Effects of Dimethyl Sulfoxide on Surface Water near Phospholipid Bilayers

Abstract

Despite much effort to probe the properties of dimethyl sulfoxide (DMSO) solution, the effects of DMSO on water, especially near plasma membrane surfaces, still remain elusive. By performing molecular dynamics simulations at varying DMSO concentrations (X_DMSO), we study how DMSO affects structural and dynamical properties of water in the vicinity of phospholipid bilayers. As proposed by a number of experiments, our simulations confirm that DMSO induces dehydration from bilayer surfaces and disrupts the H-bond structure of water. However, DMSO-enhanced water diffusivity at solvent-bilayer interfaces, an intriguing discovery reported by a spin-label measurement, is not confirmed in our simulations. To resolve this discrepancy, we examine the location of the spin label (Tempo) relative to the solvent-bilayer interface. In accord with the evidence in the literature, our simulations, which explicitly model Tempo-phosphatidylcholine, find that the Tempo moiety is equilibrated at ∼8–10 Å below the bilayer surface. Furthermore, the DMSO-enhanced surface-water diffusion is confirmed only when water diffusion is analyzed around the Tempo moiety that is immersed below the bilayer surface, which implies that the experimentally detected signal of water using Tempo stems from the interior of bilayers, not from the interface. Our analysis finds that the increase of water diffusion below the bilayer surface is coupled to the increase of area per lipid with an increasing X_DMSO$\left(\mathrm{\lesssim }10\text{mol}\text{\%}\right)$. Underscoring the hydrophobic nature of the Tempo moiety, our study calls for careful re-evaluation of the use of Tempo in measurements on lipid bilayer surfaces.

Introduction

Broadly used in biology as a cosolvent for cryoprotection at low concentrations (mole fraction of DMSO (X_DMSO), ≈0.1) and an enhancer of cell fusion and membrane permeability at high concentrations $\left(X_{\text{DMSO}}\mathrm{\gtrsim }0.6\right)$, DMSO has been a subject of great interest for many decades (1, 2, 3, 4). Although great progress has been made in understanding how DMSO affects the structural and dynamical properties of bulk water (5), the effects of DMSO on water molecules at lipid bilayer surfaces remain elusive. Surface-force-apparatus (SFA) measurement between two supported dipalmitoylphosphatidylcholine bilayers (6) and the observed decreasing repeat distance of multilamellar structures with increasing X_DMSO (7, 8) suggest that DMSO dehydrates bilayer surfaces. Employing Overhauser dynamic nuclear polarization (ODNP) measurement that uses the 2,2,6,6-tetramethylpiperidin-1-oxyl (Tempo) moiety as a spin label to probe the dynamics of water, Cheng (9) et al. reported that water diffusion was enhanced in the vicinity of bilayer surfaces with increasing X_DMSO. These companion studies (6, 9) argue that both the surface dehydration and enhanced water diffusivity at the bilayer surfaces originate from DMSO-weakened H-bonds of water with lipid headgroups. Although the properties of surface water at bilayers are known to differ from those of bulk water (10, 11), the DMSO-enhanced surface-water diffusion is both intriguing and counterintuitive, not easily reconciled with the general notion that DMSO slows down water dynamics (e.g., diffusion, H-bond lifetime) (see Fig. S1 in the Supporting Material) (5, 12). Furthermore, the assumption that a strong interaction of DMSO with lipid headgroups displaces hydration water and weakens the H-bond network near bilayer surfaces (7, 13) was made based on a few pieces of indirect evidence stitched together from measurements conducted in bulk and force-distance profiles obtained by SFA (6), not on a direct measurement probing the dynamics of water and DMSO on surfaces. We believe that this requires further study and confirmation.

To unravel the molecular origin underlying the experimental observations, we performed atomistic molecular dynamics (MD) simulations of phopholipid-DMSO-H₂O systems at various X_DMSO conditions (see Materials and Methods for details of the force fields used). In the following, we first calculate the density and diffusivity profiles of water and DMSO at palmitoyloleoylphosphatidylcholine (POPC) bilayers, visualizing the effects of DMSO on water near bilayer surfaces. Next, by explicitly modeling Tempo moieties appended to bilayer headgroups, we analyze water dynamics around each Tempo moiety. We discuss our simulation results in comparison with Cheng et al.’s spin-label measurements (9) and point out that the hydrophobic nature of Tempo is currently underestimated in the measurement. Much complication in data interpretation arises because Tempo appended to phosphatidylcholine (PC) headgroups is buried below the solvent-bilayer interfaces.

Materials and Methods

Simulations

MD simulations of POPC bilayers were performed with two different cosolvents (DMSO and sucrose). The simulation system was constructed with 128 POPC and 4740–11,664 water molecules, the number of which varied depending on DMSO concentration (Table S1). All the simulations were performed using GROMACS software (v. 4.5.4) (14, 15). The starting simulation box size was ∼6 × 6 × 14 nm³ with periodic boundary conditions, and the system was neutralized with $\sim 50$ Na⁺ and Cl⁻ ions corresponding to ∼150 mM salt concentration. The unfavorable inter-atomic contacts in the initial configurations were relieved by steepest-descent energy minimization. The system was subjected to position-restrained runs for 1 ns under the NVT ensemble at 300 K, followed by a 5 ns equilibration run under the NPT (P = 1 bar) ensemble. The temperature and pressure were semi-isotropically controlled by Nosé-Hoover thermostat (with a coupling constant of τ_T = 0.5 ps) and Parrinello-Rahman barostat (with a coupling constant of ${\tau }_{P\left(x-y\right)}={\tau }_{P\left(z\right)}$ = 2 ps), respectively. The cutoff value of 12 Å was used for both short-range van der Waals and electrostatic interactions. For long-range electrostatic potential, we used the particle-mesh Ewald method. Each system was simulated for 0.4–1 μs, and the last 0.3–0.9 μs of simulation was used for analysis.

Force fields for lipid, water, DMSO, sucrose, and Tempo

In reference to the comparative study of PC force fields by Piggot et al. (16), we selected the Berger united atom lipid force field (17), as it can best reproduce the structural and dynamical properties (e.g., area per lipid (APL), volume per lipid, isothermal area compressibility, headgroup-headgroup distance, and diffusivity of lipid) of POPC bilayers. For water and DMSO, we adopted the simple-point-charge model (18) and the rigid united-atom model (19), respectively, in the GROMOS 53a6 force field (20). The topology of sucrose (database identifier: 0ZQQ) generated by B3LYP/6-31G^∗ optimized geometry was obtained from the repository of the Automatic Topology Builder (ATB) site. Next, to model the Tempo moiety, we employed the same Lennard-Jones (LJ) parameters used in modeling POPC. Other parameters associated with bond length, angle, and partial charges of the Tempo were adopted from Kyrychenko et al. (21), who conducted density functional theory calculations at the level of UB3LYP/cc-pVDZ.

Density profile of water and cosolvent

We counted the number of molecules, N(z,t), between z − Δz/2 and z + Δz/2 with Δz = 1 Å, and divided it by a volume V(t) = x(t) × y(t) × Δz, where x(t) and y(t) are the length and width, respectively, of the simulation box. The time-dependent number density $\rho \left(z,t\right)=N\left(z,t\right)/V\left(t\right)$ was averaged over time, i.e., $\rho \left(z\right)=\left(1/T\right){\int }_0^T\rho \left(z,t\right)dt$. The number-density profiles were plotted for water, DMSO, and sucrose.

Tetrahedral order parameter

The extent of H-bond network formed among water molecules, which is critical to understand the water structure near bilayer surfaces as well as bulk, is assessed by evaluating the local tetrahedral order parameter (22, 23) averaged over the water molecules at position z,

$$\langle Q\rangle \left(z\right)=\frac{1}{N\left(z\right)}\sum _{k=1}^{N\left(z\right)}\left\{1-\frac{3}{8}\sum _{i=1}^3\sum _{j=i+1}^4{\left[\text{cos}{\psi }_{ikj}+\frac{1}{3}\right]}^2\right\},$$ (1)

where $N\left(z\right)$ is the number of particles present at z, i and j denote the nearest neighbors to water molecule k, and ${\psi }_{ikj}$ denotes the angle between water molecules i, k, and j.

Local diffusivity

The local diffusivity is calculated using the finite-difference expression (24), which is especially useful for calculating the position-dependent diffusion coefficient in anisotropic space,

$$D=\frac{\langle {\left(\overrightarrow{r}\left(t_2\right)-\overrightarrow{r}\left(t_0\right)\right)}^2\rangle -\langle {\left(\overrightarrow{r}\left(t_1\right)-\overrightarrow{r}\left(t_0\right)\right)}^2\rangle }{6\left(t_2-t_1\right)},$$ (2)

where $\overrightarrow{r}\left(t\right)$ is the position of a probed atom at time t, and angled brackets denote the average over the ensemble. For the time interval of this calculation, we selected $t_2-t_1=1$ ps, so that the bulk-water diffusion constant in isotropic space calculated from Eq. 2 quantitatively agrees with the diffusion constant calculated based on the mean-square displacement at long time limits, i.e., $D\equiv {\text{lim}}_{t\to \infty }\langle R^2\left(t\right)\rangle /6t$. To obtain the z-dependent diffusion constant $\left(D\left(z\right)\right)$ across the bilayer membrane, we evaluate Eq. 2 for the ensemble of molecules in the volume between $z-5$ Å and $z+5$ Å for a given z value.

Although subdiffusive behavior of surface water is expected at longer timescales (11), the use of Eq. 2 should be acceptable for the purpose of comparing our simulation results with experiment, as the experiment also estimates the diffusivity of solvent from short-timescale dynamics around spin labels.

Some cautionary words are in place. Although the bulk-water diffusion constant, $D_{\text{w}}^{\text{bulk}}=41\times {10}^{-10}$ m²/s, obtained from our simulation at $T=300$ K (27°C) is comparable to the value $42\times {10}^{-10}$ m²/s calculated by Rahman and Stillinger (25), it is still $\sim 1.7$-fold greater than the self-diffusion constant of water, $D_{\text{w},\text{exp}}^{\text{bulk}}=23\times {10}^{-10}$ m²/s, measured at 25°C (26). It is well known (27) that all-atom MD simulations using currently available force fields generally overestimate (underestimate) the self-diffusion constant (viscosity) of bulk water. Thus, when we compare directly the water-diffusion constants calculated from simulations with those from experiments, we will take this difference into account by multiplying a correction factor, $\varphi =D_{\text{w},\text{exp}}^{\text{bulk}}/D_{\text{w}}^{\text{bulk}}\approx 0.56$.

Potential of mean force of the Tempo moiety across lipid bilayers

The umbrella sampling technique was used to calculate the free energy of the Tempo moiety across the POPC lipid bilayer. 1) An initial simulation to generate an initial structure for each window run was conducted for ∼3 ns. We pulled the oxygen radical of the Tempo moiety appended to Tempo-PC along the z axis using a harmonic potential, $w_i\left(z\right)=\left(k_{\text{o}}/2\right){\left(z-vt\right)}^2$, with $v=0.01$ Å/ps and $k_{\text{o}}$ = 100 kJ/(mol·Å²). 2) In total, 16 window runs, which covered the range $-30\text{Å}<z<0$ Å, were performed using the initial structures generated from the procedure in step 1 and umbrella sampling at each window was conducted for 10 ns. Umbrella potentials were placed every 2 Å with a strength of k = 0.35 kJ/(mol·Å²). The strength of the harmonic umbrella potential, k, was chosen such that the positional variance of Tempo moiety, ${\sigma }^2$, from the simulation at 0 mol % DMSO satisfies $k\approx k_{\text{B}}T/{\sigma }^2$.

Analysis of solvent diffusion around the Tempo moiety

To analyze the diffusion of water around the Tempo moiety, we set the absorbing boundary condition at a distance R from the nitroxide radical oxygen of Tempo-PC and calculated the escape time (first passage time) of water molecules from the interior of a sphere $\left(r<R\right)$. Because the spin-spin interaction is dipolar $\left(\sim -1/r^6\right)$ in nature, the signal from spin-label measurement should reflect a stronger correlation with a water molecule initially closer to the nitroxide oxygen. To include this effect in our estimate of the average escape time from the Tempo moiety, we employed a weighting factor,

$$w\left(r_{\alpha }\right)=\{\begin{array}{cc}1& \text{for}r<\sigma \\ \frac{e^{{\left(\sigma /r_{\alpha ,i}\right)}^6}-1}{e-1}& \text{for}r\ge \sigma \end{array},$$ (3)

which decays from 1 to 0. We weighed the escape time, ${\tau }_{\alpha }$, for the αth water molecule with $w\left(r_{\alpha }\right)$. In the expression of $w\left(r_{\alpha }\right)$, $r_{\alpha ,i}$ is the initial position of the αth water molecule; $\sigma =3.3$ Å is the position of the first solvation shell around the nitroxide oxygen of Tempo for the case of bulk water (Fig. S2 a), and we chose $\sigma =5.8$ Å for the water molecules around Tempo moieties that are buried inside the bilayer lipid, so that the total numbers of water molecules around Tempo in both calculations are equal to each other (see Fig. S2 b). We calculated the survival probability of water molecules around the nitroxide radical oxygen using $S\left(t\right)=1-{\int }_0^{t}p\left(\tau \right)d\tau$, where $p\left(t\right)=N^{-1}{\sum }_{\alpha =1}^N\delta \left(t-t_{\alpha }\right)$ with $t_{\alpha }=w\left(r_{\alpha ,i}\right){\tau }_{\alpha }$. Finally, the average escape time of water from the spin label was calculated from $\langle \tau \rangle ={\int }_0^{\infty }S\left(t\right)dt$ (see Fig. S3).

To calculate the bulk diffusion constant of water, we conducted independent simulations also by explicitly considering the free radical Tempo in the solution. In this case, Tempo can also diffuse, so the diffusion constant of water was calculated by subtracting the contribution of Tempo as $D_{\text{w}}^{T,\text{bulk}}=D_{\text{sum}}^{\text{bulk}}-D_{\text{Tempo}}^{\text{bulk}}$. The condition $R=4.5$ Å was used for calculating the $D_{\text{sum}}^{\text{bulk}}$ (28). The DMSO-dependent bulk-water diffusion constants determined from our simulations compare well with those from experiments using Tempo (see Fig. S4).

Results

Comparison with the previous MD simulation studies

Although the effects of DMSO on lipid bilayers have been studied in a number of MD simulation studies (29, 30, 31, 32, 33), these studies were criticized (9, 13) because the simulation time was too short or the DMSO-engendered instability of the bilayer observed in these simulations was inconsistent with experimental observations. Our bilayer systems at varying DMSO concentrations remained stable. Both the APL and the bilayer thickness, quantified by the headgroup (phosphate-phosphate) distance $\left(d_{\text{PP}}\right)$, were stably maintained throughout the simulation time (∼μs) (Table S1). In their simulation study reporting DMSO-induced pore formation in a bilayer, Hughes et al. (30) used the same DMSO force field as ours (GROMOS 53a6) but a different force field (GROMOS 54a7) for the lipid (we used the Berger united-atom lipid force field (17)), and they conducted the simulations at a temperature $T=350$ K, which was 50 K higher than in our study ($T=300$ K). For simulation times (∼1 μs) much longer than other studies, we did not observe a substantial deposition of DMSO in bilayers or formation of water pores in bilayers even at high DMSO concentrations $\left(X_{\text{DMSO}}\simeq 0.3\right)$, in accord with experiments (9).

Density profiles of water and DMSO across lipid bilayers

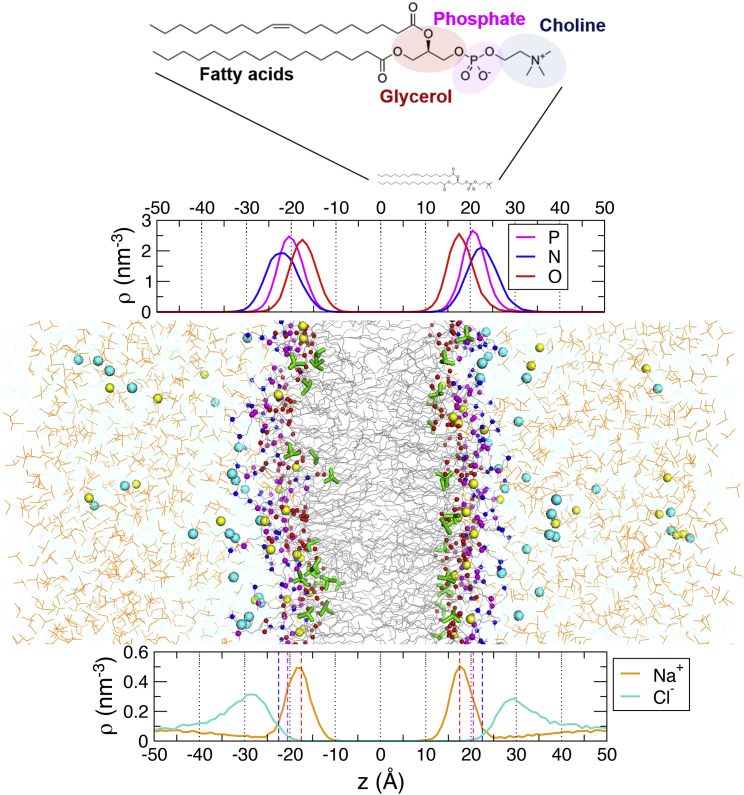
Illustrated in a snapshot from simulations (Fig. 1), the MD simulations were performed by solvating the POPC bilayer with water, DMSO, and 150 mM NaCl salt. The density profiles are presented along an axis normal to the bilayer surface (the z axis) at a spatial resolution of $\Delta z=1$ Å by averaging the statistics on the xy plane ($\sim 60\times 60$ Ų) over simulation times (see Table S1); $z=0$ is selected as the center of the bilayer. With the thickness of the POPC bilayer being ∼40 Å (Table S1), the atoms of the lipid headgroup are found at $\left|z\right|\approx 20$ Å. The distributions of choline, phosphate, and carbonyl groups along the z axis are shown in Fig. 1 in terms of the number densities of nitrogen (N), phosphorus (P), and oxygen (O) atoms, whose averages are formed at $\langle z_{\text{N}}\rangle \approx 22$ Å, $\langle z_{\text{P}}\rangle \approx 20$ Å, and $\langle z_{\text{O}}\rangle \approx 17$ Å (depicted by dashed lines in blue, red, magenta in Figs. 1, 2, 3, 5, and S5)), respectively. The number densities of salt ions (Na⁺ and Cl^–) are calculated to show the ion distribution on the lipid bilayer whose headgroups are made up of zwitterions (phosphate and choline groups) (see the density profiles in Fig. 1, bottom). Na⁺ ions are condensed on the solvent-bilayer interface with their number density maximized at $\left|z\right|\approx 17$ Å, the position corresponding to the carbonyl oxygen of the glycerol group, whereas the distribution of Cl⁻ ions is maximized at $\left|z\right|\approx 30$ Å.

Figure 1.

A snapshot from MD simulations (at 11.3 mol % DMSO concentration) performed by solvating POPC bilayers with water, DMSO (orange line), and 150 mM Na⁺ (yellow spheres), Cl⁻ (cyan spheres). Lipid bilayers are at the center ($z=0$ Å), and the solvents (water, DMSO, and ions) are at $\left|z\right|\mathrm{\gtrsim }20$ Å. DMSO molecules that penetrate inside the headgroups are shown in green sticks. On the top, the locations of the phosphate, choline, and glycerol groups in reference to the center of bilayers $\left(z=0\right)$ are calculated in terms of the number densities of phosphorus (magenta), nitrogen (blue), and oxygen (red) atoms, respectively. At the bottom are shown the number densities of Na⁺ (orange) and Cl⁻ (cyan) ions across bilayers. To see this figure in color, go online.

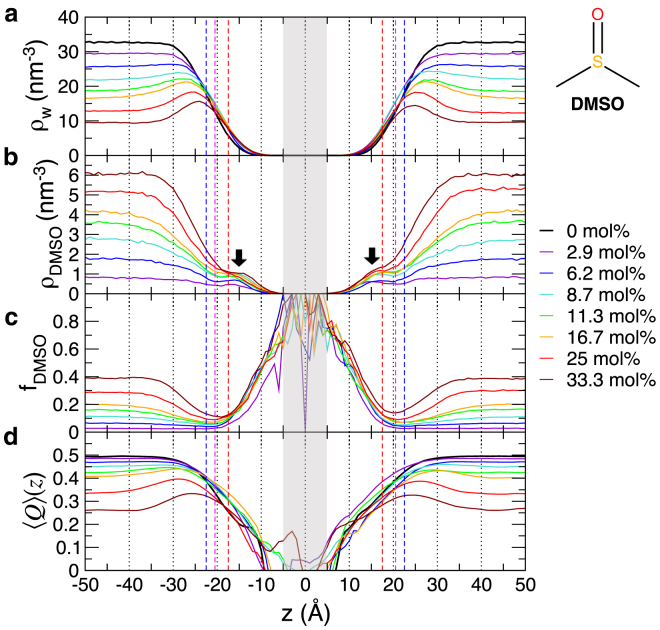
Figure 2.

Density profiles of (a) water and (b) DMSO across POPC bilayers at various DMSO concentrations. (c) Proportion of DMSO, $f_{\text{DMSO}}\left(z\right)={\rho }_{\text{DMSO}}\left(z\right)/\left({\rho }_{\text{DMSO}}\left(z\right)+{\rho }_{\text{w}}\left(z\right)\right)$. The noisy profile at $\left|z\right|\mathrm{\lesssim }5$ Å, shaded in gray, is due to the lack of statistics in the interior of bilayers and thus should be ignored. (d) Tetrahedral order parameter. The dashed lines in red, magenta, and blue are the most probable positions of glycerol, phosphate, and choline groups calculated in Fig. 1. To see this figure in color, go online.

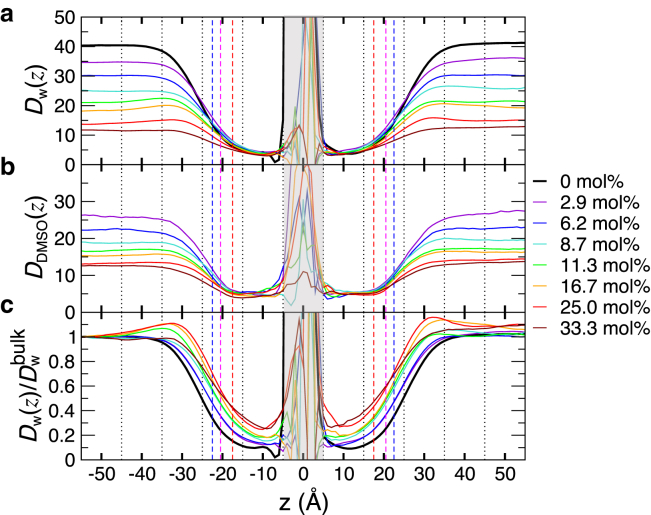
Figure 3.

Local diffusivities ($\times {10}^{-10}$ m²/s) of (a) water and (b) DMSO across the bilayers. (c) Water diffusivity normalized by the value in the bulk, $D_{\text{w}}^{\text{bulk}}\equiv D_{\text{w}}\left(z=-55\text{Å}\right)$. The dashed lines in red, magenta, and blue are the most probable positions of glycerol, phosphate, and choline groups, respectively. The noisy profiles at the bilayer core shaded in gray, ($\left|z\right|<5$ Å), are due to the paucity of water or DMSO molecules and should be ignored. To see this figure in color, go online.

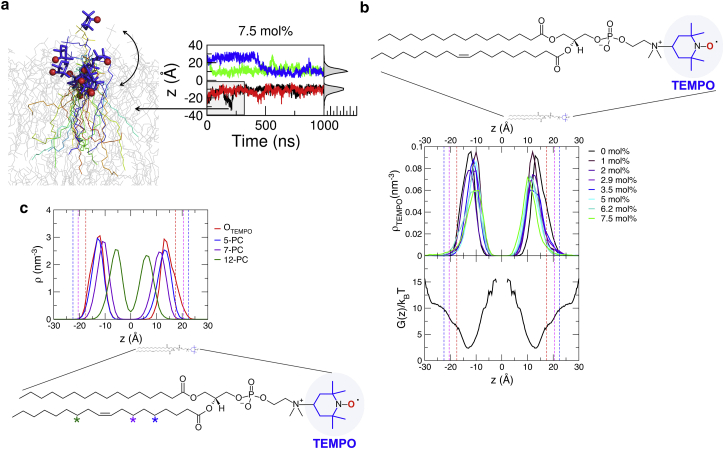
Figure 5.

Dynamics of the Tempo moiety. (a) The multiple snapshots of Tempo-PC from 0 to 300 ns using the black trajectory on the right are overlaid to depict the positions of the Tempo moiety. Tempo is highlighted in blue stick representation. The nitroxide radical oxygen is depicted as red spheres. (b) Upper: Distribution of nitroxide radical oxygens along the z axis after the position reaches a steady-state value. The corresponding time trajectories at varying DMSO concentrations are shown in Fig. S7. The equilibrium positions of the headgroup (P, N, O) are indicated by dashed lines, highlighting the positions of Tempo moieties are equilibrated beneath the bilayer surface. The structure of Tempo-PCs are shown with highlight on the Tempo moiety consisting of nine hydrocarbons. Lower: Potential of mean force of the nitroxide radical oxygen along the z axis, $G\left(z\right)/k_{\text{B}}T$, obtained from the umbrella-sampling analysis. (c) Distribution of the nth hydrocarbon in the lipid tail when bilayer lipids are equilibrated. The equilibrated positions of Tempo in the 5-PC, 7-PC, 12-PC, and Tempo-PC are displayed. Each position of the nth hydrocarbon is highlighted using a star symbol in the structure of Tempo-PC. To see this figure in color, go online.

To investigate the structure and dynamics of DMSO solution near the bilayer surfaces, we varied the mole fraction of DMSO from $X_{\text{DMSO}}=$ 0 mol % to $X_{\text{DMSO}}=$ 33.3 mol % (Figs. 2 and 3). In the absence of DMSO $\left(X_{\text{DMSO}}=0\right)$, the bulk-water density is ${\rho }_{\text{w}}\left(z\right)={\rho }_{\text{w}}^{\text{bulk}}\approx 33.3$ nm^–3 at $\left|z\right|\mathrm{\gtrsim }30$ Å (Fig. 2 a, black line), which corresponds to the typical value of 1 g/cm³. The water density begins to monotonically decrease at ∼10 Å away from the bilayer surfaces and reduces to $0.5\times {\rho }_{\text{w}}^{\text{bulk}}$ at the interface ($\left|z\right|\approx 22$ Å). The density profile of water, ${\rho }_{\text{w}}\left(z\right)$, at $X_{\text{DMSO}}=0$ mol % is described quantitatively using the interfacial density profile derived from the Cahn-Hillard equation (34, 35),

$${\rho }_{\text{w}}\left(z\right)=\frac{{\rho }_{\text{w}}^{\text{bulk}}}{2}\left[\text{tanh}\left(\frac{z-z_{\text{int}}}{\sqrt{2}\xi }\right)+1\right],$$ (4)

with ${\rho }_{\text{w}}^{\text{bulk}}=32.7$ nm^–3, $z_{\text{int}}=21.8$ Å, and $\xi =3.75$ Å, where $z_{\text{int}}$ and $2\xi$ are the position and width, respectively, of the interface. Overall, a decrease of water number density is clearly seen on bilayer surfaces with increasing $X_{\text{DMSO}}$ (Fig. 2 a), thus confirming the experimentally detected DMSO-induced dehydration of bilayer surfaces.

Notably, at high DMSO concentrations ($X_{\text{DMSO}}\ge$ 8.7 mol %), ${\rho }_{\text{w}}\left(z\right)$ displays non-monotonic variation from the bulk to the interface. ${\rho }_{\text{w}}\left(z\right)$ is maximized at $\sim 5-10$ Å away from the headgroup position ($\left|z\right|\approx 22$ Å), satisfying ${\rho }_{\text{w}}\left(\left|z\right|\approx 25-30\text{Å}\right)>{\rho }_{\text{w}}^{\text{bulk}}$. This characteristic “water-rich layer” near the bilayer surface is specific to the DMSO solution, not observed in sucrose solutions (compare ${\rho }_{\text{w}}\left(z\right)$ values in DMSO with those in sucrose solution in Fig. S5 a).

Unlike ${\rho }_{\text{w}}\left(z\right)$, a “DMSO-rich layer” above the interface is absent in ${\rho }_{\text{DMSO}}\left(z\right)$. Instead, a small population of DMSO molecules, depicted in Fig. 1 by green sticks beneath the headgroup, contribute to the small density humps at $\left|z\right|\approx 15$ Å (Fig. 2 b, black arrows). At high $X_{\text{DMSO}}$, the extent of DMSO depleted from the surfaces (Fig. 2 b) is greater than that of water, which is better demonstrated in the plot calculating the fraction of DMSO, $f_{\text{DMSO}}\left(z\right)={\rho }_{\text{DMSO}}\left(z\right)/\left({\rho }_{\text{DMSO}}\left(z\right)+{\rho }_{\text{w}}\left(z\right)\right)$ (Fig. 2 c).

To assess changes in water structure, we calculated the tetrahedral order parameter (22, 23) $\langle Q\rangle \left(z\right)$ (Eq. 1), which points to an increasing degradation of H-bond network at higher $X_{\text{DMSO}}$ values (Fig. 2 d). For a given wt %, the extent of H-bond network degradation by DMSO is greater than that by sucrose (compare Figs. 2 d and S5 c; also see Fig. S6 b), suggesting that compared with sucrose, DMSO is a more efficient cryoprotectant.

Local diffusivity profiles of water and DMSO

Local diffusivities of water and DMSO (Fig. 3) were calculated using Eq. 2 (24). In the range of $\left|z\right|>25$ Å, which spans the bilayer surface to the bulk, both water and DMSO slow down with increasing $X_{\text{DMSO}}$ (Fig. 3, a and b). Although enhancement of surface-water diffusion relative to the bulk water is seen at $\left|z\right|\approx 30$ Å (see Fig. 3 c), $\left|z\right|\approx 30$ Å is probably not the position at which the spin-label experiment in (9) probed the surface-water diffusion. The surface-water diffusivity is suppressed at $\left|z\right|\approx 22$ Å, where the experiment tried to probe it using Tempo-PC.

$D_{\text{w}}^{\text{surf}}/D_{\text{w}}^{\text{bulk}}$ values with varying $X_{\text{DMSO}}$ conditions measured from the ODNP experiment using Tempo spin labels (9) overlaid on the graph (Fig. 4 a, red asterisks) are in good agreement with our simulation results. Nevertheless, we argue below that in contradiction to the original intention, the Tempo-bilayer interaction prevents the Tempo spin labels from probing the solvent-bilayer interface, $\left|z\right|\approx 22$ Å; thus, the agreement of $D_{\text{w}}^{\text{surf}}/D_{\text{w}}^{\text{bulk}}$ between the simulation and experiment in Fig. 4 a is coincidental. In the next section, we give an in-depth discussion concerning this issue.

Figure 4.

Surface-water diffusion. (a) Plot of the diffusion constant, probed at $z=-22$ Å, i.e., $D_{\text{w}}^{\text{surf}}\equiv D_{\text{w}}\left(-22\text{Å}\right)$, and normalized with $D_{\text{w}}^{\text{bulk}}$ at each cosolvent concentration (wt %; the corresponding DMSO mole fraction is annotated at the top of the plot). The data (red asterisks) from the recent ODNP measurement (9) are overlaid for comparison. (b) Diffusion constants of surface water probed at $z=-22$ Å are compared with those from spin-label measurements in (9). To compare our simulation results directly with those from experiments (Table S2 (large unilamellar vesicles, LUV) of (9)), the correction factor $\varphi =0.56$ (see Materials and Methods) was multiplied to $D_{\text{w}}\left(-22\text{Å}\right)$. To see this figure in color, go online.

Discussion

Analysis of water dynamics around Tempo and its comparison with the spin-label measurement

To experimentally probe the surface-water dynamics, Cheng et al. (9) tethered spin labels (Tempo) to choline groups and conducted measurements assuming that the spin labels remain above or at least near the equilibrium position of the choline group ($\left|z\right|\approx 22$ Å). They obtained values of $D_{\text{w}}^{\text{surf}}$ and $D_{\text{w}}^{\text{surf}}/D_{\text{w}}^{\text{bulk}}$ with varying $X_{\text{DMSO}}$. As highlighted in Fig. 4 a, our simulation results for $D_{\text{w}}^{\text{surf}}/D_{\text{w}}^{\text{bulk}}$ are in good agreement with their observations. However, as opposed to the decreasing trend observed in the local diffusivity plot, $D_{\text{w}}\left(z\right)$, at $z=-22$ Å (overall decrease of $D_{\text{w}}\left(z=\pm 22\text{Å}\right)$ with increasing $X_{\text{DMSO}}$ (Fig. 3 a)), Cheng et al. reported an overall increase of $D_{\text{w}}^{\text{surf}}$ with $X_{\text{DMSO}}$ (Fig. 4 b, asterisks).

To investigate the origin of this discrepancy, we explicitly modeled Tempo-PCs and placed them at four different locations, two Tempo-PCs in the upper leaflet and the remaining two in the lower leaflet of the bilayer. The Tempo-PCs are placed ∼3 nm apart from each other to minimize possible interaction between them. Since the lateral diffusion constant of lipid molecules on the bilayer surfaces is $\sim 10$ nm²/μs, it is unlikely that two Tempo-PCs actively interact with each other in our simulation time of 1 μs. Compared with a recent MD study of Tempo-PC (21), the surface density of Tempo-PC in our study is much lower, precluding an inter-Tempo-PC interaction.

The position of Tempo displays large fluctuations over time, but the major depth distribution of the spin label was established in the interior of the bilayer ($10<\left|z\right|<15$ Å), instead of at the bilayer surfaces ($\left|z\right|\mathrm{\gtrsim }20$ Å) under all conditions of $X_{\text{DMSO}}=0-7.5$ mol % (Fig. 5, and see all the 32 time trajectories in Fig. S7, each of which was run for 1 μs). Furthermore, our simulation time of the bilayer system including Tempo-PC at each DMSO concentration (1 μs) is at least five times longer than that in the previous study (21), and the practically irreversible burials of Tempo moieties below bilayer surfaces after the relaxation processes appear to be robust. Furthermore, the potential of mean force of the Tempo moiety across the POPC bilayer at $X_{\text{DMSO}}=0$ (see Fig. 5 b, lower), calculated with the umbrella sampling technique (Materials and Methods), points to the identical location as the most stable location of Tempo and suggests that there is a free energy bias of $\sim 7-8$ $k_{\text{B}}T$ toward the bilayer interior ($\left|z\right|\approx 13$ Å) from the interface ($\left|z\right|\approx 22$ Å), thus giving credence to our simulation results in Figs. 5 b, upper, and S7. The hydrophobic nature of the Tempo moiety, which is composed of as many as nine hydrocarbons (see Fig. 5 b), is currently underestimated in the spin-label measurement, but this could be the driving force for this observation. We therefore assert that the Tempo moieties probe the interior not the surface of PC bilayer.

Next, to make a direct comparison of our simulation results with the spin-label experiment, we calculated water diffusion around the Tempo using

$$D_{\text{w}}^{\text{T}}=\frac{R^2}{6\langle \tau \rangle },$$ (5)

where $R=10$ Å for surface water (9) and $R=4.5$ Å for bulk water (28), and the superscript T indicates that the diffusion constant is calculated around Tempo. This is the same formula adopted by Cheng et al., and we use the same parameters (R) that they use to estimate the diffusion constant of water from ODNP measurements that provide an average spin-spin decorrelation time, $\langle \tau \rangle$ (9) (see Materials and Methods for the details of calculating $\langle \tau \rangle$ from simulations). We calculated the diffusion constant of water around Tempo moieties after the position of the Tempo moiety is equilibrated inside bilayers (Fig. S7). To make a direct comparison of water diffusivity, we multiplied the correction factor $\varphi \approx 0.56$ (see Materials and Methods) to $D_{\text{w}}^{T,\text{surf}}$ and $D_{\text{w}}^{T,\text{bulk}}$ from our simulation. The ratios of the two values $\left(D_{\text{w}}^{T,\text{surf}}/D_{\text{w}}^{T,\text{bulk}}\right)$ are in reasonable agreement with those from experiments over the range of $X_{\text{DMSO}}\le 8$ % (Fig. 6 a), now reproducing the same trends for both surface and bulk water with increasing $X_{\text{DMSO}}$. The semi-quantitative agreement of the calculated water diffusion constant around Tempo moieties with Cheng et al.’s measurement lends support to our simulation results and the finding that Tempo moieties are equilibrated below the bilayer surfaces.

Figure 6.

Diffusion coefficients for water molecules. (a) $D_{\text{w}}^{\text{surf}}$ and $D_{\text{w}}^{\text{bulk}}$ from experiment and $D_{\text{w}}^{T,\text{surf}}$ and $D_{\text{w}}^{T,\text{bulk}}$ from simulation. (b) The ratios $D_{\text{w}}^{\text{surf}}/D_{\text{w}}^{\text{bulk}}$ and $D_{\text{w}}^{T,\text{surf}}/D_{\text{w}}^{T,\text{bulk}}$ at various $X_{\text{DMSO}}$ conditions. All the data for simulations were obtained by analyzing water lifetime around Tempo moieties using Eq. 5. The experimental values of surface- and bulk-water diffusion constants are from Tables S2 (large unilamellar vesicles) and S3, respectively, of (9). To see this figure in color, go online.

Equilibrium position of the Tempo moiety in PC bilayers

Although not explicitly pointed out by the authors, evidence of the burial of the Tempo moiety inside POPC bilayer surfaces is, in fact, present in the experimental data by Subczynski et al. (36). They presented oxygen transport parameters, which contain information on the depth of Tempo in terms of the accessibility of the nitroxide moiety to the oxygen, across POPC bilayers measured at 25°C (Fig. 9 b in (36)). The data indicate that the oxygen transport parameter measured by Tempo-PC is comparable to the parameter measured by 5-PC (POPC lipid with nitroxide label at the position of the fifth hydrocarbon in the lipid tail), which is identified in our simulation at $\left|z\right|\approx 13\pm 5$ Å, approximately the same position at which a buried Tempo moiety is equilibrated (Fig. 5 c). The hydrophobicity profile across the POPC bilayer, quantified by the z-component of the hyperfine coupling tensor of the nitroxide moiety (Fig. 8 b in (36)), may indicate that Tempo in Tempo-PC is situated in a less hydrophobic environment than the interior of the bilayer; however, it should be noted that the measurement in (36) was conducted at a cryo condition (T = −165°C). The burial of Tempo appended to the PC headgroup has also been reported in MD simulation studies by Kyrychenko et al. (21, 37), who pointed out “a much broader and heterogeneous distribution for a head-group-attached Tempo spin-label of Tempo-PC lipids,” alerting the reader to “the possible sources of error in depth-dependent fluorescence quenching studies.” Kyrychenko and Ladokhin also experimentally showed that the Stern-Volmer constant $\left({\tau }_0/{\tau }_Q\right)$, corresponding to the inverse of the fluorescence quenching time, $\left({\tau }_Q\right)$, of NBD-PE increases in the order 12-Doxyl-PC < Tempo-PC < 7-Doxyl-PC < 5-Doxyl-PC, suggesting that the Tempo moiety in Tempo-PC is more deeply buried than 5- or 7-Doxyl-PC (38). The hydrophobic nature of the Tempo moiety and the inherent disorder caused by thermal motion (38), the latter especially relevant for Tempo-PC, should be taken seriously.

Thermodynamic and kinetic effects of DMSO on surface water

Now that we have reproduced the trend of surface-water diffusivity measured semi-quantitatively by the spin-label experiment, we are in a good position to examine the mechanistic proposals made in the two reports (6, 9). The results of experimental studies using SFA and ODNP measurements (6, 9) were 1) a decrease of membrane repulsion (39) and 2) enhanced local diffusivity of surface water in the presence of DMSO ($X_{\text{DMSO}}<10$ mol %), respectively. The authors surmised that the competition between DMSO and surface hydration water on the interaction with lipid headgroups led to weakening of the strength of the cohesive water network hydrating the membrane headgroups, thus enhancing surface-water diffusivity and dehydration of the bilayer surfaces. Our computational study on the lipid-DMSO-H₂O system not only reproduces these observations, but also provides a more accurate understanding of what is actually happening on the bilayer surfaces at the molecular level by making accessible the profiles of density and local diffusivity, and the tetrahedral order parameter for water structure.

Water structure

Density profiles $\left({\rho }_{\text{w}}\left(z\right)\right)$ of water across lipid bilayers visualize the dehydration due to DMSO (Fig. 2 a). The tetrahedral order parameter $\left(\langle Q\rangle \left(z\right)\right)$ indicates that the hydrogen bond network begins to be disrupted ∼10 Å away from the interface $\left(\left|z\right|=z_{\text{int}}\right)$ even in the absence of DMSO, and the degradation of the H-bond network is promoted at cosolvent concentrations (Figs. 2 d, S5 c, and S6 b). An interesting finding from our study is that the extent of change in the surface-water density $\left({\rho }_{\text{w}}\left(z\approx z_{\text{int}};X_{\text{DMSO}}\right)\right)$ is smaller than the change in the bulk-water density $\left({\rho }_{\text{w}}^{\text{bulk}}\left(X_{\text{DMSO}}\right)\right)$ (Fig. 2 a). This leads to a water-rich layer, which is specific to DMSO solutions at high $X_{\text{DMSO}}$ ($\mathrm{\gtrsim }8.7$ mol %) (Fig. 2 a).

Surface-water diffusion

We have reproduced the experimental observation of Cheng et al. (9) that surface-water diffusion increases with increasing $X_{\text{DMSO}}$ by explicitly modeling Tempo and analyzing the water dynamics around it after the Tempo was equilibrated in the interior of the bilayer surface. By contrast, the water diffusivity calculated without Tempo (see Fig. 3 a) does not show such a clear increase with $X_{\text{DMSO}}$ in the range of the Tempo moiety’s equilibrium position $\left(10\mathrm{\lesssim }\left|z\right|\mathrm{\lesssim }15\right)$. A hint to this conundrum may lie in the dependence of APL on bilayer thickness, $d_{\text{PP}}$ (Figs. 7, a and b). In the range $0<X_{\text{DMSO}}<10$ mol %, the APL increases from 55 Å² to ∼64 Å² (Fig. 7 a), whereas $d_{\text{PP}}$ decreases from 41.7 Å to 38.2 Å (Fig. 7 b) (39), a change that could effectively be induced by applying a lateral tension to the bilayer.

Figure 7.

Bilayer properties calculated using (a) APL and (b) the phosphate-phosphate distance, $d_{\text{PP}}$, at various DMSO concentrations. The error bars indicate the standard deviation. (c) The average number of DMSO molecules trapped around lipid molecules in the range $10<\left|z\right|<15$ Å as a function of $X_{\text{DMSO}}$. (d) The average time for DMSO trapped at $10<\left|z\right|<15$ Å to escape beyond $\left|z\right|>22$ Å. To see this figure in color, go online.

Although the measurements were done on the multilamellar structure of dipalmitoylphosphatidylcholine, the electron density profile across the bilayer (39) reported a decrease in bilayer thickness due to DMSO. They reported a 16% decrease of bilayer thickness from 3.79 nm to 3.16 nm in 35 wt % (≈11 mol %) DMSO after subtracting the contribution of the sulfur atom of DMSO trapped in the bilayer headgroup from the electron density profile, and the extent of decreases in bilayer thickness is even greater than our results show (3.82 nm/4.17 nm ≈ 8%). Other studies (8), again on a multilamellar structure, argue that the bilayer thickness is constant up to $X_{\text{DMSO}}\approx 0.3-0.4$, contradicting the conclusion from the above-mentioned electron density profile study (39). Compared with bilayers stacked in the gel phase, a certain amount of cosolvent deposition into bilayer in the fluid phase is physically more plausible. Thus, it appears that the issue of how DMSO $\left(X_{\text{DMSO}}<0.1\right)$ affects the bilayer thickness, especially for a fluid-phase unilamellar structure, remains inconclusive. Although the possibility of an imperfect force field cannot completely be ruled out, our simulation study straightforwardly indicates the increase (decrease) of APL $\left(d_{\text{PP}}\right)$ of unilamellar bilayers in the fluid phase (Fig. 7, a and b).

The amount of DMSO deposited below the headgroup ($10<\left|z\right|<15$ Å) increases with $X_{\text{DMSO}}$ (Fig. 7 c), providing more free space between lipids, increasing the APL, and thus contributing to the enhancement of water diffusivity around the Tempo buried below the bilayer surface (Fig. 6 a). The non-monotonic dependence of the escape time of DMSO trapped below the bilayer surface on $X_{\text{DMSO}}$ is also noteworthy (Fig. 7 d). The first decrease of the mean escape time to the surface ($X_{\text{DMSO}}<10$%) may well be an outcome of the increased APL, but the next increase of the mean escape time for $X_{\text{DMSO}}>10\%$ could be related to the increase of $X_{\text{DMSO}}$ while the APL is already saturated (Fig. 7 a). Although it is not clear how significant is the contribution of the increase (decrease) of APL $\left(d_{\text{PP}}\right)$ with $X_{\text{DMSO}}$ to the dehydration from the solvent-bilayer interface, the increase of APL is certainly a relevant factor that enhances the diffusivity of water in the interior of bilayers.

Water dynamics around the choline group

Based on the results from pulse-field-gradient NMR measurements, decrease of the hydration radii of both DMP⁻ and TMA⁺ with increasing DMSO, which is also quantitatively reproduced using our simulations (see Supporting Material text and Fig. S8 d), Schrader et al. (6) conjectured that DMSO weakens water binding to PC headgroups on bilayer surfaces and thus shortens the range of the repulsive force. However, first, the reduction of the hydrodynamic radii of DMP⁻ and TMA⁺ alone cannot be used for assessing the solvent stability (or lifetime) around DMP⁻ and TMA⁺. Second, it is not clear whether the measurement in the bulk phase can be used to explain observed phenomena on the bilayer surface, where the density of PC headgroups is much higher. In stark contrast to their conjecture, we find that lifetimes of both water and DMSO in the first solvation shell around DMP⁻ and TMA⁺ in the bulk increase with $X_{\text{DMSO}}$ (see Fig. S8 e), which indicates that an increased charge/size ratio $\left(e/r_{\text{H}}\right)$ of DMP⁻ and TMA⁺ contributes to the stability of the inner solvation shell (40).

To gain more microscopic insight, we next examined the solvent structure and its lifetime in the first solvation shell around a choline group of the phospholipid bilayer. The results summarized in Fig. 8 underscore three points: 1) the pair correlation between water and the choline group (nitrogen atom) at bilayer surfaces shows an increase in the first solvation shell with increasing $X_{\text{DMSO}}$ (Fig. 8 a); 2) the number of water molecules surrounding a PC group decreases with increasing $X_{\text{DMSO}}$ (Fig. 8 a, inset); and 3) the lifetime of water in the first solvation shell around a choline group increases with $X_{\text{DMSO}}$ and is an order of magnitude greater than that around TMA⁺ in the bulk phase (Fig. 8 b). Hence, the presence of DMSO in solution stabilizes the water-choline-group interaction and increases the lifetime of water. This is fully consistent with the decreasing diffusivity of surface water at $\left|z\right|\approx 22$ Å with increasing $X_{\text{DMSO}}$.

Figure 8.

Structure and lifetimes of water and DMSO around choline groups. (a) Radial distribution function of water oxygen (left) and DMSO oxygen (right) relative to the nitrogen atom of the choline group in varying $X_{\text{DMSO}}$ conditions. The insets show the cumulative numbers of water and DMSO around the choline group as a function of r. (b) The lifetimes of water (left) and DMSO (right) in the first solvation shell around a choline group on bilayer surfaces as a function of $X_{\text{DMSO}}$. To see this figure in color, go online.

Conclusions

This study is based on classical MD simulations, which disregard quantum mechanical effects such as polarization and ionization of water molecules near the zwitterionic PC headgroup environment. It is not clear to what extent these quantum mechanical effects would change our interpretations of DMSO-induced surface-water properties. Nevertheless, the semi-quantitative agreement between experimental measurements and simulation results on the water diffusivity probed with Tempo (see Fig. 6) and on the hydration radii of DMP⁻ and TMA⁺ (Fig. S8 d) justify the use of classical MD simulations as a computational tool.

In conclusion, our study shows clearly that DMSO dehydrates surface water from phospholipid bilayers. Concerning the more subtle point on the dynamics of water and DMSO interacting with the PC headgroup at the solvent-bilayer interface, the DMSO-enhanced surface-water diffusion reported by Cheng et al. (9) is very likely an artifact of Tempo moieties probing the water dynamics at a location below the solvent-bilayer interface. A label-free measurement of surface-water diffusion (at $\left|z\right|\approx 22$ Å) will reveal that it is a decreasing function of $X_{\text{DMSO}}$ (see Fig. 3 a at $\left|z\right|\approx 22$ Å and Fig. 4 b, cyan symbols). At present, spin-label NMR measurement is the only tool that allows us to directly probe the water dynamics on biological surfaces such as proteins and nucleic acids (41, 42). Given its significance, the actual position of the equilibrated Tempo moiety in lipid bilayers, discussed in this study, and its effect on the measurements call for a careful re-evaluation of the current biophysical techniques and accompanying theories.

Author Contributions

P.A.P. and C.H. designed the research. Y.L., P.A.P., and C.H. performed the research, analyzed the data, and wrote the manuscript.

Editor: Francesca Marassi.