Abstract
Transcription activator-like effector proteins (TALEs) contain large numbers of repeats that bind double-stranded DNA, wrapping around DNA to form a continuous superhelix. Since unbound TALEs retain superhelical structure, it seems likely that DNA binding requires a significant structural distortion or partial unfolding. In this study, we use nearest-neighbor “Ising” analysis of consensus TALE (cTALE) repeat unfolding to quantify intrinsic folding free energies, coupling energies between repeats, and the free energy distribution of partly unfolded states, and to determine how those energies depend on the sequence that determines DNA-specificity (called the “RVD”). We find a moderate level of cooperativity for both the HD and NS RVD sequences (stabilizing interfaces combined with unstable repeats), as has been seen in other linear repeat proteins. Surprisingly, RVD sequence identity influences both the overall stability and the balance of intrinsic repeat stability and interfacial coupling energy. Using parameters from the Ising analysis, we have analyzed the distribution of partly folded states as a function of cTALE length and RVD sequence. We find partly unfolded states where one or more repeats are unfolded to be energetically accessible. Mixing repeats with different RVD sequences increases the population of partially folded states. Local folding free energies plateau for central repeats, suggesting that TALEs access partially folded states where a single internal repeat is unfolded while adjacent repeats remain folded. This breakage should allow TALEs to access superhelically-broken states, and may facilitate DNA binding.
Introduction
Transcription activator-like effectors (TALEs) are bacterial proteins containing a domain of tandem 34-residue repeats that binds to specific DNA sequences and affect transcription of host genes (1, 2). TALE repeat domains have an average of 17.5 repeats, although this number varies (3). Repeats have high sequence identity, with most of the variability at repeat positions 12 and 13. These two residues, together called repeat variable diresidues (RVDs), impart DNA binding specificity, and identities at positions 12 and 13 can be used to design TALE proteins that bind specific DNA sequences (4, 5, 6). Using this specificity code, TALE nucleases (TALENs) have been engineered for genome editing purposes (7, 8). TALE repeats have also been used to design proteins that bind to DNA and activate or repress transcription (9, 10, 11, 12, 13), modify DNA by demethylation (14), and probe chromatin dynamics by encoding fluorophores with high sequence specificity (15, 16). One challenge to TALE-based genome editing is cloning difficulties resulting from the large number of repeats needed for affinity/specificity (17). Enhancing the affinity of TALE repeats would thus be beneficial for genome editing and molecular genetic studies, allowing high-specificity target recognition with fewer repeats.
TALEs in their unbound state are superhelical, with 11 repeats per turn (18) and are not likely to thread onto DNA easily. It seems likely that a conformational change is required for binding. One way to bring about such a change is a global deformation of the native state. Some degree of native-state plasticity is suggested from comparison of the free and bound states (Fig. S1 in Supporting Material) but does not seem to be enough to adequately open the structure. Alternatively, a binding competent state could be reached by a localized structural transition, either by disrupting one or more interfaces between repeats, and or by unfolding one or more repeats.
Ising analysis provides a direct means to determine the cooperativity of linear arrays of identical sequence repeats, and for quantifying the populations of partly folded states (19, 20, 21, 22). By studying the length dependence of stability, one-dimensional (1D) Ising analysis can resolve the energetics of folding individual repeats from the energetics of formation of interfaces between repeats. Two types of repeat proteins have been subjected to Ising analysis (TPR (20, 23) and ankyrin repeats (19, 21, 22)). By applying 1D Ising analysis to identical TALE repeat arrays of different lengths, we can resolve folding free energies into intrinsic and interfacial components, quantify the extent of cooperativity in folding, and determine the populations of partially folded states that may facilitate DNA binding.
Here, we characterize the equilibrium stability of a series of TALE constructs with varying length and RVD sequence using nearest-neighbor Ising analysis. The length dependence and Ising analysis demonstrate an intermediate level of coupling between repeats. Local folding free energies , calculated from intrinsic and interfacial free energies, suggest significant populations of partially unfolded states. Surprisingly, the extent of coupling and local folding free energy profiles depend on the sequence of the RVDs. This dependence leads to a stability switch between NS- and HD-containing TALE arrays at a length of eight repeats. The stabilities of mixed NS and HD constructs demonstrate that RVD sequence identity partitions asymmetrically into its N- and C-terminal interfaces, introducing further variation in local folding free energies.
Materials and Methods
Cloning, expression, and purification
Consensus TALE repeat constructs were cloned with C-terminal His6 tags via an in-house version of Golden Gate cloning (24). TALE constructs were grown in BL21(T1R) cells at 37°C to an optical density of 0.6–0.8 and induced with 1 mM isopropyl-β-D-1 thiogalactopyranoside. Following cell pelleting, resuspension, and lysis, proteins were purified by resuspending the insoluble material in 6M urea, 300 mM NaCl, and 10 mM Tris (pH 7.4). Constructs were loaded onto an Ni-NTA column. Protein was eluted using 250 mM imidazole and refolded during dialysis into 300 mM NaCl, 5% glycerol, and 10 mM Tris (pH 7.4).
Circular dichroism spectroscopy
Circular dichroism (CD) measurements were collected using an AVIV model 400 CD Spectrometer (Aviv Associates, Lakewood, NJ). Far-ultraviolet (UV) CD scans were collected at 25°C using an 0.1 cm pathlength quartz cuvette, with protein concentrations of 15–30 μM. Buffer scans were recorded and were subtracted from the raw CD data.
Urea-induced unfolding transitions
For short constructs, CD-monitored unfolding titrations at 222 nm were generated with an automated titrator. For N-capped constructs six repeats or longer, and all constructs seven repeats or longer, slow relaxation kinetics prevented us from collecting automated titrations; thus, we performed manual urea titrations for these constructs. Solutions containing 0 and 8 M urea, each with 2 μM protein, were combined in various proportions using Hamilton syringes. Samples equilibrated for 12–24 h at room temperature before monitoring CD signal at 222 nm.
Ising analysis
To determine the intrinsic and interfacial free energies for folding of cTALE arrays, and to analyze energies and populations of partly folded states, we used a 1D Ising formalism (25, 26). In this model, intrinsic folding and interfacial interaction between nearest neighbors are represented using equilibrium constants κ and τ, respectively, as follows:
| (1.1) |
| (1.2) |
| (1.3) |
| (1.4) |
| (1.5) |
In the current analysis, the intrinsic folding free energies of N (solubilizing N-terminal cap), R (consensus repeat), and C (solubilizing C-terminal cap) are each considered to be unique. The interfacial interactions of the R:R and R:C pairs are considered to be identical, but that the N:R pair is considered to be unique. Denaturant dependences are built into the intrinsic (but not the interfacial) terms. The urea dependence of the N-terminal cap is scaled by a factor of four because there are four TALE-like repeats in the N-terminal cap.
Using these equilibrium constants, a partition function q can be constructed for an n-repeat construct by multiplying two-by-two transfer matrices as follows:
| (2) |
This representation differs from several previous expressions in that the matrices in Eq. 2 correlate to the next repeat (rather than the previous repeat) (25). Though this rephrasing does not alter q, it associates the κ and τ terms for the same repeat. The fraction folded (ffolded) can be determined as follows:
| (3) |
A specific example for a three-repeat cTALE construct is given in the Supporting Material and Methods (Fig. S2).
Ising parameters were determined by nonlinear least squares using an in-house Python program (written by J. Marold) (23) by globally fitting Eq. 3 to urea-induced unfolding transitions. Confidence intervals (CI) were determined by performing 2000 bootstrap iterations (95%).
Calculation of local folding free energies within TALE arrays
Local folding free energies, , are calculated using fitted Ising parameters in Table 1 (see also Supporting Materials and Methods). Summing all statistical weights for states where the ith repeat is folded and dividing by the statistical weights where the ith repeat is unfolded gives a local equilibrium constant for folding . The local free energy of folding is calculated using the following formula:
| (4) |
Table 1.
Summary of Thermodynamic Parameters Obtained from Ising-Fit
| Intrinsic Terms | ΔGN | ΔGNS | ΔGHD | ΔGC | mi | |
|---|---|---|---|---|---|---|
| Best-Fit | −4.42 | 5.89 | 3.49 | 7.14 | −0.50 | |
| 95% CIa | −4.80, −4.03 | 5.47, 6.33 | 3.13, 3.82 | 6.78, 7.50 | −0.52, −0.48 | |
| Interfacial Terms | ΔGN, i+1 | ΔGNS, NS+1 | ΔGHD, HD+1 | ΔGC, HD-1 | ΔGNS, HD+1 | ΔGHD, NS+1 |
| Best-Fit | −0.85 | −7.79 | −5.02 | −8.49 | −7.58 | −4.73 |
| 95% CIa | −0.94, −0.76 | −8.30, −7.30 | −5.42, −4.59 | −9.00, −8.00 | −8.09, −7.09 | −5.24, −4.19 |
All values obtained are kcal/mol with the exception of mi, which is kcal/mol/M.
95% confidence intervals are from 2000 iterations of bootstrap analysis.
Results
Consensus TALE design
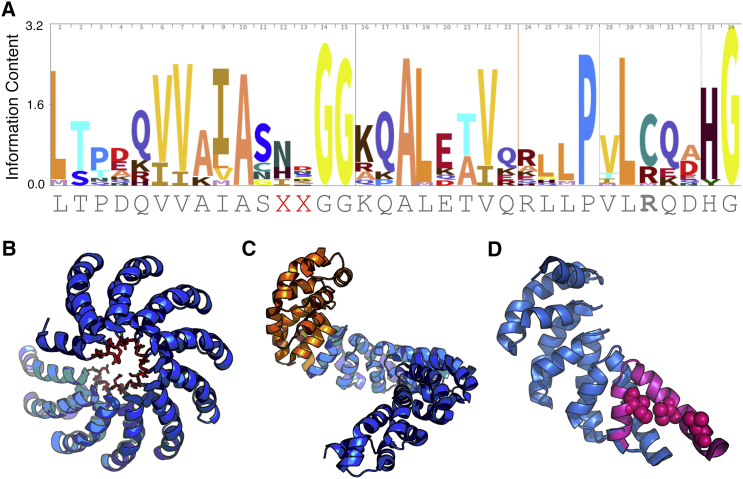
To design a consensus TALE (cTALE) repeat sequence for Ising analysis, the Hidden Markov model search tool was used to collect and align 3,667 TALE repeat sequences (27). From this alignment, Skylign was used to create an HMM logo (Fig. 1 A), where the height of each residue at each position is proportional to its conservation (28). The most-conserved residue at each position was selected for the consensus-based TALE sequence except at position 30, where arginine was chosen instead of cysteine to simplify folding studies. In addition, the two RVD residues, positions 12 and 13, were varied to generate two common recognition sequences (NS and HD; Fig. 1 B). HD is the most-common RVD sequence, and thus conforms to the consensus sequence. In contrast, NS is less frequent, and provides an interesting point of comparison, both for stability studies and in future work, DNA binding.
Figure 1.
Sequence conservation and structure of TALE repeats. (A) A sequence logo of TALE repeats showing conservation at each of the 34 positions. The sequence below is the consensus sequence used in these studies. At the RVD positions (12, 13), two common recognition motifs were selected (NS and HD). (B) Crystal structure of dHax3 highlighting location of RVDs (red sticks) (18). (C) The N-terminal cap (orange) is a conserved extension of the repeat domain composed of four TALE-like repeats (31). (D) The C-terminal cap was designed by substituting solvent exposed hydrophobic residues to polar or charged residues (pink spheres). To see this figure in color, go online.
We initially built consensus TALE arrays without terminal capping repeats, but found these constructs to self-associate by sedimentation velocity analytical ultracentrifugation (AUC; data not shown). Previous studies with ankyrin repeat and TPR consensus constructs have shown that polar N- and C-terminal caps are essential for solubility (19, 20, 22, 23, 29, 30). Thus, we designed N- and C-terminal caps to help solubilize our consensus TALE arrays.
For the N-terminal cap, we selected a conserved 149 residue N-terminal extension of the naturally occurring TALE gene product PthXo1. Crystal structures show that this N-terminal extension forms four cryptic repeats, with similar structure to TALE repeats despite significant sequence differences from the TALE consensus (Fig. 1 C) (31, 32). This N-cap has been shown to be resistant to proteolysis and is required for full transcription activation (31). The C-terminal cap was designed by changing consensus hydrophobic residues predicted to be solvent exposed to polar or charged residues (Fig. 1 D). Sedimentation velocity AUC experiments demonstrated that constructs with both the N- and C-caps are monomeric (Fig. S3). Subsequent AUC experiments showed singly capped (either N- or C-terminal) constructs are also soluble and monomeric. Including these singly capped constructs allows us to resolve the thermodynamic contributions of the capping repeats from the internal repeats.
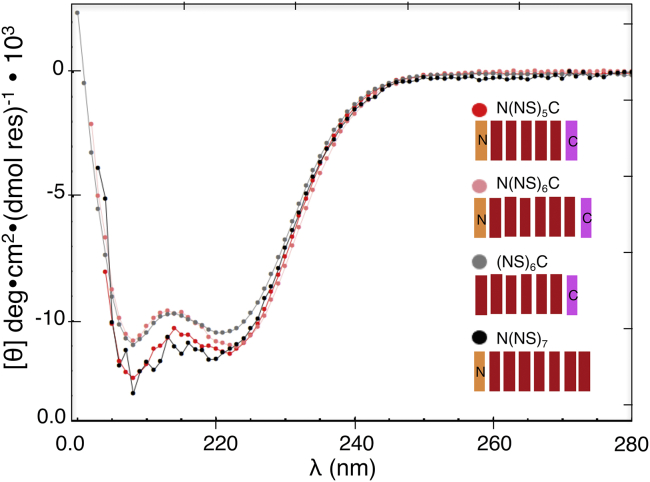
To confirm that cTALE repeats have α-helical secondary structure, far-UV CD spectra were collected for various cTALE constructs. The spectra of all constructs are consistent with α-helical structure and are similar in shape to the far-UV CD spectrum of the naturally occurring PthXo1 TALE domain (Figs. 2 and S4). Helical structure is retained when either the N- or C-cap is absent. Also, consensus TALEs retain DNA-binding activity (Fig. S5).
Figure 2.
Doubly- and singly-capped TALE consensus constructs are α-helical. Far-UV CD spectra of TALE NS repeat constructs with N-cap, C-cap, and both caps. Spectra are consistent with folded, α-helical structures. Conditions: 300 mM NaCl, 10 mM Tris HCl (pH 7.4), 5% glycerol, 25°C. To see this figure in color, go online.
The RVD sequence affects cTALE stability
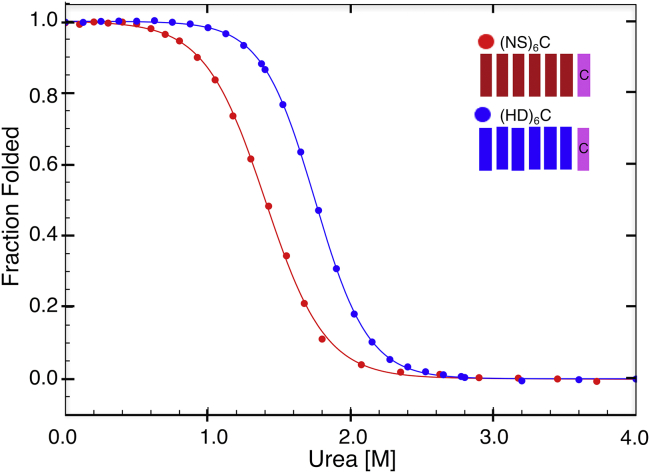
To determine the effect of RVD sequence on stability, urea-induced unfolding transitions were measured by CD spectroscopy for a construct with NS RVDs ((NS)6C, with six NS repeats and a C-cap) and an otherwise identical construct with HD repeats ((HD)6C, Fig. 3). Both unfolding transitions are sigmoidal and are well-fitted with a two-state model. The unfolding transitions of the HD and NS constructs have similar slopes (and thus, similar m-values), but have significantly different unfolding midpoints (Cm values). As a result, the NS and HD constructs have different free energies of unfolding . The sigmoidal transitions and high m-values are consistent with a high level of cooperativity in unfolding, suggesting strong interfacial coupling between repeats. The differences in values indicate that RVD identity affects intrinsic folding energy, interrepeat coupling energy, or both.
Figure 3.
Consensus TALE stability is dependent on RVD sequence. Urea-induced unfolding transitions of TALE constructs show cooperative, two-state unfolding transitions. Urea-induced unfolding transitions of each construct were fitted with a two-state model for unfolding (solid lines). Global stabilities, based on unfolding midpoints, vary significantly with RVD sequence, although slopes of the transitions do not. Conditions: 300 mM NaCl, 10 mM Tris HCl (pH 7.4), 5% glycerol, 25°C. To see this figure in color, go online.
Length and capping dependence of NS TALE stability
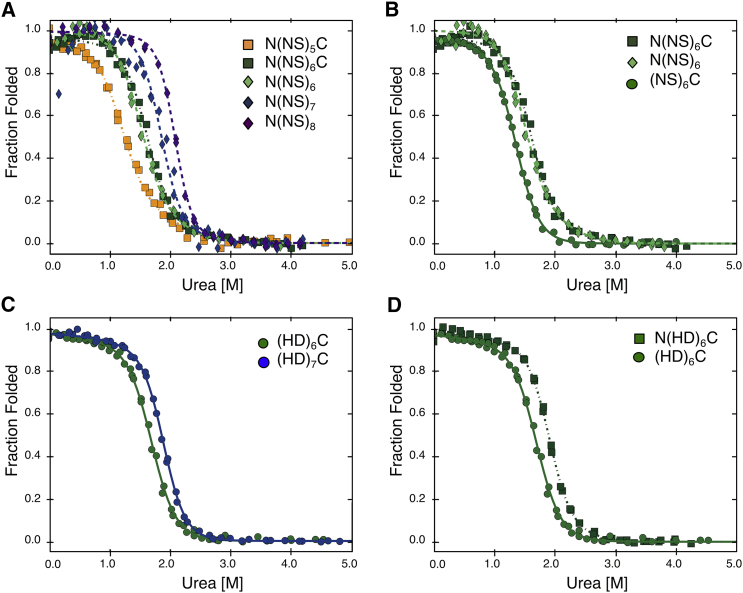
To resolve the intrinsic stability from the interfacial coupling energy between TALE repeats, urea-induced unfolding transitions were measured for constructs with different numbers of NS repeats. Because the number of repeats and interfaces in each construct differ, analyzing the unfolding of constructs of different lengths allows the intrinsic and interfacial energies to be treated as independent variables (26). To account for sequence differences in the N- and C-terminal repeat sequences, we included constructs lacking either the N- or the C-terminal cap. These constructs are crucial for untangling intrinsic and interfacial free energies from variations due to capping substitutions.
For a given capping structure, adding internal NS repeats increases stability (compare N(NS)5C and N(NS)6C, as well as N(NS)6, N(NS)7, and N(NS)8; Fig. 4 A), again consistent with strong energetic coupling between repeats. For constructs with six internal NS repeats, the construct containing both the N- and C-terminal cap has the highest midpoint, followed by the construct with only the N-terminal cap (Fig. 4 B). The construct with only the C-terminal cap has the lowest midpoint.
Figure 4.
Length- and capping-dependence of TALE HD- and NS-RVD stability. Urea-induced unfolding transitions of TALE constructs were globally fitted using a heterogeneous nearest-neighbor Ising model (N-capped, dashed lines; C-capped, solid lines; doubly capped, dotted lines). (A) NS-type repeat constructs with increasing repeat number, for N-capped and doubly capped constructs. Stability increases with number of repeats are shown. (B) Constructs with six NS-type repeats with varying capping identities are shown. N(NS)6C is most stable followed by N(NS)6. (NS)6C has the smallest Cm but the largest slope. (C) HD-type repeat constructs with increasing repeat number are shown. The increase in midpoint of the transition between (HD)6C and (HD)7C is less than the increase in midpoint between N(NS)5C and N(NS)6C (A). (D) Constructs with six HD-type repeats with varying capping identities are shown. As with the NS-type repeats (B), the doubly capped construct is more stable than the singly capped construct. Conditions: 300 mM NaCl, 10 mM Tris HCl (pH 7.4), 5% glycerol, 25°C. To see this figure in color, go online.
Transitions for N-capped constructs are not as steep as for constructs lacking N-caps. This suggests that the unfolding transitions of N-capped constructs are not two-state. It seems unlikely that adding the N-terminal cap uncouples the (NS)6C unfolding transition; rather, the decreased slope for the N-capped constructs suggests weak coupling between the N-cap and central repeats combined with a high intrinsic stability for the N-term capping segment.
Length and capping dependence of HD TALE stability
To better understand the origins of the stability differences among different RVD sequences (Fig. 3), urea-induced unfolding transitions were measured for HD-type repeats of various lengths and capping structures. Adding an internal HD repeat is stabilizing, as shown in Fig. 4 C. Although the Cm values increase with repeat number for the HD series (compare (HD)6C and (HD)7C in Fig. 4 C), this increase is smaller than the Cm increase for an NS-type repeat (compare N(NS)5C and N(NS)6C in Fig. 4 A). This suggests that addition of an NS-type repeat is more stabilizing than the addition of an HD-type repeat.
The suggestion that NS-type repeats are more stabilizing than HD-type repeats appears to be at odds with the observation that (HD)6C is more stable than (NS)6C (Fig. 3). One possible explanation for this apparent discrepancy is that stability differences between NS- and HD-type repeats are unevenly distributed between intrinsic folding and interfacial interaction energies.
Stabilities of TALEs containing mixtures of NS and HD TALE repeats
Naturally occurring TALE proteins contain “mixed RVDs,” meaning that adjacent repeats have different RVD sequences. Fig. S6 shows urea-induced unfolding transitions for constructs containing both the NS and HD RVDs, (HD)2(NS)1(HD)2C and (NS)1(HD)5C. Both mixed RVD constructs have cooperative urea-induced unfolding transitions (Fig. S6), with m-values similar to constructs composed solely of one type of repeat. These observations suggest that the size of the cooperative unit is similar for mixed and unmixed constructs.
Global Ising analysis of NS and HD TALE repeat unfolding transitions
To dissect contributions of intrinsic and interfacial stabilities to repeat-protein folding, 1D Ising models were fitted to urea-induced unfolding transitions (19, 20, 22). These models represent unfolding at the level of individual repeats, and account for all combinations of folded and unfolded repeats. The free energy of each of these 2n configurations (where n is the number of repeats) is modeled to the sum of the intrinsic energies of each folded repeat and the interfacial interaction energies of pairs of adjacent folded repeats. Because the caps differ in sequence, intrinsic energies are modeled as different from those of the internal, sequence-identical repeats.
Figs. 4 and S6 show a global fit of the Ising model to unfolding transitions for NS and HD constructs of different lengths and capping structures in which all NS-, HD-, and mixed RVD constructs are fitted simultaneously. Although each unfolding transition has separate baseline parameters, the entire family of transitions share 11 globally fitted thermodynamic parameters (Table 1). To estimate parameter uncertainties, 2000 iterations of bootstrapping were performed, and 95% confidence intervals were calculated (26).
All repeats have unfavorable intrinsic folding free energies and favorable interfacial free energies, consistent with previous Ising analyses of ankyrin repeat and some TPR proteins (19, 20, 22, 23). Intrinsic folding of individual NS repeats is more unfavorable than repeats with the HD RVD. In contrast, adjacent NS repeats are more strongly coupled than adjacent HD repeats. For interfaces between repeats with different RVD sequences, coupling is the same as for the first repeat type in the pair. That is, the identity of the RVD determines the coupling energy to the next repeat (but not the previous repeat).
Discussion
Analysis of unfolding transitions of TALE constructs of different length and RVD sequence using a nearest-neighbor Ising model provides information on coupling energies, local folding free energies, and RVD sequence-stability correlation. We find that although changes in the residues responsible for conferring DNA binding specificity have moderate effects on the constructs studied here, these sequence changes have large effects on the distribution of stability within and between repeats, and on the cooperativity of TALE repeat arrays. These results suggest that TALE proteins used for genome editing have different local as well as global stabilities based on the RVDs chosen for DNA sequence recognition.
The identity of the RVD affects stability and cooperativity
Ising analysis of the TALE constructs in this study reveals intrinsically unstable repeat units coupled by stabilizing interfaces, consistent with studies from other linear repeat proteins. This partitioning results in an overall cooperative folding transition, and gives rise to an increase in native-state stability with repeat number. However, the magnitude of the partitioning varies depending on RVD-type. For NS RVDs the intrinsic folding free energy is +5.9 kcal/mol, and the interfacial free energy is −7.8 kcal/mol. For HD RVDs the intrinsic folding energy is +3.5 kcal/mol, and the interfacial energy is −5.0 kcal/mol. That is, individual folded NS-type repeats are more intrinsically unstable, but couple more strongly with their folded neighbors. One result of this difference in partitioning is that NS-type repeats are more strongly coupled than HD-type repeats.
Because naturally occurring TALE proteins are composed of many different RVD sequences, “mixed interfaces” are formed between repeats with different RVDs. Our Ising analysis of mixed NS and HD TALE RVDs shows that for a pair of mixed RVDs, the interfacial energy is determined by the N-terminal repeat. That is, ΔGNS,i:HD,i+1 = ΔGNS,i:NS,i+1 and ΔGHD,i:NS,i+1 = ΔGHD,i:HD,i+1 (Table 1).
Weak coupling of the N-terminal cap
Although the conserved N-cap is required for DNA binding and transcription activation of the naturally occurring PthXo1 TALE array (8, 13, 31, 33, 34, 35), we find that this cap only modestly enhances stability of the central repeats. Our Ising analysis is consistent with this observation, showing that the N-cap is intrinsically stable (−4.5 kcal/mol), but it is weakly coupled (−0.82 kcal/mol) to the central repeats. In one proposed mechanism for DNA binding, the N-cap nonspecifically binds DNA and facilitates diffusion (31, 36). Weak coupling of the N-cap from the central repeats could uncouple nonspecific diffusive association from tight sequence-specific DNA binding of central repeats. In such a model, the N-cap acts to increase local concentration of TALEs on DNA while the central repeat domain can separately search for specific sequences.
TALE arrays significantly populate partly folded states
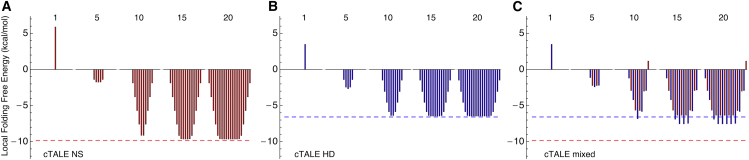
Proteins fold in a highly cooperative manner, rarifying populations of partially folded states. The Ising model allows us to determine the populations of partly folded states. These populations can be represented as a distribution of the local folding free energy of each repeat as a function of position (Fig. 5). We define folding free energy as the free energy of all states in which a given repeat is folded minus that of all states where the repeat is unfolded (see Supporting Materials and Methods). In addition to providing a picture of end-fraying, these distributions provide a picture of accessibility of conformations that are unfolded (i.e., “broken”) in the middle of the array.
Figure 5.
Distribution of local folding free energies for TALE repeat arrays as a function of length. At each position, probabilities of a repeat being folded (and unfolded) were calculated from the nearest-neighbor partition function using free energies from the Ising fit. Local folding free energies were calculated from Eq. 4. For homopolymeric TALE arrays (A, NS-type repeats in red, B, HD-type repeats in blue), the values of the central repeats decreases with repeat number until a plateau in local folding free energy is reached (dashed lines). This plateau in is lower (i.e., greater stability) for NS repeats (A) than HD repeats (B). Constructs containing both NS and HD repeat types have a heterogeneous stability distribution, with local unfolding of the C-terminal NS repeats (C). Mixing NS (red) and HD (blue) repeats in an alternating fashion decreases of HD repeats, but increases of NS repeats. All constructs show fraying of end repeats, as would be expected from a cooperative nearest-neighbor model. To see this figure in color, go online.
For short (one to four repeat) homopolymeric TALE arrays (Fig. 5, A and B), is positive, meaning it is more probable for repeats to be unfolded than folded. For homopolymer constructs with five or more repeats, becomes negative. Central repeats have more negative values than terminal repeats, consistent with end fraying. Somewhat surprisingly, the local folding free energies of internal repeats reach a plateau for long TALE arrays (15 and 20 repeats). The local folding free energies plateau at a lower value for NS-type repeats, that is, central NS-repeats are more stable than central HD-repeats (dashed lines, Fig. 5, A and B).
The values of local folding free energy plateaus are nearly equal to the sum of a single intrinsic energy and two interfacial energies (because two interfaces must be disrupted to fold an internal repeat). The close agreement between these two quantities indicates that the dominant partially unfolded state captured by the Ising model is one in which a single internal repeat unfolds, while the remainder of the TALE array remains folded. This kind of local “break” in the TALE array should disrupt the superhelix and allow direct DNA binding.
Because the intrinsic and interfacial energies for NS- and HD-type repeats are different, the plateau values for NS- and HD-type repeats are different (−9.7 kcal/mol for NS-type repeats and −6.6 kcal/mol for HD-type repeats, Fig. 5, A and B). Thus, the probability of a local unfolding reaction inside of the TALE array depends significantly (by a factor of 103.1/RT) on RVD sequence.
Fig. 5 C shows the calculated distribution for mixed constructs. Alternating NS- and HD-type repeats leads to significant heterogeneity in the distribution due to the difference in the intrinsic stabilities of NS- and HD-type repeats. Compared with unmixed arrays, mixing NS- and HD-type repeats increases the local folding free energy of NS-type repeats while decreasing the local folding free energy of HD-type repeats (Fig. 5 C). NS repeats have higher values in the mixed repeat array because the N-terminal interface in the mixed system is less favorable. HD repeats have lower values in the mixed repeat array because the N-terminal interface in the mixed system is more favorable.
Natural TALEs, such as PthXo1, contain a diverse set of RVD sequences. This extensive mixing of repeats may result in an increase in the population of partly folded states, either through end fraying, internal repeat unfolding, or interfacial fracture (see below and Fig. S7). The far UV CD spectrum of heteropolymeric PthXo1 has less α-helical signal compared with the far UV CD spectra of homopolymeric cTALEs (Fig. S4). Regions of local instability may be important for facilitating binding to DNA.
TALEs access “fractured” states
A more limited type of local structural distortion is the disruption of a single interface between two folded repeats, which can be viewed as a break internal to the folded TALE array. Such states are not included in the Ising model, which assumes that adjacent folded repeats are automatically coupled through interfacial interaction. To capture these fractures, we modified the Ising partition function to include these states (Supporting Materials and Methods). The probability of fracture is calculated for arrays of 20 cTALE repeats (homopolymeric and mixed arrays, Fig. S7). Mixed cTALEs have the greatest fracture probability, whereas homopolymeric NS cTALEs have the lowest fracture probability (3.9 × 10−3 versus 1.9 × 10−5, respectively). For comparison, the probability of fracture is calculated for consensus Ankyrin repeats (cANKS), another helical 34 residue linear repeat array that has been analyzed using the Ising formalism (19, 22); arrays of cTALEs have fracture probabilities that are four to six orders of magnitude greater than arrays of cANKs.
We have described several different ways cTALEs break: end fraying, unfolding of internal repeats, and rupturing of interfaces. Calculated probabilities for these different types of breakage are compared in Fig. S7. States where terminal repeats are unfolded (end frayed) have the greatest probability. For cTALEs, states where internal repeats are unfolded (internally unfolded) and states where consecutive repeats are folded but uncoupled (interfacially fractured) are significantly populated. These types of structural distortion are energetically accessible to cTALEs and may provide access to a state that is competent for DNA binding, thus increasing the overall binding rate.
Length-dependent stability switch
Because of differences in the energetic partitioning for the NS and HD RVDs, the relative stabilities of these two arrays are predicted to switch as repeats are added. At low repeat number, constructs containing NS-type repeats are less stable than constructs containing the HD RVD. This can be seen in Fig. 3, where the midpoint of the (NS)6C transition is at lower urea concentration than that of (HD)6C.
However, at high repeat number, the Ising model predicts that constructs composed of HD RVDs are less stable than constructs composed of NS RVDs. Although we have been unable to purify these longer constructs (N(HD)7 and N(HD)8 aggregate according to sedimentation velocity), we can use Ising parameters to estimate the free energy of the native state. (Fig. 6). At one repeat, the stability is equal to the intrinsic stability; thus, the “native state” of a single HD-repeat construct has a lower free energy than a single NS-repeat construct. Upon the addition of subsequent repeats, native state free energy decreases linearly, with a slope equal to the sum of the intrinsic and interfacial energies. Because this sum is larger (more negative) for NS repeats, the two free energy lines intersect between seven and eight repeats.
Figure 6.
Differences in energetic partitioning for NS- and HD-RVDs results in a length dependent stability switch. Using free energies from the Ising fit, folding free energies for arrays with increasing repeat number were calculated. At low repeat number, the fully folded state of NS-type constructs are less stable than HD-type constructs. However, at high repeat number, NS-type constructs are more stable than HD-type constructs. The crossover point is between seven and eight repeats. To see this figure in color, go online.
Conclusions
Through manipulation of capping sequences, we have designed a consensus TALE array that permits both length and RVD sequence variation, and we have found conditions where folded constructs remain monomeric, even with only one terminal cap. Together, our set of constructs satisfies the criteria for 1D Ising analysis, permitting high-precision determination of intrinsic stabilities and nearest-neighbor coupling energies. All constructs show moderate cooperativities (favorable coupling energies, unfavorable intrinsic stabilities). Importantly, these parameters are strongly dependent on RVD sequence. Although we have only looked at NS- and HD-RVDS, it is clear from our studies that RVD sequence identity influences not only global stability, but also intrinsic stability, coupling energy, cooperativity, and accessibility of partly folded states. Together, these factors have implications for genome editing: depending on the sequence of the genomic target, the thermodynamic profile of the cognate TALE may affect the ability to activate target sites. Taking these factors into account in genome editing experiments could improve activity.
Author Contributions
K.G-S. conducted experiments. K.G-S. and D.B. designed experiments and wrote the article.
Acknowledgments
We thank Dr. Barry Stoddard for supplying the PthXo1 plasmid, Dr. Jake Marold for writing the original program used for Ising analysis fitting, Dr. Katherine Tripp and the JHU Center for Molecular Biophysics for instrument access and technical support, Dr. Evangelos Moudrianakis for assistance with analytical ultracentrifugation, and Dr. Michael McCaffery and the JHU Integrated Imaging Center for technical support.
This work was supported by NIH grant R01 GM068462 to D.B. K.G-S. was supported by NIH training grant T32-GM008403.
Editor: Enrique De La Cruz.
Footnotes
Supporting Materials and Methods and seven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30940-7.
Supporting Material
References
- 1.Kay S., Hahn S., Bonas U. A bacterial effector acts as a plant transcription factor and induces a cell size regulator. Science. 2007;318:648–651. doi: 10.1126/science.1144956. [DOI] [PubMed] [Google Scholar]
- 2.Römer P., Hahn S., Lahaye T. Plant pathogen recognition mediated by promoter activation of the pepper Bs3 resistance gene. Science. 2007;318:645–648. doi: 10.1126/science.1144958. [DOI] [PubMed] [Google Scholar]
- 3.Boch J., Bonas U. Xanthomonas AvrBs3 family-type III effectors: discovery and function. Annu. Rev. Phytopathol. 2010;48:419–436. doi: 10.1146/annurev-phyto-080508-081936. [DOI] [PubMed] [Google Scholar]
- 4.Boch J., Scholze H., Bonas U. Breaking the code of DNA binding specificity of TAL-type III effectors. Science. 2009;326:1509–1512. doi: 10.1126/science.1178811. [DOI] [PubMed] [Google Scholar]
- 5.Moscou M.J., Bogdanove A.J. A simple cipher governs DNA recognition by TAL effectors. Science. 2009;326:1501. doi: 10.1126/science.1178817. [DOI] [PubMed] [Google Scholar]
- 6.Miller J.C., Zhang L., Rebar E.J. Improved specificity of TALE-based genome editing using an expanded RVD repertoire. Nat. Methods. 2015;12:465–471. doi: 10.1038/nmeth.3330. [DOI] [PubMed] [Google Scholar]
- 7.Li T., Huang S., Yang B. TAL nucleases (TALNs): hybrid proteins composed of TAL effectors and FokI DNA-cleavage domain. Nucleic Acids Res. 2011;39:359–372. doi: 10.1093/nar/gkq704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Christian M., Cermak T., Voytas D.F. Targeting DNA double-strand breaks with TAL effector nucleases. Genetics. 2010;186:757–761. doi: 10.1534/genetics.110.120717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cong L., Zhou R., Zhang F. Comprehensive interrogation of natural TALE DNA-binding modules and transcriptional repressor domains. Nat. Commun. 2012;3:968. doi: 10.1038/ncomms1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Geissler R., Scholze H., Boch J. Transcriptional activators of human genes with programmable DNA-specificity. PLoS One. 2011;6:e19509. doi: 10.1371/journal.pone.0019509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Y., Moore R., Bleris L. Transcription activator-like effector hybrids for conditional control and rewiring of chromosomal transgene expression. Sci. Rep. 2012;2:897. doi: 10.1038/srep00897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mahfouz M.M., Li L., Zhu J.-K. Targeted transcriptional repression using a chimeric TALE-SRDX repressor protein. Plant Mol. Biol. 2012;78:311–321. doi: 10.1007/s11103-011-9866-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang F., Cong L., Arlotta P. Efficient construction of sequence-specific TAL effectors for modulating mammalian transcription. Nat. Biotechnol. 2011;29:149–153. doi: 10.1038/nbt.1775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Maeder M.L., Angstman J.F., Joung J.K. Targeted DNA demethylation and activation of endogenous genes using programmable TALE-TET1 fusion proteins. Nat. Biotechnol. 2013;31:1137–1142. doi: 10.1038/nbt.2726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Miyanari Y., Ziegler-Birling C., Torres-Padilla M.-E. Live visualization of chromatin dynamics with fluorescent TALEs. Nat. Struct. Mol. Biol. 2013;20:1321–1324. doi: 10.1038/nsmb.2680. [DOI] [PubMed] [Google Scholar]
- 16.Ma H., Reyes-Gutierrez P., Pederson T. Visualization of repetitive DNA sequences in human chromosomes with transcription activator-like effectors. Proc. Natl. Acad. Sci. USA. 2013;110:21048–21053. doi: 10.1073/pnas.1319097110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kim H., Kim J.-S. A guide to genome engineering with programmable nucleases. Nat. Rev. Genet. 2014;15:321–334. doi: 10.1038/nrg3686. [DOI] [PubMed] [Google Scholar]
- 18.Deng D., Yan C., Yan N. Structural basis for sequence-specific recognition of DNA by TAL effectors. Science. 2012;335:720–723. doi: 10.1126/science.1215670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Aksel T., Majumdar A., Barrick D. The contribution of entropy, enthalpy, and hydrophobic desolvation to cooperativity in repeat-protein folding. Structure. 2011;19:349–360. doi: 10.1016/j.str.2010.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kajander T., Cortajarena A.L., Regan L. A new folding paradigm for repeat proteins. J. Am. Chem. Soc. 2005;127:10188–10190. doi: 10.1021/ja0524494. [DOI] [PubMed] [Google Scholar]
- 21.Mello C.C., Barrick D. An experimentally determined protein folding energy landscape. Proc. Natl. Acad. Sci. USA. 2004;101:14102–14107. doi: 10.1073/pnas.0403386101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wetzel S.K., Settanni G., Plückthun A. Folding and unfolding mechanism of highly stable full-consensus ankyrin repeat proteins. J. Mol. Biol. 2008;376:241–257. doi: 10.1016/j.jmb.2007.11.046. [DOI] [PubMed] [Google Scholar]
- 23.Marold J.D., Kavran J.M., Barrick D. A naturally occurring repeat protein with high internal sequence identity defines a new class of TPR-like proteins. Structure. 2015;23:2055–2065. doi: 10.1016/j.str.2015.07.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cermak T., Doyle E.L., Voytas D.F. Efficient design and assembly of custom TALEN and other TAL effector-based constructs for DNA targeting. Nucleic Acids Res. 2011;39:e82. doi: 10.1093/nar/gkr218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Poland D., Scheraga H.A. Academic Press; San Diego, CA: 1970. Theory of Helix-Coil Transitions in Biopolymers: Statistical Mechanical Theory of Order-Disorder Transitions in Biological Macromolecules. [Google Scholar]
- 26.Aksel T., Barrick D. Analysis of repeat-protein folding using nearest-neighbor statistical mechanical models. Methods Enzymol. 2009;455:95–125. doi: 10.1016/S0076-6879(08)04204-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Finn R.D., Clements J., Eddy S.R. HMMER web server: interactive sequence similarity searching. Nucleic Acids Res. 2011;39:gkr367. doi: 10.1093/nar/gkr367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wheeler T.J., Clements J., Finn R.D. Skylign: a tool for creating informative, interactive logos representing sequence alignments and profile hidden Markov models. BMC Bioinformatics. 2014;15:7. doi: 10.1186/1471-2105-15-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mosavi L.K., Peng Z.-Y. Structure-based substitutions for increased solubility of a designed protein. Protein Eng. 2003;16:739–745. doi: 10.1093/protein/gzg098. [DOI] [PubMed] [Google Scholar]
- 30.Tripp K.W., Barrick D. Enhancing the stability and folding rate of a repeat protein through the addition of consensus repeats. J. Mol. Biol. 2007;365:1187–1200. doi: 10.1016/j.jmb.2006.09.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gao H., Wu X., Han Z. Crystal structure of a TALE protein reveals an extended N-terminal DNA binding region. Cell Res. 2012;22:1716–1720. doi: 10.1038/cr.2012.156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mak A.N.-S., Bradley P., Stoddard B.L. The crystal structure of TAL effector PthXo1 bound to its DNA target. Science. 2012;335:716–719. doi: 10.1126/science.1216211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Miller J.C., Tan S., Rebar E.J. A TALE nuclease architecture for efficient genome editing. Nat. Biotechnol. 2011;29:143–148. doi: 10.1038/nbt.1755. [DOI] [PubMed] [Google Scholar]
- 34.Mussolino C., Morbitzer R., Cathomen T. A novel TALE nuclease scaffold enables high genome editing activity in combination with low toxicity. Nucleic Acids Res. 2011;39:9283–9293. doi: 10.1093/nar/gkr597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sun N., Liang J., Zhao H. Optimized TAL effector nucleases (TALENs) for use in treatment of sickle cell disease. Mol. Biosyst. 2012;8:1255–1263. doi: 10.1039/c2mb05461b. [DOI] [PubMed] [Google Scholar]
- 36.Meckler J.F., Bhakta M.S., Baldwin E.P. Quantitative analysis of TALE-DNA interactions suggests polarity effects. Nucleic Acids Res. 2013;41:4118–4128. doi: 10.1093/nar/gkt085. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.