Abstract
Alzheimer's disease (AD) is a progressive and irreversible neurodegenerative disorder that has recently seen serious increase in the number of affected subjects. In the last decade, neuroimaging has been shown to be a useful tool to understand AD and its prodromal stage, amnestic mild cognitive impairment (MCI). The majority of AD/MCI studies have focused on disease diagnosis, by formulating the problem as classification with a binary outcome of AD/MCI or healthy controls. There have recently emerged studies that associate image scans with continuous clinical scores that are expected to contain richer information than a binary outcome. However, very few studies aim at modeling multiple clinical scores simultaneously, even though it is commonly conceived that multivariate outcomes provide correlated and complementary information about the disease pathology. In this article, we propose a sparse multi-response tensor regression method to model multiple outcomes jointly as well as to model multiple voxels of an image jointly. The proposed method is particularly useful to both infer clinical scores and thus disease diagnosis, and to identify brain subregions that are highly relevant to the disease outcomes. We conducted experiments on the Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset, and showed that the proposed method enhances the performance and clearly outperforms the competing solutions.
Index Terms: Alzheimer's Disease, Magnetic Resonance Imaging, Multiple Responses, Region Selection, Tensor Regression
I. Introduction
Alzheimer's disease (AD), characterized by progressive impairment of cognitive and memory functions, is an irreversible neurodegenerative disorder and the leading form of dementia in elderly subjects. The number of affected subjects increases significantly every year, and is projected to be 1 in 85 by the year 2050 [1]. Amnestic mild cognitive impairment (MCI) is often a prodromal stage to AD, and individuals with MCI may convert to AD at an annual rate of as high as 15% [2]. There has been a vast body of literatures studying AD and MCI using one or more neuroimaging technologies (modalities), including magnetic resonance imaging (MRI), functional magnetic resonance imaging (fMRI), positron emission tomography (PET), diffusion tensor imaging (DTI), among many others.
The majority of AD/MCI studies have been concentrating on differentiating AD and MCI subjects from the general population, because an accurate diagnosis of AD and MCI is particularly important for timely therapy and possible delay of the disease. This can be formulated as a classification problem, and a variety of statistical machine learning techniques have been employed for imaging-based diagnosis. See [3]–[5] for some excellent reviews. Moreover, in addition to classifying a binary or categorical disease outcome given brain image scans, there were studies establishing associations between image activity patterns and a continuous clinical outcome. A variety of cognitive and memory scores have been used as the response, including the Mini-Mental State Examination (MMSE) [6]–[9], Boston Naming Testing [9], Dementia Rating Scale, Alzheimer's Disease Assessment Scale-Cognitive Subscale (ADAS-Cog), and Auditory Verbal Learning Test [8].
More recently, there have emerged studies that associate image scans with multiple clinical outcomes [10], [11]. Our motivating data example consists of 194 subjects from the Alzheimer's Disease Neuroimaging Initiative (ADNI), among which 93 are AD patients and 101 healthy controls. For each subject, the collected data include a 32 × 32 × 32 MRI scan, after proper preprocessing and downsizing, and two clinical scores. One is the MMSE, which examines orientation to time and place, immediate and delayed recall of three words, attention and calculation, language and visuo-constructional functions [12]. The other is ADAS-Cog, which is a global measure encompassing the core symptoms of AD [13]. The ADAS-Cog is usually more sensitive, but requires more than 30 minutes for participants to complete all tasks. In contrast, the administration of MMSE takes only 10–15 minutes and thus is often used for fast screening for dementia. While both can be used to measure the severity of cognitive impairment, the scores of MMSE and ADAS-Cog carry, respectively, “local” and “global” information with respect to the cognitive capability, given the fact that the examination in MMSE is conducted on more specific tasks than in ADAS-Cog. Furthermore, recent studies have shown that the two scores are correlated, as they reflect on similar cognitive aspects such as orientation and memory [8], [14]. In these regards, it is beneficiary to jointly consider these scores in AD/MCI studies. Our aim in this article is to jointly model multiple clinical outcomes given brain structural patterns, under the belief that the multivariate scores provide correlated and complementary information.
Whereas there is an enormous body of statistics literature on modeling multivariate predictors, there have been much fewer works on modeling multivariate responses. Some popular multi-response solutions include partial least squares [15]–[17], canonical correlations [18], reduced-rank regressions [19]–[21], sparse regressions with various penalties [22]–[24], and sparse reduced-rank regressions [25]. All existing multi-response modeling methods universally treat the predictors as a vector and estimate a corresponding vector of coefficients. However, in neuroimaging analysis, the predictors take a more complex form of multi-dimensional array, a.k.a. tensor. Naively turning an array into a vector would result in extremely high dimensionality. For instance, a 32 × 32 × 32 MRI image would imply 323 = 32,768 parameters. Moreover, vectorizing an array would also destroy all the inherent spatial structural information of the image.
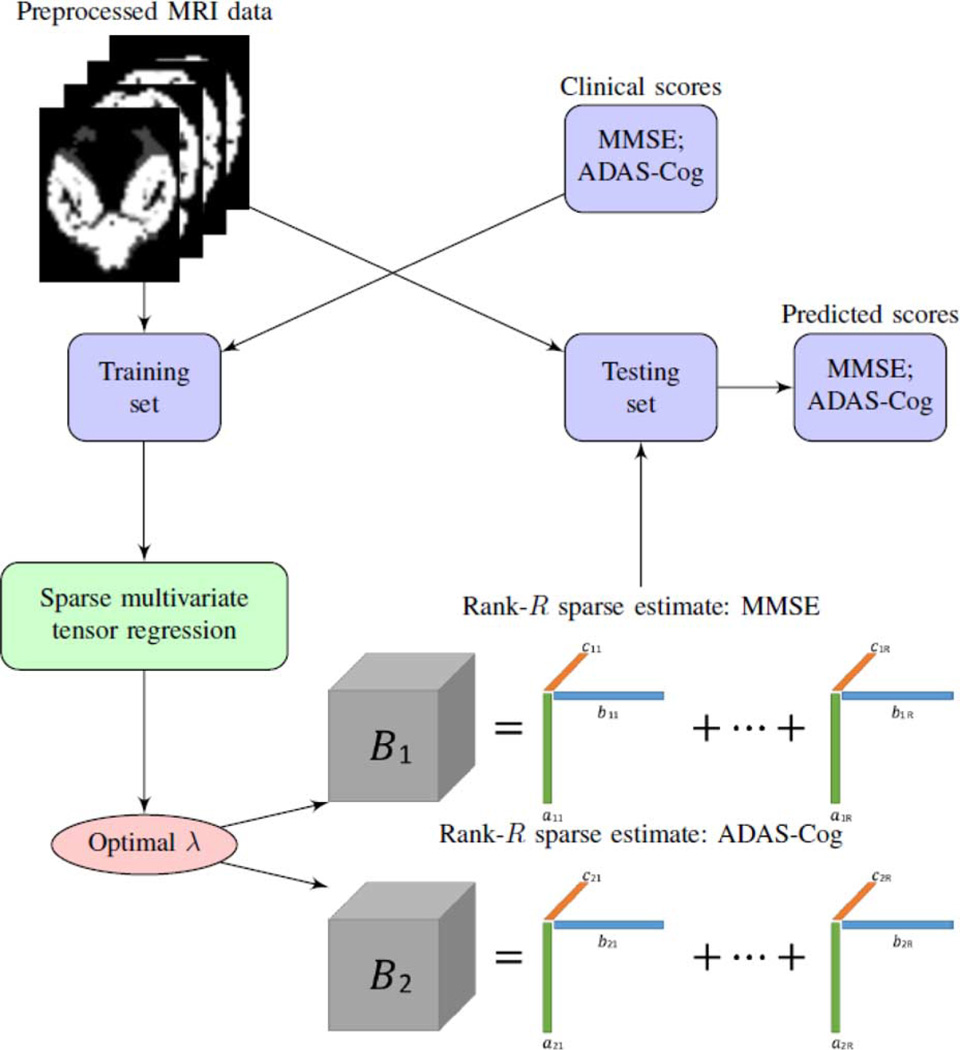
In this article, we propose a sparse multi-response tensor regression model to simultaneously infer multiple outcome variables and to identify brain subregions that are highly relevant to the clinical outcomes. A schematic overview of our proposed method is given in Fig. 1. The new method enjoys a number of appealing features. First, it models the multiple responses jointly rather than separately, by employing a penalty function accounting for correlated multivariate responses while inducing group sparsity. Second, the new method models brain image predictor in the form of a tensor rather than a vector. This is achieved by extending and generalizing a recent proposal of tensor predictor regression [26]. Directly modeling a tensor image predictor takes into account spatial correlations among the voxels, and is intuitively superior than the one-voxel-at-a-time modeling solution that ignores such correlations. This extension, however, is far from trivial, since [26] only considered a univariate response, and our proposal for multi-response requires a new form of penalty and a new optimization algorithm. Third, our method offers a competitive alternative to the common modeling strategy in neuroimaging literature that first groups individual voxels by predefined regions of interest (ROI) and then extracts a vector of useful features from ROIs. By contrast, our solution does not rely on any prior knowledge of ROIs but derives highly relevant features suggested directly by the data. Moreover, instead of conducting feature extraction and association modeling at two separate steps, our method simultaneously derives relevant features and builds their association with the outcomes. Last but not least, we develop a highly scalable computational algorithm that makes our method applicable to a range of massive imaging data.
Fig. 1.
A schematic overview of the proposed sparse multi-response tensor regression with multivariate cognitive assessments.
II. Materials
A. Subjects
We analyzed a dataset from the ADNI database (http://adni.loni.usc.edu/). The data included 93 subjects with mild AD and 101 normal controls (NC), and each subject had both MMSE and ADAS-Cog scores recorded. The subjects were in the age between 55 and 90, with a study partner, who provided an independent evaluation of functioning. All of 194 subjects met the following general inclusion criteria: (a) NC subjects: an MMSE between 25 and 30 (inclusive), a clinical dementia rating (CDR) of 0, non-depressed, non-MCI, and non-demented; (b) mild AD subjects: an MMSE score between 18 and 27 (inclusive), a CDR of 0.5 or 1.0, and met the National Institute of Neurological and Communicative Disorders and Stroke and the Alzheimer's Disease and Related Disorders Association (NINCDS/ADRDA) criteria for probable AD. The AD and NC groups were matched in age (with the two-sample t-test p-value = 0.68) and gender (with the two-sample proportion test p-value = 1.00). Table I presents the demographic characteristics of the subjects.
TABLE I.
Demographic and Clinical Information of the Subjects.
| Group | AD (n = 93) | NC (n = 101) |
|---|---|---|
| Female/Male | 36/57 | 39/62 |
| Age (Mean ± SD) | 75.5 ± 7.4 | 75.9 ± 4.8 |
| MMSE (Mean ± SD) | 23.5 ± 2.1 | 28.9 ± 1.1 |
| ADAS-Cog (Mean ± SD) | 27.7 ± 10.7 | 10.4 ± 4.2 |
SD: Standard Deviation
B. Preprocessing
All anatomical MRI data in this study were acquired using 1.5T scanners. The baseline MRI data were downloaded from ADNI in the neuroimaging informatics technology initiative (NIfTI) format, which had already been processed for spatial distortion correction caused by gradient nonlinearity and B1 field inhomogeneity. We further performed prevalent preprocessing procedures on all images, including Anterior Commissure-Posterior Commissure (AC-PC) correction, skull-stripping, and cerebellum removal. Specifically, for the AC-PC correction, we used MIPAV software to resample images to 256 × 256 × 256, and applied N3 algorithm [27] for non-uniform tissue intensity correction. Skull-stripping [28] was then performed, followed by cerebellum removal. We visually checked the skull-stripped images to ensure clean and dura removal. We next employed FAST of the FSL package (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) to segment the MR images into three tissue types: gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). We used HAMMER [29] to spatially normalized all three tissues onto a standard space, based on a brain atlas aligned with the MNI coordinate space. Next, we generated the regional volumetric maps, called RAVENS maps, using a tissue preserving image warping method [30]. In this study, we considered only the spatially normalized GM densities (GMD), due to its relatively high relevance to AD compared to WM and CSF [31]. Finally, we downsized the GMD maps to 32 × 32 × 32 voxels. Downsizing is for estimation and computational convenience, as it would considerably reduce the number of unknown parameters and save computation time and cost. It is a tradeoff and admittedly does lose some image information; however, our results and previous studies [32] suggest that the sacrifice in prediction is relatively limited.
III. Method
A. Model
Let Y = (Y1, …, Yq)⊤ ∈ ℝq denote a vector of q responses. For our AD data, q = 2, and Y = (Y1, Y2)⊤, where Y1 = MMSE and Y2 = ADAS-Cog. Let X ∈ ℝp1 × ⋯ × pD denote a D-way tensor predictor. For our AD data, D = 3, p1 = p2 = p3 = 32, and X denotes MRI scan. We propose the following multivariate tensor regression model,
| (1) |
where Bj ∈ ℝp1 × ⋯ × pD, j = 1, …, q, denotes the tensor coefficient that captures association between the tensor predictor X and the jth response Yj. The inner product 〈Bj, X〉 between two tensors Bj and X is defined as
where vec(X) denotes a tensor operator that stacks the entries of X into a column vector, and βji1, …, iD, xi1, …, iD denotes the (i1, …, iD)th element of Bj and X, respectively. e = (e1, …, eq)⊤ ∈ ℝq denotes a vector of q errors, each of which follows a normal distribution with zero mean and constant variance. Without loss of generality, we omit the intercept term in (1).
The tensor coefficients in (1) are the parameters of interest and require estimation given the observed data. If imposing no additional constraint, the total number of unknown parameters in Bj, which equals , is prohibitive. For instance, for our AD data, there are 323 = 32,768 parameters to estimate for each Bj, j = 1, 2, while the sample size is only n = 194. To alleviate the extremely high dimensionality, [26] introduced a low-rank structure on the coefficient tensor Bj that substantially reduces the number of unknown parameters. Specifically, a D-way tensor Bj ∈ ℝp1× ⋯ × pD is said to follow a rank-R CANDECOMP/PARAFAC (CP) decomposition [33], if
| (2) |
where are all column vectors, d = 1, …, D, r = 1, …, R, and ◦ denotes an outer product among vectors. For convenience, the CP decomposition is often represented by a shorthand, Bj = 〚Bj1, …, BjD〛, where for d = 1, …, D. With this low-rank decomposition, the number of unknown parameters in Bj decreases substantially from the order of to that of . For the 32 × 32 × 32 MRI image in the AD example, the dimensionality reduces from 32,768 to the order of 96 for a rank-1 model, and 288 for a rank-3 model.
Introducing this CP decomposition to , model (1) becomes
| (3) |
This is our base model for multivariate responses and tensor predictors, upon which the subsequent regularization and estimation are built.
To help concretize model (3), we consider one of its special cases when q = 2, D = 2, R = 1. That is, there are two response variables Y = (Y1, Y2)⊤, a matrix-valued predictor X, and Bj is assumed to follow a rank-1 CP structure such that Bj = 〚βj1, βj2〛 = βj1 ◦ βj2, j = 1, 2. Then (3) reduces to
| (4) |
where ⊗ denotes the Kronecker product. The first equality in (4) comes from the fact that 〈Bj, X〉 = 〈(βj2 ◦ βj1), vec(X)〉, when the matrix Bj admits a rank-1 CP decomposition (2). Furthermore, the Kronecker product equals the outer product when βj1 and βj2 are both column vectors. The second equality in (4) holds because , j = 1, 2. Examining model (4), we see that our proposed multivariate response tensor regression model in this special case essentially postulates that the relation between the jth response variable Yj and the matrix predictor X is in the form of left multiplying a coefficient vector then right multiplying another coefficient vector βj2 with the matrix image X. This relation is a natural extension of the classical linear model when X is a vector and the response-predictor relation is governed by β⊤ X.
B. Penalized Likelihood
Imposing the CP low-rank structure on the coefficient tensor Bj substantially reduces the ultrahigh dimensionality of model (1) to a manageable level, leading to feasible estimation and prediction. However, the resulting number of unknown parameters can still be much larger than the available sample size. For instance, for our AD example, imposing a rank-3 CP structure yields 576 = 2 × 3 × (32 + 32 + 32) parameters, and the sample size is merely n = 194. Moreover, model (3) itself treats the components of multivariate response Y1, …, Yq separately, while it is commonly conceived that the multivariate outcomes, i.e., MMSE and ADAS-Cog in this work, are correlated and often provide complementary information. Regularization through penalized estimation is particularly useful to both handle the small-n-large-p challenge and to incorporate potential correlations among the response variables. Therefore, we further introduce regularization into our multivariate response tensor regression model (3), and propose penalized likelihood estimation.
Given n independent and identically distributed sample observations {(X1, Y1), …, (Xn, Yn)}, we propose to minimize the following objective function over ,
| (5) |
In this function, the first component L is the usual negative log likelihood after imposing the CP structure, i.e.,
where Yij is the jth response variable of subject i. The second component J in the objective (5) is a penalty function, which could have multiple choices. Here, we choose the group lasso penalty [34], which, in our context, takes the form,
| (6) |
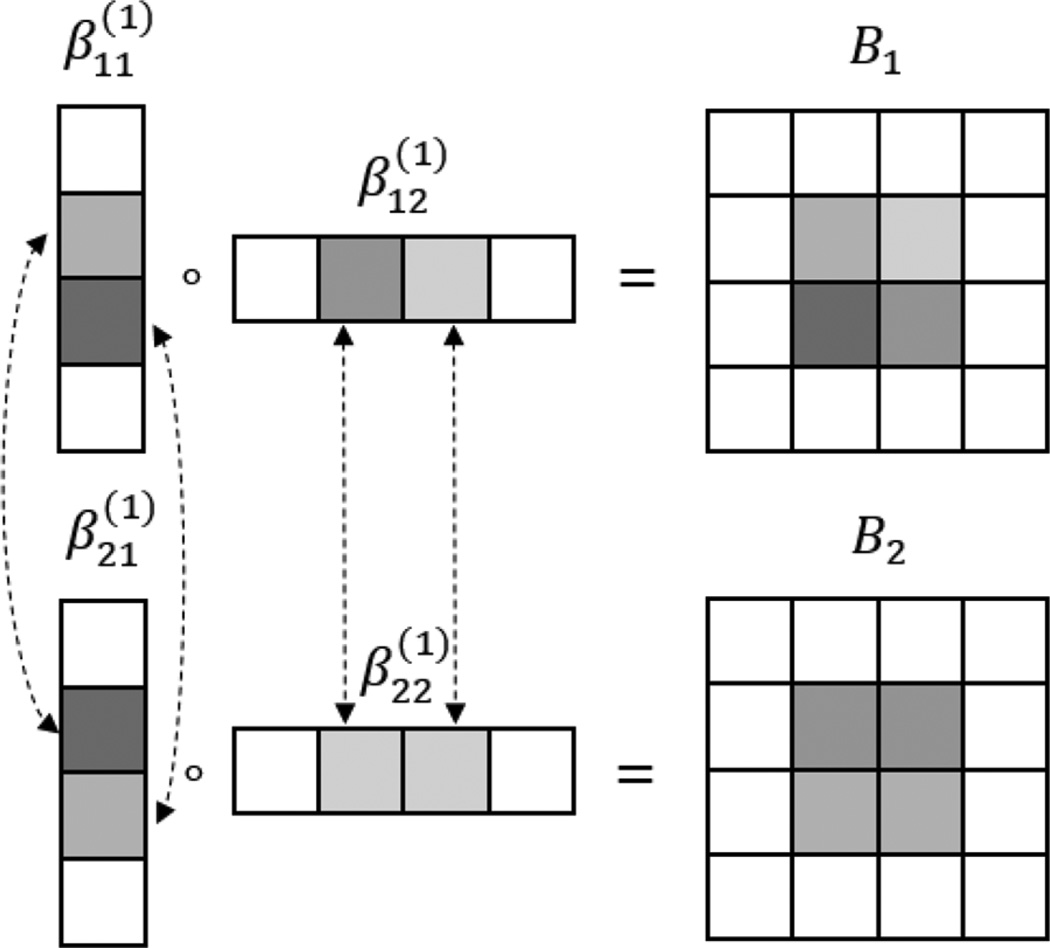
where is the kth element of in the CP decomposition (2). By imposing such a penalty, the individual coefficients that correspond to same subregion in an image but across different response variables are penalized as a group. As such, (6) encourages a subregion to drop out as a group if it is not associated with any of the multivariate response variables, which in effect takes into account potentially correlated responses. To further illustrate how the low-rank structure works and how the sparsity is imposed by this group penalty function, we consider a special case when q = 2, D = 2, R = 1, and p1 = p2 = 4. Fig. 2 shows that, for each response variable and its associated coefficient Bj, j = 1, 2, element-wise sparsity in the column vectors , j = 1, 2, d = 1, 2 translates into region-wise sparsity in the coefficient matrix Bj. Meanwhile, the group penalty (6) encourages that the subset of elements in , d = 1, 2, that correspond to the same region but across different response variables would enter or drop from the model simultaneously. A similar group penalty was also used in the classical multi-response model [23]. It encourages identification of the same subregions of the coefficient images across different responses. Meanwhile, it permits different magnitude of , i.e., strength of association, for different responses.
Algorithm 1.
Algorithm for minimizing ℓ(B1, …, Bq).
| Initialize Bjd ∈ IRpd × R as a random matrix, j = 1, …, q, d = 1, …, D. |
| repeat |
| for d = 1, …, D do |
| Update , given . |
| end for |
| for j = 1, …, q do |
| Update , |
| given . |
| end for |
| until converges. |
Fig. 2.
An illustration of the low-rank and sparse estimation of the coefficient signal when q = 2, D = 2, R = 1 and p1 = p2 = 4. ◦ denotes the outer product. Dotted lines connect the elements corresponding to the same region but across different responses, which are encouraged to enter or drop from the model simultaneously. Different colors denote different strength of association.
C. Estimation
Next, we investigate optimization of the objective function ℓ(B1, …, Bq) in (5). We first summarize the optimization procedure in Algorithm 1, then present details for individual steps. The optimization is achieved through the variational method [25] based on the following result,
when c = |x|−1, x ≠ 0. Consequently, minimizing (5) over B1, …, Bq is equivalent to minimizing the following objective function
| (7) |
over both Bj and , where . Optimization of (7) can then be achieved in an alternating fashion, updating iteratively with one set of parameters renewed and the others fixed.
Specifically, with Bj fixed, the update of is simply
With fixed, the update of Bj is achieved through a block relaxation algorithm [26]. That is, by imposing the CP structure on Bj = 〚Bj1, …, BjD〛, the first part of (7) can be written as
where Xi(d) denotes the mode-d matricization that maps tensor Xi into a pd × ∏d′ ≠ d matrix such that the (i1, …, iD)th element of Xi maps to the (id, 1 + ∑d′ ≠ d(id′ − 1) ∏d″ < d′, d″ ≠ d pd″)th element of Xi(d), and ⊙ denotes the Khatri-Rao product [35]. This reformulation allows one to focus the estimation Bjd on while keeping all the other parameters fixed. Meanwhile, the second part of (7) can be written as
Therefore, the objective in (7) is essentially a quadratic function of individual Bjd when all the other parameters are fixed. There is a closed form solution for Bjd, such that vec(Bjd) equals
where
We make a few remarks about the above optimization procedure. First, although the objective value decreases monotonically through iterations, the convergence to a global optimum is not guaranteed, since (5) involves a nonconvex optimization and there exist potentially multiple local minima. We adopt the common practice of using multiple starting values. In our setup, the stability of the algorithm with respect to initial values depends on several factors. A large sample size, a stronger signal strength, and a low-rank true image signal would all foster fast convergence and increase the chance to locate the global optimum from different initializations. In Section IV-B, we report the numerical convergence behavior of our algorithm with multiple starting values. Second, the computation of our method is fast, since both steps of iterations have closed form solutions. Actually the computational complexity for each iteration is O(np2q + p3q) for D ≤ 2, and O(npDq) for D > 2, when p1 = ⋯ = pD = p. In addition, since X̃ijd only depends on Bjd′, d′ ≠ d, {B1d, …, Bqd} can be updated simultaneously within each iteration. Again in Section IV-B, we report the computation time in simulations. Third, we note that the variational method rarely produces estimates that are exactly zero in practice. Consequently, we set a thresholding value for to achieve the desired sparsity, which is a common practice in the applications of the variational method [25]. Last but not least, in addition to the variational method, one may also consider using the alternating direction method of multipliers (ADMM) for solving the optimization of (5). We have experimented with ADMM, and found it produced similar results as the variational method, but was slower. This is partly due to that, within each block update, our problem simplifies into minimizing a quadratic function plus a group lasso penalty. The variational method can further simplify the problem by optimization over {B1d, …, Bqd} separately, whereas ADMM cannot and has to construct relatively large matrices involving {B1d, …, Bqd} jointly. For that reason, we choose the variational method as our optimization solution.
IV. Results
In this section, we first carry out Monte Carlo simulations to investigate the empirical performance of our proposed method. We then investigate its stability, convergence and computation time. Finally, we analyze the ADNI dataset to illustrate the efficacy of the new method.
A. Signal Recovery and Prediciton
We evaluate the empirical performance by two criteria: the prediction accuracy of the responses measured by root mean squared error (RMSE), and the estimation accuracy of the tensor coefficient shown by a plot. We compare our method with two alternative solutions. The first is to fit a tensor regression model for one response at a time. A comparison with this method would clearly show the gain of our method that jointly models the multivariate responses. The second is to vectorize the image predictor, ignoring all potential correlations among the image voxels, then fit a mluti-response linear regression model with a group lasso penalty [23]. This comparison would show the gain of our method that respects the image tensor structure. For abbreviation, we call our method and the two alternatives as “Multi-Resp”, “Uni-Resp”, and “Vectorized”, respectively.
The data are simulated from model (3), with a 64 × 64 matrix predictor X whose entries independently follow a normal distribution, and q coefficient matrices Bj ∈ ℝ64×64, j = 1, …, q, which take the value of 0 or 1 following specified patterns. We consider two scenarios: (i) We let all Bj follow the same pattern of “cross”, “triangle”, and “butterfly”, respectively. (ii) We let half of Bj's take the shape of “cross”, and the other half “triangle”. Among the three patterns, “cross” is of an exact rank 2, while “triangle” and “butterfly” are of infinitely high rank, whereas we use a fixed rank 3 to approximate all three patterns. We then generate q response variables following (3), with the errors e ∈ ℝq following a normal distribution with mean zero and covariance σ2Σ, where Σ ∈ ℝq×q has diagonal elements equal to 1 and off-diagonals equal to ρ. Consequently, the pairwise correlation among the q responses is governed by ρ, while σ2 controls the relative noise level. We examine a series of values of q, σ2 and ρ to investigate the empirical performance of different methods under varying response correlation strength and noise level. We marginally standardize the response variables, by subtracting mean and dividing by standard deviation. The models are fitted on a training set of size n = 750, tuned on an independent validation set, and evaluated on another independent testing set of the same size.
Table II shows RMSE of prediction of “future” responses in the testing data under 50 Monte Carlo replications, whereas Fig. 3 gives a graphical summary of the estimated coefficient signal based on one data replication under the scenario (i). Since the underlying true patterns are the same for all responses here, we only report the estimator for the first one. We present in the table the results when q = 3, 9, σ = 10, 15, 20, and ρ = 0, 0.9, respectively, but in the figure omit the results when ρ = 0.9, since they are visually similar to those of ρ = 0. We also omit in the figure the case q = 9 for “Uni-Resp”, because it fits each response variable separately, and thus the coefficient estimate is not affected by the number of responses q. It is clearly seen that our proposed method outperforms the univariate solution. The difference is more dominant when the signal is relatively more noisy, as one would often encounter in real imaging data, and when the number of response variables is large, as they provide more complementary information. In addition, both the multivariate and univariate tensor regression solutions have produced a much better estimation than the vectorized solution, which fails to identify any meaningful patterns.
TABLE II.
RMSE of Prediction Under Varying Noise Level (σ = 10, 15, 20), Number of Response Variables (q = 3, 9), and Response Pairwise Correlation (ρ = 0, 0.9). Reported are the Mean RMSE and Standard Error (in Parenthesis) Based on 50 Data Replications
| Signal | Parameter | Root mean squared error | ||||
|---|---|---|---|---|---|---|
| q | ρ | σ | Multi-Resp | Uni-Resp | Vectorized | |
| Cross | 3 | 0 | 10 | 0.599 (0.003) | 0.614 (0.003) | 0.993 (0.003) |
| 15 | 0.766 (0.003) | 0.804 (0.003) | 0.996 (0.003) | |||
| 20 | 0.895 (0.005) | 0.961 (0.004) | 0.998 (0.002) | |||
| 0.9 | 10 | 0.619 (0.005) | 0.613 (0.003) | 0.994 (0.003) | ||
| 15 | 0.798 (0.006) | 0.808 (0.005) | 0.998 (0.003) | |||
| 20 | 0.966 (0.006) | 0.976 (0.005) | 1.000 (0.003) | |||
| 9 | 0 | 10 | 0.615 (0.005) | 0.613 (0.002) | 0.974 (0.002) | |
| 15 | 0.767 (0.005) | 0.810 (0.002) | 0.986 (0.002) | |||
| 20 | 0.875 (0.004) | 0.981 (0.003) | 0.993 (0.002) | |||
| 0.9 | 10 | 0.632 (0.008) | 0.612 (0.003) | 0.986 (0.003) | ||
| 15 | 0.794 (0.006) | 0.808 (0.005) | 1.000 (0.003) | |||
| 20 | 0.904 (0.005) | 0.977 (0.005) | 1.001 (0.003) | |||
| Triangle | 3 | 0 | 10 | 0.668 (0.002) | 0.696 (0.002) | 0.996 (0.003) |
| 15 | 0.847 (0.003) | 0.871 (0.005) | 1.000 (0.002) | |||
| 20 | 0.956 (0.006) | 0.981 (0.004) | 1.000 (0.002) | |||
| 0.9 | 10 | 0.696 (0.004) | 0.697 (0.004) | 0.997 (0.003) | ||
| 15 | 0.855 (0.005) | 0.868 (0.006) | 1.001 (0.003) | |||
| 20 | 0.966 (0.007) | 0.979 (0.006) | 1.003 (0.003) | |||
| 9 | 0 | 10 | 0.678 (0.002) | 0.696 (0.002) | 0.978 (0.003) | |
| 15 | 0.805 (0.002) | 0.873 (0.004) | 0.988 (0.002) | |||
| 20 | 0.875 (0.001) | 0.982 (0.003) | 0.995 (0.002) | |||
| 0.9 | 10 | 0.702 (0.003) | 0.696 (0.003) | 0.994 (0.003) | ||
| 15 | 0.817 (0.004) | 0.868 (0.005) | 1.009 (0.003) | |||
| 20 | 0.895 (0.004) | 0.980 (0.006) | 1.003 (0.003) | |||
| Butterfly | 3 | 0 | 10 | 0.766 (0.005) | 0.801 (0.004) | 0.996 (0.003) |
| 15 | 0.860 (0.003) | 0.921 (0.003) | 0.998 (0.002) | |||
| 20 | 0.949 (0.004) | 0.998 (0.002) | 0.999 (0.002) | |||
| 0.9 | 10 | 0.797 (0.005) | 0.799 (0.004) | 0.996 (0.003) | ||
| 15 | 0.925 (0.005) | 0.922 (0.004) | 0.998 (0.002) | |||
| 20 | 1.014 (0.006) | 0.999 (0.003) | 0.999 (0.002) | |||
| 9 | 0 | 10 | 0.766 (0.004) | 0.799 (0.003) | 0.990 (0.003) | |
| 15 | 0.861 (0.002) | 0.923 (0.003) | 1.000 (0.002) | |||
| 20 | 0.909 (0.002) | 1.000 (0.002) | 1.000 (0.002) | |||
| 0.9 | 10 | 0.811 (0.004) | 0.798 (0.004) | 0.999 (0.002) | ||
| 15 | 0.996 (0.005) | 0.922 (0.004) | 1.000 (0.002) | |||
| 20 | 0.944 (0.004) | 1.000 (0.003) | 1.000 (0.002) | |||
Fig. 3.
Estimated coefficient images under varying noise level (σ = 10, 15, 20) and number of response variables (q = 3, 9). The coefficient patterns are the same for all responses.
Similarly, Table III and Fig. 4 provide a summary of the results for the scenario (ii). Again, the proposed method clearly outperforms the two competitors. If one assumes the resulting criteria from multiple replications are normally distributed, then the two-sample t-test would yield significant differences between “Multi-Resp” and “Uni-Resp” (with p-values less than 0.001) for all combinations of (q, ρ, σ), except for (q, ρ, σ) = (2, 0, 10) (p-value = 0.61) and (q, ρ, σ) = (2, 0.9, 10) (p-value = 0.08). Moreover, differences between “Multi-Resp” and “Vectorized” are significant for all situations (p-values = 0). It is also noteworthy that, in most multi-response literatures, the models are of a similar form as in the scenario (i). This does not necessarily imply that all the multiple response variables must admit exactly the same association with the predictors. The magnitude of those coefficients could vary. In our simulation, for simplicity, we only let the signal Bj take the value of 0 or 1. The proposed method works best under the scenario (i), but outperforms the competing solutions under the scenario (ii) as well.
TABLE III.
Root Mean Squared Error of Prediction Under Varying Noise Level (σ = 10, 15, 20), Number of Response Variables (q = 2, 6), and Response Pairwise Correlation (ρ = 0, 0.9). Reported are the Mean RMSE and Standard Error (in Parenthesis) Based on 50 Data Replications
| Signals | Parameter | Root mean squared error | ||||
|---|---|---|---|---|---|---|
| q | ρ | σ | Multi-Resp | Uni-Resp | Vectorized | |
| Cross & Triangle |
2 | 0 | 10 | 0.424 (0.004) | 0.427 (0.003) | 0.999 (0.005) |
| 15 | 0.655 (0.005) | 0.711 (0.007) | 1.000 (0.005) | |||
| 20 | 0.837 (0.006) | 0.963 (0.008) | 1.002 (0.005) | |||
| 0.9 | 10 | 0.421 (0.004) | 0.431 (0.004) | 1.002 (0.005) | ||
| 15 | 0.673 (0.006) | 0.713 (0.007) | 1.005 (0.005) | |||
| 20 | 0.886 (0.009) | 0.960 (0.011) | 1.007 (0.006) | |||
| Cross & Triangle |
6 | 0 | 10 | 0.411 (0.002) | 0.429 (0.002) | 0.976 (0.004) |
| 15 | 0.682 (0.003) | 0.720 (0.004) | 0.989 (0.004) | |||
| 20 | 0.805 (0.003) | 0.967 (0.005) | 0.995 (0.003) | |||
| 0.9 | 10 | 0.450 (0.004) | 0.429 (0.004) | 0.982 (0.005) | ||
| 15 | 0.700 (0.006) | 0.777 (0.009) | 0.999 (0.005) | |||
| 20 | 0.833 (0.007) | 0.966 (0.009) | 1.009 (0.006) | |||
Fig. 4.
Estimated coefficient images under varying noise level (σ = 10, 15, 20) and number of response variables (q = 2, 6). The coefficient patterns are different for different responses. One half adopts “cross”, while the other half “triangle”.
B. Stability, Convergence and Computation Time
We next investigate the stability of the algorithm with respect to the regularization parameter λ and the rank R of the CP decomposition. We adopt the setting of scenario (i), the “triangle” signal, q = 3, σ = 10, ρ = 0 and n = 750. Fig. 5 shows the results of applying different values of λ and R. For all combinations, the method successfully identifies the signal region. However, insufficient or excessive penalty would both adversely affect the quality of the recovered signal. The rank R of the CP decomposition essentially offers a bias-variance tradeoff. A larger rank implies a more flexible model and a smaller bias, but also more unknown parameters and thus a larger variation, whereas a smaller rank implies a more parsimonious model and a smaller estimation variability, but possibly a larger bias. In reality, the true signal tensor is hardly of an exactly low-rank structure. However, given the usually limited sample size in imaging studies, a low-rank estimate often provides a reasonable approximation to the true tensor regression parameter, even when the true signal is of a high rank [26]. In our analysis, we usually fix the rank at R = 3, which offers a good balance between model complexity and estimation accuracy.
Fig. 5.
Algorithm stability with respect to the varying regularization parameter λ = 0, 10, 100 and varying rank R = 1, 2, 3.
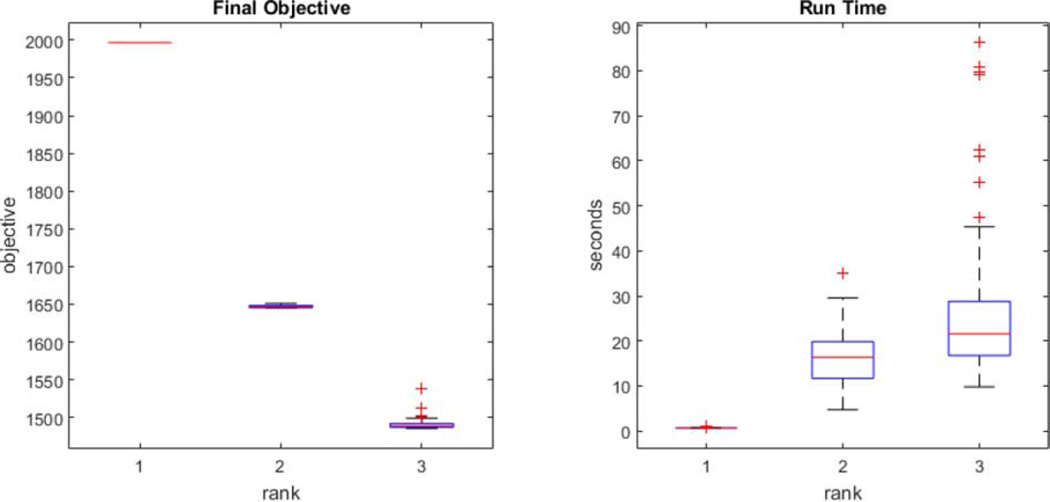
Fig. 6 shows the convergence behavior of the algorithm, as reflected by the objective value, under 100 randomly generated starting values, and the corresponding computation time. We see that, although there exist multiple local minima, the algorithm often converges to the same or similar point. The run time is recorded on a standard laptop computer with 2.9 GHz Inter i7 CPU. For instance, the median run time of fitting a rank-3 model in this example takes about 21 seconds.
Fig. 6.
Convergence behavior with 100 randomly generated starting values and the corresponding run time.
C. ADNI Data Analysis
We analyze the ADNI dataset reviewed in Section II. The analysis consists of two parts: estimation of clinical scores and identification of brain subregions that are highly relevant to the clinical outcomes.
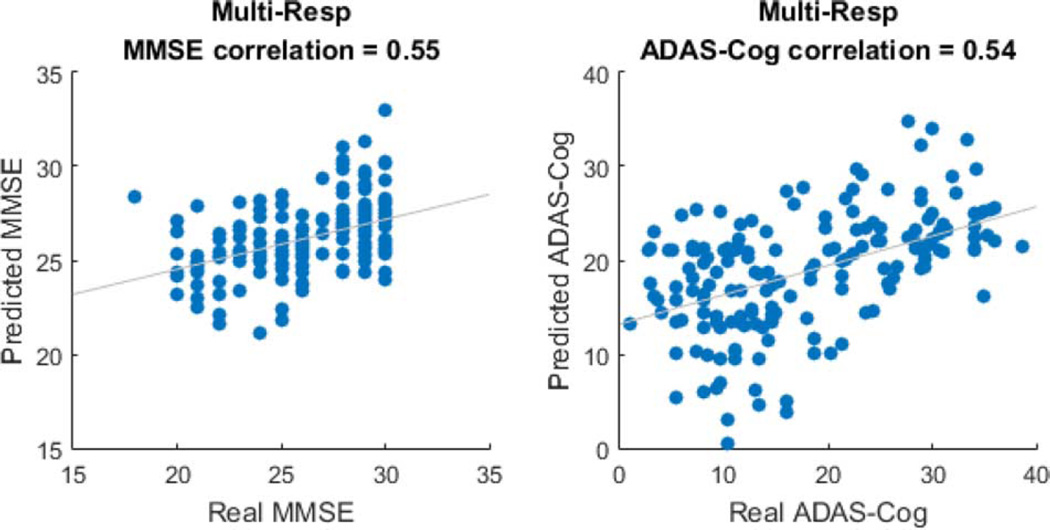
We first aim to infer the clinical scores of MMSE and ADAS-Cog given the MRI scans. Such prediction is useful for both disease diagnosis as well as understanding of disease progression. The two clinical scores are normalized (subtracted the mean and divided by standard deviation) to avoid different response scales. A 10-fold cross-validation is performed. The rank of the coefficient tensor is set as R = 3, and the regularization parameter λ is optimized based solely on the training set with another nested 10-fold cross-validation. We then employ the resulting model to estimate the clinical scores on the testing data. The RMSE (the smaller the better), and the Pearson correlation coefficient (the larger the better), between the predicted and the observed clinical scores on the testing data are reported in Table IV. Moreover, we show the scatter plots of the predicted versus observed scores for MMSE and ADAS-Cog in Fig. 7.
TABLE IV.
Estimation of the two Clinical Scores by Various Methods. Reported are the Average and Standard Error (in Parenthesis) of the Root Mean Square Error and the Pearson Correlation Coefficient Between the Predicted and the Observed Scores Based on 10-Fold Cross-Validation
| Method | Correlation coefficient | Root-mean-square error | ||
|---|---|---|---|---|
| MMSE | ADAS-Cog | MMSE | ADAS-Cog | |
| Multi-Resp | 0.55 (0.03) | 0.54 (0.04) | 2.83 (0.17) | 10.13 (0.53) |
| Uni-Resp | 0.27 (0.08) | 0.28 (0.10) | 3.18 (0.11) | 11.12 (0.57) |
| Vectorized | 0.55 (0.05) | 0.49 (0.07) | 2.83 (0.12) | 10.31 (0.57) |
| M3T | 0.56 (0.05) | 0.58 (0.06) | 2.78 (0.13) | 9.94 (0.73) |
| SVR + lasso | 0.58 (0.06) | 0.54 (0.06) | 2.73 (0.16) | 10.14 (0.68) |
| SVR | 0.42 (0.06) | 0.49 (0.06) | 3.58 (0.20) | 11.67(0.52) |
Fig. 7.
Scatter plots of the predicted MMSE and ADAS-Cog versus the observed scores.
We also compare our method (“Multi-Resp”) to two sets of alternative solutions. The first set consists of the univariate response solution (“Univ-Resp”), and the vectorized solution (“Vectorized”), as reported in Section IV-A. Both methods, as well our proposed method, directly model an image tensor and jointly incorporate all voxels of an image. The second set of alternatives include the multi-task method (“M3T”) comprised of feature selection via a group lasso penalty and estimation via support vector regression [10], support vector regression with feature selection via lasso (“SVR + lasso”), and without any feature selection (“SVR”). It is important to note that, this family of methods do not directly handle a tensor image, but a vector of features extracted from an image. As such, we employ the Automated Anatomical Labeling (AAL) [36] to partition the image into 90 regions of interest (ROI) and then use the average intensity of each ROI as the extracted features. The results are again reported in Table IV. We see that, our solution clearly outperforms the one that models one response at a time, demonstrating the advantage of jointly modeling the multivariate responses that are correlated and complementary. We also see that, after taking the standard error into account, our new method performs essentially as well as the best solutions in the literature such as “M3T” and “SVR + lasso”. On the other hand, our method works without requiring a specific image atlas, and thus avoid its dependence and the choice among different atlases.
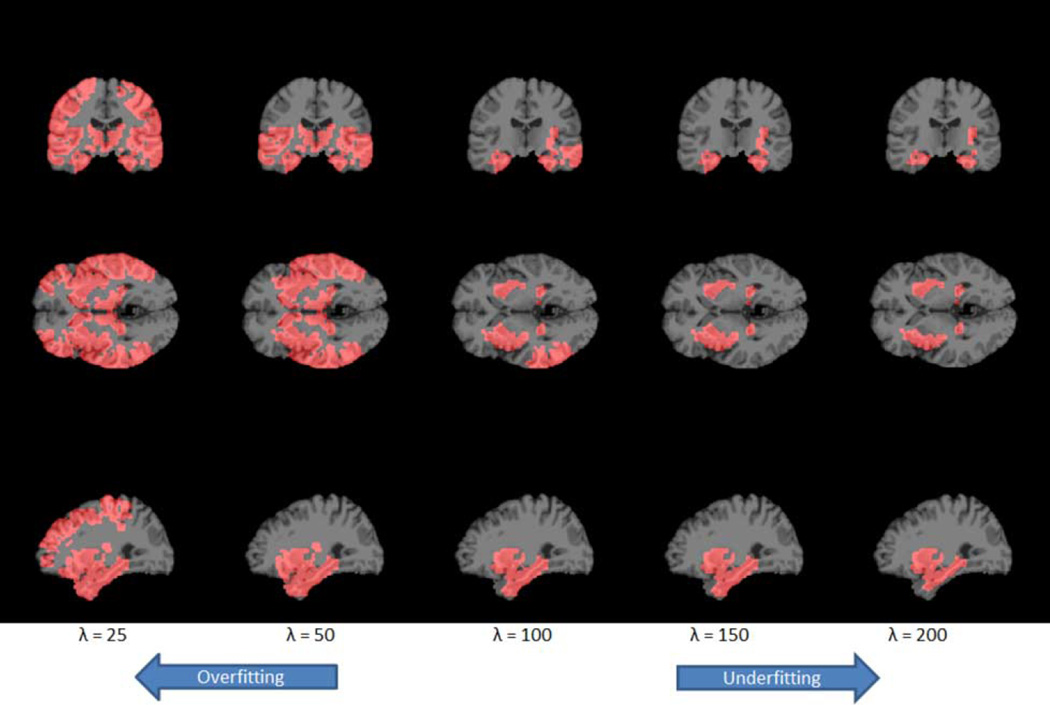
In addition to the estimation of multiple clinical scores, the proposed method can simultaneously serve as a tool to select relevant brain regions. Our multivariate method is advantageous, since different clinical scores reflect the same underlying pathology while they also offer complementary information [8], [10], [14]. For this data, we use the optimal tuning parameter from the cross-validation to fit the full dataset. The voxels selected are those with non-zero regression coefficient estimates. To help visualize the selected regions, we next partition the brain into 90 ROIs based on the AAL. Then we plot the corresponding ROIs with at least 10% of its voxels selected by our method. Ordered by the percentage of selected voxels from highest, the identified regions that are relevant to the two clinical scores are: amygdala (left and right), hippocampus (left and right), parahippocampal gyrus (right and left), olfactory cortex (left), superior temporal gyrus (left), middle temporal gyrus (left), putamen (right and left), and insula (left). These regions have been shown by numerous studies to be highly relevant to AD. See Table V for a summary of the associated literatures. Moreover, to show the path of region selection, we repeat the same procedure with a gradually increasing sparsity tuning parameter λ. We summarize the results in Fig. 8, where we map the estimate back to the original high-resolution 256 × 256 × 256 MRI image, and Table V. It is worth noting that a smaller tuning parameter would result in a larger number of selected regions and the potential problem of overfitting. Conversely, a larger tuning parameter would result in a smaller number of selected regions and potentially underfitting.
TABLE V.
AAL Regions (Colored Cells) Selected by the Sparse Multivariate Tensor Regression Model With Varying Tuning Parameters, Along With Their Support in the Literature. 13 Additional Regions Which are Only Selected When λ = 50 are not Shown Here in the Interest of Space.
| AAL Region | λ = 50 | λ = 100 | λ = 150 | λ = 200 | Literature Support |
|---|---|---|---|---|---|
| AMYGD_L | [37], [38] | ||||
| AMYGD_R | |||||
| HIPPO_L | [37], [39], [40] | ||||
| HIPPO_R | |||||
| NL_L | [41], [42] | ||||
| NL_R | |||||
| IN_L | [37], [38] | ||||
| IN_R | |||||
| PARA_HIPPO_L | [39], [43] | ||||
| PARA_HIPPO_R | |||||
| COB_L | [44] | ||||
| T1A_L | [39] | ||||
| T1A_R | |||||
| T2_L | [39] | ||||
| T2_R | |||||
Abbreviations: AMYGD = Amygdala; HIPPO = Hippocampus; NL = Lenticular Nucleus, Putamen; IN = Insula; PARA_HIPPO = Parahippocampal Gyrus; COB = Olfactory Cortex; T1A = Temporal Pole: Superior Temporal Gyrus; T2 = Middle Temporal Gyrus
Fig. 8.
Regions (red part) selected by the sparse multivariate tensor regression model that are relevant to the Alzheimer's disease. The optimal tuning parameter based on cross-validation is λ = 100.
V. Discussion
We have proposed a sparse multivariate response tensor regression model in this article. Our proposed method models multiple response variables jointly, so as to exploit the correlated and complementary information possessed in multivariate responses. It also models multiple voxels in an image tensor jointly, so as to account for inherent spatial correlation in image covariates. The method is designed to simultaneously infer multiple responses and to identify brain subregions highly relevant to the outcomes. As such it is useful for both AD/MCI diagnosis, and for locating brain regions contributing to the disease. Our numerical analyses have demonstrated that the proposed method outperformed its competitors.
There are some alternative choices within our proposed model formulation. One is to consider a different penalty function than the group lasso penalty (6), and the other is an alternative tensor regression model formulation than (3). First, an alternative to the group lasso penalty (6) for multi-response regression is the L∞ type penalty [22]. In our context, the penalty function takes the form,
| (8) |
This penalty, similar to the group lasso penalty, also induces row-wise sparsity to the regression parameters. However, it differs from the group lasso penalty in that, the L∞ penalty selects predictors based on their maximum contribution to any of the response variables, whereas the group lasso penalty selects predictors based on their joint contribution to all of the response variables. As a result, the L∞ penalty tends to select more variables than the group lasso penalty. The optimization with the L∞ penalty (8) is a linearly constrained quadratic optimization problem, which can be solved by an interior-point algorithm [45].
Second, an alternative to the multi-response tensor regression model (3) is the model
| (9) |
where B is a (D + 1)-dimensional tensor that is assumed to admit a rank-R CP decomposition, and B(D+1) denotes its mode-(D + 1) matricization. That is, B = 〚B1, …, BD+1〛 where , for d = 1, …, D, and BD+1 ∈ ℝq×R. To better understand this model, we again consider its special case when q = 2, D = 2, R = 1, i.e., two response variables with a matrix image predictor. In this case, B is a p1 × p2 × 2 tensor that admits a rank-1 decomposition, B = 〚β1, β2, β3〛 = β1 ◦ β2 ◦ β3, and β3 = [β31, β32]⊤. Then model (9) becomes
| (10) |
A few remarks are in order for the comparison of model (10) with model (4), which is a special case of model (3) under the same setup of q = 2, D = 2, R = 1. While model (4) permits different coefficient vectors β11 ⊗ β12 and β21 ⊗ β22 for different response variables Y1 and Y2, model (10) imposes the same coefficient vectors β1 ⊗ β2 except for allowing a different scalar β31 and β32 for different Y's. Consequently, model (4) enjoys more flexibility, while (10) requires fewer number of parameters and thus induces less estimation variability. For our problem, we note that, since the scores of MMSE and ADAS-Cog carry different levels of information with respect to the cognitive capability, it is more reasonable to assign different coefficients in predicting the two clinical scores. This is the reason we have primarily focused on model (3).
Finally, an alternative tensor decomposition, the Tucker decomposition [33], can be employed in our solution. The Tucker decomposition is more flexible than the CP decomposition, by allowing different number of factors along each mode of the tensor. However, it may introduce a larger number of unknown parameters than CP and require more parameter tunings. As such we have chosen the CP decomposition in this article.
Acknowledgments
Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904). This work was supported in part by the National Science Foundation under Grant AG049371, and Grant AG042599. The work of H.-I. Suk was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2015R1C1A1A01052216). The work of D. Shen was supported by the NIH under Grant EB006733, Grant EB008374, Grant EB009634, MH100217, Grant AG041721, Grant AG049371, and Grant AG042599.
ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Abbott, AstraZeneca AB, Bayer Schering Pharma AG, Bristol-Myers Squibb, Eisai Global Clinical Development, Elan Corporation, Genentech, GE Healthcare, GlaxoSmithKline, Innogenetics, Johnson and Johnson, Eli Lilly and Co., Medpace, Inc., Merck and Co., Inc., Novartis AG, Pfizer Inc, F. Hoffman-La Roche, Schering-Plough, Synarc, Inc., as well as non-profit partners the Alzheimer's Association and Alzheimer's Drug Discovery Foundation, with participation from the U.S. Food and Drug Administration. Private sector contributions to ADNI are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuron Imaging at the University of California, Los Angeles.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Zhou Li, Email: zli15@ncsu.edu, Department of Statistics, North Carolina State University, Raleigh, NC 27695 USA.
Heung-Il Suk, Email: hisuk@korea.ac.kr, Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, South Korea.
Dinggang Shen, Email: dgshen@med.unc.edu, Biomedical Research Imaging Center (BRIC) and Department of Radiology, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA, and also with the Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, South Korea.
Lexin Li, Email: lexinli@berkeley.edu, Division of Biostatistics, University of California at Berkeley, Berkeley, CA 94720 USA.
References
- 1.Brookmeyer R, Johnson E, Ziegler-Graham K, Arrighi HM. Forecasting the global burden of Alzheimer's disease. Alzheimer's Dementia. 2007;3(3):186–191. doi: 10.1016/j.jalz.2007.04.381. [DOI] [PubMed] [Google Scholar]
- 2.Petersen RC, et al. Mild cognitive impairment, clinical characterization and outcome. Arch. Neurol. 1999;56(3):303–308. doi: 10.1001/archneur.56.3.303. [DOI] [PubMed] [Google Scholar]
- 3.Fox MD, Greicius M. Clinical applications of resting state functional connectivity. Front. Syst. Neurosci. 2010;4:19. doi: 10.3389/fnsys.2010.00019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nordberg A, Rinne JO, Kadir A, Långström B. The use of PET in Alzheimer disease. Nature Rev. Neurol. 2010;6(2):78–87. doi: 10.1038/nrneurol.2009.217. [DOI] [PubMed] [Google Scholar]
- 5.Cuingnet R, et al. Automatic classification of patients with Alzheimer's disease from structural MRI: A comparison of ten methods using the ADNI database. NeuroImage. 2011;56(2):766–781. doi: 10.1016/j.neuroimage.2010.06.013. [DOI] [PubMed] [Google Scholar]
- 6.Duchesne S, Caroli A, Geroldi C, Frisoni GB, Collins DL. Medical Image Computing and Comput.-Assisted Intervention-MICCAI 2005, ser. LNCS. 3749, ch. 49. Berlin, Germany: Springer; 2005. Predicting clinical variable from MRI features: Application to MMSE in MCI; pp. 392–399. [DOI] [PubMed] [Google Scholar]
- 7.Duchesne S, Caroli A, Geroldi C, Collins DL, Frisoni GB. Relating one-year cognitive change in mild cognitive impairment to baseline MRI features. NeuroImage. 2009;47(4):1363–1370. doi: 10.1016/j.neuroimage.2009.04.023. [DOI] [PubMed] [Google Scholar]
- 8.Stonnington CM, et al. Predicting clinical scores from magnetic resonance scans in Alzheimer's disease. NeuroImage. 2010;51(4):1405–1413. doi: 10.1016/j.neuroimage.2010.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wang Y, Fan Y, Bhatt P, Davatzikos C. High-dimensional pattern regression using machine learning: From medical images to continuous clinical variables. NeuroImage. 2010;50(4):1519–1535. doi: 10.1016/j.neuroimage.2009.12.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang D, et al. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer's disease. NeuroImage. 2012;59(2):895–907. doi: 10.1016/j.neuroimage.2011.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhu X, Suk H-I, Shen D. A novel matrix-similarity based loss function for joint regression and classification in AD diagnosis. NeuroImage. 2014;100:91–105. doi: 10.1016/j.neuroimage.2014.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Folstein MF, Folstein SE, McHugh PR. Mini-mental state: A practical method for grading the cognitive state of patients for the clinician. J Psychiatric Res. 1975;12(3):189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- 13.Rosen WG, Mohs RC, Davis KL. A new rating scale for Alzheimer's disease. Am. J. Psychiatry. 1984 doi: 10.1176/ajp.141.11.1356. [DOI] [PubMed] [Google Scholar]
- 14.Fan Y, Kaufer D, Shen D. Joint estimation of multiple clinical variables of neurological diseases from imaging patterns. Proc. IEEE Int. Symp. Biomed. Imag. From Nano to Macro. 2010:852–855. [Google Scholar]
- 15.Helland IS. Partial least squares regression and statistical models. Scand. J. Stat. 1990:97–114. [Google Scholar]
- 16.Helland IS. Maximum likelihood regression on relevant components. J. R Stat. Soc B. 1992:637–647. [Google Scholar]
- 17.Chun H, Keleş S. Sparse partial least squares regression for simultaneous dimension reduction and variable selection. J. R Stat. Soc. B. 2010;72(1):3–25. doi: 10.1111/j.1467-9868.2009.00723.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou J, He X. Dimension reduction based on constrained canonical correlation and variable filtering. Ann. Stat. 2008;36:1649–1668. [Google Scholar]
- 19.Izenman AJ. Reduced-rank regression for the multivariate linear model. J Multivariate Anal. 1975;5(2):248–264. [Google Scholar]
- 20.Velu R, Reinsel GC. Multivariate Reduced-Rank Regression: Theory and Applications. Vol. 136. New York: Springer; 2013. [Google Scholar]
- 21.Yuan M, Ekici A, Lu Z, Monteiro R. Dimension reduction and coefficient estimation in multivariate linear regression. J. R Stat. Soc. B. 2007;69(3):329–346. [Google Scholar]
- 22.Turlach BA, Venables WN, Wright SJ. Simultaneous variable selection. Technometrics. 2005;47(3):349–363. [Google Scholar]
- 23.Similä T, Tikka J. Input selection and shrinkage in multiresponse linear regression. Comput. Statist. Data Anal. 2007;52(1):406–422. [Google Scholar]
- 24.Peng J, et al. Regularized multivariate regression for identifying master predictors with application to integrative genomics study of breast cancer. Ann. Appl. Stat. 2010;4(1):53. doi: 10.1214/09-AOAS271SUPP. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chen L, Huang JZ. Sparse reduced-rank regression for simultaneous dimension reduction and variable selection. J Am. Stat. Assoc. 2012;107(500):1533–1545. [Google Scholar]
- 26.Zhou H, Li L, Zhu H. Tensor regression with applications in neuroimaging data analysis. J Am. Stat. Assoc. 2013;108(502):540–552. doi: 10.1080/01621459.2013.776499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imag. 1998 Feb.17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- 28.Wang Y, et al. Knowledge-guided robust MRI brain extraction for diverse large-scale neuroimaging studies on humans and non-human primates. PLOS ONE. 2014;9(1):E77810. doi: 10.1371/journal.pone.0077810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shen D, Davatzikos C. HAMMER: Hierarchical attribute matching mechanism for elastic registration. IEEE Trans. Med. Imag. 2002 Nov.21(11):1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- 30.Davatzikos C, Genc A, Xu D, Resnick SM. Voxel-based morphometry using the RAVENS maps: Methods and validation using simulated longitudinal atrophy. NeuroImage. 2001;14(6):1361–1369. doi: 10.1006/nimg.2001.0937. [DOI] [PubMed] [Google Scholar]
- 31.Liu M, et al. Ensemble sparse classification of Alzheimer's disease. NeuroImage. 2012;60(2):1106–1116. doi: 10.1016/j.neuroimage.2012.01.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu M, Zhang D, Shen D. Hierarchical fusion of features and classifier decisions for Alzheimer's disease diagnosis. Human Brain Map. 2014;35(4):1305–1319. doi: 10.1002/hbm.22254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kolda TG, Bader BW. Tensor decompositions and applications. SIAM Rev. 2009;51(3):455–500. [Google Scholar]
- 34.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J. R Stat. Soc. B. 2006;68(1):49–67. [Google Scholar]
- 35.Rao CR, Mitra SK. Generalized Inverse of Matrices and its Applications. Vol. 7. New York: Wiley; 1971. [Google Scholar]
- 36.Tzourio-Mazoyer N, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- 37.Misra C, Fan Y, Davatzikos C. Baseline and longitudinal patterns of brain atrophy in MCI patients, and their use in prediction of short term conversion to AD: Results from ADNI. NeuroImage. 2009;44(4):1415–1422. doi: 10.1016/j.neuroimage.2008.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Karas G, et al. Global and local gray matter loss in mild cognitive impairment and Alzheimer's disease. NeuroImage. 2004;23(2):708–716. doi: 10.1016/j.neuroimage.2004.07.006. [DOI] [PubMed] [Google Scholar]
- 39.Convit A, et al. Atrophy of the medial occipitotemporal, inferior, and middle temporal gyri in non-demented elderly predict decline to Alzheimer’s disease. Neurobiol. Aging. 2000;21(1):19–26. doi: 10.1016/s0197-4580(99)00107-4. [DOI] [PubMed] [Google Scholar]
- 40.Chetelat G, et al. Mapping gray matter loss with voxel-based morphometry in mild cognitive impairment. Neuroreport. 2002;13(15):1939–1943. doi: 10.1097/00001756-200210280-00022. [DOI] [PubMed] [Google Scholar]
- 41.De Jong L, et al. Strongly reduced volumes of putamen and thalamus in Alzheimer's disease: An MRI study. Brain. 2008;131(12):3277–3285. doi: 10.1093/brain/awn278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dai Z, et al. Discriminative analysis of early Alzheimer's disease using multi-modal imaging and multi-level characterization with multi-classifier (M3) NeuroImage. 2012;59(3):2187–2195. doi: 10.1016/j.neuroimage.2011.10.003. [DOI] [PubMed] [Google Scholar]
- 43.Chetelat G, Baron J-C. Early diagnosis of Alzheimer’s disease: Contribution of structural neuroimaging. NeuroImage. 2003;18(2):525–541. doi: 10.1016/s1053-8119(02)00026-5. [DOI] [PubMed] [Google Scholar]
- 44.Devanand D, et al. Olfactory deficits in patients with mild cognitive impairment predict Alzheimer's disease at follow-up. Am. J. Psychiatry. 2000;157(9):1399–1405. doi: 10.1176/appi.ajp.157.9.1399. [DOI] [PubMed] [Google Scholar]
- 45.Friedman J, et al. Pathwise coordinate optimization. Ann. Appl. Stat. 2007;1(2):302–332. [Google Scholar]