Modeling a dynamic bi-layer contact network of injection drug users and the spread of blood-borne infections

Abstract

Injection drug users (IDUs) are at high risk of acquiring and spreading various blood-borne infections including human immunodeficiency virus (HIV), hepatitis C virus (HCV), hepatitis B virus (HBV) and a number of sexually transmitted infections. These infections can spread among IDUs via risky sexual and needle-sharing contacts. To accurately model the spread of such contagions among IDUs, we build a bi-layer network that captures both types of risky contacts. We present methodology for inferring important model parameters, such as those governing network structure and dynamics, from readily available data sources (e.g., epidemiological surveys). Such a model can be used to evaluate the efficacy of various programs that aim to combat drug addiction and contain blood-borne diseases among IDUs. The model is especially useful for evaluating interventions that exploit the structure of the contact network. To illustrate, we instantiate a network model with data collected by a needle and syringe program in Chicago. We model sexual and needle-sharing contacts and the consequent spread of HIV and HCV. We use the model to evaluate the potential effects of a peer education (PE) program under different targeting strategies. We show that a targeted PE program would avert significantly more HIV and HCV infections than an untargeted program, highlighting the importance of reaching individuals who are centrally located in contact networks when instituting prevention programs.

1. Introduction

Many injecting drug using populations experience high prevalence of communicable diseases that are spread via risky injection practices and risky sexual contacts [1, 2]. These include human immunodeficiency virus (HIV), hepatitis C virus (HCV), hepatitis B virus (HBV) and a number of sexually transmitted infections (STIs). Such diseases lead to significant morbidity and mortality – and subsequent health care costs – among injection drug users (IDUs). Controlling these diseases among IDUs is a key public health priority [3, 4].

A variety of harm reduction measures aim to limit the spread of blood-borne diseases among IDUs [5]. These measures include infection screening and treatment, needle exchange programs, opioid replacement therapy and peer education programs. However, funds for such programs are limited. Thus, it is important to evaluate the effectiveness and cost-effectiveness of these interventions so as to maximize the health impact of available resources.

Compartmental models are frequently used to evaluate the cost-effectiveness of disease control interventions (e.g., [6]). Such models divide the population into compartments corresponding to various combinations of infection status, awareness and treatment status. A key limitation of compartmental models is the assumption of homogeneous mixing, which is not likely to be the case for an IDU population [7].

Individual-based models such as network models do not require the assumption of homogeneous mixing. Such models simulate the transmission and progression of communicable diseases on an individual basis, and thus can capture features of the underlying contact network as well as biological and behavioral heterogeneity. Individual-based models are thus well suited for assessing the effects of disease control efforts that exploit the underlying contact network. For example, efforts to curb the spread of HIV by reducing risky injection practices may have the greatest impact on reducing HIV spread if they are targeted to drug injectors who are centrally located in needle-sharing networks [8, 9, 10].

However, determining the underlying contact networks in even the smallest populations can be complicated by a variety of factors. First, determination of actual network structure requires knowledge of every relationship between individuals – a time-consuming task. Second, individuals may not recall all of their contacts and, even if they do, may not want to report them. Third, relationships do not remain steady: contact networks are constantly reshaping and it is impractical to monitor their dynamics over time. For these reasons, researchers typically simulate the structure and evolution of contact networks [11, 12].

A number of network models have been introduced to model epidemics among IDUs (e.g., [13, 14, 15, 16]). For example, one study developed a model based on an empirical network of 258 IDUs in Melbourne, Australia [16]. The sample size was small due to the difficulty in contact tracing. The authors employed a static network, and thus only reported numerical results over one simulated year. These and other published network models of IDU populations consider only needle-sharing as the route of disease transmission, and do not consider sexual transmission of disease. However, sexual transmission of diseases among IDUs may be significant, so existing models may inaccurately estimate the effects of programs that aim to control blood-borne disease among IDUs.

In this paper we introduce a bi-layer network model that captures both sexual and needle-sharing contacts (Figure 1). We present methodology for inferring important parameters, such as those governing network structure and dynamics, from readily available data. Using this model, we can simulate the spread of one or more diseases among IDUs and evaluate the efficacy of different drug abuse and disease control interventions. We provide an illustrative example of HIV and HCV transmission among IDUs in a representative US urban center, and we estimate the relative effectiveness of peer education programs under different targeting strategies.

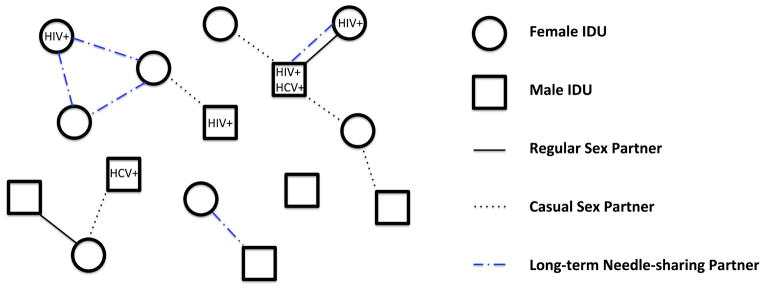
Figure 1.

Model schematic. We consider a population of male and female IDUs. At each time step t = 1, 2, … individuals can join or leave the population through initiating or abstaining from injection drug use. Each IDU can be associated with a number of characteristics including gender, age, disease status, disease awareness and treatment status, and drug abuse treatment status. We consider heterosexual and needle-sharing relationships, and one or more diseases (e.g., HIV, HCV) being spread via risky sexual and/or needle-sharing contacts. We distinguish two types of sexual partnerships: regular and casual partnerships. We distinguish two types of needle-sharing relationships: long-term needle-sharing and one-time needle-sharing (not represented in the risk network). We allow relationships to dissolve and form dynamically; thus the disease(s) can spread to any individuals who ever engage in risky behaviors.

2. Methods

Our objective is to generate networks that capture important properties of real IDU networks. IDU behavioral surveillance systems often collect data on the total number of IDUs in a respondent’s social network, whether the respondent shares needles with each of these individuals and, if so, at what frequency. From this data, one can infer a population-level degree distribution describing the proportion of individuals who have 0, 1, 2, or more needle-sharing partners during the survey period. Higher-order network features are usually not inferable from the data gathered by such surveys. Take clustering coefficient as an example: to compute this value for a needle-sharing network, each respondent has to identify the number of needle-sharing partnerships among his/her needle-sharing partners, yet many respondents may not possess such information. To avoid the difficulty in obtaining certain data, we create a needle-sharing network (and similarly a sexual contact network) that matches the empirical degree distributions of needle-sharing partnerships, while imposing no requirements on their higher-order properties.

Sexual partnerships may vary in many respects, such as duration, frequency, commercial or not, vaginal or anal, and consistency of condom use. Therefore it is reasonable to divide partnerships into subtypes based on differential characteristics. Here, we distinguish between regular versus casual sexual partnerships. A regular sex partner is defined as an individual’s main partner (spouse or girlfriend/boyfriend) with whom one has sex at regular intervals. We assume that individuals can have at most one regular sex partner at any point in time. Casual sex partners are those who fall outside the definition of regular partner, with whom one has casual sex (possibly more than once).

Similarly, we distinguish two types of needle-sharing partnerships: long-term and one-time sharing. The term ‘long-term sharing’ describes sharing needles on a regular basis; such sharing typically occurs between friends, family and sex partners. ‘One-time sharing’ is non-repeating and is not restricted to intimate relationships.

Sex partners may share needles; thus the sexual contact network and needle-sharing network in our model are not independent. Many studies suggest that a significant proportion of regular sex partners are also injecting partners, due in part to greater trust and lower perceived risks of infection [9, 17, 18, 19]. To incorporate this correlation in our model, we further divide long-term needle-sharing relationships into two classes: sharing between regular sex partners and between other social dyads (e.g., casual partners, friends and family). We will use the term ‘steady needle-sharing partnership’ to refer to a long-term sharing relationship between other social dyads exclusively.

Sexual and needle-sharing relationships may form and dissolve over time. To capture these dynamics we need to determine appropriate rules for updating the network at every time step. We assume that the degree distributions of the sexual contact network and needle-sharing network remain steady over time, and we model the number of sexual/needle-sharing partners of each IDU with a Markov chain whose steady state distribution corresponds to the degree distribution of sexual/needle-sharing network. As described in Section 2.1 and 2.2, we infer the values of transition probabilities of the Markov chains using a quadratic optimization approach. Specifically, we assume that the most likely values of the parameters are those that maintain a dynamic network whose degree structure best matches empirically observed degree distributions.

Notation

We represent the IDU sexual contact network as a graph 𝒮 = (V, E_S), where the vertices in V represent IDUs and the edges in E_S represent sexual partnerships. E_S comprises two subsets since we have defined two mutually exclusive types of edges, i.e. $E_S=E_{\text{regular}}^S\cup E_{\text{casual}}^S$. Upon initialization of the network, V consists of N_m male and N_f female vertices. At each time step t = 1, 2, …, new vertices are added to V as individuals initiate drug injection. We denote by r_m and r_f the rates of men and women entering the population, respectively. Similarly, vertices are deleted from V when individuals stop injection behaviors as a result of either death or abstention.

Each vertex is described by a set of attributes. These could include, for example, age, gender, disease state (e.g., HIV positive/negative) and treatment status (e.g., receiving antiretroviral therapy (ART), receiving opiate replacement therapy (ORT)). At time t = 0, age and gender can be randomly generated to match demographic data of the IDU population, and number infected to match disease prevalence in IDUs. New individuals entering the population are assigned a gender drawn from the same demographic data, age from the distribution of initiating age, and disease state from the disease prevalence in the population.

Similarly, we represent the needle-sharing network as a graph 𝒩 = (V, E_N), with $E_N=E_{\text{regular}}^N\cup E_{\text{steady}}^N$. Note that we do not include one-time needle-sharing relationships in E_N. Instead we examine one-time sharing events in the disease transmission model, as described below in Section 2.3. This is because one-time sharing relationships form and then immediately dissolve; inclusion of these relationships would add needless complexity to the network model.

By definition, $E_{\text{regular}}^N\subset E_{\text{regular}}^S$. Letting γ denote the proportion of IDUs who share needles with their regular sex partner, we have $\mid E_{\text{regular}}^N\mid =\gamma \mid E_{\text{regular}}^S\mid$ in expectation. We refer to 𝒮 ∪ 𝒩 as the risk network because all edges in this network are associated with potential risk of infection transmission.

2.1. Modeling the sexual contact network 𝒮

Network initialization

We consider sexual disease spread via heterosexual contacts. We denote the overall partnership distributions of men and women, respectively, by m(p) and f(p) (p = 0, …, L where L is the maximum number of sex partners any individual can have at the same time). Since the network is comprised solely of IDUs, the distributions m(p) and f(p) reflect only the number of an IDU’s sex partners who are involved in injection drug use. We do not include an incidence rate to reflect the probability of an IDU being infected by his/her non- IDU sex partners, for two reasons. First, studies show a high level of preferential sexual mixing of IDUs with other IDUs [20, 21, 22, 23]. Second, the prevalence of diseases such as HIV and HCV in non-IDUs is relatively low, implying that the dominant mode of disease transmission is from IDUs to non-IDUs rather than the other way around.

At time t = 0, the overall number of partners men have must equal the overall number of partners women have; that is

$$N_m\sum _{p=0}^{L}pm(p)=N_f\sum _{p=0}^{L}pf(p)$$ (1)

This constraint is not always satisfied by reported values of m(p) and f(p), for a variety of reasons such as recall error, underrepresentation of sex workers, and sample bias [24, 25]. In our analysis we adjust N_f so as to maintain the reported gender differences in concurrent behaviors.

Since we distinguish between regular and casual sex partners, knowledge of the joint distribution over these two types of partnerships is required. We denote the joint distribution by π_m(k₁, k₂) = π_m(k) and π_f(k₁, k₂) = π_f(k), where k₁ and k₂ denote the number of regular and casual sexual partnerships, respectively, and k is the vector (k₁, k₂). To be consistent with the overall partnership distribution, the distributions π_m and π_f must satisfy

$$\sum _{\mathbf{k}\in \{{\mathbf{k}}^{\prime }\mid k_1^{\prime }+k_2^{\prime }=p\}}{\pi }_m(\mathbf{k})=m(p),\text{for}p=0,\dots ,L$$ (2)

$$\sum _{\mathbf{k}\in \{{\mathbf{k}}^{\prime }\mid k_1^{\prime }+k_2^{\prime }=p\}}{\pi }_f(\mathbf{k})=f(p),\text{for}p=0,\dots ,L$$ (3)

Suppose that the proportion of male and female IDUs having a regular sex partner is known, denoted by s_m and s_f, respectively. Then a second constraint for π_m and π_f is

$$\sum _{k_2=0}^{L-1}{\pi }_m(1,k_2)=s_m$$ (4)

$$\sum _{k_2=0}^{L-1}{\pi }_f(1,k_2)=s_f$$ (5)

The total number of men involved in regular sexual partnerships should equal that of women. Thus s_m and s_f should satisfy,

$$N_m{s}_m=N_f{s}_f$$ (6)

If the above constraint is not met by the reported values of s_m and s_f, then we adjust the value of s_f accordingly.

There are 2L variables in Eq.2 and 4 (Eq.3 and 5). Hence we need additional constraints in order to obtain a unique solution for π_m (π_f). We assume that having a regular sex partner does not affect one’s concurrent partnership behavior; that is

$${\pi }_m(0,k_2)=C{\pi }_m(1,k_2-1),\text{for}{k}_2=1,\dots ,L$$ (7)

$${\pi }_f(0,k_2)=C^{\prime }{\pi }_f(1,k_2-1),\text{for}{k}_2=1,\dots ,L$$ (8)

where C and C′ are constants. This assumption can be easily relaxed if additional information on concurrent partnership behavior is available. Solving Eq.2, 4 and 7 (Eq.3, 5 and 8) yields the desired distribution π_m (π_f).

To initialize the sexual contact network, each IDU is randomly assigned a vector (k₁, k₂), with values for (k₁, k₂) drawn from the empirical partnership distribution π_m (π_f). Next we randomly pair up men and women seeking the same type of partners. In cases of individuals being matched to the same partner more than once, the duplicate partnership is exchanged with another randomly chosen partnership until no duplication remains.

Network dynamics

The sexual contact network evolves as old partnerships dissolve and new partnerships form. We assume that in this evolution the joint partnership distribution is steady over time; that is, we assume that the distributions π_m and π_f we deduced from survey data (a snapshot of the network degree distribution over the survey period) approximate the true degree distribution throughout the time horizon of the simulation.

Using an approach similar to that of Enns et al. [26] (who considered only the sexual contact network), we model the degree of each individual as a Markov chain. Then π_m (π_f) is the stationary distribution of male (female) IDUs. We need to find a transition matrix P_m (P_f) that satisfies the steady-state equations:

$$\sum _{\mathbf{k}\in \mathrm{\Omega }}{P}_{\mathbf{k}\to {\mathbf{k}}^{\prime }}^m{\pi }_m(\mathbf{k})={\pi }_m({\mathbf{k}}^{\prime }),\forall {\mathbf{k}}^{\prime }\in \mathrm{\Omega }$$ (9)

$$\sum _{\mathbf{k}\in \mathrm{\Omega }}{P}_{\mathbf{k}\to {\mathbf{k}}^{\prime }}^f{\pi }_f(\mathbf{k})={\pi }_f({\mathbf{k}}^{\prime }),\forall {\mathbf{k}}^{\prime }\in \mathrm{\Omega }$$ (10)

where Ω denotes the state space, i.e. the set of all possible partnership combinations. We modify the above equations to account for entry of new IDUs into the population, assuming that individuals have no IDU sex partners when they become IDUs. The adjusted steady-state equations are

$$\frac{1}{1+r_m}\sum _{\mathbf{k}\in \mathrm{\Omega }}{P}_{\mathbf{k}\to {\mathbf{k}}^{\prime }}^m{\pi }_m(\mathbf{k})+\frac{r_m}{1+r_m}{\delta }_{{\mathbf{k}}^{\prime }}={\pi }_m({\mathbf{k}}^{\prime }),\forall {\mathbf{k}}^{\prime }\in \mathrm{\Omega }$$ (11)

$$\frac{1}{1+r_f}\sum _{\mathbf{k}\in \mathrm{\Omega }}{P}_{\mathbf{k}\to {\mathbf{k}}^{\prime }}^f{\pi }_f(\mathbf{k})+\frac{r_f}{1+r_f}{\delta }_{{\mathbf{k}}^{\prime }}={\pi }_f({\mathbf{k}}^{\prime }),\forall {\mathbf{k}}^{\prime }\in \mathrm{\Omega }$$ (12)

where δ_k = 1 if k = (0, 0) and δ_k = 0 otherwise.

We now consider the effect on the network degree distribution of individuals leaving the population. We assume that each IDU is equally likely to abstain from injecting drugs at each time step; hence every partnership state is affected by the same rate of individuals quitting drug use and no differential flows arise. Mortality also leads to exit from the population, yet its rate depends on age, gender, and disease and treatment state, so it is impossible to write down an explicit formula for the aggregated mortality rate of any state in the Markov chain. We make the simplifying assumption that the effect of mortality is minimal and thus can be neglected when solving the above equations.

We decompose each entry in the transition matrix, expressing the entries as

$$\begin{array}{l}{P}_m((k_1,k_2)\to (k_1^{\prime },k_2^{\prime }))={\mathbb{P}}_m(k_1^{\prime },k_2^{\prime }\mid k_1,k_2)\\ ={\mathbb{P}}_m(k_1^{\prime }\mid k_1,k_2){\mathbb{P}}_m(k_2^{\prime }\mid k_1,k_2,k_1^{\prime })\end{array}$$ (13)

$$\begin{array}{l}{P}_f((k_1,k_2)\to (k_1^{\prime },k_2^{\prime }))={\mathbb{P}}_f(k_1^{\prime },k_2^{\prime }\mid k_1,k_2)\\ ={\mathbb{P}}_f(k_1^{\prime }\mid k_1,k_2){\mathbb{P}}_f(k_2^{\prime }\mid k_1,k_2,k_1^{\prime })\end{array}$$ (14)

where ℙ_m and ℙ_f are conditional probabilities.

We simulate partnership dissolution with a constant hazard model, where each regular (casual) sexual partnership is dissolved at a constant rate σ_r (σ_c) per incremental time step. The value of σ_r (σ_c) is chosen so that 1/σ_r (1/σ_c) matches the average duration of regular (casual) sexual partnerships. We assume that in a single time step neither of the following two situations can occur: loss and gain of the same type of partnership; gain of more than one of the same type of partnership. Then we have the probabilities below, given by a binomial probability mass function:

$${\mathbb{P}}_m(k_1^{\prime }=0\mid k_1=1,k_2)={\mathbb{P}}_f(k_1^{\prime }=0\mid k_1=1,k_2)={\sigma }_r,\text{for}{k}_2=0,\dots ,L-1$$ (15)

$${\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=1,k_2)={\mathbb{P}}_f(k_1^{\prime }=1\mid k_1=1,k_2)=1-{\sigma }_r,\text{for}{k}_2=0,\dots ,L-1$$ (16)

$${\mathbb{P}}_m(k_2^{\prime }=k_2-i\mid k_1,k_2,k_1^{\prime })={\mathbb{P}}_f(k_2^{\prime }=k_2-i\mid k_1,k_2,k_1^{\prime })=\left(\begin{array}{c}{k}_2\\ i\end{array}\right){\sigma }_c^i{(1-{\sigma }_c)}^{k_2-i},\text{for}i=1,\dots ,k_2$$ (17)

$$\begin{array}{l}{\mathbb{P}}_m(k_2^{\prime }=k_2\mid k_1,k_2,k_1^{\prime })+{\mathbb{P}}_m(k_2^{\prime }=k_2+1\mid k_1,k_2,k_1^{\prime })={\mathbb{P}}_f(k_2^{\prime }=k_2\mid k_1,k_2,k_1^{\prime })+{\mathbb{P}}_f(k_2^{\prime }=k_2+1\mid k_1,k_2,k_1^{\prime })\\ ={(1-{\sigma }_c)}^{k_2},\text{for}\mathbf{k}\in \{\mathbf{k}\mid k_1+k_2<L\}\end{array}$$ (18)

Eq.18 requires the probability of retaining the same number of casual sexual partners or gaining one more casual sexual partner to be (1 − σ_c)^k₂, which is the probability that none of the current k₂ casual sexual partnerships dissolve.

For simplicity, we assume that the probability of gaining a regular sexual partnership is independent of the number of casual sexual partnerships that an individual currently has. That is,

$${\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0,k_2)={\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0)$$ (19)

$${\mathbb{P}}_f(k_1^{\prime }=1\mid k_1=0,k_2)={\mathbb{P}}_f(k_1^{\prime }=1\mid k_1=0)$$ (20)

Now that the transition probability of k₁ is independent of k₂ and $k_2^{\prime }$, the marginal transition matrix of k₁ must satisfy the following constraint so as to maintain the marginal degree distribution of k₁,

$$\frac{1}{1+r_m}\left[\begin{array}{cc}1-s_m& s_m\end{array}\right]P_m^{k_1}+\frac{r_m}{1+r_m}\left[\begin{array}{cc}1& 0\end{array}\right]=\left[\begin{array}{cc}1-s_m& s_m\end{array}\right]$$ (21)

where $P_m^{k_1}$ is the transition matrix of k₁, and

$$P_m^{k_1}=\left[\begin{array}{cc}1-{\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0)& {\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0)\\ {\sigma }_r& 1-{\sigma }_r\end{array}\right]$$ (22)

With ${\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0)$ being the only unknown variable, Eq.21 can be readily solved, yielding

$${\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0)=\frac{({\sigma }_r+r_m)s_m}{1-s_m}$$ (23)

Similarly,

$${\mathbb{P}}_f(k_1^{\prime }=1\mid k_1=0)=\frac{({\sigma }_r+r_f)s_f}{1-s_f}$$ (24)

At time t, the total number of regular sex partners of males in the population must equal that of females. Neglecting exit out of the population we have

$$N_m{(1+r_m)}^t{s}_m=N_f{(1+r_f)}^t{s}_f$$ (25)

which requires

$$r_m=r_f$$ (26)

We denote by β_m and β_f the only unknown probabilities,

$$\begin{array}{l}{\beta }_m(k_1,k_2,k_1^{\prime })\triangleq {\mathbb{P}}_m(k_2^{\prime }=k_2+1\mid k_1,k_2,k_1^{\prime })\\ {\beta }_f(k_1,k_2,k_1^{\prime })\triangleq {\mathbb{P}}_f(k_2^{\prime }=k_2+1\mid k_1,k_2,k_1^{\prime })\end{array}$$

We need to find the values of β_m and β_f in order to calculate P_m (P_f). We do so by solving the following optimization problem, P:

$$\begin{array}{ll}\underset{{\beta }_m,{\beta }_f}{\text{minimize}}\hfill & {\Vert {\mu }_m-{\pi }_m\Vert }_2^2+{\Vert {\mu }_f-{\pi }_f\Vert }_2^2\hfill \\ \text{subject}\text{to}\hfill & {\mu }_m=\frac{{\pi }_m{P}_m}{1+r_m}+\frac{r_m{e}_1}{1+r_m}\hfill \end{array}$$ (27)

$${\mu }_f=\frac{{\pi }_f{P}_f}{1+r_f}+\frac{r_f{e}_1}{1+r_f}$$ (28)

$$P_m((k_1,k_2)\to (k_1^{\prime },k_2^{\prime }))={\mathbb{P}}_m(k_1^{\prime }\mid k_1){\mathbb{P}}_m(k_2^{\prime }\mid k_1,k_2,k_1^{\prime })$$ (29)

$$P_f((k_1,k_2)\to (k_1^{\prime },k_2^{\prime }))={\mathbb{P}}_f(k_1^{\prime }\mid k_1){\mathbb{P}}_f(k_2^{\prime }\mid k_1,k_2,k_1^{\prime })$$ (30)

$${\mathbb{P}}_m(k_1^{\prime }\mid k_1)=\left[\begin{array}{cc}1-\frac{({\sigma }_r+r_m)s_m}{1-s_m}& \frac{({\sigma }_r+r_m)s_m}{1-s_m}\\ {\sigma }_r& 1-{\sigma }_r\end{array}\right]$$ (31)

$${\mathbb{P}}_f(k_1^{\prime }\mid k_1)=\left[\begin{array}{cc}1-\frac{({\sigma }_r+r_f)s_f}{1-s_f}& \frac{({\sigma }_r+r_f)s_f}{1-s_f}\\ {\sigma }_r& 1-{\sigma }_r\end{array}\right]$$ (32)

$$\begin{array}{l}{\mathbb{P}}_m(k_2^{\prime }=k_2-i\mid k_1,k_2,k_1^{\prime })={\mathbb{P}}_f(k_2^{\prime }=k_2-i\mid k_1,k_2,k_1^{\prime })\\ =\left(\begin{array}{c}{k}_2\\ i\end{array}\right){\sigma }_c^i{(1-{\sigma }_c)}^{k_2-i},\text{for}i=1,\dots ,k_2\end{array}$$ (33)

$${\mathbb{P}}_m(k_2^{\prime }=k_2\mid k_1,k_2,k_1^{\prime })={(1-{\sigma }_c)}^{k_2}-{\beta }_m(k_1,k_2,k_1^{\prime })$$ (34)

$${\mathbb{P}}_f(k_2^{\prime }=k_2\mid k_1,k_2,k_1^{\prime })={(1-{\sigma }_c)}^{k_2}-{\beta }_f(k_1,k_2,k_1^{\prime })$$ (35)

$$0\le {\beta }_m\le 1$$ (36)

$$0\le {\beta }_f\le 1$$ (37)

$$N_m\sum _{\mathbf{k}\in \{\mathbf{k}\mid (k_1,k_2+1)\in \mathrm{\Omega }\}}{\pi }_m(\mathbf{k})P_m(\mathbf{k}\to (k_1,k_2+1))=N_f\sum _{\mathbf{k}\in \{\mathbf{k}\mid (k_1,k_2+1)\in \mathrm{\Omega }\}}{\pi }_f(\mathbf{k})P_f(\mathbf{k}\to (k_1,k_2+1))$$ (38)

where e₁ is the unit vector with the first coordinate being 1. The objective is to minimize the mean squared error between the stationary distribution and the achieved distribution after one time step. Eq.38 requires that the overall number of new casual sexual partnerships gained by men equals that of women in expectation.

P is a convex optimization problem and can easily be solved via optimization software such as CVX [27]. Convexity is guaranteed because the objective function is quadratic in the optimization variables, and the constraints are linear.

Simulation

We now describe how sexual partnerships evolve in the simulation of the IDU population. At each time step, we first independently dissolve sexual partnerships according to their type-specific dissolution rates. We denote an intermediate degree by k̃.

Then for each male (female) node with $k_1(t)=\stackrel{\sim }{k_1}(t)=0$, we generate a Bernoulli random variable with success rate $\frac{({\sigma }_r+r_m)s_m}{1-s_m}(\frac{({\sigma }_r+r_f)s_f}{1-s_f})$. If the trial succeeds then that node gains a new regular sexual partnership (i.e., k₁(t + 1) = 1). We randomly pair up men and women who are to gain new regular sex partners at time t. If the two pools are of different sizes, we repeat the above procedure until no discrepancy remains.

We carry out a similar procedure for the evolution of casual sexual partnerships. For each male (female) node with $k_2(t)=\stackrel{\sim }{k_2}(t)<L$, we generate a Bernoulli random variable with success probability ${\beta }_m(k_1,k_2,\stackrel{\sim }{k_1})({\beta }_f(k_1,k_2,\stackrel{\sim }{k_1}))$. A successful trial indicates that the node gains a new casual sexual partnership (i.e., k₂(t + 1) = k₂(t) + 1). We randomly pair up men and women who are to gain new casual sex partners, being careful not to duplicate existing partnerships. If the two pools are of different sizes, we repeat the above procedure until no discrepancy remains.

2.2. Modeling the needle-sharing network 𝒩

Network initialization

We denote by n(p) the distribution of total needle-sharing relationships (p = 0, …, M where M is the maximum number of allowable concurrent needle-sharing partners). Many surveys on needle-sharing patterns provide such information [28, 29].

We need to derive the joint degree distribution of sharing with a regular sex partner and a steady needle-sharing partner. We denote the joint distribution by π_n(j₁, j₂) = π_n(j), where j₁ is the number of regular sex partners an individual shares needles with, and j₂ the total number of steady needle-sharing partners. The marginal distribution of j₁ is determined by s_m, s_f and γ:

$$\mathbb{P}(j_1=1)=\frac{\gamma (N_m{s}_m+N_f{s}_f)}{N_m+N_f}$$ (39)

Similar to the way we derived π_m in the previous subsection, we assume that no difference in concurrent needle-sharing patterns exists between IDUs with j₁ = 1 and IDUs with j₁ = 0. Then π_n is the solution to the following equations,

$$\sum _{\mathbf{j}\in \{{\mathbf{j}}^{\prime }\mid j_1^{\prime }+j_2^{\prime }=p\}}{\pi }_n(\mathbf{j})=n(p),\text{for}p=0,\dots ,M$$ (40)

$$\sum _{j_2=0}^{M-1}{\pi }_n(1,j_2)=\mathbb{P}(j_1=1)$$ (41)

$${\pi }_n(0,j_2)=C^{″}{\pi }_n(1,j_2-1),\text{for}{j}_2=1,\dots ,M$$ (42)

where C″ is a constant.

After initialization of the sexual contact network 𝒮, we determine, with probability γ, for each regular sexual partnership whether it involves needle-sharing behavior. We then assign each IDU with a value of j₂ according to the conditional distribution of j₂ given j₁, which can be calculated from the joint distribution π(n) and the marginal distribution of j₁. We randomly pair up IDUs seeking needle-sharing partners, again being careful to avoid duplicate edges.

Network dynamics

Unlike the sexual contact network, where an edge links two nodes of opposite sex, needle-sharing relationships can be between any IDUs in the network. Once again we search for a transition matrix P_n that satisfies the steady-state equations,

$$\frac{1}{1+r_m}\sum _{\mathbf{j}\in \mathrm{\Phi }}{P}_{\mathbf{j}\to {\mathbf{j}}^{\prime }}^n{\pi }_n(\mathbf{j})+\frac{r_m}{1+r_m}{\delta }_{{\mathbf{j}}^{\prime }}={\pi }_n({\mathbf{j}}^{\prime }),\forall {\mathbf{j}}^{\prime }\in \mathrm{\Phi }$$ (43)

where Φ denotes the state space, i.e. the set of all possible needle-sharing relationship combinations, and δ_j = 1 if j = (0, 0) and δ_j = 0 otherwise. Similar to our approach for the sexual contact network, we write each transition probability as the product of two conditional probabilities,

$$\begin{array}{l}{P}_n((j_1,j_2)\to (j_1^{\prime },j_2^{\prime }))={\mathbb{P}}_n(j_1^{\prime },j_2^{\prime }\mid j_1,j_2)\\ ={\mathbb{P}}_n(j_1^{\prime }\mid j_1,j_2){\mathbb{P}}_n(j_2^{\prime }\mid j_1,j_2,j_1^{\prime })\end{array}$$ (44)

We assume that long-term needle-sharing relationships with regular sex partners dissolve if and only if the corresponding regular sexual partnerships dissolve; and such relationships form with probability γ if new regular sexual partnerships form. Hence $j_1^{\prime }$ is determined by j₁, k₁ and $k_1^{\prime }$, and is independent of j₂. The marginal transition matrix of j₁, denoted as $P_n^{j_1}$, can be deduced from $P_m^{k_1}$,

$$P_n^{j_1}=\left[\begin{array}{cc}1-{\mathbb{P}}_n(j_1^{\prime }=1\mid j_1=0)& {\mathbb{P}}_n(j_1^{\prime }=1\mid j_1=0)\\ {\sigma }_r& 1-{\sigma }_r\end{array}\right]$$ (45)

$${\mathbb{P}}_n(j_1^{\prime }=1\mid j_1=0)=\frac{2N_m(1-s_m){\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0)\gamma }{N_m+N_f-2N_m{s}_m\gamma }$$ (46)

The dissolution rate of steady needle-sharing partnerships is σ_n. We assume that each IDU gains at most one new needle-sharing partner within a single time step. However, ${\mathbb{P}}_n(j_2^{\prime }=j_2-i\mid j_1,j_2,j_1^{\prime })$ no longer follows a binomial distribution. This is due to the random effect that dissolution of needle-sharing partnerships exerts on degree distribution. Thus we must calculate ${\mathbb{P}}_n(j_2^{\prime }=j_2-i\mid j_1,j_2,j_1^{\prime })$ at each time step.

We denote the only unknown probabilities as β_n,

$${\beta }_n(j_1,j_2,j_1^{\prime })\triangleq {\mathbb{P}}_n(j_2^{\prime }=j_2+1\mid j_1,j_2,j_1^{\prime })$$

We find their values by solving the following convex optimization problem, Q:

$$\begin{array}{ll}\underset{{\beta }_n}{\text{minimize}}\hfill & {\Vert \frac{{\pi }_n{P}_n}{1+r_m}+\frac{r_m{e}_1}{1+r_m}-{\pi }_n\Vert }_2^2\hfill \\ \text{subject}\text{to}\hfill & P_n((j_1,j_2)\to (j_1^{\prime },j_2^{\prime }))={\mathbb{P}}_n(j_1^{\prime }\mid j_1){\mathbb{P}}_n(j_2^{\prime }\mid j_1,j_2,j_1^{\prime })\hfill \end{array}$$ (47)

$${\mathbb{P}}_n(j_1^{\prime }\mid j_1)=\left[\begin{array}{cc}1-{\mathbb{P}}_n(j_1^{\prime }=1\mid j_1=0)& {\mathbb{P}}_n(j_1^{\prime }=1\mid j_1=0)\\ {\sigma }_r& 1-{\sigma }_r\end{array}\right]$$ (48)

$${\mathbb{P}}_n(j_1^{\prime }=1\mid j_1=0)=\frac{2N_m(1-s_m){\mathbb{P}}_m(k_1^{\prime }=1\mid k_1=0)\gamma }{N_m+N_f-2N_m{s}_m\gamma }$$ (49)

$$\sum _{i=0}^M{\mathbb{P}}_n(j_2^{\prime }=i\mid j_1,j_2,j_1^{\prime })=1$$ (50)

$$0\le {\beta }_n\le 1$$ (51)

Simulation

We now describe how needle-sharing partnerships evolve in the simulation of the IDU population. At each time step, we first dissolve needle-sharing relationships with regular sex partners if the corresponding regular sexual partnership dissolves, and we form needle-sharing relationships with regular sex partners if the corresponding regular sexual partnership forms and a Bernoulli (γ) random trial succeeds. We then dissolve steady needle-sharing partnerships according to σ_n, and calculate the conditional probabilities ${\mathbb{P}}_n(j_2^{\prime }=j_2-i\mid j_1,j_2,j_1)$ by solving Q. For nodes with no steady needle-sharing partnership dissolved, we simulate the gain of a partner with a Bernoulli ( ${\mathbb{P}}_n(j_2^{\prime }=j_2+1\mid j_1,j_2,j_1^{\prime })$) random variable. We randomly pair up IDUs seeking new needle-sharing partners, avoiding duplicate edges. If an odd number of IDUs require new needle-sharing partners, we regenerate the pool until the total number is even.

2.3. Modeling disease transmission and progression

At each time step t, an edge in the contact network is associated with a probability of infection transmission, contingent on various factors, such as the type of pathogen, the type and frequency of risky contacts, infectivity of the host partner, vulnerability of the susceptible partner, and protective measures taken. Then for every susceptible node, we can compute a risk of infection acquisition as a function of the transmission probabilities of its edges, and simulate its contraction of infectious disease(s) according to the risk(s).

As mentioned above, we do not represent one-time sharing relationships in the risk network. Instead, we model one-time sharing events at each time step. We assume that IDU i has a probability λ_i of participating in one-time needle sharing. This probability can vary over time, and can be modeled as a function of injections per day, fraction of injections shared with strangers, access to clean needles, and so on. We sample according to the probability λ_i to determine whether IDU i engages in one-time sharing at time t, then we randomly pair up those IDUs who do, and obtain a temporary edge list E_O.

As for disease progression, individuals can progress through multiple disease stages, and at different rates, depending on their infection status (for example, mono or co-infected, under treatment or not) and individual characteristics (for example, responsive to treatment or not). Because network-based models allow one to simulate the trajectory of each individual separately, an essentially unlimited set of stochastic elements can be included in the model. In the illustrative example presented in Section 3, we examine the impact of a peer education program on averting new HIV and HCV infections in an IDU population; thus we develop a disease model that incorporates key elements relevant to those diseases (e.g., disease progression rates, proportion of treatment-eligible IDUs receiving treatment, mean time to treatment, responsiveness to treatment).

2.4. Model calibration

We verify model validity by calibration to empirical data. The general procedure is to first select target variables (e.g., disease prevalence and incidence, population growth), and then adjust input parameters so that model projections match the targets [30]. In our example below, the two model components –a network model that captures the potential routes of infection and a disease model that governs disease transmission and progression – interact with each other and cannot be disentangled when assigning credit to the resulting epidemics. For the example analysis, we take a simple yet intuitive approach which adjusts model parameters to yield disease prevalence trends that match observed trends.

3. Illustrative Example

3.1. Model instantiation

We instantiated the model for the case of HIV and HCV spreading in an open IDU population in a representative US urban center. We obtained sexual and needle-sharing data from a needle and syringe program operated by Community Outreach Intervention Projects (COIP) at the University of Illinois at Chicago [35]. In particular, we obtained data for the proportion of IDUs having a regular sex partner, concurrent sexual partnership distribution, and needle-sharing relationship distribution. We then adjusted these values in model calibration to compensate for the fact that IDUs who enroll in a needle and syringe program are potentially more risk-aware and less prone to risky behaviors than those who do not. Table A1 shows the values for parameters of the network model after calibration. Using these parameters as an input and following the method described in Section 2, we inferred the joint degree distribution over regular and casual sexual partnerships, the joint degree distribution over regular and steady needle-sharing partnerships, and the transitional matrices P_m and P_f, as shown in Table 1.

Table A1.

Input parameters of the network model.

Parameter name	Value	Source
Demographic parameters
Population size
Number of men, Nm	5,000	Assumed
Number of women, Nf	3,503	Calculated
Female-to-Male Ratio	1.43	Calculated§
Monthly entry rate, rm and rf(%)	0.10, 0.10	[39]
Non-HIV, Non-HCV annual mortality rate (%)	1.10	[40, 41]
HIV prevalence (%)
IDU	7.39	[31]
Non-IDU	0.40	[39, 42]
HCV prevalence (%)
IDU	35	[43]
Non-IDU	1.30	[39, 44]
Access to treatment (%)
HIV	69	[45]
HCV	25	[46, 47]
Sexual partnership characteristics
Have a regular partner (%)
Male IDU, sm	58	[35]
Female IDU, sf	82	Calculated
Partnership duration (months)
Regular, σr	24	[20]
Casual, σc	6	Estimated*
Concurrent partnership distributions, m(p) and f(p) (%)		Estimated*†, [35]
0 partners	26, 15
1 partner	51, 48
2 partners	17, 12
3 partners	6, 25
Needle-sharing relationship characteristics
Share needles with regular partner (%)	20	[35]
Steady needle-sharing relationship duration, σn (months)	36	[48]
Sharing relationship distribution, n(p) (%)		Estimated*†, [35]
0 partners	64
1 partner	21
2 partners	11
3 partners	3
4 partners	1

^§Close to the figure reported in [42].

^*Estimated through calibration.

^†Adjustment through calibration was minimal; thus these values closely reflect the Community Outreach Intervention Project (COIP) data.

Table 1.

Inferred parameters of the network model.

Parameter name	Value
Sexual contact network
Stationary distributions of sexual partnership, πm and πf, (%)
0 regular, 0 casual partners	26.00, 15.00
0 regular, 1 casual partners	11.03, 1.25
0 regular, 2 casual partners	3.68, 0.31
0 regular, 3 casual partners	1.30, 0.65
1 regular, 0 casual partners	39.97, 46.75
1 regular, 1 casual partners	13.32, 11.69
1 regular, 2 casual partners	4.70, 24.35
Monthly partnership formation probabilities, Pm and Pf, (%)
Gain a regular and a casual partnership with
0 regular, 0 casual partners	2.19, 6.98
0 regular, 1 casual partners	2.06, 8.09
Gain a regular and no casual partnership with
0 regular, 0 casual partners	3.26, 12.00
0 regular, 1 casual partners	3.39, 10.89
0 regular, 2 casual partners	5.45, 18.98
Gain no regular and a casual partnership with
0 regular, 0 casual partners	6.00, 0
0 regular, 1 casual partners	10.47, 0
0 regular, 2 casual partners	17.00, 0
Lose no regular partnership and gain a casual partnership with
1 regular, 0 casual partners	4.15, 4.90
1 regular, 1 casual partners	8.70, 65.27
Lose a regular partnership and gain a casual partnership with
1 regular, 0 casual partners	1.51, 0
1 regular, 1 casual partners	1.48, 0
1 regular, 2 casual partners	0, 2.14
Needle-sharing network
Stationary distributions of long-term needle-sharing partnership, πn (%)
0 regular, 0 steady partners	63.90
0 regular, 1 steady partners	12.88
0 regular, 2 steady partners	7.09
0 regular, 3 steady partners	1.56
0 regular, 4 steady partners	0.93
1 regular, 0 casual partners	7.82
1 regular, 1 casual partners	4.31
1 regular, 2 casual partners	0.94
1 regular, 3 casual partners	0.57

We employed a disease model that allows for varying infectivity dependent on disease state and treatment status, and interplay between HIV and HCV. A detailed description of the disease model can be found in Appendix A, and values for related parameters are shown in Table A2.

Table A2.

Input parameters of the disease model.

Parameter name	Value	Source
HIV progression
Duration of acute phase (weeks)	12	[49]
Monthly transition rate
CD4>500 → CD4<500 cells/mm3
ART−	0.011	[50]
ART+	HR 1	[51, 52]
CD4<500 cells/mm3 → death
ART−	0.014	[50]
ART+	HR 0.22	[53, 54]
HCV+	HR 1.35	[55]
HCV progression
Duration of acute phase (weeks)	26	[56]
Mean time to treatment (weeks)	520	[57]
Treatment response (%)	80	[58, 59, 60]
Duration of treatment (weeks)	24	[61, 62]
Sexual behavior
Coital acts per week	1	[35]
Fraction that use condom consistently (%)
Regular partnership	16	[20, 21, 63]
Casual partnership	50	[64]
HIV transmission via sex
HIV transmission rate per coital act
Asymptomatic phase (CD4>500 cells/mm3) (%)	0.06	[65]
Acute phase	HR 12	[66, 67]
Symptomatic phase (CD4<500 cells/mm3)	HR 6	[66, 67, 68]
Effect of treatment (ART+) on infection risk	HR 0.10	[69, 70, 71]
Effect of condom use on infection risk	RR 0.20	[69, 72]
Needle-sharing behavior
Number of injections per week	14	[73, 74, 75]
Fraction of injections shared with strangers (%)	1	Estimated*
Distribution of long-term-sharing frequency (%)		[76]
0.25 times/week (monthly)	38
1 time/week (weekly)	45
7 times/week (daily)	17
HIV transmission via needle
Transmission rate per injection with a contaminated syringe (%)
Acute phase	1.00	[39]
Asymptomatic phase (CD4>500 cells/mm3)	0.12	[77, 78]
Symptomatic phase (CD4<500 cells/mm3)	0.30	[77, 78]
Effect of treatment on infection risk	HR 0.50	[68]
HCV transmission via needle
Transmission rate per injection with a contaminated syringe
HIV− (%)	0.40	[79, 80]
HIV+	HR 2	[81]
Effect of treatment on infection risk	HR 0.50	[82, 83]

HR, hazard ratio; RR, relative risk.

^*Estimated through calibration.

We developed the model in Mathworks Matlab R2014b. We simulated the population over a ten-year time horizon. We modeled one-time needle-sharing and disease acquisition and progression with weekly events. We modeled the dynamics of 𝒮 and 𝒩 with monthly events, because sexual relationships and long-term needle-sharing relationships typically last for months and a finer resolution adds little accuracy at significant computational cost. Because the model is stochastic, we ran the model 100 times for each scenario considered and then calculated quartiles which roughly depict the distribution of the numerical results (e.g., the number of new HIV/HCV infections).

By varying parameters with uncertainty (i.e., average duration of casual sexual partnerships, the degree distributions of concurrent partnerships and needle-sharing relationships, fraction of injections shared with strangers), we manually calibrated the model to match projections of HIV and HCV incidence [31, 34] over the next 10 years under the status quo (Figure 2).

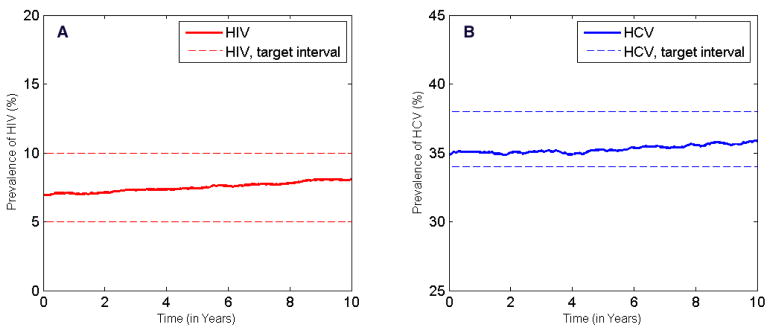
Figure 2.

Results of calibration. A: Across the US, HIV prevalence in the IDU population remained relatively constant around 7% for the past decade [31, 32, 33]. We assumed this trend would carry into the next 10 years and defined a target interval of 5–10% HIV prevalence. After calibration, the projection of HIV prevalence simulated by our model (averaged over 100 runs) lies within the target interval. B: HCV prevalence in the IDU population in the US increased slightly in the past decade [34]; thus we assumed an increasing trend in the future and defined a target interval of 34–38% HCV prevalence. The simulated HCV prevalence (averaged over 100 runs) falls within the target interval.

3.2. Example analysis

We illustrate our model by evaluating the impact of scaling up peer education (PE) programs. Such programs hire community members (in this case, mostly former and current drug users) to provide information and resources to their peers, who are generally hard to reach. PE leverages the power of peer pressure and role modeling, and has been proven to be an effective means of disseminating risk-reduction messages and promoting behavior change in IDU communities [36]. PE can be operated at comparatively low cost and thus is particularly suitable in resource-constrained settings.

In our simulation, we assumed that IDUs reached by PE are motivated to reduce sharing frequency with their long-term needle-sharing partners and to use condoms consistently with their sex partners. We considered two extreme cases regarding implementation of the program: 1) untargeted PE that reaches random IDUs in the population, 2) targeted PE that reaches IDUs with the greatest number of sexual and needle-sharing partners (i.e., the highest degree centrality in the risk network). While there are various definitions of node centrality in a network, it makes intuitive sense to consider degree centrality: an IDU with more risky partners faces a higher chance of contracting contagion(s) if not yet infected and has a higher chance of spreading contagion(s) if already infected. Such IDUs serve as hubs that facilitate the spread of diseases in the population. To simulate targeted PE, we ranked IDUs by their degree in the risk network and then enrolled the top IDUs into PE. Because the risk network is evolving over time, we re-selected IDUs according to their degrees every 6 months. We assumed that IDUs who are not in PE resume their risky behaviors at the same level as before participating in the program (a conservative assumption).

Besides the extreme cases, we examined a third scenario in which IDUs are identified for enrollment in PE via contact tracing. We start by randomly selecting 100 IDUs to enroll in PE. We then trace their sexual and needle-sharing contacts, enroll these IDUs, and then trace their contacts in turn. We repeat this procedure until we have enrolled a prespecified proportion of the population. Note that each IDU can only be enrolled once.

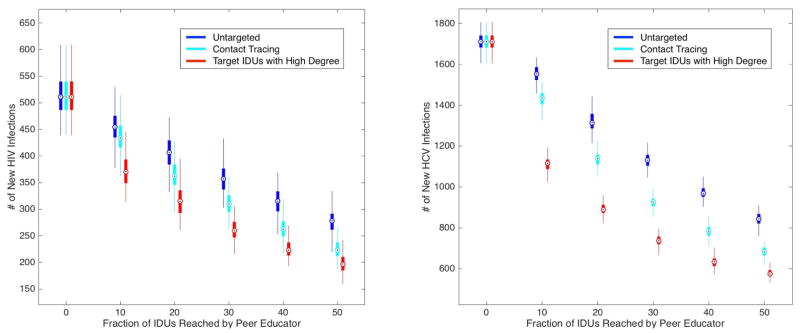
Figure 3 shows that untargeted PE is effective in averting new HIV and HCV infections. For example, an untargeted PE program that reaches 10% of IDUs could reduce new HIV infections by approximately 11% and new HCV infections by 9% by the end of the 10-year horizon. The benefits of targeted PE are approximately three times as high as the benefits of untargeted PE. For example, when the top 10% of centrally located IDUs are reached by peer educators, new HIV infections decrease by approximately 28% and new HCV infections decrease by 35%. The effect of PE when IDUs are identified for enrollment by contact tracing lies between that of untargeted and targeted PE. This can be explained by the fact that individuals with higher degree are more likely to be enrolled by contact tracing than those with lower degree, since there are more paths leading to them, but contact tracing only imperfectly finds IDUs at highest risk and thus is not as effective as the targeted program.

Figure 3.

Number of new HIV infections and new HCV infections over 10 simulated years for a peer education (PE) program that promotes condom use and discourages needle-sharing. Quartiles of the 100 simulation runs are indicated with the Tukey boxplot. We compare three scenarios: 1) untargeted PE (dark blue boxes) in which peer educators reach random IDUs in the population; 2) PE in which IDUs are identified for enrollment via contact tracing (light blue boxes); 3) targeted PE (red boxes) in which peer educators reach IDUs with the greatest number of partners (both sexual and needle-sharing).

Our analysis highlights the importance of targeting – and reaching – key groups of individuals when instituting prevention programs. Of course, targeted PE is an idealized strategy that requires perfect knowledge of the risk network, information that is usually unavailable. However, it is likely that the peer educators – ‘insiders’ of IDU communities – possess partial knowledge of the risk network and thus can identify the relatively high-risk IDUs. A practical way to circumvent the difficulty in obtaining degree information for every node in the network is by contact tracing. As shown in Figure 3, contact tracing to identify IDUs to enroll in PE achieves a significant portion of the benefits of targeted PE.

4. Discussion

We have described a methodology to infer the network structure and network dynamics of an injecting drug-using population based on readily available data. The contact network captures multiple types of sexual partnerships and needle-sharing relationships, all with the potential to spread blood-borne infectious diseases such as HIV, HCV and STIs. We applied this modeling framework to evaluate the effectiveness of a PE program under various forms of targeting to illustrate the benefits of exploiting the contact network.

Our analysis has several limitations. We modeled the needle-sharing network as an undirected network, and assumed that in any sharing event partners are equally likely to use the needle first. But this assumption does not always hold. For example, studies show that IDUs with fewer resources to share are more often engaged in receptive needle sharing than distributive needle sharing [37]. Our model can be extended to incorporate this power imbalance by specifying a direction for each edge in 𝒩. An edge from individual i to j means that i has a higher status than j in their relationship, and i injects first for Δ percent of the time (0.5 < Δ ≤ 1). Note that status is transitive: if i is superior to j and j superior to l, then naturally we would expect l to be inferior to i. To put it in terms of edge direction, given two edges i → j and j → l, if an edge ever forms between i and l, it should go from i to l to guarantee consistency. The theory of status has been studied extensively in social network settings [38] and can be applied in constructing (inferring) a directed needle-sharing network.

We did not address gender differences in injecting risk behaviors. Some studies have found that female IDUs have more sharing partners than male IDUs [19, 84] and tend to form more dense and homogeneous injecting groups [85, 86]. The former distinction can be included in the model by constructing a needle-sharing network that matches the gender-specific degree distributions. This would be an easy extension: analogous to our approach for the sexual contact network, we would now solve Q_m and Q_f to maintain a steady n_m(p) and n_f(p). It is not immediately clear how to capture the phenomenon of denser and more homogeneous injecting groups; this is an area for future work.

We did not model risk behavior as a function of disease status (e.g., individuals with symptomatic infection may be less likely to engage in risky behaviors than individuals with asymptomatic infection). Modeling such differences in behavior is a straightforward extension of our analysis.

Our model incorporates a parameter γ that reflects the tendency of regular sex partners to share needles with each other. Thus the sexual and needle-sharing contact networks are not independent. Another type of correlation between the two networks could occur if IDUs who have a high number of needle-sharing partners also have a high number of sexual partners. For the COIP data, the correlation coefficient between the number of needle-sharing partners and the number of sexual partners is 0.008, so we did not incorporate such correlation in our model. However, our model can be readily extended to reflect a population in which the numbers of sexual and needle-sharing contacts are correlated. To do so, we would compute the joint degree distribution of regular sex partners, casual sex partners and needle-sharing partners, and then use a method similar to that we have presented to infer network parameters and dynamics.

Our model of the sexual contact network can be extended in a variety of ways. While we assumed heterosexual contacts only, one could easily combine a heterosexual network with a homosexual network to account for disease transmission among IDUs who are men who have sex with men (MSM). The two networks are disjoint if we assume that no individuals are bisexual; in this case, we can infer the structure and dynamic parameters for each network independently. Currently there is no representation of sex workers in our model, though they constitute a non-negligible proportion of the IDU population. A survey of IDUs in San Francisco found that 15% of female IDUs and 13% of male IDUs had ever engaged in sex for money [19]. One could simulate commercial sex as one-time events each week (similar to the way we modeled one-time needle sharing). By modeling the IDU population exclusively, we made the implicit assumption that the sex partners of an IDU also inject drugs. This assumption can be relaxed by bringing non-IDUs into the model. Non-IDU – IDU partnerships will then serve as the bridge for disease transmission from the IDU population to the general population and vice versa (though less likely).

Despite these limitations, our framework is a significant step forward in modeling the spread of blood-borne contagions among injecting drug-using populations, capturing both sexual and needle-sharing transmission in a dynamic network model, and allowing for accurate assessment of the effects of interventions targeted to individuals in such networks.

Highlights.

• A bilayer network model of injection drug users (IDUs) is developed.

• The model incorporates sexual and needle-sharing contacts.

• The model can capture diseases spreading among IDUs (e.g., HIV, HCV).

• The model can evaluate efficacy of drug abuse and disease interventions among IDUs.

Appendix A. Details of Illustrative Example

Population dynamics

We initialized the model with 5,000 male and 3,503 female IDUs. The number of female IDUs is calculated so as to maintain the reported sexual partnership distribution. The resulting female-to-male ratio is less than 1, consistent with the fact that males usually outnumber females in IDU populations. Each month, individuals enter the model due to initiation of injection drug use and leave the model due to death. We assumed that the population size would remain constant over the 10-year time horizon, and calibrated the monthly entry rate to balance mortality. We did not include abstinence from injection drug use because of its low probability and subsequent high relapse rate.

Disease progression

We employed a discrete HIV disease model with four stages: susceptible, acute infection, asymptomatic infection and symptomatic infection. We obtained monthly progression rates from the literature. Consistent with US statistics [45], we assumed that 69% of treatment-eligible IDUs receive antiretroviral therapy (ART).

The HCV disease model has three stages: susceptible, acute and chronic. We do not distinguish chronic HCV infection stages (typically characterized by the progression of hepatic fibrosis) because we find no evidence suggesting that patient infectivity varies in the chronic disease stages. If we wished to estimate the total number of quality-adjusted life years (QALYs) accumulated over time or the cost of treating HCV infection, a more detailed model of HCV infection would be appropriate. We assumed that 25% of HCV-infected IDUs receive treatment [46, 47].

Disease transmission

In each week, every susceptible node is investigated by examining its edges shared with infected nodes.

First consider transmission via sexual contacts. We assumed that all sexual partnerships involve a frequency of coital acts of once per week, regardless of the type of partnership. HIV transmission rate per coital act is determined by the viral load of the infected individual: a host in the acute/symptomatic phase is much more infectious than an asymptomatic host, and a host on ART is much less infectious since treatment suppresses HIV viral load. We also accounted for levels of condom use and assumed that 20% of regular partners and 50% of casual partners use condoms consistently. We did not include a sexual transmission risk of HCV, as HCV rarely spreads via heterosexual sex.

The probability that a susceptible individual i acquires HIV in a given week, $d_i^{\text{HIV},\text{sex}}$, can be computed as,

$$d_i^{\text{HIV},\text{sex}}=1-\prod _{j\in \{j\mid j\text{HIV}+,(i,j)\in E_S\}}(1-p_{ij})$$ (A1)

where p_ij denotes the per-act transmission risk between individuals i and j.

Next consider transmission via needle sharing. We assigned each edge in 𝒩 with an attribute that describes the frequency of sharing behaviors. We made a simple generalization of three sharing patterns – monthly, weekly and daily – to incorporate behavioral variability in the population. This attribute remains the same throughout the simulation unless one of the sharing partners is reached by peer educators. Similar to the way in which we modeled the chance of transmission per coital act, the chance of HIV/HCV transmission per injection with an infected syringe depends on the disease and treatment status of the infected individual. Since HIV-infected individuals are more vulnerable to viruses, we assumed that the risk of acquiring HCV infection increases if the HCV-susceptible individual is HIV-infected [81]. We found no evidence suggesting that infection with HCV makes an individual more susceptible to HIV, so we assumed no increased risk of acquiring HIV among HCV-infected individuals.

We assumed that IDUs inject twice per day and 1% of the injections involve one-time sharing, resulting in an average of 0.14 one-time needle shares per week, i.e. λ_i = 0.14, ∀i ∈ V.

The probability that a susceptible individual i contracts HIV/HCV via needle sharing is

$$d_i^{\text{HIV},\text{needle}}=1-\prod _{j\in \{j\mid j\text{HIV}+,(i,j)\in E_N\cup E_O\}}{(1-q_{ij}^{\text{HIV}})}^{f_{ij}}$$ (A2)

$$d_i^{\text{HCV},\text{needle}}=1-\prod _{j\in \{j\mid j\text{HCV}+,(i,j)\in E_N\cup E_O\}}{(1-q_{ij}^{\text{HCV}})}^{f_{ij}}$$ (A3)

where $q_{ij}^{\text{HIV}},q_{ij}^{\text{HCV}}$ denote HIV, HCV transmission risk along the edge between i and j, respectively. We set f_ij = Ber(0.5 × 0.25)/Ber(0.5)/Binomial(0.5, 7) if the sharing frequency between i and j is monthly/weekly/daily. The constant 0.5 takes into account the order of needle use: an individual cannot ac-quire the contagion if injecting first with a clean needle, and we assume an equal probability of injecting first.

Combining the risks of transmission via the two routes, the weekly probabilities of an IDU becoming infected with HIV and HCV, respectively, are

$$d_i^{\text{HIV}}=1-(1-d_i^{\text{HIV},\text{sex}})(1-d_i^{\text{HIV},\text{needle}})$$ (A4)

$$d_i^{\text{HCV}}=d_i^{\text{HCV},\text{needle}}$$ (A5)