Visualization of Small-Diameter Vessels by Reduction of Incoherent Reverberation with Coherent Flow Power Doppler

Abstract

Power Doppler (PD) imaging is a widely used technique for flow detection. Despite the wide use of Doppler ultrasound, limitations exist in the ability of Doppler ultrasound to assess slow flow in small-diameter vasculature, such as the maternal spiral arteries and fetal villous arteries of the placenta and focal liver lesions. The sensitivity of PD in small vessel detection is limited by the low signal produced by slow flow and the noise associated with small vessels. The noise sources include electronic noise, stationary or slowly moving tissue clutter, reverberation clutter, and off-axis scattering from tissue, among others. In order to provide more sensitive detection of slow flow in small diameter vessels, a coherent flow imaging technique, termed coherent flow power Doppler (CFPD), is characterized and evaluated with simulation, flow-phantom experiment studies, and an in vivo animal small vessel detection study. CFPD imaging was introduced as a technique to detect slow blood flow. It has been demonstrated to detect slow flow below the detection threshold of conventional power Doppler (PD) imaging using identical pulse sequences and filter parameters. In this study, we compare CFPD to PD in the detection of blood flow in small-diameter vessels. The results from the study suggest that CFPD is able to provide 7.5–12.5 dB increase in the signal-to-noise ratio (SNR) over power Doppler images for the same physiological conditions, and is less susceptible to reverberation clutter and thermal noise. Due to the increase in SNR, CFPD is able to detect small vessels in high channel noise cases, for which PD was unable to generate enough contrast to observe the vessel.

I. INTRODUCTION

Power Doppler (PD) imaging is a widely used technique for flow detection and monitoring in various organs [1]–[4]. Conventionally, PD imaging detects the temporally varying components of backscattered echoes from blood. It provides higher sensitivity to slow flow than color Doppler imaging at the expense of flow velocity and direction information.

Despite its higher sensitivity than color Doppler imaging, limitations exist in the clinical application of PD imaging. For example, the frame rate of PD imaging is low, because it requires an ensemble length of 8 to 16 pulses in order to provide effective detection of flow. Other limitations include thermal noise and motion artifact that may obscure the vasculature and long transmit pulse lengths that limit resolution. Other limitations exist in the ability of PD in the detection of slow flow and small vessels. These limitations are associated with the noise sources of PD images, because the contrast of PD images is determined by the power of the temporally changing signal produced by backscattered waves from blood relative to the power of background noise.

Two major noise sources exist in flow imaging: thermal noise, and clutter. Thermal noise is associated with the electronics of the scanner and remain at the same level as depth increases. Because the echo signal strength decreases with depth due to frequency dependent attenuation, thermal noise causes the decrease in SNR with depth. The classic Doppler clutter is stationary or slowly changing clutter, referring to any unwanted signal that is temporally stable (i.e. high temporal coherence) over the Doppler ensemble, which obscures signals from blood and other clinical targets. This is often stationary tissue signal, referring to the typical single scattering event in pulse-echo ultrasound. It is spatially coherent in the aperture domain and temporally coherent in the slow time domain. In small vessel imaging, however, tissue clutter can also have relatively low temporal coherence because the flow associated with small vessels may be slow and the clutter motion may overlap the blood signals in the temporal frequency domain. Another type of clutter is reverberation clutter, referring to the unwanted image signal produced by multiple reflections or multipath scattering. Reverberation clutter can be distinguished by its spatial coherence properties in the aperture domain. In Dahl and Sheth [5], the two different types of reverberation clutter are described as coherent and diffuse, refer to spatially coherent and spatially incoherent signals in the aperture domain, respectively. Coherent reverberation occurs when there is a multiple reflection event between specular reflecting boundaries. Diffuse reverberation is spatially incoherent and is produced by the multipath scattering in subcutaneous or other inhomogeneous tissue layers.

In the following text, we define clutter according to their different origins and spatial coherence properties. Table I summarizes the four categories of clutter in Doppler imaging according to their spatial coherence in the receive aperture domain and temporal coherence in the slow time domain. Type I clutter has high spatial and temporal coherence, and include stationary tissue clutter and stationary coherent reverberation clutter. Type II clutter has high spatial coherence and low temporal coherence and is generated by fast moving tissue or moving specular reflecting boundaries. Type III clutter has low spatial coherence and high temporal coherence and is produced with stationary diffuse-reverberation-clutter-generating layers. Type IV clutter has low spatial and temporal coherence and is generated by moving layers.

TABLE I.

Clutter categories according to their temporal and spatial coherence properties

		Temporal coherence
		high	low
Spatial coherence	High	Type I Stationary tissue clutter or coherent reverberation	Type II Moving tissue clutter or coherent reverberation
	Low	Type III Stationary diffuse reverberation	Type IV Moving diffuse reverberation

PD imaging relies on high-pass and band-pass filters to suppress noise. However, thermal noise is a white noise process, and thus cannot be effectively suppressed by the high-pass and band-pass filters. In addition, for slow flow detection, the filters have very low cut-off frequencies so as not to attenuate the signal produced by slowly flowing blood. In such cases, the filter is only capable of suppressing clutter with high temporal coherence (Type I and III), and is not able to effectively suppress Type II and Type IV clutter because of the overlap in tissue or reverberation motion and blood scatterer movement. If the power of the thermal noise or clutter is close to or greater than the power of the blood signal, PD imaging has limited performance in the detection of slow flow and small vessels.

One recent advancement in PD imaging is the ultrafast Doppler imaging technique [6], which combines the plane-wave synthetic transmit focusing technique and PD imaging. This technique utilizes plane wave transmits at multiple angles to coherently synthesize radio-frequency (RF) signals or IQ signals that have similar quality as those of conventional focused transmit. PD processing is then applied to the ensemble of coherently synthesized RF signals. Because a smaller number of plane-wave transmits than focused transmits are used for the same field-of-view, the technique reduces acquisition time for each packet in the ensemble while maintaining a similar pulse repetition rate, and enables the acquisition of a very large ensemble length (on the order of 200) for Doppler imaging [6], thus producing high quality PD images. The large ensemble length also enables the use of a spatiotemporal filter [7], which is effective at suppressing tissue motion signals. The technique has been applied to rat brain imaging at a frame rate of 1.42 Hz [8], as well as neonatal brain imaging [9]. However, ultrafast Doppler imaging is still limited at large imaging depths, where focusing quality and image SNR must be traded off to maintain frame rate or ensemble length.

Improvement of PD imaging in slow flow and small vessel detection, including those at large depths, e.g., placental vasculature detection and focal liver lesion flow detection, is desirable. Placental vasculature play critical roles in placental development in the early gestation period. The absence of growth of the spiral arteries of the placenta is thought to lead to early-onset preeclampsia, intrauterine growth restriction (IUGR), and early pregnancy loss [10]. However, the observation of these vessels in the human placenta has been challenging. Histological assessment of placental vasculature [10], [11] suggests that the vessel sizes within the placental bed are within the diffraction limits of ultrasound imaging. However, current Doppler imaging technology has been unable to directly visualize the remodeling process of the spiral arteries due to the slow blood flow within these arteries. Direct visualization of spiral artery remodeling could be used to assess the relation between preeclampsia and IUGR and the spiral arteries, but PD has been limited in its ability to detect the small-diameter vessels in the placental vasculature [12], [13]. Although effects have been made to detect the blood flow withing the placenta of rabbits [14], it is challenging to translate scientific discovery from lower order organisms, including rabbits, to humans, because the placenta is strikingly distinct in humans when compared with other animals. Three-dimensional (3D) ultrasound power Doppler has been demonstrated to provide more information than 2D power Doppler, but can only detect the ends of spiral arteries rather than the entire spiral arteries [15], which limits its diagnostic value. In addition, PD is unable to provide adequate detection of flow in focal liver lesions [16], [17]. The perfusion characteristics in focal liver lesions may provide definite differentiation of liver tumor, even when other characteristics of the lesions are similar [17], [18]. However, due to the poor flow signal, power Doppler has low sensitivity and specificity in the detection of flow in focal liver lesions. Currently, sonographers rely on micro-bubbles as contrast agents for Doppler imaging in the assessment of focal liver lesions [16], [19]–[21], which can only detect flow in focal liver lesions with diameters above 3 mm [22].

Coherent Flow Power Doppler (CFPD) imaging has been proposed to circumvent some of the limitations of PD imaging with respect to noise to improve sensitivity [23], and has been demonstrated to detect flow with velocities approximately 50% lower than the limit of conventional power Doppler. CFPD imaging detects flow from the spatial coherence of backscattered acoustic waves from blood. The method utilizes the short-lag spatial coherence (SLSC) beamformer, which was recently introduced as an alternative beamforming method that produces images similar to those of delay-and-sum (DAS) beamformers. The SLSC imaging method suppresses spatially incoherent noise, such as thermal noise and diffuse reverberation clutter, and produces images with higher speckle SNR and higher contrast-to-noise ratio (CNR) compared to DAS beamforming [24], [25]. Because the method replaces the DAS beamformer, it can be extended to harmonic spatial coherence imaging [26], synthetic aperture SLSC imaging [27], flow imaging [23], and a number of other ultrasound imaging modalities that use DAS beamforming. The CFPD method rejects signals that pass through the wall filter based on a different property of the signal, therefore work in conjunction with the wall filter rather than as a replacement to existing wall filters. However, because phase information is lost after SLSC beamforming, it has limited applications in detecting velocity magnitude and direction. In addition, it is worth noting that CFPD only suppresses noise sources that are spatially incoherent, including thermal noise and diffuse reverberation clutter (i.e., Type III and Type IV clutter), but not stationary or moving tissue clutter or coherent reverberation clutter (Type I and II). Advanced filters, including the spatiotemporal filter [7] and the blind-source separation filter [28], can be used to suppress clutter signals with high spatial coherence but low temporal coherence. Because blood signal is similar to Type II clutter in therms of coherence, this would require other adaptive filtering techniques.

CFPD does not rely on a specific transmit focusing technique, so it can be applied in conjunction with conventional or synthetic focusing, including plane wave transmit and virtual source techniques. After channel data is acquired, the time-delayed RF channel signals are filtered across the slow-time dimension on a per-channel basis to remove stationary signal and slowly moving tissue signal.

In our previous study, we have shown that CFPD is less susceptible to thermal noise in flow detection than PD imaging in major vessels [23]. An improvement of 7.5–12.5 dB in Doppler SNR was observed with CFPD, as compared with PD. The SNR improvement enables CFPD to detect flow with velocities 50% lower than the limit of PD, or to provide a frame rate that is 3 times that of PD. However, the impact of reverberation clutter was not previously assessed. The impact of incoherent reverberation clutter generated by near-field tissue layers are often further complicated by motion artifacts due to patient breathing or transducer motion. The relative motion between the near-field tissue and transducers may create a temporally changing reverberation clutter, which is challenging for high-pass filters to suppress if the velocity of such motion is close to the velocity of the slow blood flow. In this study, we demonstrate performance CFPD in slow flow and small vessel detection, and characterize its performance in the presence of thermal noise, reverberation clutter, and motion artifact with simulations, flow phantom studies, and in vivo animal studies.

Because CFPD is capable of suppressing spatially incoherent noise, it is hypothesized that, for small vessel imaging, CFPD will produce higher Doppler image SNR than PD in the presence of noise and artifacts induced by near-field clutter sources.

Preliminary results of this study were presented in Li and Dahl [29], which only explored the performance of CFPD in detecting cross-sections of small vessels. Here, we expanded our analysis to longitudinal sections of small vessels, and include a more extensive framework of our simulations, including tissue motion, and demonstrate the method in phantoms and in vivo studies on small diameter vessels.

II. Methods

A. Principles of CFPD

A CFPD pulse sequence collects an ensemble of RF channel data in the same manner that PD collects an ensemble of beamformed RF signals [23]. Received RF channel data are then time-delayed and filtered across the ensemble dimension with a high-pass or band-pass filter to remove stationary tissue signal. The filtered RF channel data for each scan are processed using the SLSC beamformer [24]. The SLSC method computes the normalized covariance of the signals received on every pair of transducer elements, denoted by s_i(n) for element i and s_i+m(n) for element i + m of the transducer, in which n is the fast-time index. The normalized covariance of the signal is defined as

$$\widehat{R}(m)=\frac{1}{N-m}\sum _{i=1}^{N-m}\frac{{\sum }_{n=n_1}^{n_2}{s}_i(n)s_{i+m}(n)}{\sqrt{{\sum }_{n=n_1}^{n_2}{s}_i^2(n){\sum }_{n=n_1}^{n_2}{s}_{i+m}^2(n)}},$$ (1)

in which m, defined as lag, is the spacing between elements. N is the number of transducer elements in the active aperture and is determined by the F-number and focal depth of the system, and n₂ – n₁ is the kernel size for cross-correlation calculation.

The SLSC metric is computed by summing the spatial correlation values produced with Equation (1) over M lags

$$V_{\mathit{slsc}}=\sum _{m=1}^M\widehat{R}(m),$$ (2)

where M is an integer number of elements, corresponding to approximately 5–30% of the size of the transmit aperture.

A modified Loupas power estimator is then applied to the SLSC metric data to produce CFPD image:

$$\text{CFPD}(x,z)=\sum _{p=1}^P{V}_{\mathit{slsc}}^2(x,z,p),$$ (3)

where V_slsc(x, z, p) is the SLSC signal calculated with Equation (2) for the pth acquisition, (x, z) are the spatial coordinates, and P is the ensemble length used in the estimator. Equation 3 is the power of the integrated normalized and windowed spatial correlation function (i.e., the power of the SLSC beamformed data). Note that the original power Doppler estimator by Loupas et al. [30] is

$$\text{PD}(x,z)=\sum _{z=z-\mathrm{\Delta }z}^{z+\mathrm{\Delta }z}\sum _{p=1}^P{S}^2(x,z,p),$$ (4)

in which, S(x, z, p) is the delay-and-summed RF signal, and Δz is the axial averaging kernel length. The estimator used for CFPD differs from the original Loupas power estimator, which employs axial averaging. Axial averaging is not used in the power estimation of CFPD, because it is already applied in the SLSC beamformer as shown in Eq. 1. For display of CFPD and PD images, the pixel values (i.e., CFPD(x, z) and PD(x, z)) are converted to decibel (dB) scale with the 10 log₁₀(·) function.

B. Image Quality Evaluation

The SNR of the Doppler images were measured as the root-mean-square (RMS) power of the signal in the vessel relative to the RMS power of background noise [23].

$$\text{SNR}=10·{log}_{10}\left(\frac{\sqrt{\frac{1}{{\mathrm{N}}_{\text{pixel}}}·{\sum }_{i=1}^{{\mathrm{N}}_{\text{pixel}}}{\mathrm{I}}_{\mathit{sig}}^2(i)}}{\sqrt{\frac{1}{{\mathrm{N}}_{\text{pixel}}}·{\sum }_{i=1}^{{\mathrm{N}}_{\text{pixel}}}{\mathrm{I}}_{\mathit{bkgd}}^2(i)}}\right),$$ (5)

in which, I_sig(i) and I_bkgd(i) are the pixel values of the ith pixel in the vessel region, and the ith pixel in the background region, respectively, in the CFPD and PD images. The pixel values of CFPD and PD images are defined according to Eq. 3 and Eq. 4, respectively. N_pixel is the total number of pixels in each region used for the SNR measurement.

C. Field II Simulations

Field II [31], [32] simulations were performed to observe the performance of CFPD as a function of vessel diameter under different noise conditions. A 7.5 MHz, 0.2 mm pitch, 128 element linear transducer was used to simulate a longitudinal view of 0.2- to 2-mm-diameter vessels. The vessels were embedded in homogeneous scatterers at 3 cm depth with a 30° angle to the axis. To simulate blood, scatterers within the vessel were given a scattering amplitude 60 dB lower than the surrounding tissue scatterers. Blood flow was simulated with the scatterers moving at 10 mm/s along the vessel axis. The scatterer density for both the blood and the surrounding tissue was 20 scatterers per resolution voxel. Five different speckle realizations were generated and used in each case of the simulations.

Two imaging sequences were utilized in the study: a conventional focused transmit (FT) sequence, and a plane wave synthetic transmit focusing (PWT) sequence [33]. For both sequences, 3-cycle pulses are used for Doppler pulse transmissions. In the FT sequence, transmit pulses were focused at 3 cm depth at the center of vessel with an F-number of 2. 50 beams were formed with 0.25 mm beam spacing. For each lateral location in the image, an ensemble of 15 A-scans were acquired at an f_prf of 1 kHz with a sampling rate of 40 MHz. The PWT sequence fires 17 transmit plane wave pulses using the entire aperture. The plane waves have an angular spacing of 1 degree, covering a ±8° range. The plane wave firing frequency is 17 kHz, corresponding to a Doppler pulse repetition frequency of 1 kHz [6] and a maximum imaging depth of 44.8 mm. In the PWT case, the RF channel data acquired from different transmits are first time-delayed and then added coherently to produce synthetic transmit aperture channel data. An ensemble length of 15 was obtained. Data were sampled at 40 MHz and dynamically focused on receive.

Thermal noise was simulated by adding white Gaussian noise at levels of −20 to 20 dB relative to the blood signal (i.e. −80 to −40 dB relative to the stationary tissue signal). A 2-tap projection-initialized Butterworth filter [34], [35] with a cutoff frequency of 5 Hz was used to remove stationary clutter. The projection-initialization of the filter removes the components of the output signal in the transient subspace and improves the performance of the filters when only a small ensemble length is used [34]. The filtered data were then processed to produce CFPD images, as well as conventional PD images with the same parameters for comparison. In the CFPD processing, a maximum lag (M) of 20 was used. The cross-correlation kernel size is chosen to be 1.5 times the wavelength. Shorter kernel length would induce higher jitter for the normalized cross-correlation computation, while longer ones would cause deterioration of resolution without providing significant reduction in jitter [36].

D. Full-wave Simulation Studies

Full-wave simulations were conducted to study the performance of CFPD in the presence of reverberation clutter created by abdominal tissues with physiological motion. Motion is a significant challenge in Doppler imaging, especially when blood flow is slow, because the spectra of blood flow signals and tissue motion signals or clutter signals created by moving abdominal layers may overlap and is not separable by conventional high-pass filters. Tissue motion signals can be effectively suppressed using advanced filters, including adaptive clutter filtering based on blind source separation [28] and spatiotemporal filtering [7]. These filters can separate blood flow signals and the signals created by the backscattering of moving tissue near the vessel, because blood flow signals have lower spatial coherence than tissue motion signals. However, because reverberation clutter signals created with moving abdominal layers also have lower spatial coherence than tissue motion signals, the blind source separation filter or the spatiotemporal filter may not be fully effective in suppression of such clutter signals.

The full-wave simulation numerically solves the Westervelt equation, simulating wave propagation through heterogeneous media including multiple scattering and nonlinear wave propagation [37]. A two-dimensional (2D) human abdominal tissue model developed by Mast et al. [38] was used to generate reverberation clutter. Aberration was excluded from the simulations by using an isovelocity method and acoustic properties (e.g., speed of sound, attenuation, density and nonlinear properties) described in Pinton et al. [39]. In addition, the amplitude of the reverberation clutter signal was varied by adjusting impedance mismatch of the tissue layers from 0% to 300% of the nominal values to explore the impact of clutter strength on the performance of Doppler imaging. Five different speckle realizations were generated and used in the simulations.

The tissue and vessel simulation model is illustrated in Fig. 1. The abdominal layer has a thickness of approximately 2 cm. A 1.8-mm diameter vessel is placed below the abdominal layer, centered at a depth of 3 cm and tilted at an angle of 30° relative to the azimuth. Blood flow at 10 mm/s is generated by translating the scatterers along the vessel axis. Physiological motion is also simulated. In practice, transducer motion from the sonographer and physiological motion from patient breathing or muscle vibration when breath is held limits the detectable velocities [40]. The involuntary oscillation of muscle under sustained contraction has a frequency of approximately 10 Hz and a maximum velocity of approximately 1.6 mm/s [40], and adult breathing has a frequency of 0.2 to 0.3 Hz [41] with an abdominal displacement of approximately 6 mm [42]. Because the physiological motion frequencies are much lower than the Doppler pulse repetition rate of the sequence, the tissue motion can be considered linear during each acquisition. In the simulation, physiological motion was created by adding an axial linear motion of 0–3 mm/s of the clutter generating tissue layer, covering the velocity range from no motion to the maximum velocity of the superposition of the transducer motion and patient breathing or muscle vibration. The model was imaged with a focused transmit sequence having a transmit center frequency of 2.5 MHz, a pulse length of 3 cycles, and an ensemble length of 15. The received data for each channel was sampled at 20 MHz, and white Gaussian noise at the level of 0 dB relative to blood signal was added to simulate thermal noise. The channel data was then filtered with a spatiotemporal filter [7] to remove tissue motion signals. Then the data were processed with both PD and CFPD techniques. In the CFPD processing, a maximum lag (M) of 20 was used. The Doppler image SNR was measured for both cases. The cut-off threshold of the filter was adjusted to maximize the SNR of the Doppler images. In addition, the signal-to-clutter ratio (SCR) was also measured as the ratio of the RMS power of the flow signal to the reverberation clutter appearing above the vessel. The computation of SCR is the same as SNR shown in Eq. 5, except that the sample location for the noise is different. The approximate sample locations for signal, background, and clutter are shown in Fig. 1 with white dashed boxes.

Fig. 1.

Illustration of the tissue model and vessel location in the full-wave simulations. In the original tissue model from Mast [38], different tissue types correspond to different speeds of sound (shown with gray scale values in the figure), densities, absorption coefficients, and nonlinear coefficients. The red area in the figure indicates the center and angle of the vessel used in the simulations. The three white dashed boxes from top to bottom represent the approximate sample locations for clutter signal, flow signal, and background signal, respectively, in the SNR and SCR measurements.

E. Flow Phantom Experiments

Experimental studies were conducted to study the performance of CFPD in small vessel detection in the presence of near field reverberation clutter and aberration. All experimental studies were done on a Verasonics Vantage 256 research scanner (Verasonics, Inc., Redmond, WA) and an L12-3v linear transducer. In the experiments, 128 transducer elements were used to transmit a 4.8 MHz 8-cycle pulse. The flow was generated with an IDEX ISM596D flow pump (Oakharbor, WA 98277 USA) through a 2-mm diameter vessel tubing in an ATS flow phantom (Model 527 Bridgeport, CT). The vessel was angled at 30° relative to the phantom surface. The fluid utilized in the phantom was based on ATS Model 707 Doppler Test Fluid (Bridgeport, CT) with 3% corn starch to simulate blood scattering. The flow velocity was calibrated to be 10 mm/s with the method described in [23].

A 1-cm thick porcine abdominal tissue model containing skin, fat, and muscle was placed between the flow phantom and the transducer to generate reverberation clutter in the flow images. Control images were obtained by placing the transducer directly upon the flow phantom, with reflective index matching gel between the transducer and the phantom.

In both experiments, longitudinal sections of the vessel at approximately 3.5 cm depth were acquired with a plane-wave synthetic transmit focusing sequence. Similar to the transmit sequence in the simulations, 17 transmit angles with 1 degree spacing were used, corresponding to a transmit F-number of 3.5. The firing frequency of the plane waves was 8.5 kHz, corresponding to a Doppler pulse repetition frequency of 500 Hz, limited by the hardware of the scanner. A Doppler ensemble of 16 was created from the synthetic aperture data. The received data were sampled at 31.2 MHz, and then synthetically focused. The focused data were then filtered at a cut-off frequency of 12.5 Hz with the same filter described in the Field II simulation section and processed with the same methods described in the simulation studies to produce CFPD and PD images. The SNR of the images were then measured using Eq. 5.

F. In Vivo Animal Experiments

A porcine study was conducted to demonstrate the feasibility of CFPD for in vivo small vessel detection. The study was approved by the Institutional Animal Care and Use Committee (IACUC) of Stanford University (IACUC 25727). Three 12-week-old female pigs (Yorkshire; Pork Power Farms, Turlock, CA; approximate weight, 31 kg) were used in this study. The animal was housed in an Association for Assessment and Accreditation of Laboratory Animal Care-accredited and U.S. Department of Agriculture-registered facility, and fed a commercially prepared balanced ration (Natures Match Sow and Pig Complete; Purina Mills, St Louis, Mo) ad libitum.

The pig was sedated with tiletamine hydrochloride and zolazepam hydrochloride (each at 8 mg/kg, Telazol; Pfizer, New York, NY), and anesthetized with 2%–4% isoflurane in oxygen (2 L/min). The pig was placed in supine position for ultrasound imaging, which was performed by a board-certified radiologist (JKW). The femoral vein and artery of the pig were targeted using the plane-wave synthetic transmit focusing sequence on the Verasonics Vantage 256 scanner described in the phantom experiments. Plane waves with a center frequency of 4.8 MHz were steered at 7 angles covering a range of ±3° with a maximum imaging depth of 4.5 cm. The Doppler pulse repetition rate was 500 Hz. All other parameter were similar to the flow phantom studies. Received radio-frequency (RF) channel data were acquired and processed in the same way as used in the flow phantom experiments.

III. Results

A. Field II Simulations

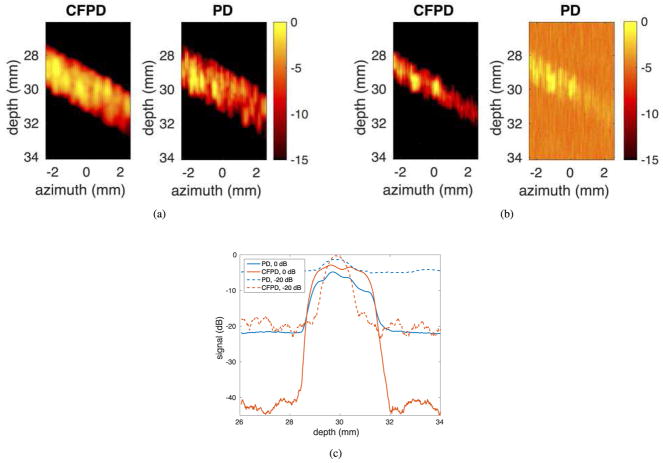
Fig. 2 (a) and (b) present a comparison of simulated CFPD and PD images of 1.6 mm diameter vessels with two different channel SNR levels (0 dB and −20 dB, respectively, relative to blood signal). These images are from simulations using a conventional FT sequence, and are displayed with a dynamic range of 15 dB. The images in (a) were produced with 0 dB channel SNR. At this channel SNR level, both CFPD and PD produce vessel images with high Doppler image SNR. The images in (b) were produced with −20 dB channel SNR. It can be seen that at this SNR level, PD begins to degrade and generates spurious background signal, making it more difficult to observe the vessel. CFPD produces a clear image of the vessel free from background noise. Fig. 2 (c) shows the center axial cross-sections of the images in Fig. 2 (a) and (b). CFPD shows approximately 10 dB improvement in SNR. In addition, for the −20 dB channel noise case, the vessel signal of PD is indistinguishable from background noise, but the vessel signal in CFPD is well separated from the background noise.

Fig. 2.

Simulated CFPD and PD images with conventional focused transmits, and center axial cross-sections of the images. For each set in (a) and (b), the CFPD image is on the left, and the PD image is on the right. (a) 0 dB channel SNR; (b) −20 dB channel SNR; (c) Center axial cross-sections of the images (a) and (b). The dashed lines in (a) and (b) indicate the approximate azimuthal locations of the cross-sections.

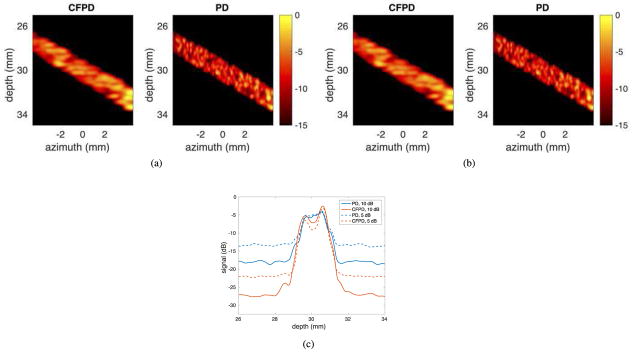
Fig. 3 (a) and (b) show simulated CFPD and PD images of a 1.6 mm diameter vessel, using the PWT sequence. Images produced with 10 dB and 5 dB channel SNR are presented. In the 10 dB case, both CFPD and PD generate enough contrast to adequately visualize the vessel. In the 5 dB case, the CFPD image has higher SNR than PD image, although it may be more easily visualized by reducing the display dynamic range.

Fig. 3.

Simulated CFPD and PD images with the plane wave synthetic transmit aperture sequence. (a) CFPD and PD images produced from data with 10 dB channel SNR. (b) CFPD and PD images produced with data containing 5 dB channel SNR. The dashed lines in (a) and (b) indicate the approximate azimuthal locations of the cross-sections.

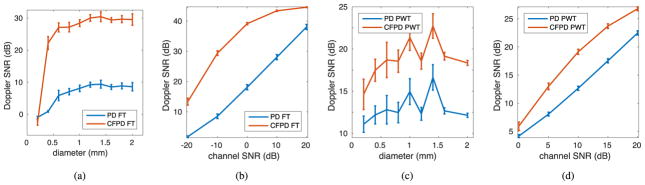
Fig. 4 presents the quantitative SNR measurements of the simulated CFPD and PD images as a function of vessel diameter and SNR. Fig. 4 (a) and (b) are from a conventional FT sequence, and Fig. 4 (c) and (d) are from a PWT sequence. Fig. 4 (a) and (c) show SNR as a function of vessel diameter with a channel SNR of −10 dB and 10 dB, respectively, and Fig. 4 (b) and (d) show SNR as a function of channel SNR for the 1.6 mm diameter vessel. A typical improvement of 5–15 dB in Doppler image SNR can be obtained with CFPD compared to PD with these imaging conditions

Fig. 4.

SNR of simulated CFPD and PD images. The curves represent the average measurement from the 5 speckle realizations, and the error bars represent the standard deviation of the measurements. (a) and (b) are from the FT sequence simulation; (c) and (d) are from the PWT case. (a) and (c) plot Doppler image SNR as functions of vessel radii, with a channel SNR level of −10 dB for (a) and 10 dB for (c) relative to blood signal; (b) and (d) presents the Doppler image SNR as functions of channel SNR for the 1.6 mm diameter vessel.

B. Full-wave Simulations

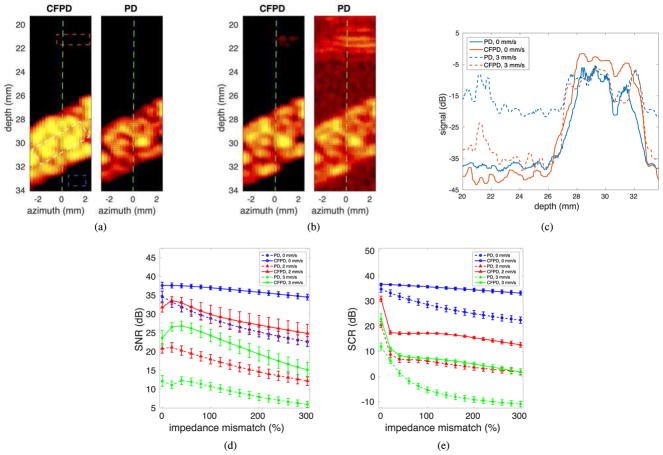
Fig. 5 shows the images and quantitative measurements on image quality from the full-wave simulations with an abdominal layer model at various simulated physiological motion velocities. Fig. 5 (a) shows the CFPD and PD images produced with 60 dB channel SNR and tissue clutter created with 60% of the nominal impedance mismatch of the abdominal tissue model and 0 mm/s tissue motion. The white, red, and blue squares indicate the approximate sample locations for flow signal, background signal, and clutter signal, respectively, in the SNR and SCR measurement. Fig. 5 (b) shows the CFPD and PD images produced with the same tissue model as (a), and 3 mm/s tissue motion. The display dynamic range for the images is 25 dB. Fig. 5 (c) shows the measured SNR of the images as a function of impedance mismatch (0–300% of the nominal values) with two simulated physiological motion velocities: 0 mm/s, 2 mm/s, and 3 mm/s. Fig. 5 (d) shows the measured SCR of the images as a function of impedance mismatch for the same parameter ranges as in Fig. 5 (c).

Fig. 5.

(a) The CFPD and PD images from full-wave simulation produced with no clutter motion. Clutter is generated with impedance matches that are 60% of the nominal values of the human model. The white, blue, and red squares indicate the approximate sample locations for flow signal, background signal, and clutter signal, respectively, in the SNR and SCR measurements. (b) The CFPD and PD images from full-wave simulation produced with 3 mm/s clutter motion. (c) Center axial cross-sections of the images in (a) and (b). The green dashed lines in (a) and (b) indicate the approximate azimuthal locations of the cross-sections. (d) Doppler SNR for the PD and CFPD images as a function of clutter level, created with impedance mismatch of 0–300% of the nominal values, for three different simulated physiological motion velocities: 0 mm/s, 2 mm/s, and 3 mm/s. (e) Signal-to-clutter ratio (SCR) as a function of impedance mismatch for three different motion velocities. In (d) and (e), the curves represent the average measurement from the 5 speckle realizations, and the error bars represent the standard deviation of the measurements.

In Fig. 5 (a), for the 0 mm/s case, the vessel is visible in both CFPD and PD images. For the 3 mm/s case in Fig. 5 (b), strong reverberation clutter from the tissue layer is visible above the vessel for the PD image. In addition, the background noise has increased in the PD image. The reverberation clutter in the CFPD image is low. Fig. 5 (c) shows that for all motion velocities, the SNR of the the CFPD images remain higher than the SNR of the PD images with a maximum improvement of approximately 12.5 dB. Fig. 5 (d) shows that the SCR of the CFPD images is higher than the SCR of the PD images by approximately 10 dB. The SNR and SCR of the CFPD images with no motion decrease slower than those of the PD images as impedance mismatch increases, indicating that CFPD is less susceptible to clutter noise than PD. As tissue motion velocity increases, the SNR and SCR of CFPD images decrease at a similar rate as the PD images, but remain 10–15 dB higher than those of the PD images, even when the spatiotemporal filter is applied to remove tissue motion signals.

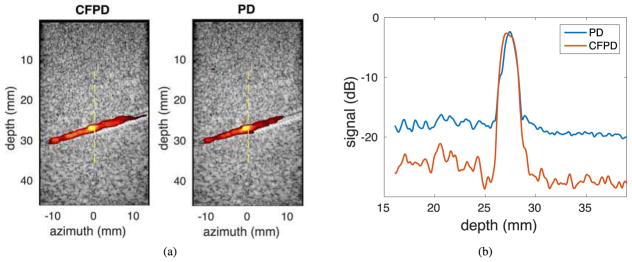
C. Flow Phantom Experiments

Fig. 6 (a) shows one example of CFPD and PD images from the control phantom with no reverberation clutter. The dynamic range for both images is 12.5 dB. Both CFPD and PD images adequately show the vessel with a few minor differences. In Fig. 6 (b), the center axial cross-section of the image is shown, where CFPD shows a lower noise floor by 7.5 dB.

Fig. 6.

(a) Experimental CFPD (left) and PD (right) images acquired with a plane wave synthetic transmit aperture sequence on a flow phantom with a 2-mm diameter vessel with no additional reverberation. The display dynamic range is 12.5 dB. The vessel is visible in both images. (b) Axial center cross-sections of the CFPD and the PD images. The white dashed lines in (a) indicates the approximate locations of axial cross-sections. CFPD shows a noise floor that is approximately 7.5 dB lower than that of PD.

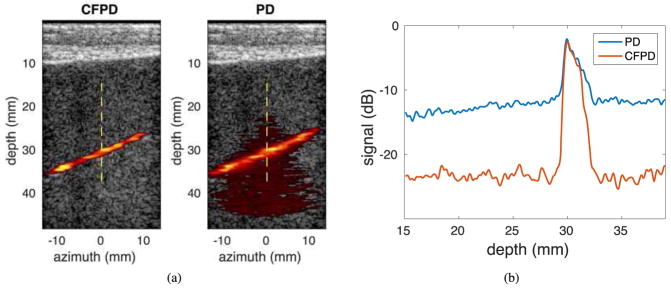
Fig. 7 (b) shows the CFPD and PD images from the phantom studies in the presence of a porcine abdominal model, which produces reverberation clutter, aberration, and attenuation. The abdominal tissue is visible in the shallow part of the images. The Doppler images are shown with the same dynamic range of 12.5 dB as in Fig. 6 (a). Fig. 7 (b) shows the center axial cross-sections of the CFPD and PD images. The noise floor in the PD image increases from −17.5 dB to −12.5 dB, while the noise floor in the CFPD image increases by only 1.5 dB compared to Fig. 6 (b). The SNR in the PD image is 7.5 dB while the SNR in the CFPD image is 17.5 dB.

Fig. 7.

(a) Experimental CFPD (left) and PD (right) images with 12.5 dB dynamic range for display. Data were acquired with a plane wave synthetic transmit aperture sequence on a flow phantom with a 2-mm diameter vessel with reverberation clutter produced with a 1-cm thick porcine abdominal tissue. The vessel is visible in both images; however, the noise in the PD image reduces image quality. (b) Center axial cross-section of the images in (a). The dashed lines in (a) indicates the approximate locations for axial cross-sections. The PD noise floor increases by 5 dB from approximately −17.5 dB to approximately −12.5 dB, while the noise floor in CFPD increases by only 1.5 dB.

D. In Vivo Animal Experiments

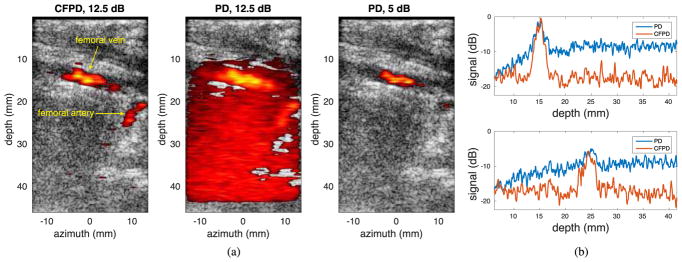
Fig. 8 (a) shows one example of the CFPD and PD images from the in vivo animal studies. The CFPD image is displayed with 12.5 dB dynamic range, and the PD image is displayed with 12.5 dB and 5 dB dynamic ranges. Two vessels, identified by the radiologist (JKW) as femoral vein (upper, approximate diameter: 3.0 mm) and femoral artery (lower, approximate diameter: 2.2 mm), are visible in the CFPD image. In the PD image with 12.5 dB dynamic range, the femoral vein at the shallow depth is visible, but the femoral artery in deeper tissue is obscured by noise. In order to suppress the noise, the dynamic range was reduced to 5 dB. However, with the dynamic range of 5 dB, the femoral artery is no longer visible in the PD image. Fig. 8 (b) shows axial cross-sections of the femoral vein at an azimuthal location of 0 mm and femoral artery at an azimuthal location of 10 mm, both near the middle of the vessels. For the femoral vein, the vessel signal in the CFPD image has an SNR of 14 dB relative to the background, compared to 5.5 dB in the PD image. For the femoral artery, the vessel signal in the PD image is indistinguishable from background noise, while the signal in the CFPD image has an SNR of 10 dB.

Fig. 8.

(a) In-vivo experimental CFPD and PD images acquired from the porcine model. The CFPD image is displayed with a dynamic range of 12.5 dB; the PD image is displayed with two different dynamic ranges: 12.5 dB and 5 dB. The two vessels visible in the CFPD image are femoral vein (upper), and femoral artery (lower). In the PD image with 12.5 dB dynamic range, excessive noise is visible, and the femoral artery is obscured by noise. To completely remove the noise in the lower part of the image, the dynamic range of the PD image has to be reduced to 5 dB. However, with a dynamic range of 5 dB, the femoral artery is not visible in the PD image. (b) Axial cross-section of CFPD and PD images at the center of the femoral vein (upper) and the femoral artery (lower). CFPD shows approximately 10 dB improvement in SNR for both vessels. For PD, the signal of the femoral artery is close to the noise floor, making the vessel difficult to detect.

IV. Discussions

In the Field II simulation of the FT case, Fig. 4 (a) shows that the Doppler image SNR is relatively constant with respect to vessel radii, except when the vessel is smaller than the diffraction limited resolution of the imaging system, which is 0.4 mm for the simulations with focused transmit and 0.7 mm for the simulations with plane-wave transmit. For vessels that are larger than the resolution limit, CFPD improves the Doppler image SNR by approximately 15 dB over PD. Fig. 4 (b) shows that the Doppler image SNR for CFPD and PD are functions of channel SNR. As channel SNR increases from 40 to 80 dB, the PD image SNR increases linearly. The Doppler image SNR improvement with CFPD is 5–20 dB, depending on channel SNR. Although the difference between the CFPD and PD image SNR decreases when channel SNR is high, for current clinical scanners, the channel SNR is unlikely to exceed 60 dB, corresponding to a Doppler image SNR of 10–20 dB, and where methods like CFPD are not needed or have minimal impact. For the PWT case, Fig. 4 shows the similar trend as in the FT case.

In the full-wave simulation studies, physiological motion with clutter generating abdominal layers is studied. As reported previously, the tissue motion signals can be effectively suppressed with advanced filters, including the adaptive blind-source separation filter [28], and the spatiotemporal filter [7], using the higher spatial coherence of the tissue motion signals. However, because reverberation clutter signals produced by the abdominal layers with physiological motion have low spatial coherence [43], they pass through these filters. Fig. 5 shows that this reverberation clutter can be suppressed by CFPD. In Fig. 5 (b), the clutter above the vessel in the CFPD image simulated with 3 mm/s motion velocity is significantly reduced compared with the PD image. Fig. 5 (c) and (d) shows that the Doppler image SNR and SCR of the CFPD images are higher than the PD images by more than 10 dB for most cases. With no motion, the Doppler image SNR and SCR of the CFPD images also decrease at a slower rate than those of the PD images with increasing impedance mismatch. This is because the reverberation clutter that has leaked through the filter has low spatial coherence and can be suppressed by the CFPD technique. At higher physiological motion velocities, additional reverberation clutter leaks through the filter, causing the rate of SNR and SCR decrease to change in CFPD images. These results demonstrate that CFPD and the adaptive filter are synergistic. Note that the SNR and SCR of the CFPD and the PD images are affected by a number of factors, including the amount of suppression of incoherent noise by the CFPD technique, the velocities of the tissue layer movement, and the performance of the spatiotemporal filter. The data presented in Fig. 5 are meant to demonstrate examples with parameters close to clinical settings. For almost all cases, the SNR and SCR of the CFPD images are approximately 7.5–12.5 dB higher than those of the PD images under the same imaging conditions. In addition, qualitatively, the trend of the SNR curve of the CFPD images agrees with the noise performance of the SLSC spatial coherence beamformer [25], [44], for which the SNR peaks as noise is increased. This similarity is likely due to coherent tissue signal leaking through the wall or spatiotemporal filter. As reverberation noise begins to increase from physiological motion, the incoherent noise dominates the leaked tissue signal and signal in this region is suppressed by the SLSC beamforming process. Because the flow signal is strong, the noise has little or no impact on the flow signal. As the reverberation noise (or impedance mismatch) increases, the leaked tissue signal is completely overwhelmed by the incoherent reverberation noise and the flow signal is partially suppressed, decreasing the Doppler SNR.

In the flow phantom studies, as shown in the Fig. 6 (a) and Fig. 7 (a), CFPD produces images with no significant loss of image quality, while the PD images are impacted by thermal noise and reverberation clutter introduced by the porcine abdominal model. From the center axial cross-sections of CFPD and PD images shown in Fig. 7 (b) and Fig. 6 (b), CFPD signals has approximately a 3.5 dB loss of SNR, and PD has approximately a 8 dB loss of SNR, demonstrating that CFPD is less susceptible to the artifacts induced by image degrading abdominal layers, which produce reverberation clutter, attenuation, and aberration. The impact of these different image degrading effects were not individually explored experimentally.

The display dynamic range affects the visualization of vessels in both CFPD and PD images. Extending the dynamic range may reveal vessels with low signal levels; however, the choice of dynamic range is ultimately limited by the noise floor of the signal so as to avoid showing background noise as Doppler signals. Therefore, if the signal of a vessel is close to the noise floor, it cannot be adequately visualized by extending the dynamic range.

In Fig. 8 (a), the femoral artery is clearly visible in the CFPD image displayed with a dynamic range of 12.5 dB. With the same displayed dynamic range, the artery is not differentiable from the noise in the PD image. If the dynamic range is reduced to 5 dB to make the femoral vein in the CFPD and the PD images appear equal, the artery is not visible in the PD image.

The reason of this can be found in the axial cross-section plots in Fig. 8 (b). The PD signal of the femoral artery is barely above the noise floor and either cannot be confidently distinguished from noise or the proper dynamic range setting would likely require extremely fine control. Comparatively, the CFPD signal of the femoral artery is approximately 10 dB above the noise floor, and can be confidently distinguished from the noise. Therefore, it is shown that improvement in Doppler image SNR brings improvement in vessel detection.

In all simulation and experimental studies with PWT synthetic aperture, CFPD results in 5–12.5 dB improvement in SNR over PD. The improvement in SNR can be translated to a reduction of ensemble length and acquisition time without loss of image quality. For example, assuming all other conditions to be the same, 5 dB SNR improvement is approximately equivalent to averaging 9–10 PD images, each produced with an ensemble length of 16. Therefore, the SNR improvement obtained with CFPD has the potential to reduce the amount of data and acquisition time required to produce high-quality images with FT and PWT synthetic aperture imaging technique. In addition, the method has also been demonstrated to improve detection of small vessels by reducing spatially incoherent noise and thus increasing the ratio of the flow signal to the noise so that the vessels are easier visualized by the clinician. Therefore, the method would be useful, particularly in imaging small vessels, such as those in the placenta, and patients with high body mass index (BMI) that produce significant amounts of reverberation clutter.

V. Conclusion

For small vessel detection, we have shown that the CFPD method produces images with 7.5–12.5 dB higher Doppler image SNR than PD under similar imaging conditions. The improvement occurs because of suppression of spatial incoherent noise sources, including thermal noise and reverberation clutter. In the presence of reverberation clutter with physiological motion, CFPD provides approximately 10 dB improvement in SNR and SCR. For in-vivo small vessel imaging, the suppression of incoherent noise including reverberation clutter and thermal noise in high noise environment enables CFPD to provide more effective detection of vessels in deeper part of the tissue that are obscured by noise in PD images.

Biographies

You Leo Li (S’14) was born in Wuhan, China, in 1986. He received the B.Eng. degree in electronics and information engineering from Huazhong University of Science and Technology in 2009, and the M.S. degree in biomedical engineering from Duke University in 2011. He is currently a Ph.D. student in biomedical engineering at Duke University, and a Student of New Faculty in bioengineering at Stanford University. His research interests include Doppler flow imaging, coherence imaging, and computational imaging.

Dongwoon Hyun received the B.S.E. degree in biomedical engineering from Duke University in 2010. He is currently a Ph.D. student at Duke University, and a Student of New Faculty in bioengineering at Stanford University. His research interests include beamforming, coherence imaging, and real-time algorithm implementation.

Lotfi Abou-Elkacem, is a postdoctoral fellow in the Department of Radiology at the Stanford University School of Medicine. He received Ph.D. degree from Rheinisch-Westfalische Technische Hochschule in 2013, and Diplom from J. W. Goethe Universitat Frankfurt in 2008. His research focuses on contrast-enhanced ultrasound imaging, and ultrasound molecular imaging for early pancreatic cancer detection.

Juergen K. Willmann, M.D. is Professor of Radiology at the Stanford University School of Medicine and clinical division chief of Body Imaging in the Department of Radiology. He received his M.D. from the University of Freiburg in Germany and did his clinical radiology training at the University of Zurich in Switzerland. His research focuses on the development and clinical translation of novel molecular and functional ultrasound imaging strategies with special focus on earlier detection and monitoring of breast as well as abdominal and pelvic diseases.

Jeremy J. Dahl (M’11) was born in Ontonagon, MI, in 1976. He received the B.S. degree in electrical engineering from the University of Cincinnati, Cincinnati, OH, in 1999. He received the Ph.D. degree in biomedical engineering from Duke University in 2004. He is currently an Assistant Professor with the Department of Radiology, School of Medicine at Stanford University. His research interests include adaptive beamforming, noise in ultrasonic imaging, contrast-enhanced ultrasound imaging, and radiation force imaging methods.