An Approach to Developing a Prediction Model of Fertility Intent among HIV-Positive Women and Men in Cape Town, South Africa: A Case Study

Abstract

As a ‘case-study’ to demonstrate an approach to establishing a fertility-intent prediction model, we used data collected from recently diagnosed HIV-positive women (N=69) and men (N=55) who reported inconsistent condom use and were enrolled in a sexual and reproductive health intervention in public sector HIV care clinics in Cape Town, South Africa. Three theoretically-driven prediction models showed reasonable sensitivity (0.70 to 1.00), specificity (0.66 to 0.94), and area under the receiver operating characteristic curve (0.79 to 0.89) for predicting fertility intent at the six-month visit. A k-fold cross-validation approach was employed to reduce bias due to over-fitting of data in estimating sensitivity, specificity, and area under the curve. We discuss how the methods presented might be used in future studies to develop a clinical screening tool to identify HIV-positive individuals likely to have future fertility intent and who could therefore benefit from sexual and reproductive health counseling around fertility options.

Introduction

With increased availability and access to antiretroviral (ARV) drugs, many HIV-positive women and men have begun to feel more assured that they can lead healthy and productive lives, including realizing their desires to have children. While it often has been assumed that HIV-positive individuals do not want children, accumulating evidence indicates that some HIV-positive individuals throughout the HIV care trajectory -- from recent diagnosis to achievement of viral suppression as a result of ARVs -- wish to have children [1–10]. South Africa has been the site of numerous studies of fertility intentions among HIV-positive persons. For example, in Cape Town, South Africa, about 50% of HIV-positive women and men who entered the HIV care system were found to be seeking or were open to the possibility of having children [11]. Eleven percent of women attending HIV Care services in Cape Town had been pregnant since becoming aware of their diagnosis, and nearly all pregnancies were unintended [8].

Many studies have identified correlates of fertility intent among HIV-positive persons [5–19], with the majority examining the cross-sectional association between variables of interest and participants’ fertility intent. However, use of prior information to predict future fertility intent, often referred to as a “prediction model”, has rarely been undertaken. Prediction models serve an additional purpose beyond that of testing associations between single variables and the outcome. In an association study, the main focus is to examine the relationship between the outcome and independent variables. While the primary goal is to predict a diagnostic or prognostic outcome, the strength of the association may not provide sufficient information for prediction. For example, in our prior analysis of baseline data from a study of fertility intentions among HIV-positive women and men, we found a significant association between gender and fertility intent (OR=5.64, p<0.001), as well as educational level and fertility intent (OR=0.79, p<0.001) [18]. Such findings indicated that men are 5.64 times as likely as women to have fertility intent, and participants with less than a high school education are 3.22 times as likely as those who graduated from high school to have fertility intent. However, an odds ratio or any other statistics measuring the strength of association (such as risk ratio and risk difference) does not reveal the probability of fertility intent for a particular individual. That is to say that knowing a patient’s gender and educational level as well as their strength of association with the outcome is not enough for a clinician to determine the likelihood of patients’ future fertility intentions. To answer a question such as “Does a person with certain characteristics (e.g., highly educated women) have a high likelihood of fertility intent?” a prediction model for fertility intent is needed. A prediction model with good ability to discriminate allows one to properly predict a binary outcome that may be difficult or costly to obtain at the current time, such as cancer or neurological disease, using information that is relatively easy to collect or available prior to the development of the outcome [19–23].

Prediction models have been widely used in studies evaluating responses to clinical interventions, combining a number of characteristics to predict a diagnostic or prognostic outcome [22]. This modeling approach guides the selection and interpretation of subsequent diagnostic tests, and provides estimates of the clinical probability of having certain diseases [23–25]. Thus, identification of potential clinical markers can help clinicians predict which patients are at high risk for a particular disease. In behavioral studies, a prediction model could be used to predict participants’ future behavior or intentions based on certain characteristics included in the model. Such models have been established and applied to predict depression [26] and suicidal intent [27] in various populations.

In this paper, a case-study is used to illustrate an approach to developing a prediction model rather than trying to establish a “definitive” prediction model of fertility intent. The models are employed to illustrate how such information could help clinicians and counselors address reproductive health issues more effectively with their HIV-positive patients -- by identifying those who might benefit from discussion of pregnancy desires, regardless of where they fall on the HIV care continuum. We further illustrate the added value of a prediction model for clinical and social scientists above what we can learn from testing associations between predictor variables and outcomes, by developing and evaluating several prediction models for fertility intent among a sample of HIV-positive women and men in Cape Town, South Africa. Such a statistical approach provides a useful tool for future researchers seeking to model determinants not only of fertility intent but of other behaviors that have public health significance.

Methods

Study population, recruitment and intervention

We used available data from Emtonjeni (spring of knowledge), a recently completed Phase II randomized futility trial focused on promoting reproductive choices and sexual health among women and men living with HIV. This study was designed to evaluate a multi-level intervention to integrate sexual and reproductive health into care for newly-diagnosed HIV-positive persons who were ineligible for antiretroviral therapy (ART) due to CD4+ counts ≥200mm. Although this pre-ART group was monitored every six months for ARV eligibility, they were not viewed as high a priority for services relative to individuals seen in HIV testing, PMCT+ and ART settings. Our focus on HIV-positive persons at their entry point into the HIV care system allowed for “early” intervention, as significant numbers of women become pregnant prior to becoming eligible for ART [8;28]. At the time of study implementation, between August 2010 and August 2011, neither general medical nor HIV-specific treatment practices routinely addressed concurrent HIV/STI and sexual and reproductive health needs of people living with HIV.

Four typical public sector HIV care clinics in Cape Town, South Africa serving low-income individuals from the surrounding townships were pair matched, and the two clinics within each pair were randomized to either a three-session provider-delivered enhanced intervention or a standard-of-care counselor-delivered intervention. Through values-neutral counseling, the enhanced intervention aimed to help individuals explore the pros and cons of conception vs. pregnancy prevention, and approaches to STI prevention within their unique life circumstances, with the goal of facilitating personal decision-making to optimize their own health and that of existing and future child(ren). In addition to counselling of HIV-positive individuals, the enhanced intervention included on-site contraceptive services and a brief “milieu intervention” for staff. The major outcome was adherence to safer sex guidelines (no condom-unprotected sex) among those wishing to avoid pregnancy, or adherence to safer conception guidelines among those seeking conception. Data from this study allowed us to delineate the proportion of HIV-positive women and men who did and did not opt to seek pregnancy, and whether pregnancies were pursued in line with best practices recommendations.

Prior to receiving their CD4+ cell count results, a clinic nurse gave clients in the waiting area an Information Sheet describing the study (as one about sexual and reproductive health services for HIV-positive women and men aimed at increasing understanding about how to improve the quality of these services within the HIV care system). Those who were interested were referred to study staff for more information. Potential participants were not informed of the study eligibility criteria.

Eligible participants had to be ≥18 years, attending the clinic to receive their first CD4⁺ cell count results since testing HIV-positive and therefore not on ARVs, not pregnant, report unprotected sex in prior three months and/or intent to conceive within the next six months, and be willing and able to provide informed consent. These criteria were selected because our intervention focused on both avoidance of pregnancy and adherence to safer conception among HIV-positive individuals who were intending to conceive. The sample for this analysis was limited to 197 participants who reported inconsistent condom use in the past 3 months, some with and without immediate fertility intent at baseline. There were 151 valid records on their fertility intent at FU2, and 127 valid records on baseline CD4+ count. We excluded 73 participants due to incomplete information on predictor or outcome variables. Thus, analyses in this paper are based on 124 complete cases (for all predictors and outcomes).

Ethical considerations

Informed consent (including for access to medical records) was obtained from all interested eligible participants. Ethical approval was obtained from [Names Removed for Blind Review].

Data collection

Face-to-face interviews were conducted in isiXhosa or English, according to client preference, by experienced gender-matched interviewers in privacy in the clinic. The baseline interview was administered prior to participants’ receipt of CD4⁺ cell count results, except for eight participants, who completed this interview within one month of receiving their results. Participants were again interviewed three months (FU1) and six months (FU2) after baseline, although only baseline and FU2 data were included in this analysis. Participants received 50 rand ($7.00 US at the time of the study) for completing the baseline interview, and 100 rand ($14.00 US at the time of the study) for the 6-month follow-up interview.

Measures

The outcome of interest was the participant’s future intention for conception measured at the FU2 interview. This binary outcome was created based on the participant’s response to the question, “Are you thinking about trying to have a child in the next 12 months?” Independent variables considered in the prediction models included baseline measures of (1) demographic characteristics (gender, age, educational level, work status [working full-time or part-time; self-employed; unemployed], place of residence [living in an informal dwelling/rents a room in someone else’s home, or owns/rents home], and number of children currently under participant’s care); (2) health status (years since HIV diagnosis and CD4⁺ cell count [from the medical record]); (3) sexual partners and practices (whether the participant had a main partner currently or in past 3 months, and if so, whether s/he lived with that partner); (4) disclosure of HIV status to main partner; (5) reproductive history over past 3 months (contraceptive practices, number of biological children, relying on a hormonal method in relationship with current/recent main partner, and participant’s perception of main partner’s fertility intent [interested in immediately conceiving a child, no immediate intent, uncertain about partner’s intent, or partner uninterested in conceiving a child]); and (6) intervention condition (three-session provider-delivered enhanced sexual and reproductive health intervention). We asked about fertility intent only of participants, not specifically with which partner. “Main” partner variables were used as covariates since presumably women and men would know more about main and less about their casual partners; slightly more than two-thirds (68.4%) of participants had only a main partner. Although participants were asked about the HIV status of their partners, many did not know their partners’ statuses; therefore, we excluded this variable from the analysis.

The participant’s fertility intent at baseline also was considered as a potential predictor of FU2 fertility intent. In addition, we assessed self-efficacy for communicating with one’s partner about safer sex and sexual and reproductive health, a measure comprising 9 items with responses in a 4-point Likert format (sample item: ‘How confident are you that you could convince [a/your] regular partner in the next 3 months to use condoms?’, response options ranging from ‘very unconfident = 1’ to ‘very confident = 4’; Cronbach’s alpha = 0.61), and self-efficacy for obtaining information on SRH services, consisting of 4 items and using the same format (sample item: ‘How confident are you that you could find additional information about contraceptive options at a clinic or hospital?’; Cronbach’s alpha = 0.63).

Procedures to establish a prediction model

To establish a prediction model for fertility intent, we first used the data collected from our sample to identify a list of potential predictors for this outcome. A variable was considered a potential predictor if it had theoretical relevance, clinical importance (e.g., gender and intervention condition), or showed significance in a simple logistic regression [14] to predict our outcome. We then used these variables to fit a multiple logistic regression model of the form $log\left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+\cdots +{\beta }_m{X}_m$, where p is the probability of fertility intent (yes vs. no) at six months follow-up (FU2) given male gender (X₁), years of education (X₂), participant had fertility intent at baseline(X₃), number of biological children (X₄), pill/injectable contraceptive use (X₅), and other potential predictors (X₆ to X_m). After obtaining the estimated regression coefficients β̂₀, β̂₁, β̂₂, β̂₃, β̂₄, ... , β̂_m, the predicted probability of fertility intent at FU2, p̂, was then calculated using the formula p̂ = exp (β̂₀, + β̂₁X₁ + β̂₂X₂ +β̂₃X₃ + β̂₄X₄ + ··· + β̂_mXm )/{1 + exp(β̂₀ + β̂₁X₁ + β̂₂X₂ + β̂₃X₃ + β̂₄X₄ + ··· + β̂_mXm)}.

Once p̂ for each participant was calculated, we then aimed to choose an optimal cut-off point (of p̂) to distinguish between participants with and without fertility intent at FU2. The criteria used to select an optimal cut-off point are thoroughly discussed in the literature. There are simple criteria that involve only sensitivity and specificity such as (1) setting a minimum value for specificity and maximizing sensitivity, or setting a minimum value for sensitivity and maximizing specificity [29–31]; (2) maximizing the product of specificity and sensitivity [32]; (3) maximizing the sum of specificity and sensitivity (i.e., maximizing Youden’s Index) [33]; and (4) maximizing the diagnostic odds ratio [34–36]. More complex criteria further take costs of misclassifications into consideration such as (1) the Generalized Youden Index [35, 37–38]; (2) cost-benefit methodology [39–41]; and (3) the misclassification cost term [42–44]. Criteria based on maximization of the Kappa Index [35; 45] make full use of the information in the confusion matrix (a 2X2 table that reports the number of false positives, false negatives, true positives, and true negatives) to assess the improvement over chance prediction.

Costs of misclassifications can also be included in criteria such as the Weighted Kappa Index [34; 46]. Alternatively, researchers/clinicians can base their selection of optimal cut-points on positive predictive value (PPV) and negative predictive value (NPV). Vermont et al. [31] discussed criteria (1) to set a minimum value for PPV or NPV or (2) to maximize the sum or product of PPV and NPV. Likelihood-based methods such as setting a particular value for the negative or positive diagnostic likelihood ratio [47–48], and test-based approaches such as minimizing the p-value associated with the statistical Chi-squared test which measures the association between the marker and the binary result obtained on using the cut-point [49–52] have also been discussed. In cases where prevalence is the parameter of primary important, one can use criteria based on setting (1) the closest value to observed prevalence [53] or (2) sample prevalence to predicted prevalence [53–54]. Given that many more criteria in addition to the above mentioned ones are available to select the optimal cut-point, researchers/clinicians should choose the one that best fits their practical needs. Most importantly, whatever method is going to be used to select a cut-point, it should be specified a priori to preclude researchers from changing the selection criteria after having seen the data, to avoid diminishing the scientific rigor and replicability of the study. For simplicity of discussion, we chose to maximize the Youden index, which is equal to the sensitivity + specificity -1 [33], as our criterion for selecting the optimal cut-point. Once that optimal cut-point was identified, the predicted fertility intent status at FU2 for each of our study participants was determined by the following algorithm: if p̂ was greater than the selected cut-point, that participant was classified by the model as having immediate fertility intent at 6-month follow-up; alternatively, if p̂ was at or below the optimal cut-point, the participant was classified by the model as having no immediate fertility intent at 6 months follow-up.

Evaluation of prediction model

To determine the accuracy of a prediction model, we evaluated the model’s discrimination ability, i.e., the “ability of the model to distinguish correctly the two classes of outcomes” [55]. Sensitivity, specificity, and the area under a receiver operating characteristic (ROC) curve (AUC) are often used to evaluate a model’s predictive capacity (probability of correct classification), and thus model fit. In Table 1, we define ‘condition’ as the outcome, fertility intent at 6-month follow-up, for the prediction model, as determined by a “gold standard” as used in medical diagnostics to refer to “disease diagnosis” using the most appropriate and widely accepted methods. Results based on a gold standard are usually treated as a substitute for the true ‘disease’ status to test a diagnostic method, or, as in this paper, a prediction model. In our study, the gold standard was the actual reported fertility intent at FU2, and the expected fertility intent from the prediction model was compared to it to evaluate the accuracy of the prediction model. Subjects in area A are true positives (tested positive and condition positive), subjects in area B are false positives (tested positive but condition negative), subjects in area C are false negatives (tested negative but condition positive), and subjects in area D are true negatives (tested negative and condition negative). Sensitivity refers to the proportion of true positives among total condition positives (A/(A+C) in the table), i.e., probability of testing positive, given that the subject is condition positive (having certain disease or intent), whereas specificity refers to the proportion of true negatives among total condition negatives (D/(B+D) in the table), i.e., probability of testing negative, given that the subject is condition negative. An ROC curve, on the other hand, provides detailed visual information about the performance of a prediction model. In an ROC curve, plotting the sensitivity against 1-specificity for various cut-points from 0 to 1 can help researchers to select a better prediction model and corresponding optimal cut-point. Specifically, the intercept of the ROC curve with the line at 90 degrees to the no-discrimination line is equivalent to the Youden index (i.e., sensitivity + specificity −1), so the larger the intercept the better the performance of the prediction model. Furthermore, if one chooses the Youden index as the selection criterion for identifying the optimal cut-point, the corresponding cut-point of the largest intercept in the ROC curve will be the optimal cut-point. Another useful statistic generated by the ROC curve is the area under the curve (AOC). It represents the probability that a randomly chosen condition positive (diseased, or in this case, having fertility intent) subject is (correctly) rated or ranked with greater suspicion (probability tested positive) than a randomly chosen condition negative (non-diseased, or in this case, no fertility intent) subject [19]. Thus, the prediction model with the greater area under the curve will have better ability to discriminate patients with and without the disease. The classification of sensitivity, specificity, and AUC vary with the nature of the ‘disease’. For those statistics, one generally considers a value of 0.90 or above as excellent and 0.80 or greater as good.

Table 1.

Explanatory table for sensitivity and specificity

		Condition (as determined by “Gold standard”)
		positive	negative
Test outcome	Positive	A	B
	Negative	C	D

Correction for potential bias in estimating sensitivity, specificity and AUC

As the cut-point for the predicted probability is based on selecting an optimal combination of sensitivity and specificity from the data used to build the model, the direct estimate of these two statistics using data from the entire sample is upwardly biased [33,56]. Therefore, if we take another independent sample from the same population, fit the same model, and use the same cut-point to estimate the sensitivity and specificity, the result may not be as good as that obtained from the current data. This is called overfitting. To reduce the potential for bias due to overfitting, we used a k-fold cross-validation procedure to estimate the sensitivity, specificity, and AUC for the derived prediction model [55; 57]. In k-fold cross-validation, the original sample is randomly partitioned into k equal (or nearly equal) sized subsamples. Of the k subsamples, a single subsample is retained as the validation set for testing the model, and the remaining k-1 subsamples are used as the training set. The cross-validation process is then repeated k times, with each of the k subsamples used exactly once as the validation set. For each cross-validation process, we used one training set to fit a logistic regression model (as shown above), obtained the estimated regression coefficients, calculated the predicted probability of fertility intent at FU2 (i.e., p̂), and selected an optimal cut-point to distinguish participants with fertility intent from those without fertility intent according to the algorithm described above. We then applied the same regression coefficients obtained from that training set to calculate p̂ for each participant in the corresponding validation set, used the selected optimal cut-point (chosen from the training set) to classify the participant’s fertility intent, and obtained one estimate of the sensitivity, specificity, and AUC. The entire process was repeated k times and the final estimate of sensitivity, specificity and the AUC was the average of the k estimates.

For the k-fold cross-validation procedure, there are no definitive guidelines or rules for choosing the number k. Generally speaking, k=5 and 10 are the most common selections of k for cross-validation. However, as the sample we used for illustration in this paper for the prediction model was relatively small (N=124) and had low prevalence (of outcome) (only 20 cases of fertility intent at FU2), we chose a 3-fold and 5-fold cross-validation method to avoid potential issues caused by the small sample size for the validation set. With such choice of cross-validation procedure, we were able to allow for a reasonable number of records in each validation set (41 or 42 records (6 or 7 positives) for 3-fold method and 24 or 25 records (4 positives) for 5-fold method). However, as the number of positives in each set was still relatively small (when k=5, there are only 4 cases in each validation set), the validated sensitivity will be sensitive to the selection of random partition. Therefore, we iterated the cross-validation procedure (100, 1000, and 5000 times) to study the stability of our estimated statistics. Data were managed using the PASW SPSS version 18.0 (SPSS Inc., Chicago, IL); and all analyses were conducted using SAS software version 9.3 [58].

Results

Background characteristics

Participants were, on average, 30.7 years of age and had completed about 10 years of school. There was a greater proportion of women (55.6%) than men (44.4%). More than half of participants worked full- or part-time, and 63.7% resided in an informal dwelling or lived with someone else. On average, they had two biological children and cared for three children. Three-quarters were diagnosed with HIV within the previous year, and the median CD4⁺ cell count was 408 cells/mm³ (values ranged from 73 to 1260, IQR = 216); 32.3% had CD4 <350). All participants reported having a main partner, and 48.4% lived with their main partner. Nearly two-thirds (64.1%) indicated that their main partner knew they were HIV-positive. About two-fifths (43.6%) of participants reported that they or their partner used hormonal contraception.

Establishing prediction models

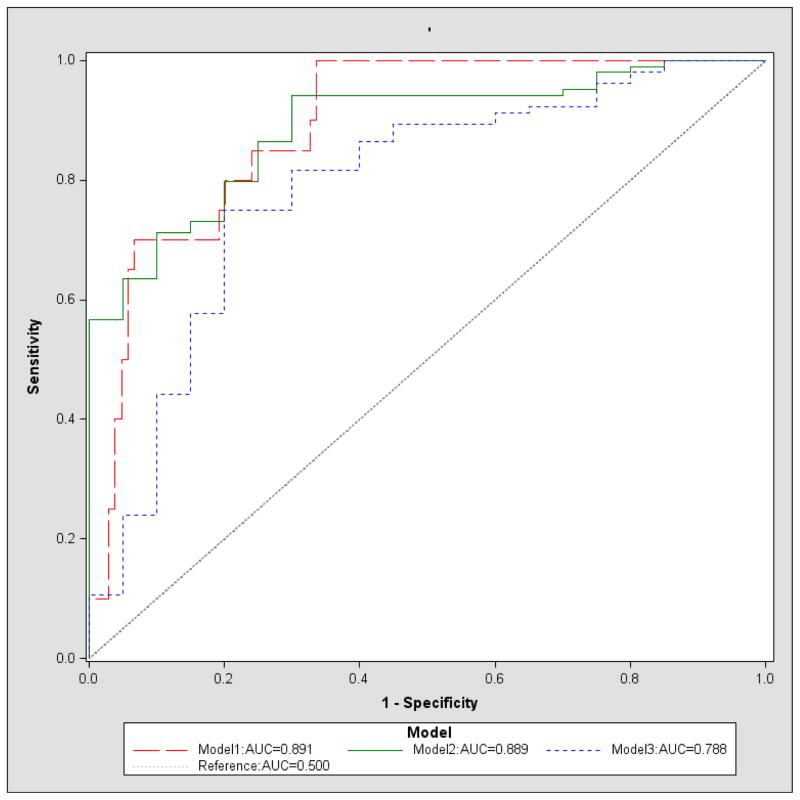
To illustrate a procedure for establishing prediction models, we used the information obtained from 124 study participants to build three models to predict fertility intent. Model 1 included all potential predictors listed above in the Measures Section (Table 2). Model 2 contained all of the predictors in Model 1, with the exception of age, education, and diagnosis within one year, due to the weak association these variables had with the outcome in Model 1 (Table 3). Model 3 was the model identified by a stepwise selection procedure in which all variables considered in Model 2 were entered. It required a significance level of 0.10 for variable entry and 0.05 for variable retention in the model. These inclusion and exclusion criteria are commonly used for larger sample studies, but again, since our analysis was for illustrative purposes, we employed the same significance levels for the selection criteria. Based on these criteria, only three predictors were selected for entry in Model 3: hormonal contraception use (pill/injectable), participant’s fertility intent at baseline, and log transformed CD4⁺ cell count (Table 4). ROC curves for the three models (using the data from entire sample of 124 participants) are shown in Figure 1.

Table 2.

Model 1 regression coefficients, adjusted OR estimates and 95% Wald CIs, and p-values of Wald Chi-squared tests for baseline predictors of reported fertility intent at 6-month follow-up

Baseline predictors	β coefficient estimates	Adjusted OR estimates	95% Wald Confidence Limits		Pr > ChiSq
Intercept	−3.91				0.572
Gender: male	−0.50	0.37	0.09	1.60	0.183
Age	−0.06	0.94	0.85	1.06	0.315
Education (in years)	−0.13	0.88	0.65	1.20	0.417
Home/living status: Shack or lives with someone else	0.89	5.98	0.95	37.61	0.056
Number of biological children	−0.32	0.73	0.38	1.41	0.348
Number of children under participant care	0.20	1.22	0.85	1.77	0.288
Pill/injectable hormonal contraception use	−0.54	0.34	0.06	2.06	0.239
Condition: Intervention	0.20	1.50	0.35	6.43	0.583
Participant fertility intent at baseline	0.87	5.72	1.11	29.49	0.037
Diagnosis within one year	−0.08	0.85	0.20	3.71	0.832
Self-efficacy for obtaining information on SRH	−0.50	0.61	0.19	1.99	0.411
Self-efficacy for communicating with partner re: safer sex & SRH	−2.32	0.10	0.01	1.10	0.060
Lives with main partner	0.36	2.06	0.39	10.82	0.394
Main partner knows participant is HIV-positive	0.51	2.78	0.36	21.54	0.328
Partner fertility intent	0.46	2.53	0.60	10.67	0.208
Work status: employed	0.55	3.03	0.65	14.18	0.160
CD4+ cell count (Log transformed)	2.36	10.62	1.66	67.87	0.013

Table 3.

Model 2 regression coefficients, adjusted OR estimates and 95% CIs, p-values of Wald Chi-squared tests for baseline predictors of reported fertility intent at 6-month follow-up

Baseline predictors	β coefficient estimates	Adjusted OR estimates	95% Wald Confidence Limits		Pr > ChiSq
Intercept	−6.86				0.257
Gender: male	−0.48	0.38	0.10	1.52	0.173
Home/living status: Shack or lives with someone else	1.02	7.67	1.31	44.76	0.024
Number of biological children	−0.30	0.74	0.40	1.37	0.338
Number of children caring under participant care	0.14	1.16	0.82	1.63	0.416
Pill/injectable hormonal contraception use	−0.52	0.36	0.06	2.09	0.253
Condition: Intervention	0.32	1.91	0.48	7.54	0.356
Participant fertility intent at baseline	0.90	6.05	1.20	30.37	0.029
Self-efficacy for obtaining information on SRH	−0.53	0.59	0.18	1.93	0.380
Self-efficacy for communicating with partner	−2.11	0.12	0.01	1.21	0.072
re: safer sex & SRH Lives with main partner	0.16	1.38	0.32	5.92	0.669
Main partner knows participant is HIV-positive	0.58	3.17	0.42	23.99	0.264
Partner fertility intent	0.53	2.87	0.70	11.71	0.141
Work status: employed	0.53	2.87	0.63	12.99	0.172
CD4+ cell count (Log transformed)	2.25	9.53	1.54	59.12	0.016

Table 4.

Model 3 regression coefficients, adjusted OR estimates and 95% CIs, p-values of Wald Chi-squared tests for baseline predictors of reported fertility intent at 6-month follow-up

Baseline predictors	β coefficient estimates	Adjusted OR estimates	95% Wald Confidence Limits		Pr > ChiSq
Intercept	−12.10				0.006
Pill/injectable hormonal contraception use	−0.70	0.25	0.06	1.00	0.050
Participant fertility intent at baseline	0.62	3.49	1.12	10.88	0.032
CD4+ cell count (Log transformed)	1.67	5.32	1.31	21.61	0.019

Figure 1.

ROC curve for models 1–3

k-fold cross-validation

For each of the three models, we report the average sensitivity, specificity, and AUC obtained from 100, 1000, and 5000 iterations of k-fold (k=3, 5) cross-validations, respectively (Table 5). As shown in Table 5, the sum of sensitivity and specificity, as well as AUC estimated through the cross-validation procedure, were uniformly smaller than those obtained via a procedure without cross-validation for all three models. Such findings demonstrated the existence of over-fitting. For example, for Model 3, the sensitivity, specificity, and AUC are 0.800, 0.750, and 0.788, respectively, without cross-validation; however, those values drop to 0.640, 0.750, and 0.758, respectively, for 3-fold cross-validation (with 5000 iterations).

Table 5.

Models 1–3 sensitivity, specificity, AUC for complete case sample, averages for 100, 1000, 5000 iterations of k-fold (k=3, 5) Cross-Validation

Model	k	Iterations	Sensitivity	Specificity	AUC
Model 1	Estimates w/o Cross-Validation		1.000	0.663	0.891
	3	100	0.413	0.788	0.667
		1000	0.439	0.784	0.676
		5000	0.437	0.784	0.676
	5	100	0.512	0.761	0.694
		1000	0.511	0.761	0.699
		5000	0.515	0.761	0.698
Model 2	Estimates w/o Cross-Validation		0.700	0.942	0.889
	3	100	0.492	0.782	0.718
		1000	0.514	0.776	0.722
		5000	0.516	0.775	0.722
	5	100	0.553	0.760	0.737
		1000	0.559	0.759	0.737
		5000	0.561	0.760	0.739
Model 3	Estimates w/o Cross-Validation		0.800	0.750	0.788
	3	100	0.638	0.750	0.758
		1000	0.640	0.748	0.758
		5000	0.640	0.748	0.758
	5	100	0.641	0.745	0.759
		1000	0.640	0.745	0.759
		5000	0.644	0.744	0.759

To illustrate the potential clinical utility of a prediction model, we provide a “diagnosis” chart that is easy for a clinician to use, based on Model 3 (Table 6). For any patient, based on responses to the two dichotomized questions in the prediction model and the cut-point of CD4+ count for each category, a clinician could easily predict the patient’s fertility intent six months after their initial baseline assessment. For example, if an HIV-positive patient with a CD4+ count over 643 reports current fertility intent and hormonal contraceptive (pill/injectable) use (Row 1, Table 6), it indicates her high probability of having fertility intent in the future according to our prediction model. In such a case, the provider would consider initiating a discussion about safer conception strategies to prevent possible HIV transmission due to unsafe sex. Or, if a patient at baseline indicated hormonal contraceptive use, and no fertility intent (Row 2, Table 6), and had a CD4+ count greater than about 935, the model suggests that there may be a change in fertility intent at 6-month follow-up visit – and that it is worth a provider’s time to initiate a discussion with a patient who, based on their initial contraceptive use and intentions, would not necessarily have been ‘flagged’ as someone with whom to explore reproductive issues again. Thus, without a prediction model, this could be difficult for a clinician to predict. Although the diagnosis chart we built from Model 3 is easy to interpret and use in practice, we need to keep in mind that the accuracy of the prediction is imperfect.

Table 6.

CD4+ Cut-points for clinical application

Pill/Injectable Hormonal Contraception Use	Fertility Intent at Baseline	logCD4+ Count	CD4+ Count	Predicted Fertility Intent at FU2
1	1	> 6.47	>643	Yes
		≤6.47	643	No
1	0	>6.84	>935	Yes
		≤6.84	935	No
0	0	>6.42	>616	Yes
		≤6.42	616	No
0	1	>6.05	>424	Yes
		≤6.05	424	No

Discussion

Addressing the reproductive health needs of HIV-positive women and men remains a challenge. The primary purpose of this paper is to highlight the need for developing and testing prediction models to estimate the probability of future fertility intent among HIV-positive individuals, and to provide a methodological approach for establishing a prediction model and evaluating its ability to correctly discriminate. We used available baseline data from a recently completed intervention study that promoted the integration of sexual and reproductive health into HIV care services to demonstrate an approach. This study was not designed to develop a screening or prediction model for fertility intent for application in clinical settings. Instead, the final selected model in our case study was for illustrative purposes only. The models we fitted were not intended to have clinical meaning nor lead to change in practice. Therefore, some important predictors were not measured and the sample size was insufficient for drawing definitive conclusions.

Statistical and clinical considerations for model selection

There are statistical and clinical considerations for model selection. Statistically speaking, the model with higher accuracy of discrimination and greater generalizability is more preferable. Therefore, we would choose Model 3 over Models 1 or 2 due to its higher sensitivity, specificity, and AUC after cross-validation. Note that, as we previously pointed out, the criterion for model selection should not rely on the crude estimate of sensitivity, specificity, and AUC because they are upwardly biased. While Model 1 looks superior from the crude estimates (due to a greater overfitting), Model 3 is still more favorable because its cross-validated statistics are better. Clinically, a prediction model with few variables is more appealing, as the information is easier to obtain. Therefore, from a clinical stand point, Model 3 is still the most preferable model among the three candidates.

When evaluating a prediction model, we often face the question of which is more important -- sensitivity or specificity? It depends. For some severely adverse outcomes, for example, suicide intent, we definitely would want the sensitivity to be as high as possible (with a clinically acceptable corresponding specificity) to preclude missing any persons with suicide intent and to initiate preventative actions. For diseases whose treatment might be painful or time-consuming to the patient, we would want the specificity to be high (with a clinically acceptable corresponding sensitivity) to avoid imposing a burden on true negatives. The Youden index is one of the most common ways to choose a cut-point for a prediction model, but there may be situations in which two or more cut-points have optimal and very close Youden indices; for example, if two cut-points A and B have very close Youden indices of 1.61 vs. 1.60, A with sensitivity 0.75 and specificity 0.86, B with sensitivity 0.85 and specificity 0.75. A researcher will then have to select the final cut-point based on A and B; if sensitivity is more important, one may want to choose B even its Youden index is not optimal. In our case example of identifying HIV-positive persons interested in conception, the cost-benefit issues to be weighed involve risks to uninfected partners and infection of the child, benefits for averting new infections, balanced with providers’ time to address other medical concerns/issues. In such a case we would argue for higher and more stable sensitivity so that we can offer related information and support to people with positive fertility intent. Since these are HIV-positive individuals, a clinician would want to identify those who are likely to want to conceive so that he/she can give them information about how to do so while minimizing the risk of HIV transmission to an uninfected partner. From the results, Model 1 is the least stable, and Model 2 has lower sensitivity and less stability than Model 3. Therefore, Model 3 would be the best choice; also, it has few predictors (only three) and information on the predictors is easy to obtain.

Our case study, designed to illustrate the establishment of a clinical prediction model to estimate the probability of future fertility intent, has a number of limitations. We developed and tested the model on a small sample with unique characteristics and with a relatively limited number of predictor variables. Even though we found that Model 3 was superior to the other two models we tested, this model is not yet primed for clinical application. A considerably larger and more representative sample of our HIV-positive target population and a greater array of predictor variables (e.g., motivation for childbearing, gender norms, social support) are needed to establish a fertility intent prediction model for application in clinical practice. However, our study begins to provide data on an approach to developing a clinical practice model, based on a larger and more representative sample. Clients actively attempting pregnancy as opposed to having intent for pregnancy will additionally need to be considered by clinicians. Given that fertility desires and ability to report these are likely to be highly context-specific and vary between clinic populations (e.g., hospital vs. primary care) and communities (e.g., settings with heavy social expectations for childbearing vs. more limited expectations in others), a single generalizable prediction model for all populations is neither realistic nor ideal. Rather, the approach used in our case study could be applied in different settings to assist in deriving local predictors.

Our sample was limited to HIV-positive women and men who were inconsistent condom users and linked to HIV care and therefore is not representative of all HIV-positive individuals in Cape Town. Also, our case example has a limited follow-up period -- fertility intentions are likely to evolve over a much longer time period than six months, and to be dynamic with changing health as well as with life and partnership circumstances. Therefore, anyone seeking to build a practical prediction model for fertility intentions in clinical care needs to recognize that fertility intent is a moving target. Additional studies are needed to identify variables significantly associated with fertility intent for building an initial prediction model. A well-defined k-fold cross-validation procedure could help to reduce potential bias of over-fitting and to assess the predictive accuracy of the model in the target population. Moreover, a much larger sample of HIV-positive individuals will be needed to give greater confidence in the precision and predictive power of a prediction model of fertility intent that has clinical relevance. Note that once a prediction model is established, it is necessary to evaluate its performance in datasets that were not used to develop the model before its use in clinical practice [59]. This is often referred to as external validation. External validation is essential as it quantifies optimism from model overfitting or deficiencies during the development of a prediction model and evaluates the validity of the model in different locations with a similar population [60]. We did not conduct external validation for any of three models discussed in this paper because they were used only for illustration.

Fertility planning should be an integral part of comprehensive care for HIV-positive women and men, introduced once an HIV-positive individual is engaged in HIV care. Numerous studies have shown that health care providers often refrain from asking HIV-positive individuals, especially men, about their fertility desires [61]. Among many clinicians there is low awareness of safer conception options and that HIV serodiscordance can be maintained in a couple [61]. There is also a perception that in the pre-ART period couples do not consider fertility issues [61], despite the fact that fertility planning is critical in this group. Use of a brief screening tool consisting of variables identified in a prediction model can serve to jumpstart health care providers’ discussion of fertility intent with HIV-positive individuals, prepare providers to develop a plan with their patients, and guide patients to make informed decisions about both contraception and safer conception options in a non-judgmental manner [62]. Both The Southern African Clinicians Society [63] and the South African National Contraception and Fertility Planning Policy and Service Delivery Guidelines [64] call for a stronger move toward routine assessment of fertility options for people living with HIV (PLHIV). In both resource-rich and resource-limited settings where time constraints increasingly challenge the amount of time health care providers spend with patients, an evidence-based screening tool derived from a prediction model could be utilitarian, helping providers to use their time more effectively while accelerating early interventions for PLHIV.