Abstract
Context
Recent analyses of epidemiological data including the National Health and Nutrition Examination Survey (NHANES) have suggested that the harmful effects of obesity may have decreased over calendar time. The shifting BMI distribution over time coupled with the application of fixed broad BMI categories in these analyses could be a plausible “nuisance contributor” to this observed change in the obesity-associated mortality over calendar time.
Objective
To evaluate the extent to which observed temporal changes in the obesity-mortality association may be due to a shifting population distribution for body mass index (BMI), coupled with analyses based on static, broad BMI categories.
Design, Setting, and Participants
Simulations were conducted using data from NHANES I and III linked with mortality data. Data from NHANES I were used to fit a “true” model treating BMI as a continuous variable. Coefficients estimated from this model were used to simulate mortality for participants in NHANES III. Hence, the population-level association between BMI and mortality in NHANES III was fixed to be identical to the association estimated in NHANES I. Hazard ratios (HRs) for obesity categories based on BMI for NHANES III with simulated mortality data were compared to the corresponding estimated HRs from NHANES I.
Main Outcome Measures
Change in hazard ratios for simulated data in NHANES III compared to observed estimates from NHANES I.
Results
On average, hazard ratios for NHANES III based on simulated mortality data were 29.3% lower than the estimates from NHANES I using observed mortality follow-up. This reduction accounted for roughly three-fourths of the apparent decrease in the obesity-mortality association observed in a previous analysis of these data.
Conclusions
Some of the apparent diminution of the association between obesity and mortality may be an artifact of treating BMI as a categorical variable.
Keywords: obesity, mortality, simulations, BMI distribution and categories
Background
Because of the rapid increase in the prevalence of overweight and obesity in the United States,1,2 and the association of obesity with various diseases,3 there has been consistent research to quantify the public health impact of obesity, particularly with respect to mortality. In 2005, Flegal et al.,4 found a very interesting and, to our knowledge, novel result using data from the National Health and Nutrition Examination Surveys (NHANES). Specifically, they reported that the deleterious association of body mass index (BMI)-derived categories of overweight and obesity on mortality may have weakened over the last four decades or so. It can be speculated that such patterns of results may be due to medical advances in the treatment of obesity-related co-morbidities.
Results from other studies have been mixed. Using a prospective cohort from the Cancer Prevention Study II, Calle et al.5 found no indication that the relative mortality rates (MRs) associated with BMI-derived categories of overweight or obesity have decreased. In contrast, three recent studies provided supportive evidence that the deleterious association of obesity with mortality has diminished over time, at least in certain subpopulations.6–8 These diverse results have spurred considerable speculation as to whether methodological factors or data artifacts such as regression-dilution and reverse-causation may have influenced the findings.9–15 However, as discussed previously in Mehta et al. (2014), all of the studies evaluating change in the obesity-mortality association are potentially confounded by unstable study-level factors.7
One potential distorting factor is the effect of categorizing BMI in the analysis coupled with a shifting population BMI distribution. BMI is often modeled as a categorical variable using cutoffs based on sample quantiles or predefined cut-points from federal guidelines.4,16 Treating BMI as a categorical variable is one way of allowing for nonlinearity, and some find it easier to interpret and communicate findings from categorical analyses. In this study, we evaluate the effect of BMI categorization and a shifting population BMI distribution as a plausible “nuisance contributor,” using the same data from NHANES as in the study of Flegal et al.4 We use the term nuisance contributor in the sense of a nuisance statistical parameter, that is, an aspect of the model distribution that is not of primary interest, but must be accounted for. Specifically, we hypothesize that even if the true effect of BMI as a continuous variable has not changed, changes in the BMI distribution could affect the calculated estimates for specific BMI categories. Within each BMI category is a distribution of continuous BMI values. Those within-category distributions may have changed over time as the overall distribution of BMI has markedly changed over time.1,2,17,18 To the extent that different BMI values within a BMI category are associated with different MRs, then absolute categorical MRs, which would be functions of the absolute MRs integrated over the within-category probability density function of BMI, can change over time even though the absolute rate associated with any specific value of BMI may not have changed.
Materials and Methods
Separate waves of a large publicly available complex cross-sectional health examination survey designed to represent the United States non-institutionalized civilian population were used. Both studies reported here used NHANES I (1971–1975) and III (1988–1994) baseline data. NHANES I Epidemiologic Follow-Up Study (NHEFS) (1982–84) was used to retrospectively impute smoking data.15,19 Design and sampling methods for NHANES I and NHANES III have been previously reported.20–22 Mortality information for NHANES I participants was obtained from the 1992 NHEFS Vital and Tracing Status file with follow-up until 1992.23,24 Mortality information for NHANES III was available from the NHANES III public-use National Center for Health Statistics (NCHS) linked mortality file with follow-up until 2000.
Adults aged 25 years and older at baseline were included in our analyses, and pregnant women were excluded.25 Our model and covariate coding reflected Flegal et al.’s4 including smoking, race, sex, and alcohol consumption as covariates. The smoking variable was coded as never, current, and former smokers and sex as male or female. Alcohol consumption categories were defined as 0, <0.07, 0.07 to 0.35, and ≥0.35 oz/d. Race was coded as “white,” “black,” or “other.” Our primary analysis models were conducted to account for the complex sampling design of NHANES as described elsewhere.26 Attained age at death or end of follow-up was chosen as the time scale,4,27 and left truncation at the age of study entry was accounted for in each survey Cox model. Publicly available mortality data were used to create 3 different attained age subpopulations (25 to <60, 60 to <70, and ≥70 years of age) for NHANES I and III. Before evaluating our hypothesis, we replicated the analysis done by Flegal et al.4 to reproduce the hazard ratios (HRs) of the NHANES I and III subpopulations published in their Figure 1. This was important because analyzing NHANES data is complex and the choice of sample weights, variables, and derived variable coding can affect the analysis.15 R 2.7.228 and the R/survey package 3.1029 were used to perform all analyses.
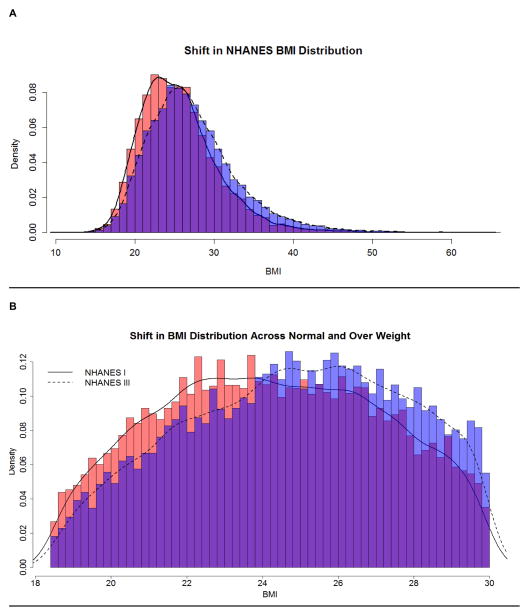
Figure 1. Changes in BMI Distribution over Time Illustrated using NHANES I and NHANES III.
BMI on the x-axis and density on the y-axis.
A simulation procedure was used to evaluate the impact of shifting BMI distribution along with broad fixed BMI categories
Our simulation procedure was designed to assess the impact of applying broad static BMI categories by first estimating the BMI-mortality relationship in NHANES I. We then forced this relationship to hold in NHANES III by simulating mortality follow-up conditional on its observed baseline data, thus implying no change in the BMI-mortality relationship and yet allowing for a shifting population BMI distribution.
-
Fitting a ‘true’ model for NHANES I sub-population with BMI as a continuous predictor:
Within each attained age strata of NHANES I (e.g. age strata 25–<60) linked to the NHEFS mortality data, a Cox proportional hazards model was fit treating mean-centered BMI as a cubic polynomial. Race, sex, age, smoking status and alcohol consumption were included as covariates. To improve model fit, age was modeled as a quadratic polynomial.
-
Simulating survival times for NHANES III Subpopulation.
We applied the simulation procedure described in Bender et al.30,31 to approximate the baseline survival distribution from the Cox model. Within each NHANES I attained age strata, the baseline hazard was approximated by an exponential distribution. We simulated survival times for each NHANES III attained age strata, using the estimated parameters for the derived distribution and estimated coefficients of the predictors from the corresponding ‘true’ model with observed BMI and covariate data from corresponding sub-population of NHANES III (e.g. attained age strata 25–<60).
-
Simulating right censoring and events (death).
In order to induce similar lengths of follow-up and patterns of right-censoring within our simulations, we fit an analogous logistic regression model to the NHANES I dataset with whether or not death was observed as the outcome, using the same set of predictors included in the Cox regression model. Using the resulting estimates, we then inverted the logistic model to calculate predicted probabilities of observing the death time for each individual in NHANES III. Within each simulated data set, we randomly assigned each simulated mortality time as observed/censored according to this predicted probability. Moreover, individuals simulated to live longer than their assigned attained age subpopulation (based on observed mortality) were censored at the following attained age cutoffs: 59.9 for 25 to <60 and 69.9 for 60 to <70. We generated 2000 simulated mortality datasets for each attained age strata of NHANES III.
-
Evaluating the effect of shifting BMI distribution and categorical BMI variable in the model.
For each simulated attained age NHANES III data, a Cox proportional hazards model was then fit with BMI split into five categories based on recommendations from federal guidelines4 and described earlier. Percentile based confidence intervals for the HRs for each of these BMI categories of each sub-population for NHANES III were computed from the empirical distribution of the 2000 simulated datasets. Point estimates of the HRs from the simulated follow-up data were calculated as the medians of the empirical distributions of the log HRs. We then evaluated the percentage reduction in the HRs of grade 1 and 2/3 obesity in NHANES III by using simulated follow-up data with respect to the corresponding categories in NHANES I that could be attributed to this nuisance contributor.
Sensitivity Analyses
We performed additional simulations in the attained age category 25 to <60 as sensitivity analyses to evaluate the robustness of our findings with another parametric specification functional form used as a true model in NHANES I. We also conducted simulations to account for the uncertainty in the coefficients estimated from NHANES I. To assess the robustness of our findings to the functional form of the parametric model, we simulated mortality follow-up of NHANES III by choosing a penalized spline model using the ‘pspline’ function (with degree=4) available in the survival package of R with degree=4. In these simulations we did not account for complex sampling design. Hence, we also recomputed the obesity category HRs in NHANES I and III using observed mortality follow-up without incorporating the complex sampling design. We then compared the HRs of obese categories from NHANES III simulated mortality follow-up with corresponding hazard ratios of obesity categories from NHANES I based on observed mortality follow-up.
Further, to account for uncertainty in the estimates, we generated bootstrap replicates of NHANES I data. We fitted the penalized spline parametric form and redid our simulations. That is, for each iteration of our simulation in these analyses, the true model was estimated from a bootstrap replicate of NHANES I. The observed mortality-follow-up based HRs of obese categories for bootstrap replicates of NHANES I were estimated and compared to corresponding hazard ratios in NHANES III using simulated mortality.
Results
Descriptive measures of NHANES I and NHANES III can be found in Table 1. These descriptive measures illustrate that our baseline data was very similar to the published analyses of Flegal et al. There were 3,773 deaths observed for NHANES I from an unweighted sample size of 13,551 and 2,793 deaths observed for NHANES III from an unweighted sample size of 14,985. There is an increase in the prevalence of overweight, grade 1 obesity, and grade 2/3 obesity moving from NHANES I to NHANES III. As seen in panels A and B of Figure 1 the BMI distribution has shifted from the 1970s (NHANES I) to 1990s (NHANES III).
Table 1.
Descriptive measures of the NHANES I and III survey data
| NHANES I | NHANES III | |
|---|---|---|
| Baseline years | 1971–1975 | 1988–1994 |
| Mortality follow-up | 1992 | 2000 |
| Unweighted sample sizes | 13,551 | 14,985 |
| Person years of follow-up | 219,030 | 123,603 |
| Number of women | 7,537 | 7,888 |
| Age (minimum, mean, maximum) | (25, 48.98, 74) | (25, 52.69, 90) |
| Number of deaths* | 3,773 | 2,793 |
| Prevalence of BMI level (%) | ||
| BMI <18.5 | 3.37 | 2.14 |
| BMI 18.5 – <25 | 46.28 | 35.58 |
| BMI 25 – < 30 | 33.47 | 35.82 |
| BMI 30 – <35 | 12.07 | 16.9 |
| BMI ≥35 | 4.81 | 9.57 |
Changes in obesity-associated mortality using observed mortality data
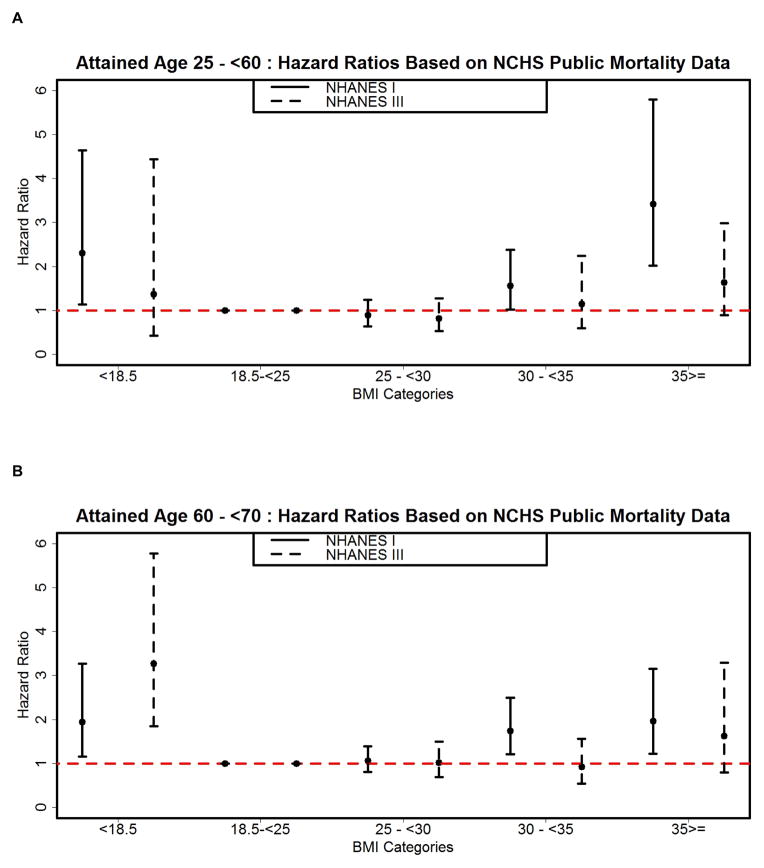
The HRs estimated for the different subpopulations of NHANES I and III by use of the NCHS linked mortality files (observed mortality) are shown in Figure 2 A, B, and C. In general, these results were similar to the findings published previously 4 where it was suggested that the deleterious effects of overweight and obesity on mortality have reduced over calendar time.
Figure 2. Hazard Ratios (with 95 % confidence intervals) of Mortality Rate by BMI Category for Different Attained Age Strata using the NCHS linked Publicly Available Mortality Data.
BMI categories on the x-axis are underweight (BMI < 18.5), normal weight (BMI 18.5 to <25), overweight (BMI 25 to <30), grade 1 obesity (BMI 30 to < 35), and grade 2/3 obesity (BMI ≥ 35).
In the attained age stratum of 25 to <60 years, the percentage reduction in the HRs for grade 1 and 2/3 obesity of NHANES III versus NHANES I were 26.28% and 52.33%, respectively. The interval estimates for grade 1 and grade 2/3 obesity in NHANES I were 1.56 (1.02, 2.38) and 3.42 (2.02, 5.8). Corresponding estimates for NHANES III were 1.15 (0.59, 2.24) and 1.63 (0.89, 2.98). In the attained age stratum of 60 to <70 years, the percentage reduction in the HRs of grade 1 and 2/3 obesity were 47.12% and 17.34% respectively. The HR estimates for grade 1 obesity were 1.74 (1.21, 2.49) for NHANES I and 0.92 (0.54, 1.56) for NHANES III. The HRs for grade 2/3 obesity were 1.96 (1.22, 3.15) and 1.62 (0.80, 3.29) in NHANES I and III respectively. In the attained age stratum of 70 years or more, the percentage reduction in the HRs of grade 1 and 2/3 obesity were 28.57% and 49.73%, respectively. The HR of grade 1 obese in NHANES I was 1.26 (1.05, 1.51) and 0.90 (0.74, 1.11) in NHANES III. The HR for grade 2/3 obese in NHANES I was 1.89 (1.40, 2.55) and in NHANES III was 0.95 (0.65, 1.38).
BMI Categorization and Shifting BMI Distributions
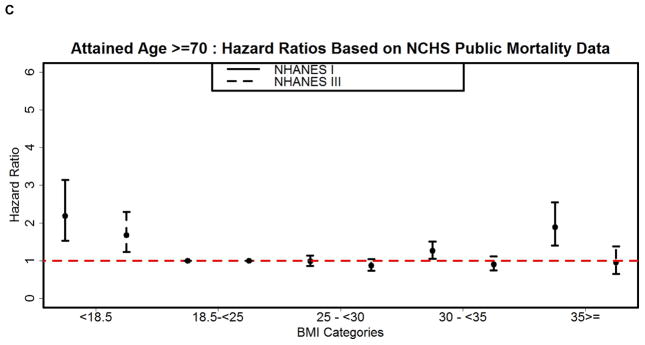
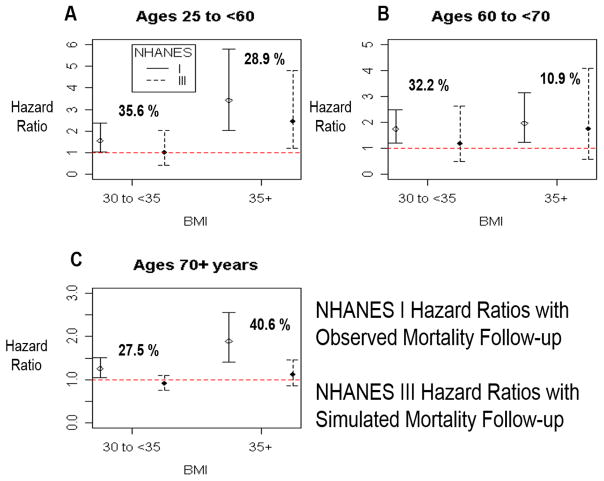
We next generated HRs for NHANES III corresponding to different attained age strata from the simulated follow-up data so that the true association of BMI with mortality was forced to be the same as what was estimated in NHANES I. The HR point estimates for NHANES III are median values from the empirical distribution. Except for the underweight category in the attained age stratum of 25 to <60 years, the mean HR estimates from the empirical distribution were very similar to the median HR estimates of the empirical distribution (Figure 3 A, B, and C). This figure also includes the HRs for NHANES I computed from the publicly available NHEFS linked mortality data.
Figure 3. Hazard Ratios (with 95 % confidence intervals) of Mortality Rate by BMI Category for Different Attained Age Strata using Simulated Mortality Data for NHANES III. Estimates for NHANES I based on the observed NHEFS linked mortality data.
BMI categories on the x-axis are underweight (BMI < 18.5), normal weight (BMI 18.5 to <25), overweight (BMI 25 to <30), grade 1 obesity (BMI 30 to < 35), and grade 2/3 obesity (BMI ≥35).
As shown in Figure 3A, for the attained age stratum of 25 to <60 years, grade 1 obesity in NHANES III had a HR of 1.0 (0.43, 2.01) while grade 2/3 obesity had a HR of 2.43 (1.21, 4.81). The percentage reduction in the HR for grade 1 obesity in NHANES III with the simulated follow-up data versus the NHANES I HR with observed mortality follow-up was 35.58%, with a similar relative reduction for grade 2/3 obesity (28.87%). These reductions were 135.40% and 55.16% of the corresponding decreases estimated using the observed mortality data for NHANES III.
As shown in Figure 3B, for the attained age stratum of 60 to <70 years, the percentage reduction in the HR for grade 1 obesity of NHANES III with the simulated follow-up data versus NHANES I was 32.23%, with a reduction of 10.87% for grade 2/3 obesity. This reduction was 68.61% and 62.66% of the decrease found in the HRs of NHANES III using the observed NHANES III mortality data. The HR estimate for grade 1 obesity and grade 2/3 obesity in NHANES III with simulated mortality data was 1.17 (0.49, 2.63) and 1.74 (0.57, 4.08) respectively.
For the attained age stratum of ≥70 years, the percentage reduction in the HR of grade 1 obesity of NHANES III with the simulated follow-up data versus NHANES I was 27.47%, with a reduction of 40.60% for grade 2/3 obesity. This reduction was 96.16% and 81.64% of the decrease found in the HR estimates of NHANES III by using the observed mortality data. The HR associated with grade 1 obesity and grade 2/3 obesity in NHANES III with simulated mortality data was 0.91 (0.75, 1.1) and 1.12 (0.86, 1.46) respectively.
Sensitivity Analyses
Table 2 provides the complete set of sensitivity analyses results. As expected the HR estimates of obese categories in NHANES I and III using observed mortality follow-up but without accounting for the complex sampling design were different than the estimates that were generated using the complex sampling design. However, the original pattern of obesity category hazard ratios still showed a decline from NHANES III to I. The first set of sensitivity analysis focused on understanding the robustness of our findings to the choice of the functional form of the parameters in the model. When a penalized spline model was fitted as true model to NHANES 1 and mortality follow-up simulated for NHANES III in attained age 25 to <60, the percentage reduction in the HR for grade 1 obesity in NHANES III with the simulated follow-up data versus the NHANES I HR with observed mortality follow-up was 31.85%. The percentage reduction for grade 2/3 obesity in NHANES III compared to NHANES I was 63.44%.
Table 2.
Sensitivity Analyses Results Based on Attained Age 25 to <60
| NHANES | BMI Category | HR | 95% CI | Analysis Type | |
|---|---|---|---|---|---|
| I | 30 to <35 | 1.35 | 0.98 | 1.86 | Observed mortality follow-up but without complex sampling design |
| 35 or above | 2.79 | 1.97 | 3.95 | ||
| III | 30 to <35 | 0.95 | 0.72 | 1.27 | Observed mortality follow-up but without incorporating complex sampling design |
| 35 or above | 1.15 | 0.83 | 1.6 | ||
| III | 30 to <35 | 0.92 | 0.55 | 1.43 | Simulated mortality follow-up based on penalized spline fitted to NHANES I. Complex sampling design not incorporated. |
| 35 or above | 1.02 | 0.545 | 1.66 | ||
| I | 30 to <35 | 1.35 | 0.97 | 1.82 | Simulated mortality follow-up based on penalized spline fitted to NHANES I. Complex sampling design not incorporated. |
| 35 or above | 2.78 | 1.69 | 3.84 | ||
| III | 30 to <35 | 1 | 0.54 | 1.62 | Simulated mortality follow-up based on penalized spline fitted to bootstrap replicates of NHANES I. Complex sampling design not incorporated. |
In the second set of sensitivity analysis we incorporated the uncertainty in the true model estimates from NHANES I by fitting the penalized spline model to NHANES I bootstrap replicates. We found that the percentage reduction in the HR for grade 1 obesity in NHANES III with the simulated follow-up data versus the NHANES I HR with observed mortality follow-up was 25.93%. The percentage reduction for grade 2/3 obesity in NHANES III compared to NHANES I was 66.9%.
Discussion
Changes observed in the obesity-mortality association have been attributed to medical advances in the treatment of obesity-related co-morbidities over calendar time.4,6,7,32 However, all of the previous studies that have indicated a decline are potentially confounded by unstable study-level confounders.7 One such confounder discussed here is a shifting population BMI distribution coupled with analyses based on static, broad BMI categories. We used the widely cited nationally representative study by Flegal et al. to illustrate the influence of this nuisance contributor in studies evaluating changes in obesity-associated mortality over time.4 Because we simulated follow-up data for NHANES III such that the relationship between BMI and mortality was identical to that in NHANES I, the expectation is that the point estimates for each BMI categories in the respective attained age subgroup of the NHANES series would be similar. In other words, if the population BMI distribution had no influence, we would not see lower HRs for the grade 1 and grade 2/3 obesity over calendar time. The results shown in Figure 3 indicate that in all attained age subgroups, the grade 1 and 2/3 obesity HRs for NHANES III from the simulated follow-up data were lower than what was estimated in NHANES I. In general, the decreases in the HR of NHANES III compared with NHANES I were very similar to the patterns seen in Figure 2, in which the public mortality data for NHANES III were used. On average, the HRs of NHANES III from simulated mortality follow-up were approximately 29.3% lower than the NHANES I estimates using observed mortality-follow-up. Overall, this trend suggests that the effect of BMI categorization and altered population BMI distributions between NHANES I and III may have contributed up to 75% of the apparent change in the obesity-mortality association over calendar time.
Replicating previously published work is a challenge, especially for complex data sets like NHANES.15,33 We recognize that analyzing the NHANES data correctly involves choosing variables appropriately, and we made an earnest effort to replicate the NHANES analyses according to the NCHS guidelines. While to the best of our knowledge we used the same exclusion criteria as that of the 2005 manuscript by Flegal et al.,4 we did notice a discrepancy in the unweighted sample size of NHANES I we derived compared to what has been published in 2005. One aspect of data merging specific to NHANES I that could have led to these different sample sizes was the use of NHANES I Epidemiologic Follow-Up Study (NHEFS) (1982–84) to retrospectively impute smoking data. While we replicated this step, there may have been additional data steps/details unknown to us limiting our ability to replicate their dataset. However, we want to stress that we used Flegal’s influential analysis as an illustration only to evaluate the role of plausibility of the nuisance contributor (unstable study-level confounder) since this was one of the first studies that showed significant declines in the obesity-associated mortality across period. Overall, our results for NHANES III were very similar to those published in 2005.4 Our results for the NHANES I data followed the overall trend, and most of the estimates were comparable to those previously published.4 However, a few point estimates of certain NHANES I BMI categories differed by more than 10%.
To verify our data, we reproduced the results published in Table 3 (HR estimates with baseline and retrospective smoking data) of Flegal et al. 2010.15 Because the results published for NHANES I in 201015 did not include alcohol in the model, we speculate that the variability between our results and those of Flegal et al.4 for the NHANES I data may be attributed to differences in the coding of the alcohol consumption covariate, as well as any perturbation introduced from using the publicly available mortality data. As illustrated in Figure 2, compared with NHANES I, in which the baseline data were collected in 1971–1975, the HR of death in NHANES III for overweight and obesity was lower or equal across all attained age subpopulations. In general, these trends were similar to the findings published previously,4 where it was suggested that the deleterious effects of overweight and obesity on mortality have reduced over calendar time. Recent studies have indicated a similar trend at least for the certain subpopulations of the US population.
One of the limitations of our simulations is that our true model for NHANES I was estimated, and does not fully explain the variability in that dataset. Therefore, the reduction in the HR of NHANES III (in Figure 3) estimated using simulated follow-up data may in part be a function of the choice of estimated model and the parametric approximation used to model the baseline hazard distribution. Our sensitivity analyses, however, assessed the robustness of our findings by assuming a different, much more flexible functional form of the parametric approximation as well as accounting for the uncertainty in the estimates. The overall trends of our findings were similar even when we switched from a cubic polynomial to a penalized spline approach and later accounted for the uncertainty in the estimates of the true model. Although we were not able to incorporate the complex sampling design when fitting the penalized spline model, interestingly, this limitation in the sensitivity analyses helped us assess whether our findings are sensitive to complex sampling design. However, we caution readers that the HR estimates of NHANES presented in the sensitivity analyses should not be considered estimates for the US population since the complex sampling design was not used.
Another complexity in our simulation stems from the attained age stratification as a means of addressing violations of proportional hazards assumption by stratifying on attained age when age is the time scale.27 This type of modeling implied that if the simulated follow-up of a NHANES III subject belonging to the original age stratum of 25 to <60 was death at 69, then our simulation procedure censored this individual at 59.9 years of age. If we chose not to follow this procedure, we would not be analyzing the simulated data and the observed data consistently. This mutually exclusive situation was a challenge to handle and may lead to some confounding in our simulations, especially in the age stratum of 25 to <60. However, this confounding was minimal or none in the age stratum of ≥70, for which we also found large effects that could be attributed to a shifting population BMI distribution.
In brief, our simulations based on an existing analysis in the literature suggest that the attenuation of the obesity-mortality association may in part be a function of treating BMI as a categorical variable combined with a change in the US population BMI distribution. One likely implication of this finding is that were the relationship in the NHANES data estimated using a parametric form such as a cubic polynomial or other flexible continuous functional form in a parametric survival regression, it is plausible that that the marginal effects at any BMI would be much closer for the two surveys than if BMI is categorized. The implications of our findings are not limited to the outcome of mortality. This phenomenon could also influence findings on the association of obesity with other outcomes such as disability.34 Because obesity-mortality analyses can influence obesity-related clinical practice and public health policy, the identification of these nuisance contributors is potentially of great importance. We recommend supplementing categorical analyses by also treating BMI as a continuous variable in future BMI-mortality analyses, especially those assessing changes in the relationship over calendar time. Further, we advise caution in interpreting the apparent reduction in the obesity-mortality association as being driven by treatment advances. Future work in this area also needs to quantify rigorously the extent to which successes in medicine explain the any apparent reduction in the obesity-mortality association.
Acknowledgments
Funding/Support:
This work was supported in part by NIH grants R01DK076771, P30DK056336, T32HL072757, and R21DK077959. The opinions expressed are those of the authors and not necessarily those of the NIH or any other organization with which the authors are affiliated.
Footnotes
Author Contributions:
Dr. Mehta had full access to all of the data and takes responsibility for the integrity of the data and the accuracy of the analysis.
Study concept and design: Allison
Acquisition of data: Mehta
Drafting of the manuscript: Mehta, Allison, Fontaine, Keith, Pajewski
Critical revision of the manuscript for important intellectual content: Allison, Fontaine, Keith, Mehta, Pajewski
Statistical analysis: Mehta
Analysis and interpretation of data: Mehta and Pajewski
Simulation Code Implementation: Mehta and Pajewski
Conflicts of Interest and Financial Disclosures: Dr. Allison has received numerous grants, donations, and consulting fees as well as book royalties from non-for-profit and for profit entities with interests in obesity.
Conflict of Interest Disclosures:
Dr. Allison has received payments from non-profit and for-profit organizations with interests in obesity. Dr. Mehta has consulted with Gjording Fouser PLLC. Drs. Kevin Fontaine, Scott Keith and Nicholas Pajewski have no financial disclosure and conflict of interest to report.
Role of the Sponsors: The sponsors had no role in influencing the content of this paper.
Contributor Information
Tapan Mehta, Email: tapan@uab.edu.
Nicholas M. Pajewski, Email: npajewsk@wakehealth.edu.
Scott W. Keith, Email: scott.keith@jefferson.edu.
Kevin Fontaine, Email: kfontai1@uab.edu.
David B. Allison, Email: dallison@uab.edu.
References
- 1.Hedley A, Ogden C, Johnson C, Carroll M, Curtin L, Flegal K. Prevalence of overweight and obesity among US children, adolescents, and adults, 1999–2002. JAMA. 2004 Jun;291(23):2847–2850. doi: 10.1001/jama.291.23.2847. [DOI] [PubMed] [Google Scholar]
- 2.Ogden C, Carroll M, Curtin L, McDowell M, Tabak C, Flegal K. Prevalence of overweight and obesity in the United States, 1999–2004. JAMA. 2006 Apr;295(13):1549–1555. doi: 10.1001/jama.295.13.1549. [DOI] [PubMed] [Google Scholar]
- 3.Misra A, Khurana L. Obesity and the metabolic syndrome in developing countries. J Clin Endocrinol Metab. 2008 Nov;93(11 Suppl 1):S9–30. doi: 10.1210/jc.2008-1595. [DOI] [PubMed] [Google Scholar]
- 4.Flegal K, Graubard B, Williamson D, Gail M. Excess deaths associated with underweight, overweight, and obesity. JAMA. 2005 Apr;293(15):1861–1867. doi: 10.1001/jama.293.15.1861. [DOI] [PubMed] [Google Scholar]
- 5.Calle E, Thun M, Petrelli J, Rodriguez C, Heath CJ. Body-mass index and mortality in a prospective cohort of U.S. adults. N Engl J Med. 1999 Oct;341(15):1097–1105. doi: 10.1056/NEJM199910073411501. [DOI] [PubMed] [Google Scholar]
- 6.Mehta NK, Chang VW. Secular Declines in the Association Between Obesity and Mortality in the United States. Popul Dev Rev. 2011 Sep;37(3):435–451. doi: 10.1111/j.1728-4457.2011.00429.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mehta T, Fontaine KR, Keith SW, et al. Obesity and mortality: are the risks declining? Evidence from multiple prospective studies in the United States. Obesity Reviews. 2014 doi: 10.1111/obr.12191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Afzal S, Tybjærg-Hansen A, Jensen GB, Nordestgaard BG. Change in Body Mass Index Associated With Lowest Mortality in Denmark, 1976–2013. JAMA. 2016 May;315(18):1989–1996. doi: 10.1001/jama.2016.4666. [DOI] [PubMed] [Google Scholar]
- 9.Greenberg J. Biases in the mortality risk versus body mass index relationship in the NHANES-1 Epidemiologic Follow-Up Study. Int J Obes Relat Metab Disord. 2001 Jul;25(7):1071–1078. doi: 10.1038/sj.ijo.0801648. [DOI] [PubMed] [Google Scholar]
- 10.Greenberg J. Hypothesis - the J-shaped follow-up relation between mortality risk and disease risk-factor is due to statistical confounding. Med Hypotheses. 2002 Nov;59(5):568–576. doi: 10.1016/s0306-9877(02)00155-x. [DOI] [PubMed] [Google Scholar]
- 11.Greenberg J. Correcting biases in estimates of mortality attributable to obesity. Obesity (Silver Spring) 2006 Nov;14(11):2071–2079. doi: 10.1038/oby.2006.242. [DOI] [PubMed] [Google Scholar]
- 12.Greenberg J, Fontaine K, Allison D. Putative biases in estimating mortality attributable to obesity in the US population. Int J Obes (Lond) 2007 Sep;31(9):1449–1455. doi: 10.1038/sj.ijo.0803615. [DOI] [PubMed] [Google Scholar]
- 13.Greenberg J. Biased corrections or biased about corrections? Obesity (Silver Spring) 2009 May;17(5):939–940. doi: 10.1038/oby.2009.10. author reply 940. [DOI] [PubMed] [Google Scholar]
- 14.Flegal K, Graubard B, Williamson D, Gail M. Simple examples should not be extrapolated to the US population. Int J Obes (Lond) 2008 May;32(5):875. doi: 10.1038/sj.ijo.0803788. author reply 876–877. [DOI] [PubMed] [Google Scholar]
- 15.Flegal K, Graubard B, Williamson D, Gail M. Sources of differences in estimates of obesity-associated deaths from first National Health and Nutrition Examination Survey (NHANES I) hazard ratios. Am J Clin Nutr. 2010 Mar;91(3):519–527. doi: 10.3945/ajcn.2009.28222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Panel NOEIE. Clinical Guidelines on the Identification, Evaluation, and Treatment of Overweight and Obesity in Adults. NIH; 1998. Vol 98-4083. http://www.nhlbi.nih.gov/guidelines/obesity/ob_home.htm. [PubMed] [Google Scholar]
- 17.Flegal K, Carroll M, Ogden C, Johnson C. Prevalence and trends in obesity among US adults, 1999–2000. JAMA. 2002 Oct;288(14):1723–1727. doi: 10.1001/jama.288.14.1723. [DOI] [PubMed] [Google Scholar]
- 18.Wang Y, Beydoun M, Liang L, Caballero B, Kumanyika S. Will all Americans become overweight or obese? estimating the progression and cost of the US obesity epidemic. Obesity (Silver Spring) 2008 Oct;16(10):2323–2330. doi: 10.1038/oby.2008.351. [DOI] [PubMed] [Google Scholar]
- 19.Cohen B, Barbano H, Cox C, et al. Plan and operation of the NHANES I Epidemiologic Followup Study: 1982–84. Vital Health Stat 1. 1987 Jun;(22):1–142. [PubMed] [Google Scholar]
- 20.Plan and operation of the health and nutrition examination survey: United States-1971–1973. Vital Health Stat 1. 1973 Feb;(10b):1–77. [PubMed] [Google Scholar]
- 21.McQuillan G, Gunter E, Lannom L. Field issues for the plan and operation of the laboratory component of the Third National Health and Nutrition Examination Survey. J Nutr. 1990 Nov;120( Suppl 11):1446–1450. doi: 10.1093/jn/120.suppl_11.1446. [DOI] [PubMed] [Google Scholar]
- 22.Plan and operation of the Third National Health and Nutrition Examination Survey, 1988–94. Series 1: programs and collection procedures. Vital Health Stat 1. 1994 Jul;(32):1–407. [PubMed] [Google Scholar]
- 23.Cox C, Mussolino M, Rothwell S, et al. Plan and operation of the NHANES I Epidemiologic Followup Study, 1992. Vital Health Stat 1. 1997 Dec;35:1–231. [PubMed] [Google Scholar]
- 24.DID, MMD SERVICES USDOHAH, editor. Statistical Issues in Analyzing the NHANES I Epidemiologic Followup Study. Vol Series 2: Data Evaluation and Methods Research No. 121. NCHS website : http://www.cdc.gov/nchs/data/series/sr_02/sr02_121.pdf1994. [PubMed]
- 25.Graubard B, Korn E. Survey inference for subpopulations. Am J Epidemiol. 1996 Jul;144(1):102–106. doi: 10.1093/oxfordjournals.aje.a008847. [DOI] [PubMed] [Google Scholar]
- 26.Korn E, Graubard B. Epidemiologic studies utilizing surveys: accounting for the sampling design. Am J Public Health. 1991 Sep;81(9):1166–1173. doi: 10.2105/ajph.81.9.1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Flegal K, Graubard B, Williamson D, Gail M. Impact of smoking and preexisting illness on estimates of the fractions of deaths associated with underweight, overweight, and obesity in the US population. Am J Epidemiol. 2007 Oct;166(8):975–982. doi: 10.1093/aje/kwm152. [DOI] [PubMed] [Google Scholar]
- 28.Team RDC. R: A Language and Environment for Statistical Computing. Vienna, Austria: 2010. [Google Scholar]
- 29.Lumley T. Analysis of complex survey samples. Journal of Statistical Software. 2004;9(1):1–19. [Google Scholar]
- 30.Bender R, Augustin T, Blettner M. Generating survival times to simulate Cox proportional hazards models. Stat Med. 2005 Jun;24(11):1713–1723. doi: 10.1002/sim.2059. [DOI] [PubMed] [Google Scholar]
- 31.Bender R, Augustin T, Blettner M. Generating survival times to simulate Cox proportional hazards models by Ralf Bender, Thomas Augustin and Maria Blettner, Statistics in Medicine 2005; 24:1713–1723. Stat Med. 2006 Jun;25(11):1978–1979. doi: 10.1002/sim.2059. [DOI] [PubMed] [Google Scholar]
- 32.Finkelstein EA, Brown DS, Wrage LA, Allaire BT, Hoerger TJ. Individual and aggregate years-of-life-lost associated with overweight and obesity. Obesity (Silver Spring) 2010 Feb;18(2):333–339. doi: 10.1038/oby.2009.253. [DOI] [PubMed] [Google Scholar]
- 33.Peng R, Dominici F, Zeger S. Reproducible epidemiologic research. Am J Epidemiol. 2006 May;163(9):783–789. doi: 10.1093/aje/kwj093. [DOI] [PubMed] [Google Scholar]
- 34.Alley D, Chang V. The changing relationship of obesity and disability, 1988–2004. JAMA. 2007 Nov;298(17):2020–2027. doi: 10.1001/jama.298.17.2020. [DOI] [PubMed] [Google Scholar]