Abstract
In this paper, extensive simulations are performed to compare two statistical methods to analyze multiple correlated quantitative phenotypes: (1) approximate F-distributed tests of multivariate functional linear models (MFLM) and additive models of multivariate analysis of variance (MANOVA), and (2) Gene Association with Multiple Traits (GAMuT) for association testing of high-dimensional genotype data. It is shown that approximate F-distributed tests of MFLM and MANOVA have higher power and are more appropriate for major gene association analysis (i.e., scenarios in which some genetic variants have relatively large effects on the phenotypes); GAMuT has higher power and is more appropriate for analyzing polygenic effects (i.e., effects from a large number of genetic variants each of which contributes a small amount to the phenotypes). MFLM and MANOVA are very flexible and can be used to perform association analysis for: (i) rare variants, (ii) common variants, and (iii) a combination of rare and common variants. Although GAMuT was designed to analyze rare variants, it can be applied to analyze a combination of rare and common variants and it performs well when (1) the number of genetic variants is large and (2) each variant contributes a small amount to the phenotypes (i.e., polygenes). MFLM and MANOVA are fixed effect models which perform well for major gene association analysis. GAMuT can be viewed as an extension of sequence kernel association tests (SKAT). Both GAMuT and SKAT are more appropriate for analyzing polygenic effects and they perform well not only in the rare variant case, but also in the case of a combination of rare and common variants. Data analyses of European cohorts and the Trinity Students Study are presented to compare the performance of the two methods.
Keywords: rare variants, common variants, association mapping, quantitative trait loci, complex traits, functional data analysis, multivariate functional linear models (MFLM), multivariate analysis of variance (MANOVA)
Introduction
Since multi-phenotype analysis can increase power to dissect complex disorders, analysis of pleiotropic traits has become a very important topic. One method to analyze pleiotropic traits is to analyze a single polymorphism at a time to evaluate the effect of common variants as is routinely done in genome-wide association studies (GWAS) or exome studies [Allison et al., 1998; Chavali et al.; 2010; Ferreira and Purcell, 2009; Galesloot et al., 2014; Huang et al., 2011; O'Reilly et al., 2012; Ried et al. 2012; Sivakumaran et al., 2011; Solovieff et al., 2013]. In recent years, next-generation sequencing technologies have provided rich resources to search for causal genetic variants. Researchers are facing ever-increasing amounts of data and the need to analyze such data efficiently to enable novel discoveries [Ansorge, 2009; Mardis, 2008; Metzker, 2010; Rusk and Kiermer, 2008; Shendure and Ji, 2008]. There are increasing interest in developing gene-based methods to analyze next-generation sequencing data of pleiotropic traits [Broadaway et al., 2016; Maity et al., 2012; Vsevolozhskaya et al., 2016; Wang et al., 2015]. The gene-based methods have several advantages such as combining multiple variants for a unified analysis, thereby increasing power, and reducing the number of multiple comparisons. In practice, the advantages of different methods are not always clear. In this article, we aim at evaluate the performance of two gene-based procedures described below to understand the pros and cons of each procedure.
In Wang et al. (2015), multivariate functional linear models (MFLM) were proposed to perform gene-based analysis of pleiotropic traits. The MFLM are very flexible and can be used to analyze rare variants or common variants or a combination of the two. Here the rare variants’ minor allele frequencies (MAF) are less than 0.01 ~ 0.05. Broadaway et al. [2016] proposed a method of Gene Association with Multiple Traits (GAMuT) for association testing of phenotypes with high-dimensional rare variant data. By using simulated data of 30 kb regions using COSI [Schaffner et al.; 2005], the authors compared power levels of GAMuT and approximate F-distributed tests of MFLM, and found that GAMuT had higher power than the approximate F-distributed tests of MFLM for 6 and 10 correlated quantitative phenotypes. In addition, Broadaway et al. [2016] analyzed four phenotypic measures of cardiovascular health using data from the Genetic Epidemiology Network of Arteriopathy (GENOA) [Daniels et al., 2004], and found that MFLM inflates p-values. An interesting question is: why and how this happens?
The data analyzed in Broadaway et al. [2016] included 48,712 rare genetic variants (MAF < 3%) that fell within 3,277 genes. Hence, each gene region has about 15 rare variants in the data analysis. Note that MFLM are designed to analyze high-dimensional next-generation sequencing data of multiple quantitative traits [Wang et al., 2015]. For a gene region with about 15 rare variants, the number of parameters of MFLM is about 60 for four phenotypes if one uses B-spline basis functions suggested by Wang et al. [2015]. Therefore, the number of parameters is much larger than the number of rare variants in the data analysis making it almost impossible for MFLM to perform well. If there is only a small number of variants in a gene region, it would be possible to use linear regressions to perform model selection to pick up the important variants, and then one may be able to get a final optimal model to analyze the data. In that case, neither MFLM nor GAMuT is necessary since they are mainly for large number of variant analysis.
In the simulation studies of Wang et al. [2015], genetic variants located in 3 kb regions were simulated using the package COSI [Schaffner et al., 2005]. In the simulations of rare variants (defined as MAF < 3%), the 3 kb regions contain a mean of 53 variants. In the case that some variants are rare and some are common, the 3 kb regions contain a mean of 59 variants and about 10% are common. If the simulated data used in Broadaway et al. [2016] are similar, the 30 kb regions would contain more than 500 rare variants (and each causal variant contributes a small amount to the traits). Hence, the simulation studies of Broadaway et al. [2016] were based on high-dimensional genotype data. In the Supplemenatry Information, Broadaway et al. [2016] presented a power comparison using genetic variants located in 3 kb regions for three phenotypes and found that GAMuT performed similarly to MFLM when genetic effect sizes are relatively large.
Some interesting questions and issues stand out: how do the two methods of GAMuT and MFLM perform for more simulation scenarios? When does the GAMuT perform better and when do the fixed models including MFLM perform better and why? MFLM are very flexible and can be used to perform association analysis for: (i) rare variants, (ii) common variants, and (iii) a combination of rare and common variants. Can GAMuT be used to analyze a combination of rare and common variants (or just common variants), although it was designed to analyze rare variants only? Here we perform extensive simulations to evaluate the performance of the approximate F-distributed tests of fixed effect models and GAMuT for quantitative traits by using genetic variants located in 3 - 30 kb regions of simulated COSI data. Data analyses of European cohorts and Trinity Students Study are presented to compare the performance of the two methods.
Models
In gene-based association analysis, the research goal is to model the association between multiple genetic variants and phenotypic traits. In this section, we briefly introduce the two procedures (i.e., GAMuT and MFLM) for gene-based analysis of pleiotropic traits.
Gene Association with Multiple Traits (GAMuT)
GAMuT utilizes a kernel distance-covariance to build a nonparametric test of independence between multiple phenotypes and multiple genetic variants, and can be viewed as an extension of sequence kernel association tests (SKAT) [Ionita-Laza et al., 2013; Lee et al., 2012; Wu et al., 2011]. GAMuT can analyze both quantitative and categorical phenotypes adjusting for covariates. The kernel distance-covariance framework used by GAMuT assesses if pairwise phenotypic similarity is independent of pairwise rare-variant genotypic similarity. The phenotypic similarity and genotypic similarity can be formulated as matrices using a projection or a weighted linear kernel function. An MAF weighted linear kernel is recommended for the genotypic similarity [Broadaway et al., 2016].
Multivariate Fixed Effect Models
Consider n individuals who are sequenced in a genomic region that has m variants. We assume that the m variants are located in a region with ordered physical positions 0 ≤ t1 < ··· < tm = T. To make the notation simpler, we normalize the region [t1, T] to be [0, 1]. For the i-th individual, let Xi = (xi(t1), ··· , xi(tm))′ denote her/his genotypes at the m variants and Zi = (zi1, ··· , zic)′ denote her/his covariates. Hereafter, ′ denotes the transpose of a vector or matrix. For genotypes, we assume that xi(tj)(= 0, 1, 2) is the number of minor alleles of the individual at the j-th variant located at the position tj. For each individual, we assume that there are L quantitative traits, L ≥ 1. We assume that the quantitative traits are normally distributed. For the i-th individual, let denote her/his quantitative traits, respectively.
Traditional Additive Effect Models of MANOVA
To model the relationship between the quantitative traits and the m variants, one may use the following additive effect models of multivariate analysis of variance (MANOVA)
| (1) |
where is the overall mean, is a c × 1 column vector of regression coefficients of covariates, is the effect of genetic variant xi(tj), and is an error term. For each i, the error vector εi = (εi1, ···, εiL)′ is normally distributed with a mean vector of zeros and a L × L variance-covariance matrix Σ. Moreover, ε1, ··· , εn are assumed to be independent. When the number of genetic variants is large, the number of parameters in the model (1) can be large which may lead to low power. Before fitting the model (1), the QR decomposition can be applied to the genotype data to remove the redundancy. Since dense variants in a region can be highly correlated to each other, the QR decomposition could signi cantly reduce the dimensionality and could be useful in data analysis.
General Multivariate Functional Linear Models
In this subsection, we introduce general MFLM to connect genetic variants to the traits [Fan et al., 2013, 2014, 2015, 2016a, 2016b, 2016c; Ramsay and Silverman, 2005; Wang et al., 2015]. We view the i-th individual's genotype data as a genetic variant function (GVF) as Xi(t), t ∈ [0, 1]. We assume that the GVF Xi(t) is continuous, but this assumption can be removed as in the beta-smooth models (6).
Note that the sample includes n discrete realizations or observations Xi = (xi(t1),··· , xi(tm))′ of the human genome. By using the genetic variant information Xi, we may estimate the related GVF Xi(t). To relate the GVF to the quantitative traits adjusting for covariates, we consider the following MFLM
| (2) |
where is the genetic effect of GVF Xi(t) at the position t, and the other terms are similar to those in the MANOVA model (1).
Estimation of Genetic Variant Functions
To estimate the GVF Xi(t) from the genotypes Xi, we use an ordinary linear square smoother [Fan et al., 2013, 2014; Wang et al., 2015]. The ordinary linear square smoother method assumes that the GVF is smooth. Let ϕk(t), k = 1,··· , K, be a series of K basis functions, such as the B-spline basis and Fourier basis functions. Denote ϕ(t) = (ϕ1(t),··· , ϕK(t))′. Let Φ denote the m by K matrix containing the values ϕk(tj), where j ∈ 1,··· , m. Using the discrete realizations Xi = (xi(t1),··· ,xi(tm))′, we may estimate the GVF Xi(t) using an ordinary linear square smoother as follows [Ramsay and Silverman, 2005]
| (3) |
We consider two types of basis functions: (1) the B-spline basis: ϕk(t) = Bk(t, k = 1, ··· , K; and (2) the Fourier basis: ϕ1(t) = 1, ϕ2r+1(t) = sin(2πrt), and ϕ2r(t) = cos(2πrt), r = 1, ··· , (K – 1)/2. Here for the Fourier basis, K is taken as a positive odd integer [de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay et al., 2009; Ramsay and Silverman, 2005].
Revised Functional Regression Models
The genetic effect functions are assumed to be continuous/smooth. One may expand them by B-spline or Fourier basis functions. Formally, let φk(t), k = 1, ··· , Kβ, be a series of Kβ basis functions. We expand the genetic effect function by φ(t) = φ1(t), ··· , φKβ(t))′ as
| (4) |
where is a vector of coefficients . Replacing Xi(t) in MFLM (2) by X̂i(t) in (3) and by the expansion (4), we have the following revised MFLM
| (5) |
where .
Multivariate Functional Linear Models: beta-smooth Only Approach
We now introduce a simplified version of our MFLM, i.e., beta-smooth only model [Fan et al., 2013, 2014; de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay et al., 2009; Ramsay and Silverman, 2005; Wang et al., 2015]. The beta-smooth only MFLM were developed to define the relationship between the ℓ-th quantitative trait and the m variants [Wang et al., 2015]
| (6) |
where is the genetic effect at the physical position tj, and the other terms are similar to those in the model (1). As for the general MFLM (2), the genetic effect are expanded by a series of basis functions by relations (4). Replacing by the expansion, the models (6) can be revised as
| (7) |
where . In the model (6) and its revised version (7), we use the raw genotype data Xi = (xi(t1), ··· ,xi(tm))′. The genetic effect functions are assumed to be smooth. Thus, the models are called beta-smooth only. In our previous work, we showed that beta-smooth only models perform similarly to the general MFLM in real data analysis and simulation studies [Fan et al., 2013, 2014, 2015, 2016a, 2016b, 2016c; Wang et al., 2015].
Null Hypotheses and Test Statistics
Consider the additive effect model of MANOVA (1) and the revised MFLM (5) and (7). To test for association between the m genetic variants and the quantitative traits as a group, the null hypothesis is , for model (1) and , for models (7) and (5). We may test the null H0: β1 = ··· = βL = 0 by approximate F-distributed tests based on Pillai-Bartlett trace, Hotelling-Lawley trace, and Wilks's Lambda using standard statistical approaches [Anderson, 1984; Rao, 1973].
Functional Data Analysis Parameters
In the data analysis and simulations, we used the functional data analysis procedure in the statistical package R. We used two functions from the functional data analysis (fda) R package as follows to create the bases:
basis = create.bspline.basis(norder = order, nbasis = bbasis) basis = create.fourier.basis(c(0,1), nbasis = fbasis)
The three parameters were taken as order = 4, bbasis = 15, fbasis = 21 for quantitative traits in all simulations. Specifically, the order of B-spline basis was 4, and the number of B-spline basis functions was K = Kβ = 15, the number of Fourier basis functions was K = Kβ = 21. To make sure that the results are valid and stable, we tried a wide range of parameters that 10 ≤ K = Kβ ≤ 21 and the results are very close to each other (data not shown).
Simulation Studies
We utilize two fixed models: (1) MFLM and (2) additive models (1) of multivariate analysis of variance (i.e., MANOVA). Simulations were performed to evaluate the performance of the fixed models and GAMuT with sample sizes 500, 1,000, and 1,500. We used the European ancestry simulated sequence data [Lee et al., 2012; Wu et al., 2011]. The sequence data are from 10,000 simulated chromosomes covering a 1 Mb region simulated using the calibrated coalescent model programmed in COSI [Schaffner et al., 2005]. The generated European haplotypes mimic CEPH Utah individuals with ancestry from northern and western Europe in terms of site frequency spectrum and linkage disequilibrium pattern.
Type I error Simulations
To evaluate whether the approximate F-distributed tests control false positive rates accurately, we consider either three or six correlated phenotypes for each individual. For the three phenotype case, we generated three correlated quantitative traits using the model
| (8) |
where zi1 is a continuous covariate from a standard normal distribution N(0, 1), zi2 is a dichotomous covariate taking values 0 and 1 with a probability of 0.5, and (εi1, εi2, εi3)′ follows a normal distribution with a mean vector of 0 and a 3 × 3 variance-covariance matrix . The is taken from of 3 × 3 variance-covariance matrix Σ is taken from an empirical analysis of three traits from The Trinity Students Study [Wang et al., 2015].
For the six phenotype case, we use the same strategy of Broadaway et al. [2016] to generate the correlation matrix Σ. That is, we consider scenarios of low residual correlation among phenotypes [pairwise correlation among phenotypes selected from a uniform (0, 0.3) distribution], moderate residual correlation [pairwise correlation selected from a uniform (0.3, 0.5) distribution], and high residual correlation [pairwise correlation selected from a uniform (0.5, 0.7) distribution]. The six correlated quantitative traits were generated using the model
| (9) |
where zi1 and zi1 are the same as those of (8).
To be sure that the false positives are properly controlled, empirical type I errors are calculated for the approximate F-distributed tests. For the three trait case, the type one error rates were reported in Tables 3 and 4 of Wang et al. (2015). For six traits, the type I errors of the approximate F-distributed tests are reported in Tables 1 and 2, and they are around the nominal levels and so the false positive rates are accurately controlled.
Table 1.
Empirical Type I Error Rates of the Approximate F-distribution Tests based on Pillai-Bartlett Trace of Six Traits and Moderate Correlation, When the Variants Are either Rare or Common. The results of “Basis of both GVF and ” were based on smoothing both GVF and genetic effect functions of model (5), the results of “Basis of beta-Smooth Only” were based on the smoothing only approach of model (7). The order of B-spline basis was 4, and the number of basis functions of B-spline was K = Kβ = 15; the number of Fourier basis functions was K = Kβ = 21.
| Region Size | Sample Size | Nominal | Basis of both GVF and | Basis of beta-Smooth Only | MANOVA Model (1) | ||
|---|---|---|---|---|---|---|---|
| Level α | B-sp Basis | Fourier Basis | B-sp Basis | Fourier Basis | |||
| 6 kb | 500 | 0.001 | 0.000896 | 0.000986 | 0.000894 | 0.000987 | 0.000942 |
| 0.0001 | 0.000082 | 0.000090 | 0.000082 | 0.000090 | 0.000087 | ||
| 1000 | 0.001 | 0.000994 | 0.001006 | 0.000994 | 0.001006 | 0.000957 | |
| 0.0001 | 0.000103 | 0.000100 | 0.000103 | 0.000100 | 0.000094 | ||
| 1500 | 0.001 | 0.001035 | 0.000974 | 0.001034 | 0.000974 | 0.000974 | |
| 0.0001 | 0.000093 | 0.000097 | 0.000093 | 0.000097 | 0.000098 | ||
| 9 kb | 500 | 0.001 | 0.000910 | 0.000897 | 0.000910 | 0.000897 | 0.000887 |
| 0.0001 | 0.000089 | 0.000081 | 0.000089 | 0.000081 | 0.000105 | ||
| 1000 | 0.001 | 0.000995 | 0.000976 | 0.000995 | 0.000976 | 0.000934 | |
| 0.0001 | 0.000094 | 0.000113 | 0.000094 | 0.000113 | 0.000091 | ||
| 1500 | 0.001 | 0.000969 | 0.000996 | 0.000969 | 0.000996 | 0.000947 | |
| 0.0001 | 0.000098 | 0.000085 | 0.000098 | 0.000085 | 0.000088 | ||
| 12 kb | 500 | 0.001 | 0.000907 | 0.000944 | 0.000907 | 0.000944 | 0.000881 |
| 0.0001 | 0.000095 | 0.000096 | 0.000095 | 0.000096 | 0.000090 | ||
| 1000 | 0.001 | 0.000930 | 0.000954 | 0.000930 | 0.000954 | 0.000928 | |
| 0.0001 | 0.000083 | 0.000088 | 0.000083 | 0.000088 | 0.000101 | ||
| 1500 | 0.001 | 0.001012 | 0.000948 | 0.001012 | 0.000948 | 0.000989 | |
| 0.0001 | 0.000088 | 0.000092 | 0.000088 | 0.000092 | 0.000115 | ||
| 15 kb | 500 | 0.001 | 0.000931 | 0.000953 | 0.000931 | 0.000953 | 0.000997 |
| 0.0001 | 0.000086 | 0.000102 | 0.000086 | 0.000102 | 0.000094 | ||
| 1000 | 0.001 | 0.000976 | 0.000958 | 0.000976 | 0.000958 | 0.000955 | |
| 0.0001 | 0.000115 | 0.000088 | 0.000115 | 0.000088 | 0.000102 | ||
| 1500 | 0.001 | 0.000955 | 0.000889 | 0.000955 | 0.000889 | 0.001003 | |
| 0.0001 | 0.000111 | 0.000100 | 0.000111 | 0.000100 | 0.000106 | ||
| 18 kb | 500 | 0.001 | 0.000870 | 0.000943 | 0.000870 | 0.000943 | 0.000938 |
| 0.0001 | 0.000076 | 0.000081 | 0.000076 | 0.000081 | 0.000098 | ||
| 1000 | 0.001 | 0.000958 | 0.001013 | 0.000958 | 0.001013 | 0.000966 | |
| 0.0001 | 0.000099 | 0.000113 | 0.000099 | 0.000113 | 0.000099 | ||
| 1500 | 0.001 | 0.000937 | 0.000956 | 0.000937 | 0.000956 | 0.000925 | |
| 0.0001 | 0.000077 | 0.000089 | 0.000077 | 0.000089 | 0.000083 | ||
| 21 kb | 500 | 0.001 | 0.000923 | 0.000917 | 0.000923 | 0.000917 | 0.000893 |
| 0.0001 | 0.000089 | 0.000065 | 0.000089 | 0.000065 | 0.000088 | ||
| 1000 | 0.001 | 0.000945 | 0.000961 | 0.000945 | 0.000961 | 0.000969 | |
| 0.0001 | 0.000073 | 0.000089 | 0.000073 | 0.000089 | 0.000102 | ||
| 1500 | 0.001 | 0.000947 | 0.000986 | 0.000947 | 0.000986 | 0.000980 | |
| 0.0001 | 0.000093 | 0.000100 | 0.000093 | 0.000100 | 0.000101 | ||
| 24 kb | 500 | 0.001 | 0.000939 | 0.000919 | 0.000939 | 0.000919 | 0.000914 |
| 0.0001 | 0.000093 | 0.000095 | 0.000093 | 0.000095 | 0.000093 | ||
| 1000 | 0.001 | 0.000984 | 0.000959 | 0.000984 | 0.000959 | 0.000961 | |
| 0.0001 | 0.000104 | 0.000091 | 0.000104 | 0.000091 | 0.000100 | ||
| 1500 | 0.001 | 0.001003 | 0.000931 | 0.001003 | 0.000931 | 0.001003 | |
| 0.0001 | 0.000086 | 0.000089 | 0.000086 | 0.000089 | 0.000104 | ||
| 27 kb | 500 | 0.001 | 0.000979 | 0.001003 | 0.000979 | 0.001003 | 0.000925 |
| 0.0001 | 0.000091 | 0.000081 | 0.000091 | 0.000081 | 0.000091 | ||
| 1000 | 0.001 | 0.000919 | 0.000966 | 0.000919 | 0.000966 | 0.000956 | |
| 0.0001 | 0.000088 | 0.000101 | 0.000088 | 0.000101 | 0.000114 | ||
| 1500 | 0.001 | 0.000933 | 0.000922 | 0.000933 | 0.000922 | 0.000976 | |
| 0.0001 | 0.000085 | 0.000089 | 0.000085 | 0.000089 | 0.000079 | ||
| 30 kb | 500 | 0.001 | 0.000981 | 0.001031 | 0.000981 | 0.001031 | 0.000895 |
| 0.0001 | 0.000102 | 0.000104 | 0.000102 | 0.000104 | 0.000093 | ||
| 1000 | 0.001 | 0.000979 | 0.000972 | 0.000979 | 0.000972 | 0.001001 | |
| 0.0001 | 0.000092 | 0.000093 | 0.000092 | 0.000093 | 0.000087 | ||
| 1500 | 0.001 | 0.000966 | 0.000969 | 0.000966 | 0.000969 | 0.000971 | |
| 0.0001 | 0.000096 | 0.000097 | 0.000096 | 0.000097 | 0.000102 | ||
Table 2.
Empirical Type I Error Rates of the Approximate F-distribution Tests based on Pillai-Bartlett Trace of Six Traits and Moderate Correlation, When the Variants Are Only Rare. The results of “Basis of both GVF and ” were based on smoothing both GVF and genetic effect functions of model (5), the results of “Basis of beta-Smooth Only” were based on the smoothing only approach of model (7). The order of B-spline basis was 4, and the number of basis functions of B-spline was K = Kβ = 15; the number of Fourier basis functions was K = Kβ = 21.
| Region Size | Sample Size | Nominal | Basis of both GVF and | Basis of beta-Smooth Only | MANOVA Model (1) | ||
|---|---|---|---|---|---|---|---|
| Level α | B-sp Basis | Fourier Basis | B-sp Basis | Fourier Basis | |||
| 6 kb | 500 | 0.001 | 0.000906 | 0.000919 | 0.000906 | 0.000916 | 0.000921 |
| 0.0001 | 0.000091 | 0.000088 | 0.000093 | 0.000090 | 0.000085 | ||
| 1000 | 0.001 | 0.000996 | 0.000930 | 0.000998 | 0.000930 | 0.000918 | |
| 0.0001 | 0.000096 | 0.000091 | 0.000096 | 0.000091 | 0.000089 | ||
| 1500 | 0.001 | 0.000985 | 0.000991 | 0.000985 | 0.000991 | 0.000984 | |
| 0.0001 | 0.000094 | 0.000099 | 0.000094 | 0.000099 | 0.000095 | ||
| 9 kb | 500 | 0.001 | 0.000940 | 0.000925 | 0.000940 | 0.000923 | 0.000912 |
| 0.0001 | 0.000090 | 0.000095 | 0.000090 | 0.000095 | 0.000100 | ||
| 1000 | 0.001 | 0.000906 | 0.000969 | 0.000906 | 0.000969 | 0.000900 | |
| 0.0001 | 0.000092 | 0.000086 | 0.000092 | 0.000086 | 0.000092 | ||
| 1500 | 0.001 | 0.000981 | 0.000980 | 0.000981 | 0.000980 | 0.000952 | |
| 0.0001 | 0.000111 | 0.000091 | 0.000111 | 0.000091 | 0.000076 | ||
| 12 kb | 500 | 0.001 | 0.000930 | 0.000901 | 0.000930 | 0.000901 | 0.000909 |
| 0.0001 | 0.000086 | 0.000089 | 0.000086 | 0.000089 | 0.000078 | ||
| 1000 | 0.001 | 0.000905 | 0.000930 | 0.000905 | 0.000930 | 0.000946 | |
| 0.0001 | 0.000094 | 0.000085 | 0.000094 | 0.000085 | 0.000094 | ||
| 1500 | 0.001 | 0.000965 | 0.000983 | 0.000965 | 0.000983 | 0.000984 | |
| 0.0001 | 0.000099 | 0.000099 | 0.000099 | 0.000099 | 0.000097 | ||
| 15 kb | 500 | 0.001 | 0.000950 | 0.000947 | 0.000950 | 0.000947 | 0.000940 |
| 0.0001 | 0.000093 | 0.000099 | 0.000093 | 0.000099 | 0.000093 | ||
| 1000 | 0.001 | 0.000951 | 0.000946 | 0.000951 | 0.000946 | 0.000965 | |
| 0.0001 | 0.000103 | 0.000094 | 0.000103 | 0.000094 | 0.000098 | ||
| 1500 | 0.001 | 0.000925 | 0.000966 | 0.000925 | 0.000966 | 0.000987 | |
| 0.0001 | 0.000098 | 0.000089 | 0.000098 | 0.000089 | 0.000104 | ||
| 18 kb | 500 | 0.001 | 0.000896 | 0.000957 | 0.000896 | 0.000957 | 0.000913 |
| 0.0001 | 0.000077 | 0.000088 | 0.000077 | 0.000088 | 0.000105 | ||
| 1000 | 0.001 | 0.000979 | 0.000955 | 0.000979 | 0.000955 | 0.000946 | |
| 0.0001 | 0.000093 | 0.000078 | 0.000093 | 0.000078 | 0.000105 | ||
| 1500 | 0.001 | 0.000969 | 0.000985 | 0.000969 | 0.000985 | 0.000962 | |
| 0.0001 | 0.000083 | 0.000114 | 0.000083 | 0.000114 | 0.000105 | ||
| 21 kb | 500 | 0.001 | 0.000888 | 0.000929 | 0.000888 | 0.000929 | 0.000936 |
| 0.0001 | 0.000086 | 0.000085 | 0.000086 | 0.000085 | 0.000077 | ||
| 1000 | 0.001 | 0.000879 | 0.000940 | 0.000879 | 0.000940 | 0.001018 | |
| 0.0001 | 0.000092 | 0.000095 | 0.000092 | 0.000095 | 0.000093 | ||
| 1500 | 0.001 | 0.000919 | 0.000932 | 0.000919 | 0.000932 | 0.000989 | |
| 0.0001 | 0.000086 | 0.000079 | 0.000086 | 0.000079 | 0.000086 | ||
| 24 kb | 500 | 0.001 | 0.000943 | 0.000846 | 0.000943 | 0.000846 | 0.000931 |
| 0.0001 | 0.000087 | 0.000091 | 0.000087 | 0.000091 | 0.000076 | ||
| 1000 | 0.001 | 0.000968 | 0.000986 | 0.000968 | 0.000986 | 0.000975 | |
| 0.0001 | 0.000085 | 0.000084 | 0.000085 | 0.000084 | 0.000085 | ||
| 1500 | 0.001 | 0.000989 | 0.000990 | 0.000989 | 0.000990 | 0.001014 | |
| 0.0001 | 0.000110 | 0.000096 | 0.000110 | 0.000096 | 0.000090 | ||
| 27 kb | 500 | 0.001 | 0.000935 | 0.000960 | 0.000935 | 0.000960 | 0.000946 |
| 0.0001 | 0.000105 | 0.000107 | 0.000105 | 0.000107 | 0.000092 | ||
| 1000 | 0.001 | 0.000988 | 0.000974 | 0.000988 | 0.000974 | 0.000984 | |
| 0.0001 | 0.000105 | 0.000106 | 0.000105 | 0.000106 | 0.000098 | ||
| 1500 | 0.001 | 0.000999 | 0.000993 | 0.000999 | 0.000993 | 0.000966 | |
| 0.0001 | 0.000097 | 0.000113 | 0.000097 | 0.000113 | 0.000097 | ||
| 30 kb | 500 | 0.001 | 0.000900 | 0.000916 | 0.000900 | 0.000916 | 0.000942 |
| 0.0001 | 0.000069 | 0.000082 | 0.000069 | 0.000082 | 0.000083 | ||
| 1000 | 0.001 | 0.000953 | 0.000940 | 0.000953 | 0.000940 | 0.000938 | |
| 0.0001 | 0.000109 | 0.000083 | 0.000109 | 0.000083 | 0.000104 | ||
| 1500 | 0.001 | 0.000997 | 0.000940 | 0.000997 | 0.000940 | 0.000980 | |
| 0.0001 | 0.000095 | 0.000098 | 0.000095 | 0.000098 | 0.000097 | ||
Empirical Power Simulations
For empirical power simulations of quantitative traits, we assumed that 5% of the variants were causal. We considered two scenarios: (1) all causal variants are rare (MAF < 0.03), and (2) some causal variants are rare and some are common. Once a subregion of size 3 - 30 kb was selected from the 1 Mb region, a subset of p causal variants located in the subregion was then randomly selected to obtain ordered genotypes (xi(t1),··· ,xi(tp)). Then, we generated the quantitative traits by adding genetic contributions to models (8) and (9). For instance, the three quantitative traits were generated by
| (10) |
where zi1; zi2, and (εi1; εi2; εi3)′ are the same as in the model (8), and the βs are additive effects for the causal variants defined as follows. We used |βij| = cij log10(MAFj)|, where MAFj was the MAF of the j-th variant. For the three trait model (10), we assume that 5% of the variants were causal and the constants ci are defined by
| (11) |
for the six trait case, we also assume that 5% of the variants were causal and the constants ci = 4.0/k for all six traits, where k depends on region size. The constants k and genetic effect sizes decrease as region sizes increase:
| (12) |
It can be seen that the effect sizes |βij| are smaller and smaller when the region sizes in (12) increase. In particular, the number of causal variants is large and each causal variant contributes a small amount to the traits if the region sizes are larger than 12 kb for the three trait case (i.e., ci ≤ log(10)/(2 * 4) ≈ 0.29). For the six trait case, the constant ci = 0.4 when region size is 30 kb and this is the same as that in the simulations of Figure 3, Broadaway et al. [2016], except for an additional random contribution N(0, 1)| log10(MAFj)|. For the three trait case, we also consider a second type of constants: k = 3.0, i.e., effect sizes |βij| do not depend on region sizes and are relatively large.
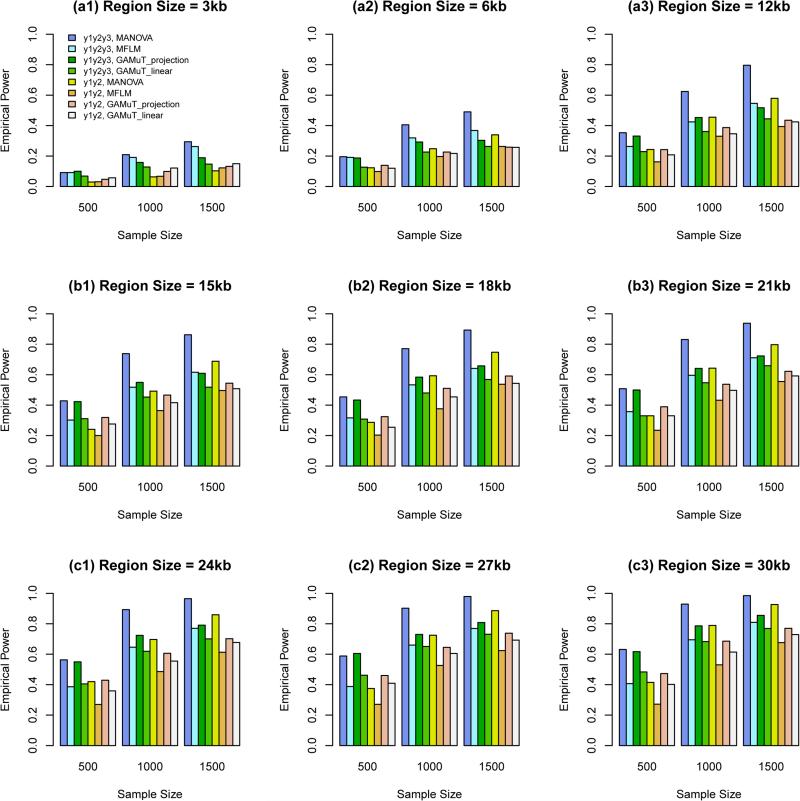
Figure 3.
The empirical power of the approximate F-distributed tests of the additive models of MANOVA (1) and MFLM (7) using B-spline basis based on Pillai-Bartlett trace and GAMuT at α = 0.01, when some causal variants are rare and some are common, the constant k = 30, 20%/80% causal variants have negative/positive effects for each of three traits, and 5% variants are causal. The order of B-spline basis was 4, and the number of B-spline basis functions was K = Kβ = 15.
For each setting of empirical power calculations, 1,000 datasets were simulated to calculate the empirical power levels as the proportion of p-values which are smaller than a given α = 0.01 level. The results of two combinations of traits are reported: one tri-variate combination (y1, y2, y3) and one bivariate combination (y1, y2) for three trait case. We calculated the empirical power levels for the approximate F-distributed tests based on Pillai-Bartlett trace, Hotelling-Lawley trace, and Wilks's Lambda. The results of approximate F-distributed tests based on the Pillai-Bartlett trace are reported, which are similar to the results of approximate F-distributed tests based on Hotelling-Lawley trace and Wilks's Lambda. An MAF weighted linear kernel is used for the genotypic similarity.
Three Traits
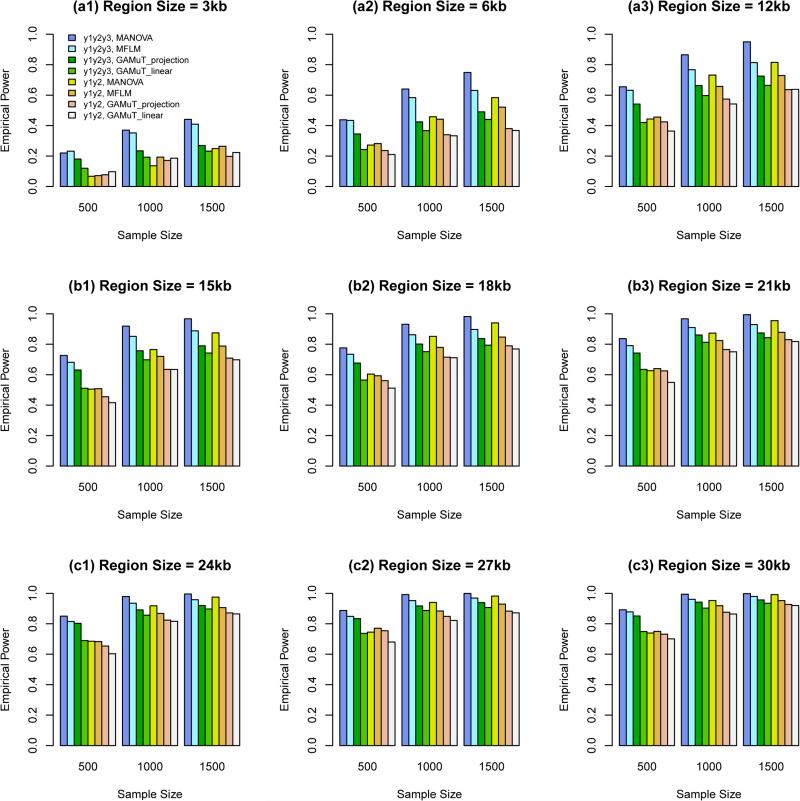
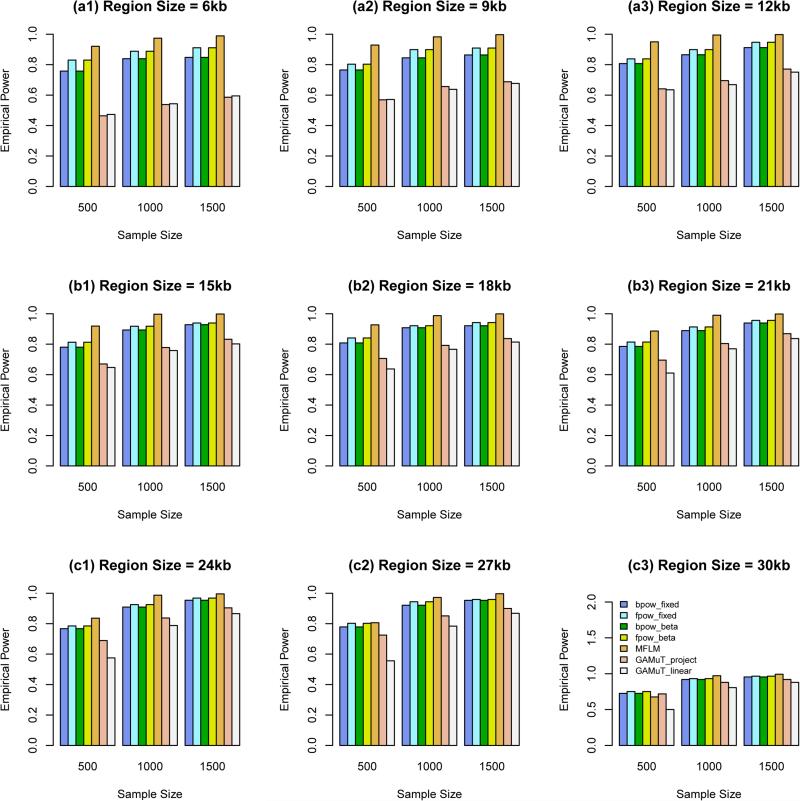
Power Comparison When the Constants k are Given by Relations (12). In this case, genetic effect sizes |βij| decrease as region sizes increase. When some causal variants are rare and some are common, we report in Figure 1 the empirical power of the approximate F-distributed tests of additive models of MANOVA (1) and MFLM (7) and GAMuT at α = 0.01. When the region sizes are between 3 kb and 12 kb, both the additive models of MANOVA and MFLM perform better than GAMuT, and the additive models of MANOVA perform better than MFLM. When the region sizes are 15 kb and 18 kb, both the additive models of MANOVA and MFLM perform similarly to GAMuT based on projection matrix, and the additive models of MANOVA start to perform worse than MFLM. When the region sizes are between 21 kb and 27 kb, both the additive models of MANOVA and MFLM perform worse than GAMuT based on projection matrix, and the additive models of MANOVA perform worse than MFLM.
Figure 1.
The empirical power of the approximate F-distributed tests of the additive models of MANOVA (1) and MFLM (7) using B-spline basis based on Pillai-Bartlett trace and GAMuT at α = 0.01, when some causal variants are rare and some are common, the constants k are given by relations (12), 20%/80% causal variants have negative/positive effects for each of three traits, and 5% variants are causal. The order of B-spline basis was 4, and the number of B-spline basis functions was K = Kβ = 15.
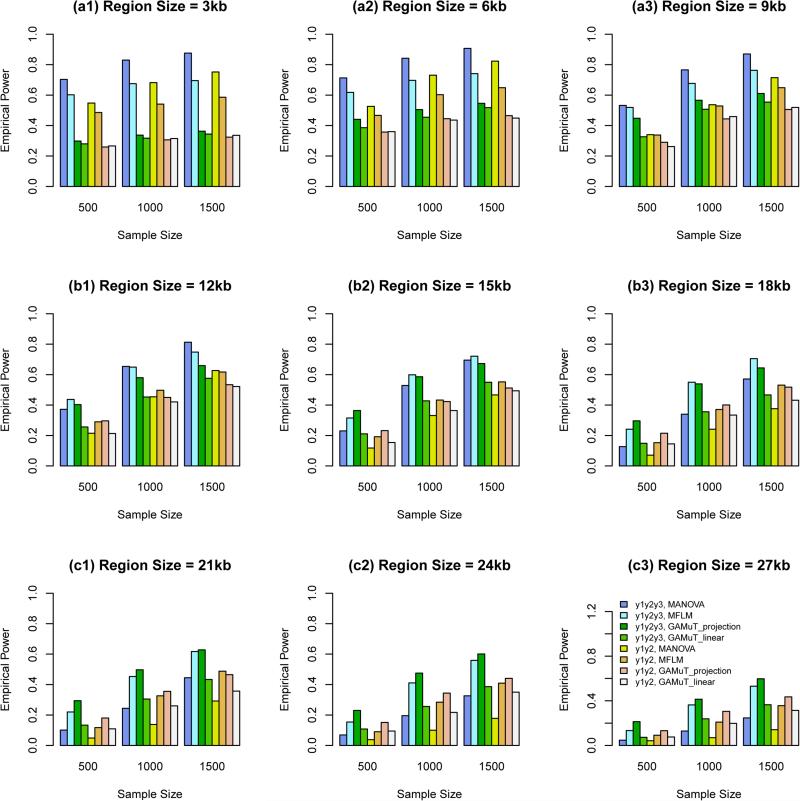
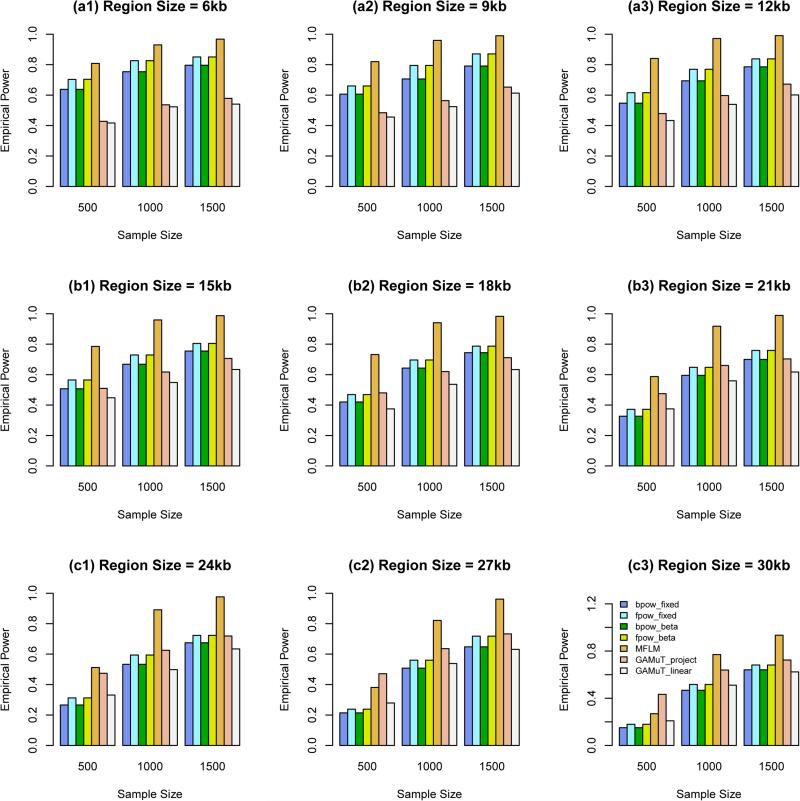
When all causal variants are rare, we report empirical power levels in Figure 2. When the region sizes are between 3 kb and 9 kb, the additive models of MANOVA perform the best (i.e., better than GAMuT and MFLM), and MFLM performs better than or similar to GAMuT. When the region sizes are 12 kb and 15 kb, the additive models of MANOVA perform similarly to GAMuT based on projection matrix. When the region sizes are between 18 kb and 27 kb, the GAMuT based on projection matrix performs the best.
Figure 2.
The empirical power of the approximate F-distributed tests of the additive models of MANOVA (1) and MFLM (7) using B-spline basis based on Pillai-Bartlett trace and GAMuT at α = 0.01, when all causal variants are rare, the constants k are given by relations (12), 20%/80% causal variants have negative/positive effects for each of three traits, and 5% variants are causal. The order of B-spline basis was 4, and the number of B-spline basis functions was K = Kβ = 15.
In the Figures 1 and 2, GAMuT based on projection matrix performs similarly to GAMuT based on linear kernel when the region sizes are between 3 kb and 9 kb; When the region sizes are between 12 kb and 27 kb, GAMuT based on projection matrix perform better than GAMuT based on linear kernel.
Three Traits
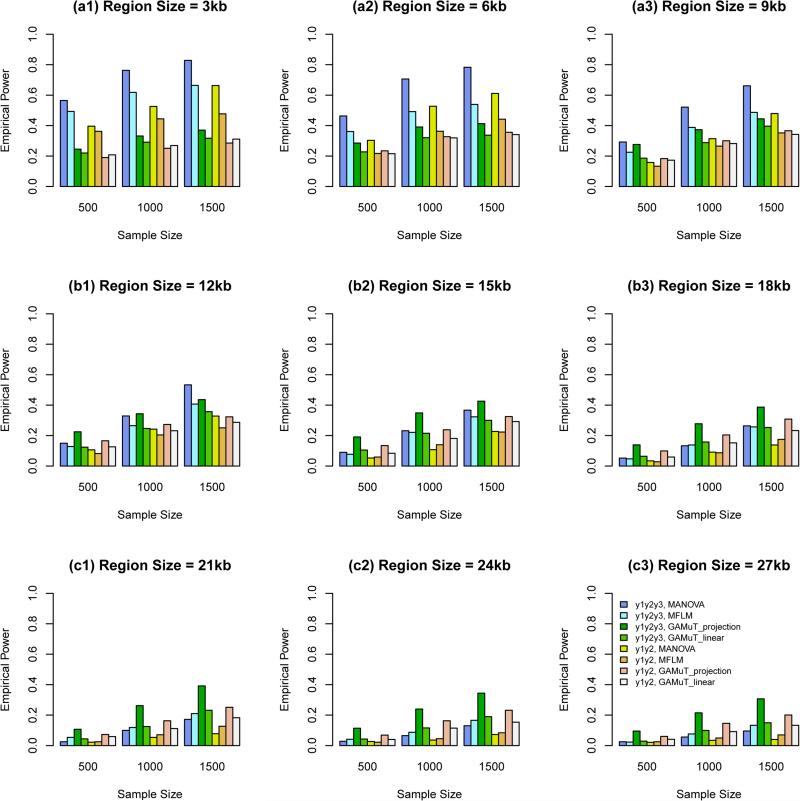
Power Comparison When the Constant k = 3.0. In these cases, genetic effect sizes |βij| do not depend on the region sizes and are relatively large. When some causal variants are rare and some are common, the power levels are presented in Figure 3. When all causal variants are rare, the power levels are presented in Figure 4. In these Figures, the results of 9 kb region sizes are not plotted since they are the same as those in plots (a3) of Figures 1 and 2. The obvious features of Figures 3 and 4 are that the additive models of MANOVA perform the best (i.e., better than GAMuT and MFLM). When some causal variants are rare and some are common, MFLM perform better than GAMuT. When all causal variants are rare, MFLM perform worse than GAMuT.
Figure 4.
The empirical power of the approximate F-distributed tests of the additive models of MANOVA (1) and MFLM (7) using B-spline basis based on Pillai-Bartlett trace and GAMuT at α = 001, when all causal variants are rare, the constant k = 30, 20%/80% causal variants have negative/positive effects for each of three traits, and 5% variants are causal. The order of B-spline basis was 4, and the number of B-spline basis functions was K = Kβ = 15.
Six Traits: Power Comparison When the Constants k are Given by Relations (12)
If the residual correlations are moderate, the empirical power levels are plotted in Figures 5 and 6. When some causal variants are rare and some are common, the power levels are presented in Figure 5. When all causal variants are rare, the power levels are presented in Figure 6. It can be seen that the additive models of MANOVA perform the best (i.e., better than GAMuT and MFLM) in Figures 5 and 6. When some causal variants are rare and some are common, MFLM perform better than GAMuT. When all causal variants are rare, MFLM perform better than GAMuT when the region sizes are between 6 kb and 15 kb, MFLM perform similarly to GAMuT when the region sizes are between 18 kb and 24 kb, and MFLM perform similarly to or worse than GAMuT when the region sizes are 27 kb and 30 kb.
Figure 5.
The empirical power of the approximate F-distributed tests of the additive models of MANOVA (1) and MFLM (5) and (7) based on Pillai-Bartlett trace and GAMuT at α = 2.5 × 10−6 for six traits and moderate correlation, when some causal variants are rare and some are common, 20%/80% causal variants have negative/positive effects for each of six traits, and 5% variants are causal. The order of B-spline basis was 4, the number of B-spline basis functions was K = Kβ = 15, and the number of Fourier basis functions was K = Kβ = 21.
Figure 6.
The empirical power of the approximate F-distributed tests of the additive models of MANOVA (1) and MFLM (5) and (7) based on Pillai-Bartlett trace and GAMuT at α = 2.5 × 10−6 for six traits and moderate correlation, when all causal variants are rare, 20%/80% causal variants have negative/positive effects for each of six traits, and 5% variants are causal. The order of B-spline basis was 4, the number of B-spline basis functions was K = Kβ = 15, and the number of Fourier basis functions was K = Kβ = 21.
In Figures S.1 and S.2, the power levels are plotted when the residual correlations are low. In Figures S.3 and S.4, the power levels are plotted when the residual correlations are high. The features of Figures S.1 and S.3 are similar to those of the Figure 1 when some causal variants are rare and some are common, and the features of Figures S.2 and S.4 are similar to those of the Figure 2 when all causal variants are rare.
Application to Real Data
In Wang et al. [2015], we analyzed data from the Trinity Students Study (TSS) and European lipid studies by fixed models. In this report, we analyzed the data by GAMuT. Table 3 reports results of MFLM, additive models of MANOVA, and GAMuT. In the European lipid studies, four lipid quantitative traits were analyzed in 22 gene regions: high-density lipoprotein (HDL) levels, low-density lipoprotein (LDL) levels, triglycerides (TG), and total cholesterol (CHOL). Three quantitative traits (i.e., A, B, and C) from the Trinity Students Study were analyzed in the region of an enzyme gene. The associations that attain a threshold signi cance of P < 3.1 × 10−6 are highlighted in red [Liu et al., 2014]. If the p-values are around 10−5 but larger than 3.1 × 10−6, we claim the association as tentative.
Table 3.
Results of Association Analysis of Four Lipid Traits in 5 European Studies in the Regions of APOE, LPL, and LDLR Genes and Three Traits of the Trinity Students Study in the Region of An Enzyme Gene Using the F-approximation Based on Pillai-Bartlett Trace. The associations that attain a threshold significance of P < 3.1 × 10−6 are highlighted in red [Liu et al. 2014]. The results of “Basis of both GVF and ” were based on smoothing both GVF and genetic effect functions of model (5), and the results of “Basis of β-smooth only” were based on smoothing only approach of model (7).
| Study | Gene | Combinations of Traits | P-values of the F-approximation Based on Pillai-Bartlett Trace | P-values of GAMuT | |||||
|---|---|---|---|---|---|---|---|---|---|
| Basis of both GVF and | Basis of beta-Smooth Only | MANOVA Model (1) | Projection Matrix | Linear Kernel | |||||
| B-sp Basis | Fourier Basis | B-sp Basis | Fourier Basis | ||||||
| D2d-2007 | APOE | LDL,TG | 4.33 × 10−23 | 8.96 × 10−23 | 4.33 × 10−23 | 8.96 × 10−23 | 4.92 × 10−22 | 2.01 × 10−4 | 2.01 × 10−4 |
| LDL,CHOL | 1.21 × 10−20 | 2.08 × 10−19 | 1.21 × 10−20 | 2.08 × 10−19 | 7.91 × 10−19 | 4.62 × 10−4 | 4.62 × 10−4 | ||
| TG,CHOL | 2.98 × 10−18 | 2.69 × 10−18 | 2.98 × 10−18 | 2.69 × 10−18 | 1.20 × 10−17 | 1.61 × 10−3 | 1.61 × 10−3 | ||
| LDL,TG,CHOL | 9.10 × 10−20 | 3.45 × 10−19 | 9.10 × 10−20 | 3.45 × 10−19 | 1.84 × 10−18 | 7.31 × 10−5 | 3.51 × 10−4 | ||
| LPL | LDL,TG | 5.15 × 10−2 | 2.85 × 10−2 | 5.15 × 10−2 | 2.85 × 10−2 | 4.32 × 10−1 | 4.36 × 10−5 | 4.36 × 10−5 | |
| FUSION | APOE | LDL,TG | 3.05 × 10−7 | 2.02 × 10−8 | 3.05 × 10−7 | 2.02 × 10−8 | 3.83 × 10−8 | 1.90 × 10−1 | 1.90 × 10−1 |
| LDL,CHOL | 1.20 × 10−7 | 1.29 × 10−8 | 1.20 × 10−7 | 1.29 × 10−8 | 1.75 × 10−8 | 4.88 × 10−2 | 4.88 × 10−2 | ||
| TG,CHOL | 4.25 × 10−4 | 1.06 × 10−5 | 4.25 × 10−4 | 1.06 × 10−5 | 1.93 × 10−5 | 4.95 × 10−1 | 4.95 × 10−1 | ||
| LDL,TG,CHOL | 8.02 × 10−6 | 6.44 × 10−7 | 8.02 × 10−6 | 6.44 × 10−7 | 1.11 × 10−6 | 1.33 × 10−1 | 9.41 × 10−2 | ||
| LPL | LDL,TG | 7.11 × 10−5 | 2.82 × 10−3 | 7.11 × 10−5 | 2.82 × 10−3 | 2.73 × 10−2 | 2.71 × 10−5 | 2.71 × 10−5 | |
| LDL,TG,CHOL | 8.51 × 10−4 | 1.79 × 10−2 | 8.51 × 10−4 | 1.79 × 10−2 | 6.32 × 10−2 | 2.29 × 10−6 | 8.61 × 10−4 | ||
| Norway | APOE | LDL,TG | 1.42 × 10−25 | 8.16 × 10−25 | 1.42 × 10−25 | 8.16 × 10−25 | 4.72 × 10−24 | 2.43 × 10−4 | 2.43 × 10−4 |
| LDL,CHOL | 8.12 × 10−29 | 1.64 × 10−27 | 8.12 × 10−29 | 1.64 × 10−27 | 6.70 × 10−27 | 1.13 × 10−4 | 1.13 × 10−4 | ||
| TG,CHOL | 5.32 × 10−20 | 1.46 × 10−19 | 5.32 × 10−20 | 1.46 × 10−19 | 6.08 × 10−19 | 1.66 × 10−3 | 1.66 × 10−3 | ||
| LDL,TG,CHOL | 1.18 × 10−24 | 3.06 × 10−23 | 1.18 × 10−24 | 3.06 × 10−23 | 1.68 × 10−22 | 8.33 × 10−b | 2.20 × 10−4 | ||
| DIAGEN | APOE | LDL,TG | 1.78 × 10−8 | 1.76 × 10−7 | 1.78 × 10−8 | 1.76 × 10−7 | 4.47 × 10−7 | 3.73 × 10−3 | 3.73 × 10−3 |
| LDL,CHOL | 1.24 × 10−9 | 1.44 × 10−8 | 1.24 × 10−9 | 1.44 × 10−8 | 3.24 × 10−8 | 1.60 × 10−1 | 1.60 × 10−1 | ||
| TG,CHOL | 2.99 × 10−6 | 2.49 × 10−5 | 2.99 × 10−6 | 2.49 × 10−5 | 4.51 × 10−5 | 1.71 × 10−1 | 1.71 × 10−1 | ||
| LDL,TG,CHOL | 1.81 × 10−10 | 4.43 × 10−9 | 1.81 × 10−10 | 4.43 × 10−9 | 1.19 × 10−8 | 1.25 × 10−3 | 1.83 × 10−2 | ||
| METSIM | APOE | LDL,TG | 2.70 × 10−7 | 3.45 × 10−7 | 2.70 × 10−7 | 3.45 × 10−7 | 7.77 × 10−7 | 6.29 × 10−4 | 6.29 × 10−4 |
| LDL,CHOL | 3.87 × 10−5 | 5.63 × 10−5 | 3.87 × 10−5 | 5.63 × 10−5 | 9.45 × 10−5 | 3.08 × 10−3 | 3.08 × 10−3 | ||
| LDL,TG,CHOL | 1.09 × 10−6 | 2.08 × 10−6 | 1.09 × 10−6 | 2.08 × 10−7 | 3.91 × 10−6 | 9.51 × 10−4 | 1.06 × 10−3 | ||
| LDLR | LDL,TG | 1.20 × 10−4 | 2.59 × 10−5 | 1.20 × 10−4 | 2.59 × 10−5 | 2.51 × 10−5 | 2.85 × 10−4 | 2.85 × 10−4 | |
| LDL,CHOL | 3.24 × 10−5 | 2.99 × 10−7 | 3.24 × 10−5 | 2.99 × 10−7 | 7.83 × 10−7 | 1.12 × 10−5 | 1.12 × 10−5 | ||
| TG,CHOL | 5.49 × 10−4 | 2.03 × 10−5 | 5.49 × 10−4 | 2.03 × 10−5 | 2.09 × 10−5 | 1.76 × 10−5 | 1.76 × 10−5 | ||
| LDL,TG,CHOL | 4.26 × 10−5 | 1.19 × 10−6 | 4.26 × 10−5 | 1.19 × 10−6 | 1.72 × 10−6 | 6.16 × 10−5 | 3.24 × 10−5 | ||
| Trinity Students Study | An Enzyme Gene | A,B | 2.14 × 10−20 | 3.14 × 10−10 | 2.14 × 10−20 | 3.14 × 10−18 | 7.67 × 10−17 | 4.21 × 10−3 | 2.44 × 10−3 |
| A,C | 1.08 × 10−17 | 9.53 × 10−16 | 1.08 × 10−17 | 9.53 × 10−16 | 4.46 × 10−15 | 2.36 × 10−3 | 2.53 × 10−3 | ||
| B,C | 6.54 × 10−15 | 9.51 × 10−12 | 6.54 × 10−15 | 9.51 × 10−12 | 1.05 × 10−10 | 8.96 × 10−2 | 5.83 × 10−2 | ||
| A,B,C | 2.30 × 10−21 | 5.87 × 10−18 | 2.30 × 10−21 | 5.87 × 10−18 | 1.56 × 10−16 | 7.42 × 10−3 | 3.91 × 10−3 | ||
Abbreviation: GVF = Genetic Variant Function.
In Table 3, the results of GAMuT are new but the other results are mainly from Wang et al. [2015]. GAMuT detected only one association signal at gene LPL in the FUSION study based on projection matrix for a combination of (LDL, TG, CHOL) [p = 2.29 × 10−6], and this is one of the two cases that MFLM and MANOVA failed to detect an association (the other instance is from a combination of (LDL, TG) at gene LPL in study of D2d-2007). In addition, GAMuT based on projection matrix detected seven tentative association signals and GAMuT based on linear kernel detected five. By MFLM and additive models of MANOVA, however, quite a few combinations of lipid traits from the 5 European studies showed associations or tentative association signals in the regions of the APOE and LDLR genes, and all combinations of three traits (i.e., A, B, and C) in the Trinity Students Study showed association with the enzyme gene (Table 3). Moreover, the p-values of the approximate F-distributed tests of fixed models are generally much smaller than those of GAMuT. Therefore, the fixed effect MFLM and MANOVA perform better than GAMuT.
In Tables S.3 and S.4, we report the results of data analysis of the European lipid studies by dividing the data into rare and common variants based on a cutoff of 0.03. It is worth noting that the gene regions contain both rare and common variants and the associations are mainly from common variants. GAMuT detected a tentative association at gene LPL in the FUSION study in Table S.4 based on common variants for the combination (LDL, TG, CHOL) [p = 2.99 × 10−5], but no association signal was detected in Table S.3 based on rare variants [p = 3.02 × 10−1]. After combining rare and common variants into one group, GAMuT detected an association signal at gene LPL in the FUSION study based on projection matrix in Table 3 [p = 2.29 × 10−6]. Interestingly, GATuT was designed to analyze rare variants while the only association was detected in a combination of rare and common variants at gene LPL.
Discussion
In this study, extensive simulations were performed to evaluate the performance of tests of fixed effect models and GAMuT, by using simulated genetic variants located in 3 - 30 kb regions. We carried out simulation analyses for two scenarios: (1) all causal variants are rare; (2) some causal variants are rare and some are common. No matter which scenario, fixed effect MFLM and MANOVA perform better than GAMuT when the genetic effect sizes are relatively large, and GAMuT performs better when the region sizes are large and the genetic effect sizes are small. When the region size grows, MFLM and MANOVA gradually perform worse and GAMuT performs better if the genetic effect sizes are smaller and smaller. In short, MFLM and MANOVA perform well if the effective sizes are relatively large and GAMuT performs well when the effective sizes are small, which was also pointed out in Broadaway et al. [2016].
In prior studies, fixed effect functional regression models were found to outperform SKAT, its optimal unified test (SKAT-O), and a combined sum test of rare and common variant effect (SKAT-C) in most cases [Fan et al., 2013, 2014, 2015, 2016a, 2016b, 2016c; Luo et al., 2011, 2012, 2013; Svishcheva et al., 2015; Vsevolozhskaya et al., 2014, 2016]. In Fan et al. (2016c), we compared the performance of MFLM and MANOVA, and the performance of SKAT/SKAT-O/SKAT-C and the univariate fixed models [Fan et al., 2013]. For multivariate analysis, no comparison was made since there was no multivariate version of SKAT/SKAT-O/SKAT-C to compare with in Fan et al. (2016c). In this paper, we fill the gap by comparing the performance of MFLM and MANOVA with GAMuT.
Geneticists have long known of the existence of polygenes which have small effects on phenotypes [Fisher, 1918]. If the number of causal genetic variants at a gene locus is very large and each variant contributes a small amount to the traits, SKAT/SKAT-O/SKAT-C and GAMuT perform better than the tests of fixed models. Thus, SKAT/SKAT-O/SKAT-C as well as GAMuT are more appropriate for analyzing polygenic effects. In major gene association analysis, we look for genes which have relatively large effects (otherwise, they are not major genes). When the number of causal genetic variants at a major gene locus is not very large and the contribution of a few causal variants to the traits is reasonably large, the fixed models should work well, which should be the case for most complex disorders.
The GAMuT procedure was designed for the analysis of rare variants but we use GAMuT to analyze a combination of common and rare variants. As noted in Ionita-Laza et al. [2013], this would be suboptimal and would lead to the common variants drowning out the effects of rare variants. It is very likely that GAMuT can be revised to improve power to analyze a combination rare and common variants by implementing a strategy similar to the combined sum test outlined in Ionita-Laza et al. [2013]. In terms of MFLM, it does not need to be weighted by MAF. The genetic effect functions is actually the effect of the genetic variant functions at the location t, which can be thought of as a weighted effect. In Fan et al. (2014), we explored the issues using weighted genetic variant functions defined by the MAF, and found that the power is very similar to the power without weights. Hence, it is not necessary to add weights in functional regression models. One benefit of treating genotype data functionally is that the genetic effect function naturally serves as a weighting function; this function is determined by the data, and takes marker spacing and linkage disequilibrium (LD) and similarity among individuals into account. In short, the functional regression models are data driven approaches.
By using gene-based tests, one may discover associations with a variant set. Gene-based tests do not reveal precisely which variants are associated with the disease, but the findings can suggest targeted follow-up and laboratory investigation [Zuk et al., 2014]. If all variants had small effects on the phenotypes, it would be hard to locate them. If the contribution of some causal variants to the traits is reasonably large, it would be possible to locate them. We argue that MFLM and MANOVA perform better in most major gene association studies.
In our real data analysis, we found that multivariate fixed models perform better than GAMuT in most gene regions. Note that the European lipid data contain both rare and common variants. As argued by Ionita-Laza et al. [2013], it is reasonable to assume that a combination of rare and common variants affects the risk of many complex disorders. GAMuT detected only one association signal at gene LPL while multivariate fixed models failed to confirm it. Hence, the two methods can be complementary instead of competing with each other. It is our hope that our work may shed more light in gene-based association analysis to facilitate dissection of complex disorders.
Supplementary Material
Acknowledgement
Two anonymous reviewers and the editors, Dr. Shete and Dr. Cordell, provided very good and insightful comments for us to improve the manuscript. We greatly thank the European cohorts groups for letting us analyze the data and using them as examples. Dr. Heather M. Stringham and Dr. Tanya M. Teslovich kindly sent us the data of the European cohorts and patiently answered many questions about the cohorts, and we greatly appreciate their help. This study was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (Ruzong Fan, Chi-yang Chiu, and James L. Mills), by the Intramural Research Program of the National Human Genome Research Institute (Alexander F. Wilson and Joan E. Bailey-Wilson), National Institutes of Health, Bethesda, MD. This study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov).
Footnotes
Computer Program. The methods proposed in this paper are implemented by using procedures from functional data analysis (fda) R package. The R codes for multivariate fixed models are available from the web site http://www.nichd.nih.gov/about/org/diphr/bbb/software/fan/Pages/default.aspx
Reference
- Allison DB, Thiel B, St Jean P, Elston RC, Infante MC, Schork NJ. Multiple phenotype modeling in gene-mapping studies of quantitative traits: power advantages. The American Journal of Human Genetics. 1998;63:1190–1201. doi: 10.1086/302038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson TW. An Introduction to Multivariate Statistical Analysis. Second Edition John Wiley & Sons; New York: 1984. [Google Scholar]
- Ansorge WJ. Next-generation DNA sequencing techniques. New Biotechnology. 2009;25:195–203. doi: 10.1016/j.nbt.2008.12.009. [DOI] [PubMed] [Google Scholar]
- Broadaway KA, Cutler DJ, Duncan R, Moore JL, Ware EB, Jhun MA, Bielak LF, Zhao W, Smith JA, Peyser PA, Kardia SLR, Ghosh D, Epstein MP. A statistical approach for testing cross-phenotype effects of rare variants. The American Journal of Human Genetics. 2016;98:525–540. doi: 10.1016/j.ajhg.2016.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chavali S, Barrenas F, Kanduri K, Benson M. Network properties of human disease genes with pleiotropic effects. BMC Syst Biol. 2010;4:78. doi: 10.1186/1752-0509-4-78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniels PR, Kardia SL, Hanis CL, Brown CA, Hutchinson R, Boerwinkle E, Turner ST, Genetic Epidemiology Network of Arteriopathy Study Familial aggregation of hypertension treatment and control in the Genetic Epidemiology Network of Arteriopathy (GENOA) study. Am J Med. 2004;116:676–681. doi: 10.1016/j.amjmed.2003.12.032. [DOI] [PubMed] [Google Scholar]
- de Boor C. Applied Mathematical Sciences 27. A Practical Guide to Splines, revised version. Springer; New York: 2001. [Google Scholar]
- Fan R, Wang Y, Mills JL, Wilson AF, Bailey-Wilson JE, Xiong MM. Functional linear models for association analysis of quantitative traits. Genetic Epidemiology. 2013;37:726–742. doi: 10.1002/gepi.21757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R, Wang Y, Mills JL, Carter TC, Lobach I, Wilson AF, Bailey-Wilson JE, Weeks DE, Xiong MM. Generalized functional linear models for case-control association studies. Genetic Epidemiology. 2014;38:622–637. doi: 10.1002/gepi.21840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan RZ, Wang YF, Boehnke M, Chen W, Li Y, Ren HB, Lobach I, Xiong MM. Gene level meta-analysis of quantitative traits by functional linear models. Genetics. 2015;200:1089–1104. doi: 10.1534/genetics.115.178343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan RZ, Wang YF, Chiu CY, Chen W, Ren HB, Li Y, Boehnke M, Amos CI, Moore JH, Xiong MM. Meta-analysis of complex diseases at gene level with generalized functional linear models. Genetics. 2016a;202:457–470. doi: 10.1534/genetics.115.180869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan RZ, Wang YF, Qi Y, Ding Y, Weeks DE, Lu ZH, Ren HB, Cook RJ, Xiong MM, Chen W. Gene-based association analysis for censored traits via functional regressions. Genetic Epidemiology. 2016b;40:133–143. doi: 10.1002/gepi.21947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan RZ, Chiu CY, Jung JS, Weeks DE, Wilson AF, Bailey-Wilson JE, Amos CI, Chen Z, Mills JL, Xiong MM. A comparison study of xed and mixed effect models for gene level association studies of complex traits. Genetic Epidemiology. 2016c doi: 10.1002/gepi.21984. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferraty F, Romain Y. The Oxford Handbook of Functional Data Analysis. Oxford University Press; New York: 2010. [Google Scholar]
- Ferreira MA, Purcell SM. A multivariate test of association. Bioinformatics. 2009;25:132–133. doi: 10.1093/bioinformatics/btn563. [DOI] [PubMed] [Google Scholar]
- Fisher RA. The correlation between relatives on the supposition of Mendelian inheritance. Philos Trans R Soc Edinb. 1918;52:399–433. [Google Scholar]
- Galesloot TE, van Steen K, Kiemeney LA, Janss LL, Vermeulen SH. A comparison of multivariate genome-wide association methods. PLoS ONE. 2014;9:e95923. doi: 10.1371/journal.pone.0095923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J, Johnson AD, ODonnell CJ. PRIMe: a method for characterization and evaluation of pleiotropic regions from multiple genome-wide association studies. Bioinformatics. 2011;27:1201–1206. doi: 10.1093/bioinformatics/btr116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horváth L, Kokoszka P. Inference for Functional Data With Applications. Springer; New York: 2012. [Google Scholar]
- Ionita-Laza I, Lee S, Makarov V, Buxbaum JD, Lin X. Sequence kernel association tests for the combined effect of rare and common variants. The American Journal of Human Genetics. 2013;92:841–853. doi: 10.1016/j.ajhg.2013.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Emond MJ, Bamshad MJ, Barnes KC, Rieder MJ, Nickerson DA, NHLBI GO Exome Sequencing Project—ESP Lung Project Team. Christiani DC, Wurfel MM, Lin X. Optimal uni ed approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. The American Journal of Human Genetics. 2012;91:224–237. doi: 10.1016/j.ajhg.2012.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu DJ, Peloso GM, Zhan X, Holmen OL, Zawistowski M, Feng S, Nikpay M, Auer PL, Goel A, Zhang H, et al. Meta-analysis of gene-level tests for rare variant association. Nat Genet. 2014;46:200–204. doi: 10.1038/ng.2852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Boerwinkle E, Xiong MM. Association studies for next-generation sequencing. Genome Research. 2011;21:1099–1108. doi: 10.1101/gr.115998.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Zhu Y, Xiong MM. Quantitative trait locus analysis for next-generation sequencing with the functional linear models. J Med Genet. 2012;49:513–524. doi: 10.1136/jmedgenet-2012-100798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Zhu Y, Xiong MM. Smoothed functional principal component analysis for testing association of the entire allelic spectrum of genetic variation. European Journal of Human Genetics. 2013;21:217–224. doi: 10.1038/ejhg.2012.141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maity A, Sullivan PF, Tzeng JY. Multivariate phenotype association analysis by marker-set kernel machine regression. Genetic Epidemiology. 2012;36:686–695. doi: 10.1002/gepi.21663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardis ER. Next-generation DNA sequencing methods. Annu Rev Genom Hum Genet. 2008;9:387–402. doi: 10.1146/annurev.genom.9.081307.164359. [DOI] [PubMed] [Google Scholar]
- Metzker ML. Sequencing technologies the next generation. Nat Rev Genet. 2010;11:31–46. doi: 10.1038/nrg2626. [DOI] [PubMed] [Google Scholar]
- O'Reilly PF, Hoggart CJ, Pomyen Y, Calboli FC, Elliott P, Jarvelin MR, Coin LJ. MultiPhen: joint model of multiple phenotypes can increase discovery in GWAS. PLoS ONE. 2012;7:e34861. doi: 10.1371/journal.pone.0034861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JO, Hooker G, Graves S. Functional Data Analysis With R and Matlab. Springer; New York: 2009. [Google Scholar]
- Ramsay JO, Silverman BW. Functional Data Analysis. 2nd edition Springer; New York: 2005. [Google Scholar]
- Rao CR. Linear statistical inference and its applications. Second Edition John Wiley & Sons; New York: 1973. [Google Scholar]
- Ried JS, Döring A, Oexle K, Meisinger C, Winkelmann J, Klopp N, Meitinger T, Peters A, Suhre K, Wichmann HE, Gieger C. PSEA: Phenotype Set Enrichment Analysis - a new method for analysis of multiple phenotypes. Genetic Epidemiology. 2012;36:244–252. doi: 10.1002/gepi.21617. [DOI] [PubMed] [Google Scholar]
- Rusk N, Kiermer V. Primer: Sequencingthe next generation. Nat Methods. 2008;5:15. doi: 10.1038/nmeth1155. [DOI] [PubMed] [Google Scholar]
- Schaffner SF, Foo C, Gabriel S, Reich D, Daly MJ, Altshuler D. Calibrating a coalescent simulation of human genome sequence variation. Genome Research. 2005;15:1576–1583. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shendure J, Ji H. Next-generation DNA sequencing. Nat Biotechnol. 2008;26:1135–1145. doi: 10.1038/nbt1486. [DOI] [PubMed] [Google Scholar]
- Sivakumaran S, Agakov F, Theodoratou E, Prendergast JG, Zgaga L, Manolio T, Rudan I, McKeigue P, Wilson JF, Campbell H. Abundant pleiotropy in human complex diseases and traits. The American Journal of Human Genetics. 2011;89:607–618. doi: 10.1016/j.ajhg.2011.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovieff N, Cotsapas C, Lee PH, Purcell SM, Smoller JW. Pleiotropy in complex traits: challenges and strategies. Nat Rev Genet. 2013;14:483–495. doi: 10.1038/nrg3461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svishcheva GR, Belonogova NM, Axenovich TI. Region-based association test for familial data under functional linear models. PLoS ONE. 2015;10:e0128999. doi: 10.1371/journal.pone.0128999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vsevolozhskaya OA, Zaykin DV, Greenwood MC, Wei C, Lu Q. Functional analysis of variance for association studies. PLoS ONE. 2014;9(9):e105074. doi: 10.1371/journal.pone.0105074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vsevolozhskaya OA, Zaykin DV, Barondess DA, Tong X, Jadhav S, Lu Q. Uncovering local trends in genetic effects of multiple phenotypes via functional linear models. Genetic Epidemiology. 2016;40:210–221. doi: 10.1002/gepi.21955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang YF, Liu AY, Mills JL, Boehnke M, Wilson AF, Bailey-Wilson JE, Xiong MM, Wu CO, Fan RZ. Pleiotropy analysis of quantitative traits at gene level by multivariate functional linear models. Genetic Epidemiology. 2015;39:259–275. doi: 10.1002/gepi.21895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. The American Journal of Human Genetics. 2011;89:82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuk O, Schaffner SF, Samocha K, Do R, Hechter E, Kathiresan S, Daly MJ, Neale BM, Sunyaev SR, Lander ES. Searching for missing heritability: Designing rare variant association studies. Proceedings of the National Academy of Sciences. 2014;111(4):E455E464. doi: 10.1073/pnas.1322563111. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.