Abstract
Many genetic epidemiological studies collect repeated measurements over time. This design not only provides a more accurate assessment of disease condition, but allows us to explore the genetic influence on disease development and progression. Thus, it is of great interest to study the longitudinal contribution of genes to disease susceptibility. Most association testing methods for longitudinal phenotypes are developed for single variant, and may have limited power to detect association, especially for variants with low minor allele frequency. We propose Longitudinal SNP-set/Sequence Kernel Association Test (LSKAT), a robust, mixed-effects method for association testing of rare and common variants with longitudinal quantitative phenotypes. LSKAT uses several random effects to account for the within-subject correlation in longitudinal data, and allows for adjustment for both static and time-varying covariates. We also present a longitudinal-trait burden test (LBT), where we test association between the trait and the burden score in linear mixed models. In simulation studies, we demonstrate that LBT achieves high power when variants are almost all deleterious or all protective, while LSKAT performs well in a wide range of genetic models. By making full use of trait values from repeated measures, LSKAT is more powerful than several tests applied to a single measurement or average over all time points. Moreover, LSKAT is robust to misspecification of the covariance structure. We apply the LSKAT and LBT methods to detect association with longitudinally-measured body mass index in the Framingham Heart Study, where we are able to replicate association with a circadian gene NR1D2.
Keywords: longitudinal study, association testing, linear mixed model, variant set, quantitative trait
1. INTRODUCTION
Over recent years, genome-wide association studies (GWAS) have been successful in identifying thousands of susceptibility variants for common diseases and complex traits. However, these genetic variants have explained only a small proportion of heritability [Eichler et al., 2010; Manolio et al., 2009]. To date, most of the GWAS have focused on case/control status of particular diseases or cross-sectional measurements of phenotypic traits. Many genetic epidemiological studies have been conducted in cohorts, in which repeated measures on the trait of interest are collected on each participant over a period of time. Such studies not only provide a more accurate assessment of disease condition, but enable us to investigate genes influencing the trajectory of a trait and disease progression, which are likely to reduce the remaining missing heritability of these traits [Wu and Lin, 2006]. Recently, complementary to traditional epidemiological studies, electronic medical records (EMR) have become an emerging resource for genomic research [Dumitrescu et al., 2015; Gottesman et al., 2013; Kullo et al., 2010; MaCarty et al., 2011]. EMR-derived data offer rich phenotype information including longitudinal measures and lengthy follow-up. As a result, more and more longitudinal studies have been introduced in GWAS to understand how genetic variants affect changes over time of a particular phenotype [Cousminer et al., 2013; Smith et al., 2010; Tang et al., 2014].
In longitudinal data analysis, it is important to account for the non-independence of repeated measurements from the same subject. To estimate growth trajectories or changes of trait values over time, several statistical methods have been developed, such as random effects models [Laird and Ware, 1982], hierarchical linear models [Raudenbush and Bryk, 2002], empirical Bayes models [Hui and Berger, 1983], and growth mixture models [Muthen, 2004]. Association analyses that incorporate these methods have been applied to longitudinal GWAS to test individual genetic variant [Das et al., 2011; Fan et al., 2012; Furlotte et al., 2012; Londono et al., 2013; Meirelles et al., 2013; Sikorska et al., 2013; Wang et al., 2012]. However, single-variant association tests suffer from restricted power to detect association, especially for variants with low minor allele frequency (MAF) which are commonly seen in high-throughput sequencing studies and exome chip genotyping arrays. It would be advantageous to consider the joint effect of multiple markers in a variant set. Such analyses offer greater power by reducing the multiple testing burden and aggregating signals on the basis of genomic features such as genes or linkage disequilibrium (LD)-based haplotype blocks [Neale and Sham, 2004; Wu et al., 2010].
Most existing methods for region-based association analysis are designed for phenotypes from a single time point, including two broad classes of methods referred to as “burden tests” [Han and Pan 2010; Li and Leal, 2008; Lin and Tang 2011; Madsen and Browning, 2009; Morgenthaler and Thilly, 2007; Morris and Zeggini, 2010; Price et al., 2010] and “variance component tests” [Chen et al., 2013; Neale et al., 2011; Schifano et al., 2012; Wu et al., 2011]. Burden tests collapse information from multiple variant sites in a region into a single genetic burden score, and then test for association between the trait and the burden score. In contrast, variance component tests aggregate statistics from individual variant sites for measuring association. Omnibus tests that combine burden tests and variance component tests have also been proposed in population samples [Derkach et al., 2013; Lee et al., 2012] and family studies [Jiang and McPeek, 2014]. The performance of various burden and variance component tests have been extensively evaluated for rare genetic variants [Derkach et al., 2014]. In general, the power of a test depends on the nature of association, such as proportion of causal variants, directions of association, variants frequencies and genetic effects.
For longitudinal data, there has been limited literature on statistical methods for region-based association analysis [Beyene and Hamid, 2014; Chien et al., 2016; Wu et al., 2014; Yan et al., 2015]. Linear mixed model is one of the popular methods for longitudinal data. Kernel-based methods offer a flexible and powerful platform to combine complex or high-dimensional genomic information [Schaid, 2010], e.g. the sequence kernel association test (SKAT) for rare variants [Wu et al., 2011]. In this study, we propose LSKAT (Longitudinal SNP-set/Sequence Kernel Association Test), a longitudinal trait association testing approach, which combines features of linear mixed models and kernel machine methods to test for association between variants in a genomic region and a longitudinal quantitative phenotype. LSKAT can be viewed as an extension of the SKAT test of a single measurement to repeated measurements. It effectively accounts for the within-subject correlations by using several random effects and allows for adjustment for both static and time-varying covariates. We also present a longitudinal-trait burden test (LBT), where we test association between the trait and the burden score in linear mixed models. Through simulation studies, we evaluate the type I error rates of LSKAT and LBT, and compare their power to that of SKAT and burden test. We further investigate the performance of LSKAT and LBT when the assumptions on the correlation structure of the random effects are violated. Our simulation results show that LSKAT has an increased power over the SKAT and burden tests with a single time point measurement or the average value across time points. When a high proportion of the variants are causal and they are almost all deleterious or all protective, LBT achieves the highest power. However, when both deleterious and protective variants are present, or the fraction of the causal variants is low, LSKAT outperforms LBT. Moreover, LSKAT is robust to misspecified covariance structure in all of our simulation settings. Finally, we illustrate the utility of the two approaches by evaluating genome-wide association with longitudinally-measured body mass index in the Framingham Heart Study, where we replicate association with a circadian gene NR1D2.
2. METHODS
2.1 Kernel-based linear mixed model for longitudinal trait
Suppose a quantitative trait is measured over time on n sampled individuals. We consider the problem of association testing between the trait and all variants in a genomic region, e.g. a single gene, an exon, or a multigene region. Let yij be the trait value measured on the ith subject at time tij, and xij be a p × 1 covariate vector, where xij always includes an intercept, i.e., the first entry of xij is 1. We allow that xij includes both static and time-varying covariates. Suppose the genomic region of interest contains m variants that have been selected in the test. Let Gi = (Gi1, …, Gim)T denote an m × 1 genotype vector at the m variant sites, and Gik = 0, 1 or 2, according to whether the ith subject has 0, 1 or 2 copies of minor allele at the kth variant site. We model the trait value using a linear mixed effects model:
| (1) |
where β is a p × 1 vector of the regression coefficients for the covariates, γ = (γ1, …, γm)T is an m × 1 vector of random effects for the m genetic variants. We assume that the variant random effects vector γ does not change with time, and follows an arbitrary distribution with E(γk) = 0 and , where τ is the variance component of genetic effects, and wk is a fixed, pre-specified weight for the kth variant that depends on particular features of the variant. Various weighting schemes have been proposed. For example, the weight of a variant is some function of its MAF [e.g., Madsen and Browning, 2009; Wu et al., 2011], or the weight is determined by prior information on function or annotation. Uniform weighting can be used if no prior information is available.
In Model (1), the dependency among repeated measures of the trait values is captured by several random effects: ai represents the individual random effect, rij is the individual-specific time-dependent random effect, and eij is the measurement error. We assume ai’s are independent and . Here we allow individuals to have measures at different time points. The correlation between each pair of rij and rij′, the random effects at two measurement times tij and tij′ of the ith subject, depends on the time lag between the two time points and the degree of influence on the trait. For example, we assume has a multivariate normal distribution, , where ni is the number of repeated measurements on the ith subject, and the correlation matrix Ri can be modeled with the first-order autoregressive correlation structure [AR(1)] with , where |φ| < 1 [Diggle, 1988]. The error term eij is assumed to be i.i.d. .
Writing in a matrix form, we have the following conditional phenotypic model:
| (2) |
where , the phenotype vector of length N = Σini, X is the N × p covariate matrix, and G is the n × m genotype matrix. That is, conditional on γ, X and G, Y has a multivariate normal distribution with mean vector Xβ + MGγ and covariance matrix Σ, where M is an N × n design matrix for measurement clustering structure, with Mli being the indicator that the lth entry of Y belongs to the measurements on subject i. The conditional covariance matrix Σ includes three terms: the first term, , summarizes the individual-level time-independent correlation; the second term, , models the individual-level time-dependent correlation, where R = diag(R1, …, Rn) is a block diagonal matrix; and the last term, , represents the measurement error, where I is an N-dimensional identity matrix. Note that, by converting the genotype matrix G to the design matrix MG in Model (2), we extend the genetic mean vector from the individual level to the measurement level. The overall mean also depends on the covariate values at each time point that are allowed to change over time.
To detect association between the trait and the genomic region of interest, we test H0 : γ = 0 vs. H1 : γ ≠ 0 in Model (1), which is equivalent to test H0 : τ = 0 vs. H1 : τ > 0. The null maximum likelihood estimates (MLEs) of β, φ, , , and can be obtained by fitting the null model to the data without performing a genome scan. We then estimate the null covariance matrix by replacing φ, , and with their null MLEs. Finally, we obtain the LSKAT statistic, given by
| (3) |
where is an m × m diagonal weight matrix. Since the covariance matrix Σ in Model (2) is specified as a block diagonal matrix, the LSKAT statistic TK can further be expressed as the weighted sum of the individual variant score statistics
where , the phenotype vector on the ith subject, Xi is the covariate matrix on subject i, is the ith diagonal block of , and is an ni-vector of 1’s. Thus, LSKAT belongs to the class of quadratic statistics considered by Derkach et al., [2014].
To evaluate the P-value of the LSKAT statistic, we define
Under the null hypothesis, TK asymptotically follows a mixture of chi-square distributions, i.e. , where (λ1, …, λr) are the nonzero eigenvalues of the matrix , and the ’s are independent variables. The P-value can then be evaluated by a moment-matching method [Liu et al., 2009].
2.2 Burden score-based linear mixed model for longitudinal trait
To extend the burden test to the context of repeated measures, we consider the genetic burden score as a single variable and evaluate its association with the trait in a linear mixed model. In this case, we fit the model
| (4) |
where the burden score is a weighted sum of genotypes at all variants being tested, and θ is the parameter of interest. Here yij, xij, β, ai, rij, eij are as defined in Model (1). The LBT statistic is a score test for testing H0 : θ = 0 vs. H1 : θ ≠ 0, given by
| (5) |
where w = (w1, …, wm)T is an m × 1 weight vector. We can also write the LBT statistic TB as
It can be seen that LBT belongs to the class of linear statistics specified by Derkach et al., [2014]. Under the null hypothesis, TB asymptotically follows a scaled distribution.
3. RESULTS
3.1 Simulation studies
We conduct simulation studies in order to (1) evaluate the type I error rates of LSKAT and LBT; (2) compare their power to that of SKAT and burden test (BT); and (3) assess sensitivity of the two tests to misspecified covariance structure. Because SKAT and BT are only applicable to a single measurement, we consider both tests when they are applied to the baseline measures (SKATBL and BTBL) and the average across multiple time points (SKATAVG and BTAVG).
In the simulations, we first generate 10,000 chromosomes over a 1 Mb region using a coalescent model that implements a population genetic model to mimic the LD pattern, recombination rates, and the population history of Europeans [Schaffner et al., 2005]. We then simulate 1,000 sets of genotype data from randomly selected sets of regions within the 1 Mb chromosome. The lengths of the regions range from 5 kb to 30 kb. We further remove the variants with less than 4 copies of minor allele in the n samples, where we set n = 500, 1000, and 2500. The selected regions contain 47 observed variants on average, and the number of observed variants in any given data set varies across the sample size n.
3.1.1 Type I error simulations
In the assessment of type I error rates, for each of the 1,000 simulated genotype data sets, we simulate 1,000 sets of trait values at eight time points using the model
where Xij1 is a continuous, time-varying covariate that is generated from a standard normal distribution, Xi2 is a binary, time-independent covariate taking values 0 or 1 with a probability of 0.5, ai is an individual random effect generated from a distribution, , where R is an 8 × 8 correlation matrix specified by the AR(1) model with a correlation coefficient φ, and eij is independently generated from a distribution at each time point. Here the variance components are set to and φ = 0.75. Note that this null model indicates that the trait values are not related to the genotypes in the type I error experiments. Putting all together, we obtain 106 genotype-phenotype data sets.
In linear mixed models, we commonly model the covariance structure of random effects. There has not been much investigation on whether misspecification of the covariance structure affects the type I error and power in genetic association analysis with longitudinal phenotypes. Therefore, we further investigate the robustness of LSKAT and LBT when the correlation matrix R is misspecified. We simulate trait values under two correlation structures commonly used for growth curves:
compound symmetry model, where the correlations within a subject are constant over time, i.e., Rjk = φ when j ≠ k, and Rjj = 1;
- first-order structured antedependence [SAD(1)] model specified as in Jaffrézic et al. [2003] with
Here the correlation function in the SAD model is non-stationary and depends not only on the time interval, but also on the start and end points of the interval.
For each of the 106 replicates of genotype-phenotype data, we apply the LSKAT and LBT methods to test association with all variants, including X1 and X2 as covariates in the analysis. We use the weights suggested by Wu et al. [2011] for rare variants with MAF < 5% and that suggested by Madsen and Browning [2009] for common variants with MAF ≥ 5%. We estimate the type I error rates with nominal levels set at 10−3, 10−4, and 10−5. Table 1 gives the empirical type I error rates of LSKAT and LBT under various correlation structures and sample sizes. In all simulations, the type I error of LSKAT does not exceed the nominal, though when the true correlation is compound symmetry, LSKAT is slightly conservative. In contrast, LBT has inflated type I error under the SAD(1) model when sample size is small (n = 500). These results suggest that the type I error rate of LSKAT is protected and robust against deviation from the assumed within-subject AR(1) correlation structure, whereas the type I error of LBT is more sensitive to sample size and correlation structure.
Table 1.
Empirical type I error of LSKAT and LBT under different correlation structures, based on 106 simulated replicates. Rates that are significantly larger than the nominal levels are in bold.
| Sample Size | Correlation | Empirical Type I Error
|
|||||
|---|---|---|---|---|---|---|---|
| LSKAT
|
LBT
|
||||||
| α = 10−3 | α = 10−4 | α = 10−5 | α = 10−3 | α = 10−4 | α = 10−5 | ||
| AR(1) | 8.9 × 10−4 | 6.1 × 10−5 | 4 × 10−6 | 1.0 × 10−3 | 8.2 × 10−5 | 5 × 10−6 | |
| 500 | CS | 6.1 × 10−4 | 4.3 × 10−5 | 5 × 10−6 | 5.6 × 10−4 | 4.7 × 10−5 | 2 × 10−6 |
| SAD(1) | 1.0 × 10−3 | 9.8 × 10−5 | 4 × 10−6 | 1.5 × 10−3 | 1.5 × 10−4 | 1.6 × 10−5 | |
|
| |||||||
| AR(1) | 8.8 × 10−4 | 8.6 × 10−5 | 8 × 10−6 | 1.0 × 10−3 | 8.3 × 10−5 | 4 × 10−6 | |
| 1000 | CS | 6.0 × 10−4 | 4.8 × 10−5 | 5 × 10−6 | 6.7 × 10−4 | 4.2 × 10−5 | 5 × 10−6 |
| SAD(1) | 8.6 × 10−4 | 7.9 × 10−5 | 5 × 10−6 | 8.2 × 10−4 | 6.2 × 10−5 | 4 × 10−6 | |
|
| |||||||
| AR(1) | 8.4 × 10−4 | 7.9 × 10−5 | 7 × 10−6 | 7.4 × 10−4 | 6.3 × 10−5 | 4 × 10−6 | |
| 2500 | CS | 6.8 × 10−4 | 5.9 × 10−5 | 4 × 10−6 | 6.7 × 10−4 | 4.5 × 10−5 | 4 × 10−6 |
| SAD(1) | 9.4 × 10−4 | 8.7 × 10−5 | 7 × 10−6 | 9.0 × 10−4 | 4.7 × 10−5 | 6 × 10−6 | |
AR(1): first-order autoregressive model
CS: compound symmetry model
SAD(1): first-order structured antedependence model
An important feature of the LSKAT and LBT methods is the use of several random effects to capture the within-subject correlation in linear mixed models. We conduct additional simulations to assess the impact on type I error if the individual-level time-dependent correlation is not accounted for. For each of the 106 genotype-phenotype data sets, we apply alternative versions of LSKAT and LBT without considering the term rij in Models (1) and (4). The empirical type I error rates are inflated for both LSKAT and LBT at all three nominal levels when sample size is 2500, and LBT has slightly inflated type I error at the nominal 10−3 level when sample size is 1000 (Table 2). We also apply the SKAT and BT methods to the genotype-phenotype data sets without modeling the within-subject correlation. In this case, the type I error rates of SKAT and BT are severely inflated (results not shown). These simulation studies demonstrate that it is critical to account for the non-independence of repeated measurements and model the time-dependent correlation in association testing with longitudinal data.
Table 2.
Empirical type I error of LSKAT and LBT without modeling the individual-level time-dependent correlation, based on 106 simulated replicates. Rates that are significantly larger than the nominal levels are in bold.
| Sample Size | Empirical Type I Error | |||||
|---|---|---|---|---|---|---|
| LSKAT | LBT | |||||
| α = 10−3 | α = 10−4 | α = 10−5 | α = 10−3 | α = 10−4 | α = 10−5 | |
| 500 | 9.3 × 10−4 | 8.2 × 10−5 | 8 × 10−6 | 1.0 × 10−3 | 9.5 × 10−5 | 7 × 10−6 |
| 1000 | 1.0 × 10−3 | 7.9 × 10−5 | 7 × 10−6 | 1.1 × 10−3 | 1.1 × 10−4 | 8 × 10−6 |
| 2500 | 1.5 × 10−3 | 2.7 × 10−4 | 4.3 × 10−5 | 1.7 × 10−3 | 3.0 × 10−4 | 5.7 × 10−5 |
3.1.2 Power simulations
To compare the power of LSKAT and LBT to that of SKAT and BT, we use the 1,000 simulated genotype data sets to generate phenotypes. The genomic regions contain on average 47 observed variants. We set the proportion of the causal variants at two levels, 30% and 90%, where only a small percentage of variants are associated with the trait at the first level, while majority of variants are associated at the second level. We simulate trait values using the model
where i = 1, …, n and j = 1, …, 8. Here Xij1, Xi2, ai, rij, and eij are as defined for the type I error experiments, s is the total number of causal variants, Gi1, …, Gis are the genotypes for the s causal variants coded as 0, 1 or 2, and the γs are the fixed genetic effects for the causal variants. In the first scenario with 30% of variants being causal, we set the magnitude of each γk to 0.12 for common variants and 0.08|log10MAFk| for rare variants. When the proportion of the causal variants is 90%, the genetic effects are reduced to 1/3 of the values in the first scenario. The sign of γk is determined by the pre-specified percentage of causal variants with positive and negative effects, where the proportion of positive effects is set at 100%, 80%, and 50%. We consider three parameter settings for the variance components , , and . The parameter values are listed as Models I–III in Table 3. In all three models, the correlation coefficient in the AR(1) model is set at φ = 0.75. To evaluate power of all methods when the correlation structure is misspecified, we also generate trait values using the compound symmetry correlation matrix and the SAD(1) model (Models IV and V in Table 3).
Table 3.
Correlation structures and variance component parameters in power simulations
| Model | Correlation | Variance Components | |
|---|---|---|---|
| I | AR(1) |
|
|
| II | AR(1) |
|
|
| III | AR(1) |
|
|
| IV | CS |
|
|
| V | SAD(1) |
|
AR(1): first-order autoregressive model
CS: compound symmetry model
SAD(1): first-order structured antedependence model
We perform association testing with all observed variants using the same weights specified in the type I error experiments. Empirical power is obtained for LSKAT, LBT, SKATAVG, BTAVG, SKATBL, and BTBL at the significance level 10−5, based on 1,000 replicates. Figure 1 demonstrates the power results of the first scenario when a substantial fraction of the variants are not associated with the phenotype. In each of Models I–III, when the proportion of causal variants that are positively associated with the trait is 100% or 80%, LSKAT and LBT are more powerful than the other four methods. This is because both LSKAT and LBT gain power by directly using the trait information from all time points, while SKAT and BT tend to lose information when they are applied to either the baseline measures or the time point average of each sample. When all effects of causal variants are in the same direction (100% positive), LSKAT and LBT have comparable power, with LBT having a slightly higher power when sample sizes are 500 and 1000. In contrast, LSKAT is more powerful than LBT when the effects for the causal variants are 80% positive. However, when the percentage of positive effects drops to 50%, LBT loses power, and the power of SKATAVG and SKATBL improves such that SKATAVG outperforms LBT in all three models, and SKATBL performs better than LBT in some cases; while LSKAT is consistently the most powerful of all the tests in all three models. In the second scenario when the fraction of the causal variants increases to 90%, the power results in Figure 2 are slightly different. When the effects of causal variants are all positive, LBT achieves the highest power, and LSKAT remains to be more powerful than the other four tests in all three models. As the proportion of the positive causal variants declines, LBT gradually loses power, and is less powerful than LSKAT when the effects for the causal variants are 50% positive. This suggests that LBT performs better when variants are almost all deleterious or all protective, while LSKAT is better when both deleterious and protective variants are present. When causal variants are all deleterious or all protective, but a large fraction of the variants are not associated with the trait, the power gain of LBT over LSKAT is less prominent. These results are in agreement with the power comparison between linear and quadratic tests for rare variant association with a trait value measured at a single time point [Derkach et al., 2014].
Figure 1.
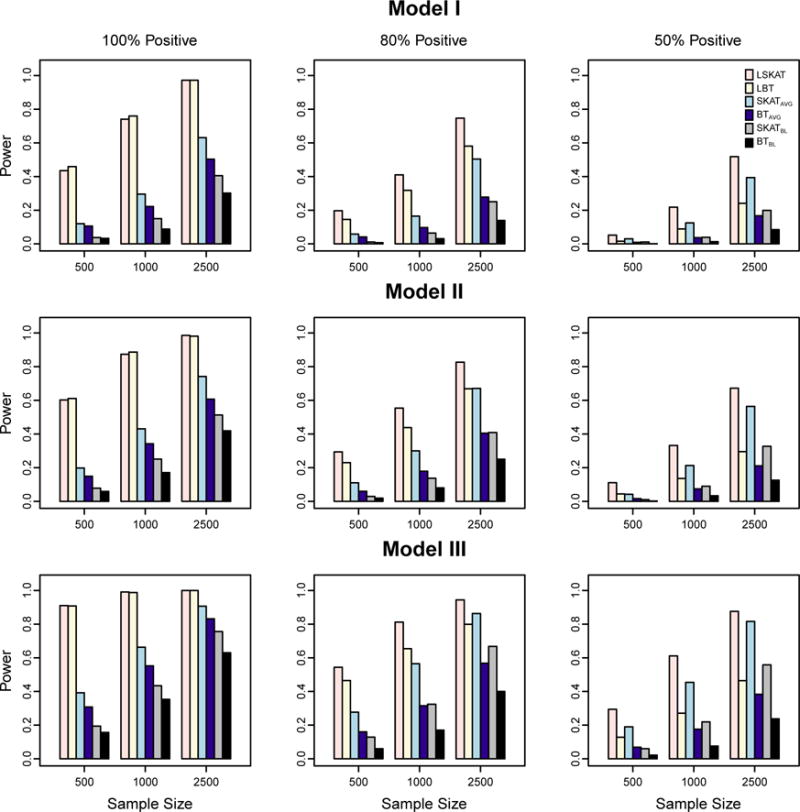
Empirical power of LSKAT, LBT, SKATAVG, BTAVG, SKATBL, and BTBL in Models I–III when 30% of variants are causal. Empirical power is based on 1000 simulated replicates at eight time points with α = 10−5. Total sample sizes considered are 500, 1000, and 2500. From the left to right columns, the plots illustrate settings in which the coefficients for the causal variants are 100% positive, 80% positive, and 50% positive.
Figure 2.
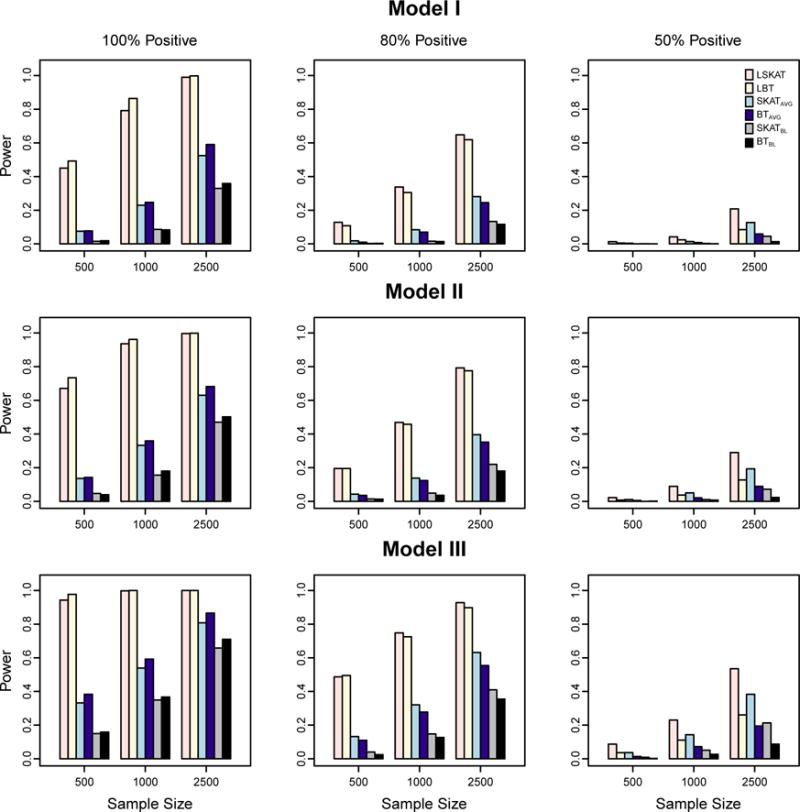
Empirical power of LSKAT, LBT, SKATAVG, BTAVG, SKATBL, and BTBL in Models I–III when 90% of variants are causal. Empirical power is based on 1000 simulated replicates at eight time points with α = 10−5. Total sample sizes considered are 500, 1000, and 2500. From the left to right columns, the plots illustrate settings in which the coefficients for the causal variants are 100% positive, 80% positive, and 50% positive.
Overall we find that, among the three variance component tests (LSKAT, SKATAVG, and SKATBL), the LSKAT method that jointly considers all time points has the highest power; SKATAVG that uses the average over all time points comes the second; and SKATBL which uses only one time point has the lowest power. The same pattern is also observed in the three burden tests LBT, BTAVG, and BTBL. This is consistent with what we expected because the average of trait values over eight time points has a smaller variation than the trait value from a single time point. Then the variants in the region of interest explain a larger proportion of the variance of the mean phenotypic values than that of the phenotypic variance at one time point. As a result, the average approaches are more powerful than their counterpart with a single time point measure. When the number of repeated measures is large, the methods that jointly consider all time points gain more power than the average approaches. Similar patterns were also reported in the simulation studies of Furlotte et al., [2012], where they compared the single-marker association with a single time point, the average, and all time point measurements in longitudinal phenotypes.
We further assess the impact of misspecified covariance structure on the power of the six methods. Figure 3 shows the power results for Models IV and V in which the true correlation matrix on the subject-specific random effects is compound symmetry and the SAD model, respectively, where the fraction of the causal variants is 30%. Because the type I error of LBT based on the asymptotic distribution tends to be inflated when sample size is small, we use the empirical cutoff values at the significant level 10−5 in power assessment. For both the LSKAT and LBT methods, as we fit the null model under the AR(1) correlation model, we expect the power to be reduced. This can be illustrated by comparing the power results of Models IV and V to that of Model I, where the overall variances are the same in these three models. For example, when sample size is 1000, and all effects of causal variants are in the same direction (100% positive), the power of LSKAT is 0.51 and 0.64 in Models IV and V respectively, while the power is 0.74 in Model I. Similarly, under the same setting, the power of LBT is 0.47 and 0.66 in Models IV and V respectively, while the power is 0.76 in Model I. In contrast, the power of SKATAVG, BTAVG, SKATBL, and BTBL do not change much across Models I, IV and V. Under the misspecified covariance structure in Models IV and V, LSKAT remains to be the most powerful or has power approximately equal to the most powerful of all the tests in all scenarios. When 90% of the variants are causal, we observe slightly different results (Figure 4). The power of LBT is higher than that of LSKAT when the effects of all causal variants are in the same direction. When the proportion of positive effects drops to 50%, LBT becomes powerless and LSKAT has improved power. Overall, the power of LSKAT and LBT in Models IV and V is lower than that in Model I.
Figure 3.
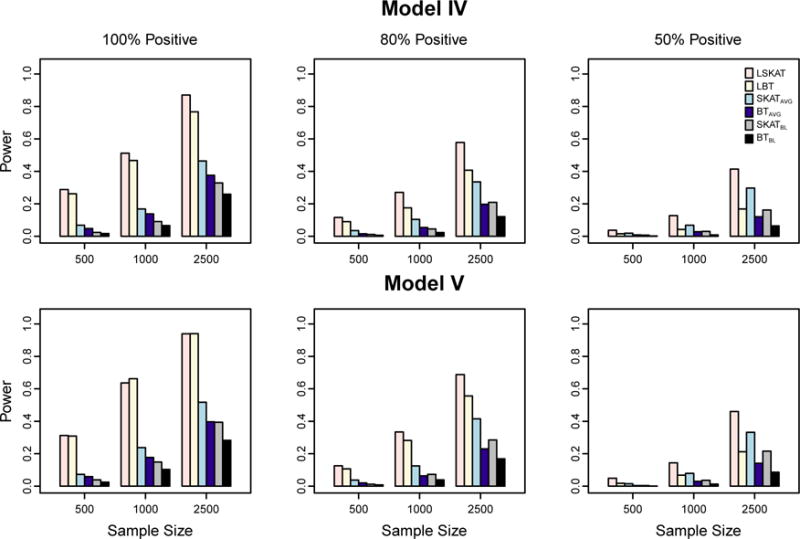
Empirical power of LSKAT, LBT, SKATAVG, BTAVG, SKATBL, and BTBL in Models IV and V when 30% of variants are causal. Empirical power is based on 1000 simulated replicates at eight time points with α = 10−5. Total sample sizes considered are 500, 1000, and 2500. From the left to right columns, the plots illustrate settings in which the coefficients for the causal variants are 100% positive, 80% positive, and 50% positive.
Figure 4.
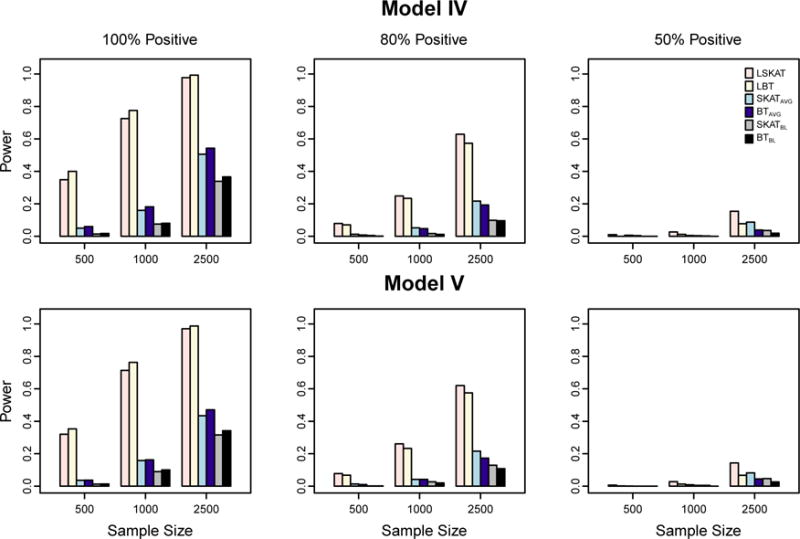
Empirical power of LSKAT, LBT, SKATAVG, BTAVG, SKATBL, and BTBL in Models IV and V when 90% of variants are causal. Empirical power is based on 1000 simulated replicates at eight time points with α = 10−5. Total sample sizes considered are 500, 1000, and 2500. From the left to right columns, the plots illustrate settings in which the coefficients for the causal variants are 100% positive, 80% positive, and 50% positive.
3.2 Analysis of body mass index from the Framingham Heart Study
To illustrate the use of our methods, we analyze a GWAS dataset from the Framingham Heart Study (FHS) [Splansky et al. 2007]. FHS is a multicohort, longitudinal study of risk factors for cardiovascular disease. We investigate association with body mass index (BMI). BMI is a heuristic measure of body weight based on a person’s weight and height, and is the most widely used diagnostic tool to assess whether an individual is underweighted, normal, overweighted or obese. It is a strong risk factor for obesity-related diseases, such as hypertension, type 2 diabetes, and cardiovascular diseases [Frayling 2007]. The FHS sample consists of unrelated individuals as well as individuals from multigenerational pedigrees. We focus on a set of 2,104 unrelated individuals from the first two generation cohorts (original and offspring cohorts), where the original cohort has data from 28 exams, and the offspring cohort has data from 8 exams.
All samples were genotyped on the Affymetrix 500K array. We include in the analysis individuals who satisfy the following criteria: (1) completeness (i.e., proportion of variants for which genotype is called) > 95% and (2) empirical self-kinship < .525 (i.e., empirical inbreeding coefficient < .05). In addition, we exclude 72 individuals who appear to be far apart from the rest of the sample in the principal components plot. The resulting data set has 1,678 individuals who have both genotype and phenotype information, of which 728 are males and 950 are females. These individuals were measured for BMI at multiple time points from age 19 to age 86. For individuals in the original cohort, we use the data from exams 1–28, and for individuals in the offspring cohort, we use the data from exams 1–8. The number of measures on each subject ranges from 3 to 22, and the intervals between measurements are highly variable among subjects.
We perform a genome-wide gene-based longitudinal association analysis with BMI. For each gene region that is either protein-coding or RNA genes, we extract all variants that are on the Affymetrix 500K chip and are within 100 kb of the gene. We exclude sites that do not meet all of the following conditions: (1) call rate > 90%, (2) Hardy-Weinberg χ2 statistic P-value > 10−6, and (3) at least 4 copies of minor allele. We then impute any missing genotypes using the software IMPUTE2 [Howie et al., 2009]. All together we test association of 32,393 genes with BMI, including sex, age at each exam, and the top 5 principal components as covariates in the analysis.
We consider four tests LSKAT, LBT, SKATAVG, and BTAVG, where the weights specified in the type I error experiments are used. All tests are reasonably calibrated based on the Q-Q plots (Figure 5). The genomic control inflation factors are 0.983, 1.048, 0.995, and 0.971 for LSKAT, LBT, SKATAVG, and BTAVG, respectively. Table 4 reports the top six gene regions for which at least one of the four tests gives a P-value < 5 × 10−5. The first two genes are located at 20p11.23, where the P-values of LSKAT and LBT are much smaller than that of SKATAVG and BTAVG. The LINC00237 gene is significantly associated with BMI after Bonferroni correction, with a nominal P-value of 7.9 × 10−7 by LBT. This gene leads to the production of a non-coding RNA. It has previously been reported to be a candidate gene for macrosomia, obesity, macrocephaly, and ocular abnormalities (MOMO) syndrome (Vu et al., 2012). The SGK1 gene on chromosome 6 encodes a serine/threonine protein kinase. High levels of expression of this gene may contribute to hypertension and diabetic nephropathy [Ferrelli 2015]. The NR1D2 gene on chromosome 3 is a nuclear hormone receptor gene. It plays an important role in circadian rhythms and carbohydrate and lipid metabolism. Several studies have reported association of this circadian gene with obesity [Garaulet et al., 2014; Goumidi et al., 2013]. For the two genes on chromosome 21, LSKAT yields a smaller P-value than the other three methods (P-value is 2.8 × 10−5 for AP001347.6 and 4.4 × 10−5 for LIPI). AP001347.6 is an antisense gene. The LIPI gene encodes a phospholipase that hydrolyzes phosphatidic acid to produce lysophosphatidic acid. Defects in this gene have been reported to be associated with hypertriglyceridemia which increases the risk of obesity and heart disease [Wen et al., 2003].
Figure 5.
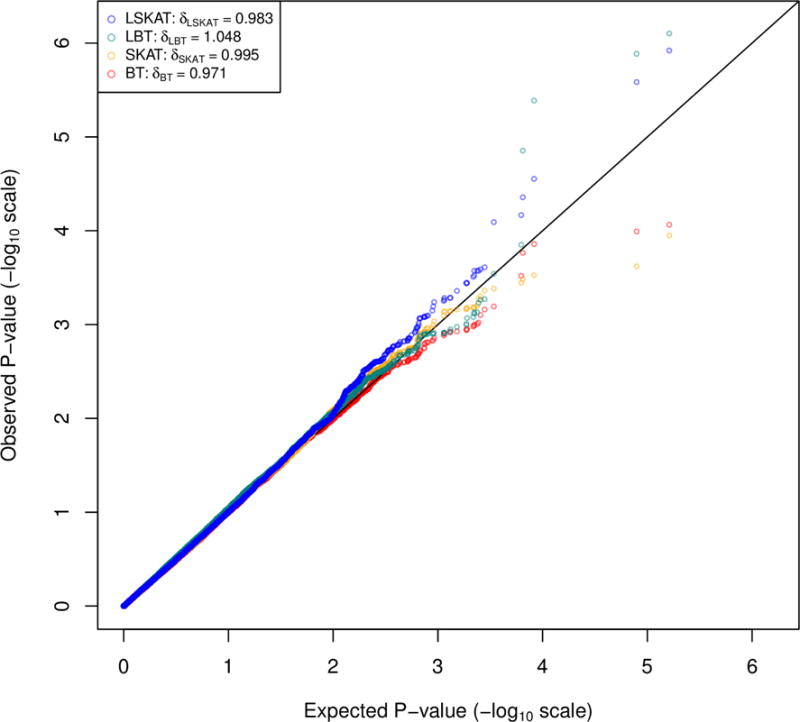
Q-Q plots of LSKAT, LBT, SKATAVG, and BTAVG in the Framingham Heart Study BMI data.
Table 4.
Genes with P-value < 5 × 10−5 in the Framingham Heart Study BMI data
| Gene | Chr | # SNPs in Test | P-value
|
|||
|---|---|---|---|---|---|---|
| LSKAT | LBT | SKATAVG | BTAVG | |||
| LINC00237 | 20 | 49 | 1.2 × 10−6 | 7.9 × 10−7 | 1.7 × 10−2 | 1.1 × 10−2 |
| PLK1S1 | 20 | 52 | 2.6 × 10−6 | 1.3 × 10−6 | 2.7 × 10−3 | 3.6 × 10−3 |
| SGK1 | 6 | 56 | 6.8 × 10−5 | 4.1 × 10−6 | 2.4 × 10−2 | 2.2 × 10−1 |
| NR1D2 | 3 | 16 | 8.1 × 10−5 | 1.4 × 10−5 | 6.3 × 10−1 | 2.8 × 10−1 |
| AP001347.6 | 21 | 46 | 2.8 × 10−5 | 8.2 × 10−3 | 2.2 × 10−2 | 6.7 × 10−2 |
| LIPI | 21 | 58 | 4.4 × 10−5 | 1.9 × 10−2 | 5.0 × 10−1 | 8.9 × 10−1 |
3.3 Computation time
The computational burden of LSKAT and LBT comes from the inversion of the correlation matrix. Additionally, LSKAT requires the eigenvalue decomposition of the correlation matrix to calculate the P-value. Thus, the computational cost largely depends on the sample size, the number of variants, and the number of measurements. When a study is balanced, i.e., all samples have the same number of measurements, the identical structure of the correlation matrix allows the inversion and decomposition to be performed only once for each tested region, which can substantially reduce the computation time. The Framingham BMI data we analyze contain unbalanced data. For instance, the number of measures on each subject ranges from 3 to 22, and the intervals between measurements are highly variable among subjects. Therefore we need to perform matrix inversion and decomposition separately for each individual. The combined analysis of LSKAT and LBT on the whole genome 32,393 genes took 2.1 hours on an Intel Xeon 2.6 GHz CPU computing cluster with 15 nodes. This result demonstrates that LSKAT and LBT are computationally feasible for large-scale studies.
4. DISCUSSION
Longitudinal studies have recently been introduced in GWAS and provided a valuable resource for exploring genetic and environmental factors that affect diseases and complex traits. Repeated measures in phenotypic data can yield advantages such as (i) more accurate assessment of disease condition, and (ii) the opportunity to explore temporal variations of trait values, disease development and progression, which leads to improved power to detect association. One study has shown that jointly considering trait values from all time points can gain power by as much as eight folds over the traditional mapping procedure utilizing only one time point in the single-marker association analysis [Furlotte et al., 2012].
In this article, we introduce two methods, LSKAT and LBT, to analyze longitudinal phenotypic data in GWAS and/or sequencing studies. They are useful for detecting association between a set of rare and common variants and a longitudinally-measured quantitative trait. Both tests are constructed on the basis of a mixed-effects model that can not only account for the within-subject correlation, but also adjust for static and time-varying covariates. LSKAT and LBT can be viewed as extensions of the SKAT and BT methods from a single time point measure to repeated measures. We demonstrate in simulation studies that LBT achieves high power when variants are almost all deleterious or all protective, while LSKAT performs well in a wide range of genetic models, particularly when a small fraction of tested variants are causal, and they are mixed with both protective and deleterious variants with different magnitude of effect sizes. This is desirable in practice because the true biological mechanism and genetic architecture is usually unknown and can vary across genes and traits. We have shown that by utilizing multiple measurements, LSKAT achieves increased power over SKAT and BT with either a single time point measurement or average over multiple time points. We apply LSKAT and LBT to a genome-wide gene-based association analysis of BMI in the Famingham Heart Study, in which we identify six novel genes that may associated with BMI. Among them, the circadian gene NR1D2 has previously been reported as association with obesity. In the data analysis, both the LSKAT and LBT methods use the phenotype information from all time points to increase power to detect association over SKAT and BT.
The models we use for constructing the LSKAT and LBT statistics are under a certain set of assumptions, however, the framework is very general and may work for a larger class of problems. We further simulate longitudinal data to assess the type I error and power for association with all variants in a genomic region when the linear mixed model is misspecified with covariance structure. We have shown that the type I error of LSKAT has no inflation with misspecified correlation structure in our simulations, however the power is lower than that using the correct covariance model; while LBT has inflated type I error when sample size is small. In longitudinal data analysis, there are always a variety of consideration when selecting the covariance structure, including the number of parameters, the interpretation of the structure, and the impact on tests and estimates of fixed effects. In practice, one could fit various correlation models and choose one based on the information criteria, such as Akaike’s Information Criteria (AIC) or Bayesian Information Criteria (BIC). Furthermore, when samples contain related individuals, familial correlation needs to be accounted for to ensure correct calibration of type I error in longitudinal data. For example, additional random effect can be incorporated in the anlysis to account for genetic relationship (kinship) between individuals.
Both the LSKAT and LBT tests are developed for repeated measures of quantitative traits on the basis of linear mixed models, and they are not directly applicable to dichotomous outcomes. For binary traits, one possible solution is to incorporate kernel function or burden score into the generalized linear mixed models for non-normal data. We are currently exploring this direction and will report it in a future communication. In the absence of prior information on the genetic architecture of the phenotype, it is useful to develop omnibus tests for longitudinal data that combine the strengths of both the LSKAT and LBT tests, similar to the SKAT-O statistic of Lee et al. [2012]. In addition, the LSKAT and LBT methods assume constant genetic effects for each variants. It would be possible to extend the method to allow for time-varying genetic effects, as the relative influence from genetic and environmental factors on a trait of interest can fluctuate over time [Li et al., 2015]. A simple approach would be to replace the genetic parameter γ with γj in Model (1) such that the genetic effects could vary at different time points. Another solution would be to include the variant by time interaction terms, and to jointly test the mean genetic effects and the variant by time interaction effects. This will be a direction of investigation in our future study.
Supplementary Material
Acknowledgments
This study was supported by National Institutes of Health grants R21 AA022870, K01 AA023321, and K12 DA000167, American Cancer Society grant IRG-58-012-56, and National Natural Science Foundation of China grant 31470675. The Framingham Heart Study is conducted and supported by the National Heart, Lung, and Blood Institute (NHLBI) in collaboration with Boston University (Contract No. N01-HC-25195). This manuscript was not prepared in collaboration with investigators of the Framingham Heart Study and does not necessarily reflect the opinions or views of the Framingham Heart Study, Boston University, or NHLBI. Funding for SHARe Affymetrix genotyping was provided by NHLBI Contract N02-HL-64278. SHARe Illumina genotyping was provided under an agreement between Illumina and Boston University.
Footnotes
The authors declare no conflicts of interest.
WED RESOURCES
LSKAT and LBT source code is available at https://github.com/ZWang-Lab/LSKAT/.
SUPPORTING INFORMATION
Additional Supporting Information may be found online in the supporting information tab for this article.
References
- Beyene J, Hamid JS. Longitudinal data analysis in genome-wide association studies. Genet Epidemiol. 2014;38(Suppl 1):S68–73. doi: 10.1002/gepi.21828. [DOI] [PubMed] [Google Scholar]
- Chen H, Meigs JB, Dupuis J. Sequence kernel association test for quantitative traits in family samples. Genet Epidemiol. 2013;37:196–204. doi: 10.1002/gepi.21703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chien LC, Hsu FC, Bowden DW, Chiu YF. Generalization of Rare Variant Association Tests for Longitudinal Family Studies. Genet Epidemiol. 2016;40:101–112. doi: 10.1002/gepi.21951. [DOI] [PubMed] [Google Scholar]
- Cousminer DL, Berry DJ, Timpson NJ, Ang W, Thiering E, Byrne EM, Taal HR, Huikari V, Bradfield JP, Kerkhof M, et al. Genome-wide association and longitudinal analyses reveal genetic loci linking pubertal height growth, pubertal timing and childhood adiposity. Hum Mol Genet. 2013;22:2735–2747. doi: 10.1093/hmg/ddt104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das K, Li J, Wang Z, Tong C, Fu G, Li Y, Xu M, Ahn K, Mauger D, Li R, et al. A dynamic model for genome-wide association studies. Hum Genet. 2011;129:629–639. doi: 10.1007/s00439-011-0960-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derkach A, Lawless JF, Sun L. Robust and powerful tests for rare variants using Fisher’s method to combine evidence of association from two or more complementary tests. Genet Epidemiol. 2013;37:110–121. doi: 10.1002/gepi.21689. [DOI] [PubMed] [Google Scholar]
- Derkach A, Lawless JF, Sun L. Pooled association tests for rare genetic variants: a review and some new results. Stat Sci. 2014;29:302–321. [Google Scholar]
- Diggle PJ. An approach to the analysis of repeated measurements. Biometrics. 1988;44:959–971. [PubMed] [Google Scholar]
- Dumitrescu L, Goodloe R, Bradford Y, Farber-Eger E, Boston J, Crawford DC. The effects of electronic medical record phenotyping details on genetic association studies: HDL-C as a case study. BioData Min. 2015;8:15. doi: 10.1186/s13040-015-0048-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichler EE, Flint J, Gibson G, Kong A, Leal SM, Moore JH, Nadeau JH. Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev Genet. 2010;11:446–450. doi: 10.1038/nrg2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R, Zhang Y, Albert PS, Liu A, Wang Y, Xiong M. Longitudinal association analysis of quantitative traits. Genet Epidemiol. 2012;36:856–869. doi: 10.1002/gepi.21673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrelli F, Pastore D, Capuani B, Lombardo MF, Blot-Chabaud M, Coppola A, Basello K, Galli A, Donadel G, Romano M, et al. Serum glucocorticoid inducible kinase (SGK)-1 protects endothelial cells against oxidative stress and apoptosis induced by hyperglycaemia. Acta Diabetol. 2015;52:55–64. doi: 10.1007/s00592-014-0600-4. [DOI] [PubMed] [Google Scholar]
- Frayling TM. Genome-wide association studies provide new insights into type 2 diabetes aetiology. Nat Rev Genet. 2007;8:657662. doi: 10.1038/nrg2178. [DOI] [PubMed] [Google Scholar]
- Furlotte NA, Eskin E, Eyheramendy S. Genome-wide association mapping with longitudinal data. Genet Epidemiol. 2012;36:463–471. doi: 10.1002/gepi.21640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garaulet M, Smith CE, Gomez-Abellan P, Ordovas-Montanes M, Lee YC, Parnell LD, Arnett DK, Ordovas JM. REV-ERB-ALPHA circadian gene variant associates with obesity in two independent populations: Mediterranean and North American. Mol Nutr Food Res. 2014;58:821–829. doi: 10.1002/mnfr.201300361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottesman O, Kuivaniemi H, Tromp G, Faucett WA, Li R, Manolio TA, Sanderson SC, Kannry J, Zinberg R, Basford MA, et al. The Electronic Medical Records and Genomics (eMERGE) network: past, present, and future. Genet Med. 2013;15:761–771. doi: 10.1038/gim.2013.72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goumidi L, Grechez A, Dumont J, Cottel D, Kafatos A, Moreno LA, Molnar D, Moschonis G, Gottrand F, Huybrechts I, et al. Impact of REV-ERB alpha gene polymorphisms on obesity phenotypes in adult and adolescent samples. Int J Obes. 2013;37:666–672. doi: 10.1038/ijo.2012.117. [DOI] [PubMed] [Google Scholar]
- Han F, Pan W. A data-adaptive sum test for disease association with multiple common or rare variants. Hum Hered. 2010;70:42–54. doi: 10.1159/000288704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howie BN, Donnelly P, Marchini J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009;5:e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hui SL, Berger JO. Empirical Bayes estimation of rates in longitudinal studies. J Am Stat Assoc. 1983;78:753–760. [Google Scholar]
- Jaffrézic F, Thompson R, Hill WG. Structured antedependence models for genetic analysis of repeated measures on multiple quantitative traits. Genet Res. 2003;82:55–65. doi: 10.1017/s0016672303006281. [DOI] [PubMed] [Google Scholar]
- Jiang D, McPeek MS. Robust rare variant association testing for quantitative traits in samples with related individuals. Genet Epidemiol. 2014;38:10–20. doi: 10.1002/gepi.21775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong S-Y, Freimer NB, Sabatti C, Eskin E. Variance component model to account for sample structure in genome-wide association studies. Nat Genet. 2010;42:348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kullo IJ, Fan J, Pathak J, Savova GK, Ali Z, Chute CG. Leveraging informatics for genetic studies: use of the electronic medical record to enable a genome-wide association study of peripheral arterial disease. J Am Med Inform Assoc. 2010;17:568–574. doi: 10.1136/jamia.2010.004366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- Lee S, Wu MC, Lin X. Optimal tests for rare variant effects in sequencing association studies. Biostatistics. 2012;13:762–775. doi: 10.1093/biostatistics/kxs014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet. 2008;83:311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Wang Z, Li R, Wu R. Bayesian group Lasso for nonparametric varying-coefficient models with application to functional genome-wide association studies. Ann Appl Stat. 2015;9:640–664. doi: 10.1214/15-AOAS808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Tang ZZ. A general framework for detecting disease associations with rare variants in sequencing studies. Am J Hum Genet. 2011;89:354–367. doi: 10.1016/j.ajhg.2011.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Tang Y, Zhang HH. A new chi-square approximation to the distribution of non-negative definite quadratic forms in non-central normal variables. Comput Stat Data Anal. 2009;53:853–856. [Google Scholar]
- Londono D, Chen KM, Musolf A, Wang R, Shen T, Brandon J, Herring JA, Wise CA, Zou H, Jin M, et al. A novel method for analyzing genetic association with longitudinal phenotypes. Stat Appl Genet Mol Biol. 2013;12:241–261. doi: 10.1515/sagmb-2012-0070. [DOI] [PubMed] [Google Scholar]
- Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5:e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarty CA, Chisholm RL, Chute CG, Kullo IJ, Jarvik GP, Larson EB, Li R, Masys DR, Ritchie MD, Roden DM, et al. The eMERGE network: a consortium of biorepositories linked to electronic medical records data for conducting genomic studies. BMC Med Genet. 2011;4:13. doi: 10.1186/1755-8794-4-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meirelles OD, Ding J, Tanaka T, Sanna S, Yang HT, Dudekula DB, Cucca F, Ferrucci L, Abecasis G, Schlessinger D. SHAVE: shrinkage estimator measured for multiple visits increases power in GWAS of quantitative traits. Eur J Hum Genet. 2013;21:673–679. doi: 10.1038/ejhg.2012.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgenthaler S, Thilly WG. A strategy to discover genes that carry multi-allelic or mono-allelic risk for common diseases: a cohort allelic sums test (CAST) Mutat Res. 2007;615:28–56. doi: 10.1016/j.mrfmmm.2006.09.003. [DOI] [PubMed] [Google Scholar]
- Morris AP, Zeggini E. An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet Epidemiol. 2010;34:188–193. doi: 10.1002/gepi.20450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthen B. Latent variable analysis: growth mixture modeling and related techniques for longitudinal data. In: Kaplan D, editor. The Sage Handbook of Quantitative Methodology for the Social Sciences. Thousand Oaks, CA: Sage; 2004. [Google Scholar]
- Neale BM, Rivas MA, Voight BF, Altshuler D, Devlin B, Orho-Melander M, Kathiresan S, Purcell SM, Roeder K, Daly MJ. Testing for an unusual distribution of rare variants. PLoS Genet. 2011;7:e1001322. doi: 10.1371/journal.pgen.1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale BM, Sham PC. The future of association studies: Gene-based analysis and replication. Am J Hum Genet. 2004;75:353–362. doi: 10.1086/423901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Kryukov GV, de Bakker PI, Purcell SM, Staples J, Wei LJ, Sunyaev SR. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical linear models: application and data analysis methods. Thousand Oaks, CA: Sage; 2002. [Google Scholar]
- Schaffner SF, Foo C, Gabriel S, Reich D, Daly MJ, Altshuler D. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 2005;15:1576–1583. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ. Genomic similarity and kernel methods II: methods for genomic information. Hum Hered. 2010;70:132–140. doi: 10.1159/000312643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schifano ED, Epstein MP, Bielak LF, Jhun MA, Kardia SLR, Peyser PA, Lin X. SNP set association analysis for familial data. Genet Epidemiol. 2012;36:797–810. doi: 10.1002/gepi.21676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sikorska K, Rivadeneira F, Groenen PJ, Hofman A, Uitterlinden AG, Eilers PH, Lesaffre E. Fast linear mixed model computations for genome-wide association studies with longitudinal data. Stat Med. 2013;32:165–180. doi: 10.1002/sim.5517. [DOI] [PubMed] [Google Scholar]
- Smith EN, Chen W, Kahonen M, Kettunen J, Lehtimaki T, Peltonen L, Raitakari OT, Salem RM, Schork NJ, Shaw M, et al. Longitudinal genome-wide association of cardiovascular disease risk factors in the Bogalusa heart study. PLoS Genet. 2010;6:e1001094. doi: 10.1371/journal.pgen.1001094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Splansky GL, Corey D, Yang Q, Atwood LD, Cupples LA, Benjamin EJ, D’Agostino RB, Fox CS, Larson MG, Murabito JM, et al. The third generation cohort of the National Heart, Lung, and Blood Institute’s Framingham Heart Study: design, recruitment, and initial examination. Am J Epidemiol. 2007;165:1328–1335. doi: 10.1093/aje/kwm021. [DOI] [PubMed] [Google Scholar]
- Tang W, Kowgier M, Loth DW, Soler Artigas M, Joubert BR, Hodge E, Gharib SA, Smith AV, Ruczinski I, Gudnason V, et al. Large-scale genome-wide association studies and meta-analyses of longitudinal change in adult lung function. PLoS One. 2014;9:e100776. doi: 10.1371/journal.pone.0100776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vu PY, Toutain J, Cappellen D, Delrue MA, Daoud H, El Moneim AA, Barat P, Montaubin O, Bonnet F, Dai ZQ, et al. A homozygous balanced reciprocal translocation suggests LINC00237 as a candidate gene for MOMO (macrosomia, obesity, macrocephaly, and ocular abnormalities) syndrome. Am J Med Genet A. 2012;158A:2849–2856. doi: 10.1002/ajmg.a.35694. [DOI] [PubMed] [Google Scholar]
- Wang Y, Huang C, Fang Y, Yang Q, Li R. Flexible semiparametric analysis of longitudinal genetic studies by reduced rank smoothing. J R Stat Soc Ser C Appl Stat. 2012;61:1–24. doi: 10.1111/j.1467-9876.2011.01016.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen XY, Hegele RA, Wang J, Wang DY, Cheung J, Wilson M, Yahyapour M, Bai Y, Zhuang L, Skaug J, et al. Identification of a novel lipase gene mutated in lpd mice with hypertriglyceridemia and associated with dyslipidemia in humans. Hum Mol Genet. 2003;12:1131–1143. doi: 10.1093/hmg/ddg124. [DOI] [PubMed] [Google Scholar]
- Wu MC, Kraft P, Epstein MP, Taylor DM, Chanock SJ, Hunter DJ, Lin X. Powerful SNP-set analysis for case-control genome-wide association studies. Am J Hum Genet. 2010;86:929–942. doi: 10.1016/j.ajhg.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet. 2011;89:82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu R, Lin M. Functional mapping – how to map and study the genetic architecture of dynamic complex traits. Nat Rev Genet. 2006;7:229–237. doi: 10.1038/nrg1804. [DOI] [PubMed] [Google Scholar]
- Wu Z, Hu Y, Melton PE. Longitudinal data analysis for genetic studies in the whole-genome sequencing era. Genet Epidemiol. 2014;38(Suppl 1):S74–80. doi: 10.1002/gepi.21829. [DOI] [PubMed] [Google Scholar]
- Yan Q, Weeks DE, Tiwari HK, Yi N, Zhang K, Gao G, Lin WY, Lou XY, Chen W, Liu N. Rare-variant kernel machine test for longitudinal data from population and family samples. Hum Hered. 2015;80:126–38. doi: 10.1159/000445057. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


