Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jan 1.
Published in final edited form as: J Mech Behav Biomed Mater. 2016 Sep 16;65:490–501. doi: 10.1016/j.jmbbm.2016.09.020

Characterizing white matter tissue in large strain via asymmetric indentation and inverse finite element modeling

Yuan Feng a,b,*,#, Chung-Hao Lee c,d,#, Lining Sun a,b, Songbai Ji e, Xuefeng Zhao a
PMCID: PMC5154882  NIHMSID: NIHMS818761  PMID: 27665084

Abstract

Characterizing the mechanical properties of white matter is important to understand and model brain development and injury. With embedded aligned axonal fibers, white matter is typically modeled as a transversely isotropic material. However, most studies characterize the white matter tissue using models with a single anisotropic invariant or in a small-strain regime. In this study, we combined a single experimental procedure—asymmetric indentation—with inverse finite element (FE) modeling to estimate the nearly incompressible transversely isotropic material parameters of white matter. A minimal form comprising three parameters was employed to simulate indentation responses in the large-strain regime. The parameters were estimated using a global optimization procedure based on a genetic algorithm (GA). Experimental data from two indentation configurations of porcine white matter, parallel and perpendicular to the axonal fiber direction, were utilized to estimate model parameters. Results in this study confirmed a strong mechanical anisotropy of white matter in large strain. Further, our results suggested that both indentation configurations are needed to estimate the parameters with sufficient accuracy, and that the indenter-sample friction is important. Finally, we also showed that the estimated parameters were consistent with those previously obtained via a trial-and-error forward FE method in the small-strain regime. These findings are useful in modeling and parameterization of white matter, especially under large deformation, and demonstrate the potential of the proposed asymmetric indentation technique to characterize other soft biological tissues with transversely isotropic properties.

Keywords: soft tissue, mechanical properties, transversely isotropic material, indentation, genetic algorithm

1 Introduction

Characterizing the mechanical properties of brain tissue is important to understand and model the underlying mechanobiological mechanisms of brain injury (Bayly et al., 2005; Meaney and Smith, 2011; Prange et al., 2000). Among many brain injury forms, diffuse axonal injury (DAI) is one of the most common and devastating types (Iwata et al., 2004). It has been hypothesized that the myelin-sheathed axonal fibers of white matter undergoing stretch and shear deformation contribute to DAI. To investigate injury mechanisms, finite element (FE) simulations have been widely adopted (Ji et al., 2015; Wright and Ramesh, 2012; Zhang et al., 2004). A critical component of these FE models, is to accurately characterize the material properties of the brain, including the white matter. Unfortunately, challenges remain in describing the tissue behavior and/or estimating the model parameters using proper experimental techniques, despite decades of active research (Chatelin et al., 2010; Cheng et al., 2008).

Mechanical testing is the most straightforward procedure considered as a verification method for in vivo measurements (Reiter et al., 2014; Zhang et al., 2015). The mechanical properties of white matter have been studied using various mechanical testing methods, including oscillatory shear test (Arbogast and Margulies, 1998; Arbogast et al., 1997; Hrapko et al., 2008; Nicolle et al., 2005; Rashid et al., 2013), simple (Destrade et al., 2015) or ultrasound shear test (Jiang et al., 2015), compression test (Cheng and Bilston, 2007; Hrapko et al., 2008), and indentation test (Elkin et al., 2011; van Dommelen et al., 2010). Nevertheless, many existing testing techniques were carried out in the small-strain regime. For example, in shear test, strains were usually between 0.1% and 1% (Hrapko et al., 2008; Nicolle et al., 2005), with some reaching 5% (Feng et al., 2013) or 7.5% (Arbogast and Margulies, 1998), lower than that thought to induce injury (Bain and Meaney, 2000). Notably, a recent study by Destrade et al. (2015) used the simple shear test to characterize brain tissue with shear strain up to 60%. For the indentation and compression tests, although tests in the large-strain regime were carried out, isotropic material models were adopted (Budday et al., 2015; Gefen and Margulies, 2004; Miller et al., 2000; van Dommelen et al., 2010). Few studies have investigated the white matter in the large-strain regime using anisotropic material models (Velardi et al., 2006). Thus, there is a pressing need to characterize white matter in the large-strain regime using an anisotropic material model for realistic computational modeling of brain tissue.

Indentation test is widely used to characterize soft tissues (Budday et al., 2015; Elkin et al., 2011; Hatami-Marbini and Etebu, 2013; Slomka et al., 2011; Svensson et al., 2010; Yang et al., 2012). To-date, however, most existing indentation techniques assume tissue isotropy, which are often limited when characterizing transversely isotropic materials. Recently, an anisotropic quarter punch test (AQPT) was utilized to characterize the transversely isotropic behaviors of human ligament (Hortin et al., 2015; Robertson et al., 2013). But their experimental setup was specifically designed for testing ligament tissue with a special sample clamping and stretching device, which may not be easily adapted to other transversely isotropic tissues such as white matter. In this study, we aimed at exploring the capability of using a single asymmetric indentation test (Bischoff, 2004) to characterize white matter. Brain white matter, with its aligned axonal fiber bundles, is typically idealized as a fiber-reinforced material and the tissue's mechanical responses are commonly modeled by a transversely isotropic material (Kulkarni et al., 2014; Ning et al., 2006; Velardi et al., 2006), which is the simplest, yet the most representative anisotropic form in many soft biological tissues (Liu et al., 2014; Thomopoulos and Genin, 2012). In a previous study, a minimal form of a transversely isotropic material model was used to explain the experimental observations of mechanical anisotropy of white matter in both shear and indentation tests in the small-strain regime (Feng et al., 2013). In estimating the model parameters, anisotropic hyperelastic models combined with inverse FE modeling were widely employed to study the cornea (Nguyen and Boyce, 2011), sclera (Coudrillier et al., 2013), mitral valve leaflet (Lee et al., 2015a; Lee et al., 2013; Lee et al., 2014; Lee et al., 2015b), and right ventricle tissue (Witzenburg et al., 2012). However, characterization of white matter using a hyperelastic model with both I4 and I5 invariants in the large-strain regime remains limited.

Therefore, the goal of this study is to characterize white matter in the large-strain regime. Here, we focused on developing an integrated experimental-computational technique to characterize the elastic properties of white matter using a hyperelastic, transversely isotropic material model. Specifically, we extended the previous investigation on white matter (Feng et al., 2013) to the large-strain regime using a minimal form of transversely isotropic model (Feng et al., 2016). We also developed an integrated experimental-computational technique, which combines asymmetric indentation and inverse FE modeling for effective characterization of white matter. Previous white matter test data in the small strain regime (Feng et al., 2013) were used for method validation. This study may provide important insights in characterizing white matter's behavior in the large strain regime.

2 Materials and Methods

2.1 Sample preparation

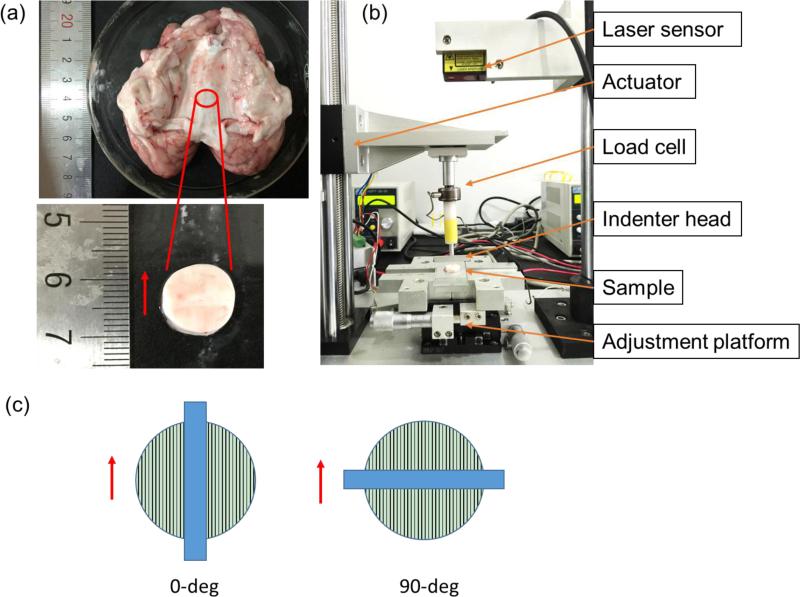
Porcine brains (3-5 month old, weight ~90 kg) were obtained from a local slaughterhouse 2 to 4 hours post-mortem. White matter samples were dissected from the central corpus callosum region, where axonal fibers can be seen connecting the left and right hemisphere (Figure 1a). Tissue samples were carefully sliced using a surgical blade (Type 10, CangSong Medical Instruments Co. Ltd., Shanghai, China) and were further trimmed to ensure that they were flat and clean before being punched with a circular punch. Cylindrical samples were carefully punched out and the sample edge was trimmed and cleaned. A total of 12 samples were acquired with an average sample thickness of 3.3 mm and a diameter of 14 mm. During the experiment, samples were moisturized with phosphate-buffered saline solution.

Figure 1.

Figure 1

Open in a new tab

(a) Porcine brain with the flat corpus callosum region exposed. The red circle indicates where the tissue sample was dissected from for asymmetric indentation testing. The red arrow shows the fiber direction. (b) The custom-built asymmetric indentation device. (c) Schematic of the 0-deg and 90-deg indentation configurations. The red arrow shows the axonal fiber direction and the blue rectangular bar indicates the indenter's long side.

2.2 Asymmetric indentation

A custom-built asymmetric indentation device was used to characterize white matter (Figure 1b). Indenter head movement was actuated by a motor (Model NDTSD422-RS485, Huikong Intellectual Tech Co. Ltd., Suzhou, China) with a minimum linear travel distance of 8 m. Indenter displacement was recorded by a laser sensor (Model HG-C1050-30mm, Panasonic, Japan). A load cell (Honey-well Sensotec, Model 31, USA) was used to measure the indentation force. Signals from the load cell and laser sensor were sampled at 1000 Hz using a synchronous analog-to-digital data acquisition board (Model PCI-706U, Advantech, Taiwan). A custom-written MATLAB (Mathsworks, Natick, MA, USA) program was used for data acquisition and system control.

A rectangular indenter head with a width of 2 mm and a length of 20 mm was used to indent the white matter samples. To characterize the elastic properties of white mater under large deformation, a single indentation step with 10% of the sample thickness was carried out. Indentation information from two testing configurations was acquired for each sample: with the indenter's long side parallel (0-deg) and perpendicular (90-deg) to the dominating fiber direction (Figure 1c). An average strain rate of ~0.2 s−1 was considered in the indentation experiments. The force-displacement curves were analyzed at the section where the indentation velocity was constant. The indentation stiffness k was define as the slope of a linear fitting of the corresponding force-displacement curve.

2.3 FE simulations of asymmetric indentation

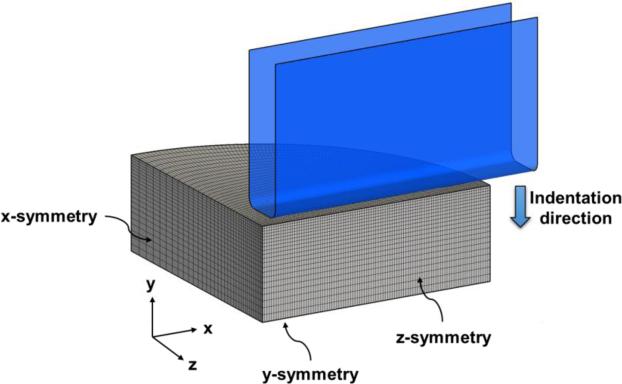
A nearly incompressible transversely isotropic material model used in a previous experimental study under the small-strain regime was adopted (Feng et al., 2016; Feng et al., 2013). Briefly, a strain energy function (SEF) ψ=μ2[(I1−3)+ζ(I4−1)2+ϕI5∗], was considered and a decoupled form was implemented with a penalty term to enforce incompressibility. To incorporate a FE-based inverse modeling method to estimate model parameters, asymmetric indentations were simulated using commercial FE software (ABAQUS 6.12, Simulia, Providence, RI). Details of the construction of the FE model for simulating asymmetric indentations were provided as follows. Due to symmetry, only a quarter model was considered. Symmetric boundary conditions were prescribed on the edges and on the bottom of the tissue sample (Figure 2). The metallic indenter was treated as a rigid body because of its distinctly larger stiffness (Cox et al., 2008). A frictional coefficient (fc) of 0.5 between the indenter and the sample was considered in the FE simulations. A comparable mesh density was adopted for both the tissue sample (39,312 C3D8H elements) and the indenter (23,600 R3D4 elements) to ensure accurate representation of the contact behavior between the tissue sample and the indenter, and to render the balance between solution accuracy and computational efficiency, with a mesh size ~1.05 mm. This was achieved via a one-way biased mesh for the tissue sample edges along the y- and z-axes (Figure 2). For modeling tissue's mechanical responses, the afore-mentioned transversely isotropic material model was implemented in a UMAT user-defined material subroutine. The indenter was offset in the y-axis with respect to the tissue sample surface prior to indentation to properly initiate the indenter-tissue contact. An indentation strain of 10% for both indentation configurations was simulated, and the numerical predictions of the indentation force-displacement response were compared with the experimental data acquired in Section 2.2. Although most of the indentation curves appeared to be linear, nonlinear behavior was observed for 90-deg indentation curves. Therefore, in this study, we used the linear fitting data to simulate the 0-deg indentation and the quadratic fitting data to simulate the 90-deg indentation.

Figure 2.

Figure 2

Open in a new tab

Schematic of the FE model for simulations of asymmetric indentation tests. A quarter model is used due to symmetry. Fibers are oriented along the x- or z-axis for 0-deg or 90-deg configuration, respectively.

2.4 Inverse modeling for parameter estimation

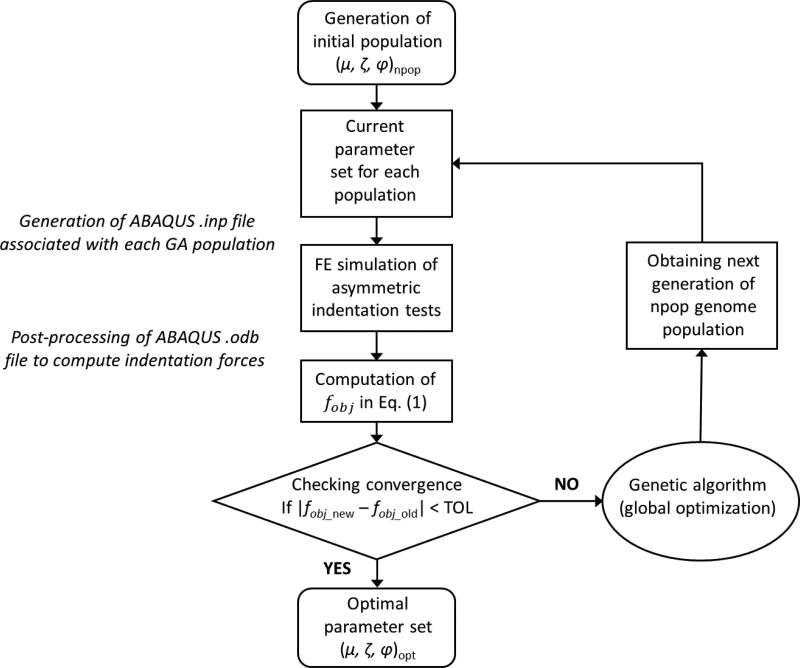
In this study, an optimization-based parameter estimation approach was developed to determine the three model parameters, μ, ζ, and ϕ. On one hand, optimization methods, such as standard derivative-based optimization algorithms, may suffer from difficulties associated with a discontinuous or highly nonlinear objective function. On the other hand, the genetic algorithm (GA) is an adaptive heuristic search approach capable of circumventing the above difficulties that generates solutions to optimization problems based on evolutionary algorithms, including inheritance, selection, crossover and mutation (Holmes, 2014; Smith and Cagnoni, 2011; Wright, 1991). Such GA-based parameter optimization approaches have been commonly employed in other biomechanics related studies of soft biological tissues (Harb et al., 2011, 2014; Khalil et al., 2006; Ning et al., 2006). Therefore, we used MATLAB's genetic algorithm function that integrates the automatic handling of ABAQUS input files and output database for global optimization-based parameter estimation (Figure 3).

Figure 3.

Figure 3

Open in a new tab

A flowchart of the GA-based inverse FE optimization for parameter estimation.

Specifically, for each set of the parameters associated with an individual genome, the corresponding ABAQUS “.inp” input file was generated and a 10% indentation strain in each indentation direction was simulated. Reaction forces of the rigid indenter (FFE) were calculated from ABAQUS “.odb” database file. An objective function defined as the root-mean-squared-errors (RMSE) of the indentation forces between the numerical predictions and experimental measurements was considered in parameter estimation:

fobj(μ,ζ,ϕ)=[w11n∑i=1n(FFEi−Fexpi)2]0−deg+[w21n∑i=1n(FFEi−Fexpi)2]90−deg, (1)

where n=25 is the total number of indentation incremental steps, FFEi and Fexpi are the FE predicted and experimentally measured indentation forces at increment i, respectively, and w1 and w2 are the weights associated with the contributions from the 0-deg and 90-deg indentation configurations, respectively. In this study, equal weights were considered:

w1+w2=1andw1=w2=0.5. (2)

An optimal set of material parameters (μ, ζ, ϕ)opt was obtained using a GA-based inverse FE modeling approach by evolutionarily updating the genomes to minimize the objective function (tolerance = 10−6).

2.5 Effects of model parameters on indentation behavior

To investigate the influences of each of the three model parameters on the tissue's mechanical responses in asymmetric indentation, we simulated the indentation processes by varying the model parameters (±15%) based on the optimal parameter values obtained in Section 2.4. Moreover, the effect of friction between the indenter head and the sample on the predicted indentation force-displacement response was also investigated by considering various friction coefficients (fc = 0.25, 0.3, 0.4 and 0.5).

3 Results

3.1 Indentation force-displacement responses

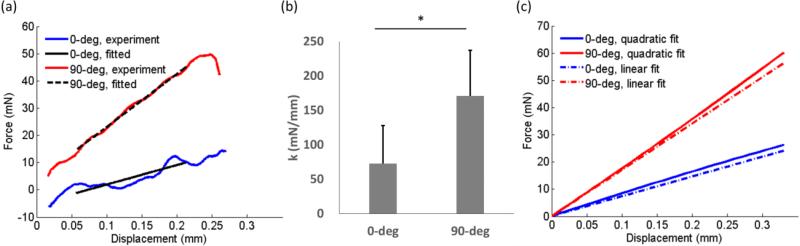
A typical force-displacement curve for indenting white matter showed that the indentation stiffness of the 90-deg configuration was significantly higher than that of 0-deg configuration (Figure 4a). The mean indentation stiffness for 0-deg and 90-deg configurations was 72.9 mN/mm and 170.5 mN/mm, respectively (Figure 4b). A comparison of the quadratic and linear fitting of the force-displacement data showed the two fitting were close to each other with a slightly nonlinear effect observed for the quadratic fitting of the 90-deg configuration. The indentation stiffness ratios (90-deg/0-deg) was 2.83±1.32. This observation was consistent with the previous indentation test of white matter from lamb brain tissue, indicating strong mechanical anisotropy of white matter (Feng et al., 2013).

Figure 4.

Figure 4

Open in a new tab

(a) Typical indentation force-displacement curves from both 0-deg and 90-deg indentation. The dark lines are linear fits to data obtained when the velocity of the indenter head is constant. (b) Indentation stiffness of white matter measured from asymmetric indentation (n=12). The stiffness of 90-deg indentation is significantly larger than that of 0-deg (student t-test, p<0.001). (c) A comparison of the averaged quadratic and linear fits of the force-displacement data.

3.2 Estimated optimal model parameters

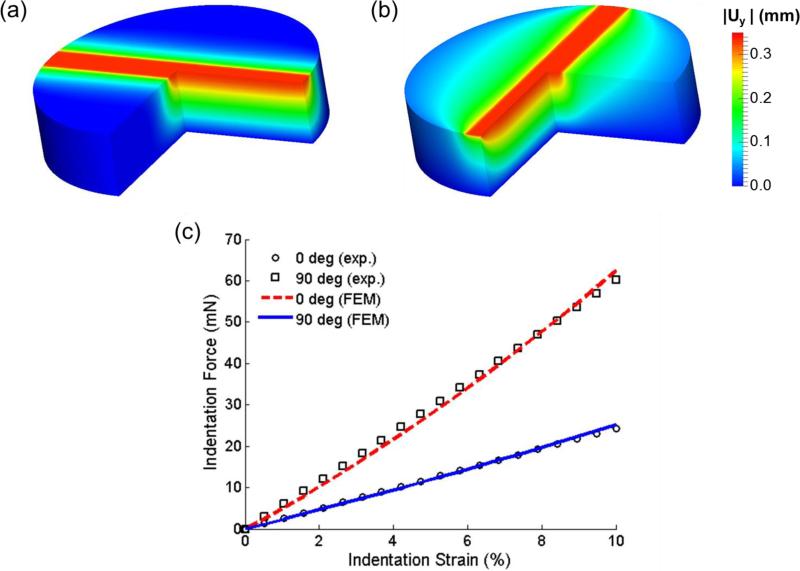
Upon optimization convergence, an objective function value of 0.832 was reached, which led to a set of estimated model parameters of μ=1.49 kPa, ζ=4.68, ϕ=0.68. The prediction of the indentation displacement uy showed that in the region close to the indenter contact area, the tissue sample had a larger magnitude of displacement distribution under the 90-deg configuration (Figure 5a, b). This finding also demonstrated the fiber reinforcement effect, where fibers tended to pull the materials around when the indentation was perpendicular to the fiber direction. Moreover, fairly good agreement between the numerically predicted and experimentally measured force-displacement responses (Figure 5c) was achieved, indicating that the indentation behaviors along and perpendicular to the fiber direction were accurately captured by the optimized parameters using the transversely isotropic model.

Figure 5.

Figure 5

Open in a new tab

Numerically predicted indentation displacement uy in (a) 0-deg and (b) 90-deg indentation at the 10% indentation strain. (c) Comparisons of the indentation force-displacement curves between the experimental measurements and the FE simulation results (with optimized model parameters: μ=1.49 kPa, ζ=4.68, ϕ=0.68).

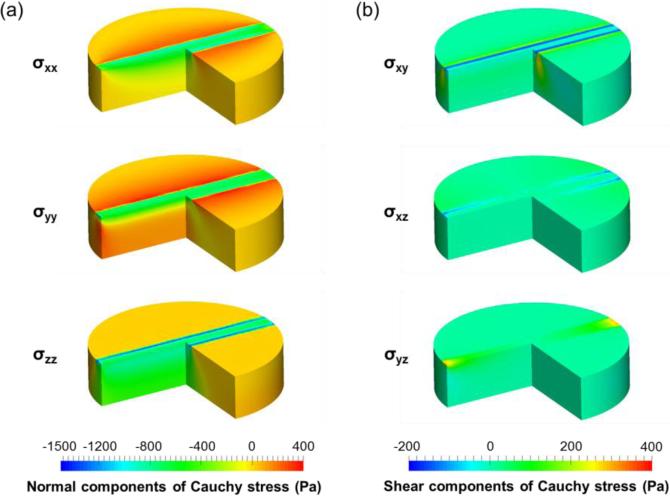
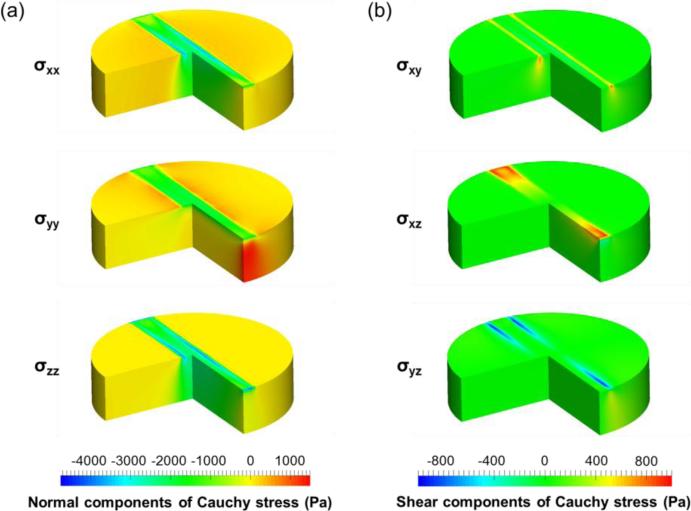
For the obtained optimal parameter set, numerically predicted Cauchy stress distribution at 10% strain of both indentation configurations showed distinct stress concentrations around the indenter for both the normal and shear stress components (Figure 6 and Figure 7). The FE predictions showed that the largest normal stress component is σzz for both 0-deg and 90-deg indentation configurations, whereas the largest shear stress component is σyz for the 0-deg configuration and σxz for the 90-deg configuration. Moreover, all the stress components from the 90-deg indentation configuration were larger than those of 0-deg configuration. These results clearly demonstrate the significance of indentation modes on tissue-level stress distributions.

Figure 6.

Figure 6

Open in a new tab

Distribution of the (a) normal (σxx, σyy, σzz,) and (b) shear (σxy, σxz, σyz) components of the numerically predicted Cauchy stresses for the 0-deg indentation.

Figure 7.

Figure 7

Open in a new tab

Distribution of the (a) normal (σxx, σyy, σzz,) and (b) shear (σxy, σxz, σyz) components of the numerically predicted Cauchy stresses for the 90-deg indentation.

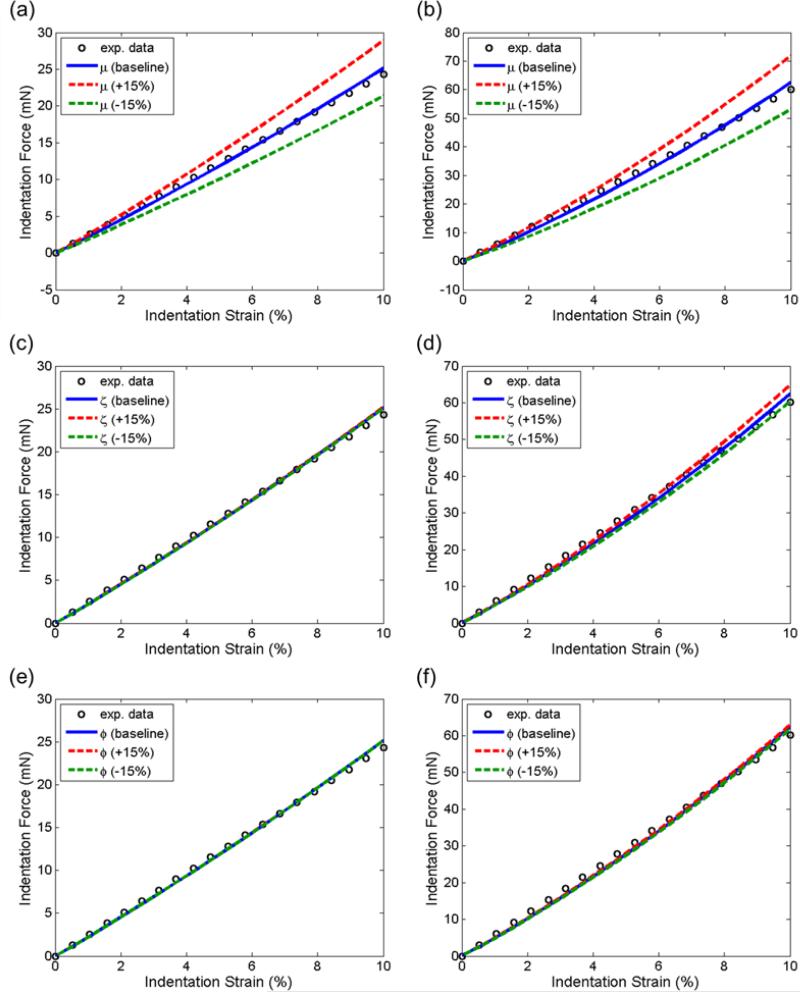
3.3 Effect of model parameters

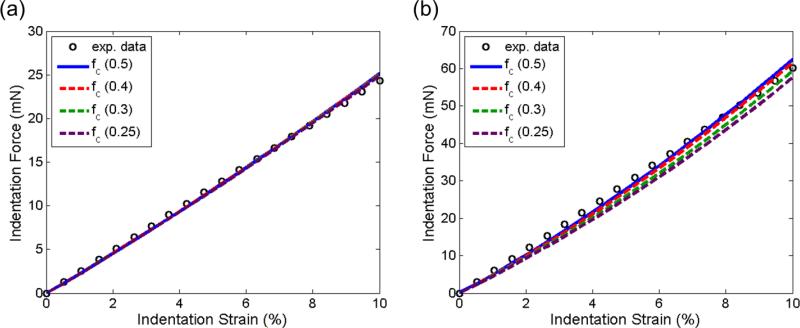
Comparisons of the force-displacement curves between each parameter variation (±15%) and its optimal value were shown in Figure 8. We found from this parameter study that the indentation force-displacement behavior appeared to be predominantly affected by the variation of μ (Figure 8a, b), and least by the variation of ϕ (Figure 8e, f). The slope of the indentation curve increased monotonically as the three parameters increased. The variation of the parameters had a greater influence for the 90-deg indentation than on the 0-deg counterpart. A similar comparison of the force-displacement curves with an fc value of 0.5, 0.4, 0.3, and 0.2 showed he variation of the value of fc did not affect the response of the 0-deg indentation (Figure 9a). However, for the 90-deg configuration, lower indentation stiffness was observed as the value of fc decreased (Figure 9b). At 10% strain, the indentation force with fc=0.2 was about 8% lower than that of fc=0.5.

Figure 8.

Figure 8

Open in a new tab

Force-displacement curves with varying parameters for (a, c, e) 0-deg and (b, d, f) 90-deg indentations. The upper and lower bounds of μ, ζ, and ϕ were set to be ±15% of the values of the optimal parameter set: μ=1.49 kPa, ζ=4.68, ϕ=0.68.

Figure 9.

Figure 9

Open in a new tab

Force-displacement curves with friction coefficients of 0.5, 0.4, 0.3, and 0.25 for (a) 0-deg and (b) 90-deg indentations.

4 Discussion

In this study, we characterized the mechanical properties of white matter in the large-strain regime, using asymmetric indentation and inverse FE modeling. We observed a strong mechanical anisotropy of white matter, which was consistent as previously observed in the small-strain regime (Feng et al., 2013). Using a nearly incompressible transversely isotropic material model with two anisotropic invariants, we estimated the three model parameters. Parametric studies showed the three model parameters have different influences on the indentation responses. We also demonstrated that information from both 0-deg and 90-deg indentations is necessary for parameter estimation and that the indenter-sample friction was not negligible.

4.1 Mesh convergence check

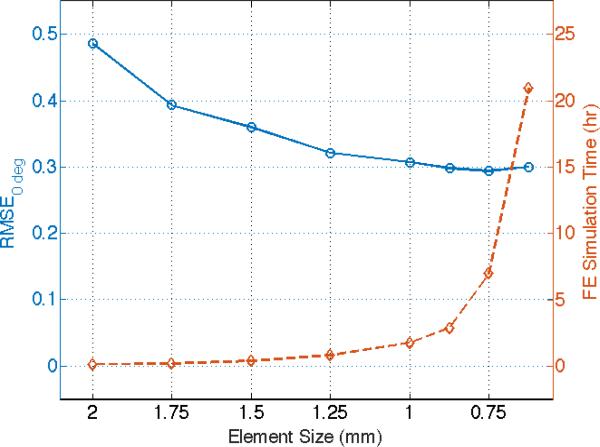
To verify the appropriateness of the chosen model mesh, a mesh convergence study was carried out with the mesh size varied from 2 mm to 0.625 mm. Using 0-deg configurations as an example, we tested the models with various mesh sizes based on the estimated optimal material parameters (μ=1.49 kPa, ζ=4.68, ϕ=0.68). The RMSE values of the indentation forces between the numerical predictions and experimental measurements, as well as the CPU time were compared among various mesh sizes (Figure 10). We observed that the RMSE values of the predicted reaction force converged with a mesh size smaller than 1.25 mm, while the computational time increased dramatically when the FE mesh size is finer than 1.25 mm. Also, the CPU time for the FE model with a mesh size of 0.875 mm exceeded 2.8 hours with limited improvement in solution accuracy, which is computationally impractical for our GA-based inverse FE technique. Similar trend in solution convergence was also observed for simulations of the 90-deg indentation configuration, but with significant increases in the CPU time for mesh sizes smaller than 1.0 mm. Therefore, the current model with a mesh size about 1.05 mm is adequate for the balance between the computational demand and solution accuracy.

Figure 10.

Figure 10

Open in a new tab

A mesh convergence study using the estimated optimal parameters (μ=1.49 kPa, ζ=4.68, ϕ=0.68). RMSE values of the indentation forces between the FE numerical predictions and experimental data, as well as the CPU time were compared with various mesh sizes.

4.2 Comparison with the forward FE estimate in small strain

As a validation of the proposed technique, we estimated the model parameters using another asymmetric indentation data set of white matter, with a 5% indentation strain, from a previously reported study (Feng et al., 2013). The estimate model parameters were μ=0.60 kPa, ζ=4.0, ϕ=0.5, by carrying out similar inverse FE modeling-based optimization procedure using the measured indentation stiffness of 27.84 mN/mm and 67.18 mN/mm for 0-deg and 90-deg configurations, respectively. The obtained parameter set for indentation under a small-strain regime was in good agreement with the previously reported result (μ=0.51 kPa, ζ=5.5, and ϕ=0.4), which was derived from a combination of both shear and indentation with trial-and-error forward FE simulations (Feng et al., 2013). Nevertheless, a larger estimated ϕ value from the current study suggested a greater influence of shear anisotropy predicted by the inverse modeling-based parameter estimation technique than the previous forward modeling method. This may be due to larger shear deformation at the corner of the indenter, which can be captured more accurately by the hyperelastic, transversely isotropic material model than the linear material model with small-strain approximations in the previous forward FE simulations. Moreover, in the previous study, the shear modulus was estimated independently from the shear testing. The shear modulus and the indentation force-displacement slopes from different experiments were subsequently used to estimate the remaining two parameters, ζ and ϕ. Using a single asymmetric indentation in the present work, we showed that our new technique was able to estimate all the three model parameters all together. By consolidating testing procedures into a single asymmetric indentation, the current technique improves testing efficiency and potentially reduces errors associated with sample transport between different testing devices. Furthermore, the previous forward FE modeling approach requires simulations with a rather large number of parameter sets in order to obtain a good estimate. Even with this computationally demanding trial-and-error approach, the estimate could still be a local minimum rather than the global minimum provided by the GA technique used in this study. However, the results from the small-strain regime provided a first-order approximation of the parameter estimate and were used to validate the proposed characterization method that is also applicable to problems under the large strain regime.

4.3 Material model

Although transversely isotropic material models have been widely used to study white matter (Ning et al., 2006; Velardi et al., 2006), most of them utilized only one invariant (I4). It has been shown that at least two anisotropic invariants (I4 and I5) are needed to characterize transversely isotropic soft tissues (Destrade et al., 2013; Feng et al., 2013), and that shear deformation-induced anisotropic behavior is closely related to invariant I5 (Feng et al., 2016). In brain injury, shear deformation is considered one of the predominant mechanisms (Laurer et al., 2002; Meaney and Smith, 2011). Therefore, characterization of white matter using a transversely isotropic material model with both I4 and I5 in this study could help improving computational models used for brain simulation and TBI related studies (Fahlstedt et al., 2015; Ji et al., 2015).

Material models with no more than three parameters have been used to study brain tissue in many different mechanical tests (Destrade et al., 2015; Ning et al., 2006; Velardi et al., 2006). The hyperelastic model with three parameters adopts the minimum number of parameters needed to characterize the transversely isotropic white matter. Although more terms and parameters can be used to capture other tissue behaviors, the primary focus of this study is to demonstrate that the minimal form is sufficient to characterize the elastic behavior in the large-strain regime.

4.4 Influence of model parameters

Larger influences of parameter μ on the predicted indentation behaviors than those of parameters ζ and ϕ (Figure 8) indicated that for white matter, the matrix material largely determined the overall mechanical properties. Theoretical analysis has showed that when stretch and shear deformation are along the fiber direction, the corresponding tensile and shear stresses are higher than those of deformations perpendicular to the fiber direction (Feng et al., 2016). In this study, we observed that as ζ and ϕ increased, the indentation force also increased, showing a clear fiber reinforcement effect by the axonal fibers. This effect was also observed by larger influences of the model parameters on the 90-deg configuration than those of 0-deg (Figure 8). This could be possibly explained by stretching and shearing fibers during the indentation process. In the 0-deg configuration, the stretch and shear deformation were mostly perpendicular to the fiber direction (Figure 11a). In the 90-deg configuration, as the indenter bending into the sample, the axonal fibers were stretched and sheared along the fiber direction (Figure 11b), inducing a larger indentation reaction force. These results also showed that a combination of information from both indentation configurations should be considered to accurately estimate the model parameter of the adopted transversely isotropic material model.

Figure 11.

Figure 11

Open in a new tab

An illustration of indentation of the white matter with axonal fibers (a) along (0-deg indentation) and (b) perpendicular (90-deg indentation) to the indenter long side. The tissue was mostly stretched and sheared perpendicular to the fiber direction in (a) while stretched and sheared parallel to the fiber direction in (b).

When characterizing isotropic materials with symmetric indenters, friction was usually not taken into account (Budday et al., 2015; Chai et al., 2014; Zhang et al., 2014). However, our study using asymmetric indentation suggested that the effect of friction might not be neglected (Figure 9). Unfortunately, an accurate quantification of the friction at the contact interface is particularly challenging. Böl et. al. (2013) recently proposed a method to estimate the frictional coefficient based on an inverse FE method in conjunction with the geometry change of the tissue sample (Böl et al., 2013). However, their method requires a larger sample thickness (10 mm) for the optical measurement, which may not be applicable to other tissue samples, such as the white matter considered in this study. A comparison of FE predictions between the 0-deg and 90-deg indentation configurations showed that the friction influences more on the 90-deg indentation (Figure 9b) than on the 0-deg configuration (Figure 9a), indicating a combined effect of fiber reinforcement and friction.

4.5 Aspects of experimental measurement

Theoretically, a combination of uniaxial stretch and shear tests can be used to characterize the transversely isotropic material parameters (Feng et al., 2016). Experiments, such as uniaxial stretch (Velardi et al., 2006) and shear along or perpendicular to the fiber direction (Ning et al., 2006), have been successfully used to characterize white matter. Other methods, such as combined extension and torsion tests (Horgan and Murphy, 2012) and combined shear and indentation tests (Feng et al., 2013; Namani et al., 2012), could also characterize the anisotropy of soft tissue. Nevertheless, tissue fixation poses a challenge for applying them to white matter. As an alternative, the asymmetric indentation technique presented in this study utilized only one instrument and did not have specific clamping and attaching requirements. Therefore, this can enhance the efficiency of the testing and prevent the tissue sample from mishandling and damage during the measurement.

Moreover, studies have shown that the Young's modulus of porcine white matter ranges from 1.79 kPa (Jiang et al., 2015; Kaster et al., 2011) to 3.08 kPa (van Dommelen et al., 2010). Using a hyperelastic, transversely isotropic material model, our estimate of the shear modulus of white matter was slightly higher. This is probably due to the strain-rate effect that the measured elastic modulus increases with the loading rate, as shown in Budday et al. (2015) in indentation and Rashid et al. (2013) in shear tests.

4.6 Limitations

Although measurement at larger deformation is possible, indentation could damage the tissue, making it difficult to acquire data of intact tissues. In addition, our current method does not yet consider the viscous effect of the white matter tissue. Nevertheless, our method, which provides parameter estimates of the elastic component, is a useful and important first step to establish more realistic hyperelastic, viscoelastic anisotropic models for modeling brain tissues in the future.

5 Conclusions

A custom-built asymmetric indentation device in conjunction with an optimization-based inverse FE modeling technique was used to characterize white matter. Our results indicated the potential of using a single experimental procedure, asymmetric indentation, to characterize transversely isotropic soft tissues. The method does not require multiple testing techniques to characterize one material sample, enhancing the testing efficiency and reducing the experimental error. An inverse method was used to estimate the parameters of a transversely isotropic, hyperelastic material model with two anisotropic invariants. We have shown that indentation information from both indentation configurations (parallel and perpendicular to fiber direction) is necessary to estimate the transversely isotropic model parameters with sufficient accuracy. Moreover, parameter μ has a larger influence on the indentation response than parameters ζ and ϕ, suggesting that the matrix material plays an important role in white matter. We have also shown that inclusion of the frictional effect is necessary in estimating model parameters. Further, the estimated optimal parameters based on the proposed inverse modeling technique were comparable to those obtained via forward FE simulations, suggesting the consistency between the two techniques. Future work includes a study of different weighting ratios for the two configurations, inclusion of the strain-rate effect, and applications of the proposed technique to quantify other biological tissues, such as tendon and ligament.

Acknowledgement

Funding is provided by grant 61503267 (YF) from National Natural Science Foundation, grant BK20140356 (YF), 16KJB460018 (YF) from Jiangsu Province, and by grant K511701515 (YF) from Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry. In addition, supports from the NIH R01 NS092853 (SJ) and the start-up funds from the School of Aerospace and Mechanical Engineering (AME) at the University of Oklahoma (CHL) are also acknowledged.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest statement

No conflict of interest exists.

References

  1. Arbogast KB, Margulies SS. Material characterization of the brainstem from oscillatory shear tests. J Biomech. 1998;31:801–807. doi: 10.1016/s0021-9290(98)00068-2. [DOI] [PubMed] [Google Scholar]
  2. Arbogast KB, Thibault KL, Pinheiro BS, Winey KI, Margulies SS. A high-frequency shear device for testing soft biological tissues. J Biomech. 1997;30:757–759. doi: 10.1016/s0021-9290(97)00023-7. [DOI] [PubMed] [Google Scholar]
  3. Böl M, Kruse R, Ehret AE. On a staggered iFEM approach to account for friction in compression testing of soft materials. J Mech Behav Biomed. 2013;27:204–213. doi: 10.1016/j.jmbbm.2013.04.009. [DOI] [PubMed] [Google Scholar]
  4. Bain AC, Meaney DF. Tissue-Level Thresholds for Axonal Damage in an Experimental Model of Central Nervous System White Matter Injury. Journal of Biomechanical Engineering. 2000;122:615–622. doi: 10.1115/1.1324667. [DOI] [PubMed] [Google Scholar]
  5. Bayly PV, Cohen TS, Leister EP, Ajo D, Leuthardt EC, Genin GM. Deformation of the human brain induced by mild acceleration. J Neurotrauma. 2005;22:845–856. doi: 10.1089/neu.2005.22.845. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bischoff JE. Static Indentation of Anisotropic Biomaterials Using Axially Asymmetric Indenters—a Computational Study. Journal of Biomechanical Engineering. 2004;126:498–505. doi: 10.1115/1.1785808. [DOI] [PubMed] [Google Scholar]
  7. Budday S, Nay R, de Rooij R, Steinmann P, Wyrobek T, Ovaert TC, Kuhl E. Mechanical properties of gray and white matter brain tissue by indentation. J Mech Behav Biomed. 2015;46:318–330. doi: 10.1016/j.jmbbm.2015.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chai C-K, Speelman L, Oomens CWJ, Baaijens FPT. Compressive mechanical properties of atherosclerotic plaques—Indentation test to characterise the local anisotropic behaviour. J Biomech. 2014;47:784–792. doi: 10.1016/j.jbiomech.2014.01.018. [DOI] [PubMed] [Google Scholar]
  9. Chatelin S, Constantinesco A, Willinger R. Fifty years of brain tissue mechanical testing: From in vitro to in vivo investigations. Biorheology. 2010;47:255–276. doi: 10.3233/BIR-2010-0576. [DOI] [PubMed] [Google Scholar]
  10. Cheng S, Bilston LE. Unconfined compression of white matter. J Biomech. 2007;40:117–124. doi: 10.1016/j.jbiomech.2005.11.004. [DOI] [PubMed] [Google Scholar]
  11. Cheng S, Clarke EC, Bilston LE. Rheological properties of the tissues of the central nervous system: A review. Med. Eng. Phys. 2008;30:1318–1337. doi: 10.1016/j.medengphy.2008.06.003. [DOI] [PubMed] [Google Scholar]
  12. Coudrillier B, Boote C, Quigley H, Nguyen T. Scleral anisotropy and its effects on the mechanical response of the optic nerve head. Biomech Model Mechanobiol. 2013;12:941–963. doi: 10.1007/s10237-012-0455-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cox MAJ, Driessen NJB, Boerboom RA, Bouten CVC, Baaijens FPT. Mechanical characterization of anisotropic planar biological soft tissues using finite indentation: Experimental feasibility. J Biomech. 2008;41:422–429. doi: 10.1016/j.jbiomech.2007.08.006. [DOI] [PubMed] [Google Scholar]
  14. Destrade M, Gilchrist MD, Murphy JG, Rashid B, Saccomandi G. Extreme softness of brain matter in simple shear. International Journal of Non-Linear Mechanics. 2015;75:54–58. [Google Scholar]
  15. Destrade M, Mac Donald B, Murphy JG, Saccomandi G. At least three invariants are necessary to model the mechanical response of incompressible, transversely isotropic materials. Comput Mech. 2013;52:959–969. [Google Scholar]
  16. Elkin BS, Ilankova A, Morrison B. Dynamic, regional mechanical properties of the porcine brain: indentation in the coronal plane. Journal of biomechanical engineering. 2011;133:071009. doi: 10.1115/1.4004494. [DOI] [PubMed] [Google Scholar]
  17. Fahlstedt M, Depreitere B, Halldin P, Sloten JV, Kleiven S. Correlation between Injury Pattern and Finite Element Analysis in Biomechanical Reconstructions of Traumatic Brain Injuries. J Biomech. 2015;48:1331–1335. doi: 10.1016/j.jbiomech.2015.02.057. [DOI] [PubMed] [Google Scholar]
  18. Feng Y, Okamoto RJ, Genin GM, Bayly PV. On the accuracy and fitting of transversely isotropic material models. J Mech Behav Biomed. 2016;61:554–566. doi: 10.1016/j.jmbbm.2016.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Feng Y, Okamoto RJ, Namani R, Genin GM, Bayly PV. Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J Mech Behav Biomed. 2013;23:117–132. doi: 10.1016/j.jmbbm.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gefen A, Margulies SS. Are in vivo and in situ brain tissues mechanically similar? J Biomech. 2004;37:1339–1352. doi: 10.1016/j.jbiomech.2003.12.032. [DOI] [PubMed] [Google Scholar]
  21. Harb N, Labed N, Domaszewski M, Peyraut F. A new parameter identification method of soft biological tissue combining genetic algorithm with analytical optimization. Comput Method Appl M. 2011;200:208–215. [Google Scholar]
  22. Harb N, Labed N, Domaszewski M, Peyraut F. Optimization of material parameter identification in biomechanics. Struct Multidisc Optim. 2014;49:337–349. [Google Scholar]
  23. Hatami-Marbini H, Etebu E. An experimental and theoretical analysis of unconfined compression of corneal stroma. J Biomech. 2013;46:1752–1758. doi: 10.1016/j.jbiomech.2013.03.013. [DOI] [PubMed] [Google Scholar]
  24. Holmes JH. Methods and applications of evolutionary computation in biomedicine. Journal of Biomedical Informatics. 2014;49:11–15. doi: 10.1016/j.jbi.2014.05.008. [DOI] [PubMed] [Google Scholar]
  25. Horgan C, Murphy J. On the Modeling of Extension-Torsion Experimental Data for Transversely Isotropic Biological Soft Tissues. Journal of Elasticity. 2012;108:179–191. [Google Scholar]
  26. Hortin M, Graham S, Boatwright K, Hyoung P, Bowden A. Transversely isotropic material characterization of the human anterior longitudinal ligament. J Mech Behav Biomed. 2015;45:75–82. doi: 10.1016/j.jmbbm.2015.01.020. [DOI] [PubMed] [Google Scholar]
  27. Hrapko M, van Dommelen JA, Peters GW, Wismans JS. Characterisation of the mechanical behaviour of brain tissue in compression and shear. Biorheology. 2008;45:663–676. [PubMed] [Google Scholar]
  28. Iwata A, Stys PK, Wolf JA, Chen XH, Taylor AG, Meaney DF, Smith DH. Traumatic axonal injury induces proteolytic cleavage of the voltage-gated sodium channels modulated by tetrodotoxin and protease inhibitors. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2004;24:4605–4613. doi: 10.1523/JNEUROSCI.0515-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ji S, Zhao W, Ford JC, Beckwith JG, Bolander RP, Greenwald RM, Flashman LA, Paulsen KD, McAllister T. Group-wise evaluation and comparison of white matter fiber strain and maximum principal strain in sports-related concussion. Journal of neurotrauma. 2015;32:441–454. doi: 10.1089/neu.2013.3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jiang Y, Li G, Qian L-X, Liang S, Destrade M, Cao Y. Measuring the linear and nonlinear elastic properties of brain tissue with shear waves and inverse analysis. Biomech Model Mechanobiol. 2015;14:1119–1128. doi: 10.1007/s10237-015-0658-0. [DOI] [PubMed] [Google Scholar]
  31. Kaster T, Sack I, Samani A. Measurement of the hyperelastic properties of ex vivo brain tissue slices. J Biomech. 2011;44:1158–1163. doi: 10.1016/j.jbiomech.2011.01.019. [DOI] [PubMed] [Google Scholar]
  32. Khalil AS, Bouma BE, Kaazempur Mofrad MR. A combined FEM/genetic algorithm for vascular soft tissue elasticity estimation. Cardiovascular engineering (Dordrecht, Netherlands) 2006;6:93–102. doi: 10.1007/s10558-006-9013-5. [DOI] [PubMed] [Google Scholar]
  33. Kulkarni SG, Gao X-L, Horner SE, Mortlock RF, Zheng JQ. A transversely isotropic visco hyperelastic constitutive model for soft tissues. Math Mech Solids. 2014 [Google Scholar]
  34. Laurer HL, Meaney DF, Margulies SS, McIntosh TK. Modeling Brain Injury/Trauma A2 - Ramachandran, V.S, Encyclopedia of the Human Brain. Academic Press; New York: 2002. pp. 93–102. [Google Scholar]
  35. Lee C-H, Carruthers CA, Ayoub S, Gorman RC, Gorman Iii JH, Sacks MS. Quantification and simulation of layer-specific mitral valve interstitial cells deformation under physiological loading. Journal of Theoretical Biology. 2015a;373:26–39. doi: 10.1016/j.jtbi.2015.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Lee C-H, Oomen PJA, Rabbah JP, Yoganathan A, Gorman RC, Gorman JH, Amini R, Sacks MS. A High-Fidelity and Micro-anatomically Accurate 3D Finite Element Model for Simulations of Functional Mitral Valve. In: Ourselin S, Rueckert D, Smith N, editors. Functional Imaging and Modeling of the Heart: 7th International Conference, FIMH 2013, London, UK, June 20-22, 2013. Proceedings. Springer Berlin Heidelberg; Berlin, Heidelberg: 2013. pp. 416–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lee CH, Amini R, Gorman RC, Gorman JH, Sacks MS. An inverse modeling approach for stress estimation in mitral valve anterior leaflet valvuloplasty for in-vivo valvular biomaterial assessment. J Biomech. 2014;47:2055–2063. doi: 10.1016/j.jbiomech.2013.10.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Lee CH, Rabbah JP, Yoganathan AP, Gorman RC, Gorman JH, Sacks MS. On the effects of leaflet microstructure and constitutive model on the closing behavior of the mitral valve. Biomech Model Mechanobiol. 2015b;14:1281–1302. doi: 10.1007/s10237-015-0674-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Liu Y, Thomopoulos S, Chen C, Birman V, Buehler MJ, Genin GM. Modelling the mechanics of partially mineralized collagen fibrils, fibres and tissue. J. R. Soc. Interface. 2014;11:20130835. doi: 10.1098/rsif.2013.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Meaney DF, Smith DH. Biomechanics of Concussion. Clin Sport Med. 2011;30:19. doi: 10.1016/j.csm.2010.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Miller K, Chinzei K, Orssengo G, Bednarz P. Mechanical properties of brain tissue in-vivo: experiment and computer simulation. J Biomech. 2000;33:1369–1376. doi: 10.1016/s0021-9290(00)00120-2. [DOI] [PubMed] [Google Scholar]
  42. Namani R, Feng Y, Okamoto RJ, Jesuraj N, Sakiyama-Elbert SE, Genin GM, Bayly PV. Elastic characterization of transversely isotropic soft materials by dynamic shear and asymmetric indentation. J Biomech Eng. 2012;134:061004. doi: 10.1115/1.4006848. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Nguyen TD, Boyce BL. An inverse finite element method for determining the anisotropic properties of the cornea. Biomech Model Mechanobiol. 2011;10:323–337. doi: 10.1007/s10237-010-0237-3. [DOI] [PubMed] [Google Scholar]
  44. Nicolle S, Lounis M, Willinger R, Palierne JF. Shear linear behavior of brain tissue over a large frequency range. Biorheology. 2005;42:209–223. [PubMed] [Google Scholar]
  45. Ning X, Zhu Q, Lanir Y, Margulies SS. A transversely isotropic viscoelastic constitutive equation for brainstem undergoing finite deformation. J Biomech Eng. 2006;128:925–933. doi: 10.1115/1.2354208. [DOI] [PubMed] [Google Scholar]
  46. Prange MT, Meaney DF, Margulies SS. Defining brain mechanical properties: effects of region, direction, and species. Stapp Car Crash J. 2000;44:205–213. doi: 10.4271/2000-01-SC15. [DOI] [PubMed] [Google Scholar]
  47. Rashid B, Destrade M, Gilchrist MD. Mechanical characterization of brain tissue in simple shear at dynamic strain rates. J Mech Behav Biomed. 2013;28:71–85. doi: 10.1016/j.jmbbm.2013.07.017. [DOI] [PubMed] [Google Scholar]
  48. Reiter R, Freise C, Johrens K, Kamphues C, Seehofer D, Stockmann M, Somasundaram R, Asbach P, Braun J, Samani A, Sack I. Wideband MRE and static mechanical indentation of human liver specimen: Sensitivity of viscoelastic constants to the alteration of tissue structure in hepatic fibrosis. J Biomech. 2014;47:1665–1674. doi: 10.1016/j.jbiomech.2014.02.034. [DOI] [PubMed] [Google Scholar]
  49. Robertson D, Willardson R, Parajuli D, Cannon A, Bowden AE. The lumbar supraspinous ligament demonstrates increased material stiffness and strength on its ventral aspect. J Mech Behav Biomed. 2013;17:34–43. doi: 10.1016/j.jmbbm.2012.07.009. [DOI] [PubMed] [Google Scholar]
  50. Slomka N, Oomens CW, Gefen A. Evaluating the effective shear modulus of the cytoplasm in cultured myoblasts subjected to compression using an inverse finite element method. J Mech Behav Biomed. 2011;4:1559–1566. doi: 10.1016/j.jmbbm.2011.04.006. [DOI] [PubMed] [Google Scholar]
  51. Smith SL, Cagnoni S. Genetic and evolutionary computation : medical applications. Wiley; Chichester, West Sussex: 2011. [Google Scholar]
  52. Svensson RB, Hassenkam T, Hansen P, Magnusson SP. Viscoelastic behavior of discrete human collagen fibrils. J Mech Behav Biomed. 2010;3:112–115. doi: 10.1016/j.jmbbm.2009.01.005. [DOI] [PubMed] [Google Scholar]
  53. Thomopoulos S, Genin GM. Tendon and Ligament Biomechanics. Orthopaedic Biomechanics. 2012;49 [Google Scholar]
  54. van Dommelen JAW, van der Sande TPJ, Hrapko M, Peters GWM. Mechanical properties of brain tissue by indentation: Interregional variation. J Mech Behav Biomed. 2010;3:158–166. doi: 10.1016/j.jmbbm.2009.09.001. [DOI] [PubMed] [Google Scholar]
  55. Velardi F, Fraternali F, Angelillo M. Anisotropic constitutive equations and experimental tensile behavior of brain tissue. Biomech Model Mechanobiol. 2006;5:53–61. doi: 10.1007/s10237-005-0007-9. [DOI] [PubMed] [Google Scholar]
  56. Witzenburg C, Raghupathy R, Kren SM, Taylor DA, Barocas VH. Mechanical Changes in the Rat Right Ventricle with Decellularization. J Biomech. 2012;45:842–849. doi: 10.1016/j.jbiomech.2011.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Wright AH. Genetic Algorithms for Real Parameter Optimization. In: Gregory JE,R, editor. Foundations of Genetic Algorithms. Elsevier; 1991. pp. 205–218. [Google Scholar]
  58. Wright RM, Ramesh KT. An axonal strain injury criterion for traumatic brain injury. Biomech Model Mechanobiol. 2012;11:245–260. doi: 10.1007/s10237-011-0307-1. [DOI] [PubMed] [Google Scholar]
  59. Yang L, van der Werf KO, Dijkstra PJ, Feijen J, Bennink ML. Micromechanical analysis of native and cross-linked collagen type I fibrils supports the existence of microfibrils. J Mech Behav Biomed. 2012;6:148–158. doi: 10.1016/j.jmbbm.2011.11.008. [DOI] [PubMed] [Google Scholar]
  60. Zhang LY, Yang KH, King AI. J. Biomech. Eng.-Trans. Vol. 126. ASME; 2004. A proposed injury threshold for introduction mild traumatic brain injury. pp. 226–236. [DOI] [PubMed] [Google Scholar]
  61. Zhang MG, Cao YP, Li GY, Feng XQ. Spherical indentation method for determining the constitutive parameters of hyperelastic soft materials. Biomech Model Mechanobiol. 2014;13:1–11. doi: 10.1007/s10237-013-0481-4. [DOI] [PubMed] [Google Scholar]
  62. Zhang W, Feng Y, Lee C-H, Billiar KL, Sacks MS. A Generalized Method for the Analysis of Planar Biaxial Mechanical Data Using Tethered Testing Configurations. Journal of biomechanical engineering. 2015;137:064501. doi: 10.1115/1.4029266. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES