Implications of cellular models of dopamine neurons for disease

Abstract

This review addresses the present state of single-cell models of the firing pattern of midbrain dopamine neurons and the insights that can be gained from these models into the underlying mechanisms for diseases such as Parkinson's, addiction, and schizophrenia. We will explain the analytical technique of separation of time scales and show how it can produce insights into mechanisms using simplified single-compartment models. We also use morphologically realistic multicompartmental models to address spatially heterogeneous aspects of neural signaling and neural metabolism. Separation of time scale analyses are applied to pacemaking, bursting, and depolarization block in dopamine neurons. Differences in subpopulations with respect to metabolic load are addressed using multicompartmental models.

in this review, we address the present state of modeling the firing pattern of midbrain dopamine (DA) neurons and the insights that can be gained from these models into the underlying mechanisms for diseases such as addiction (Volkow and Morales 2015), schizophrenia (Weinberger 1987), and Parkinson's disease (PD) (Bernheimer et al. 1973). The review arose from a workshop at the Organization for Computational Neuroscience meeting in Prague in the summer of 2015, organized by the first author, in which all authors presented their work. Here, we begin with a tutorial explaining the analytical technique of separation of time scales and then show how this technique can produce insights into mechanisms using simplified single-compartment models. In addition, we show how morphologically realistic multicompartmental models can be used to address some spatial aspects of neural signaling. We also address variability within and across subpopulations of DA neurons defined by electrophysiology, projection targets, anatomical localization, and protein expression.

Midbrain dopaminergic neurons project to many brain regions (Bjorklund and Lindvall 1984; Yetnikoff et al. 2014), likely mediating a number of important neural computations. Distinct subpopulations within the ventral tegmental area (VTA) and the substantia nigra pars compacta (SNc) project to distinct targets (Roeper 2013) and receive afferent inputs from distinct areas (Lerner et al. 2015; Watabe-Uchida et al. 2012). In a slice preparation devoid of afferent input, DA neurons spontaneously exhibit regular pacemaker firing (Grace and Onn 1989). Presumably their ability to sustain a background level of tonic firing in the absence of synaptic input ensures that, under conditions in vivo, the firing rate can always be increased and also robustly decreased. This bidirectional signaling allows better than expected outcomes to be coded by increases in firing rate, whereas worse than expected outcomes can be coded by decreases in firing rate (Eshel et al. 2015; Schultz 1998). More recent work shows that, whereas some subpopulations indeed code for the reward prediction error based on motivational values, bursts in distinct subpopulations may instead convey information about motivational salience and novelty (Roeper 2013), which requires only unidirectional signaling, that is, increases in firing rate. Rapid increases in the firing rate are often associated with bursts of action potentials, and synaptic activation of NMDA receptors is critical for most bursting activity (Overton and Clark 1992; Tong et al. 1996; Zweifel et al. 2009). Moreover, the balance between inhibition and excitation is critical (Paladini and Roeper 2014). Bursts can also be facilitated by various manipulations of intrinsic conductances in DA neurons, including blocking the SK potassium channel, which is responsible for the Ca²⁺-mediated afterhyperpolarizing potential (AHP) (Ping and Shepard 1996). Modeling can explain the complex contributions of intrinsic currents to the propensity of DA neurons to transmit tonic or phasic signals. Phasic and tonic firing differentially affect the DA concentration in target areas and therefore have very distinct effects on the binding of DA to pre- and postsynaptic receptors (Dreyer et al. 2010), with implications for systems (Hazy et al. 2010) and algorithmic (Gruber et al. 2006; Niv et al. 2007) level models of dopaminergic signaling.

Nullclines and the Phase Plane (Tutorial)

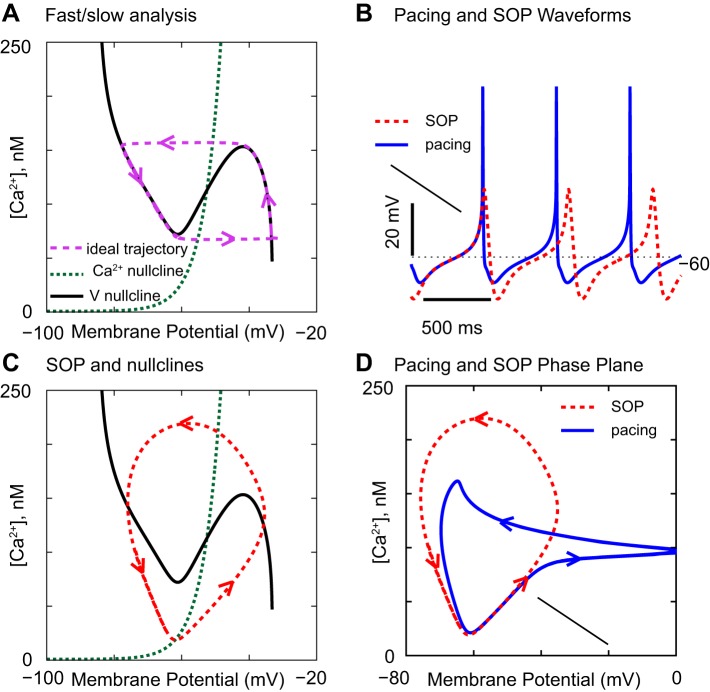
A separation of time scales, or fast/slow analysis (van der Pol 1926; Somers and Kopell 1993), can often capture the essence of a neural oscillation by assuming that one rate-limiting variable changes slowly compared with the rate of change of the membrane potential (V). In the example given in Fig. 1, the slow variable is the cytosolic concentration of free Ca²⁺. To make the chosen model (Kuznetsova et al. 2010) simple enough to capture the essence of the oscillations, we analyzed a single isolated compartment of this multicompartmental model, the proximal dendritic compartment. We eliminated a minor slow variable, the cytosolic sodium ion concentration, by setting it to a small fixed value (0.81 mM), to focus on the Ca²⁺-driven slow oscillatory potential (SOP, red trace) that results when the Na_V channel is blocked in a pacemaking (blue trace) DA neuron in Fig. 1B.

Fig. 1.

How the phase portrait with respect to V and Ca²⁺ affects the slow oscillatory potentials (SOPs) and pacemaking. The Na_V conductance was 550 μS/cm² for the blue traces and 0 for all other curves. The fraction of free, unbuffered Ca²⁺ in the model was 0.05% in A and 5% in all other panels. A: phase-plane portrait of an idealized oscillation that strictly observes the separation of time scales. B: simulation of pacemaking and of the SOP. C: nullclines only approximately shape the SOP in the model. D: blue trajectory shows the contribution of the Na_V conductance during spiking compared with during SOP.

In Fig. 1A, two important curves, the voltage (V) nullcline (solid black) and the Ca²⁺ nullcline (dotted green), influence the dynamics. All gating variables were eliminated from the analysis by assuming that they change on a fast time scale with respect to the slow time scale of Ca²⁺, so they were set to their steady-state values with respect to membrane potential (V). Along a nullcline, the time rate of change of the respective variable is 0, so each nullcline divides the plane into two halves, one in which the respective variable increases and another in which it decreases, determining in which direction the trajectory evolves in this space. The “ideal” trajectory (dashed purple) in which the nullclines precisely determine the course of an oscillation was obtained by setting the Na_V conductance to 0 and reducing the fraction of free Ca²⁺ from the default value of 5% to 0.05%, which greatly slows the rate of change of [Ca²⁺]. There are two key principles in Fig. 1A. First, the V nullcline has three branches. The middle branch of the nullcline results, in this model, from the L-type Ca²⁺ current, an inward current that regeneratively activates with increased depolarization, causing more channel opening and further depolarization, or regeneratively deactivates with increased hyperpolarization. This type of current produces positive feedback, which destabilizes the entire middle branch, because a small displacement from this branch always leads to a larger displacement. The outer branches have no such positive feedback, so, when the trajectory lands on these branches, it moves along the branch in a direction dictated by whether Ca²⁺ is increasing or decreasing on the branch. When the middle branch is reached, positive feedback resulting from Ca²⁺ channels closing or opening results in a jump to the other branch. The intersection of the nullclines is the point at which both the membrane potential and the Ca²⁺ concentration can reach a steady state. The second key principle is that, when this intersection falls on the unstable branch, the resting potential is unstable; moreover, an unstable resting potential, combined with the fold in the V nullcline, forces an oscillation.

The picture in Fig. 1A no longer strictly holds when the separation of time scales of V and Ca²⁺ is less drastic, as in Fig. 1C, in which the red trace corresponds to the SOP generated by the model in Fig. 1B. However, the two major principles that force an oscillation remain intact; the intersection of the nullclines occurs on the unstable middle branch of the V nullcline, and the rate of change of V is fast enough with respect to Ca²⁺ to enable the positive feedback to destabilize the intersection point. The oscillation will disappear when the separation of the time scales is further reduced. When the Na_V channel is reintroduced into the model (blue trace in Fig. 1D), the trajectory is very similar during the depolarization preceding an action potential; compare the blue and red traces in Fig. 1D and the first action potential in Fig. 1B, which is aligned with the SOP. The difference between the minimum and maximum Ca²⁺ levels determines the amount of Ca²⁺ that must be pumped out each cycle period. The phase plane of the two dimensions V and Ca²⁺ no longer suffices for pacemaking because there is another separation of time scales between the processes responsible for the upstroke of an action potential and its repolarization that is not captured in this portrait. This analysis is similar to one performed previously [Fig. 7 of Drion et al. (2011)] on a similarly reduced model.

Fig. 7.

SK block promotes bursting by extending the unstable middle branch of the V nullcline. A and B: simulations of pacemaking and intrinsic bursting, respectively. C and D: voltage nullclines with overlaid limit cycles for pacemaking and intrinsic bursting, respectively. Arrows indicate direction of trajectory. [Adapted from Oster et al. (2015).]

Pacemaking and PD

There may be a dark side to the spontaneous spiking activity of DA neurons. The relatively high calcium load in SNc DA neurons has been blamed for their selective vulnerability in PD (Surmeier et al. 2010, 2011, 2012). The high Ca²⁺ load is thought to result from the atypically prominent role of Ca²⁺ channels in the pacemaking mechanism (Bean 2007; Chan et al. 2007) resulting in Ca²⁺ entry that is continuously maintained (Puopolo et al. 2007) during pacemaking. The energetic burden of synthesizing ATP to fuel removal of calcium by the Ca²⁺ pump is borne primarily by the mitochondria, and mitochondrial respiration increases production of reactive oxygen species implicated in cell death in PD.

Spontaneous pacemaking activity in DA neurons in vitro has been widely hypothesized (Amini et al. 1999; Kuznetsov et al. 2006; Wilson and Callaway 2000) to be driven by an underlying oscillation in Ca²⁺ concentration. This hypothesis is based on the observation that SOPs can often be observed when spikes are blocked by the Na_V channel blocker TTX (Kang and Kitai 1993; Nedergaard et al. 1993; Ping and Shepard 1996) and that these SOPs are blocked by the L-type Ca²⁺ channel blocker nifedipine (Nedergaard et al. 1993; Mercuri et al. 1994) and disrupted by the Ca²⁺-activated SK potassium channel blocker apamin (Ping and Shepard 1996). As an illustrative example of the insight that can be gained from models of DA neurons, we performed an analysis on an existing, rather complicated, model of pacemaking (Kuznetsova et al. 2010) in DA neurons that reproduces spontaneous pacemaking and the SOP that results when the Na_V channel is blocked (Fig. 1B). In the model, the oscillation is driven by the interaction of a depolarizing, subthreshold Ca²⁺ current and a Ca²⁺-activated SK potassium channel.

Nullclines and the Phase Plane explains in detail how the mathematical analysis of neural dynamics can be reduced to just two variables (Fig. 1A), in this case V and [Ca²⁺], using a technique from nonlinear dynamics called phase-plane analysis. The gist of the technique is to identify a slow variable, then find the pairs of values of V and [Ca²⁺] for which the steady-state inward and outward currents are exactly balanced such that net membrane current flow is 0 to draw the V nullcline (recall that the current is equal to the time derivative of the voltage, so the V-nullcline defines all pairs of V and [Ca²⁺] for which there is no time change in voltage). Another set of pairs of values of V and [Ca²⁺], along which the steady-state influx and efflux of Ca²⁺ are exactly balanced, is called the [Ca²⁺] nullcline. The [Ca²⁺] nullcline has been measured experimentally in DA neurons (Wilson and Callaway 2000), using a voltage-clamp protocol combined with Ca²⁺ imaging. The first key point is that the intersection of the nullclines, where everything is in balance, determines the resting potential of the membrane, if any. However, DA neurons in general are pacemakers and do not have a resting potential. The second key point is that a current that exhibits positive feedback, otherwise called regenerative activation, folds the membrane potential nullcline, destabilizes the resting potential, and forces an oscillation in the membrane potential (Fig. 1C). The fold in the nullcline is caused by the same type of positive feedback that can result in a negative slope conductance in the current/voltage (I/V) relationship (Kaczmarek and Levitan 1987; Koch 2004). Time is not represented in the phase plane, and, for a perfectly periodic oscillation, each cycle traces out the same path in this space. The voltage dependence of the L-type Ca²⁺ channel, which produces the middle branch of the voltage nullcline in this model, is critical in pacemaking (Drion et al. 2011; Tucker et al. 2012). Ca²⁺ influx is necessary to activate the SK channel, but whether the L-type channel participates in activating the SK channel is unclear (Wolfart and Roeper 2002), so the calcium current in the model should be regarded as a composite.

In Fig. 1D, the trajectory in the phase plane with the Na_V conductance intact is compared with that with the Na_V conductance blocked. The arrow indicates the point at which the Na_V conductance turns on; during the depolarization leading up to the spike, the trajectory is indistinguishable from the SOP. However, this phase-plane representation does not capture the dynamics of action potential generation, which decouple the frequency of pacemaking from that of the SOP in the model (Drion et al. 2011; Fellous et al. 2016), consistent with experimental data (Guzman et al. 2009). Also, consistent with experimental data, Drion et al. (2011) were able to show that pacemaking is less sensitive to noise than the SOP in a reduced model similar to the one analyzed in Fig. 1. Any phase-plane portrait is a gross oversimplification of the multicompartmental, multidimensional complex dynamics of a real DA neuron but nevertheless allows us to understand and predict the effects of various manipulations.

Note that both the Ca²⁺ and Na⁺ inward currents contribute to pacemaking in the model in Fig. 1B, consistent with experimental data (Puopolo et al. 2007). Some investigators have found that bath application of dihydropyridines, selective pharmacological blockers of the L-type Ca²⁺ current, blocks pacemaking in DA neurons (Chan et al. 2007; Nedergaard et al. 1993; Putzier et al. 2009), whereas others have found that pacemaking persists when the L-type current is blocked (Drion et al. 2011; Guzman et al. 2009). Modeling can reconcile these divergent results by showing how a tiny change in a single parameter, the Na_V conductance (ḡ_Na), can cause a shift between these two opposite responses to L-type channel blockers, namely sustained vs. disrupted pacemaking. The phase diagram at the center of Fig. 2 shows the parameter region that supports pacemaking in an existing multicompartmental model (Canavier and Landry 2006). Drion et al. (2011) reduced the Na_V conductance (ḡ_Na) within this parameter region from 10,003 mS/cm² in Fig. 2A to 10,002 mS/cm² in Fig. 2B. In Fig. 2A, pacemaking persists when the L-type Ca²⁺ conductance (ḡ_Ca) is set to 0, but, at the infinitesimally smaller value of ḡ_Na in Fig. 2B, the same manipulation blocks pacemaking. Moreover, application of TTX does not always unmask a SOP; similarly, small changes in the value of the L-type Ca²⁺ conductance (ḡ_Ca) determine whether a SOP is unmasked by setting ḡ_Na to 0 to simulate the application of TTX (not shown).

Fig. 2.

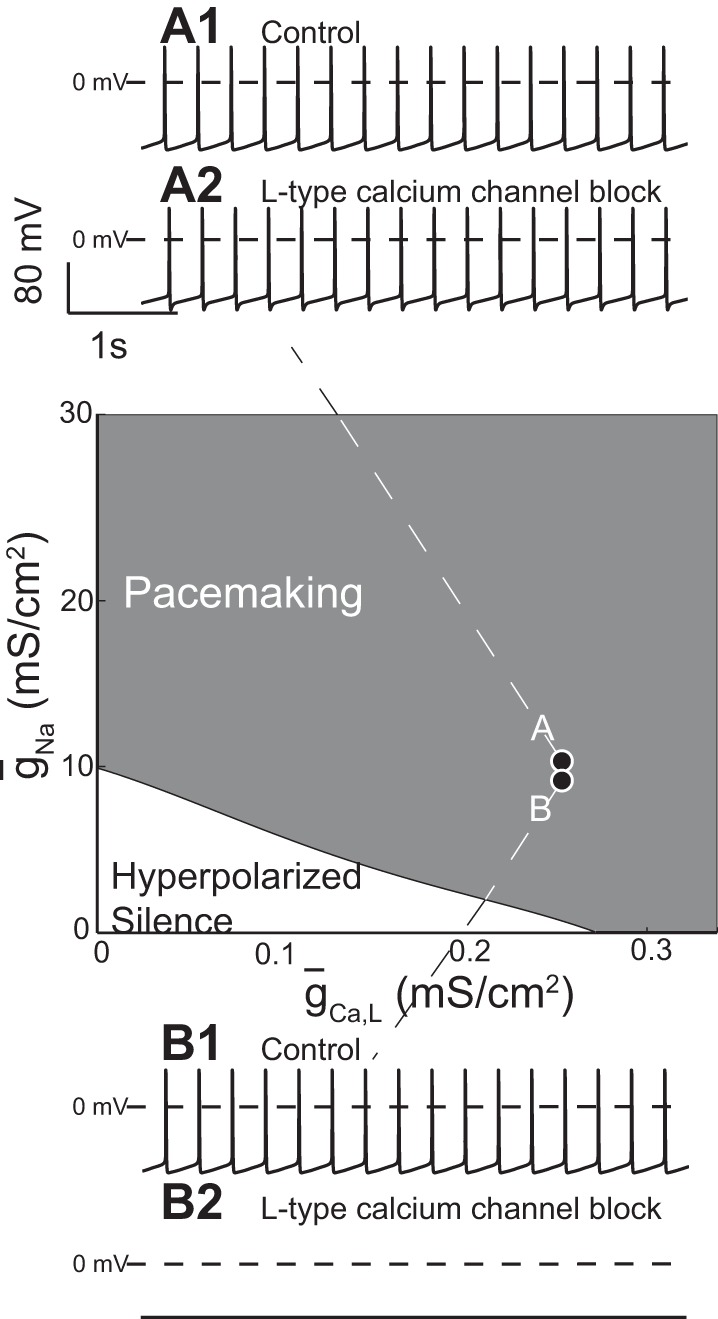
Small changes in model parameters change the predicted response to L-type Ca²⁺ or Na_V channel blockers. A1: ḡ_Na = 10,003 mS/cm², ḡ_Ca = 0.15 mS/cm². A2: ḡ_Na = 10,003 mS/cm², ḡ_Ca = 0 mS/cm². B1: ḡ_Na = 10,002 mS/cm², ḡ_Ca = 0.15 mS/cm². B2: ḡ_Na = 10,002 mS/cm², ḡ_Ca = 0 mS/cm². [Adapted from Drion et al. (2011).]

DA Subpopulations and PD

Early characterization of SNc DA neurons defined a ventral tier located directly above the substantia nigra pars reticulata and a dorsal tier, located directly above the ventral tier. Only the neurons of the dorsal tier contain calbindin, a calcium-binding protein (Gerfen et al. 1987). The calbindin-positive neurons of the dorsal tier are consistently shown to be resilient to neurodegeneration in PD and in PD model systems, whereas the calbindin-negative neurons are more vulnerable (German et al. 1992; Okamura et al. 1995; Rodríguez et al. 2001; Yamada et al. 1990). The I_h current is significantly stronger in calbindin-negative SNc neurons compared with the calbindin-positive SNc neurons (Neuhoff et al. 2002). This study also found that the calbindin-negative neurons had a higher spontaneous firing rate than the calbindin-positive neurons. Recordings of calbindin-positive and -negative DA neurons in vivo confirmed that the calbindin-negative neurons fire faster (Brown et al. 2009). Recent recordings in midbrain slices have replicated both the difference in I_h and the difference in tonic firing between the two subpopulations (Evans and Khaliq 2015a). Modeling can help us to understand which mechanisms may contribute to the increased susceptibility of calbindin-negative neurons. A multicompartmental, multichannel model of an SNc DA neuron (Evans and Khaliq 2015b) consisting of a spherical soma with two dendritic trees extending from it, each containing identical primary, secondary, and tertiary branches, was implemented using the Genesis simulation software (Bower and Beeman 1994). This model (Fig. 3) was used to explain recent experimental results (Hage and Khaliq 2015) on the supralinear summation of Ca²⁺ during pacemaking and to provide a possible explanation for the increased resilience of calbindin-positive neurons.

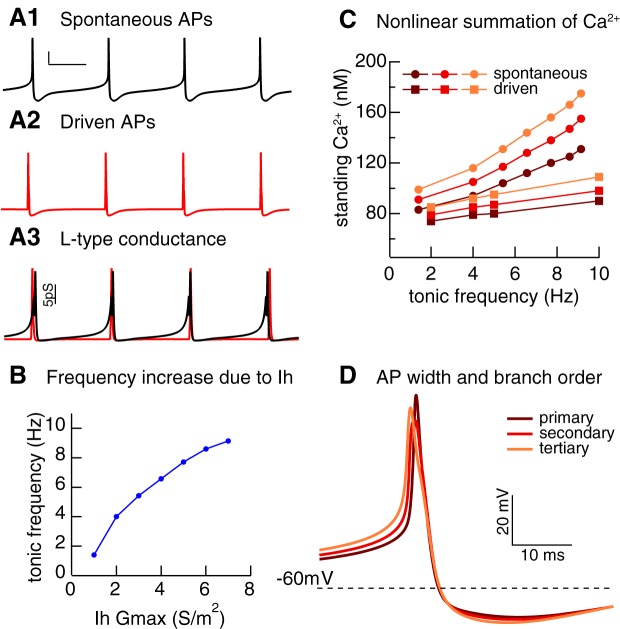
Fig. 3.

I_h alters standing calcium in model of substantia nigra pars compacta (SNc) dopamine neuron. A: spontaneous pacemaking, scale bars = 20 mV, 60 ms (A1). Action potentials (APs) evoked (A2) with a square depolarizing current pulse superimposed on a hyperpolarizing holding current to keep the neuron quiescent. A3: activation of L-type Ca²⁺ conductance in A1 (black) and A2 (red). B: tonic frequency increases with increased I_h conductance. C: standing calcium (defined as lowest calcium concentration reached between APs) increases more steeply with frequency in primary, secondary, and tertiary dendrites for pacemaking compared with driven APs as frequency is increased by stepping I_h G_max from 1 to 7 S/m². D: difference in AP width attributable to lower I_A conductance density distally accounts for the difference in C. [Unpublished simulations by R. C. Evans.]

Figure 3A shows that the membrane potential over the period of the interspike interval (ISI) is more depolarized during pacemaking (Fig. 3A1) than when action potentials are evoked by a current pulse from a silent, hyperpolarized neuron (Fig. 3A2). When the maximal conductance of I_h is increased globally throughout the model neuron but all other currents are unchanged, the tonic firing rate increases (Fig. 3B). Increasing the spontaneous firing frequency causes a much steeper increase (filled circles) in the minimum cytosolic Ca²⁺ concentration, called the standing Ca²⁺ load, observed in the model than simply evoking action potentials (filled squares) from a quiescent state at the same frequency (Fig. 3C). Figure 3A3 shows that the greater than expected increase is due to the subthreshold influx of Ca²⁺ via the L-type Ca²⁺ channel (CaV 1.3), which continues throughout the ISI during pacemaking (black trace), but not for evoked action potentials (red trace). Thus it is likely that the increased I_h in the calbindin-negative neurons will cause an increase in standing Ca²⁺ load, which may contribute to their selective vulnerability in PD. Moreover, the load increases with the dendritic branching level (Fig. 3C). In this model, A-type potassium current is highly concentrated in the soma and proximal dendrites (Gentet and Williams 2007) but absent from more distal dendrites, which leads to a more depolarized ISI and a broader action potential in the more distal branches leading to greater Ca²⁺ influx. As a result, the distal branches may be particularly susceptible to Ca²⁺ overload.

Another way in which calbindin-positive dopamine neurons differ from calbindin-negative neurons is that, recently, a novel in vivo discharge pattern was identified only in calbindin-positive dopamine neurons, sustained regular rhythmic bursting (Schiemann et al. 2012). The same study found that K-ATP channels mediate burst firing selectively in the medial nigra (Schiemann et al. 2012). Modeling work suggests that the metabolic activation of K-ATP by the metabolic load of faster spiking induced by NMDA receptor activation must be sufficient to periodically silence the cell to observe this type of bursting (Canavier and Yu 2014). Substantia nigra DA neurons in general have a relatively low Ca²⁺-buffering capacity (Foehring et al. 2009), and this may contribute to their increased vulnerability in PD. Further modeling work (Knowlton et al. 2016) postulated that in vivo calbindin-positive DA neurons have a greater buffering capacity than calbindin-negative DA neurons because calbindin is a Ca²⁺-binding protein. In this model, larger buffering capacity allows for a slower rate of change of cytosolic free Ca²⁺ during bursting activity and thereby stabilizes regular, rhythmic burst firing, consistent with the observation of this firing mode only in calbindin-positive DA neurons.

Within the SNc, as stated above, calbindin-positive neurons are less vulnerable to PD than calbindin-negative neurons. However, SNc DA neurons in general are more vulnerable to PD than the dopaminergic neurons of the VTA. Although the origin of this predisposition remains unknown, a striking feature of individual SNc DA neurons is the highly ramified and massive axon arborization they can establish (Matsuda et al. 2009), a cytoarchitecture with which VTA DA neurons can hardly compete (Prensa and Parent 2001). The axons of SNc DA neurons in rat brain have massive length and complexity, so it is likely that they exhibit high activity-dependent metabolic demands, disproportionate to those of VTA DA neurons, whose axons are smaller in size.

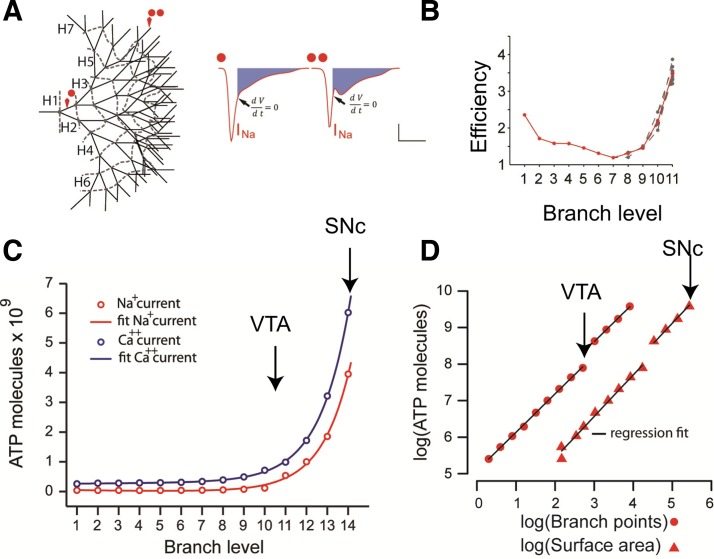
A recent modeling study (Pissadaki and Bolam 2013) examined the hypothesis that SNc neurons in PD might collapse under the energetic cost of their axons by quantifying the activity-dependent metabolic loads required for the activity of the Na⁺/K⁺ ATPase and Ca²⁺ pumps to remove the Na⁺ and Ca²⁺ ions entering during spontaneous pacemaking activity. Specifically, they estimated the bioenergetic demand required to reliably propagate a single action potential throughout the axon to the very distal terminals of axons of different size and complexity. The soma, dendrites, axon initial segment, and axon branches were constructed using the NEURON simulation package (Hines and Carnevale 1997) to conform to empirical morphological data. All compartments were equipped with active conductances and passive properties that allowed the model neurons to reproduce the typical electrophysiological profile exhibited by SNc DA neurons. To represent the axonal compartment of DA neurons that are spared vs. those that are vulnerable in PD, axonal branches were appended to an unbranched 6-mm section of axon using a bifurcating architecture in which each branch level contained 2ⁿ⁻¹ branches, where n is the number of branch levels. A model neuron (see Fig. 4A) with branch level 14 corresponds to a living SNc DA neuron with an axon with a total length of 50 cm, whereas one with branch level 10–11 corresponds to a VTA DA neuron with an axon with a total length of 3–8 cm. One main finding of this study is the exponential scaling of the energy cost with the level of branching (see Fig. 4C). The energy cost has a power law dependence on total axonal surface area and on the total number of axonal branch points (Fig. 4D). Consequently, the SNc DA neuron model has a much higher demand for ATP molecules compared with the VTA neuron model. Translating this prediction to living neurons, SNc DA neurons may be vulnerable to degeneration in PD because their cellular energetic demand is disproportionately higher than those of VTA FA neurons.

Fig. 4.

Exponentially increasing energy demand for signal propagation in neurons with increasing levels of axonal arborization. A: representative axonal tree (left). Red spots indicate the branch level (1 and 12) point at which the sodium current is plotted (right). B: AP efficiency for 10 continuous paths along a branched axon with a total length of 6.23 cm. C: number of ATP molecules required to restore membrane potential increases exponentially with respect to the length and branch level of the axon both as a result of Ca²⁺ influx (blue) and Na⁺ influx (red). D: number of ATP molecules with respect to the axonal surface area and branch points for different sizes of axonal arborizations follows a power law function. The discontinuity reflects the point where application of synaptic stimulation was required to enhance the signal to successfully invade the distal terminals of the axons with branch level higher than 10. VTA, ventral tegmental area. [Adapted from Pissadaki and Bolam (2013).]

Recent experimental results show that SNc DA neurons are at the limit of their energetic capacity, bolstered by the finding that mitochondrial density and ATP content is increased in SNc DA neurons compared with that in VTA and olfactory bulb neurons (Pacelli et al. 2015). High energy demand combined with low energy yield may contribute to functional failure (Bolam and Pissadaki 2012). According to the same study, axon endings (the terminal branches of an axon arborization) are risk factors for initiating functional failure as those that exhibit lower energetic efficiency. One measure of action potential efficiency is the ratio of actual Na⁺ flux to the theoretical minimum flux required to generate the upstroke of the action potential (Hallermann et al. 2012). The larger the ratio is above 1, the lower the energetic efficiency of action potential generation. In the model, efficiency was calculated as the ratio of sodium influx over the duration of an AP compared with the sodium influx from the start until the peak (at which the time derivative of the membrane potential is equal to 0) of the AP (blue filled area in Fig. 4A, right). For axons in the length range of the SNc and VTA, energetic efficiency was lowest in the terminal branches of the axon (Fig. 4B), supporting the idea that the axons may begin to die at the ends. Breakdown of distal axon branches is consistent with findings derived from animal models of PD (Meredith et al. 2008) and findings reporting axon loss and distal axon sensitivity as a prominent feature of many neurodegenerative and neurological diseases (Gerdts et al. 2016). Axon endings of larger axons may be more sensitive to die back, as this tendency is exacerbated at higher branch levels.

Burst Mechanisms and Addiction

DA neurons play a critical role in the processing of reward-related stimuli, and the DA neurons in the VTA that project to the shell subregion of nucleus accumbens (NAc) may be particularly critical in the processing of signals associated with drug abuse (Volkow and Morales 2015). Bursts of spikes in VTA DA neurons lead to fast DA increases sufficient to activate D1 receptors in the target area. Drugs of abuse cause increases in DA in the NAc that mimics the endogenous reward signaling mechanism of the brain (Volkow and Morales 2015). GABAergic projections from local GABAergic neurons, the accumbens, globus pallidus, and rostromedial tegmentum (RMTg) contribute to the control of burst timing (Paladini and Roeper 2014).

Because bursting in DA neurons has an important role in reward-mediated signaling, it is important to understand how bursting is generated and modulated in these neurons. Bursting in the context of midbrain DA neurons can have two definitions: 1) a simple transient, episode of high-frequency spiking, often time locked to a conditioned or unconditioned stimulus, or 2) an episode of high frequency driven by a voltage plateau. Plateau potentials in vitro can be oscillatory (Canavier et al. 2007; Johnson and North 1992; Johnson and Wu 2004; Ping and Shepard 1996), leading to a rhythmic repetitive discharge of closely spaced groups of spikes separated by quiescent periods. Classic reward prediction error signaling (Schultz 1998) is mediated by a transient increase in spike frequency that is time locked to an unexpected primary reward or a cue that has come to predict reward delivery. A burst in DA neurons has been operationally defined as beginning with an ISI <80 ms and terminating when the ISI exceeds 160 ms (Grace and Bunney 1984). Thus a burst would seem to require only increased excitation to increase the frequency. However, several pieces of evidence suggest that DA neuron burst dynamics may under some circumstances be more complex than a simple transient increase in frequency. First, intracellular bursts in vivo have been observed to be driven by a depolarizing wave (Grace and Bunney 1986) although different burst patterns can also be observed (Grace and Bunney 1984). Second, repetitive burst firing is sometimes observed in vivo, for example in calbindin-positive DA neurons (Schiemann et al. 2012) or in the presence of SK channel blockers (Waroux et al. 2005). Moreover, GABA A receptor blockers (Tepper et al. 1995) can cause most spikes to occur in bursts. Finally, there is a limit (10 Hz sustained, 20 Hz transiently) on how fast typical DA neurons can be made to fire via simple somatic depolarization (Richards et al. 1997), and this limit is often exceeded during bursts in vivo (Hyland et al. 2002). Therefore, simple depolarizing excitation appears to be an incomplete explanation; hence specific burst-generating mechanisms have been explored using modeling. Three possible burst-generating mechanisms have been suggested for dopamine neurons (Morikawa and Paladini 2011): the large excitatory postsynaptic potential model in which a burst is evoked by a particularly strong synaptic input, the plateau potential model in which a burst rides on a depolarized plateau and in which a burst requires interaction between synaptic events and intrinsic properties that cannot be mimicked by somatic current injection. There is probably some validity to all three mechanisms.

Recent studies (Ha and Kuznetsov 2013; Zakharov et al. 2016) focused on the role of tonic synaptic excitatory input in shaping the slow, Ca²⁺-dependent SOP described in Figs. 1 and 2, C3 and D3. If this oscillation is quenched, for example, by blocking the L-type Ca²⁺ channel (Fig. 2D2), spiking ceases in the absence of synaptic input because the membrane fails to reach the spiking threshold. The model of Ha and Kuznetsov (2013) is similar to the reduced single-compartment model presented in Fig. 1, except that the spiking frequency in this model is controlled by the frequency of the subthreshold oscillation, in contrast to Kuznetsova et al. (2010) and Drion et al. (2011). Moreover, this model includes tonic synaptic inputs that can be thought of as a limiting approximation of the asynchronous Poisson process synaptic input these neurons likely receive in vivo. The model responses to NMDA-mediated inputs are dependent, not only on the amplitude of the NMDA conductance, but also on the general level of the background AMPA activation (Fig. 5A) and can be explained using the nullcline analysis for three separate cases in Fig. 5B. Specifically activating an AMPA input alone can destabilize pacemaking and induce an inactive state. The AMPA conductance is ohmic, or linear, and tends to suppress the regenerative nonlinearity that is responsible for the destabilizing middle branch of the nullcline (compare the nullclines marked pacing and silent). The Ca²⁺ nullcline is unchanged by the activation of the AMPA conductance because, for simplicity, any synaptic Ca²⁺ influx was considered to be negligible in the model and intrinsic Ca²⁺ sources were considered to activate the SK channel.

Fig. 5.

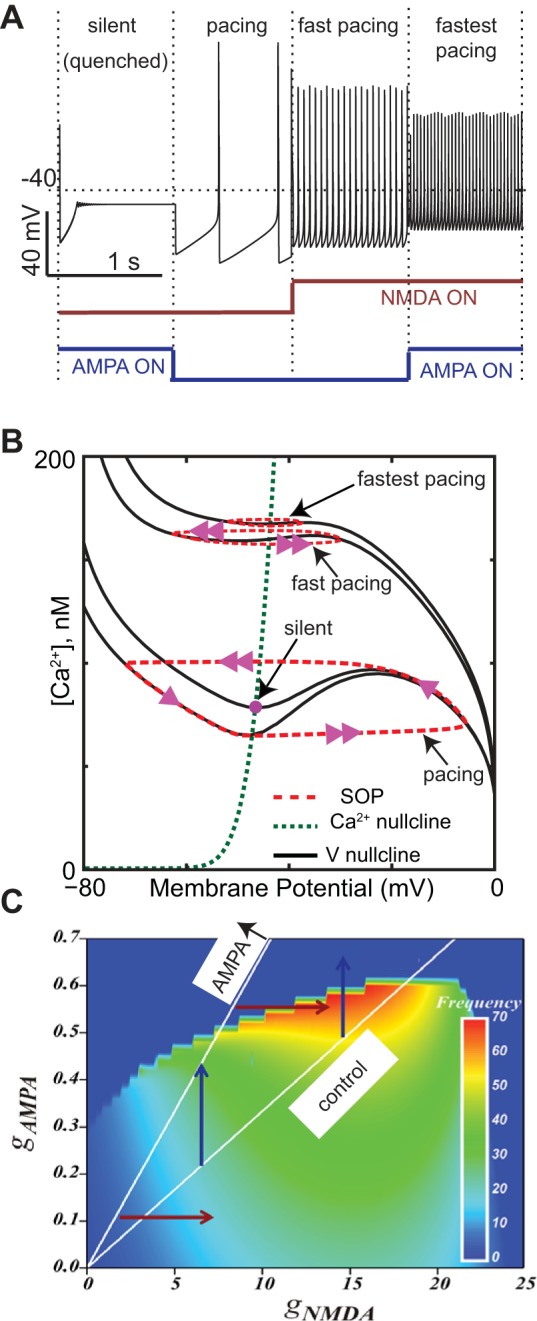
Effect of activating AMPA receptors depends on concurrent activation of NMDA receptors. A: effect of activating AMPA receptors alone (silence), control pacing, activating NMDA receptors alone, and AMPA and NMDA together. g_AMPA = 0.4 mS/cm² and g_NMDA = 18 mS/cm². B: 4 membrane potential nullclines are indicated for the silent, pacing, fast pacing, and fastest pacing cases. The middle branch of the potential nullcline (black lines) is destabilizing. The silent regime results when the Ca²⁺ nullcline (green dashes) intersects the stable left branch although this is difficult to discern by eye. The red dashed curves indicate the trajectory of the underlying SOP, and the arrowheads give the direction. C: heat map for firing rates. White lines indicate control AMPA/NMDA ratio; the AMPA ↑ line indicates a doubling of this ratio. [A and B adapted from Ha and Kuznetsov (2013) and C is patterned after Zakharov et al. (2016).] All parameters are the same as in Ha and Kuznetsov (2013) except g_ERG = 2.

Activation of a tonic AMPA conductance (arrow in Fig. 5B indicating the silent case) decreases the destabilizing middle branch of the nullcline and, more importantly, moves the intersection point rightward so that it lands on the stable left branch, which allows a stable resting potential. Biophysically speaking, a tonic excitatory AMPA input allows the Ca²⁺ and Ca²⁺-dependent K currents to balance each other instead of maintaining their alternating predominance within a subthreshold oscillation that, in this model, drives pacing. Because DA neurons spike at high-frequency firing during bursts, there must be a mechanism to circumvent the frequency limitation induced by tonic AMPA excitation, and, in this model, the mechanism is based on NMDA receptor activation. Although the nonlinear voltage dependence of this current in general enhances the unstable middle branch of the voltage nullcline, the presence of this current requires more SK current to balance the net current at each membrane potential; hence higher levels of the SK current are evoked at each membrane potential. The suppression of the middle branch of the nullcline by the SK current dominates the enhancement by NMDA receptor activation. The flattening of the nullcline results in a smaller amplitude oscillation in Ca²⁺ in the presence of NMDA than in its absence (see faster pacing compared with pacing in Fig. 5B); the smaller amplitude oscillation proceeds more rapidly, resulting in a faster spiking frequency (see Fig. 5A). In the presence of NMDA, AMPA (fastest pacing in Fig. 5, A and B) has two effects: it shifts the intersection to the right (but not so far as to move the intersection to the stable rightmost branch, thereby killing the oscillation), and it suppresses the middle branch of the nullcline enough to decrease the amplitude of the slow underlying oscillation and thereby increase the frequency.

The ability of AMPA receptor activation to either silence firing or increase its frequency depending on the level of NMDA receptor activation may have implications for the effects of the drug-induced changes in the AMPA/NMDA ratio of peak synaptic conductances (Lüscher 2013; Saal et al. 2003). Drug exposure results in increased bursting in response to drug cues but paradoxically also in a decrease in the population activity of the DA neurons (Shen et al. 2007) because a subset of DA neurons stops firing repetitively after the drug exposure and passes to an inactive state (Shen et al. 2007). The dual effects of AMPA receptor activation may help reconcile drug-induced block of repetitive firing with the increased responses to drug cues. Consider that AMPA and NMDA receptors are usually coactivated by a common glutamatergic drive at a fixed ratio (white lines labeled control and doubled AMPA/NMDA ratio labeled AMPA ↑ in Fig. 5C). As the drugs of abuse increase the AMPA/NMDA ratio, there is a transition between the white lines. Highly active neurons transition to silence as the AMPA/NMDA ratio is increased (rightmost blue vertical arrow Fig. 5C), but slower ones increase their frequency (leftmost blue vertical arrow Fig. 5C). It is important to note that neurons in the postulated silent state are not in a state of depolarization block because further depolarization can indeed evoke spikes. Nonetheless, the quenched or silenced state is indistinguishable from depolarization block using the methods of Shen et al. (2007) because hyperpolarization can restore inactive neurons to an active spiking state, just as it can rescue neurons in a true state of depolarization block. At the same time, the model suggests increased responsivity to drug cues if we assume that they are associated with NMDA receptor activation, which may be connected with learning-associated NMDA receptor plasticity (Mameli et al. 2009). In particular, in this model, an increase in the NMDA input, not only increases the frequency of the active neurons (lowermost red horizontal arrow in Fig. 5C), but also strongly reactivates the neurons from the inactive pool (Fig. 5C uppermost red horizontal arrow). Thus the relative population firing increase is greater than in the case where the AMPA/NMDA ratio has not been altered (the “drug-naïve” state). There is experimental evidence supporting a time window in which the NMDA inputs into VTA DA neurons are potentiated because of addictive drugs (e.g., even in a single acute cocaine exposure) (Mameli et al. 2009). In summary, one might surmise that, after the exposure to an addictive drug, a neuroadaptive change in the ratio between the AMPA and the NMDA-mediated inputs might silence the most highly active neurons but at the same time boost their response to the drug-related cues, provided that such cues are signaled by selectively recruiting NMDA-mediated synaptic inputs.

Complementary models (Canavier 1999; Canavier and Landry 2006; Drion et al. 2011; Komendantov et al. 2004; Oster et al. 2015; Yu and Canavier 2015) focus on the plateau potential hypothesis of bursting. One major insight from modeling is that certain voltage-dependent currents expressed in the DA neurons are well suited to induce bursts by supporting sustained depolarized plateaus that can trigger fast spiking on at least part of the plateau. To support a plateau, a current should be inward and activate with increasing depolarization and inactivate slowly or not at all. In dopamine neurons, the NMDA synaptic receptor current meets this description and likely plays an important role in burst firing (Overton and Clark 1992; Tong et al. 1996; Zweifel et al. 2009). A role has also been postulated for another such current, the intrinsic L-type voltage-dependent Ca²⁺ current (Johnson and Wu 2004; Ping and Shepard 1996). However, in vivo, inhibition likely plays a prominent role in controlling dopamine neuron firing patterns as well (Paladini and Roeper 2014). The GABAergic RMTg, or tail of the VTA, is an important contributor to the excitation/inhibition balance in midbrain DA neurons. Tonic activation of the RMTg neurons causes inhibition and decreased firing in the VTA DA neurons (Barrot et al. 2012; Lecca et al. 2012), and drugs of addiction appear to alter this balance. For example, chronic nicotine administration causes a decrease in the activity of GABA cells innervating the VTA DA neurons (especially in response to nicotine) in vitro and a depressed DA cell activity (Nashmi et al. 2007). At the same time, morphine-mediated increase in VTA DA neuron firing rate caused by disinhibition of the RMTg did not occur in the presence of blockers of glutamatergic transmission (Barrot 2015). This suggests that the excitatory/inhibitory balance in DA neurons is critical to understand the effects of drugs of abuse.

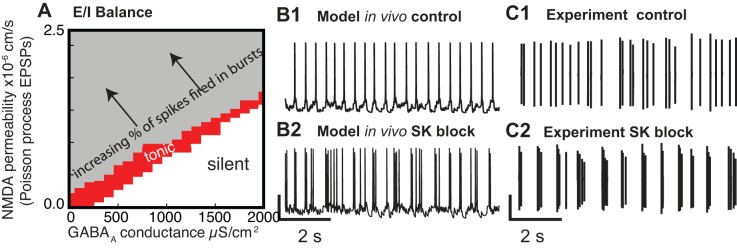
A balanced state between the excitation and inhibition impinging on a given DA neuron can enable tonic single-spike firing, whereas an imbalance can result in a phasic signal in the form of one or more bursts (Fig. 6A). The balanced state was first predicted by modeling (Canavier and Landry 2006; Komendantov et al. 2004) then confirmed by experiments (Lobb et al. 2010, 2011). The model that was used to generate Fig. 6 is a multicompartmental model with multiple slow variables. Moreover, it is subjected to a barrage of random inputs on the dendrites only, so there is no steady-state solution. In the presence of random synaptic input in the parameter region corresponding to the gray area in Fig. 6A, the phase portrait is constantly changing between one corresponding to single-spike firing and one corresponding to bursting, resulting in a variable fraction of the total spikes fired in bursts (arrow points in the direction of an increased fraction of spikes fired in bursts). The complexity and nonstationarity of this model are not amenable to a simplified phase-plane analysis. In a regime with few spikes fired in bursts, the bursts result from transient random synchronization of the inputs. In real neurons, the transient synchrony might be stimulus locked rather than random. In Fig. 6A, the AMPA/NMDA ratio was held constant, but drugs of abuse are known to increase the AMPA/NMDA ratio by inducing LTP at excitatory synapses selectively on DA neurons that project to the NAc (Lammel et al. 2011; Saal et al. 2003). Doubling the AMPA/NMDA ratio in the model, which is slightly greater than the reported effects of drugs of abuse, produced only a modest increase in the simulated proportion of spikes fired in bursts (Canavier and Landry 2006). Perhaps this increase is sufficient to allow drug cues that previously did not elicit a burst to do so after the potentiation, possibly accounting for some of the effects of drug exposure and the path to addiction.

Fig. 6.

Excitatory-inhibitory (E/I) balance in dopamine neurons and effect of SK block. A: random excitatory inputs in the presence of constant levels of inhibition show that the tonic, single-spike firing observed in vitro, corresponding to P_NMDA = 0 and g_GABAA = 0, can be preserved if synaptic inputs are balanced. [Adapted from Canavier and Landry (2006).] B1: balanced regime in a model. B2: SK channel block promotes bursting by shrinking the tonic region in A. C1: extracellular recordings of single-spike firing in vivo. C2: SK channel block promotes bursting in vivo extracellular recordings. [B and C adapted from Drion et al. (2011).]

In addition to synaptic influences, modulation of intrinsic conductances can also affect the firing pattern. The Ca²⁺-activated small conductance SK K⁺ current is known to oppose the tendency to burst in DA neurons both in vivo (Waroux et al. 2005) and in vitro (Ping and Shepard 1996). Strikingly, the complex model in Fig. 6 is able to capture the dramatic effect of SK channel block on the firing pattern. At almost all parameters corresponding to single-spike, tonic firing (red region in Fig. 6A), setting the SK conductance to 0 converts single-spike firing (Fig. 6B1) to almost all spikes fired in bursts (Fig. 6B2), matching experimental data (Fig. 6C). The AHP associated with the SK current tends to limit depolarizing waves to a single action potential per depolarization (Canavier and Landry 2006). Because repeated ethanol exposure reduces the SK current in rat VTA neurons and also increases the burst firing evoked by the application of NMDA (Hopf et al. 2007), downregulation of the SK current may play a role in the development of alcohol addiction. In the model of Canavier and Landry (2006), two slow variables (Na⁺ concentration and Ca²⁺ concentration) control bursting, and two currents drive the unstable middle branch of the nullcline (t he NMDA receptor current and the L-type Ca²⁺ current). Therefore, we will use a simpler model to illustrate how single-spike firing can be converted to bursting.

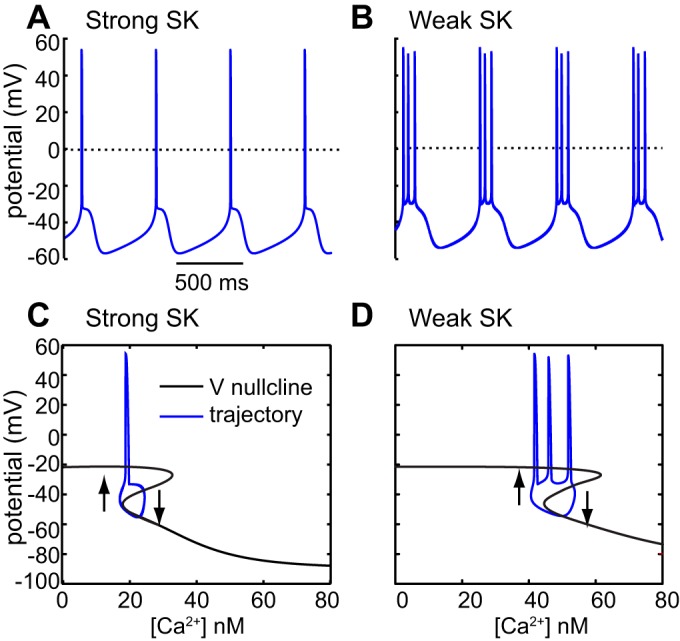
The effect of SK channel block can be explained using a simplified, single-compartment model (Oster et al. 2015) of bursting, an intrinsic model with a single slow variable (Ca²⁺ concentration) that ignores synaptic afferents for simplicity. In vitro, blocking the SK channel can sometimes convert pacemaking to burst firing (Ping and Shepard 1996), and blocking the L-type channel blocks this type of bursting (Johnson and Wu 2004). The nullcline analysis from Fig. 1 can be extended very easily to show that the duration of the depolarized plateau becomes longer as the unstable middle branch of the nullcline becomes longer. In this simple, single-compartment model, reducing the SK channel conductance transforms pacing (Fig. 7A) to bursting (Fig. 7B). In this model, as in the model of Fig. 1, the unstable middle branch results from the regenerative activation of a persistent L-type Ca²⁺ channel. Ca²⁺ influx recruits an outward current, the SK channel, which dominates at Ca²⁺ levels above 30 nM in the model, and truncates the unstable middle branch of the V nullcline, allowing only a single spike per depolarization (Fig. 7C). Reducing this conductance extends the unstable middle branch, prolonging the depolarization so that several spikes can be emitted between hyperpolarizations, resulting in bursting (Fig. 7D). Other currents affect the middle branch in a predictable way. Linear, ohmic currents such as the current mediated by GABA A receptors, flatten the V nullcline and reduce the extent of the unstable middle branch, which favors single spiking over bursting (Canavier 1999). On the other hand, the NMDA receptor current accentuates the middle branch and promotes bursting. The phase-plane analysis is only strictly accurate in the absence of spiking, as in Amini et al. (1999), but the principle illustrated by this separation of time scale analysis is very general, regardless of the exact identity of the slow variable.

Depolarization Block and Schizophrenia

DA neurons are very susceptible to depolarization block, a depolarized state in which the firing of action potentials ceases. Most DA neurons go into depolarization block (Fig. 7A) before they can achieve sustained firing rates above 10 Hz (Richards et al. 1997), including the conventional slowly firing populations, namely the SNc neurons projecting to the dorsal striatum and the VTA neurons projecting to the lateral shell of the NAc. However, an atypical population of DA neurons in the VTA has been recently identified (Lammel et al. 2008) that projects to other mesolimbic sites or to cortex and can sustain higher firing rates (up to 20 Hz). Depolarization block in DA neurons is important for two reasons. First, the very definition of a burst in DA neurons was an operational definition (Grace and Bunney 1984), which identified a burst as beginning at the point at which the maximum frequency of the single-spike firing of conventional DA neurons was exceeded. Therefore, many bursts likely require a mechanism to circumvent the limitation imposed by depolarization block to achieve the high frequencies that are often observed (Hyland et al. 2002).

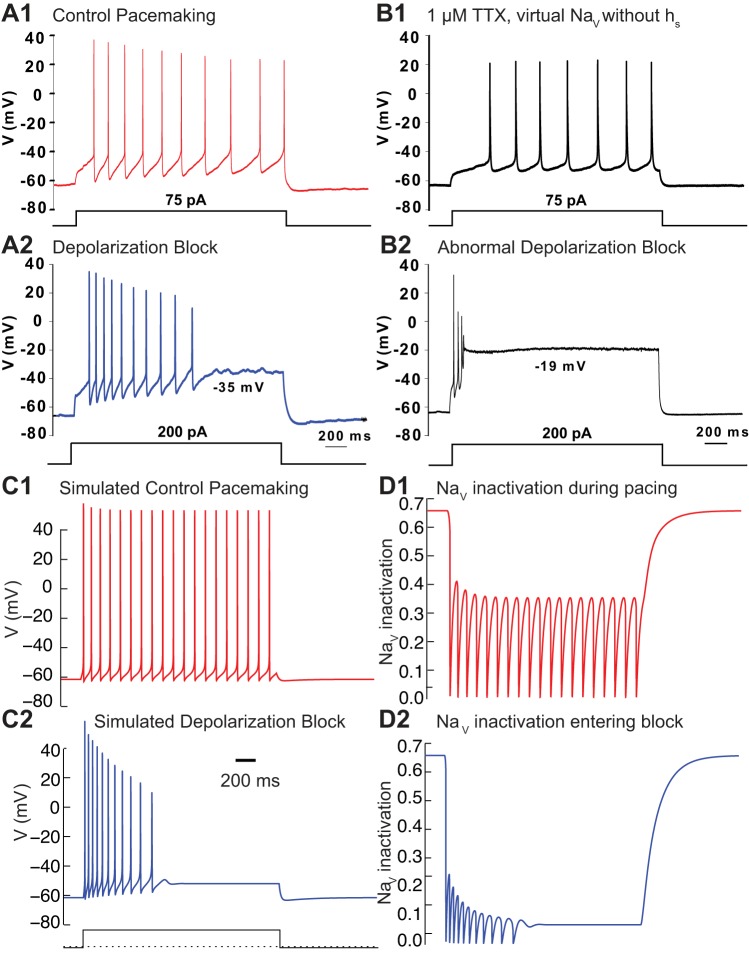
Another important reason to understand depolarization block is its postulated role in the effectiveness of drugs that are used to treat the positive symptoms of schizophrenia, such as psychosis. A common assay for the therapeutic efficacy of antipsychotic drugs is their ability to induce selective depolarization block in the VTA; on the other hand, the ability to produce extrapyramidal motor side effects is correlated with their ability to induce depolarization block in the SNc (Chiodo and Bunney 1983; White and Wang 1983). In vivo recordings have demonstrated that DA neurons in rats chronically treated with the antipsychotic haloperidol can enter depolarization block at the end of a burst (Grace and Bunney 1986). Antipsychotics have been widely theorized to exert their effects by reducing DA neurotransmission by inducing depolarization block in midbrain DA neurons (Grace et al. 1997; Lodge and Grace 2011; Valenti et al. 2011). Depolarization block in midbrain DA neurons occurs at relatively hyperpolarized potentials, ∼−40 mV (Blythe et al. 2009; Richards et al. 1997; Tucker et al. 2012). Moreover, the onset of depolarization block is abrupt and usually preceded by a full-amplitude action potential (Fig. 7A2).

Qian et al. (2014) used a minimal, modified Hodgkin Huxley (Hodgkin and Huxley 1952) model to show that failure to remove sufficient Na_V channel inactivation is the most likely mechanism underlying entry into depolarization block. This very simple model was used to mimic only the transition from pacemaking (Fig. 8, A1 and C1, for data and model, respectively) to depolarization block (Fig. 8, A2 and C2) as the magnitude of the applied current step is increased. The fraction of Na_V conductance that is not inactivated recovers sufficiently between action potentials to support pacing at low levels of applied depolarizing current (Fig. 8D1) but not at more depolarized levels (Fig. 8D2). The inactivation curve for the Na_V channel must be very steep in order for cells to enter depolarization block at −35 to −40 mV. However, the measured slope of fast inactivation of the Na_V channel is not sufficiently steep (see Table 1) to produce abrupt entry into depolarization block at −40 to −35 mV; moreover, a slow component of Na_V channel activation has been observed in SNc DA neurons (Ding et al. 2011; Seutin and Engel 2010). A similar slow component of inactivation in hippocampal pyramidal neurons (Colbert et al. 1997) has been successfully modeled (Fernandez and White 2010; Migliore et al. 1999) with a steep dependence on membrane potential. Therefore, Qian et al. (2014) added a second, slow component of Na_V channel inactivation with a steep dependence on membrane potential to the model. This manipulation adds a term to the Hodgkin-Huxley equation for the Na_V current, such that the equation for the Na_V current becomes I_Na = g_Na m³ h h_s (V − E_Na), where m is the activation, h is the usual inactivation term, h_s is the slow inactivation term, and E_Na is the reversal potential of Na⁺. Hodgkin-Huxley-type models are a simplification of more accurate Markov models of Na_V channel gating (French et al. 2016; Milescu et al. 2010) but are more amenable to analysis. In Fig. 8D, the product h h_s gives the sodium channel availability. To demonstrate the need for the slow component with a steep dependence on membrane potential, the slow component was selectively removed from the Na_V channel using the Dynamic Clamp, a technique in which a computer is used to inject a virtual conductance in a biological neuron in real time. In the presence of the Na_V channel blocker TTX, a version of the Na_V conductance from the model in Fig. 8C that set h_s to 1 was injected into the neuron. Pacing was relatively undisturbed (Fig. 8B1), but depolarization block (Fig. 7B2) occurred abnormally at an excessively depolarized potential in the middle of an action potential.

Fig. 8.

Depolarization block in response to a current step. A: small current step from a hyperpolarized holding potential leads to pacing (A1), but a large step leads to block (A2). B: Na_V current was replaced with a virtual Na_V current from the model in C but without slow inactivation. Normal pacing (B1) but abnormal depolarization block results (B2). [A and B adapted from Qian et al. (2014).] C: simulations using the model of Qian et al. (2014) with a holding current of −0.25 μA/cm² and steps to 0 in C1 and 0.375 in C2. The leak and K⁺ conductances were increased by a factor of 5 and the Na_V conductance by 4.5 to produce abrupt failure of APs. Moreover, the n activation variable was unyoked from the h inactivation variable. D: available, noninactivated fraction of Na_V channels recovers sufficiently between APs during pacing (D1) but not upon entry to block (D2).

Table 1.

Parameters of the fast sodium current

Source	Seutin and Engel (2010) (data)	Ding et al. (2011) (data)	Yu and Canavier (2015) (model)	Qian et al. (2014) (model)	Oster (2015) (model)
mHALF, mV	−9.6*	−26.7	−30	−30	−7
mSLOPE, mV	12	7.3	13	9.7	9.2†
hHALF, mV	−48.9*	−61.3	−54	−54	−38
hSLOPE, mV	−10.5	−10.1	−12.8	−10.7	−4†
hsHALF, mV			−54.8	−54.8
hsSLOPE, mV			−1.57	−1.57

The fit in Seutin and Engel (2010) did not consider simultaneous fitting of the parameters of activation and activation to the voltage clamp data, but they fit them separately assuming no inactivation occurred before the peak.

^*Goldman-Hodkin-Katz formalism was used in the fit rather than an ohmic dependence on membrane potential. The sodium current description in Qian et al. (2014) was taken from the fit given in Tucker et al. (2012) to the data from Seutin and Engel (2010), considering simultaneous activation and inactivation and ohmic dependence of driving force on membrane potential as in the original Hodgkin and Huxley (1952) formalism. †Approximate value because a Boltzman function description was not used.

The model in Fig. 8C used a slightly revised parameter set, which captures the abrupt entry into depolarization block (Fig. 8C2) better than the original model of Qian et al. (2014) for two reasons. First, for simplicity, in the original model, the n activation variable for the K⁺ conductance that helps repolarize the action potential was yoked to the h inactivation variable (Rinzel 1985). However, the analysis of depolarization block by Oster et al. (2015), which is explained in detail in Fig. 9, requires these time scales to be separated; therefore, they were unyoked for Fig. 8, C and D. Second, the rate of change membrane potential must be very fast compared with h, so the conductances were scaled up, which is mathematically equivalent to decreasing the capacitance and speeds the time course of membrane potential independently of the other variables.

Fig. 9.

The Oster et al. (2015) model replicates SK block-induced bursting (A) and explains entry into depolarization block using separation of time scales (B). The steepness of the right stable branch of the nullcline is determined by the reversal potential of Na⁺ at 55 mV. (Same as published parameters for Fig. 4, except: i₁ = 0.6, h_a = 0.72, h_a2 = −45, h_a3 = 14, h_b1 = 1.44, h_b2 = −10, p₁ = 0.9, p₂ = −7, p₃ = 19, g_KDR = 17, g_Na = 150, gpers_Na = 0, g_L = 0.3, e_L = −59, K₁ = 370, and g_CAB = 0.02 in the same units as reported previously.) Also the equation for L-type channel closing should have been multiplied by a factor of 0.05.

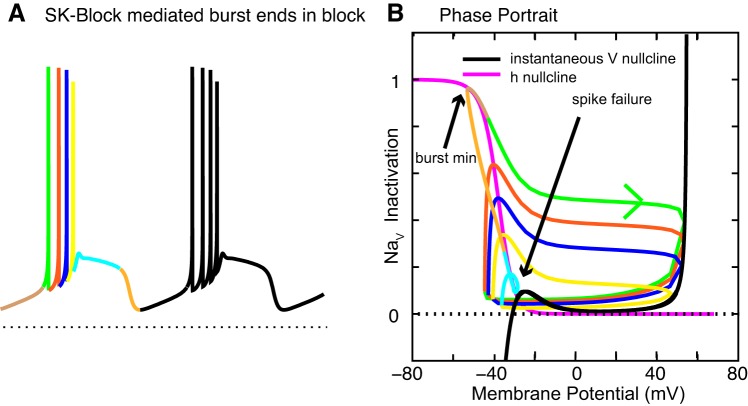
A separation of time scale analysis can be used to explain the mechanism of entry into depolarization block. Recall that bursts that terminated in depolarization block were observed DA neurons from animals chronically exposed to the antipsychotic drug haloperidol (Grace and Bunney 1986). Figure 7 illustrates bursting that does not terminate in depolarization block but with a few parameter changes; the same model (Oster et al. 2015) bursting does terminate in depolarization block (Fig. 9A). The new twist is that an intermediate time scale, corresponding to that of the h inactivation variable, has been inserted between the fast time scale of membrane potential and the slow time scale of Ca²⁺ in Figs. 1 and 6. For simplicity, Oster et al. (2015) used a single inactivation variable (Table 1) that can be regarded as the composite inactivation variable plotted in Fig. 8D.

The phase-portrait analysis in Fig. 9B was generated using the intermediate time scale variable h as the slow variable. The h nullcline (magenta) is simply the steady-state fraction of noninactivated Na_V channel conductance as a function of membrane potential, the standard inactivation curve. To isolate the very fastest time scale that is responsible for the upstroke of the action potential, the instantaneous (early) V nullcline (black curve) was utilized rather than the steady-state (late) nullcline. The assumptions that go into the generation of the instantaneous V nullcline are similar to those that underlie the concept of the instantaneous (early) I-V curve (Baxter et al. 2004; Hodgkin and Huxley 1952). Namely, the activation of the delayed rectifier, which contributes to action potential repolarization in the model at a later time point than does inactivation of the sodium channel, is ignored by calculating the V nullcline with the conductance for this channel set to 0 (g_KDR = 0). In addition, the slow variable Ca²⁺ is set to its average value during the plateau (60 nM). Under these circumstances, the peaks of the spikes occur when the trajectory hits the instantaneous voltage nullcline (Fig. 8B). Each portion of the cycle is color coded for the first burst in Fig. 9A, and the same colors are used in the trajectory of bursting in the V/h plane in Fig. 9B. Thus it is clear that the fraction of noninactivated Na_V channels (h in Fig. 9B) is maximal at the arrow indicating the burst minimum and recovers less after each successive spike (green, red, blue, and yellow loops), with the green arrow indicating the generally clockwise direction of motion. The fraction is minimal at the arrow indicating spike failure (cyan loop). The important things to note are that there is again an unstable middle branch in the V nullcline and that spiking is terminated when the trajectory touches the stable left branch (cyan loop). Other important factors are that the evolution of the slow variable pushes the trajectory (orange) to the h nullcline (magenta) during burst repolarization, and, after crossing this boundary, h begins to increase (brown), setting the stage for the next burst. The final important aspect is that during the spike upstroke the trajectories are essentially horizontal, meaning that comparatively little inactivation occurs during the upstroke; otherwise the spike amplitude would be unconstrained because intersections with the unstable branch would also be possible. In that case, all amplitudes, no matter how small, would be allowed. This elegant analysis of the depolarization block that terminates a burst also applies to burst termination during a step to a constant depolarizing current value (Fig. 8, A and C), as evidenced by the improved parameter set utilized in Fig. 8, C and D. The analysis explains the increases and decreases in frequency that precede depolarization block under the two different circumstances illustrated in Figs. 8 and 9. During bursting, the loops in the phase space are smaller and thus faster for successive spikes, matching the tendency in similar bursts evoked experimentally by application of apamin to terminate with decreasing ISIs (Ping and Shepard 1996). However, with control values for the SK conductance, the model of Oster et al. (2015) can produce a burst with increasing ISI similar to that shown in Fig. 8C2 in response to a depolarizing current step, matching the data in Fig. 8A2 and early in vivo data from the Grace laboratory (Grace and Bunney 1984). The difference is that, for a rapid, step-like depolarization, spike adaptation occurs because successive ISIs have a decreasing amount of available Na_V channels, but a ramp-like depolarization such as that observed in Fig. 9A offsets the decreased availability of Na_V with a simple increase in depolarizing current between ISIs. A more recent study (Hyland et al. 2002) in awake rats found no systematic pattern in the ISI during a burst, so perhaps both types of bursts occur naturally.

The analysis presented above is relevant to schizophrenia for the following reasons. Because Na_V channel activation is the limiting factor for entry into depolarization block, any additional AHP after a spike can delay entry into depolarization block by removing Na_V channel inactivation. Indeed, it has been shown that the ERG K⁺ current delays entry into depolarization block via this mechanism (Ji et al. 2012). Moreover, the ERG current adds in repolarizing bursts that terminate in depolarization block. Antipsychotics may combat psychosis-inducing depolarization block in midbrain DA neurons (Grace et al. 1997; Lodge and Grace 2011; Valenti et al. 2011), and all known antipsychotics block the ERG channel as a side effect (Shepard et al. 2007). Therefore, the downregulation of this current by antipsychotic drugs may contribute to their efficacy. Moreover, it is important to tease out any differences in entry into depolarization block to develop more precisely targeted therapies with fewer side effects. There is some evidence that chronic exposure to nicotine or ethanol may promote depolarization block in the VTA (Shen et al. 2007), suggesting that depolarization block may be important for understanding the long-term adaptations that lead to addiction.

Summary and Conclusions

This review summarizes recent insights gained using two complementary techniques: muticompartmental models that capture spatial aspects of the morphology of a single neuron and reduced single-compartment models that capture the essence of a single phenomenon. Multicompartmental models allow testing of hypotheses regarding the effects of heterogeneous conductance densities and different rates of Ca²⁺ accumulation attributable to diameter, for example. The separation of time scales and phase-plane analysis has frequently been used to study pacemaking (Amini et al. 1999; Kuznetsov et al. 2006; Kuznetsova et al. 2010; Wilson and Callaway 2000), bursting (Canavier 1999; Canavier et al. 2007; Li et al. 1996; Oster and Gutkin 2011; Yu and Canavier 2015), and entry into depolarization block in DA neurons.

A major contribution of the multicompartmental studies reviewed here was to examine the metabolic load as a function of branch order in the dendrites (Fig. 3) and axon (Fig. 4), respectively. These studies used different but complementary techniques to characterize the metabolic load. The dendritic study focused on the standing Ca²⁺ load, which is an indicator of the basal level of Ca²⁺ ATPase activity. The axonal study focused on the total Na⁺ and Ca²⁺ removed, as well as action potential efficiency. In both the axonal and dendritic cases, the conclusion was that the distal ends with higher branch order are predicted to be more vulnerable. The larger branch order of SNc vs. VTA axons is predicted to be a source of greater vulnerability to neurodegeneration. Moreover, the dendritic study showed that the increased expression of the hyperpolarization-activated cationic current (I_h) in a particularly vulnerable subpopulation in the SNc, the calbindin-negative neurons, could potentially contribute to their increased vulnerability. A single inhomogeneity, a greater functional contribution of the A-type K⁺ current in low-order branches, was responsible for the predicted greater vulnerability of higher-order dendritic branches. Other inhomogeneities have been suggested and may need to be considered. For example, in dissociated SNc neurons that retained a substantial portion of their dendritic trees, TTX applied proximally slowed the spontaneous frequency more than TTX applied distally (Jang et al. 2014). However, it is unclear whether this effect was mediated by the axon initial segment, which is usually located on a proximal dendrite (Gentet and Williams 2007; Hausser et al. 1995). A recent study also suggested that the density of I_h is higher in the axon-bearing dendrite (Engel and Seutin 2015). Future models may need to represent the dynamics of Na⁺ and Ca²⁺ removal and exchange in a more detailed and biophysical manner (Francis et al. 2013). In addition to the metabolic studies, a parametric examination of a multicompartmental model showed that heterogeneity within and between subpopulations in the relative contributions of Ca²⁺ and Na⁺ currents to pacemaking can account for different responses (Fig. 2) to pharmaceutical block of these currents in DA neurons and may also contribute to selective vulnerability to neurodegeneration and cell death in PD.

The insights gained from separation of time scale analysis are quite general and often may apply regardless of the precise identity of the postulated slow variable. The analyses presented herein suggest that, although there are multiple time scales operating within DA neural dynamics, by focusing on two time scales, we can often uncover a key principle underlying DA neural dynamics. For example, although the depolarizing drive for the SOP and pacemaking is the same (Fig. 1), the mechanism that terminates the oscillation is different, which can decouple the frequency of the two oscillations. An unstable region in the V nullcline associated with a so-called negative slope conductance is essential for both pacemaking and burst firing. Pacemaking can be converted to burst firing via any manipulation that broadens this region (Fig. 7). Similarly, burst firing is opposed by manipulations that reduce or obscure this region. A complication is that simple hyperpolarization or depolarization can move the operating point from the middle branch that supports bursting to the left stable silent branch or the right branch that leads to depolarization block. Therefore, a single manipulation like increasing the ohmic AMPA tone can have several effects: to move the bias point toward bursting, depolarization block, or a quiescent potential (as in Fig. 5), while at the same time dampening to some degree the overall tendency to burst. A change in the AMPA/NMDA ratio (Fig. 5) can turn off endogenous pacemaking by stabilizing a rest potential. The mechanism leading to depolarization block is not clear from Fig. 7 because a different time scale, in which Na_V channel inactivation is the intermediate slow process, must be considered (Fig. 9). The excitatory/inhibitory balance (Fig. 6A) is very important in regulating burst firing because NMDA tone accentuates the unstable middle branch, whereas GABA attenuates it. The SK channel inherits its voltage dependence from the voltage dependence of Ca²⁺ influx; it is an outward current activated by depolarization in the exact range that can truncate the unstable middle branch (Fig. 7). Therefore, blocking this current enhances bursting (Fig. 6, B and C).

An important implication of the studies on depolarization block (Figs. 8 and 9) is that currents that contribute to the AHP remove Na_V channel inactivation and oppose entry into depolarization block, which in the case of the ERG current may be clinically relevant for schizophrenia. Because the conventional Na_V inactivation variable in DA neurons is not particularly steep, a slower component likely contributes to depolarization block. The issue of how the frequency during bursts in vivo is augmented beyond the in vitro frequency limitations imposed by depolarization block (Fig. 8) is an open question. NMDA receptors have the appropriate voltage and time dependence to contribute to spiking; thus activation of NMDA receptors may increase the frequency potentially by compensating for inactivated Na_V channels (Qian et al. 2014) or, alternatively, by the mechanism suggested in Fig. 5B. The downregulation of the SK conductance has multiple effects: attenuation of the unstable middle branch of the nullcline, reduced AHP, and potentially a general reduction in hyperpolarizing currents evoked in response to a depolarizing current step. The latter effect may be responsible for the increase in the maximum frequency attainable in response to a depolarizing current step when this conductance is blocked (Shepard and Bunney 1991).

In summary, both multicompartmental modeling and the analysis of reduced models are needed to continue to advance our knowledge of the dynamics of the different subpopulations of midbrain DA neurons and to translate this knowledge to new and targeted therapies for diseases to which dopaminergic dysfunction contributes.

GRANTS

This work was supported by National Institutes of Health (NIH) National Institute of Neurological Disorders and Stroke (NINDS) Grant R01-NS-061097 to C. C. Canavier, Russian Academic Excellence Project “5-100” and L'Agence Nationale de la Recherche NEUCOMP, ANR-10-LABX-0087 IEC, and ANR-10-IDEX-0001-02 PSL to B. S. Gutkin, NIH National Institute on Alcohol Abuse and Alcoholism (NIAAA) Grant R01-AA-022821 to A. S. Kuznetsov, and Eastern Washington University Faculty Grant for Research and Creative Works to A. M. Oster. R. C. Evans was supported by NIH NINDS Intramural Research Program Grant NS-003135 to Zayd M. Khaliq.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

C.C.C., R.C.E., A.M.O., and E.K.P. performed experiments; C.C.C., R.C.E., A.M.O., and E.K.P. analyzed data; C.C.C., R.C.E., A.M.O., and E.K.P. interpreted results of experiments; C.C.C., R.C.E., A.M.O., E.K.P., A.S.K., and B.S.G. prepared figures; C.C.C., R.C.E., and A.M.O. drafted manuscript; C.C.C., R.C.E., A.M.O., E.K.P., G.D., A.S.K., and B.S.G. edited and revised manuscript; C.C.C., R.C.E., A.M.O., E.K.P., G.D., A.S.K., and B.S.G. approved final version of manuscript.