Biochemical systems analysis of signaling pathways to understand fungal apthogenicity

Abstract

Over the past decade, researchers have recognized the need to study biological systems as integrated systems. While the reductionist approaches of the past century have made remarkable advances of our understanding of life, the next phase of understanding comes from systems-level investigations. Additionally, biology has become a data-intensive field of research. The introduction of high throughput sequencing, microarrays, high throughput proteomics, metabolomics, and now lipidomics are producing significantly more data than can be interpreted using existing methods. The field of systems biology brings together methods from computer science, modeling, statistics, engineering, and biology to explore the volumes of data now being produced and to develop mathematical representations of metabolic, signaling, and gene regulatory systems. Advances in these methods are allowing biologists to develop new insights into the complexities of life, to predict cellular responses and treatment outcomes, and to effectively plan experiments that extend our understanding. In this chapter, we are providing the basic steps of developing and analyzing a small S-system model of a biochemical pathway related to sphingolipid metabolism in the regulation of virulence of the human fungal microbial pathogen Cryptococcus neoformans (Cn).

1. Introduction

In recent years, most biologists have recognized that reductionism alone cannot explain every cellular biological process and now admit that integralism or pluralism must accompany reductionism to fully explain biological phenomena. One key issue in the reductionism process is the use of appropriate methodologies in the study of the phenomenon of interest. For instance, methodologies that study molecules in the time and space of the living cell should be preferable to and complement those that study the molecules in vitro. Outside of this critical cellular context, the richness of integrated cell behavior may be lost. Systems biology can dramatically improve the selection of such experimental strategies.

Since mathematical models can be used to theoretically predict the patterns of enzymatic activity that could lead to an observed steady state phenotype, it is possible, in principle, to determine which enzyme would have the greatest effect in achieving that phenotype. Therefore, systems biology can aid in selecting which enzyme would have to be altered and in what manner to obtain the phenotype of interest. In other words, mathematical models can be used as valuable tools for exhaustive prescreening studies for all kinds of scenarios and for creating novel hypotheses that are then to be tested in the laboratory. Computational modeling can help in selecting the experiments most likely to disprove the hypothesis and further improve our conceptual model of the system under study.

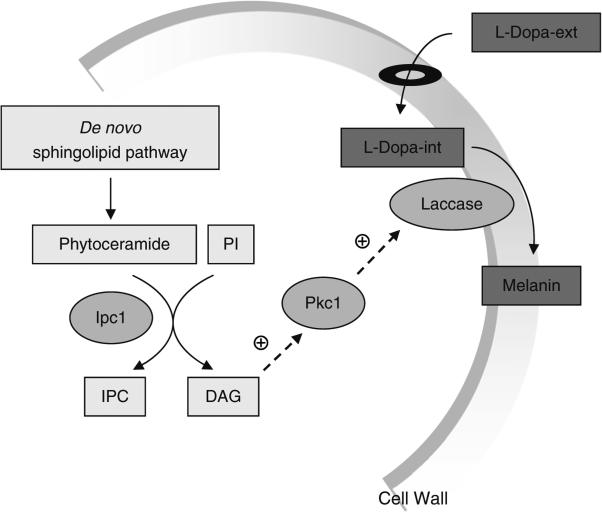
Cellular systems frequently employ cascade mechanisms to facilitate the transduction of external signals and activation of transcription factors that regulate the expression of specific genes in response to specific signals. Cascade pathways and signaling in Cryptococcus neoformans (Cn) has been extensively studied (1–17). In our studies, we found that an enzyme in the fungal sphingolipid pathway, inositol phosphoryl ceramide synthase 1 (Ipc1), controls the signaling cascade leading to the production of melanin (18). In particular, Ipc1 produces inositol-containing sphingolipids (e.g., inositol phosphoryl ceramide or IPC) and diacylglycerol (DAG) (19), which, in Cn, activates protein kinase C1 (Pkc1) (20). Although previous studies showed that DAG does not activate Pkc1 of other fungal species, such as Candida albicans (Ca) (21) and Saccharomyces cerevisiae (Sc) (22), we found that this was not the case for the Cn Pkc1. In Cn, Pkc1 activation occurs through the C1 domain of Pkc1 since deletion of this domain reduces its activation by DAG (20). The Ipc1–DAG–Pkc1 pathway appears to drive laccase to its proper location (cell wall) so that it can transform l-Dopamine into melanin in the outer leaflet of the cell wall (Fig. 1).

Fig. 1. Signaling pathway regulating melanogenesis in Cryptococcus neoformans (Cn) by sphingolipids.

Diacylglycerol (DAG) produced by Ipc1 activates Pkc1 through the C1 domain of Pkc1. Activation of Pkc1 maintains the structure of the cell wall, which enables laccase to produce melanin granules deposited in the cell wall. Melanin production is required for pathogenesis of Cn. PI phosphatidylinositol, Ipc1 inositol phosphoryl ceramide synthase 1, Pkc1 protein kinase C 1, l-DOPA-ext l-Dopamine extracellular, l-DOPA-int l-Dopamine intracellular.

In this chapter, we demonstrate the development of a simple mathematical model of the regulation of melanin by the sphingolipid pathway in the pathogenic microorganisms C. neoformans. This microbe is an environmental fungus that, upon inhalation, can cause a life-threatening meningoencephalitis, especially in immunocompromised patients (23). Cn produces a black melanin pigment deposited on the outer cell wall that protects the fungus from the environment and from the host immune response (24–27). Melanin deficient mutants are not pathogenic (28–30), thus it became important to define how its production is regulated.

Mathematical modeling of biochemical and regulatory systems is a well-developed field of research, and there are numerous strategies that could be employed to implement the sphingolipid activated production of melanin in Cn. We choose Biochemical Systems Theory (BST) as developed by Savageau in the 1960s (31, 32) and applied in numerous modeling efforts since. BST employs a power-law formalism derived from a Taylor series approximation to each process rate law in logarithmic coordinates. The resulting canonical representation greatly simplifies the construction of models, provides a rigorous basis for analyzing the stability and performance of the system, and has been successfully applied to metabolic pathways, gene regulatory networks, and signal transduction systems. BST has been successfully used to model a variety of pathways in a variety of organisms (33–35), including metabolic pathways in S. cerevisiae (36, 37) and Cn (38, 39). In the BST framework, the system's dynamic behavior is captured in a set of differential equations, where the rates of individual processes are given as the product of power laws. Each time varying quantity of interest, termed a dependent variable, is described by one of these equations. When each of the underlying processes (reaction, transport, expression, etc.) is described individually, the model is termed a Generalized Mass Action (GMA) system owing to its mathematical similarity to Mass Action systems. In many cases, this form can be further simplified by aggregating influxes and effluxes into a single product of power law terms each. Models in this form are referred to as S-systems and have distinct computational and analytical advantages. Equations giving the canonical forms for each of these forms are given below

GMA equation

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}=\sum _{k=1}^m{\alpha }_{ik}\prod _{j=1}^n{X}_j^{g_{ijk}}-\sum _{k=1}^m{\beta }_{ik}\prod _{j=1}^n{X}_j^{h_{ijk}}i=1,2,\dots ,n$$

S-system equation

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}={\alpha }_i\prod _{j=1}^{n+m}{X}_j^{g_{ij}}-{\beta }_i\prod _{j=1}^{n+m}{X}_j^{h_{ij}}i=1,2,\dots ,n$$

Here, the αs and βs are referred to as rate constants and the gs and hs as kinetic orders. More formally, these gs and hs are called apparent kinetic orders to differentiate them from the kinetic orders familiar to those describing process rates using mass action kinetics. For a more detailed explanation of the theory behind BST models, see appendix below and Voit (35).

Since this demonstration model is based on our previous experiments, model analyses show that under alteration of its parameters the simulations strictly reflect the results obtained in the previous experiments. Indeed, any mathematical model crucially depends on solid experimental data. However, once a model is established, it becomes a rich tool for analyses that are often unattainable with wet experimentation. For instance, the model can simulate the effect of Pkc1 downregulation on cell wall integrity and laccase location at the cell wall; these predictions could help to design additional experiments that specifically address this hypothesis. This chapter walks the reader through the basic steps of developing and analyzing a small S-system model of a biochemical pathway related to sphingolipid metabolism in Cn.

2. Methods

2.1. The Modeling Process

Regardless of which mathematical method is chosen to model a biological system, the same general process is followed to develop and test a model. Each step is discussed in greater detail in the appendix below, but briefly here are the main steps. The crucial first step consists of defining the pathway to be modeled and deciding which components are altered by the system (dependent variables) and which remain unchanged (independent variables). The second step is to write the system equations; each dependent variable represented by one differential equation that calculates how the amount of the associated molecular species changes. The equations are first written symbolically in terms of the dependent and independent variables and kinetic parameters and then numerically once all parameters have been estimated. Next, the quality and robustness of the model is assessed by calculating the local stability at steady state and the logarithmic gains and sensitivities of the variables and parameters. Last, simulations of known behavior are used to examine the dynamics of the model in response to perturbations. Reasonable responses indicate that the model is ready for predictive simulations. The modeling process is not strictly linear but iterative with successive rounds of experimentation and refinement as determined by the results of the analysis.

2.2. Graphical Model Design

As described in the introduction and illustrated in Fig. 1, our pathway of interest is a signaling cascade that promotes melanin production in Cn. After listing the components of the pathway (see Table 1), the most crucial step is to create a drawing or map of the biological system to be modeled, as it is from this map that the equations are written. This map connects the real biological system with the mathematical analysis. Thus, the map should be as accurate as possible based on the published literature and the researchers knowledge and should include the level of detail desired for the given problem. This map is similar to the conceptual drawings of biological pathways often found in textbooks or journal articles, but there are some simple guidelines to insure consistency between model maps and to help avoid ambiguity or confusion.

Table 1.

Model variables with initial values

Type	Symbol	Variable name	Role	Initial value	Reference
Dependent	X 1	IPCa	Metabolite	1 mol%b	(56)
	X 2	DAGc	Metabolite	38 pmol/nmol Pi	(18)
	X 3	l-DOPA-intd	Metabolite	1e	(42)
	X 4	Melanin	Metabolite	1f	(42)
Independent	X 5	Phytoceramide	Metabolite	3.8 pmol/nmol Pi	(18)
	X 6	PIg	Metabolite	4.54 mol%	(56)
	X 7	Ipc1h	Enzyme	35 pmol/min/mg	(18)
	X 8	Pkc1i	Signaling molecule	53.5 pmol/min/mgj	(18)
	X 9	l-DOPA-extk	Metabolite	106 nM	(42)
	X 10	Transport	Process	3.5 nmol/min/mg of cellsl	(43)
	X 11	Laccase	Enzyme	1,500 pmol/min/107 cells	(18)

^aInositol phosphoryl ceramide

^bThe total membrane concentration of IPC is 1 mol% under normal conditions during exponential growth, value reported by Wu et al. (56). Mol% is equivalent to the concentration of sphingoid base or phosphatidate/concentration of total phospholipid

^cDiacylglycerol

^dl-Dopamine intracellular

^eC. neoformans grown in l-3,4-dihydroxyphenylalanine (l-DOPA) external (42). The l-DOPA internal concentration is assumed equal to the relative melanin contents

^fThis concentration refers to the relative melanin contents whose value is equal to 1 (42)

^gPhosphatidylinositol

^hInositol phosphoryl ceramide synthase 1

ⁱProtein kinase C 1

^jSerine/threonine kinase whose specific activity in the absence of lipids is reported as 31.5 pmol/min/mg. In the presence of the DAG subspecies, its activity was increased by 1.7 fold (18)

^kl-Dopamine extracellular

^lV_max

The system map is represented as a network graph with two basic elements: nodes and directed edges. Nodes typically represent a pool of material, such as metabolites, cofactors, signaling molecules, proteins, enzymes, or genes. Nodes may represent dependent (time varying) or independent (fixed) variables. For example, a canonical reaction, where the substrate is transformed into a product (e.g., l-DOPA-int and melanin) by an enzyme (laccase) has two dependent and one independent variable; the substrate and product concentrations are changed by the reaction, but the enzyme typically is not. Each dependent variable has an equation that describes the influx and efflux of that variable, while independent variables have a constant value. Some typical independent variables are enzymes and cofactors.

Solid edges are used to indicate a flow or conversion of material and must connect to nodes. Single-headed arrows denote irreversible reactions and double-headed arrows indicate reversible reactions. If a different enzyme catalyzes the reverse reaction, then two single-headed arrows pointing in opposite directions are used. Several variations of flux arrows are possible depending on the number of substrates, products, enzymes, and cofactors involved in the reaction; see Sims et al. for more examples (40).

Edges are also used to indicate the flow of information, i.e., signals, from one variable that regulate some process in the model. In this case, the arrows are dashed and may have a positive or negative sign to indicate activation or inhibition, respectively. Lack of a sign on a dashed arrow is considered activation. Information flow arrows connect a node to an edge associated with a flow of material (solid arrow). Often these dashed arrows are used to indicate the relationship between an enzyme and the reactions that it modulates or the inhibition of one metabolite on some step in the pathway.

2.3. Equation Formulation, Symbolic, and Numeric

Once satisfied that the system map is accurate and includes all details relevant to the model, the differential equations can be set up from the map. It is helpful to first write the symbolic equations of the system. These indicate all the pertinent components that affect each dependent variable, but no specific numerical values, such as metabolite concentration are used. After the symbolic equations are complete, parameter values are estimated and plugged in to create the numeric equations that are used for further analysis.

It is mathematically convenient to substitute symbols for the proper names of the associated molecular species. They are represented by X_i for dependent and X_j for independent variables with the respective subscript. By convention, the numeration is consecutive beginning with i = 1 to n for the dependent variables j = n + 1 to n + m for the independent variables. Table 1 lists the components of the sample system along with the symbolic name and initial value. The fluxes between metabolites are also given symbolic names of the form v_i,j, where i and j indicate the two nodes the flux flows between. Next, for each dependent variable X_i, we identify the other variables and signals that influence its influx and efflux. A symbolic differential equation is then written for each dependent variable using either the S-system or GMA method of flux representation.

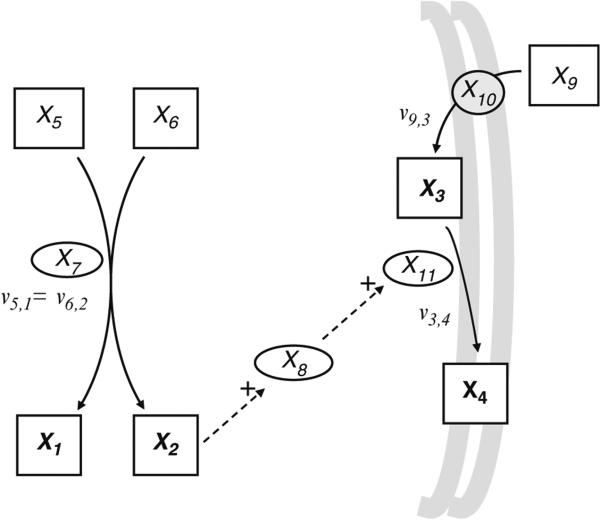
For example, Fig. 2 shows the network map with symbolic notation for the signaling cascade Ipc1–DAG–Pkc1 described in the introduction. In the first half of the cascade, the enzyme Ipc1, (X₇) transfers the phosphoryl-inositol moiety from phosphatidylinositol (PI), (X₆) to phytoceramide, (X₅) forming IPC, (X₁) and DAG, (X₂)

Fig. 2. Network map of the production of melanin via the signaling cascade: Ipc1–-DAG–Pkc1.

Based on the pathway described in Fig. 1., the system has four dependent variables X₁, X₂, X₃, X₄ and seven independent variables X₅, X₆, X₇, X₈, X₉, X₁₀, and X₁₁. Metabolites are shown as boxes with dependent variables in bold, enzymes as ovals, and the transport process as a circle. Solid arrows indicate flux and dashed arrows indicate that the variable has an effect on the system. Positive signals are indicating activation.

In the second half of the system, melanin (X₄) is synthesized from an internal concentration of l-DOPA-int, (X₃) via laccase, (X₁₁). In Cn, melanin (X₄) is produced in the presence of phenolic substrates, such as l-DOPA-ext, (X₉) (41, 42) that are actively transported into the cell (43). This transport process is identified in this relatively simple model as the variable X₁₀.

These two metabolic pathways are connected by two signals. First, DAG, (X₂) released from the production of IPC activates the enzyme Pkc1, (X₈), which then activates laccase, (X₁₁), stimulating the increased production of melanin.

This example contains four dependent variables, the metabolites: X₁, X₂, X₃, and X₄. Their synthesis is affected by their respective precursors and their degradation depends only on their own concentration. Note that the production of melanin requires numerous precursors and reactions, but has been simplified in this example as a direct substrate of l-DOPA-int. For each X_i, all components whether dependent or independent that have a part in its synthesis are aggregated in $V_i^{+}$, the influx function. Similarly, all variables dependent or independent that have a part in the degradation of X_i are aggregated in $V_i^{-}$, the efflux function. For the system shown in Fig. 2, the influx and efflux functions for each dependent variable can be represented as follows.

2.3.1. Mass Balance Equations

$$\begin{array}{c}\hfill \frac{\mathrm{d}{X}_1}{\mathrm{d}t}=V_1^{+}(X_5,X_6,X_7)-V_1^{-}\left(X_1\right)\hfill \\ \hfill \frac{\mathrm{d}{X}_2}{\mathrm{d}t}=V_2^{+}(X_5,X_6,X_7)-V_2^{-}\left(X_2\right)\hfill \\ \hfill \frac{\mathrm{d}{X}_3}{\mathrm{d}t}=V_3^{+}(X_9,X_{10})-V_3^{-}(X_2,X_3,X_8,X_{11})\hfill \\ \hfill \frac{\mathrm{d}{X}_4}{\mathrm{d}t}=V_4^{+}(X_2,X_3,X_8,X_{11})-V_4^{-}\left(X_4\right)\hfill \end{array}$$

The next step is to flesh out these influx and efflux functions. While the actual function that governs an enzymatic reaction may sometimes be described using Michaelis–Menten kinetic rate laws, often the exact mechanism is not known. This is when using the power law formalism has a great advantage. We can rewrite these flux functions as symbolic S-system equations as shown below, where each of the fluxes is given as a product of power-law terms.

2.3.2. Symbolic Equations

$$\begin{array}{c}\hfill \frac{\mathrm{d}{X}_1}{\mathrm{d}t}={\alpha }_1{X}_5^{g_{1,5}}{X}_6^{g_{1,6}}{X}_7^{g_{1,7}}-{\beta }_1{X}_1^{h_{1,1}}\hfill \\ \hfill \frac{\mathrm{d}{X}_2}{\mathrm{d}t}={\alpha }_2{X}_5^{g_{2,5}}{X}_6^{g_{2,6}}{X}_7^{g_{2,7}}-{\beta }_2{X}_2^{h_{2,2}}\hfill \\ \hfill \frac{\mathrm{d}{X}_3}{\mathrm{d}t}={\alpha }_3{X}_9^{g_{3,9}}{X}_{10}^{g_{3,10}}-{\beta }_3{X}_2^{h_{3,2}}{X}_3^{h_{3,3}}{X}_8^{h_{3,8}}{X}_{11}^{h_{3,11}}\hfill \\ \hfill \frac{\mathrm{d}{X}_4}{\mathrm{d}t}={\alpha }_4{X}_2^{g_{4,2}}{X}_3^{g_{4,3}}{X}_8^{g_{4,8}}{X}_{11}^{g_{4,11}}-{\beta }_4{X}_4^{h_{4,4}}\hfill \end{array}$$

2.4. Parameter Estimation

Once the symbolic equations are defined, it is time to provide numeric values for each parameter. Most often, this procedure occurs “bottom-up” by estimating the parameters for individual reactions based on kinetic characterizations of the associated enzymes. Recently, efforts have also focused on estimating these parameters from time series measurements of the dependent variables, the so-called top-down approach (44–47). Here, we employ the “bottom-up” approach and focus on using kinetic data for each reaction or process in the model. This step utilizes published information about the enzymes and reactions, such as Km, Ki, and V_max, although there are times when the needed data are unavailable. In such cases, custom experiments may need to be conducted, parameter values may be estimated from characterizations in other organisms, or default “guesstimates” may be used for a limited number of parameters.

On initial inspection, our system appears to have 8 rate constants and 19 kinetic orders that need to be calculated; however, there are constraints on the system that equate some parameters, thus reducing the total number to be determined. For example, the synthesis of X₁ and X₂ occur from the same process so V₁⁺ and V₂⁺ are equivalent. Also, the precursor–product relationship conserves the flux of a reaction, thus the efflux V₃⁻ must equal the influx of V₄⁺. This means that the rate constants and kinetic orders of each of these relationships must be equal resulting in the following constraints on the parameters.

$$\begin{array}{c}\hfill {\alpha }_1={\alpha }_2;g_{1,5}=g_{2,5};g_{1,6}=g_{2,6};g_{1,7}=g_{2,7}\\ \hfill {\beta }_3={\alpha }_4;h_{3,2}=g_{4,2};h_{3,8}=g_{4,8};h_{3,3}=h_{4,3};h_{3,11}=g_{4,11}\end{array}$$

2.4.1. Kinetic Orders

In BST, the kinetic order of a variable indicates the influence of that variable on the flux in which the variable appears and is derived from the slope of the rate function when expressed in logarithmic coordinates. Kinetic orders influence the stability of the system and the logarithmic gains, and sensitivities of the dependent variables (35). Several methods are available for the estimation of kinetic orders, including estimation from time series data (as in the top-down approach), estimation from kinetic data of individual enzymes, or through approximations to established rate laws for well-characterized processes. Kinetic orders are frequently determined directly from experimental data by estimating the slope in a log–log plot of rate versus concentration data (34). When a rate law is available to describe a process of interest, it is also possible to calculate kinetic orders using partial derivatives as shown below.

$$g_{i,j}=\frac{\partial V_i}{\partial X_j}\frac{X_j}{V_i}$$

This expression is derived from the partial derivative of the log rate V_i with respect to the log of the variable of interest X_j. For example, the simple Michaelis–Menten rate law produces the following kinetic order with respect to the substrate X_i.

Given

$$\begin{array}{cc}\hfill g_{i,j}& =\left[\frac{\partial }{\partial X_i}\left(\frac{V_{\max }\times X_i}{Km+X_i}\right)\right]\times \frac{X_i}{\left(\frac{V_{\max }\times X_i}{Km+X_i}\right)}\hfill \\ \hfill & =\frac{Km}{Km+X_i}\hfill \end{array}$$

For the first example, consider the enzyme Ipc1, X₇ of the sphingolipid pathway and its substrates X₅ and X₆ which are assumed to be independent variables and thus are constants. However, the products of this reaction can change; so the kinetic orders of V₁⁺ and V₂⁺ are associated with the IPC and DAG. Estimations of the kinetic orders g_1,5 and g_1,6 are illustrated in the appendix below. To determine the kinetic order of the enzyme, we assume a direct proportionality between activity and concentration of enzyme. Differentiation gives a value of 1. Recalling the constraints on parameters discussed previously, we get g_1,7 = g_2,7 = 1.

Next, we assume a simple kinetic Michaelis–Menten rate law for the laccase reaction from which we compute the kinetic orders h_3,3 and g_3,9. First, h_3,3 quantifies the effect of internal l-DOPA on its own degradation through laccase. This enzyme exhibits a constant kinetic for DOPA with a Km = 0.59 mM (48). After differentiation and substitution of measured values, we get the following:

$$h_{3,3}=\frac{Km}{Km+X_4}=\frac{0.59}{0.59+1}=0.3710$$

Similarly, the kinetic order g_3,9 is obtained by differentiation of V₃⁺ with respect to X₉. The kinetic order g_3,9 reflects the effect of l-DOPA-ext on l-DOPA-int via transport through the cell wall with a kinetic constant Km = 0.45 mM (48) as shown below.

$$g_{3,9}=\frac{Km}{Km+X_9}=\frac{0.45}{0.45+1}=0.3103$$

We note that in the calculation of these kinetic orders, we supply a value for one or more of the system variables (X₄ and X₉ in the examples above). The power-law derived in this manner is an approximation to the underlying rate law (Michaelis–Menten in this case), more formally it is a first order Taylor approximation in logarithmic coordinates. As such, we must choose a point around which to make this approximation. This becomes what is called the operating point and is often chosen to match the nominal conditions around which the system is expected to operate. At this operating point, both the rate and the slope of the power law approximation match that of the rate law being approximated.

2.4.2. Rate Constants

Rate constants represent the speed of the processes. Their values can be calculated with data for the Vmax, metabolite and enzyme concentrations along with the calculated kinetic orders (49). This is accomplished by setting the power law flux term equal to the original rate law at the operating point and solving for the rate constant this guarantees that the velocity of the original rate law and the power law approximation match.

For example, the rate constant associated with the formation of the variable X₁ is determined from the set of values for the flux rate, concentrations, and kinetic orders:

$${\alpha }_1=\frac{V_1^{+}}{X_5^{g_{1,5}}{X}_6^{g_{1,6}}{X}_7^{g_{1,7}}}=\frac{12.29}{{3.8}^{0.2621}\times {4.54}^{0.5241}\times 35}=0.1119$$

From the parameter constraints, we know that the rate constant associated with the formation of the variable X₁ is the same value as the rate constant associated with the formation of the variable X₂. Thus, α₂ = 0.1119. Similar calculations give the remaining rate constants.

Once all the values have been calculated for the kinetic orders and rate constants, those values replace the symbols to produce the numeric equations that are then ready for analysis and testing. For several detailed examples of parameter estimation, see (35) and (40).

2.4.3. S-System Representation

$$\begin{array}{c}\hfill \frac{\mathrm{d}{X}_1}{\mathrm{d}t}=0.1119{X_5}^{0.2621}{X}_6^{0.5241}{X}_7-12.29X_1\hfill \\ \hfill \frac{\mathrm{d}{X}_2}{\mathrm{d}t}=0.1119{X_5}^{0.2621}{X}_6^{0.5241}{X}_7-0.3234X_2\hfill \\ \hfill \frac{d{X}_3}{dt}=0.9474e-2X_9^{0.3103}{X}_{10}-0.7915e-6X_2{X}_3^{0.3710}{X}_8{X}_{11}\hfill \\ \hfill \frac{d{X}_4}{dt}=0.7915e-6X_2{X}_3^{0.3710}{X}_8{X}_{11}-2.413X_4\hfill \end{array}$$

2.5. Model Analysis

The system of equations that have been developed are now tested for steady state values, eigenvalues, and sensitivity or logarithmic gains. The computations associated with these analyses are somewhat more complicated; fortunately, these steps have been automated and are available in at least two freely available software packages; PLAS http://www.dqb.fc.ul.pt/docentes/aferreira/plas.html (50) and PLMaddon http://www.sbi.uni-rostock.de/plmaddon (51). At this time, it is useful to employ a software package that has been developed specifically for this task, such as PLAS. The equations and initial values (see Table 1) for the variables are entered into the software. The software can then automatically compute the steady state of the system by simultaneously setting the system of differential equations to zero. For S-systems the system of equations can be solved directly after logarithmic transformation. When the model is characterized using the GMA model, the software must use numerical integration techniques as a closed form for the steady state is not available. See appendix below and (35) for more details. Our system reaches steady state as shown in Table 2.

Table 2.

Steady state and stability assessment using PLAS software. Eigenvalues for the S-system model (Fig. 2) of cascade Ipc1–DAG–Pkc1–laccase

	Steady state		Eigenvalues
Variable	Value	Flux	Re	Im
X 1	1	12.29	−12.29	0
X 2	38	12.29	−2.41	0
X 3	1	2.41	−0.90	0
X 4	1	2.41	−0.32	0

Along with the steady state, it is necessary to check the eigenvalues of the system which indicates the local stability of the system. Stability is an indication of the system's behavior following small perturbations from the steady state. If the system eventually returns to the steady state following a perturbation it is considered stable, a desirable property of our model. Stability is assessed by examining the eigenvalues of a linear approximation to the nonlinear system, constructed at the steady state. When the real parts of all the eigenvalues are negative, the steady state of the system is considered stable. Our system has negative real parts (see Table 2) and is thus stable. Also, the imaginary parts are all zero, indicating that the system does not oscillate as it returns to the steady state following a perturbation. Next, we check the sensitivity of the parameters and independent variables. Again, the available software package implements the required calculations. Sensitivities and logarithmic gains indicate how much the steady state values of dependent variables or fluxes of the system change when a parameter or independent variable is changed by a small amount. These measures are interpreted as relative changes. For example, a sensitivity of 5 means that a 1% change in the parameter or independent variable cause a 5% change in the steady state or flux. Positive sensitivities indicate a change in the same direction, whereas negative sensitivities indicate opposite directions of change. Robust models have mostly small sensitivities; unusually, large values (e.g., >10) suggests that something may be amiss with the model or importantly, that the node in question may play a key role in the pathway.

Several types of sensitivities are calculated, but each with the dependent variables and the fluxes of the system; sensitivity with respect to kinetic orders (Table 3) and to rate constants (Table 4), and logarithmic gains of the independent variables (Table 5). As can be seen in the tables, our system has low log gains and mostly low to medium sensitivities of the kinetic orders. The primary exception is the kinetic order of laccase with respect to l-DOPA-int which equals −19.71.

Table 3.

Influence of the rate constant on the metabolite concentrations of the model in Fig. 2

		Metabolite concentration				Flux of metabolite
Equation	Rate constant	X 1	X 2	X 3	X 4	V(X1)	V(X2)	V(X3)	V(X4)
IPCa	α 1	1	–	–	–	1	–	–	–
	β 1	−1	–	–	–	–	–	–	–
DAGb	α 2	–	1	−2.7	–	–	1	–	–
	β 2	–	−1	2.7	–	–	–	–	–
l-DOPA intc	α 3	–	–	2.7	1	–	–	1	1
	β 3	–	–	−2.7	−1	–	–	–	−1
Melanin	α 4	–	–	–	1	–	–	–	1
	β 4	–	–	–	−1	–	–	–	–

^aInositol phosphoryl ceramide synthase 1

^bDiacylglycerol

^cl-Dopamine intracellular

Table 4.

Logarithmic gains of the independent variables with respect to metabolites concentration and with respect to fluxes of the model in Fig. 3. The metabolite most influenced by changes in the independent variables is l-Dopamine (l-DOPA)-int. The influence of the fluxes on metabolite concentrations shows that almost all the magnitudes are less than 1

			Metabolite concentration				Flux of metabolite
Equation	Variable	Kinetic order	X 1	X 2	X 3	X 4	V(X1)	V(X2)	V(X3)	V(X4)
IPC	PhytoCera	g(1,5)	0.35	–	–	–	0.35	–	–	–
	PIb	g(1,6)	0.79	–	–	–	0.79	–	–	–
	Ipc1c	g(1,7)	3.56	–	–	–	3.56	–	–	–
	IPCd	h(1,1)	–	–	–	–	–	–	–	–
DAG	PhytoCer	g(2,5)	–	0.35	−0.94	–	–	0.35	–	–
	PI	g(2,6)	–	0.79	−2.14	–	–	0.79	–	–
	Ipc1	g(2,7)	–	3.56	−9.58	–	–	3.56	–	–
	DAGe	h(2,2)	–	−3.64	9.80	–	–	–	–	–
l-DOPA int	l-DOPA-extf	g(3,9)	–	–	11.56	4.29	–	–	4.29	4.29
	Transport	g(3,10)	–	–	3.38	1.25	–	–	1.25	1.25
	DAG	h(3,2)	–	–	−9.80	−3.64	–	–	–	−3.64
	l-DOPA-intg	h(3,3)	–	–	–	–	–	–	–	–
	Pkc1h	h(3,8)	–	–	−10.73	−3.98	–	–	–	−3.98
	Laccase	h(3,11)	–	–	−19.71	−7.31	–	–	–	−7.31
Melanin	DAG	g(4,2)	–	–	–	3.64	–	–	–	3.64
	l-DOPA-int	g(4,3)	–	–	–	–	–	–	–	–
	Pkc1	g(4,8)	–	–	–	3.98	–	–	–	3.98
	Laccase	g(4,11)	–	–	–	7.31	–	–	–	7.31
	Melanin	h(4,4)	–	–	–	–	–	–	–	–

^aPhytoceramide

^bPhosphatidylinositol

^cInositol phosphoryl ceramide synthase 1

^dInositol phosphoryl ceramide

^eDiacylglycerol

^fl-Dopamine extracellular

^gl-Dopamine intracellular

^hProtein kinase C 1

Table 5.

Sensitivity of the kinetic orders on the metabolite concentrations and fluxes of the model in Fig. 2. The largest negative influence is on l-Dopamine (l-DOPA) concentration, X₃. This metabolite responds to a change in the kinetic order associate to degradation h_3,11; increase its concentration when this parameter decreases. Additionally, S(X₄, g_4,11) indicates an increase in melanin concentration, X₄ when its own synthesis increases

		Metabolite concentration				Flux of metabolite
Independent variable		X 1	X 2	X 3	X 4	V(X1)	V(X2)	V(X3)	V(X4)
Phytoceramide	X 5	0.26	0.26	−0.71	–	0.26	0.26	–	–
PIa	X 6	0.52	0.52	−1.41	–	0.52	0.52	–	–
Ipc1b	X 7	1.00	1.00	−2.70	–	1.00	1.00	–	–
Pkc1c	X 8	–	–	−2.70	–	–	–	–	–
l-DOPA-extd	X 9	–	–	0.84	0.31	–	–	0.31	0.31
Transport	X 10	–	–	2.70	1.00	–	–	1.00	1.00
Laccase	X 11	–	–	−2.70	–	–	–	–	–

^aPhosphatidylinositol

^bInositol phosphoryl ceramide synthase 1

^cProtein kinase C 1

^dl-Dopamine extracellular

The results presented show that the relatively simple model presented in the Fig. 2 is self-consistent with a steady state that is stable. The sensitivities are relatively small suggesting that this model is robust. Note that this model is only a preliminary analysis and consists of only four dependent variables. Additional variables and pathways could be included in the system, which would lead to a more detailed analysis of the formation of melanin and its regulation by sphingolipid metabolism in Cn. Now, we can simulate a perturbation to study the dynamics of the system.

2.6. Model Dynamics

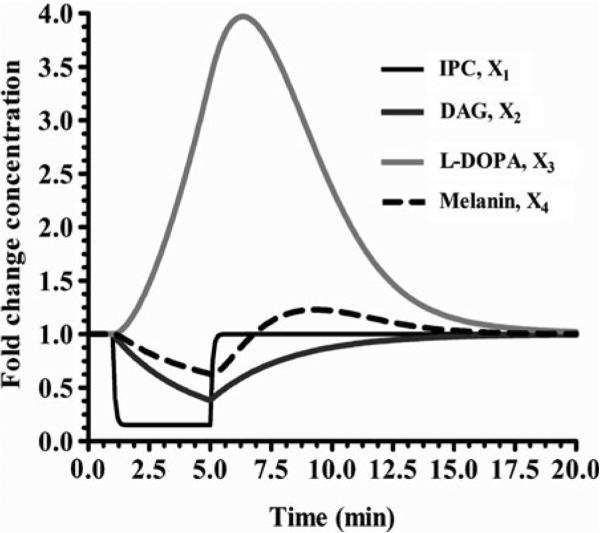
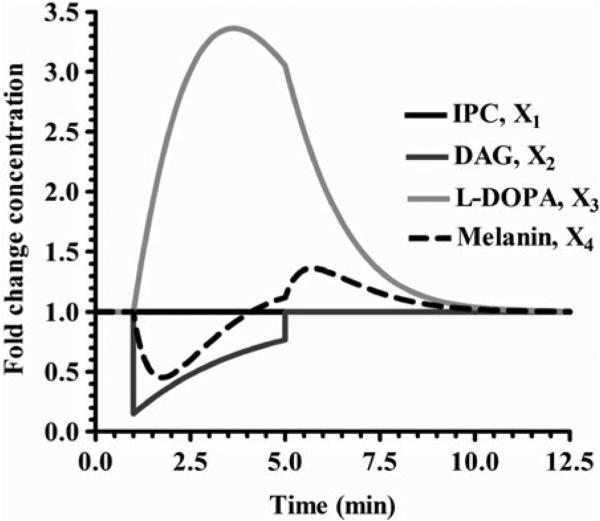
Since the analysis of our system was favorable, we can now perform simulations to see how the system behaves dynamically. This is done using the software package by adding a statement that changes a variable's value at a specific time and then returns that variable to its initial value. This is typically designed to simulate the presentation and removal of a stimulus as might be accomplished in a laboratory experiment but may also be applied to any sort of perturbation to the system. For example, Fig. 3 illustrates the dynamics when Ipc1p activity is decreased by 85% at 1 min and then returned to its initial value at 5 min. Another example is shown in Fig. 4, where the concentration of DAG is decreased by 85% at 1 min. These two simulation show that the system behaves as expected if either of the enzymes are decreased and then returns to steady state. Further scenarios could be tested as well, such as increasing the input of PI and or phytoceramide.

Fig. 3. Decrease of the enzyme Ipc1 by 85%.

The results show that X₁ and X₂ decrease and then reach the steady state. X₃ increases rapidly and significantly (approximately fourfold) and then back to the steady state. X₄ exhibits a slight S shape before reaching the steady state.

Fig. 4. Decrease of the metabolite DAG by 85%.

The results show an increase of X₃ by 3.36 fold and a decrease of X₄. This perturbation does not affect X₁. After the perturbation, all variables reach quickly their initial values.

2.7. Validation of the Model

Once the mathematical model has been established it becomes essential to perform laboratory experimentations to validate its accurateness. For instance, the downregulation or/and deletion of IPC1 or/and PKC1 genes by homologous recombination should produce mutant strains that make less or no melanin. We would expect IPC and DAG lipid measurements to be decreased in the mutant in which Ipc1 is downregulated. Also, in this mutant, Pkc1 enzymatic activity should be decreased. Experiments of this type not only help to prove (or disprove) the model but also help in finding additional components of the model (e.g., cell wall genes regulated by Pkc1 in the regulation of cell wall integrity) (52, 53). In the Chapter 16, we provide a detailed description of materials and methods used for performing molecular biology and biochemistry studies in Cn that can be used to validate theories generated by systems biology.

Ultimately, reliable models are used as tools for prescreening studies for different kind of scenario and for creating novel hypotheses. But the creation of reliable mathematical models requires substantial efforts from both biologists and mathematicians. As modeling has improved significantly during the past few decades, collaborations between biological and computational scientists have begun to show that their effort reveal insights for a better understanding of biological processes that neither biologists nor mathematicians could have obtained without each other. Thus, the development of mathematical models should be seen as a tool that can analyze the system in different ways, complementing laboratory experimentations.

3. Analytical Methods

In the sections that follow, we provide a more complete description of the analytical methods involved in the modeling of melanin regulation by the sphingolipid pathway.

3.1. Methods of System Characterization

Within the framework of BST, models are usually constructed with either the S-system or GMA system representation. In special cases such as ours, where no branch points are present, the S- and GMA representations are equivalent. In the more general case, the S-system representation can be constructed so as to be equivalent to the GMA model at the operating point by aggregating all incoming or outgoing fluxes for each dependent variable into one incoming and one outgoing flux (please see examples in (35)).

Power-Law Formalism

Synergistic System

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}={\alpha }_i\prod _{j=1}^{n+m}{X}_j^{g_{ij}}-{\beta }_i\prod _{j=1}^{n+m}{X}_j^{h_{ij}}i=1,2,\dots ,n$$

Generalized Mass Action

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}=\sum _{k=1}^m{\alpha }_{ik}\prod _{j=1}^n{X}_j^{g_{ijk}}-\sum _{k=1}^m{\beta }_{ik}\prod _{j=1}^n{X}_j^{h_{ijk}}i=1,2,\dots ,n$$

Two kinetic representations are related within the power-law formalism (33, 54). The aggregation for Synergistic System (S-System) has one differential equation for each dependent variable X_i with one term for the accumulation or synthesis and another term for the degradation. In GMA, each equation may contain one, two or more terms. In both aggregations, the derivatives of the variables with respect to time t are dX_i/dt. Each term contains all variables that affect the process that the term represents. The multiplicative rate constants α and β could be zero but not negative and the state variables X_j are positive. The exponential parameters are the kinetic order g and h that can be positive or negative real numbers; the subscript i enumerates the equations of the process, k refers to the process number of production or degradation (in GMA only), n refers to the number of dependent variables, and m to the number of independent variables.

3.1.1. S-System

The explanations below correspond with the simple model for the Ipc1–diacylglycerol–Pkc–laccase–melanin pathway. The general equation that describes the biological changes with respect to time can be written as

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}=V_i^{+}-V_i^{-},i=1,\dots ,n,$$

where $V_{\mathrm{i}}^{+}$ is a function that contains all the variables (dependent X_i and independent X_j) that influence the synthesis of the given X_i while $V_i^{-}$ is a function of all variables related with degradation of X_i. This can be written as

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}=V_i^{+}(X_1,X_2,X_3,X_n,X_{n+1},\dots ,X_{n+m})-V_i^{-}\times (X_1,X_2,X_3,X_n,X_{n+1},\dots ,X_{n+m})$$

According with the general properties of biochemical system, a good representation of $V_i^{+}$ and $V_i^{-}$ is a product of power-law functions of the variables that directly influence the production ($V_i^{+}$) or degradation ($V_i^{-}$) of the quantity X_i, n is the number of dependent variables, i corresponds to the dependent variable subscript which typically ranges from 1 to n. Each function can be written as a power-law function, as shown below

$$\begin{array}{cc}\hfill {\stackrel{.}{V}}_i^{+}(X_1,X_2,X_3,X_n,X_{n+1},\dots ,X_{n+m})& ={\alpha }_i\left(X_1^{g1}{X}_2^{g2}{X}_3^{g3}{X}_n^{gn},X_{n+1}^{gn+1},\dots ,X_{n+m}^{gn+m}\right)\hfill \\ \hfill {\stackrel{.}{V}}_i^{-}(X_1,X_2,X_3,X_n,X_{n+1},\dots ,X_{n+m})=& {\beta }_i\left(X_1^{h1}{X}_2^{h2}{X}_3^{h3}{X}_n^{hn},X_{n+1}^{hn+1}\dots ,X_{n+m}^{hn+m}\right)\hfill \end{array}$$

The parameters α and ß are positive real numbers called the rate constants and g and h are kinetic orders and can take on positive or negative values. α and g are parameters related with the synthesis of X_i, whereas ß and h are related to the degradation of X_i. Putting these two equations together and writing in compact form gives the canonical S-system representation.

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}={\alpha }_i\prod _{j=1}^{n+m}{X}_j^{g_{ij}}-{\beta }_i\prod _{j=1}^{n+m}{X}_j^{h_{ij}}i=1,2,\dots ,n$$

The S-system in our model contains four equations. Each term contains all the dependent and independent variables that have direct effect on the associated degradation or production process. Also each variable in each term has one exponent called the kinetic order. The kinetic order in the synthesis term is typically labeled g and the kinetic order in the degradation term labeled h. Each first subscript i in the kinetic order g or h refers to the dependent variable of the equation, and the second subscript j refers to the variable of the exponent. The rate constants α_i and ß_i have one subscript that identifies the equation in question. The S-system equations for the model Fig. 3 are the following:

$$\begin{array}{c}\hfill \frac{\mathrm{d}{X}_1}{\mathrm{d}t}=V_1^{+}-V_1^{-}={\alpha }_1{X}_5^{g_{1,5}}{X}_6^{g_{1,6}}{X}_7^{g_{1,7}}-{\beta }_1{X}_1^{h_{1,1}}\hfill \\ \hfill \frac{\mathrm{d}{X}_2}{\mathrm{d}t}=V_2^{+}-V_2^{-}={\alpha }_2{X}_5^{g_{2,5}}{X}_6^{g_{2,6}}{X}_7^{g_{2,7}}-{\beta }_2{X}_2^{h_{2,2}}\hfill \\ \hfill \frac{\mathrm{d}{X}_3}{\mathrm{d}t}=V_3^{+}-V_3^{-}={\alpha }_3{X}_9^{g_{3,9}}{X}_{10}^{g_{3,10}}-{\beta }_3{X}_2^{h_{3,2}}{X}_3^{h_{3,3}}{X}_8^{h_{3,8}}{X}_{11}^{h_{3,11}}\hfill \\ \hfill \frac{\mathrm{d}{X}_4}{\mathrm{d}t}=V_4^{+}-V_4^{-}={\alpha }_4{X}_2^{g_{4,2}}{X}_3^{g_{4,3}}{X}_8^{g_{4,8}}{X}_{11}^{g_{4,11}}-{\beta }_4{X}_4^{h_{4,4}}\hfill \\ \hfill X_5,X_6,X_7,X_8,X_9,X_{10},X_{11}=\text{constant}\hfill \end{array}$$

3.1.2. GMA

As with the S-system, a GMA system contains one differential equation for each dependent variable. However, each of these equations may include a sum of any number of terms. Typically, the number of terms in an equation is related to the number of reactions in which the associated dependent variable is involved. Each term has a rate constant α_ik associated with each synthesis (processes where X_i is a product) and other rate constant ß_ik associated with each degradation (processes where X_i is a reactant). In some instances, we relax the constraint on the signs of α_ik and β_ik giving a single sum with rate constant γ_ik. Each term contains all dependent and independent variables that directly affect the process of synthesis or degradation of X_i that the term represents. The index i identifies the dependent variable, j the variable influencing the process, and k gives the index of the production or degradation process (k = 1,. . .,m). Each variable X_j is raised to its kinetic order g_ijk and h_ijk (sometimes denominated as f_ijk).

$$\frac{\mathrm{d}{X}_i}{\mathrm{d}t}=\sum _{k=1}^m{\alpha }_{ik}\prod _{j=1}^n{X}_j^{g_{ijk}}-\sum _{k=1}^m{\beta }_{ik}\prod _{j=1}^n{X}_j^{h_{ijk}}i=1,2,\dots ,n$$

An important advantage, GMA representation permits the identification of each component and each process to be expressed explicitly, retaining the original the stoichiometry of influxes and effluxes. However, a significant inconvenience of GMA representation is that it does not permit the easy calculation of the steady state solution as does the S-system representation.

S- and GMA systems are closely related and, as in our example, sometimes equivalent. Models using the GMA representation explicitly represent each process in the system and preserve the system stoichiometry. S-systems are often constructed from a GMA model and thus require an additional step, the aggregation of fluxes. Despite the fact that the GMA system explicitly represents each process, research indicates that the S-system representation permits error compensation and approximates the branches of traditional rate laws more exactly than GMA representation, although S-system can introduce discrepancies in flux stoichiometry. S-systems have a distinct computational advantage in the availability of a closed form solution for the steady state. This can be a significant advantage in optimization problems and in cases where a large parameter space is being explored. In this example, the model includes four differential equations for the dependent variables X₁, X₂, X₃, and X₄ each with one production and one degradation term. In this case, the GMA equations coincide with the S-system equations as our model system has no branch points.

The GMA equations are:

$$\begin{array}{c}\hfill \frac{\mathrm{d}{X}_1}{\mathrm{d}t}={\alpha }_{1,5}{X}_5^{g_{1,5,5}}{X}_6^{g_{1,6,5}}{X}_7^{g_{1,7,5}}-{\beta }_{1,1}{X}_1^{h_{1,1,1}}{X}_2^{h_{1,2,1}}\hfill \\ \hfill \frac{\mathrm{d}{X}_2}{\mathrm{d}t}={\alpha }_{2,5}{X}_5^{g_{2,5,5}}{X}_6^{g_{2,6,5}}{X}_7^{g_{2,7,5}}-{\beta }_{2,2}{X}_1^{h_{2,1,2}}{X}_2^{h_{2,2,2}}\hfill \\ \hfill \frac{\mathrm{d}{X}_3}{\mathrm{d}t}={\alpha }_{3,9}{X}_9^{g_{3,9,9}}{X}_{10}^{g_{3,10,9}}-{\beta }_{3,3}{X}_2^{h_{3,2,3}}{X}_3^{h_{3,3,3}}{X}_8^{h_{3,8,3}}{X}_{11}^{h_{3,11,3}}\hfill \\ \hfill \frac{\mathrm{d}{X}_4}{\mathrm{d}t}={\alpha }_{4,3}{X}_2^{g_{4,2,3}}{X}_3^{g_{4,3,3}}{X}_8^{g_{4,8,3}}{X}_{11}^{g_{4,11,3}}-{\beta }_{4,4}{X}_4^{h_{4,4,4}}\hfill \end{array}$$

3.2. Kinetic Order Estimation

Kinetic orders can be estimated using several, different methods but frequently these values are obtained directly from experimental data, or from any mathematical representation of such data. In some particular cases, the slope in a log–log plot of rate versus concentration data gives the corresponding kinetic order directly (34). At steady state, when the net flux through a dependent variable is zero, the influx and efflux terms must be equal. Thus, a given exponent g (or h) can be computed via partial differentiation of V with respect to X and multiplied by the ratio of X and V all evaluated at the operating point. The expression is formulated as:

$$g_{i,j}=\frac{\partial V_i}{\partial X_j}\frac{X_j}{V_i}.$$

The kinetic orders for the influence of a reactant, derived from a Michaelis–Menten rate law are between 0 and 1, where a value of 0.5 is obtained when the operating point is such that the substrate concentration is equal to the Km of the enzyme.

For example, the production of IPC (X₁) is represented by the flux v_5,1. The process that contributes to this flux is assumed to be irreversible, and the bisubstrate reaction includes phytoceramide, X₅ and phosphatidylinositol, X₆. The enzyme Ipc1 exhibits Michaelis–Menten kinetics with a Km = 1.35 mol% for phytoceramide, Km = 5 mol% for DAG (48). The following equation includes substrate phytoceramide, X₅ and phosphatidylinositol, X₆:

$$v_{5,1}=\left(V_{\max }\times \frac{X_5}{(1.35+X_5)}\times \frac{X_6}{(5+X_6)}\right)$$

Derived from V_max, the flux was calculated from the specific activity V_Ipc1 = 35 pmol/min/mg (18). In this simple model, we are assuming that 1 L contains 1 mg of protein.

This gives the following equation for the flux v_5,1.

$$V_1^{+}=v_{5,1}=\left(35\times \frac{X_5}{(1.35+X_5)}\times \frac{X_6}{(5+X_6)}\right)$$ (1)

The kinetic order g_1,5 is then computed through partial differentiation of V₁⁺ with respect to X₅ which yields:

$$g_{1,5}=\left[\frac{\partial }{\partial X_5}\left(35\times \frac{X_5}{(K{m}_{\left(X_5\right)}+X_5)}\times \frac{X_6}{(K{m}_{\left(X_6\right)}+X_6)}\right)\right]\times \frac{X_5}{V_1^{+}}$$

The partial derivative using the initial concentrations of the substrates is

$$=\left(\frac{35}{(1.35+3.8)}\times \frac{X_6}{(5+X_6)}-\frac{35\times 3.8}{{(1.35+3.8)}^2}\times \frac{X_6}{(5+X_6)}\right)\times \frac{X_5}{V_1^{+}}$$

and the kinetic order is then calculated as

$$g_{1,5}=0.8475\times \frac{3.8}{12.29}=0.2621,$$

where 12.29 is produced from solving Eq. 1 using the initial concentrations of X₅ and X₆. The kinetic order g_1,6 is obtained in the same fashion, but its partial differentiation is with respect to X₆ resulting in g_1,6 = 0.5241.

3.3. Software Implementation

As mentioned previously, software packages such as PLAS, greatly simplify the computations associated with model analysis and simulation. With PLAS, and other software packages, the user must typically provide (1) a model description, in this case, the system of differential equations for each of the dependent variables, (2) the operating point given as a list of values for the dependent and independent variables, normally a steady state of the system, (3) equations needed to translate the predicted system response to that of the experimental measurement system, and when simulating the system, (4) a set of initial conditions, starting time, end time, and reporting time interval. The sample PLAS input given below provides these for our model. Here, each of the differential equations is given as X1’, X2’, X3’, and X4’ where the “’” indicates that this equation gives the first derivative of X_i and the expression is given as a sum of power-law terms (“^” indicates exponentiation). The operation point (and steady state) are given by the lines X1 = 1 to X11 = 1500 and the start time, end time, and reporting interval are given by t0, t1, and hr. Additional details on the PLAS model syntax and options are given in the software documentation. Below is the PLAS code for our model.

X1 ’ = .1119780350157*X5^.2621359223298*X7^1. *X6^.5241090146750-12.29000020354*X1^1.

X2 ’ = .1119780350157*X5^.2621359223298*X7^1. *X6^.5241090146750-.3234210579878*X2^1.

X3 ’ = .9474646868175e-2*X9^.3103448275861*X10^1.-.7915373351201e-6*X11^1.*X8^1.*X2^1. *X3^.3710

X4 ’ = .7915373351201e-6*X11^1.*X8^1.*X2^1. *X3^.3710-2.413793103448*X4^1.

&& X5 X6 X7 X8 X9 X10 X11

!! XX1 XX2 XX3 XX4 Ib

!! XXINDEP Ib

‘// Dependent and independent variables‘ = 1 .. 11

X1 = 1

X2 = 38

X3 = 1

X4 = 1

X5 = 3.8

X6 = 4.54

X7 = 35

X8 = 53.5

X9 = 1000000

X10 = 3.5

X11 = 1500

XX1 = X1

XX2 = 1/38*X2

XX3 = X3

XX4 = X4

// Times

t0 = 0

hr = .1

tf = 150

3.4. Steady State Solution

At steady state, the time rate of change for all dependent variables must be 0 and thus all of the equations in the S-system model (or GMA model) must equal 0. For S-systems, the resulting expression equates a difference of two power-law terms to 0. Moving the degradation term to the opposite side and taking logarithms results in a system of equations linear in the log concentrations. Given the gs, hs, αs, and βs, this system of equations can be solved for the system steady state (32).

The PLAS software executes these calculations and provides the computed steady state. The software additionally evaluates a linearized model at the computed steady state and gives us the eigenvalues for that model from which we can determine the stability of the system. In this model, the real parts are negative; the steady state is locally stable indicating that the system returns to the steady state following small perturbations.

3.5. Logarithmic Gains

We often wish to predict how the system responds to an increase or decrease in one of the independent variables to understand, for example, how over expression of an enzyme or increase in available nutrient might change the steady state of the system. Logarithmic gains indicate this relation of change between the dependent concentration X_i and the independent concentration X_j. The logarithmic gains characterize the propagation of biochemical signals throughout the system (55). These systemic properties are obtained by a single analytical solution of the steady state equations within the framework of the S-system representation (33).

Logarithmic gains can be used to understand changes in either dependent variable steady states or changes in steady state fluxes. The expression for a flux gain is given by the equation

$$L(V_i,X_j)=\left(\frac{\partial V_i}{\partial X_j}\right)\left(\frac{\partial X_j}{\partial V_i}\right)=\frac{\partial l\left(\log V_i\right)}{\partial l\left(\log X_j\right)}i=1,\dots ,n;j=n+1,\dots ,n+m$$

A similar equation can be used to compute dependent variable logarithmic gains. If the resulting log gain is greater than 0, this implies amplification of the original signal; a magnitude less than 0 indicates attenuation. If the log gain is positive, this indicates that the changes of the independent and dependent variable are in the same direction, both increase and both decrease. If the log gain is negative, this indicates that the changes are in opposite directions.

3.6. Sensitivities

Sensitivities, like logarithmic gains, provide a measure of how the system steady state concentrations and steady state fluxes change with changes to rate constants and kinetic orders. Again, these values provide a relative indication of effect.

3.6.1. Sensitivities of the Rate Constant Parameters on the Metabolites

Metabolite sensitivities with respect to a rate constant indicates a relative change in the steady state dependent concentration X_i in response to changes in the rate constant, calculated by differentiation. For S-systems, some sensitivities are linked by the structure of the equation system. Increasing a production rate constant is mathematically equivalent to decreasing the corresponding degradation rate constant. Therefore, the sensitivity of X_i with respect to α is equivalent but with negative sign to the sensitivity of X_i with respect ß. This can be expressed as the following equations giving the relative change in a dependent concentration X_i with respect to relative change in the rate constants α and ß.

$$\begin{array}{cc}\hfill S(X_i,{\beta }_j)& =\left(\frac{\partial X_i}{\partial {\beta }_j}\frac{{\beta }_j}{X_i}\right)=\frac{\partial \left(\log X_i\right)}{\partial \left(\log {\beta }_j\right)}i,j=1,2,\dots ,n\hfill \\ \hfill S(X_i,{\alpha }_j)& =\left(\frac{\partial X_i}{\partial {\alpha }_j}\frac{{\alpha }_j}{X_i}\right)=\frac{\partial \left(\log X_i\right)}{\partial \left(\log {\alpha }_j\right)}i,j=1,2,\dots ,n\hfill \end{array}$$

3.6.2. Sensitivities of the Rate Constant Parameters on the Fluxes

The equations for the sensitivities of the rate constants with respect to the fluxes are

$$\begin{array}{cc}\hfill S(V_i,{\beta }_j)& =\left(\frac{\partial V_i}{\partial {\beta }_j}\frac{{\beta }_j}{V_i}\right)=\frac{\partial \left(\log V_i\right)}{\partial \left(\log {\beta }_j\right)}i,j=1,\dots ,n\hfill \\ \hfill S(V_i,{\alpha }_j)& =\left(\frac{\partial V_i}{\partial {\alpha }_j}\frac{{\alpha }_j}{V_i}\right)=\frac{\partial \left(\log V_i\right)}{\partial \left(\log {\alpha }_j\right)}i,j=1,\dots ,n\hfill \end{array}$$

The details of these derivations of these equations can be found in (35). The PLAS program includes procedures to calculate the logarithmic gains and sensitivities.

3.6.3. Sensitivities of the Kinetic Order Parameters on the Metabolite

This sensitivity shows a relative change in X_i given a relative change in a kinetic order g_ij. This influence is given by a magnitude that correspond to S(X_i, g_ij).

The sensitivities with respect to kinetic orders are:

$$\begin{array}{cc}\hfill S(X_i,g_{jk})& =\left(\frac{\partial X_i}{\partial g_{jk}}\frac{g_{jk}}{X_i}\right)=\frac{\partial \left(\log X_i\right)}{\partial \left(\log g_{jk}\right)}i=1,2,\dots ,n;j=n+1,\dots ,m\hfill \\ \hfill S(X_i,h_{jk})& =\left(\frac{\partial X_i}{\partial h_{jk}}\frac{h_{jk}}{X_i}\right)=\frac{\partial \left(\log X_i\right)}{\partial \left(\log h_{jk}\right)}i=1,2,\dots ,n;j=n+1,\dots ,m\hfill \end{array}$$

3.6.4. Sensitivities of the Kinetic Order Parameters on the Fluxes

The change that can be generated in a flux when a kinetic order is changed is defined in the following fashion:

$$\begin{array}{cc}\hfill S(V_i,g_{jk})& =\left(\frac{\partial V_i}{\partial g_{jk}}\frac{g_{jk}}{V_i}\right)=\frac{\partial \left(\log V_i\right)}{\partial \left(\log g_{jk}\right)}i=1,2,\dots ,n;j=n+1,\dots ,m\hfill \\ \hfill S(V_i,h_{jk})& =\left(\frac{\partial V_i}{\partial h_{jk}}\frac{h_{jk}}{V_i}\right)=\frac{\partial \left(\log V_i\right)}{\partial \left(\log h_{jk}\right)}i=1,2,\dots ,n;j=n+1,\dots ,m\hfill \end{array}$$

3.7. Advantages of S-System Representation

In this analysis, we have chosen to use a modeling representation developed from BST, in particular the S-systems representation. Choosing this framework brings a wealth of theory, numerous examples from the literature, established methods for the analysis of biochemical systems, and freely available software implementing the required calculations. The S-system representation provides some additional advantages. The steady state in S-systems can be expressed in linear equations that govern the local behavior of the intact biological system (32). The formalism is consistent with biologically relevant allometric relationships that quantitatively characterize the relative growth among the parts of the biological systems. S-system equations allow explicit symbolic determination of conditions for local stability and have been shown to represent the behavior of many biological systems with sufficient accuracy. For further study, we recommend the textbook from Voit (35).