Branching patterns of root systems: comparison of monocotyledonous and dicotyledonous species

Abstract

Background and Aims Acropetal root branching is a major process which increases the number of growing tips and distributes their growth potential within the whole root system.

Methods Using a method presented in a recent paper, the defined branching traits were estimated in 140 different species, and the branching patterns of monocots (45 species) and dicots (95 species) were compared.

Key Results It was checked that the method also applied to monocots (not considered in the previous paper), and that all traits could be estimated in each species. Variations of most traits were even larger for monocots than for dicots. Systematic differences appeared between these two groups: monocots tended to have a larger range in apical diameters (stronger heterorhizy), with both finer and thicker roots; the diameters of their lateral roots were also more variable; their roots exerted a stronger dominance over lateral branches. Altogether, species exhibited two main dependencies among their traits that were illustrated using two axes: (1) the ‘fineness–density’ axis separated the species which develop very fine roots and branch densely, from species without fine roots which space out their branches; and (2) the ‘dominance–heterorhizy’ axis separated the species according to the range in their apical diameter which was positively correlated to the level of dominance of mother roots over their branches. Both axes and correlations were remarkably similar for monocots and dicots.

Conclusions Beyond the overall typology, this study went on to validate the phenotyping method in Natura, and showed its potential to characterize the differences in groups of species.

INTRODUCTION

The dynamics of the root system architecture result from the combination of several developmental processes. Among them, acropetal branching has a key role in the drastic increase of the number of root tips, and also in allotting growth potential to these new growing tips (Pagès, 2014).

The branching density, i.e. the number of lateral roots per unit length of mother root, is the most direct way of adjusting the number of new lateral meristems. Both genetic and environmental factors interact to modulate this variable, as shown by many authors (reviewed by Malamy, 2005; Hodge, 2009). Less obvious is the role of the branching process in defining the balance between the growth of a mother root and the growth of its daughter laterals. There is usually a hierarchy (or dominance) between a mother root and its lateral roots, laterals usually being finer and shorter than their mother. In his quantitative survey on different species, Pagès (2014) modelled this dominance using the relationship between the diameter of the lateral roots and that of their mother. Beyond its importance from a geometrical and economical point of view, the diameter of the root (measured in the young apical zone) is a key criterion to obtain a synthetic evaluation of its structure and fate. It can be measured on excavated roots, and correlations have been shown for many species and conditions between the diameter, internal structure and size of the apical meristem (e.g. review by Coutts, 1987; Varney et al., 1991). Regarding developmental dynamics, tip diameter has been linked to several aspects of growth: rate, duration, potential and even tropism (Coutts, 1987; Cahn et al., 1989; Pagès, 1995; Lecompte and Pagès, 2006; Wu et al., 2015, 2016). The production of branches by lateral roots is also related to their diameter in maize (Pagès and Pellerin, 1994; Wu et al., 2016). Furthermore, neighbouring lateral roots emerging along the same mother may exhibit important variations in their diameters and growth characteristics (Varney et al., 1991; Pagès, 1995; Lecompte et al., 2005). Several authors have defended the functional interest of such structural and growth variations along the same parent root (Forde, 2009; Pagès, 2011).

Considering the importance of these different aspects of root branching (i.e. number, growth potential and variation of laterals), Pagès (2014) proposed to regard acropetal branching through a set of traits dedicated to the simultaneous analysis of all these characteristics. Since the proposed method relies on excavated peripheral parts of the root system, namely tips with young laterals, it is rather easy to use, provided a careful excavation, scanning at high resolution and specific measurements on the obtained images are carried out. Like other methods, such as that of Fitter (1982, 1987) or that of Spek and Van Noordwijk (1994), it does not require the monitoring of the dynamics of the developmental processes. Therefore, it can be applied to isolated samples observed at a given stage, after excavation. However, in contrast to previous methods, it focuses on acropetal branching occurring in the young parts of the roots, not far from the growing tips. The considered diameters are those of the young and turgescent primary structures, before the influence of later radial growth or shrinkage related to desiccation and ageing further away from the tips.

In the reference paper (Pagès, 2014), the method was assessed on a set of 45 dicotyledonous species. The chosen traits were quantified for each species, and large interspecific variations were shown. Moreover, co-variations of traits were evidenced, which revealed trade-offs and branching types. This work legitimated the initial choice of regarding several attributes describing both branching density and apical diameters, which are associated with the growth potential of the laterals.

The applicability of the method, as well as the main results, deserves to be extended to a larger set of species and to monocotyledonous species. This is the main objective of this study, in which several questions are addressed. (1) Is the method also applicable and valuable for these species? (2) What are the main differences between dicots and monocots regarding their root branching patterns? (3) Are the between-trait correlations similar in this new set? The studied species were sampled from four different environments with two sites in Natura and two sites in pots.

MATERIALS AND METHODS

Sampling species and environments

The studied population contained 178 different sampling cases, each case being a species or cultivar (140 different species and cultivars) observed in a given environment (four different environments). We hereafter call this combination SE (Species × Environment). Each SE (among the 178) was sampled by excavating the roots of 3–6 different plants. Table 1 contains the information on the species (according to Tela botanica, www.tela-botanica.org, related to the French flora), cultivars and collection sites. Our aim was to characterize, through the set of quantitative traits defined in Pagès (2014), the root phenotype of each SE.

Table 1.

List of species and sampling sites

Species	Clermont	Avignon greenhouse	Nozeyrolles	Thouzon
Achillea millefolium			X
Agrostis capillaris			X
Agrostis vinealis			X
Alliaria petiolata				X
Allium cepa				X
Allium porrum			X	X
Alopecurus pratense	X
Alyssum simplex				X
Amaranthus hybridus				X
Amaranthus retroflexus				X
Ambrosia artemisiifolia				X
Anisantha sterilis				X
Anthoxanthum odoratum	X		X
Aquilegia vulgaris				X
Arabidopsis thaliana			X
Arenaria serpyllifolia				X
Arrhenatherum elatius	X
Artemisia annua				X
Artemisia vulgaris			X	X
Arum italicum				X
Arundo donax				X
Atriplex hortensis			X	X
Avena barbata				X
Brachypodium pinnatum			X
Brachypodium sylvaticum				X
Bromopsis erecta				X
Bromus hordeaceus				X
Bryonia cretica				X
Capsella bursa-pastoris			X	X
Cardamine hirsuta			X	X
Ceratochloa cathartica				X
Chelidonium majus				X
Chenopodiastrum hybridum			X
Chenopodium album			X	X
Cicer arietinum				X
Cirsium vulgare				X
Clematis vitalba				X
Cynosurus cristatus			X
Dactylis glomerata	X		X	X
Datura stramonium				X
Digitalis purpurea			X
Echinochloa crus-galli				X
Elytrigia campestris	X			X
Elytrigia repens
Erigeron canadensis				X
Erodium moschatum				X
Euonymus europaeus				X
Euonymus japonicus				X
Eupatorium cannabinum				X
Euphorbia helioscopia			X	X
Euphorbia peplus				X
Fallopia convolvulus			X	X
Festuca rubra	X			X
Fragaria vesca			X
Galeopsis segetum			X
Galium aparine			X	X
Geranium molle			X
Glaucium flavum				X
Hedera helix				X
Helianthus annuus				X
Hemerocallis species				X
Holcus lanatus	X		X	X
Hordeum murinum			X	X
Hypomea learii				X
Impatiens balfouri				X
Iris germanica				X
Lactuca serriola				X
Lamium album			X
Lamium amplexicaule				X
Lapsana communis			X	X
Lolium perenne	X		X	X
Lunaria annua				X
Lycopsis arvensis				X
Lysimachia arvensis			X	X
Malva neglecta				X
Matricaria discoidea			X
Medicago lupulina			X	X
Melilotus albus				X
Melissa officinalis				X
Mercurialis annua				X
Minuartia hybrida				X
Nigella damascena				X
Oenothera biennis				X
Oryza sativa ‘Azucena’		X
Oryza sativa ‘IAC165’		X
Oxalis corniculata				X
Panicum capillare				X
Panicum miliaceum				X
Papaver rhoeas				X
Parietaria judaica				X
Parthenocissus inserta				X
Phalaris arundinacea				X
Phleum pratense	X
Picris hieracioides				X
Pisum sativum ‘Kayanne’		X
Plantago lanceolata			X	X
Plantago major			X	X
Platycapnos spicata				X
Poa annua				X
Poa pratensis	X
Poa trivialis	X			X
Polygonum aviculare				X
Portulaca oleracea				X
Potentilla reptans			X	X
Prunus persica ‘GF’		X
Quercus suber		X
Ranunculus repens				X
Rubus species				X
Schedonorus arundinaceus	X
Senecio vulgaris			X	X
Setaria italica				X
Setaria verticillata				X
Silene latifolia				X
Silene vulgaris				X
Solanum lycopersicon				X
Solanum nigrum				X
Sonchus oleraceus			X	X
Sorghum bicolor				X
Sorghum halepense				X
Stellaria media			X	X
Tanacetum parthenium				X
Taraxacum officinale			X	X
Torilis nodosa				X
Trifolium repens			X	X
Trisetum flavescens	X
Triticum aestivum
Urtica dioica			X	X
Urtica urens				X
Verbascum nigrum			X
Verbascum sinuatum				X
Verbena officinalis				X
Veronica arvensis				X
Veronica hederifolia			X	X
Veronica persica			X	X
Vicia faba				X
Vinca major			X	X
Vinca minor			X	X
Viola odorata			X	X
Vulpia myuros				X
Zea mays ‘Palqui’		X		X

The first environment (for 13 different species, described in Pagès and Picon-Cochard, 2014) was represented by foam-insulated cylindrical pots (150 cm in length, 10 cm in diameter) filled with a natural sieved and fertilized soil (brown acid soil) and located outside under natural climate conditions near Clermont-Ferrand (Auvergne region, latitude, 45°77′; longitude, 3°14′; altitude, 339 m). These plants were sampled on two dates: mid-June and mid-July 2013.

The second environment (for two species and two rice cultivars) was also represented by insulated cylindrical pots (50 cm in length, 12 cm in diameter) filled with a mixture of sepiolite and sieved peat (60:40, v/v) located in a greenhouse near Avignon (Provence region, longitude, 43°92′, latitude, 4°88′, altitude, 33°m). For each species and cultivar, we sampled three different plants on two dates during June and July 2013. The sampled roots in pots had not reached the bottom of the pots.

The third and fourth environments were in Natura. The sampled species grew spontaneously in kitchen gardens and cultivated fields as weeds, in two different zones with uniform soils (described in Pagès, 2014). The third site was near Thouzon, in the south-east of France (Provence region, latitude, 43°57′; longitude, 4°59′; altitude, 50°m). The soil was a deep calcareous silty soil developed on loess. The fourth site was near Nozeyrolles, located in the Massif Central (Auvergne region, latitude, 44°59′; longitude, 3°24′; altitude, 1100°m). The soil was a sandy brown acid soil developed on a granitic arena.

Thus, most SE (159 out of 178) were observed in Natura (sites 3 and 4). The site of Thouzon represented 63 % of SE, while Nozeyrolles represented 26 %. The proportions of monocots and dicots were similar at the two sites (Thouzon, 27 % of monocots and 73 % of dicots; Nozeyrolles, 22 % of monocots and 78 % of dicots).

Root system excavation

When sampling in Natura (sites 3 and 4), we favoured isolated plants grown in recently cultivated soils (kitchen gardens or fields) or on recent mole-hills (in the case of pastures). A garden fork was used to demarcate a monolith around the chosen plant (radius 15–20 cm around the collar, 30–50 cm deep), and to extract it before putting it in a large bucket with water. Then, the monolith was gently washed with running water. The same washing procedure was used for pot-grown plants. When the root system was nearly free of soil and organic debris, it was left for several minutes to 1 h in a tray with salt water (5 g L⁻¹) and liquid soap to complete cleaning.

Measurements

Root systems were carefully separated and spread with mounted needles in a layer of water several millimetres deep contained in a transparent plastic tray. The densest root systems were cut into several pieces in order to minimize root overlap in the tray. Then they were scanned with a flatbed scanner (EPSON perfection V700) at a resolution of 1200–4800 dots per inch, using the transparent mode. The resolution was adjusted for each species (in this range) in order to get at least 8 pixels transversally to the finest roots and to measure them with sufficient accuracy. Previous tests had shown that this adjustment did not induce any bias, since we obtained the same values (on average) when measuring the same objects at these various resolutions.

Measurements were made manually (by eye) on the images using the ImageJ software (http://rsbweb.nih.gov/ij/) on the young branched part of the root, where acropetal branching occurs. On each identified sub-structure, we measured the diameter of the mother root, the diameter of the laterals and the distance along the mother root from each lateral to its proximal closest neighbour (see fig. 1 in Pagès, 2014). Depending on the architectural position of the mother root, the sub-structures studied had 1–15 laterals. We were careful, through a meticulous visual inspection, to sample roots with extreme diameters (finest and thickest) because these roots make it possible to estimate extreme diameters (parameters D_min and D_max) according to Pagès (2014). For each SE, we measured from 131 to 805 lateral roots, for a total number of 42 139 roots.

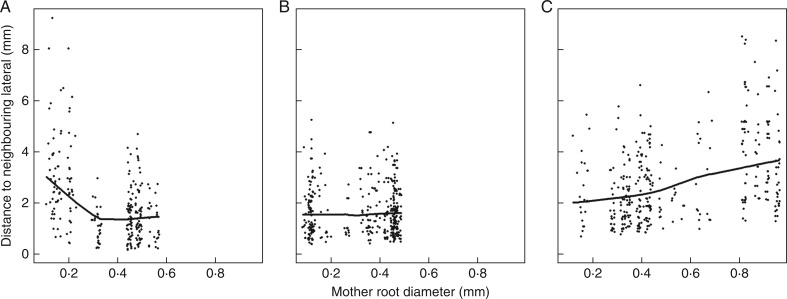
Fig. 1.

Relationships between interbranch distance and diameter of the mother root for three different species. (A) Anisantha sterilis; (B) Poa pratensis; and (C) Arrhenatherum elatius. The thick solid lines represent the trend between these variables (calculated by the ‘lowess’ smoother of R). The three graphs illustrate the three cases that we observed: (A) decrease in interbranch distance with mother root diameter; (B) independence; and (C) slight increase.

All diameters (also called ‘apical diameter’ hereafter) were measured on the young part of the root, close to the tip, at a location where it was nearly cylindrical. The distance from this position to the very tip was typically between 5 and 50 mm on the thickest roots, and from 2 to 20 on the finest ones. The youngest lateral roots, < 3 mm long, were discarded from these measurements. Zones of local thickening were observed along some roots (supposedly due to mechanical constraints), and were systematically discarded for diameter measurements. A number of root tips were broken by the procedure, but even on broken roots it was generally easy, on the high-resolution pictures, to recognize the young parts thanks to several criteria (colour, transparency of the structure, root hairs, lateral primordia).

Data analysis

All data treatments, plots and analyses were carried out with the R software (R Core Team, 2013; http://www.r-project.org/). Linear models were estimated with the ‘lm’ function in order to estimate parameters and conduct analyses of variance and covariance. In these analyses, SE was the qualitative factor. The diameter of the parent roots was the covariable to estimate the dominance slopes for each SE (see below). To study the shape of the trends between two variables graphically, we used the ‘lowess’ smoothing function of R, with the flexibility parameter at default value (f = 0·6). Principal component analyses (PCAs) were performed with the ‘ade4’ R package (Chessel et al., 2004). The PCAs were all centred and normalized.

The names and precise meanings of the considered traits are the same as in Pagès (2014). They are recalled in Table 2 and below with the results on their estimates. Each trait was estimated on each SE.

Table 2.

Abbreviations, significance, units and extreme values of the different traits (one value per species was estimated for each trait)

Parameter abbreviation	Significance	Unit	Range
Dmin	Minimal diameter (quantile 2 %)	mm	0·044–0·45
Dmax	Maximal diameter (quantile 100 %)	mm	0·24–2·6
Drange	Relative diameter range 2·0 × (Dmax − Dmin)/(Dmax + Dmin)	—	0·89–1·9
IBD	Interbranch distance on the thick roots (with a diameter above the middle value)	mm	0·51–7·0
DlDm	Slope of the regression of lateral diameter vs. mother diameter [regression passing through the point (Dmin,Dmin)]	—	0·062–0·39
VarD	Coefficient of variation of the diameter of laterals	—	0·099–0·41

RESULTS

Diameter distribution

We observed a 10-fold difference in extreme diameters among SE: between 0·044 and 0·45 mm for D_min and between 0·24 to 2·6 mm for D_max.

The correlation between minimal and maximal diameter across cases was not significant at the 5% level, showing that the range in diameters was also highly variable. Some species have both fine and thick roots (e.g. Setaria verticillata, Sorghum bicolor), while others have relatively homogeneous and intermediate diameters (e.g. Clematis vitalba, Euonymus europaeus). These variations legitimated the use of the trait called Drange (relative range in diameters) and its inclusion in the PCA below.

Interbranch distance (IBD)

Within several SEs (i.e. species in its sampling environment, as defined in the Materials and Methods), the distance between neighbouring laterals was dependent on the mother root diameter, since we obtained low but significant correlations. Three examples are illustrated in Fig. 1. In the first one (Fig. 1A), the distance decreased with the mother root diameter. In others, it was rather independent of the mother root diameter (Fig. 1B) or even tended to increase (Fig. 1C). Therefore, the IBD trait was calculated for each SE as the mean IBD on the thick roots, i.e. those thicker than the middle of the range in diameters for the given SE (Table 2). IBD exhibited large variations, between 0·51 and 7·0 mm (approx. 14-fold variations).

Relationship between diameters of mother and lateral roots

The Pearson correlation coefficients between the diameters of a mother root and those of its laterals were highly significant for all SEs. P-values were between 0·000 and 0·002. Moreover, a systematic visual inspection of each SE graph showed that the trends (represented on Fig. 2 by the smooth lines) were approximately linear. Some small deviations from the linearity were observed, but they did not show any common shape from one SE to another.

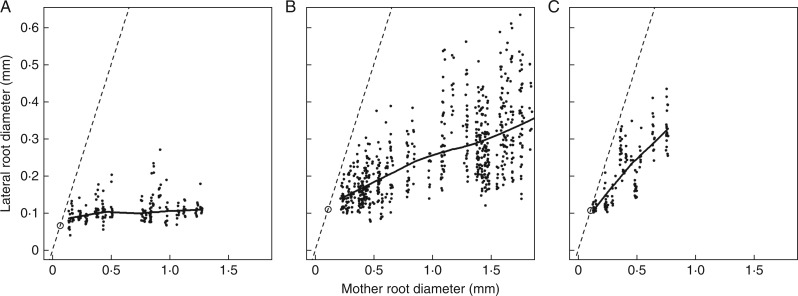
Fig. 2.

Relationships between lateral and mother diameter for three different monocots. (A) Setaria verticillata; (B) Sorghum halepense; and (C) Vulpia myuros. The thick solid lines represent the trend between these variables (calculated by the ‘lowess’ smoother of R). The bisecting line is also drawn as well as the particular point with coordinates (D_min, D_min), to show that the trends would intersect the bisecting line near this particular point.

Regression lines always intersected the bisecting line near the point of co-ordinates (D_min, D_min). Moreover, we observed on the images that the finest roots, when they branched, gave rise to laterals which had about the same diameter as themselves. Thus, the hypothesis that the regression lines passed through this point (D_min, D_min) was tested independently for all SEs. We used the test of a zero intercept for the regression of the lateral root diameter (with D_min subtracted) on that of its mother (with D_min subtracted). This test was rejected only 19 times out of 178 at the 0·001 P-level. In these cases, the estimated intercepts were very small (<0·02 mm) and were either positive or negative. Therefore, we decided to force the regression lines to pass through this particular point (D_min, D_min) for all SEs, in order to get a more robust estimate of the slope (called DlDm hereafter) following the same protocol. We also checked that we did not obtain a negative correlation between D_min and DlDm.

We also used a covariance model (the parent root diameter being the covariate, the SE being the interaction factor) to test the effect of the SE on the slope. It was shown to be highly significant, when compared with the simpler model considering a single common slope. The slope estimates (DlDm) varied within a 6-fold range, with extreme species being Setaria verticillata on the one hand, exhibiting a strong hierarchy of the mother to its laterals (slope: 0·062), and Nigella damascena on the other hand, exhibiting a low hierarchy (slope: 0·39).

Because both the average and the standard deviation of the diameter of laterals depended on the parent root diameter (see Fig. 2), we also estimated the coefficient of variation of the lateral root diameter (VarD, table 2). For this estimation, we made successive classes of mother root diameter with the same number of lateral roots (around ten in each class). For each class, we calculated the average and s.d. of the lateral root diameter. We fitted a linear model without intercept (s.d. vs. average of diameter). Its slope was the coefficient of variation (VarD). VarD exhibited large (4-fold) interspecific variations, with species having homogeneous laterals (e.g. Allium porrum) and others having highly variable laterals (e.g. Echinochloa crus-galli).

Distribution of traits between monocots and dicots

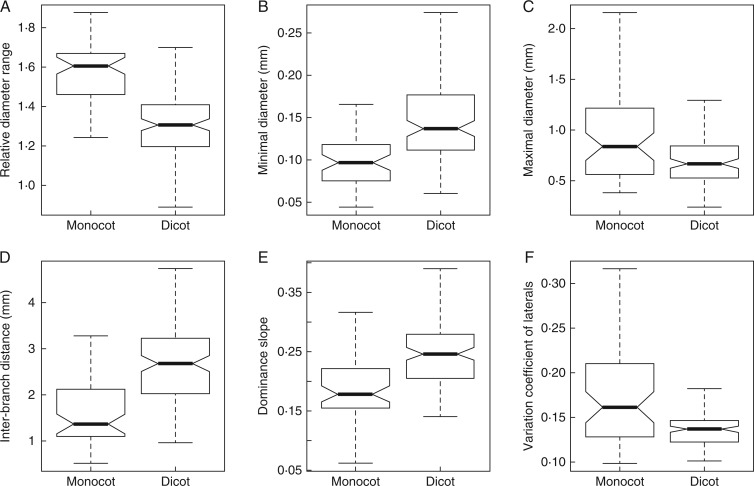
Figure 3 presents the synthesis of these comparisons through boxplots. All traits exhibited different distributions for the two sub-populations, and the median values were significantly different. The relative diameter range (Table 2; Fig. 3A) was much higher for monocots. This was due both to the minimal diameter (Fig. 3B), which tended to be lower for monocots (except for some species), and to the maximal diameter (Fig. 3C), which tended to be higher for monocots. The IBD (Fig. 3D) was higher for dicots (median: 2.7) than for monocots (median: 1·4). The dominance (Fig. 3E) was usually higher for monocots (lower slope values), and the variation coefficients (Fig. 3F) were also clearly higher. These coefficients were more homogeneously distributed among dicots than among monocots.

Fig. 3.

Boxplots showing the distribution of the traits between the two sub-populations [monocots (n = 57) and dicots (n = 121)] among all SE (i.e. Species in a given Environment). Horizontal lines represent quantiles at probability levels of 0·05, 0·25, 0·50, 0·75 and 0·95. Notches in the boxes represent the confidence intervals on the medians.

Relationships between traits

Principal component analysis was achieved for monocots and dicots separately (Fig. 4A, B) and together (Fig. 4C). The data sets contained the different SEs (Table 1) as individuals and the six traits as variables (Table 2).

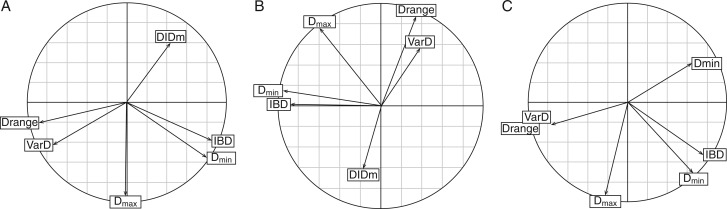
Fig. 4.

Principal component analysis. Variables (i.e. traits) located on the plane defined by component 1 (horizontally) and 2 (vertically). (A) Monocots only; (B) dicots only; (C) all species together. See the text and Table 2 for the explanations of the traits.

Figure 4A and B shows the same co-variation pattern obtained for the two sub-populations. The arrows were just rotated from one figure to the other. The first plane (containing the first two components) explained 81 % (49 plus 32 %) of the total variation on monocots and 73 % (40 plus 33 %) on dicots. Because of obvious similarities, we included all species and made a third synthetic PCA (Fig. 4C). As expected, this last PCA exhibited the same pattern. The first plane explained 80 % (48 plus 32 %) of the total variation and represented all traits correctly, since they were all close to the correlation circle.

On this plane, we can distinguish two groups of correlated variables (D_min and IBD on the one hand, and Drange, VarD and DlDm on the other hand) and an isolated one (D_max). In the first group, IBD and D_min were significantly and highly correlated (R = 0·81 for the overall population; R = 0·74 for dicots and R = 0·88 for monocots). In the second group, correlations were lower, but still highly significant (between Drange and DlDm: R = −0·59 for the overall population; R = −0·34 for monocots; R = −0·51 for dicots).

Definition of two main axes of variations

These two groups of variables, which are nearly perpendicular in the PCA plane, defined two axes which explained most variations. These two axes are presented in Figs 5 and 6 to show their general shape and the relative position of species (monocots and dicots).

Fig. 5.

Fineness vs. density relationship.

Fig. 6.

Heterorhizy vs. dominance slope relationship.

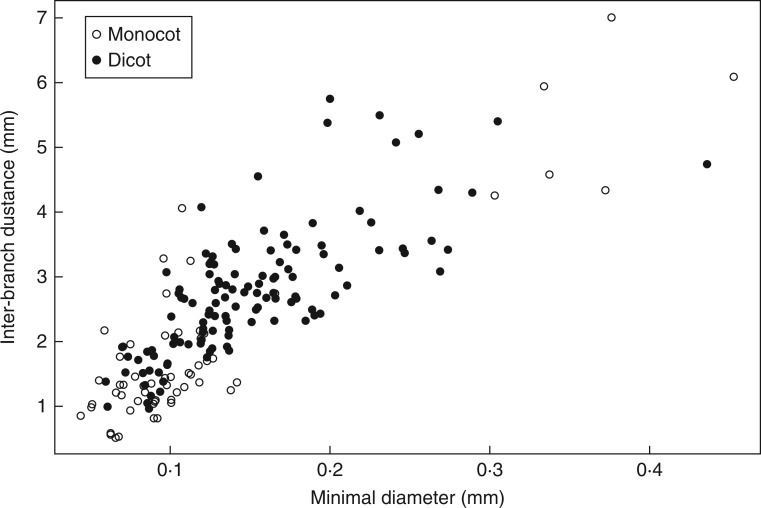
The relationship between D_min and IBD (Fig. 5) was tight and common for the two groups (monocots and dicots). Monocots had the largest range for both variables, while dicots occupied more intermediate positions. This axis was called the ‘fineness–density’ axis, since it characterizes the species simultaneously for these two visual criteria.

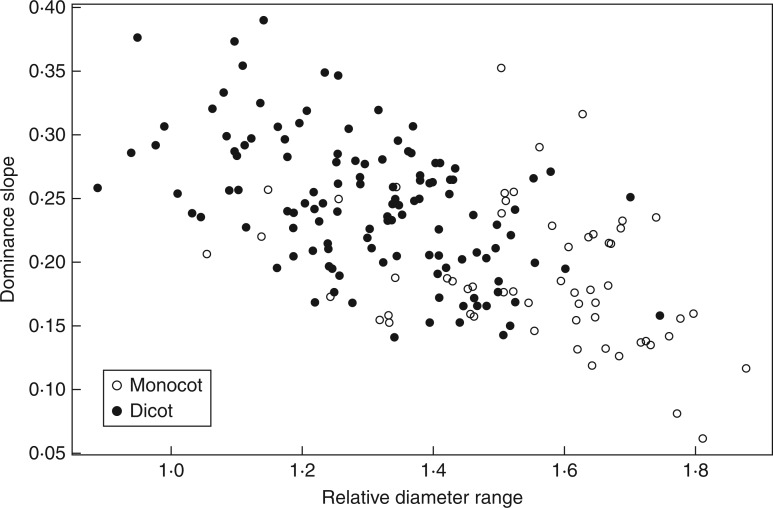
The second main axis of variation (DlDm vs. Drange; Fig. 6) was also common to the groups which followed approximately the same trend. However, they were more discriminated: monocots had larger ranges in diameters and stronger dominances. This axis was called the ‘heterorhizy–dominance’ axis. Species with a strong heterorhizy (sensu Sutton and Tinus, 1983) regarding diameter also had a strong dominance; and vice versa, species with a weak dominance had homogeneous roots.

DISCUSSION

Validation of the method for phenotyping root branching

We have further validated the new method proposed by Pagès (2014) for characterizing the acropetal branching patterns, which includes protocols for data acquisition and treatment in order to obtain a defined set of quantitative traits for each phenotype. It was applied to a large set of different species from several families, on which we could estimate all traits and checked the validity of the main correlations between the measured variables. Moreover, we demonstrated the possibility of obtaining the required data from plants sampled in various environmental conditions (in Natura and in containers). In comparison with the previous study, we have simplified the data analysis and quantification by keeping only six different traits (those presented in Table 2) because we wanted to make it as simple as possible, and the selected traits were considered to be the essential ones. Thus, we confirm that the method is rather easy to apply, although it requires meticulous measurements on high quality images. Thus, it can be integrated with various types of research approaches to characterize roots in ecosystems or plants (phenotyping; see, for example, Walter et al., 2015). At the present stage, the throughput is rather low because the different steps (excavation, sampling and measurements) are carried out manually. However, each step can be improved in the future. In the present study, our aim was first to confirm the feasibility and interest of this quantitative approach. The next steps should be dedicated to the optimization of root collection, data acquisition and treatment.

Main points of this method

The most important and original points are: (1) to focus on the peripheral parts of the root system which extend and branch; (2) to consider branching and growth indicators (diameters) simultaneously; (3) to consider extreme apical diameters instead of average ones; and (4) to make a bridge between static observations and dynamic simulations of root systems.

The first point is crucial, since the young parts exhibit several morphological indicators which can reveal the developmental processes which occurred just before excavation. For example, IBD on young roots serves to characterize acropetal branching density. Branching density can be modified later (on older roots) by other developmental processes when root decay and self-pruning occur. This approach is in line with the recommendations of several authors (Guo et al., 2008; Pagès et al., 2010; McCormack et al., 2015) who pointed out the interest in focusing on the peripheral parts of root systems. This focus might also appear as a weakness since the young parts which are affected by the sampling procedure are the most fragile. Excavation methods are important in this context: getting medium sized monoliths instead of small auger samples is an important means to get branched root samples in good condition. Therefore, this approach should be associated with suitable methods to extract and wash such monoliths, such as that proposed by Wu and Guo (2014). Application of the method to very strong or stony soils would be very challenging if not impossible.

The second point was confirmed in this work by several strong correlations between diameters and branching attributes (e.g. fineness–density axis presented on Fig. 5). It shows that these two aspects of branching are co-ordinated, and should be considered together for a better comprehension of the branching process and its consequences in root foraging.

The third point is related to the heterogeneity of root tip diameters in root systems (called ‘heterorhizy’ for brevity). This is a major aspect for the development and functioning of root systems that cannot be captured by considering only average or median diameters. Many species which are similar regarding their mean diameter are very different regarding their range, and consequently have different foraging characteristics. The differences between monocots and dicots exemplified this point, since monocots usually exhibited large Drange values (e.g. Sorghum bicolor, between 0·075 and 2·4 mm), while most dicot species have much more homogeneous diameters (e.g. Medicago lupulina, between 0·160 and 0·480 mm).

Moreover, when making the observations, we found it relatively easy (with magnifying glasses) to sample the extreme roots when the root systems were correctly disentangled and laid out in a large tray with water, and it was thus possible to characterize extreme diameter quantiles. Conversely, from our experience, average values are not easy to obtain in such populations, and the risks of bias are important because of the usual huge asymmetry of diameter distributions.

The fourth point is important as well, because we know how difficult it is to get dynamic data on root systems. Therefore, connecting static data that can be obtained in relevant environmental conditions to models of the root system architecture is an interesting task, in order to synthesize the dynamic branching patterns in silico. The link is in line with some recent models (Pagès, 2011; Pagès and Picon-Cochard, 2014) since several traits which were measured following this method are also parameters of the dynamic simulation models. For example, Pagès and Picon-Cochard (2014) showed how the architecture model could serve to interpolate data between sampling dates or to link traits at different scales.

Variations of root traits in the SE population

The six considered traits were highly variable from one SE to another. For example, we observed 14-fold variations for the IBD and 11-fold variations for the maximal diameter. The SE variations were phenotypes, which mixed species and environmental effects. Since the study was a survey of existing species on several sites, only a limited number of species was sampled from several sites. Therefore, this work could not be strictly devoted to the study of the species effects on the traits. However, we noticed on the PCA graphs that SE of the same species usually had close positions (data not shown). A systematic study on this topic will require a suitable sampling schema with a sufficient number of species on several sites.

In comparison with previous works using similar traits (Pagès, 2014; Bui et al., 2015), we observed that the addition of new species in the population extended the range of variation for all traits and confirmed the main conclusions of Pagès (2014). Conversely, the correlations that were pointed out by Bui et al. (2015) in Solanaceae species were slightly different from those presented here, probably because the genetic background of their study was much narrower. For example, the variations in minimal diameter (D_min) in Solanaceae species were very low in comparison with ours.

Comparison of monocots and dicots

Regarding the monocot and dicot groups, our survey was nearly balanced regarding the number of samples in Natura, which represented 90 % of the total SE population. Therefore, this two-level factor (monocot and dicot) was not confused with the environmental effect. Its effect could thus be presented and qualitatively tested. For this purpose, we used exploratory tools such as the ‘boxplot’ function of the R software.

The addition of monocots to the population of SE (from that of Pagès, 2014) largely contributed in extending the range of variation for several traits. A number of species, especially among the Poaceae family, exhibited very low values for their minimal diameter and IBD. Several of them were also among the species with the largest maximal diameters. Thus, we found the highest levels of heterorhizy among monocots. High heterorhizy levels were associated with a high dominance level and high coefficients of variation of laterals. Strong dominance tends to give ‘herringbone patterns’, as noticed by other authors in various Poaceae species (e.g. Fitter and Stickland, 1991; Taub and Goldberg, 1996; Roumet et al., 2006; Arredondo and Johnson, 2011), and it often produces laterals with variable diameter, length and structure. The variability among laterals (VarD) could not be quantified satisfactorily by the Fitter’s method, although it was already mentioned as a particular feature in several Poaceae species (Varney et al., 1991; Pagès and Pellerin, 1994; Lecompte and Pagès, 2006; Arredondo and Johnson, 2011). We hypothesize that the high levels of heterorhizy and dominance that we observe in monocots might be due to the inability of these species to undergo radial growth. Radial growth is a process which enables a later adjustment of the capacity of roots for water transport and anchorage strength. Species which cannot undergo radial growth must build variable roots from the beginning, i.e. from their primary structures. We can also say that lateral roots are constrained by the structure of their parent root. Their subordination can be seen as a means to cope with the fixed structure in which they appear.

Correlations between traits, and main axes of branching types

We have confirmed the correlation structure (with essentially two groups of correlated traits) that we discovered and discussed in the previous paper (Pagès, 2014). Moreover, we have shown that the same structure appeared in both groups of species, confirming the robustness of the underlying correlations and their significance in terms of developmental co-ordination. Thanks to these stable correlations, trait variations could be summarized through two axes which represent trade-offs: ‘fineness–density’ on the one hand, and ‘heterorhizy–dominance’ on the other hand. These two axes are interesting because they are nearly independent and they represented most of the variation extracted by the first plane of the PCA (approx. 80 % of the total variation). They are even simpler and clearer than the branching types which were defined in the previous companion paper (Pagès, 2014). In the latter, we discussed the possible functional significance of these two axes regarding foraging strategies. Future work, using this method, could be more specifically dedicated to defining these strategies and testing the efficiency of these various root systems for different types of resources (water and nutrients). The present characterization also opens up new avenues to study the associations of these species with mycorrhizae. For example, interesting questions could be investigated on the relationships between fineness and mycorrhizal association.

Conclusion

The proposed method devoted to the quantification of branching patterns was validated and its interest was confirmed by this study in a large set of species coming from monocots and dicots. The branching typology was made simpler and clearer thanks to the definition of two main and independent axes of variation which can be seen as developmental trade-offs. The differences between the two groups (monocots and dicots) were evidenced and quantified using several criteria. The genetic and environmental determinism of these traits should be investigated in more detail.