Multi‐arm group sequential designs with a simultaneous stopping rule

Abstract

Multi‐arm group sequential clinical trials are efficient designs to compare multiple treatments to a control. They allow one to test for treatment effects already in interim analyses and can have a lower average sample number than fixed sample designs. Their operating characteristics depend on the stopping rule: We consider simultaneous stopping, where the whole trial is stopped as soon as for any of the arms the null hypothesis of no treatment effect can be rejected, and separate stopping, where only recruitment to arms for which a significant treatment effect could be demonstrated is stopped, but the other arms are continued. For both stopping rules, the family‐wise error rate can be controlled by the closed testing procedure applied to group sequential tests of intersection and elementary hypotheses. The group sequential boundaries for the separate stopping rule also control the family‐wise error rate if the simultaneous stopping rule is applied. However, we show that for the simultaneous stopping rule, one can apply improved, less conservative stopping boundaries for local tests of elementary hypotheses. We derive corresponding improved Pocock and O'Brien type boundaries as well as optimized boundaries to maximize the power or average sample number and investigate the operating characteristics and small sample properties of the resulting designs. To control the power to reject at least one null hypothesis, the simultaneous stopping rule requires a lower average sample number than the separate stopping rule. This comes at the cost of a lower power to reject all null hypotheses. Some of this loss in power can be regained by applying the improved stopping boundaries for the simultaneous stopping rule. The procedures are illustrated with clinical trials in systemic sclerosis and narcolepsy. © 2016 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.

1. Introduction

Multi‐arm clinical trials simultaneously compare several doses, treatments or treatment regimens to a control while controlling the familywise error rate (FWER) in the strong sense. Group sequential versions of multi‐arm clinical trials in addition include interim analyses where recruitment in some or all arms may be stopped early, either for futility if no promising treatment effect is observed or because the respective null hypotheses can be rejected based on the interim data. These group sequential trials require, on average, less patients than fixed sample designs, which is particularly important in rare diseases or sensitive populations as children 1. The stopping boundaries for such group sequential designs can be determined by simulation, the Bonferroni inequality 2 or numerical integration 3. Recently, these tests (which are based on single step multiple testing procedures) have been improved by the closed testing procedure to sequentially rejective tests 4.

In this paper, we consider multi‐arm multi‐stage designs with two different stopping rules to achieve two different objectives: (i) the objective to detect at least one effective treatment and (ii) the objective to identify all effective treatments. The simultaneous stopping rule suited to accomplish objective (i) stops the whole trial as soon as for a single treatment arm, the null hypothesis of no treatment effect can be rejected. When the trial is stopped early, also for all other treatment arms, a hypothesis test is performed based on the interim data, and no additional subjects are recruited. Thus, the simultaneous stopping rule stops recruitment in all treatment arms simultaneously at the same interim analysis. On the other hand, to meet objective (ii), we consider the classical stopping rule for multi‐arm multi‐stage designs, where the stopping decision for each experimental treatment arm depends only on the test statistics comparing the respective arm to the control. We refer to the latter as the separate stopping rule. The critical boundaries derived for classical multi‐arm group sequential designs with the separate stopping rule control the FWER also if the simultaneous stopping rule is applied but are typically strictly conservative and do not exhaust the type I error rate. Therefore, we derive improved critical boundaries for closed group sequential testing procedures using the simultaneous stopping rule. The improvement of the critical values is based on a methodological approach that is closely related to the methods used to improve group sequential tests with multiple endpoints 5, 6, 7, 8, 9. Similar as in the multiple endpoint setting, the multiple testing procedure can be improved by taking into account the stopping rule. However, in the setting of multi‐arm trials considered here, the correlation between test statistics is known (in contrast to test statistics for multiple endpoints) such that sharper critical values can be derived.

Wason and Jaki 10 optimized multi‐arm group sequential designs with a simultaneous stopping rule applying single step multiple testing procedures. The testing procedures considered here uniformly improve this single step test in two ways: first, by applying a sequentially rejective test based on the closure principle as in 4 and second, by accounting for the stopping rule.

We illustrate the approach by improving O'Brien Fleming and Pocock type group sequential boundaries and compare the operating characteristics to tests with classical group sequential boundaries when simultaneous as well as separate stopping rules are applied. Furthermore, we optimize the critical boundaries to minimize the average sample number for the separate and the simultaneous stopping rule.

The paper is organized as follows: In Section 2, the model is introduced, and the level α conditions for group sequential multi‐arm clinical trials with separate and simultaneous stopping are derived. In Section 3, the operating characteristics of the improved O'Brien Fleming and Pocock type boundaries are compared with classical multi‐arm group sequential designs. In Section 4, optimal critical boundaries for simultaneous and separate stopping are derived. In Section 5, the simultaneous stopping designs are extended to four arm trials. The approach is illustrated by clinical trial examples with two and three experimental treatment arms in Section 6. Finally, in Section 7, we investigate the procedure in settings with small sample sizes.

2. Model and notation

Consider a two‐stage, three‐arm group sequential clinical trial comparing the means μ _i,i = A,B,0 of a normally distributed outcome of two experimental treatments (A and B) to a control (0) testing the one‐sided hypotheses

$$H_A:{\mu }_A\le {\mu }_0\text{vs.}{H}_A^{\prime }:{\mu }_A>{\mu }_0\text{and}{H}_B:{\mu }_B\le {\mu }_0\text{vs.}{H}_B^{\prime }:{\mu }_B>{\mu }_0.$$

The overall FWER is to be controlled at level α in the strong sense. Let n ₁,n denote the first stage and maximum sample sizes in the two experimental treatment arms, r n ₁,r n the respective sample sizes in the control group for some allocation ratio r > 0, and Z _ij the standard z‐test statistics for treatment group i = A,B at stage j = 1,2. Note that Z _i2,i = A,B denote the cumulative test statistics based on the observations from both stages. Then, under the assumption of known and equal variances across treatment groups, the vector (Z _A1,Z _B1,Z _A2,Z _B2) follows a multivariate normal distribution with mean $({\delta }_A\sqrt{r{n}_1/(r+1)},{\delta }_B\sqrt{r{n}_1/(r+1)},{\delta }_A\sqrt{\mathrm{rn}/(r+1)},{\delta }_B\sqrt{\mathrm{rn}/(r+1)})$ and covariance matrix

$$\mathrm{\Sigma }=\left(\begin{array}{cccc}1& \rho & \sqrt{\frac{n_1}{n}}& \rho \sqrt{\frac{n_1}{n}}\\ \rho & 1& \rho \sqrt{\frac{n_1}{n}}& \sqrt{\frac{n_1}{n}}\\ \sqrt{\frac{n_1}{n}}& \rho \sqrt{\frac{n_1}{n}}& 1& \rho \\ \rho \sqrt{\frac{n_1}{n}}& \sqrt{\frac{n_1}{n}}& \rho & 1\end{array}\right),$$

where δ _A=μ _A−μ ₀,δ _B=μ _B−μ ₀ denote the effect sizes and ρ = 1/(1 + r) the correlation because of the common control. Next, we state the level α conditions for the group sequential designs with separate and simultaneous stopping rules and derive improved rejection boundaries for the latter.

2.1. Stopping boundaries for the separate stopping rule

Following Magirr et al. 4, we apply the closure principle to define a sequentially rejective group sequential test and specify group sequential local level α tests for the intersection hypothesis $H_A\cap H_B$ and the elementary hypotheses H _A, H _B. Then, the closed test rejects an elementary hypothesis H _i,i = A,B at multiple level α if the intersection hypothesis $H_A\cap H_B$, and the corresponding elementary hypothesis H _i are rejected with the respective group sequential local level α tests.

Let u ₁,u ₂ (which we call global boundaries) denote the rejection boundaries for the intersection hypothesis test at the interim and the final analysis. Similarly, let v ₁,v ₂ (the elementary boundaries) denote the rejection boundaries for the local elementary hypothesis tests of H _A and H _B. We assume that the same elementary boundaries v ₁,v ₂ are applied for H _A and H _B. Furthermore, l ₁ denotes an interim futility boundary. Then, with the separate stopping rule, recruitment stops at the interim analysis for treatment arm i = A,B if Z _i1<l ₁ (stopping for futility) or $Z_{i1}\ge v_1$ and ${\max }_{i=A,B}{Z}_{i1}\ge u_1$ (early rejection). To control the local level α, the stopping boundaries of the intersection hypothesis test have to satisfy

$$\begin{array}{c}{P}_{H_A\cap H_B}(\underset{i=A,B}{\max }{Z}_{i1}\ge u_1)+P_{H_A\cap H_B}\left\{\left(\underset{i=A,B}{\max }{Z}_{i1}<u_1\right)\wedge \right.\\ \left.\left[\left(Z_{A1}\ge l_1\wedge Z_{A2}\ge u_2\right)\vee \left(Z_{B1}\ge l_1\wedge Z_{B2}\ge u_2\right)\right]\right\}\le \alpha ,\end{array}$$ (1)

where $P_{H_A\cap H_B}$ denotes the probability under $H_A\cap H_B$. Note that, as shown in 3, the least favourable configuration (defined as the parameter configuration that maximizes the probability of an erroneous rejection) under the global null hypothesis where δ _A≤0,δ _B≤0 is δ _A=δ _B=0.

The stopping boundaries for the elementary tests have to satisfy

$$P_{H_i}(Z_{i1}\ge v_1)+P_{H_i}(l_1\le Z_{i1}<v_1\wedge Z_{i2}\ge v_2)\le \alpha .$$ (2)

In addition, we require the critical boundaries for the elementary hypothesis H _i,i = A,B to satisfy v ₁≤u ₁ and v ₂≤u ₂ to obtain a consonant closed test such that the rejection of the intersection hypothesis implies rejection of at least one elementary hypothesis. Then, the closed test simplifies to a sequentially rejective testing procedure, where first the critical boundaries u ₁,u ₂ are applied, and, if at least one of the hypotheses can be rejected, the remaining hypothesis is tested with the critical boundaries v ₁,v ₂ 11.

Note that when directly applying the closed testing procedure, there are outcomes where the trial continues to the final analysis and an elementary hypothesis is rejected because an interim test statistics crosses a rejection boundary, while the final test statistics does not. Consider, for example, the outcome where the interim test statistics for treatment B crosses the interim boundary of the elementary hypothesis test ( $Z_{1,B}\ge v_1$), both treatments are continued to the second stage because the intersection hypothesis cannot be rejected (i.e. l ₁≤Z _1,A≤u ₁,l ₁≤Z _1,B≤u ₁), but at the final analysis, the intersection hypothesis (and H _A) can be rejected, because, for example $Z_{2,A}\ge u_2$. Now, if Z _2,B<v ₂, then H _B could be rejected in retrospect based on the interim data only (even though the test statistics at the final analysis does not cross the respective rejection boundary). While this does not inflate the type I error rate, it disregards the second stage data for that treatment, which is undesirable in the application to clinical trials. Therefore, we modify the local hypothesis tests of H _A and H _B in the closed testing procedure by excluding retrospective rejections from the rejection regions. Then, for H _A the rejection region of the local level α test is given by $R_A^{}={\bigcup }_{i=1}^5{R}_i$, where

$$\begin{array}{cc}{R}_1^{}& =\{Z_{1,B}<u_1\wedge Z_{1,A}\ge u_1\}\\ R_2^{}& =\left\{Z_{1,B}\ge u_1\wedge \left[Z_{1,A}\ge v_1\vee \left(l_1\le Z_{1,A}\wedge Z_{2,A}\ge v_2\right)\right]\right\}\\ R_3^{}& =\{Z_{1,B}<l_1\wedge l_1\le Z_{1,A}<u_1\wedge Z_{2,A}\ge u_2\}\\ R_4^{}& =\{l_1\le Z_{1,B}<u_1\wedge l_1\le Z_{1,A}<u_1\wedge Z_{2,B}\ge u_2\wedge Z_{2,A}\ge v_2\}\\ R_5^{}& =\{l_1\le Z_{1,B}<u_1\wedge l_1\le Z_{1,A}<u_1\wedge Z_{2,B}<u_2\wedge Z_{2,A}\ge u_2\}.\end{array}$$ (3)

The rejection region R _B for H _B is defined by analogy with A and B exchanged. Some comments are as follows: (i) If the modified rejection regions R _A, R _B are applied, this results in a strictly conservative test for certain parameter configurations. However, the respective level α conditions cannot be relaxed as the test still exhausts the level α in the least favourable configurations. The least favourable configuration for the local hypothesis test of H _A is the setting where treatment A has no effect (δ _A=0), and the effect size of the other treatment approaches infinity (δ _B→∞) (Figure 1). The type I error rate under this parameter configuration approaches α. Similar as in 3, one can show that scenarios where δ _A<0 lead to a lower type I error rate. (ii) The closed testing procedure based on the intersection and elementary hypotheses tests defined previously exhausts the FWER in two scenarios: if one of the treatments has no effect but the effect size of the other approaches infinity and under the global null hypothesis, if δ _A=δ _B=0. For comparison, in the single step testing procedure considered in 3 (which corresponds to a closed test where both, the intersection and the elementary hypotheses, are tested with the boundaries u ₁,u ₂), only δ _A=δ _B=0 is a least favourable configuration. (iii) The rejection regions $R_A^{},R_B^{}$ are contained in the rejection regions of the intersection hypothesis test. Therefore, they are also the rejection regions of the closed testing procedure. (iv) The level α conditions ((1)) and ((2)) apply when assuming a binding stopping for futility rule. If the futility stopping boundaries are not binding (i.e. the data monitoring committee may override them), then the level conditions ((1)) and ((2)) have to be modified by replacing l ₁ by −∞. The actually performed test will be strictly conservative if a non‐binding stopping rule for futility is applied.

Figure 1.

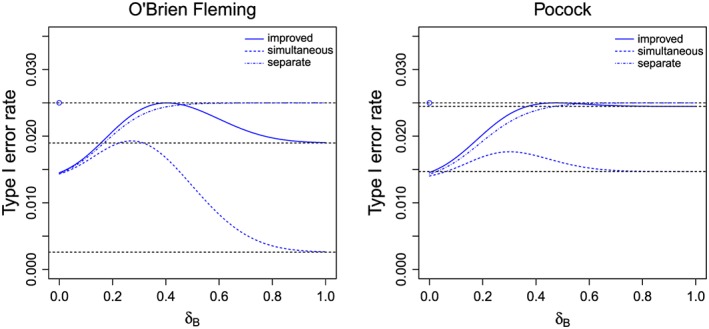
The type I error rate $P_{0,{\delta }_B}\left(R_A^{\prime }\right)$ to reject H _A as function of δ _B when applying the simultaneous stopping rule or separate stopping rule for boundaries v ₁,v ₂ satisfying ((2)) (dashed curves) or the simultaneous stopping rule for improved boundaries v1′,v2′ = v ₂ where v1′ solves ((4)) (solid curves) for O'Brien Fleming boundaries (left graph) and Pocock boundaries (right graph). No futility bound is applied (l ₁=−∞). The horizontal dashed lines show the nominal α level and the levels corresponding to v1′ and v ₁.

2.2. Stopping boundaries for the simultaneous stopping rule

If the critical boundaries u ₁,u ₂ and v ₁,v ₂ satisfying ((1)) and ((2)) derived for the separate stopping rule are applied, but the simultaneous stopping rule is followed, the FWER will still be controlled. This holds because the test of the intersection hypothesis $H_A\cap H_B$ has the same type I error rate for the simultaneous and the separate stopping rule. Furthermore, the tests of the elementary hypotheses will have a type I error rate lower than α under simultaneous stopping: if the closed test rejects only one of the elementary hypotheses at the interim analysis, the other hypothesis will not be tested at the final analysis, even if its interim test statistic lies in the continuation region (see Figure 1 for the actual type I error rates when Pocock (POC) or O'Brein Fleming (OBF) boundaries are used).

Consider, for example, the local test of H _A. If the test statistic for H _B crosses a rejection boundary at the interim analysis, the trial is stopped and H _A cannot be rejected in the final analysis. However, the probability to stop at the interim analysis without rejecting H _A(and as a consequence the actual type I error rate) depends on the effect size of treatment B. For example, at nominal level α = 0.025, the maximum type I error rate over all δ _B to reject H _A under simultaneous stopping is 0.018 (0.019) for the Pocock (O'Brien Fleming) design. Thus, the stopping boundaries v ₁,v ₂ can be relaxed such that the maximum type I error rate over all effect sizes of treatment B is equal to α, and the improved stopping boundaries v1′,v2′ for the test of the elementary hypothesis H _A satisfy

$$\underset{{\delta }_B}{\max }{P}_{0,{\delta }_B}\left(R{\prime }_A\right)=\alpha ,$$ (4)

where $P_{{\delta }_A,{\delta }_B}$ denotes the probability under μ _i−μ _c=δ _i,i = A,B. The rejection region for H _A is modified to $R_A^{\prime }={\bigcup }_{i=1}^5{R}_i^{\prime }$ with $R_2^{\prime }=\{Z_{1,B}\ge u_1\wedge Z_{1,A}\ge v_1^{\prime }\}$ and $R_i^{\prime }=R_i^{},i=1,3,4,5$ where v ₁,v ₂ is substituted by v1′,v2′ in ((3)). The type I error rate is maximal for δ _A=0 and decreases for negative δ _A, as can be shown along the lines of 3, where the monotonicity of the type I error rate in the effect sizes is shown for single step tests. Exchanging A and B, we obtain the rejection region R _B for the test of H _B.

Note that, compared with the separate stopping rule, the boundaries v ₁,v ₂ in the elementary hypotheses tests can be improved for simultaneous stopping but the boundaries u ₁,u ₂ for the intersection hypothesis test cannot. As the latter test exhausts the type I error rate under the global null hypothesis also under simultaneous stopping, the same rejection boundaries as for the separate stopping rule have to be applied.

Table 1 gives Pocock (POC) type (where v ₁=v ₂,u ₁=u ₂) and O'Brien Fleming (OBF) type (where $u_2=u_1\sqrt{n_1/n},v_2=v_1\sqrt{n_1/n}$) boundaries for equal per arm per stage sample sizes (r = 1,n ₁=n/2) and α = 0.025. It also shows the improved boundaries v1′,v2′ for the Pocock and the O'Brien Fleming designs, which exhaust the type I error rate in the least favourable configuration as shown in Figure 1. Here we set v2′ = v ₂ (where v ₂ is the respective boundary in the separate stopping design) and compute v1′ by solving ((4)). By this choice, given the null hypothesis for one of the treatments is rejected at the interim analysis, the other is tested at a level as close to α as possible. An alternative strategy to choose improved boundaries is to fix a certain boundary shape by setting, for example v1′ = v2′ for Pocock or $v_1^{\prime }=v_2^{\prime }\sqrt{n_1/n}$ for O'Brien Fleming designs, and then solve ((4)) for v2′.

Table 1.

Pocock and O'Brien Fleming type boundaries for the intersection and the elementary null hypothesis if no binding futility stopping rule is applied (l ₁=−∞) and equal per arm per stage allocation (r = 1,n ₁/n = 1/2). The global boundaries (u ₁,u ₂) fullfill Equation ((1)). The elementary boundaries (v ₁,v ₂) computed for the separate stopping rule satisfy ((2)), $v_1^{{}^{\prime }}$ is calculated for the simultaneous stopping rule to achieve ((4)) with $v_2^{{}^{\prime }}=v_2.$

	Intersection hypothesis		Elementary hypotheses
Boundary type	u 1	u 2	v 1	v1′	v 2=v2′
Pocock	2.42	2.42	2.18	1.97	2.18
O'Brien Fleming	3.14	2.22	2.80	2.08	1.98

3. Operating characteristics of group sequential designs with separate and simultaneous stopping

For Pocock and O'Brien Fleming stopping boundary types, we investigate the reduction of the average sample number (ASN) under the simultaneous compared with the separate stopping rule and compute the disjunctive power, defined as the probability to reject at least one null hypothesis (for simplicity, no distinction between correct and incorrect rejections is made which has, however, only a minimal impact on the results as all procedures control the FWER at the nominal level). Furthermore, we compare the conjunctive power (defined as the probability to reject both null hypotheses) of the designs with separate and simultaneous stopping rules and quantify the gain in power by using the improved stopping boundaries.

We consider the following: (i) the separate stopping rule with boundaries satisfying ((1)) and ((2)) (separate design); (ii) the simultaneous stopping rule with the same boundaries (simultaneous design); and (iii) the simultaneous stopping rule with the improved boundaries satisfying ((1)) and ((4)) (improved simultaneous design). Note that, by construction, the improved simultaneous design has (compared with the simultaneous design) a larger conjunctive power, but the two designs have the same average sample size and disjunctive power.

For example, consider a trial powered to achieve a disjunctive power of at least 90% given δ _A=0.5,δ _B=0, that is assuming that for only one experimental treatment, the alternative holds. We assume that n ₁/n = 1/2, r = 1 and n ₁ is rounded up such that the maximum sample size N = 6·n ₁ is a multiple of 6. The operating characteristics of the Pocock and O'Brien Fleming designs with separate and simultaneous stopping rules are given in Table 2.

Table 2.

Operating characteristics of the separate stopping design (Sep.), the simultaneous stopping design (Sim.) and the improved simultaneous stopping design (Imp.) with Pocock and O'Brien Fleming type boundaries and n ₁=n/2,r = 1: disjunctive power, conjunctive power and average sample number (ASN) under different effect sizes. The maximum sample size N is chosen to achieve a disjunctive power of 0.9 for δ _A= 0.5 and δ _B= 0. The settings where l ₁=−∞ indicate designs with no stopping for futility boundary.

Boundary		Effect size		Disj.	Conjunctive power			ASN
Type	l 1	δ A	δ B	Power	Sep.	Sim.	Imp.	Sep.	Sim.	N
Pocock	−∞	0.5	0.5	0.970	0.890	0.689	0.756	230	205
		0.5	0	0.904	0.025	0.016	0.025	292	232	324
		0	0	0.025	0.004	0.003	0.004	323	322
O'Brien	−∞	0.5	0.5	0.970	0.894	0.716	0.840	260	241
Fleming		0.5	0	0.906	0.025	0.012	0.024	287	261	300
		0	0	0.025	0.004	0.004	0.004	300	300
Pocock	0	0.5	0.5	0.970	0.889	0.687	0.755	230	205
		0.5	0	0.903	0.025	0.016	0.025	253	215	324
		0	0	0.025	0.004	0.003	0.004	251	250
O'Brien	0	0.5	0.5	0.970	0.891	0.711	0.836	259	240
Fleming		0.5	0	0.905	0.025	0.012	0.024	276	238	300
		0	0	0.025	0.004	0.004	0.004	233	233

If no futility stopping rule is applied, the simultaneous and improved simultaneous designs lead, compared with the separate design, to savings in the average sample number of 11% for the Pocock and 7% for the O'Brien Fleming design if both treatments are equally effective (δ _A=δ _B=0.5). This comes at the cost of a lower conjunctive power which drops by 20 percentage points for the Pocock and 18 percentage points for the O'Brien Fleming type tests. When applying the improved boundaries, the conjunctive power increases again by 7 (12) percentage points for the Pocock (O'Brien Fleming) design, compared with the simultaneous design. If for only one treatment arm the alternative holds (δ _A=0.5,δ _B=0), the simultaneous stopping rule leads to a reduction in average sample size by 21% (9%) for the Pocock (O'Brien Fleming) design. In the setting where only one treatment is effective, the actual FWER is given by the conjunctive power (the probability to reject both null hypotheses). Similarly, under the global null hypothesis the actual FWER is given by the disjunctive power. According to the closed testing principle, these FWERs are bounded by the nominal FWER 0.025.

Applying a futility boundary of l ₁=0 leads to a substantially lower average sample number under the global null hypothesis for all designs. Everything else kept equal, the introduction of the futility bound leads to a slightly lower power such that in general, a larger maximum sample size needs to be applied to reach the nominal disjunctive power of 90% under the alternative that only one of the treatments is effective. However, because of the discreteness of the sample size, for both designs the same maximum sample size is required with and without futility stopping and the obtained disjunctive and conjunctive power values are almost identical.

In addition, we investigated the impact of a futility bound on the operating characteristics. We applied the critical boundaries from Table 1 (which were computed without a futility stopping boundary) and account for the futility stopping only in the computation of the power and the maximum and average sample numbers. Then FWER control is guaranteed even if the futility boundaries are not adhered to. We find that a futility boundary of l ₁=0 (which corresponds to a stop for futility if a negative trend is observed) leads in all considered scenarios to lower or equal average sample numbers (Table 2).

Figure 2 shows the conjunctive power and average sample number as function of the effect size δ _B for δ _A=0,0.25,0.5. For all considered designs, the average sample number is highest for intermediate effect sizes δ _B, where the probability that the trial continues to the second stage because neither the futility stopping bound (l ₁=0) nor the efficacy bounds are crossed is highest. As expected, the average sample number under the simultaneous stopping rule is consistently lower than under the separate stopping rule and approaches the first stage sample size as δ _B increases. The difference in average sample number between the simultaneous and separate stopping design is maximal if the treatment effect in one treatment arm is very large but in the other it is only moderate.

Figure 2.

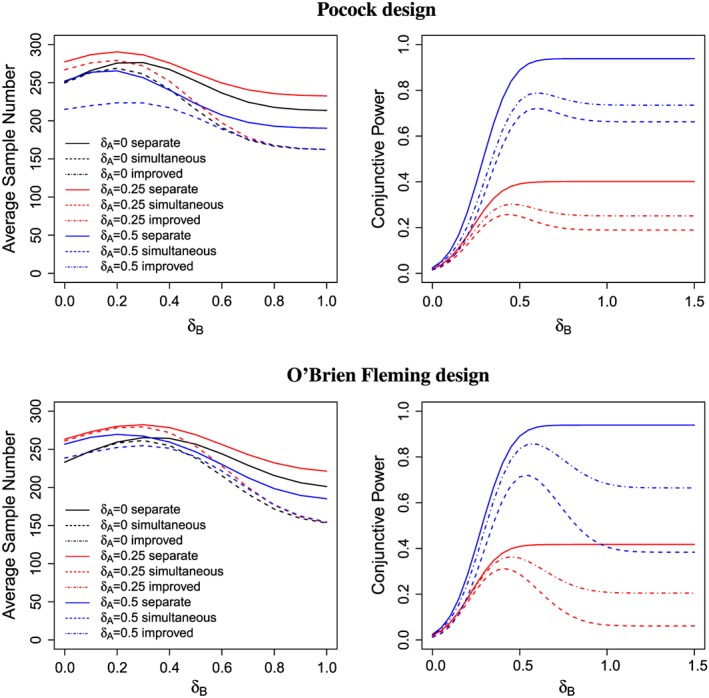
The average sample number and conjunctive power for different values of δ _A and δ _B, l ₁=0. The average sample number is the same for the simultaneous stopping design as for the improved stopping design (dashed lines). The maximum sample size N is chosen to achieve a disjunctive power of 90% under δ _A=0.5,δ _B=0. For the settings where δ _A=0 and only one alternative hypothesis is true, no conjunctive power is shown.

While for the separate stopping designs, the conjunctive power is monotonically increasing in δ _B; this does not hold for the designs under the simultaneous stopping rule. For the latter, the probability to stop in the interim analysis increases with δ _B, and, as a consequence, the conjunctive power for the test of H _A begins to decrease at a certain point. For large δ _B, the trial will practically always stop at the interim analysis, restricting the test for treatment A essentially to a fixed sample test with sample size n ₁ and applying the interim significance level. This leads to a smaller conjunctive power compared with designs using the separate stopping rule. Using the improved boundaries can regain some of the lost conjunctive power because a relaxed significance level is applied. This gain is larger for the O'Brien Fleming than for the Pocock design.

4. Optimized group sequential boundaries

The Pocock and O'Brien Fleming type stopping boundaries considered previously are frequently considered for group sequential trials but do not satisfy specific optimality properties. In this section, we derive optimized boundaries for the separate, the simultaneous and the improved simultaneous designs as defined in Section 3. In all scenarios, for given stopping boundaries, the maximum sample size N is chosen such that the disjunctive power is 90% if only one of the treatments is effective (δ _A=0.5,δ _B=0 ) and we set r = 1,n ₁/n = 1/2. Optimization is performed with the R‐function optimize for one dimensional and optim with the L‐BFGS‐B method for multidimensional optimization.

4.1. Designs with optimized rejection boundaries (no futility stopping)

For the separate design (where the average sample number depends on the global and the elementary boundaries), we choose u ₁,u ₂,v ₁,v ₂(satisfying ((1)) and ((2))) to minimize the ASN under a specified alternative hypothesis. For the simultaneous and improved simultaneous designs (where the average sample number depends on the global boundaries only), we also choose the boundaries u ₁,u ₂ to minimize the average sample number for a given alternative hypothesis δ _A,δ _B. Furthermore, we choose boundaries v ₁,v ₂ satisfying ((2)) (simultaneous design) or improved boundaries v1′,v2′ satisfying ((4)) (improved simultaneous design) such that the conjunctive power is maximized under this alternative hypothesis. The resulting optimized boundaries and operating characteristics for the separate, the simultaneous and the improved simultaneous designs with no futility stopping rule (setting l ₁=−∞) are given in Table 3. If both treatments are equally effective (δ _A=δ _B=0.5), the simultaneous stopping designs have a 9% lower average sample number, slightly larger maximum sample size and the conjunctive power is reduced by 14 percentage points for the simultaneous but only 9 percentage points for the improved simultaneous design. If only one treatment is effective (δ _A=0.5,δ _B=0), the reduction in average sample number is 17%. In this case, the conjunctive power corresponds to the FWER.

Table 3.

Characteristics of the optimized separate (sep.), simultaneous (sim.) and improved simultaneous (imp.) designs: stopping boundaries, average sample number (ASN) under H ₀(δ _A=δ _B=0), H ₁(δ _A,δ _B), maximum sample size (N) and the conjunctive and disjunctive power under H ₁. The power and, for designs with no futility stopping (where l ₁=−∞), the A S N are optimized under the alternative H ₁ specified in the table. For designs with futility stopping, $\overline{\mathrm{ASN}}$, defined as the mean of the ASN under H ₁ and the ASN under the global null hypothesis, is optimized. The maximum sample size N is chosen such that the disjunctive power is 90% given δ _A=0,δ _B=0.5. The columns v _i(v i ′),i = 1,2 denote the stopping boundary v _i for the separate and simultaneous design and the boundary v i ′ for the improved simultaneous design.

	Effect size		Stopping boundaries					ASN			Power
Design	δ A	δ B	l 1	u 1	u 2	v 1(v1′)	v 2(v2′)	H 1	H 0	N	conj.	disj.
Sep.	0.50	0.50	−∞	2.47	2.38	2.05	2.38	225	317	318	0.85	0.97
Sim.	0.50	0.50	−∞	2.41	2.43	2.06	2.37	205	322	324	0.71	0.97
Imp.	0.50	0.50	−∞	2.41	2.43	2.00	2.06	205	322	324	0.76	0.97
Sep.	0.50	0.00	−∞	2.79	2.26	2.11	2.26	279	300	300	0.02	0.90
Sim.	0.50	0.00	−∞	2.42	2.42	2.04	2.42	232	322	324	0.02	0.90
Imp.	0.50	0.00	−∞	2.42	2.42	2.00	2.06	232	322	324	0.02	0.90
Sep.	0.50	0.50	0.91	2.55	2.33	2.07	2.33	228	200	330	0.84	0.97
Sim.	0.50	0.50	0.91	2.51	2.35	2.10	2.28	211	203	336	0.71	0.97
Imp.	0.50	0.50	0.91	2.51	2.35	1.98	2.12	211	203	336	0.76	0.97
Sep.	0.50	0.00	0.94	2.68	2.28	2.10	2.28	235	199	330	0.02	0.90
Sim.	0.50	0.00	0.89	2.58	2.32	2.10	2.28	216	200	330	0.02	0.90
Imp.	0.50	0.00	0.88	2.58	2.32	1.97	2.20	216	201	330	0.02	0.90

4.2. Designs with optimized rejection and futility boundaries

As for the Pocock and O'Brien Fleming designs, we do not account for futility stopping for the computation of the stopping boundaries and set l ₁=−∞ in the level α conditions ((1)), ((2)), ((4)) such that the tests control the level α even if the futility stopping rule is not adhered to. For the computation of power and sample sizes, however, we account for the futility boundary.

Because the benefit of futility stopping in terms of average sample number is most substantial under the global null hypothesis, we optimize the mean average sample number $\overline{\mathrm{ASN}}$ (instead of the average sample number under the alternative), taking the mean of the average sample number under a specified alternative and the global null hypothesis. Besides the different objective function, the optimization strategy is analogous to the case without futility stopping: For the separate design we choose l ₁,u ₁,u ₂,v ₁,v ₂ (satisfying ((1)) and ((2))) to minimize $\overline{\mathrm{ASN}}$. For the simultaneous and improved simultaneous designs, we choose the boundaries l ₁,u ₁,u ₂ to minimize $\overline{\mathrm{ASN}}$. Furthermore, we choose boundaries v ₁,v ₂ satisfying ((2)) (simultaneous design) or improved boundaries v1′,v2′ satisfying ((4)) (improved simultaneous design) such that the conjunctive power is maximized under the assumption that both treatments have effect sizes δ _A,δ _B.

The simultaneous stopping designs have a 3% to 4% lower mean average sample number $\overline{\mathrm{ASN}}$ and 7% to 8% lower ASN under the considered alternative then the separate stopping design (Table 3). In the scenario δ _A=δ _B=0.5, this comes at the cost of a drop in conjunctive power of 13 percentage points for the simultaneous but only 8 percentage points for the improved simultaneous design.

5. Four arm trials

To extend the designs to the comparison of three experimental treatment arms A, B, C to a control, by the closed testing principle local group sequential tests for all intersection hypotheses need to be defined (see Figure 3). For simplicity, we consider the case without futility stopping. For the separate stopping design, rejection boundaries v ₁,v ₂ for the elementary null hypotheses and u ₁,u ₂ for the intersections of two null hypotheses can be computed similarly as for the case of three arm trials (see the Appendix for computational details). For the global null hypothesis $H_A\cap H_B\cap H_C$, boundaries w ₁,w ₂ are defined such that

$$P_{H_A\cap H_B\cap H_C}\left(\underset{i=A,B,C}{\max }{Z}_{1,i}\ge w_1\vee \underset{i=A,B,C}{\max }{Z}_{2,i}\ge w_2\right)=\alpha .$$

As in the case of three arm trials, the actual type I error of the closed test may be lower than α, if null hypotheses are not rejected retrospectively.

Figure 3.

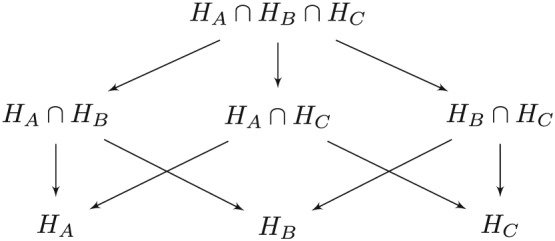
Closure principle for testing three hypotheses

Tables 4 and 5 show Pocock and O'Brien Fleming boundaries as well as the operating characteristics for the separate, the simultaneous and the improved simultaneous designs. As in the three arm trial setting, we improved only the first stage boundaries. In addition, we applied as lower bound the 1 − α standard normal quantile to avoid critical values falling below this threshold. In the four arm trial, the savings in average sample size with the simultaneous stopping rule is more pronounced compared with the separate stopping rule. In addition, in the scenario where all three treatments are effective, the gain in conjunctive power (defined as the probability to reject all three null hypotheses) by the improved simultaneous design (compared to the simultaneous design) is substantial. In all other scenarios, the conjunctive power is bounded by the FWER.

Table 4.

Pocock and O'Brien Fleming type boundaries for the intersection of three and two hypotheses and the elementary hypothesis if no binding futility stopping rule is applied l ₁=−∞,r = 1 and n ₁/n = 1/2.

	$H_i\cap H_j\cap H_k$		$H_i\cap H_j$			H i
Boundary type	w 1	w 2	u 1	u1′	u 2=u2′	v 1	v1′	v 2=v2′
Pocock	2.56	2.56	2.42	2.21	2.42	2.18	1.96	2.18
O'Brien Fleming	3.33	2.36	3.14	2.23	2.22	2.80	1.96	1.98

Table 5.

Operating characteristics of the different three‐arm designs for Pocock and O'?Brien Fleming design types with equal allocation: disjunctive power, conjunctive power and average sample number (ASN) under different parameter configurations and maximum sample size N for a disjunctive power of 0.9 under δ _A=0.5andδ _B=δ _C=0.

Boundary		Effect size			Disj.	Conjunctive power			ASN
Type	l 1	δ A	δ B	δ C	Power	Sep.	Sim.	Imp.	Sep.	Sim.	N
Pocock	−∞	0.5	0.5	0.5	0.99	0.72	0.49	0.60	330	279
		0.5	0.5	0	0.97	0.011	0.008	0.014	395	297
		0.5	0	0	0.90	0.003	0.001	0.003	431	336	464
		0	0	0	0.025	0.0007	0.0005	0.0010	463	461
O'Brien	−∞	0.5	0.5	0.5	0.98	0.80	0.54	0.76	373	334
Fleming		0.5	0.5	0	0.97	0.015	0.004	0.019	398	351
		0.5	0	0	0.90	0.003	0.0008	0.003	412	376	424
		0	0	0	0.025	0.0008	0.0007	0.0009	424	424

6. Applications

6.1. Example: A three‐arm trial in systemic sclerosis

We illustrate the approach in a setting along the lines of a randomized, double‐blind, placebo‐controlled clinical trial in patients with diffuse cutaneous systemic sclerosis 12 to compare two doses of recombinant human relaxin (10 and 25 μg/kg/day for 24 weeks) with a placebo. The objective of this fixed sample trial was to show clinically efficacy in improving skin disease and reducing functional disability. The primary endpoint was the modified Rodnan skin thickness score measured at week 24, which is based on a clinical evaluation of skin thickness in 17 body surface areas and ranges from 0 to 51. The original trial was powered to detect a difference of 4 points in the score assuming a standard deviation of 10 points but did not account for multiple testing to control the FWER.

To account for multiplicity, assume a single stage Dunnett test at a one‐sided level of 2.5% is applied. Then, to achieve a disjunctive power of 80% if only one of the two treatment arms is effective, a total sample size of 354 patients, 118 per group, is required. We compare this single stage design with optimized separate, simultaneous and improved simultaneous designs with futility stopping and assume an interim analysis is performed after half of the patients have been observed. The designs are optimized as described in Section 4 assuming standardized effect sizes of 0.4.

Compared with the fixed sample design, the maximum sample size of the optimized group sequential design increases by a factor of 1.10 (1.14) for the separate (simultaneous) stopping rule, but the saving in mean average sample number (taking the mean over the null hypothesis and the alternative scenario with equal effect sizes) is 89 (98) patients. If the treatment is equally effective in both dose groups (δ _A=δ _B=0.4), the ASN under simultaneous stopping is 23 patients lower than under separate stopping. This comes at the cost of a loss of 12 percentage points in conjunctive power, which reduces to 6 percentage points if the improved simultaneous stopping boundaries are used.

Note that in this example, because the endpoint is measured only at 24 weeks, the benefit of early stopping may be limited, especially if the recruitment speed is high. Unless recruitment is halted before the interim analysis, at the time of the interim analysis, only part of the responses of the patients recruited in the first stage will be observed. This reduces the savings in average sample number that can be obtained by the group sequential design and leads to the problem of potential reversals of test decisions once the complete data becomes available (see 13 for an approach to address this issue in two‐armed trials). Potential reversals of test decisions are of special concern for the simultaneous stopping rule, because early rejection of a single null hypothesis stops the whole trial and makes it difficult to start recruitment again, once a reversal has been observed.

Table 6.

Operating characteristics of the group sequential designs in the systemic sclerosis example. The average sample number and conjunctive power are computed for δ _A/σ = δ _B/σ = 0.4. The maximum sample size N is chosen such that the disjunctive power is 80% given δ _A/σ = 0.4, δ _B=0. The rejection and futility boundaries are optimized as in Section 4.

	Boundaries					Sample size				Power
Design	u 1	u 2	l 1	v 1	v 2	$\overline{\mathrm{ASN}}$	H 1	H 0	N	conj.	disj.
Sep.	2.64	2.30	0.94	2.09	2.30	265	295	235	390	0.70	0.91
Sim.	2.51	2.35	0.97	2.10	2.28	256	272	239	402	0.58	0.92
Imp.	2.52	2.35	0.97	1.99	2.07	256	272	239	402	0.64	0.92

6.2. Example: A four‐arm trial in narcolepsy

The second example is motivated by a randomized, double blind, placebo‐controlled multicenter trial to compare three doses (3, 6 or 9g) of sodium oxybate with placebo in the treatment of Narcolepsy, a chronic debilitating disease of the central nervous system leading to sleep disorder characterized by attacks of excessive daytime sleepiness 14. With a prevalence of 25 to 50 per 100 000 people, it is considered as a rare disease. The primary endpoint was the change from baseline of weekly cataplexy attacks after a 4‐week treatment period. The trial included 136 patients, but no power calculation was reported in the publication. However, we note that a fixed sample size Dunnett test with disjunctive power of 90% for standardized effect sizes δ _A=0.86,δ _B=δ _C=0 at a one sided level of 0.025 requires a total sample size of 136 patients, that is 34 per group, and use this standardized effect size in the example.

We derive optimized group sequential boundaries along the lines of Section 4, setting the maximum sample size such that, given the treatment is efficient in only one arm, the disjunctive power is 90%(Table 7). The maximum sample size is larger than in the fixed sample test (inflation factor 1.12 for separate and 1.35 for simultaneous stopping). If there is a homogeneous effect size in all treatment arms (δ _A=δ _B=δ _C=0.86), the group sequential test with separate (simultaneous) stopping requires, on average, 28 (35) patients less than the fixed sample test. Under the same alternative, the conjunctive power to reject all three null hypothesis is 22 (18) percentage points larger in the separate than in the (improved) simultaneous stopping design.

Table 7.

Operating characteristics for a clinical trial for narcolepsy with standardized effect sizes of δ _A=δ _B=δ _C=0.86 and sample size for a disjunctive power of 90% if only one treatment is effective (δ _A=0.86, δ _B=0, δ _C=0)

	Boundaries						Sample size		Power
Design	w 1	w 2	u 1	u 2	v 1	v 2	ASN	N	conj.	disj.
Sep.	2.63	2.50	2.36	2.50	2.02	2.50	108	152	0.81	0.98
Sim.	2.40	2.88	2.24	2.88	1.97	2.88	101	184	0.59	0.99
Imp.	2.40	2.88	2.22	2.50	1.96	2.20	101	184	0.63	0.99

7. Type I error rate control in trials with small sample sizes

The derivations of the stopping boundaries are based on z‐tests and are valid for t‐statistics only asymptotically. For small sample sizes, however, the type I error rate of group sequential tests is substantially inflated if critical boundaries based on the normal approximation are applied to t‐statistics 15. To better control the type I error rate in the small sample case, a nominal p‐value approach has been proposed 15, 16, 17, 18 to adjust for the unknown variance case: the group sequential boundaries computed for the z‐test are transformed to significance levels (by applying the cumulative distribution function of the standard normal distribution). These significance levels are then applied to p‐values of the t‐test. While this procedure improves the type I error rate control, it is not exact and still leads to a small inflation of the type I error rate (a minor inflation persists because the correlation of the cumulative t‐statistics is lower than the correlation of the corresponding z‐statistics because the variance estimates in the t‐statistics introduce additional variability). Note that the type I error rate of the nominal p‐value approach depends only on the stage‐wise sample sizes and not on the unknown variance 19.

To investigate the type I error rate of the multi‐arm group sequential tests considered here, we performed a small simulation study for three‐arm trials applying the z‐test boundaries u _i,v _i,v i ′ either directly to the t‐statistics or the corresponding significance levels 1−Φ(x),x = u _i,v _i,v i ′ to the p‐values of the t‐test (Figure 4). Applying the nominal p‐value approach, the type I error rate is overall well controlled, and we observe only a minimal inflation in the worst case scenarios. The z‐test generally leads to a larger type I error rate than the nominal p‐value approach, with one exception: For the simultaneous stopping rule with the non‐improved boundaries and intermediate values of δ _B, the type I error rate of the nominal p‐value approach and the z‐test are almost identical. While this is at first sight surprising, there is a simple explanation. With the nominal p‐value approach the trial is more likely to continue to the second stage compared with the z‐test and rejections after the second stage become slightly more likely because for intermediate δ _B, the increased probability to reach the second stage dominates the impact of the more conservative test. On the other hand, the probability to reject in the interim analysis with the nominal p‐value approach is lower than with the z‐test. For the simultaneous stopping with the non‐improved boundaries, however, the difference is very small (because both probabilities are very small) and the differences in type I error probabilities at the first and second stage cancel out. The difference is larger for the improved boundary, and therefore, we observe a larger overall type I error rate.

Figure 4.

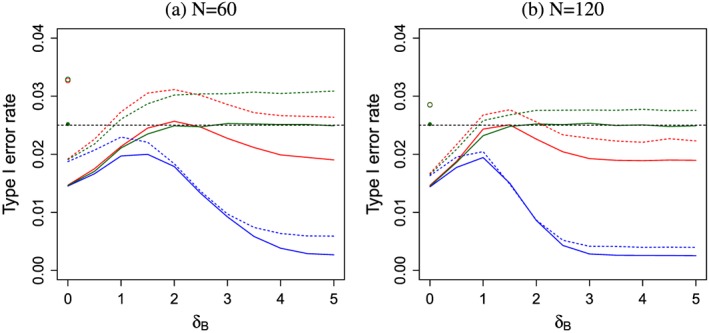
The FWER as function of δ _B if δ _A=0 for the separate (green), simultaneous (blue) and improved simultaneous (red) designs using z‐test O'Brien Fleming boundaries (dashed) or the nominal p‐value approach (solid) applied to t‐statistics. No futility bound is applied. 10⁶ simulation runs for each scenario. The FWER under the global null hypothesis δ _A=δ _B=0 for the nominal p‐value approach (z‐test) represented by the full (empty) dot is the same for all three designs. The dashed horizontal line denotes nominal level α = 0.025. Left graph for maximum total sample size N = 60, right graph N = 120.

8. Discussion

In this manuscript, we consider multi‐arm clinical trials with separate and simultaneous stopping rules. We derive improved critical boundaries for designs with a simultaneous stopping rule that uniformly improve the group sequential boundaries with separate stopping for multi‐arm trials. Furthermore, we optimize the boundary shape and determine the operating characteristics of the resulting designs.

If the separate or the simultaneous stopping rule should be chosen for a multi‐arm, clinical trial will depend on the trial objectives: For the objective to demonstrate a treatment effect for all experimental treatments that are effective, the separate stopping design is favourable, because it has the largest conjunctive power. If the objective is, however, to identify at least one effective treatment, designs with a simultaneous stopping rule may be preferred because they can lead to a saving in the average sample number. The improved stopping boundaries can alleviate the reduction in conjunctive power, which the simultaneous stopping rule entails. However, this comes at the cost that the simultaneous stopping rule must be adhered to in order to control the FWER. If a Data Monitoring Committee overrules the stopping rule and continues the trial after a hypothesis has been rejected in an interim analysis, the type I error rate will be inflated. For example, in the setting of Section 2.2, with improved Pocock (O'Brien Fleming) type boundaries, the maximum type I error rate increases to 0.033 (0.036) instead of 0.025 and is achieved if the separate instead of the simultaneous stopping rule is applied.

We defined disjunctive power as the probability to reject at least one null hypothesis, making no distinction between correct and incorrect rejections. With this simplification the disjunctive power only depends on the group sequential boundaries of the intersection (but not the elementary) hypothesis test and is the same for the simultaneous, improved simultaneous and the separate stopping designs. If, instead, only correct rejections are considered, the improved boundaries for simultaneous stopping also lead to a slightly improved disjunctive power. While for Phase III designs, where very small significance levels are applied, this difference is negligible; it can be more pronounced if larger significance levels are applied, as in some Phase II trials.

The computation of the stopping boundaries relies on the assumption of normally distributed test statistics. However, for small clinical trials with low sample sizes, we demonstrated that the FWER can be controlled by applying t‐tests and the nominal p‐value approach.

Several extensions of the proposed designs can be considered. Improved stopping boundaries for designs with simultaneous stopping rules can be computed also for more than three treatment arms by considering all relevant intersection hypotheses in the closed test. Another extension are group sequential trials with more than two stages. If a binding simultaneous stopping rule is applied, the critical boundaries of the corresponding group sequential design with separate stopping can be improved similarly as in the two stage setting. To this end, the rejection regions for the local tests for the elementary hypotheses ((3)) are generalized for three stage designs, accounting for the possibility that the trial can stop at the first, second or final analysis. Then the corresponding improved stopping boundaries are chosen as in ((4)) such that the maximum type I error rate across all effect sizes where the elementary hypothesis holds is bounded by α. A further extension of the proposed designs is to define the first stage stopping boundaries based on an error spending function such that the first stage sample size need not to be fixed in advance. Such a strategy will control the FWER as long as the first stage sample size does not depend on the trial outcomes. Furthermore, the multi‐arm group sequential designs can be generalized to adaptive designs with unblinded interim analyses where the sample size may be reassessed. This can be implemented either with a combination function approach 4, 20 or the conditional error rate principle 21, 22. Finally, a further improvement of the critical boundaries could be achieved by applying the confidence intervall approach by Berger and Boos 23. Instead of controlling the familywise error rate for the least favourable configuration (as for the δ _B that maximizes the type I error rate in the test of H _A, see Figure 1), a 1 − ε(for some ε > 0) confidence interval for the relevant nuisance parameter is computed, and the FWER is controlled at level α − ε for the least favourable configuration within that confidence interval. The resulting procedure then has an overall FWER bounded by α.

Appendix A.

A.1. A.1. Rejection regions for the four‐arm designs

For both stopping rules, the level α condition of the test of $H_A\cap H_B\cap H_C$(which defines a condition on w ₁,w ₂) is

$$\begin{array}{cc}{P}_{H_A\cap H_B\cap H_C}\left(\underset{i=A,B,C}{\max }{Z}_{1i}\ge w_1\right)+P_{H_A\cap H_B\cap H_C}& \left\{\left(Z_{A1}<w_1\wedge Z_{A2}\ge w_2\right)\vee \left(Z_{B1}<w_1\wedge Z_{B2}\ge w_2\right)\right.\\ \left.\vee \left(Z_{C1}<w_1\wedge Z_{C2}\ge w_2\right)\right\}\le \alpha .\end{array}$$ (A.1)

Boundaries for the Separate Stopping Rule The level α conditions on u ₁,u ₂ for the intersection of two hypotheses and on v ₁,v ₂ for the elementary tests are given by ((1)) and ((2)). Again, the critical boundaries, in addition, have to satisfy the monotonicity condition v ₁≤u ₁≤w ₁ and v ₂≤u ₂≤w ₂ to obtain a sequentially rejective test.

Improved Simultaneous Design For the test of the intersection of two hypotheses, say, $H_A\cap H_B$, we write the rejection region of the simultaneous stopping design as the union of the first and second stage rejection regions given by $R_{A\cap B}=R_{1A\cap B}\cup R_{2A\cap B}$ where $R_{\mathrm{iA}\cap B}={\bigcup }_j{R}_{\mathrm{ij}}$ for i,j = 1,2 and

$$\begin{array}{cc}{R}_{11}^{}& =\{Z_{1,C}<w_1\wedge (Z_{1,A}\ge w_1\vee Z_{1,B}\ge w_1\left)\right\}\\ R_{12}^{}& =\{Z_{1,C}\ge w_1\wedge (Z_{1,A}\ge u_1\vee Z_{1,B}\ge u_1\left)\right\}\\ R_{21}^{}& =\{Z_{1,A}<w_1\wedge Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{2,C}<w_2\wedge (Z_{2,A}\ge w_2\vee Z_{2,B}\ge w_2\left)\right\}\\ R_{22}^{}& =\{Z_{1,A}<w_1\wedge Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{2,C}\ge w_2\wedge (Z_{2,A}\ge u_2\vee Z_{2,B}\ge u_2\left)\right\}.\end{array}$$

Note that the rejection regions for the other two way intersection hypotheses are obtained by exchanging the treatment labels. Now, the level α condition for the improved stopping boundaries (u1′,u2′) is given by

$$\underset{{\delta }_C}{\max }{P}_{0,0,{\delta }_C}\left(R_{A\cap B}\right)=\alpha .$$ (A.2)

Similarly, the rejection regions for the elementary hypotheses, for example. H _A, can be written as the union of the first and second stage rejection regions $R_A=R_{1A}\cup R_{2A}$, where $R_{\mathrm{iA}}={\bigcup }_j{R}_{\mathrm{ij}}$, i = 1,2 and

$$\begin{array}{cc}{R}_{11}^{}& =\{Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{1,A}\ge w_1\}\\ R_{12}^{}& =\{Z_{1,B}\ge w_1\wedge Z_{1,C}<u_1\wedge Z_{1,A}\ge u_1\}\cup \{Z_{1,B}<u_1\wedge Z_{1,C}\ge w_1\wedge Z_{1,A}\ge u_1\}\\ R_{13}^{}& =\{Z_{1,B}\ge w_1\wedge Z_{1,C}\ge u_1\wedge Z_{1,A}\ge v_1\}\cup \{Z_{1,B}\ge u_1\wedge Z_{1,C}\ge w_1\wedge Z_{1,A}\ge v_1\}\\ R_{21}^{}& =\{Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{1,A}<w_1\wedge Z_{2,B}<w_2\wedge Z_{2,C}<w_2\wedge Z_{2,A}\ge w_2\}\\ R_{22}^{}& =\{Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{1,A}<w_1\wedge Z_{2,B}\ge w_2\wedge Z_{2,C}<u_2\wedge Z_{2,A}\ge u_2\}\cup \\ \{Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{1,A}<w_1\wedge Z_{2,B}<u_2\wedge Z_{2,C}\ge w_2\wedge Z_{2,A}\ge u_2\}\\ \end{array}$$

$$\begin{array}{cc}{R}_{23}^{}& =\{Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{1,A}<w_1\wedge Z_{2,B}\ge w_2\wedge Z_{2,C}\ge u_2\wedge Z_{2,A}\ge v_2\}\cup \\ \{Z_{1,B}<w_1\wedge Z_{1,C}<w_1\wedge Z_{1,A}<w_1\wedge Z_{2,B}\ge u_2\wedge Z_{2,C}\ge w_2\wedge Z_{2,A}\ge v_2\}.\end{array}$$

The level α condition for the improved boundaries (v1′,v2′) for the elementary hypothesis test of H _A is given by

$$\underset{{\delta }_B,{\delta }_C}{\max }{P}_{0,{\delta }_B,{\delta }_C}\left(R_A\right)=\alpha .$$ (A.3)

Because the rejection region of H _A contains the rejection regions of $H_A\cap H_B$, $H_A\cap H_C$ and $H_A\cap H_B\cap H_C$, it follows by the closed testing principle that applying the rejection regions R _A,R _B,R _C to test H _A,H _B,H _C leads to a test that controls the FWER at level α.

Rejection regions for the separate stopping rule Note that we do not allow for ‘retrospective rejections’, where a null hypothesis is rejected because a test statistic crosses a rejection boundary in the interim analysis, but the respective treatment arm is continued to the second stage, because some intersection hypothesis containing it cannot be rejected at interim, and the test statistics does not cross the boundary in the final analysis. Therefore, the actual rejection regions for the separate stopping rule are smaller than the rejection regions that are used in the level α conditions ((A.1)), ((1)) and ((2)). This has to be considered when computing the power of the procedure (unfortunately it cannot be exploited to obtain improved boundaries because the test still exhausts the level in the least favourable configuration).

Under separate stopping, the rejection region of the intersection hypothesis, for example $H_A\cap H_B$, can be constructed by adding to the region $R_{A\cap B}$(defined for the aforementioned simultaneous stopping rule) the events where H _C is rejected in the interim analysis and $H_A\cap H_B$ is rejected in the final analysis, that is by adding $R_{2,3}^{}=\{Z_{1,A}<u_1\wedge Z_{1,B}<u_1\wedge Z_{1,C}\ge w_1\wedge (Z_{2,A}\ge u_2\vee Z_{2,B}\ge u_2\left)\right\}$.

The rejection region of the elementary tests, for example H _A, is obtained by adding to R _A, defined previously, the events where one or two arms are stopped at interim and H _A is rejected after the second stage. Therefore, the rejection region in addition contains the rejection regions

$$\begin{array}{cc}{R}_{2,4}^{}& =\{Z_{1,B}\ge w_1\wedge Z_{1,C}<u_1\wedge Z_{1,A}<u_1\wedge Z_{2,C}<u_2\wedge Z_{2,A}\ge u_2\}\cup \\ \{Z_{1,B}<u_1\wedge Z_{1,C}\ge w_1\wedge Z_{1,A}<u_1\wedge Z_{2,B}<u_2\wedge Z_{2,A}\ge u_2\}\\ R_{2,5}^{}& =\{Z_{1,B}\ge w_1\wedge Z_{1,C}<u_1\wedge Z_{1,A}<u_1\wedge Z_{2,C}\ge u_2\wedge Z_{2,A}\ge v_2\}\cup \\ \{Z_{1,B}<u_1\wedge Z_{1,C}\ge w_1\wedge Z_{1,A}<u_1\wedge Z_{2,B}\ge u_2\wedge Z_{2,A}\ge v_2\}\\ R_{2,6}^{}& =\{Z_{1,B}\ge w_1\wedge Z_{1,C}\ge u_1\wedge Z_{1,A}<v_1\wedge Z_{2,A}\ge v_2\}\cup \\ \{Z_{1,B}\ge u_1\wedge Z_{1,C}\ge w_1\wedge Z_{1,A}<v_1\wedge Z_{2,A}\ge v_2\}.\end{array}$$

Urach, S. , and Posch, M. (2016) Multi‐arm group sequential designs with a simultaneous stopping rule. Statist. Med., 35: 5536–5550. doi: 10.1002/sim.7077.