Propensity score weighting for a continuous exposure with multilevel data

Abstract

Propensity score methods (e.g., matching, weighting, subclassification) provide a statistical approach for balancing dissimilar exposure groups on baseline covariates. These methods were developed in the context of data with no hierarchical structure or clustering. Yet in many applications the data have a clustered structure that is of substantive importance, such as when individuals are nested within healthcare providers or within schools. Recent work has extended propensity score methods to a multilevel setting, primarily focusing on binary exposures. In this paper, we focus on propensity score weighting for a continuous, rather than binary, exposure in a multilevel setting. Using simulations, we compare several specifications of the propensity score: a random effects model, a fixed effects model, and a single-level model. Additionally, our simulations compare the performance of marginal versus cluster-mean stabilized propensity score weights. In our results, regression specifications that accounted for the multilevel structure reduced bias, particularly when cluster-level confounders were omitted. Furthermore, cluster mean weights outperformed marginal weights.

1. Introduction

Many essential research questions in the fields of behavioral science, public health, and health policy research are best answered using observational study designs, as randomization is often not feasible. Causal comparisons are often of interest, and statistical methods for causal inference have become increasingly well-developed and adopted in health research. These methods strive to generate unbiased estimates of exposure effects by carefully accounting for differences across exposure groups in the absence of randomization. Propensity score methods, proposed by Rosenbaum and Rubin (1983), have gained widespread popularity for balancing dissimilar exposure groups with respect to baseline covariates.

Exposure groups may be dissimilar in the absence of randomization, potentially with regard to confounders, variables associated with both the exposure and the outcome. Failure to account for confounding can result in a biased effect estimate that conflates the true effect and baseline group differences. The propensity score is defined as the probability of exposure, given the observed covariates. Propensity score methods first estimate propensity scores for each individual and then use the scores to statistically balance exposure groups. Specifically, the estimated propensity scores are used to match, weight, or stratify individuals across exposure groups to create groups that are similar with respect to the propensity score distribution. Rosenbaum and Rubin showed that groups with similar propensity score distributions have similar distributions with respect to all covariates that were used to estimate the propensity score (Rosenbaum and Rubin 1983). Thus, propensity score methods can be used to remove the association between covariates and exposure group, thereby reducing confounding and facilitating unbiased exposure effect estimates.

Propensity score methods were developed in the context of independence among observations (Rosenbaum and Rubin 1983), but in many health research applications the data have a clustered or hierarchical structure that is of substantive importance, such as individuals clustered within geographic region or within healthcare providers. Recent work has extended propensity score methods to a multilevel setting for a binary exposure (Arpino and Mealli 2011; Eckardt 2012; Leyrat et al. 2013; Li et al. 2013; McCormick et al. 2013; Thoemmes and West 2011; Xiang and Tarasawa 2015). Through simulations, previous studies compared estimating the propensity score with a single-level model (SLM) with cluster-level covariates, a fixed effects model (FEM), or a random effects model (REM). Simulation results consistently showed that both the FEM and REM outperformed the SLM, indicating the importance of taking the clustered nature of the data into account when estimating the propensity score (Arpino and Mealli 2011).

While existing methodological work on propensity score methods with multilevel data have focused on binary exposures, Zhu et al. (2014) highlight that continuous exposures or treatments are quite common in health research. Examples include physical or mental health conditions assessed by a scale, dosage of a medication, or exposure duration measured in continuous time. Recent examples in the medical literature of multisite studies with a continuous exposure or treatment include a study examining the effect of systolic blood pressure at hospital admission on mortality among individuals with a traumatic brain injury (Fuller et al. 2014), and a study of the effect of door-to-needle times for administration of tissue plasminogen activator among individuals experiencing an acute ischemic stroke (Fonarow et al. 2014). Existing studies of continuous exposures in multilevel data rely on regression adjustment to account for individual-level and cluster-level confounders, yet propensity score methods offer a less parametric alternative to regression adjustment (Austin 2011; Stuart 2010). While propensity score weighting methods have been developed for continuous exposures (Imbens 2000; Hirano and Imbens 2004), these methods have not yet been extended to the multilevel setting.

This paper provides a methodological framework for propensity score weighting for a continuous exposure or treatment in a multilevel setting. Throughout, we use the terms exposure and treatment interchangeably. We focus on settings in which both the exposure and outcomes are defined at the individual level. Through simulations, we assess the performance of various propensity score regression and weighting approaches. Specifically, we compare various combinations of regression specifications (SLM, FEM, and REM) for the propensity score and outcome models, as well as comparing marginal and cluster-mean stabilized weights. Furthermore, we investigated robustness of these regression and weighting options to omission of cluster-level confounders. We show that regression specifications that account for the multilevel structure reduced bias, particularly when the cluster-level confounder was omitted, and that cluster-mean weights outperformed marginal weights.

1.1 Propensity score weighting estimators

The basis for propensity score weighting is similar to that of survey weighting: in each exposure group, those who are underrepresented in the sample relative to the population of interest (with respect to baseline covariates) are up-weighted, and those who are overrepresented are down-weighted. Inverse probability weighting (IPW) is one of the most commonly used propensity score weighting estimators in the health research literature. Consider an exposure T, a vector of individual-level covariates X, and an outcome Y. For a binary exposure, the propensity score is defined as $e\left({\mathit{X}}_i\right)=\text{Pr}\left(T_i=1\text{|}{X}_i\right)$ and the weights are defined as $w_i=\frac{1}{e\left({\mathit{X}}_i\right)}$ for individuals in the exposure group and $w_i=\frac{1}{1-e\left({\mathit{X}}_i\right)}$ for individuals in the control group (Lunceford and Davidian 2004; Robins et al. 2000). The ATE can then be estimated as follows: $\mathit{ATE}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\frac{T_i{Y}_i}{e(X_i)}-\frac{(1-T_i)Y_i}{1-e(X_i)}}$. Additionally, there are doubly-robust weighting estimators that combine propensity score weighting and regression adjustment (Hirano and Imbens 2001; Kang and Schafer 2007; Robins et al. 2007). One such estimator can be obtained from weighted regression: one fits an outcome regression model for $\mathrm{E}\left(Y\text{|}T,\mathit{X}\right)=\alpha +{\beta }_{T}T+\mathit{\gamma }\mathit{X}$, using IPW. The ATE estimate can be obtained as ${\widehat{\beta }}_T$, the weighted regression coefficient of T. Under appropriate conditions, this estimator is doubly robust in that it will yield unbiased ATE estimates if either the outcome regression or the propensity score regression that generated the weights was consistently estimated (e.g., correctly specified in the case of parametric regression).

For a continuous exposure, the generalized propensity score is defined as $e_i=\text{Pr}\left(T_i=t\text{|}{\mathit{X}}_i\right)$, where t ∈ τ for some continuous domain (Hirano and Imbens 2004). One approach to propensity score weighting for continuous exposures was introduced by Robins et al. (2000), who proposed the use of stabilized weights of the form $w_i=\frac{\text{Pr}\left(T_i=t\right)}{e_i}$. In the continuous case, unlike in the binary case, the weights must be stabilized with a numerator other than 1 because unstabilized weights will have infinite variance. If the exposure of interest is continuous (or nearly continuous) and approximately normally distributed, then $\text{Pr}(T_i=t|{\mathit{X}}_i)$ can be estimated by a linear regression propensity score model of the form $T=\mathit{\beta }\mathit{X}+\epsilon$, where $\epsilon ~N(0,{\sigma }^2)$. In the binary exposure case, the propensity score is often modeled using logistic regression and thus yields a model-predicted probability estimate between 0 and 1 that is directly interpretable as a propensity score. However, in the case of a continuous exposure, estimates from the linear regression propensity score model must be transformed to the probability scale. As Robins et al. (2000) details, after obtaining estimates of ${\widehat{\epsilon }}_i$ and $\widehat{\sigma }$ from the propensity score model, $\text{Pr}(T_i=t|{\mathit{X}}_i)$ can be estimated by the normal density, $\frac{1}{\sqrt{2\pi }\widehat{\sigma }}\mathit{exp}\left\{-\frac{{\widehat{\epsilon }}_i^2}{2{\widehat{\sigma }}^2}\right\}$.

Likewise, $\text{Pr}\left(T_i=t\right)$ can be estimated by first fitting the intercept-only model $T={\beta }_0+\epsilon$ and then using the corresponding normal density. Note that the propensity score model can alternatively be estimated with a non-parametric approach, such as generalized boosted modeling (Zhu et al. 2014). Furthermore, a non-parametric approach, such as kernel density estimation, could be used to transform estimates from the propensity score model to the probability scale (Zhu et al. 2014). For simplicity, in this paper we will estimate the propensity score model with linear regression and use the corresponding normal density to obtain the propensity score weights.

When calculating the ATE for a continuous exposure, one must specify the desired comparison between exposure levels: this is often taken to be an increase of one unit or one standard deviation in T. Using propensity score weights, this is estimated from a weighted outcome regression of the form $\mathrm{E}\left(Y\text{|}T\right)=\alpha +{\beta }_{T}T$, where T is scaled such that ${\widehat{\beta }}_T$ reflects the effect of interest. Alternatively, one could use an outcome regression that included covariates, $\mathrm{E}\left(Y\text{|}T,\mathit{X}\right)=\alpha +{\beta }_{T}T+\mathit{\gamma }\mathit{X}$, for a doubly robust approach.

In order to interpret the ATE as a causal effect, several assumptions are required. One causal assumption, formalized by Rubin, is the stable unit treatment value assumption (SUTVA), which states that an individual’s exposure status does not affect the potential outcomes of any other individuals and that the exposure level is the same for all individuals who received a given exposure level (Rubin 1980, 1986). Additionally, the assumption of no unmeasured confounders – namely, that all covariates associated with both the exposure and the outcome have been measured – is needed to identify the ATE. This assumption is formalized as $\left({\mathit{Y}}_{\mathbf{1}},{\mathit{Y}}_{\mathbf{0}}\right)\perp \mathit{T}|\mathit{X}$, namely that the exposure and potential outcomes are independent after conditioning on the covariates (both individual-level and cluster-level) (Greenland and Robins 1986). Additionally, the positivity assumption states that within strata of X, each individual has a nonzero probability of receiving every level of the exposure (Petersen et al. 2012).

1.2 Propensity score weighting in a multilevel setting

In the multilevel setting, in order to estimate the causal effect of an individual’s treatment on his or her outcome, one must adjust for confounding arising at both the individual and cluster level. In this paper, our multilevel structure consists of two levels, where level 1 represents the individual level and level 2 represents the cluster level. Our sample is comprised of n total individuals, each in cluster j, where $\mathit{j}=\mathbf{1},\dots ,\mathit{J}$. for each individual, we observe a vector of individual-level covariates ${\mathit{X}}_{\mathit{ij}}$ and a vector of cluster-level covariates ${\mathit{W}}_{\mathit{j}}$. The outcome of interest is denoted ${\mathit{Y}}_{\mathit{ij}}$. In the multilevel setting, the propensity score is estimated using both individual-level covariates $\mathit{X}$ and cluster-level covariates $\mathit{W}$, and is defined as ${\mathit{e}}_{\mathit{ij}}=\mathbf{\text{Pr}}({\mathit{T}}_{\mathit{i}}=\mathbf{1}\mathbf{\text{|}}{\mathit{X}}_{\mathit{ij}},{\mathit{W}}_{\mathit{j}})$ for a binary treatment. In the multilevel setting, the no unmeasured confounders assumption states that the exposure and potential outcomes are independent after conditioning on the covariates, both individual-level and cluster-level.

When estimating the propensity score in multilevel data, common approaches include: a single level model (SLM), a fixed effect model (FEM), and a random effects model (REM). A single level model ignores the clustered structure of the data, whereas both the FEM and REM include a cluster-specific intercept for each of the j clusters in order to account for unobserved heterogeneity across clusters. A single level propensity score regression includes the individual-level covariates, cluster-level covariates, and an overall intercept: ${\mathit{T}}_{\mathit{ij}}={\mathit{\alpha }}_{\mathbf{0}}+{\mathit{X}}_{\mathit{ij}}\mathit{\beta }+{\mathit{W}}_{\mathit{j}}\mathit{\gamma }+{\mathit{\epsilon }}_{\mathit{ij}}$. A fixed effects propensity score regression includes the individual-level covariates, cluster-level covariates, and cluster-specific intercept: ${\mathit{T}}_{\mathit{ij}}={\mathit{\alpha }}_{\mathbf{0}\mathbf{j}}+{\mathit{X}}_{\mathit{ij}}\mathit{\beta }+{\mathit{W}}_{\mathit{j}}\mathit{\gamma }+{\mathit{\epsilon }}_{\mathit{ij}}$, where α_0j is assumed to be distribution free and is commonly estimated through j dummy variables. A random effects propensity score regression (specified with only random intercepts) includes the individual-level covariates, cluster-level covariates, and cluster-specific intercept: ${\mathit{T}}_{\mathit{ij}}={\mathit{\alpha }}_{\mathbf{0}\mathbf{j}}+{\mathit{X}}_{\mathit{ij}}\mathit{\beta }+{\mathit{W}}_{\mathit{j}}\mathit{\gamma }+{\mathit{\epsilon }}_{\mathit{ij}}$, where ${\mathit{\alpha }}_{\mathbf{0}\mathbf{j}}~\mathit{N}\left(\mathbf{0},{\mathit{\sigma }}_{{\mathit{\alpha }}_{\mathbf{0}}}^{\mathbf{2}}\right)$. Additionally, a REM can be specified to allow random slopes, in which the covariate coefficients are allowed to vary across clusters, in addition to the cluster-specific intercepts. As discussed in the multilevel data literature, a FEM performs poorly with regard to statistical inference when there is a large number of small clusters, due to the large number of ${\mathit{\alpha }}_{\mathbf{0}\mathit{j}}$ cluster-specific intercept parameters that must be estimated with relatively little information. When the number of clusters is large, the REM has considerable advantages over the FEM because specifying a distribution on ${\mathit{\alpha }}_{\mathbf{0}\mathit{j}}$ reduces the number of parameters. A REM may offer greater flexibility because cluster-specific slopes can also be included.

In typical multilevel analysis settings, the multilevel regression is used for statistical inference, and thus properly accounting for clustering when calculating the standard errors is essential. In the context of propensity score estimation, we are interested in the point estimate of the propensity score, and thus correct specification with regard to the confounders is of primary importance rather than standard error estimation. Past research on propensity score estimation for a binary exposure in the context of clustered data has examined a SLM with cluster-level covariates, a FEM with cluster-level specific intercepts, and random effects models. Some authors preferred a FEM (Arpino and Mealli 2011), and others preferred a REM (Kim and Seltzer 2007), which include random intercept-only and random-intercept-and-slopes models with and without cluster-level covariates. When REMs are used to estimate propensity scores, Thoemmes and West (2011) noted that the propensity score estimate may be based on only the fixed effects or on both the fixed and random effects.

A FEM specifies the cluster-specific intercepts as a set of dummy variables and estimates each intercept from observations in the given cluster; in contrast, a REM uses partial pooling across clusters to estimate cluster intercepts, which may obscure some cluster heterogeneity. As Li et al. (2013) discuss, the cluster-specific intercepts in a FEM may better capture both observed and unobserved cluster-level variability, making a FEM more robust than a REM to misspecification of cluster-level covariates. In contrast, due to cluster shrinkage, a REM does not guarantee balance on cluster-level variables, and thus is more sensitive to incorrect specification of cluster-level variables (Li et al. 2013).

After estimation of the propensity score, a variety of estimators can be used to calculate causal effects in the multilevel setting. If the ATE is the effect of interest, then IPW or doubly robust weighting methods may be used (see Li et al. 2013). Li et al. (2013) assessed the performance of a doubly robust weighted regression estimator and found that ignoring the multilevel structure of the data in the outcome regression results in larger bias than ignoring the multilevel structure in the propensity score regression.

In this paper, we focus on the multilevel extension of the generalized propensity score for a continuous exposure, which is estimated using both individual-level and cluster-level covariates. Let $T_{ij}$ denote the exposure level of individual $i$ in cluster $j$, where $T_{ij}$ is defined for all $t\in \tau$, some continuous domain. We denote our propensity score of interest as $e_{ij}=\text{Pr}(T_i=t|{\mathit{X}}_{ij},{\mathit{W}}_j)$.

1.3 Assessing covariate balance for clustered data

For clustered data structures, balance could be obtained either within or across clusters depending on the research question of interest. Balancing individuals across clusters allows the estimation of the average effect. Often, the cluster-specific effect is not of substantive interest, and the objective is simply to adjust for across-cluster variability. Conversely, balancing individuals on covariates within clusters allows estimation of both the average effect and the variability of this effect across clusters (Kelcey 2011). Within cluster balance is only driven by individual-level covariates, as within-cluster matching guarantees balance on cluster-level covariates. However, within-cluster matching is often infeasible for small cluster sizes (Arpino and Mealli 2011).

In multilevel data, conventional balance diagnostics can be used to assess either across-cluster or within-cluster balance (Li et al. 2013). When seeking across-cluster balance, covariate balance should be assessed for both individual-level and cluster-level covariates. When the exposure is binary, covariate balance is often assessed using standardized mean differences (SMD) between exposure groups (Austin 2011). A standardized mean difference less than |0.2| is often taken to indicate sufficient covariate balance; this SMD corresponds to a small effect size (Cohen 1988). Zhu et al. (2014) proposed using the exposure–covariate correlation to assess balance for continuous exposures and proposed, on the basis of simulations, that a correlation less than |0.1| is a reasonable rule-of-thumb for achieving balance in the context of continuous exposures and non-clustered data. A correlation of 0.1 in the continuous exposure setting is analogous to a standardized mean difference of 0.2 in the binary exposure setting (Zhu et al. 2014). As with binary exposures and clustered data structures, balance for continuous exposures may be obtained either within or across clusters. In this paper, we will focus on across cluster balance, as our primary interest is estimating the ATE rather than cluster-specific effects.

2. Simulation study design

Our simulation design is similar to that of Arpino and Mealli (2011) and Li et al. (2013). We simulated data with a clustered structure to represent individuals (denoted $i$) nested within clusters (denoted $j$). Each simulation consisted of 4,000 individuals, nested within $J$ equally sized clusters of size $n_j$; we varied $n_j$ and $J$ across replications, considering $\left(J,n_j\right)=\left\{\left(5,800\right),\left(20,200\right),\left(200,20\right)\right\}$. Our data comprised a continuous exposure $T$, three individual-level confounders $\mathit{X}=\left(X_1,X_2,X_3\right)$, one cluster-level confounder $W$, and a continuous outcome $Y$.

Two individual-level covariates, $X_1$ and $X_2$, were generated to be independent of cluster membership, and were generated as $X_{1ij}~N\left(1,1\right)$ and $X_{2ij}~\mathit{Bernoulli}\left(0.5\right)$. One individual-level covariate, $X_3$, was generated to be dependent on cluster membership, and was generated as $X_{3ij}~N\left(0.01j,1\right)$, where $j=1,\dots ,J$. One cluster-level variable, $W$, was generated as $W_j~N\left(1,2\right)$, such that all individuals in the same cluster have identical values for $W$. $W$ and $\mathit{X}$ are uncorrelated. The continuous exposure, $T$, was generated as a linear combination of an individual’s covariates $X_1,X_2,X_3,$ and $W$ as follows: $T_{ij}={\beta }_{0i}+{\beta }_1{X}_{1ij}+{\beta }_2{X}_{2ij}+{\beta }_3{X}_{3ij}+{\beta }_4{W}_j+{\epsilon }_{ij}$, where ${\beta }_{0i}~N\left(0,{\sigma }_{{\beta }_0}^2\right),$ and $\left({\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\right)=\left(0.4,-0.3,0.4,-0.4\right)$. We considered two different specifications for the continuous outcome, $Y$, which was generated as a linear combination of an individual’s covariates $X_1,X_2,X_3,$ and $W$ and the exposure, $T$. First, we specified $Y$ as a function of main effect terms only (No differential confounding): $Y_{ij}={\gamma }_{0i}+{\gamma }_T{T}_{ij}+{\gamma }_1{X}_{1ij}+{\gamma }_2{X}_{2ij}+{\gamma }_3{X}_{3ij}+{\gamma }_4{W}_j+{\epsilon }_{ij}$, where ${\gamma }_{0i}~N\left(0,{\sigma }_{{\gamma }_0}^2\right)$ and $\left({\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4\right)=\left({\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\right)\times 0.8$. Additionally, we specified Y as a function of both main effect and interaction terms (Differential confounding): $Y_{ij}={\gamma }_{0i}+{\gamma }_T{T}_{ij}+{\gamma }_1{X}_{1ij}+{\gamma }_2{X}_{2ij}+{\gamma }_3{X}_{3ij}+{\gamma }_4{W}_j+{\gamma }_5(X_{1ij})(W_j)+{\gamma }_6(X_{2ij})(W_j)+{\epsilon }_{ij}$, where ${\beta }_{0i}~N\left(0,{\sigma }_{{\beta }_0}^2\right),$ and $\left({\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4,{\gamma }_5,{\gamma }_6\right)=\left(0.4,-0.3,0.4,-0.4,-0.3,0.2\right)$. We specified the true exposure effect in terms of ${\gamma }_T$; for all simulations ${\gamma }_T=0.5$. Across-cluster variability was specified as ${\sigma }_{{\alpha }_0}^2={\sigma }_{{\beta }_0}^2=0.4$.

We considered three different regression models for estimating the propensity score: a SLM in which the clustered structure of the data are ignored, a FEM, which includes a cluster-specific intercept ${\beta }_{0j}$ for each of the $J$ clusters; and a random effects model (REM), which includes a cluster-specific intercept arising from the distribution ${\beta }_{0j}~N\left(0,{\sigma }_{{\beta }_0}^2\right)$. We estimated the ATE using a weighted outcome regression, and considered three different outcome models: SLM, a FEM, and REM. In total, we implemented five combinations of propensity score and outcome models: SLM-SLM, SLM-REM, FEM-FEM, FEM-REM, and REM-REM (Table 1). Simulations investigated the effect of (1) misspecification of cluster-level confounder (2) the form of the propensity score weights, and (3) cluster size.

Table 1.

Simulation overview: Combinations of propensity score regression, outcome regression, and propensity score weight implemented in our simulations.

Propensity score regression	Outcome regression	PS weight form
Single level (SLM)	Single level (SLM)	Marginal weight
Single level (SLM)	Random effects (REM)	Marginal weight
Fixed effects (FEM)	Fixed effects (FEM)	Cluster-mean weight
Fixed effects (FEM)	Fixed effects (FEM)	Marginal weight
Fixed effects (FEM)	Random effects (REM)	Cluster-mean weight
Fixed effects (FEM)	Random effects (REM)	Marginal weight
Random effects (REM)	Random effects (REM)	Cluster-mean weight
Random effects (REM)	Random effects (REM)	Marginal weight

In order to assess robustness to misspecification of the cluster-level confounder, we considered three conditions: (1) generating $Y$ with no differential confounding; inclusion of cluster-level covariate $W$ in the propensity score regression, (2) generating $Y$ with no differential confounding; omission of the cluster-level covariate $W$ in the propensity score regression, and (3) generating $Y$ with differential confounding; omission of the cluster-level covariate $W$ in the propensity score regression. For all conditions, all individual-level confounders $\mathit{X}$ were included in the propensity score regression. Additionally, the covariates included in the outcome model for each condition were the same as those included in the propensity model: either all covariates (X and W), or only the individual-level covariates X.

Additionally, when the propensity score was estimated with a FEM or REM, we assessed two different forms for the propensity score weight. These weights differed in terms of the propensity score weight numerators: (1) the cluster-specific exposure mean (“cluster-mean weight”) and (2) the overall exposure mean (“marginal weight”). The cluster-specific exposure mean was estimated with a regression of the form $T_{ij}={\alpha }_{0\mathrm{j}}+{\epsilon }_{ij}$. When using cluster-specific means, the numerator was estimated using the same model type as the denominator (e.g., both were FEMs or both were REMs). The overall exposure mean was estimated with a regression of the form $T_{ij}={\alpha }_0+{\epsilon }_{ij}$, yielding the observed mean of the exposure. For both, the denominator of an individual’s weight was the estimated propensity score. When the propensity score was estimated with a SLM, the numerator was the overall mean. Table 1 summarizes the eight different regression/weighting combinations we assessed.

Our primary interest was estimation of the exposure effect, ${\widehat{\beta }}_T$, as obtained from a weighted outcome regression. We assessed performance of the various combinations of regression and weight specifications in terms of average absolute bias, root mean squared error (RMSE), and 95% confidence interval coverage rates. Coverage rates were calculated empirically using the bootstrap method, which resampled at the cluster level (e.g., resampling J clusters with replacement, using all individuals within each resampled cluster), as recommended by Li et al. (2013). Covariate balance was assessed before and after weighting by the following procedure. First, within each simulated dataset we resampled individuals with replacement with probability equal to their estimated propensity scores. Second, within each bootstrap sample we calculated the Pearson correlation between the continuous exposure and each covariate. Finally, this procedure was repeated 500 times; the balance metric was calculated as the average across 500 correlations for each covariate. All data were simulated and analyzed in R (R Core Team 2015). Random effects models for the propensity score and outcome were estimated using the lme4 package in R (Bates et al. 2015). Simulation code is provided in Appendix 1.

2.1 Simulation study results

Table 2 presents the covariate balance, both before and after propensity score weighting, across our three simulation conditions. Covariate balance was assessed for the three individual-level confounders (X₁–X₃) and the cluster-level confounder $W$ by calculating the Pearson correlation between each confounder and the exposure variable $T$. Prior to propensity score weighting (i.e., unadjusted), each confounder was associated with the exposure, with Pearson correlations ranging in magnitude from 0.13 to 0.60. When $W$ was included in the propensity score regression (Table 1, column 1), propensity score weights estimated with SLM, FEM and REM all significantly improved balance on all confounders. Balance improved as cluster size increased: for J=20 and J=5, all confounders yielded Pearson correlations less than |0.05| after weighting. Propensity score weights estimated with the SLM achieved the best balance for J=200 and J=20, while all weights achieved similar very good balance for the largest cluster size, $\left(J,n_j\right)=\left(5,800\right)$. Given that the SLM is correctly specified when $W$ is included, we would expect the SLM to perform well under this condition.

Table 2.

Balance tables from simulation study: Mean Pearson correlation between confounders and exposure across 500 bootstrapped samples for various propensity score regression specifications under three different simulation conditions.

Propensity score form	No differential confounding: W included				No differential confounding: W omitted				Differential confounding: W omitted
	X1	X2	X3	W	X1	X2	X3	W	X1	X2	X3	W
	(J, nj) = (200, 20)
Unadjusted	0.260	−0.595	0.131	−0.257	0.260	−0.596	0.131	−0.257	0.260	−0.596	0.131	−0.257
SLM	0.067	−0.096	0.062	−0.065	0.051	−0.077	0.046	−0.405	0.011	−0.039	0.011	−0.398
FEM	0.081	−0.142	0.063	−0.079	0.080	−0.141	0.063	−0.080	0.047	−0.123	0.024	−0.045
REM	0.074	−0.123	0.060	−0.073	0.073	−0.123	0.058	−0.120	0.041	−0.104	0.019	−0.102
	(J, nj) = (20, 200)
Unadjusted	0.315	−0.244	0.157	−0.303	0.315	−0.245	0.157	−0.303	0.315	−0.245	0.157	−0.303
SLM	0.032	−0.028	0.025	−0.038	0.020	−0.017	0.013	−0.356	0.002	−0.001	−0.002	−0.358
FEM	0.048	−0.043	0.041	−0.049	0.049	−0.042	0.042	−0.049	0.009	−0.010	0.005	−0.015
REM	0.047	−0.042	0.040	−0.049	0.047	−0.041	0.041	−0.051	0.009	−0.009	0.005	−0.022
	(J, nj) = (5, 800)
Unadjusted	0.323	−0.243	0.162	−0.266	0.323	−0.243	0.162	−0.266	0.323	−0.243	0.162	−0.266
SLM	0.011	−0.008	0.006	−0.017	0.006	−0.004	0.004	−0.310	0.006	−0.004	0.004	−0.310
FEM	0.012	−0.013	0.008	−0.011	0.012	−0.013	0.008	−0.011	0.012	−0.013	0.008	−0.011
REM	0.012	−0.013	0.007	−0.011	0.012	−0.013	0.007	−0.013	0.012	−0.013	0.007	−0.013

Abbreviations: SLM = single level model, FEM = fixed effects model, REM = random effects model, J = number of clusters, n_j = number of individuals in each cluster, W = cluster-level covariate.

When W was omitted from the propensity score regression (Table 2, columns 2 and 3), propensity score weights estimated with the SLM no longer balanced on W (post-weighting correlation ranged in magnitude from 0.31 to 0.41), as this variable was not included in the propensity score model. In contrast, propensity score weights estimated with either a FEM or REM did achieve balance on W, despite the fact that it was not included in the propensity score regression. The use of a multilevel model (FEM or REM) for the propensity score regression accounts for cluster-level variability, even when not directly measured, through the estimation of cluster-specific intercepts. For the REM and FEM, balance on W improved as cluster size increased: post-weighting correlation with T for REM was −0.10 when $\left(J,n_j\right)=\left(200,20\right)$ and −0.01 when $\left(J,n_j\right)=\left(5,800\right)$. Note that our simulation design considered two forms of propensity score weights when the propensity score was estimated with either a FEM or REM: (1) weights stabilized by the marginal exposure mean and (2) weights stabilized by the cluster-specific exposure mean. Table 1 presents balance diagnostics using the marginal weight. Balance diagnostics using the cluster mean weights were similar (results not shown), except that these weights did not balance on the cluster-level variable as it appears in both the numerator and denominator of the weight, an issue highlighted in the marginal structural model literature (Almirall et al. 2014). Appendix 2 presents boxplots of the Pearson correlation.

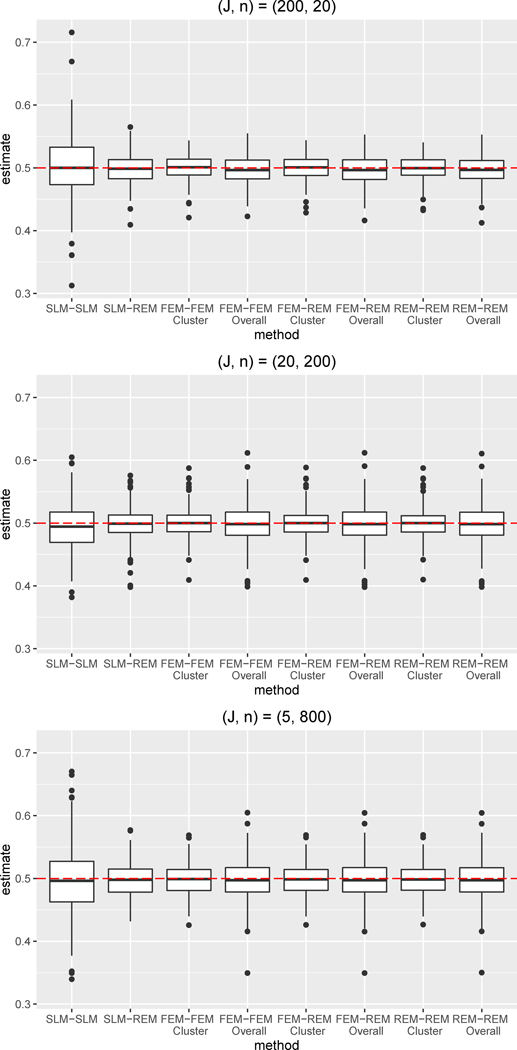
The ATE estimation results from our simulation study are presented in Table 3 and Figures 1–3. Our simulations assessed the performance of each propensity score/outcome regression combination under the three simulation conditions: (1) no differential confounding, W included, (2) no differential confounding, W omitted, and (3) differential confounding, W omitted. When W was included, the propensity score regression included all confounders, fulfilling the assumption of no unmeasured confounding. Under this condition, the FEM-FEM, FEM-REM, REM-REM combinations performed very well across the three different clustering designs considered (J=5, J=20, J=200). Specifically, for J=20, the FEM-FEM, FEM-REM, and REM-REM combinations had nearly identical results, with mean bias of 0.019 and 92% coverage (for cluster-mean weights). The SLM-SLM combination consistently yielded the largest bias, while SLM-REM performed relatively similarly to the multilevel combinations. When W was included, cluster size minimally impacted performance of a given regression combination (except for SLM-SLM): for each regression combination, the absolute bias, RMSE and coverage were very similar across J=5, J=20, and J=200. Note that SLM-SLM yielded markedly lower coverage (64%) for J=5.

Table 3.

Simulation results: Absolute bias, root mean square error (RMSE) and 95% confidence interval (CI) coverage of the ATE estimate under different propensity score/outcome regression specifications and propensity score weight form. Results are shown for under three simulation conditions.

		No differential confounding: W included			No differential confounding: W omitted			Differential confounding: W omitted
PS – outcome regression	PS weight	Absolute Bias	RMSE	95% CI coverage	Absolute Bias	RMSE	95% CI coverage	Absolute Bias	RMSE	95% CI coverage
		(J, nj) = (200, 20)
SLM-SLM		0.039	0.053	92%	0.096	0.106	24%	0.114	0.129	27%
SLM-REM		0.021	0.026	92%	0.026	0.032	86%	0.025	0.031	91%
FEM-FEM	cluster	0.016	0.021	94%	0.016	0.021	94%	0.017	0.022	96%
FEM-FEM	marginal	0.020	0.025	95%	0.020	0.025	95%	0.020	0.026	95%
FEM-REM	cluster	0.017	0.021	93%	0.021	0.026	86%	0.018	0.023	93%
FEM-REM	marginal	0.020	0.025	94%	0.021	0.026	94%	0.021	0.026	95%
REM-REM	cluster	0.017	0.021	93%	0.022	0.027	86%	0.019	0.023	92%
REM-REM	marginal	0.020	0.025	94%	0.021	0.026	94%	0.021	0.026	95%
		(J, nj) = (20, 200)
SLM-SLM		0.033	0.044	93%	0.089	0.102	57%	0.142	0.161	10%
SLM-REM		0.021	0.027	94%	0.017	0.022	91%	0.019	0.026	94%
FEM-FEM	cluster	0.019	0.023	92%	0.019	0.024	92%	0.021	0.028	93%
FEM-FEM	marginal	0.024	0.031	94%	0.024	0.031	94%	0.026	0.036	94%
FEM-REM	cluster	0.019	0.023	92%	0.019	0.024	93%	0.021	0.028	93%
FEM-REM	marginal	0.024	0.031	94%	0.024	0.031	94%	0.026	0.036	94%
REM-REM	cluster	0.019	0.023	92%	0.019	0.024	93%	0.021	0.028	93%
REM-REM	marginal	0.024	0.031	94%	0.024	0.030	94%	0.026	0.035	94%
		(J, nj) = (5, 800)
SLM-SLM		0.042	0.055	64%	0.088	0.113	29%	0.141	0.177	20%
SLM-REM		0.021	0.027	93%	0.019	0.023	94%	0.020	0.026	95%
FEM-FEM	cluster	0.020	0.025	94%	0.020	0.025	94%	0.021	0.027	96%
FEM-FEM	marginal	0.025	0.034	94%	0.025	0.034	94%	0.026	0.036	95%
FEM-REM	cluster	0.020	0.025	94%	0.020	0.025	94%	0.021	0.027	96%
FEM-REM	marginal	0.025	0.034	94%	0.025	0.034	94%	0.026	0.036	96%
REM-REM	cluster	0.020	0.025	94%	0.020	0.025	94%	0.021	0.027	96%
REM-REM	marginal	0.025	0.034	94%	0.025	0.034	94%	0.026	0.036	96%

Abbreviations: SLM = single level model, FEM = fixed effects model, REM = random effects model, PS = propensity score, J = number of clusters, n_j = number of individuals in each cluster, W = cluster-level covariate.

Figure 1.

Boxplots of bias for the ATE estimate for simulation condition with no differential confounding and W included in both the propensity score and outcome regression (i.e., both regressions correctly specified).

Abbreviations: SLM = single level model, FEM = fixed effects model, REM = random effects model

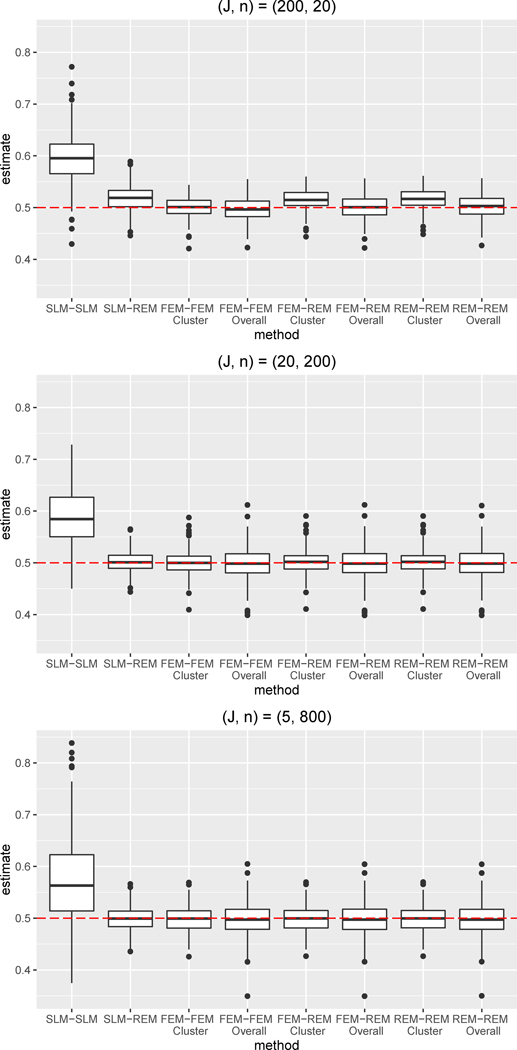
Figure 3.

Boxplots of bias for the ATE estimate for simulation condition with differential confounding and W omitted from both the propensity score and outcome regression.

Abbreviations: SLM = single level model, FEM = fixed effects model, REM = random effects model

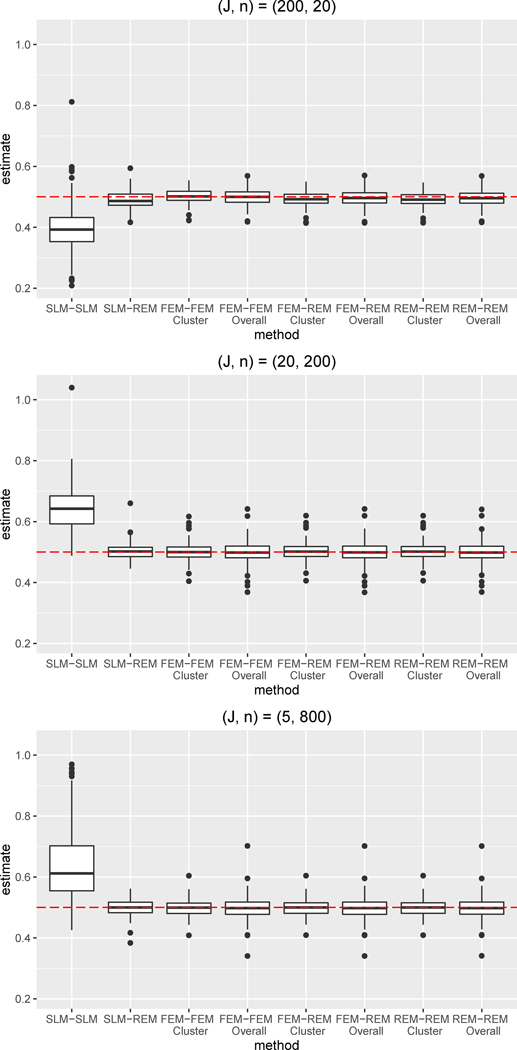
We also assessed robustness to omission of W in both the absence and presence of differential confounding. For both conditions, the SLM-SLM combination performed worst, as the cluster-level confounder was not being adjusted for in either the propensity score or outcome regression. Compared to when W was included, the SLM-SLM bias was approximately 2.5 times larger, on average, in the absence of differential confounding and approximately 3.5 times larger, on average, in the presence of differential confounding. SLM-SLM coverage was quite low, ranging from 24–57% under no differential confounding and from 10–27% under differential confounding. In general, only the SLM-SLM combination showed worse performance under differential confounding; the remaining combinations performed quite similarly in the presence and absence of differential confounding for a given cluster size. The SLM-REM combination performed consistently better than the SLM-SLM combination —even though W was omitted from the regressions, the use of a REM for the outcome regression accounted for cluster-level differences and yielded ATE estimates with little bias. Indeed, the SLM-REM combination was able to account for non-linear, differential confounding by W. Furthermore, the FEM-FEM, FEM-REM, and REM-REM combinations performed very well, also significantly outperforming the SLM-SLM combination. Even though the propensity score and outcome models were misspecified due to omission of W, these combinations yielded estimates with small absolute bias, even in the presence of differential confounding, because the cluster variability was accounted for through the use of a FEM or REM. Note that, across all combinations, the performance of the FEM-FEM, FEM-REM, and REM-REM combinations were the most similar across the three simulation, indicating that these combinations were the most robust to omission of cluster-level confounders. Comparison of the results across all three simulation conditions indicates that the omission of W did not notably impact the bias or RMSE for the FEM-FEM, FEM-REM, and REM-REM combinations, even in the presence of differential confounding. Omission of W did somewhat reduce the coverage for the FEM-REM and REM-REM combinations when cluster size was the smallest, $\left(J,n_j\right)=\left(200,20\right)$.

Additionally, when either a FEM or REM was specified for the propensity score regression, we compared the performance of two forms of the numerator for stabilizing the propensity score weights: the marginal mean and the cluster-specific mean. Note that this choice of the numerator is not applicable when a SLM is specified for the propensity score regression, as either a FEM or REM is required to estimate cluster-specific means. Across the three simulation conditions, the cluster-mean weights almost always yielded lower mean bias and RMSE than the marginal weights. The only exception was for J=200 with no differential confounding and W omitted, when the FEM-REM and REM-REM combinations with cluster-mean weights and marginal weights had similar or identical bias. The larger bias for the marginal weights relative to the cluster-mean weights reflects both poorer covariate balance arising from these weights and greater variability of the marginal weights relative to the cluster-mean weights. Coverage also varied across the cluster-mean and marginal weights. Specifically, for J=200 with no differential confounding and W omitted, the FEM-REM combinations using the marginal and the cluster-mean weights both had mean bias of 0.021, yet the coverage was 86% with the cluster-mean weights and 94% with the marginal weights. The lower coverage arising from the cluster-mean weights indicates lower variability of the weights (range=0.05–25.37, SD=0.79) compared to the marginal weights (range = 0.01–161.12, SD=3.23). Finally, Figures 1–3 highlight that cluster-mean weights yield ATE estimates with smaller variance than marginal weights. Overall, in the context of a continuous exposure and a multilevel data structure, we recommend stabilizing propensity score weights by the cluster-specific mean.

Finally, our simulations assessed the impact of cluster size by considering three different clustering designs (J=5, J=20, J=200). When W is included and all regressions are correctly specified, cluster size did not notably impact performance with the exception of reduced coverage for SLM-SLM for the largest cluster size. Yet, cluster size had a greater impact for the two simulation conditions for which W is omitted. In the absence of W, the SLM-SLM combination had relatively similar bias across cluster sizes, but coverage rates varied across cluster size. When cluster size was large, FEM-FEM, FEM-REM, REM-REM combinations with cluster-mean weights and SLM-REM generally performed similarly. Indeed, for both J=20 and J=5, the FEM-FEM, FEM-REM, REM-REM combinations yielded identical or very similar results for a given simulation condition. In contrast, for the smallest cluster size (J=200), the FEM-FEM combination with cluster-mean weights yielded smaller bias, lower RMSE, and higher coverage than either FEM-REM or REM-REM with cluster-mean weights. Furthermore, the multilevel combinations with cluster-mean weights outperformed SLM-REM for the smallest cluster size.

3. Discussion

In general, accounting for the clustered nature of the data in both the propensity score and outcome regressions yielded the best performance with respect to bias, RMSE, and 95% confidence interval coverage. The SLM-SLM combination, which did not account for the clustered nature of the data in either the propensity score or outcome regression, consistently performed the worst, yielding larger bias and poor coverage. The SLM-REM combination yielded lower bias and higher coverage than the SLM-SLM combination, as it was able to adjust for cluster-level confounders omitted in the propensity score through the REM outcome model. Yet this approach generally provided lower coverage than the FEM-FEM, FEM-REM, and REM-REM combinations, particularly when the cluster-level confounder was omitted and cluster size was small.

Overall, multilevel regression combinations (FEM-FEM, FEM-REM, REM-REM) using cluster-mean weights performed the best across all simulation settings. These combinations consistently yielded the lowest absolute bias and had coverage rates near nominal levels for all conditions. For large cluster sizes, the SLM-REM combination also performed quite well. Regression specification was most important when cluster size was small (i.e., 20 individuals). For the smallest cluster size, our results indicate that FEM-FEM with cluster-mean weights was optimal, and that SLM-REM showed suboptimal performance relative to the multilevel regression combinations.

Unobserved confounders are a primary concern in the context of propensity score estimation because unbiased causal estimation relies on the fundamental assumption of no unmeasured confounders. Our covariate balance results indicate that a key advantage of using a multilevel model (i.e., FEM or REM) for propensity score estimation is that these models account for cluster heterogeneity through the use of cluster-specific intercepts. Our simulation results examine robustness to omission of the cluster-level confounder both in the absence and presence of differential confounding (namely, the true relationship between Y and W differs across individual-level confounders $X_1$ and $X_2$). Our results suggest that under certain conditions (e.g., when the underlying data structure is linear in the parametric sense), these models can achieve good balance with regard to cluster-level covariates, whether or not these covariates are included in the propensity score model. This robustness to omission of cluster-level confounders helps to satisfy the underlying causal inference assumption of no unmeasured confounders, and may be particularly advantageous in cases in which cluster-level characteristics have not been measured or are not available to the researcher. While our results indicated robustness when differential confounding is present, this robustness may not hold in the case of more complex data structures, including complex correlations across covariates or violations of normality. Additionally, multilevel models are not robust to omission of individual-level confounders. Therefore, while the use of multilevel modeling for propensity score estimation may provide some protection against unmeasured or omitted cluster-level confounders, unbiased estimation of the ATE still requires that there are no unmeasured or omitted individual-level confounders.

In general, the multilevel modeling literature recommends that random effects models are preferable to fixed-effects models when the data structure includes a large number of small clusters, as the data are too sparse to estimate a large number of fixed-effect terms. Partial pooling across small clusters helps REMs achieve more precise standard error estimates. However, achieving covariate balance across treatment groups is the primary objective in propensity score estimation, and accurate standard error estimation is of less concern than in the typical inferential application. Consistent with previous results regarding propensity score weighting for a binary exposure in multilevel data (Li et al. 2013), in our simulation, the FEM-FEM combination outperformed both the FEM-REM and REM-REM combinations for the condition with the smallest clusters. A FEM specifies the cluster-specific intercepts as a set of dummy variables and estimates each intercept from observations in the given cluster; in contrast, a REM uses partial pooling across clusters to estimate cluster intercepts, smoothing over cluster heterogeneity. As Li et al. (2013) discuss, the cluster-specific intercepts in a FEM may better capture both observed and unobserved cluster-level variability, making a FEM more robust than a REM to misspecification of cluster-level covariates. In contrast, due to cluster shrinkage, a REM does not guarantee balance on cluster-level variables, and thus is more sensitive to incorrect specification of cluster-level variables (Li et al. 2013). In the context of propensity score estimation, the ability of the FEM to achieve better balance on cluster-level variables is particularly advantageous. It should be noted that in our simulation study, the smallest clusters were comprised of 20 individuals, which may be sufficiently large so as not to compromise the performance of the FEM. Furthermore, a FEM is typically preferred when the observed clusters represent the total population of interest, whereas a REM is more appropriate when the clusters represent a random sample from the population. In propensity score applications, balance within the observed sample is of primary importance; in that sense, the observed clusters represent the totality of the population of interest. While a general advantage of REM is generalization beyond the observed data, in the context of propensity score weighting, optimizing within sample balance is the objective.

The existing literature regarding propensity score weighting for a continuous exposure indicates that unstabilized inverse probability of exposure weights (which have a numerator of 1) must be stabilized with an alternative numerator in order to reduce weight variability. When extending to the multilevel setting, one could stabilize the weights with either the cluster means or the marginal mean. Our simulation results indicated that across conditions, the cluster-mean weights almost always yielded lower mean bias and RMSE than the marginal weights. This is consistent with findings (Li et al. 2013) that indicated that cluster-mean weights outperformed marginal weights in the context of a binary exposure in the multilevel setting. In our simulations, we also considered unstabilized weights (numerator of 1; results not presented); both the unstabilized weights and the resulting post-weighting exposure-covariate correlations had large variance, in keeping with previous findings (Robins et al. 2000). It is likely that the cluster-mean stabilized weights work well for the same reason that subgroup-mean stabilized weights work well when estimating moderating effects of a treatment; that is, the weights are stabilized to a group rather than overall mean. In summary, use of the cluster-mean stabilized weights is recommended.

Our simulation study was not exhaustive. In particular, our simulations only assessed performance when either the regression models were correctly specified or when the cluster-level confounder was omitted (a scenario unique to multilevel structured data). There are a variety of data structures of greater complexity for which our results may not fully generalize. Specifically, we did not examine performance of these methods under conditions of correlated covariates, or treatment heterogeneity (interactions between T and W). Also, we did not consider misspecified or omitted individual-level confounders; misspecification of individual-level confounders in the propensity score model would be expected to bias the effect estimate. We examined a total sample size of 4,000, with cluster size ranging from 20 to 800; performance may be impacted by either a smaller total sample size or smaller cluster sizes. Finally, an important consideration in the multilevel setting is the implications of SUTVA, particularly with regard to interference between units. This assumption requires that an individual’s potential outcomes are not affected by the exposure assignment of any other individual. In some multilevel applications, this assumption may prove untenable, given concerns regarding contamination (spill-over) effects among individuals within the same cluster (Arpino and Mealli 2011). Interference across clusters essentially induces a cluster-level effect that is not measured with any of the covariates. In keeping with our simulation results and as highlighted by Li et al. (2013), the use of either a FEM or REM for the propensity score regression can help account for cluster-level interference, as these multilevel models account for cluster-level similarity arising from both measured and unmeasured variables. Of greater concern is interference with respect to some higher level clustering (e.g., individuals nested within doctors nested within hospitals; Li et al. 2013). If higher-level clustering is present but not accounted for in the propensity score regression and outcome analyses, then interference may still be present.

4. Guidance for the applied practitioner

In summary, we discuss some practical advice for implementation of propensity score weighting in a multilevel setting with a continuous treatment. The first objective is to carefully define the ATE of interest and identify potential confounders at both the individual and cluster level. The methods discussed in this paper are appropriate when both the treatment and outcome are measured at the individual level. Treatment assignment may occur at either the individual level (i.e., individuals within a cluster vary on treatment level) or at the cluster level (i.e., individuals within a cluster have the same treatment level). When assignment occurs at the individual level, both individual and cluster characteristics may influence treatment – for example, the level of pain medication prescribed to an individual may relate to both her individual characteristics (e.g., pain severity) as well as cluster characteristics (e.g., hospital prescribing trends). When interventions or policy changes are implemented at the cluster level (i.e., schools, hospitals), individual-level factors do not influence treatment assignment, yet clusters may still vary with regard to individual characteristics. Understanding the treatment assignment mechanism will help inform which variables (both individual-level and cluster-level) may be potential confounders. No special consideration regarding the structure of the data is necessary when both the exposure and outcome are measured at the cluster level, since there is no higher level clustering of the data (see (Stuart 2007)).

While the stabilized form of weights used for continuous treatments are designed to limit weight variability, in practice, one should examine the range of weights. When particularly large weights are observed, weight trimming may be used to reduce variability (Cole and Hernan, 2008; Lee et al., 2011; Potter, 1993; Scharfstein et al., 1999). In addition, balance should always be assessed in practice by assessing the Pearson correlation between each covariate and the exposure. After weighting, these correlations should be close to 0; Pearson correlation of 0.10 is equivalent to a standardized mean difference of 0.20. See Zhu et al. (2014) for more details.

In general, using a multilevel model (FEM or REM) for the outcome regression is strongly recommended. When deciding between a SLM and multilevel model for the propensity score regression, cluster size should be considered. When clusters are of sufficient size (e.g., 200+ individuals), weights estimated from a SLM regression perform very similarly to cluster-mean weights estimated from a FEM or REM regression. Thus, the applied practitioner may choose to use a SLM for propensity score estimation. Note that when using a SLM regression to estimate the propensity score, it is strongly recommended to use a multilevel outcome regression in order to provide robustness to misspecified or omitted cluster-level confounders, as this was not provided in the propensity score regression. When clusters are small (e.g., 20 individuals), cluster-mean weights estimated from a FEM or REM regression can reduce bias and improve coverage relative to weights estimated from a SLM, in the likely setting that important cluster-level confounders are measured with error or unmeasured. Furthermore, in this case, propensity score estimation with FEM outperforms propensity score estimation with REM, and FEM-FEM appears to be the optimal combination. Thus, when cluster-size is small, the specification of both the propensity score and outcome models is of greater importance.

While multilevel regression can provide some protection against misspecified or omitted cluster-level confounders, bias may still arise if individual-level confounders are misspecified or omitted. As correct parametric specification of both the propensity score and outcome regressions is unlikely in the context of complex observational data, use of nonparametric machine learning algorithms can be advantageous. These methods (e.g., generalized boosted regression, random forests, classification and regression trees, super learning) use data-driven algorithms to identify nonlinear or higher-order relationships among variables, which may reduce model misspecification. Machine learning methods have been shown to outperform parametric propensity score estimation in some contexts (Lee et al., 2009; McCaffrey et al., 2004; Piracchio et al., 2015; Setoguchi et al., 2004). In the multilevel setting, use of nonparametric machine learning methods for the propensity score regression may also be advantageous.

5. Conclusion

Propensity score methods are powerful statistical methods for balancing exposure or exposure groups with respect to covariates. Propensity score methodology was developed in the context of data with no hierarchical structure, and there is limited literature regarding propensity scores in the context of multilevel data. Yet, in many applications in health research, the data have a clustered structure that is of substantive importance, such as when individuals are clustered within healthcare providers or geographic region. When estimating the ATE in a multilevel setting, accounting for both individual-level and cluster-level confounders is imperative for unbiased effect estimates.

Figure 2.

Boxplots of bias for the ATE estimate for simulation condition with no differential confounding and W omitted from both the propensity score and outcome regression.

Abbreviations: SLM = single level model, FEM = fixed effects model, REM = random effects model