Denoising of diffusion MRI using random matrix theory

Abstract

We introduce and evaluate a post-processing technique for fast denoising diffusion-weighted MR images. By exploiting the intrinsic redundancy in diffusion MRI using universal properties of the eigenspectrum of random covariance matrices, we remove noise-only principal components, thereby enabling signal-to-noise ratio enhancements, yielding parameter maps of improved quality for visual, quantitative, and statistical interpretation. By studying statistics of residuals, we demonstrate that the technique suppresses local signal fluctuations that solely originate from thermal noise rather than from other sources such as anatomical detail. Furthermore, we achieve improved precision in the estimation of diffusion parameters and fiber orientations in the human brain without compromising the accuracy and/or spatial resolution.

1. Introduction

In vivo exploration of microstructure of biological tissues has been made possible by the development of diffusion Magnetic Resonance Imaging (dMRI) (Jones, 2010a). The dMRI signal is sensitized to the stochastic thermal motion of water molecules and their interaction with surrounding microstructure by applying diffusion-encoding gradients. Unfortunately, due to the signal-attenuation induced by diffusion-sensitization and T₂ relaxation resulting from the long echo time necessary to accommodate gradient pulses, the signal-to-noise ratio (SNR) of the diffusion-weighted (DW) MR signals is inherently low (Jones, 2010b).

Thermal noise that corrupts dMRI measurements propagates to the diffusion parameters of interest and, as such, hampers visual inspection and quantitative interpretation of the underlying diffusion process. Although attempts have been made to minimize the noise propagation by optimizing diffusion encoding settings (Jones et al., 1999; Poot et al., 2010; Hansen et al., 2013, 2015), scan time limitations put a bar on what is to gain with protocol optimization in terms of precision. Therefore, image denoising, i.e. minimizing the variance of the dMRI signals in a post-processing step, is essential to raise that bar.

Denoising has been an important and long-standing problem in image processing. Some of the proposed techniques were adopted by the dMRI community in the last few years because of their ability to deal with the spatially varying and non-Gaussian nature of noise in magnitude MR data. Overall, many of these methods share an underlying similarity in terms of their structure, which is based on weighted averages of voxels, where the voxels (and weights) are selected by metric similarity of patches (Buades et al., 2005; Coupé et al., 2006; Manjón et al., 2008, 2010; Orchard et al., 2008; Rajan et al., 2011, 2012; Foi, 2011). Limitations are typically loss of spatial resolution of the image (blur) and introduction of additional partial volume effects that lead to complications in further quantitative analyses or to biases in diffusion modeling. An alternative approach was pioneered by Rudin et al. (1992), who proposed total variation (TV) minimization, which is a method based on the principle that local signal fluctuations increase the L₁ norm of image gradient. The main benefit of such TV-based noise removal techniques is that they are well-suited to remove local noise variations while preserving the edges in the images. Limitations are the dependency on a regularization term, introduction of reconstruction artifacts, and the fact that thermal noise is not the sole source of local variations. Indeed, fine anatomical details might be removed as well by this non-selective technique (Block et al., 2008; Knoll et al., 2011; Veraart et al., 2015; Perrone et al., 2015).

In 1933, Hotelling seeded the idea of noise removal by means of transforming a redundant dataset into a principal component basis and preserving only the signal-carrying principal components by suggesting “perhaps neglecting those whose contributions to the total variance are small.” (Hotelling, 1933). Indeed, the principal component analysis (PCA) of redundant data shows that most of the signal-related variance is contained in a few components, whereas the noise is spread over all components. Redundancy in data is commonly pursued by a local or non-local selection of image patches, a non-trivial and time-consuming approach, especially in case of spatially varying noise (Deledalle et al., 2011; Manjón et al., 2015). Fortunately, it has been shown that typical dMRI data exhibit sufficient redundancy due to common practice of oversampling the q-space (Veraart et al., 2016).

The number of signal-carrying principal components, i.e. the number of components that significantly contribute to the description of the underlying diffusion process, is unknown and is expected to depend on imaging factors such as resolution, b-value and SNR. Hence, an objective criterion to discriminate between the signal-carrying and noise-only components has been missing. In other words, it had remained unclear what “small contributions to the total variance” (Hotelling, 1933) actually means. Commonly used criteria include thresholding of the eigenvalues associated with the principal components by an empirically set value (Manjón et al., 2013).

In this work, we will objectify the above-mentioned threshold for PCA denoising by exploiting the fact that noise- only eigenvalues are expected to obey the universal Marchenko-Pastur law, a result of the random matrix theory for noisy covariance matrices (Marchenko and Pastur, 1967). This article is an extension of our previous work that was concerned with the estimation of spatially varying noise maps using random matrix theory (Veraart et al., 2016). Whereas we previously focused on the noise level estimation, here we will demonstrate that an objective threshold on the eigenvalues for PCA denoising can be derived from the noise level. We will show that the proposed technique preserves the underlying signal better than other state-of-the-art techniques at the level of the diffusion sensitized images and diffusion MR parameters of general interest. Indeed, we propose here a denoising technique that preserves local signal fluctuations of any origin different than thermal noise, including fine anatomical detail. The noise level, being an additional product of the method (Veraart et al., 2016), offers the opportunity to correct the denoised signal for Rician or noncentral-χ distributed noise bias (Aja-Fernández et al., 2011; Gudbjartsson and Patz, 1995) using the method of moments (Koay and Basser, 2006).

2. Materials and Methods

2.1. Marchenko-Pastur distribution

A redundant M × N data matrix X is the one that can be synthesized by a combination of a few, P ≪ min{M, N} linearly independent sources, or principal components, derived via the singular value decomposition of X:

$$\mathit{X}=\sqrt{N}\mathit{U}\mathbf{\Lambda }{\mathit{V}}^T,$$ [1]

with U and V unitary matrices whose columns are the left-singular and right-singular vectors of X, respectively. Without loss of generality, we assume M < N. The diagonal elements Λ_1,1, ···,Λ_M,M of the M × N matrix Λ are the singular values, with ${\mathrm{\Lambda }}_{ii}^2={\lambda }_i$ being the i^th eigenvalue of the M × M matrix:

$$\mathrm{\sum }=\frac{1}{N}\mathit{X}{\mathit{X}}^T=\mathit{U}{\mathbf{\Lambda }}^2{\mathit{U}}^T.$$ [2]

In agreement with an asymptotic universal law resulting from random matrix theory for noisy covariance matrices, the M̃ = M − P smallest nonzero eigenvalues λ_P+1 ≥ ··· ≥ λ_M are described by the Marchenko-Pastur (MP) distribution if the noise level is constant amongst all elements of X (Marchenko and Pastur, 1967):

$$p(\lambda \mid \sigma ,\gamma )=\{\begin{array}{ll}\frac{\sqrt{({\lambda }_{+}-\lambda )(\lambda -{\lambda }_{-})}}{2\pi \gamma \lambda {\sigma }^2}\hfill & \text{if}{\lambda }_{-}\le \lambda \le {\lambda }_{+}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ [3]

where ${\lambda }_{\pm }={\sigma }^2{(1\pm \sqrt{\gamma })}^2$ with γ = M̃/N and σ the noise level if M̃ ≫ P (see Fig. 1). Note that the width of the MP bulk spectrum equals:

$${\lambda }_{+}-{\lambda }_{-}=4\sqrt{\gamma }{\sigma }^2,$$ [4]

and the expectation value of an MP distribution is given by:

$${\int }_{{\lambda }_{-}}^{{\lambda }_{+}}p(\lambda \mid \sigma ,\gamma )\lambda d\lambda ={\sigma }^2.$$ [5]

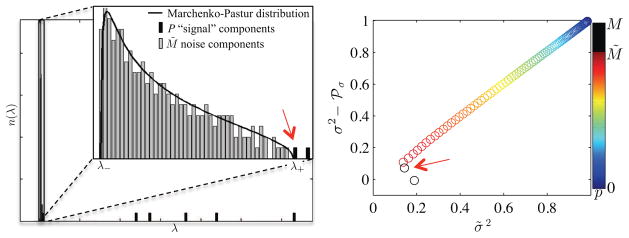
Figure 1.

(left) The upper edge λ₊ of the Marchenko-Pastur distribution, a universal signature of noise in sample covariance matrices, distinguishes between noise- and significant signal-carrying principal components. (right) Validitiy of Eq. [8] as function of p nullified eigenvalues (color encoding). if p > M̃, suppressed signal leaks into the residuals and, as such, the variability of the residual map, σ̃², start to deviate from σ² − ℘_σ with σ² being the noise variance and ℘_σ the noise variance accumulated in the p omitted eignvalues. Simulated data (cf. Data) with M = 90 and N = 250 was used to generate the graphs.

However, the coherent repulsion of the pure noise eigenvalues by the signal-carrying eigenvalues will introduce an error of order $\mathcal{O}(\frac{P}{N})$ to Eq. [5] (Johnstone, 2006).

The distribution edge λ₊ distinguishes between noise- and significant signal carrying principal components. Nullifying all λ ≤ λ₊, Λ → Λ̃, and reconstructing the matrix results in a denoised matrix:

$$\widehat{\mathit{X}}=\sqrt{N}\mathit{U}\stackrel{\sim }{\mathbf{\Lambda }}{\mathit{V}}^T.$$ [6]

Using Eq. [5], one can derive that the variance accumulated in the omitted eigenvalues is given by:

$${\mathcal{P}}_{\sigma }=\sum _{i=P+1}^M\frac{{\lambda }_i}{M}=\frac{\stackrel{\sim }{M}}{M}{\sigma }^2+\mathcal{O}(\frac{P}{N}).$$ [7]

Since the omitted and residual principal components are linearly uncorrelated, the variance σ̃² of the residual noise, contained within the P significant components, can be computed as:

$${\stackrel{\sim }{\sigma }}^2={\sigma }^2-{\mathcal{P}}_{\sigma }.$$ [8]

Combining Eqs. [7] and [8] gives an estimate of the noise reduction achieved by nullifying the M̃ lowest eigenvalues:

$${\stackrel{\sim }{\sigma }}^2\approx \left(1-\frac{\stackrel{\sim }{M}}{M}\right){\sigma }^2=\frac{P}{M}{\sigma }^2.$$ [9]

The SNR after denoising should thus scale with $\sqrt{M/P}$.

In what follows, X will be a real-valued dMRI matrix, with rows representing M dMRI measurements and columns representing N voxels within a local neighborhood, typically a sliding window (note that M and N are re-denoted compared to Veraart et al. (2016)). To comply with the MP theory, we assume the noise level to be constant and uncorrelated within the local neighborhood and across the dMRI measurements (Veraart et al., 2013a; Blackledge et al., 2011).

2.2. Denoising algorithm

We aim to remove M̃ “pure noise” eigenvalues (see Fig. 1). For that, we need to estimate the noise level σ and the number of significant signal components P simultaneously. The simultaneous estimation of σ and P roots in the idea that the mean of the lowest p eigenvalues will exceed the expectation value of the MP distribution p(λ|σ, γ_p) with γ_p = (M − p)/N if at least one of the p eigenvalues corresponds to a signal-carrying component.

In particular, we estimate the number P̂ of significant components by incrementally increasing p until

$$\sum _{i=p+1}^M{\lambda }_i\ge (M-p){\widehat{\sigma }}^2(p).$$ [10]

Given that λ_P+1 and λ_M serve as a proxy for, respectively, λ₊ and λ₋, Eq. [4] results in:

$${\widehat{\sigma }}^2(p)=\frac{{\lambda }_{p+1}-{\lambda }_M}{4\sqrt{{\gamma }_p}}.$$ [11]

After solving Eqs. [10–11] for p, we update our estimate of σ̂²:

$${\widehat{\sigma }}^2=\frac{{\sum }_{i=\widehat{P}+1}^M{\lambda }_i}{M-\widehat{P}},$$ [12]

to avoid the discretization bias inherent to Eq. [11]. Then, we nullify λ_P+1, ···, λ_M and reconstruct the signal using Eq. [6]. Afterwards, P̂ and σ̂ can be corrected for the Rician or noncentral-χ biases using the well documented inversion technique described by Koay and Basser (2006). The same routine is then applied to different neighborhoods, or sliding windows, until the entire region-of-interest is processed. In case of a sliding window operation, the user can choose to adopt the center voxel only, or to average the results of overlapping voxels from multiple windows (Manjón et al., 2013). Here, we use the latter strategy with a sliding window of [5 × 5 × 5] voxels unless stated otherwise.

Note that the proposed technique to fit the MP distribution to the PCA eigenspectrum is conceptually different than the approach presented in our previous work (Veraart et al., 2016). Although no significant differences in terms of accuracy or precision have been observed, the new approach reduces the computation time dramatically. More details are given in the Discussion.

Hereafter, we will refer to the proposed method as MPPCA. The accuracy and precision of MPPCA will be compared to two widely adopted state-of-the-art techniques: adaptive non-local means (Manjón et al., 2010) (ANLM) and second order total generalized variation (Knoll et al., 2011) (TGV). Source code of both techniques was kindly provided by the respective authors. Default parameters were used for ANLM, whereas the regularization term of TGV was optimized according to Veraart et al. (2015). Unlike MPPCA, ANLM and TGV are applied on the individual 3D imaging volumes.

2.3. Data

Simulations I

A set of 1000 Rician distributed M × N data matrices was computed by projecting N, ranging from 100 to 2500, axially symmetric diffusion tensors onto M = 30, 60, and 90 diffusion gradient directions with b = 1ms/μm². The first eigenvectors of the diffusion tensors were uniformly distributed on a hemisphere. The underlying FA and MD for each tensor was sampled from a distribution with mean 0.6 and 0.8 μm²/ms, respectively, and standard deviation 0.1.

Next, we fixed M = 90, N = 125, and SNR = 25, but varied the diffusion encoding protocol used to generate the simulated diffusion-weighted signals. We evaluated two single-shell protocols: (Ia) 90 × 1ms/μm² and (Ib) 90×2.5ms/μm², as well as (II) 2-, (III) 3-, (V) 5-, and (VI) 6-shell protocols. For the n-shell protocols, we distributed or repeated the M = 90 diffusion gradient directions equally over the number shells, whereas the b-values were equidistantly spread in the range [2.5/n, 2.5] ms/μm². Note that for the former, M is consistently 90 (or M/n directions per shell), whereas in the latter, M = n × 90, with n being the number of shells.

Simulations II

We derived simulated DW data from a hybrid diffusion atlas that was created from DW measurements of 10 healthy subjects (Dhollander et al., 2011). The DW atlas data provides high precision and a high order parameterization of the underlying diffusion signal by spherical harmonics, allowing us to employ it as a noise-free “ground truth” that represents a typical human brain. The b = 1ms/μm²-shell of the atlas data was resampled on 30, 60, and 90 isotropically distributed gradient directions. After adding complex Gaussian noise, the magnitude images were computed to generate Rician distributed DW data. The noise level was spatially uniform and the average SNR of the skullstripped b = 0 image varied between 25 and 50.

Clinical data

A healthy volunteer underwent imaging on a Siemens Prisma (3T) MR scanner (Siemens AG, Siemens Medical Solutions, Erlangen, Germany) after obtaining informed consent, using a 64-channel receiver head coil. The body coil was used for transmission. An EPI-DWsequence was used to acquire 3 repetitions of the following dMRI data. Besides the acquisition of 6 nondiffusion-weighted images, diffusion weighting was applied along 90 isotropically distributed gradient directions for b = 1 and 2.5ms/μm², resulting in a total of 186 images per repetition. Following imaging parameters were kept constant throughout the data acquisition sequences: TR/TE : 4000/76, ms, matrix: 92×92, voxel dimensions: 2.5×2.5 mm, slice thickness: 2.5 mm, slices: 50, parallel imaging factor: GRAPPA with acceleration factor 2, reconstructed using the adaptive combine algorithm and simultaneous multisclice factor 2.

We will refer to subsets of this data as follows, e.g. M_b=1 = 30 represents a subset of 30 DW images of the dMRI data that was acquired with b = 1μm²/ms. Alternatively, M_b={1,2.5} = {30, 30} indicates a subset of 30 DW images with b = 1ms/μm² and 30 DW images with b = 2.5ms/μm² that are analyzed simultaneously. Six non-DW images were always included in the subsets. Hence, M_b=0 = 6 without further notice. M equals sum of the number DW images per analyzed shell, that is, respectively, 36 and 66 in the examples above.

HCP data

We used a randomly chosen single subject from the MGH Adult Diffusion Data of the Human Connectome Project (HCP) for this study. While the diffusion acquisition is covered in detail in (Setsompop et al., 2013), a brief summary is given here. Whole-brain EPI acquisitions were acquired with a 64-channel, tight-fitting brain array coil (Keil et al., 2013) on the customized Siemens 3T Connectom scanner with TR = 8800 ms, TE = 57 ms, BW = 1984 Hz/Px, in-plane FOV = 210 × 210 mm, 96 slices, 1.5 mm isotropic voxels, with iPAT factor of 3. Diffusion weighting was applied along 64, 64, 128, and 256 DWgradient directions for b = 1, 2, 5, and 10 ms/μm², respectively. Additionally, 41 nondiffusion-weighted images were acquired.

2.4. Diffusion MR analysis

Without loss of generality, we limit ourselves to studying the effect of denoising on diffusion parameters such as the fractional anisotropy (FA), mean diffusivity (MD) and main fiber orientations. Both the FA and MD were calculated from the eigenvalues of the diffusion tensors, which were estimated from dMRI data with b ≤ 1ms/μm² with Diffusion Tensor Imaging (DTI) (Basser et al., 1994) using the weighed linear least squares estimator (Veraart et al., 2013b).

Constrained spherical deconvolution (CSD) was used to estimate the fiber orientations (Tournier et al., 2007). First, the fiber orientation distribution function (fODF) is estimated by deconvolving the b = 2.5ms/μm²-images with a data-specific single-fiber response function. By expressing the components of the CSD in terms of spherical harmonics, here up to the 6th order, the deconvolution becomes a linear estimation problem. The single-fiber voxels are identified using the recursive response function calibration technique proposed by Tax et al. (2014). Second, the fiber orientations are selected as the distinct peaks of the fODF with an amplitude exceeding a user-defined threshold (Jeurissen et al., 2013). Note that all data was corrected for eddy current distortion and subject motion prior to diffusion MR analyses (Glasser et al., 2013). Finally, probabilistic streamline fiber tractography was performed to investigate the effect of denoising on the tractogram using the MRtrix software package (Jeurissen et al., 2013; Tournier et al., 2012).

2.5. Bootstrapping

Bootstrapping is a non-parametric statistical procedure that enables the estimation of the uncertainty of a given statistic by randomly selecting individual measurements from repetitions of the same measurement (Efron, 1992). Note that all bootstrap realizations (n = 500) have an identical diffusion encoding scheme. However, they are all unique because of the random drawing of individual data points from one out of three repetitions. By computing the diffusion parameters of interest from each of many bootstrap realizations, with or without denoising, and measuring the variability of those parameters amongst the different realizations, we evaluate the effect of denoising on the precision of diffusion parameter estimators. Diffusion parameters were estimated after correcting the resultant images for eddy current distortions and subject motion. Affine transformation matrices for motion and distortion correction were estimated from original images and applied to denoised data, regardless of the used technique, to exclude difference in registration quality after denoising. We also analyze systematic differences between the bootstrap realizations and all b ≤ 1ms/μm² data to evaluate the effect of denoising on accuracy.

In particular, we probe the variability of the principal diffusion peaks ζ_i(x), i = 1, ···, n in voxel x by means of a coherence metric κ(x)(Jones, 2003):

$$\kappa (\mathit{x})=1-\sqrt{\frac{{\beta }_2(\mathit{x})-{\beta }_3(\mathit{x})}{2{\beta }_1(\mathit{x})}},$$ [13]

with β₁(x) ≥ β₂(x) ≥ β₃(x) the eigenvalues of the average dyadic tensor Ξ:

$$\mathrm{\Xi }=\frac{1}{n}\sum _{i=1}^n{\mathit{\zeta }}_i(\mathit{x}){\mathit{\zeta }}_i{(\mathit{x})}^T,$$ [14]

and n the number of bootstrap realizations. The first eigenvector of the dyadic tensor, ζ̄ (x), represents the average principal diffusion directions over all realizations (Basser and Pajevic, 2000). The angular error to a certain peak ψ(x) is given by θ(x) = arccos(ζ̄(x) · ψ(x)). We repeat this calculation for the secondary diffusion peak extracted from the orientation distribution functions. Note, however, that we order the diffusion peaks based on their alignment with the directions associated to the respective non-denoised data instead of the magnitude of the respective fODF peaks, to avoid a sorting bias.

3. Results

For the human DW data, Rician noise correction was not applied because denoising and bias corrections are technically independent problems that need to be evaluated separately. In particular, we demonstrated that MPPCA is signal preserving, i.e. accurate, by studying the residuals. Evaluating the statistics of residuals is a powerful way to study the performance of post processing techniques when no real ground truth exists. Unfortunately, Rician bias correction would distort the residual maps, making them unsuited for the evaluation of accuracy of the denoising technique. Moreover, the accuracy of the Rician bias correction technique has been demonstrated independently in previous work (Koay and Basser, 2006; Veraart et al., 2016). Nonetheless, in the simulations, ground truth was available and, as such, the errors were used to assess the accuracy of denoising in combination with Rician bias correction.

Simulation I

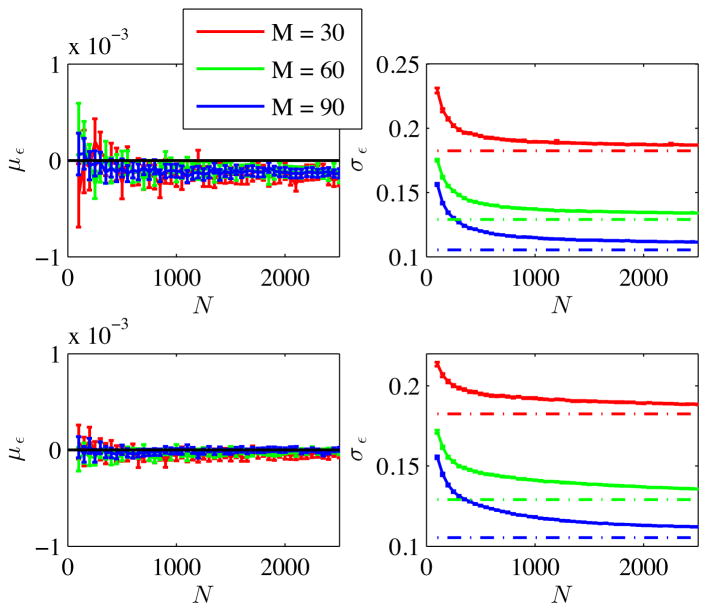
The accuracy of the denoising method, including Rician bias correction, as a function of M and N is evaluated. In Fig. 2, the average and standard deviation of the error, that is, the difference between denoised and noise-free signal, are plotted as function of M, N, and SNR. First, overall, the accuracy of denoising is very high. Indeed, the mean error, normalized by noise-free data, μ_ε is unbiased with a significance of α = 0.05 for SNR=50, whereas the underestimation of the signal for SNR=25 is limited to 0.01% after Rician bias correction. The standard deviation of the error, that is the standard deviation of the non-suppressed noise, normalized by $\sigma \sqrt{\widehat{P}}$, σ_ε decays with M and N. A universal expression of the decay for finite N is missing though.

Figure 2.

The bias [%] in the estimation of the noise-free signal is shown as function of N for different values for M and SNR (top row: SNR=25, bottom row: SNR=50). After Rician correction, the maximal error reduced to ~ 0.01%. The remaining noise standard deviation, normalized by $\sigma \sqrt{\widehat{P}}$, converges to $1/\sqrt{M}$ (dashed line).

In Fig. 2, it is shown that MPPCA is unbiased for the different diffusion encoding protocols for fixed M, N, and SNR. Indeed, the error in the estimation of noise-free signal is not significantly different than zero. However, we observe a slight, yet significant, elevated residual noise level for multi-shell protocols in comparison with the single-shell protocols if M is kept constant (blue). This observation demonstrates that more significant components are needed to approximate the diffusion-weighted signal as function of b-value in the PCA eigenbasis. However, simulations also show that combining multiple shells (M = n × 90) boost the performance of MPPCA due to the increased redundancy (red).

Simulation II

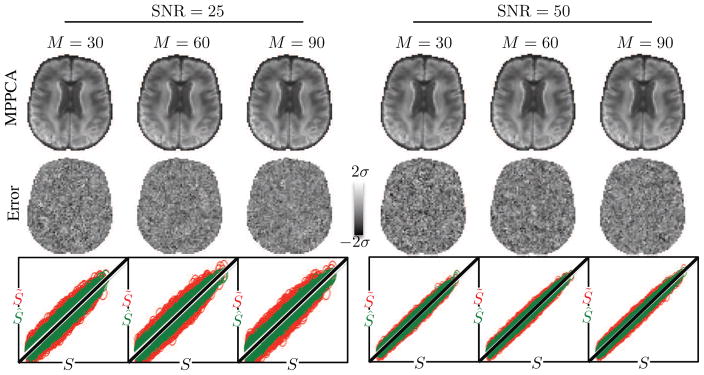
Fig. 4 shows the results of denoising the simulated data with M=30, 60, and 90 using MPPCA with a sliding window size of [5 × 5 × 5] for SNR=25 and 50. Next to a randomly chosen DW image (top row), the corresponding error maps are shown (middle row). The errors are computed as the difference between the denoised images, corrected for Rician noise bias, and the noise-free ground truth data. Scatter plots show the noise-free simulated data (S ) against the corresponding noisy data points (S̃ ; red) and against the corresponding denoised and Rician corrected data points (S̃ ; green) (bottom row). The lack of anatomy in the error maps indicates high accuracy of denoising and signal-preservation. More quantitatively, the relative errors, that is the error normalized by the noise-free data, are centered around zero. Indeed the center of the distribution of relative errors are not significantly different from zero with p = 0.05. The average signal of the skullstripped b = 0 image divided by the standard deviation of the error gives the SNR of the denoised data. For SNR=25, the resulting SNR after denoising equals 54, 63, and 68 for M=30, 60, and 90, respectively. The respective denoised SNR values for SNR=50 are 92, 110, and 117.

Figure 4.

(top row) A randomly chosen DW image after denoising the simulated whole brain data with M=30, 60, and 90 using MPPCA for SNR=25 and 50. (middle row) The corresponding error maps, computed as the difference between the denoised images, corrected for Rician noise bias, and the noise-free ground truth data, do not show anatomical features. (bottom row) Scatter plots show the noise-free simulated data (S ) against the corresponding noisy data points (S̃ ; red) and against the corresponding denoised and Rician corrected data points (S̃ ; green)

In vivo data

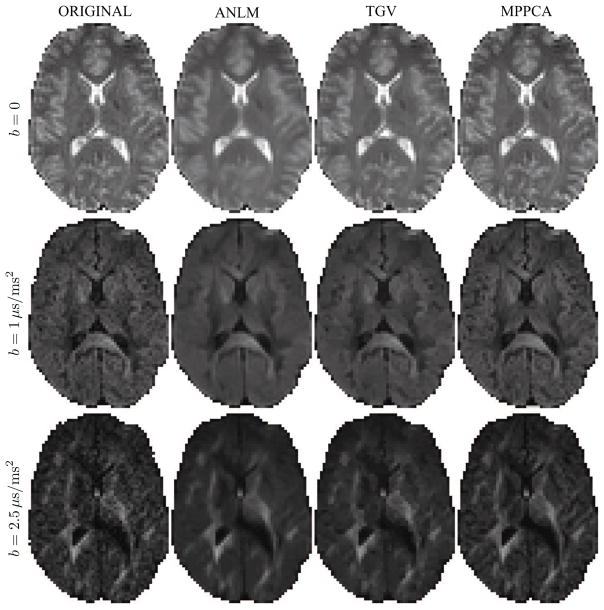
We applied the proposed denoising method, excluding the Rician bias correction, to subsets M_b=1 = 60 and M_b={1,2.5} = {60, 60} of the first repetition with a sliding window size of [5 × 5 × 5], i.e. N = 125, and compared the result to ANLM and TGV. The resultant maps for a single dMRI image of b = 0, 1, and 2.5ms/μm² are shown for qualitative comparison in Fig. 5. Note that the results for b = 0 and 1ms/μm² are derived from the M_b=1 = 60 subset, whereas b = 2.5ms/μm² resulted from the multishell M_b={1,2.5} = {60, 60} subset.

Figure 5.

Denoised diffusion-weighted images for different b-values. Although the noise reduction is clearly visible in all denoising techniques, ANLM and TGV introduce image blur and/or reconstruction artifacts.

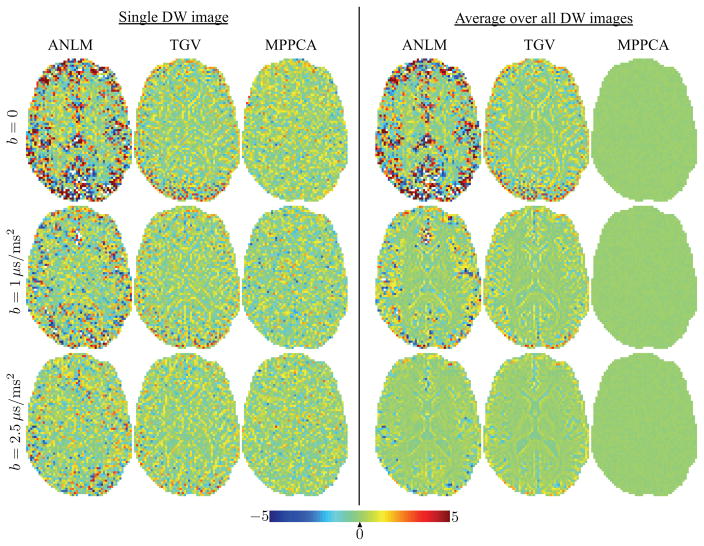
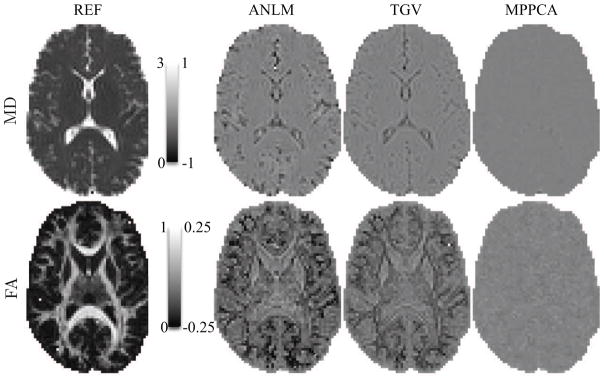
The maps of the σ-normalized residuals r(x), i.e. the residuals at coordinate x divided by σ̂ (x), for those images are shown in the left panel of Fig. 6. Although anatomical structure can already be observed in the normalized residual maps of ANLM and TGV, these effects become really pronounced after averaging the residual maps of all images per b value. The lack of anatomical structure and zero-centered residuals indicate good preservation of signal, or accuracy. Clearly, MPPCA outperforms ANLM and TGV in that respect.

Figure 6.

(left panel) The σ-normalized residual maps between the denoised diffusion-weighted images from Fig. 5 and the original data. (right panel) The presence of anatomical structure in ANLM and TGV anatomical maps indicates interference of the denoising algorithm with the “signal”. The effect becomes more visible after averaging the residual maps of the M_b>0 = 60 images per b value.

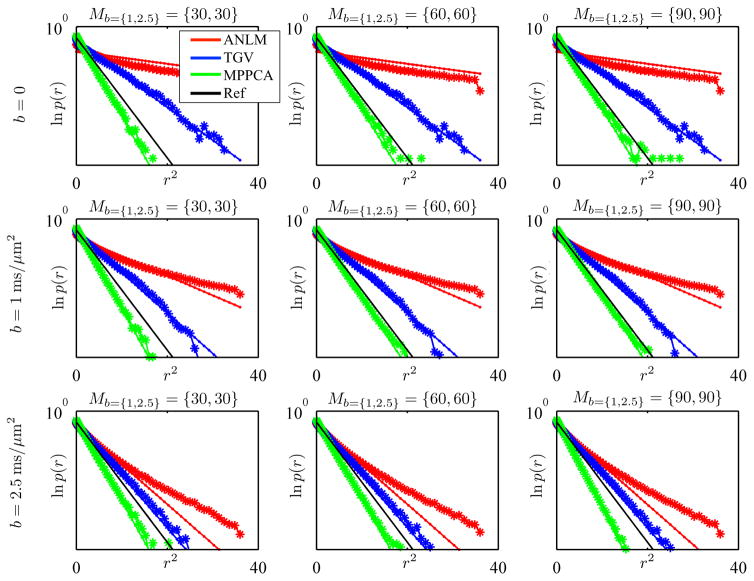
The distribution of the σ-normalized residuals, r, resulting from denoising following subsets M_b=1 = 30, 60, and 90 or M_b=1,2.5 = {30, 30}, {60, 60}, and {90, 90} of the first repetition of the clinical data are shown in Fig. 7. The logarithm of the distribution p(r) is shown as function of r². A zero-centered normal distribution with variance σ² is then represented by a straight line with slope 1/2. Ideally, normalized residuals are described by the standard normal distribution because only then all the noise is accumulated in the residuals. First, we observe that MPPCA residuals are well approximated by a normal distribution. Small deviations in the distribution’s tail are to attributed to Rician noise effects. Second, more importantly, MPPCA has a lower variance than unity, whereas TGV and ANLM have a higher variance. In the latter, the residuals contain more variance than explained by the noise. Indeed, genuine signal fluctuations (e.g. fine anatomical details) are removed by ANLM and TGV and add to the variance of the residuals. Conversely, MPPCA does not remove anatomical details, conservatively removing only noise. The variance of the MPPCA residuals ranges from 68% to 89% of the estimated noise variance. This translates to an MPPCA induced SNR increase between 77% and 201%.

Figure 7.

The logarithm of the distribution of normalized residuals p(r) as a function of r² for different b-values, M_b>0, and methods as observed (*) and best fitting normal distribution (solid line). The standard normal distribution is shown for reference (black line). ANLM and TGV clearly over-do the denoising (i.e. standard deviation >1) by interfering with the underlying signal.

The apparent blurring for ANLM and TGV is quantitatively confirmed by comparing the differential k-energy density as function of the distance to the k-space center k (Fig. 8, cf. Veraart et al. (2015)). Given a discrete k-space û_k, [n_x × n_y], with frequency step Δk, the k-energy density is computed as ||û_k(Ω;(n_kΔk))||₂ for n_k = 1 to min(n_x, n_y) with Ω;(n_kΔk) being the 2d square shell centered around the k-space center. A reference energy density is predicted by subtracting the noise power N_Ω;σ² with N_Ω; the number of samples falling within the shell Ω; from the corresponding kspace density of the original data (black line). This normalized quantity shows the observed loss of higher frequencies for ANLM and TV (cf. low-pass filtering). Spatial resolution loss and blur are the direct consequence. The suppression of frequencies that are not strictly rooted in thermal noise also results in residuals that follow a distribution with standard deviation exceeding the noise standard deviation (meaning that they are contaminated by signal). We can see that MPPCA preserves the actual signal better than competing methods.

Figure 8.

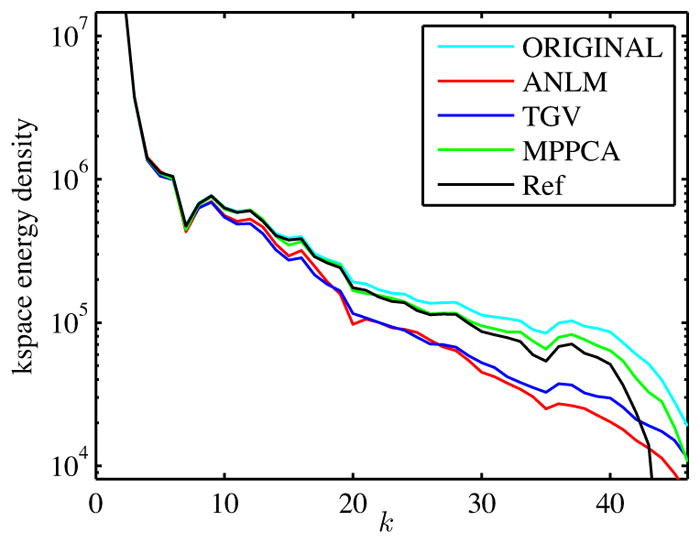
k-space energy density as function of the distance to the k-space center. ANLM and TGV have a low-pass filtering effect resulting in spatial resolution loss. MPPCA overshoots the predicted k-space density (black), i.e. Ref = Original - N_Ω;σ². This observation indicated incomplete noise suppression.

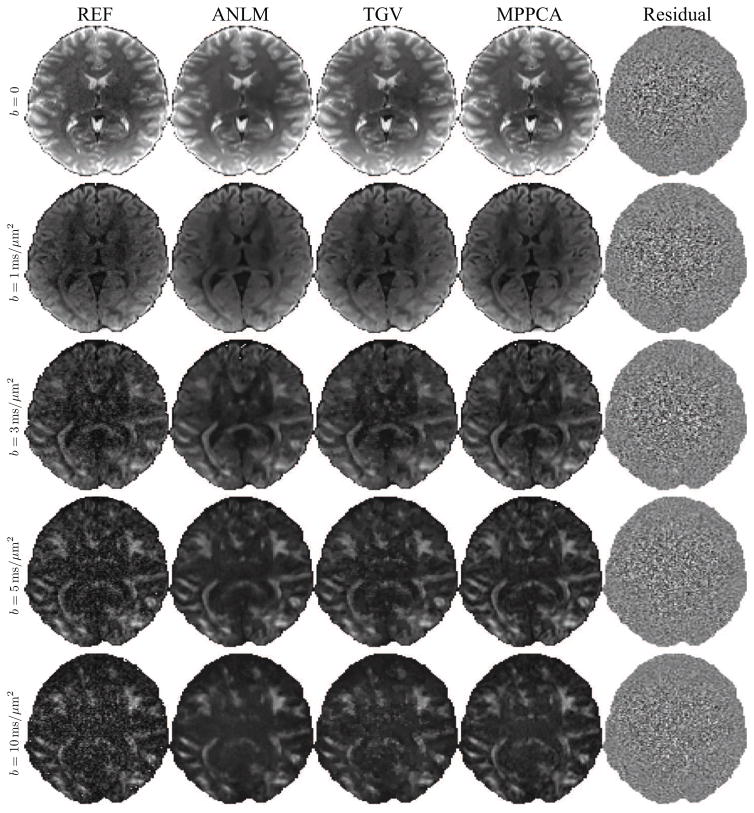
In Fig. 9, denoised DW images of the HCP data with b = {0, 1, 3, 5, and 10} ms/μm² are shown. Here, the sliding window size was [7 × 7 × 7]. The data quality enhancement is clearly visible in all methods. However, significant differences are noticeable. Overall, MPPCA preserves anatomical detail better than ANLM and TGV. Moreover, artifactual features present in TGV at high b are not shown in MPPCA. The MPPCA residuals do not show anatomical details. Indeed only a spatially varying noise trend can be observed and this is, in line with previous results, a marker for accuracy.

Figure 9.

Denoised single DW images for different methods and b-values and the corresponding residuals maps for MPPCA.

Diffusion parameter maps

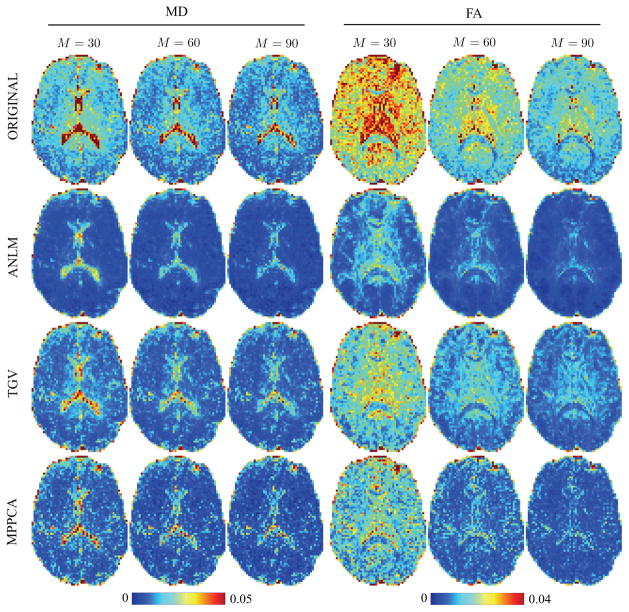
Bootstrapping (n = 500) with replacement based on the 3 repetitions was used to assess the effect of the different denoising strategies on the variability in FA and MD maps (Fig. 10). Note that the gradient directions for every single generated data set were the same. All denoising techniques improve the precision of diffusion parameter estimators, in all structures of the brain. The excelling results of ANLM in terms of precision are superficial. It may look as if ANLM does a good job, however studying the residuals between the denoised results and a ground truth derived from a concatenation of the 3 repetitions of all DW data up to b = 1ms/μm², i.e. 3×[5×b = 0] and 3×[90×b = 1ms/μm²], one reveals severe biases. Indeed, by averaging the residual maps between parameters maps with and without denoising, one clearly notices systematic differences for ANLM and TGV in every brain structure (Fig. 11). The differences root in the accumulation of signal inaccuracies introduced during denoising of the individual images. MPPCA shows structure-free, zero-centered residuals for MD and FA.

Figure 10.

Effect of denoising on the variability in the estimated MD [μm²/ms] and FA as function of the denoising method and the number of measurements M

Figure 11.

Effect of denoising on the bias in the estimation of MD [μm²/ms] and FA. MD and FA maps, derived from a concatenation of the 3 repetitions of all DW data up to b = 1ms/μm², are shown for reference.

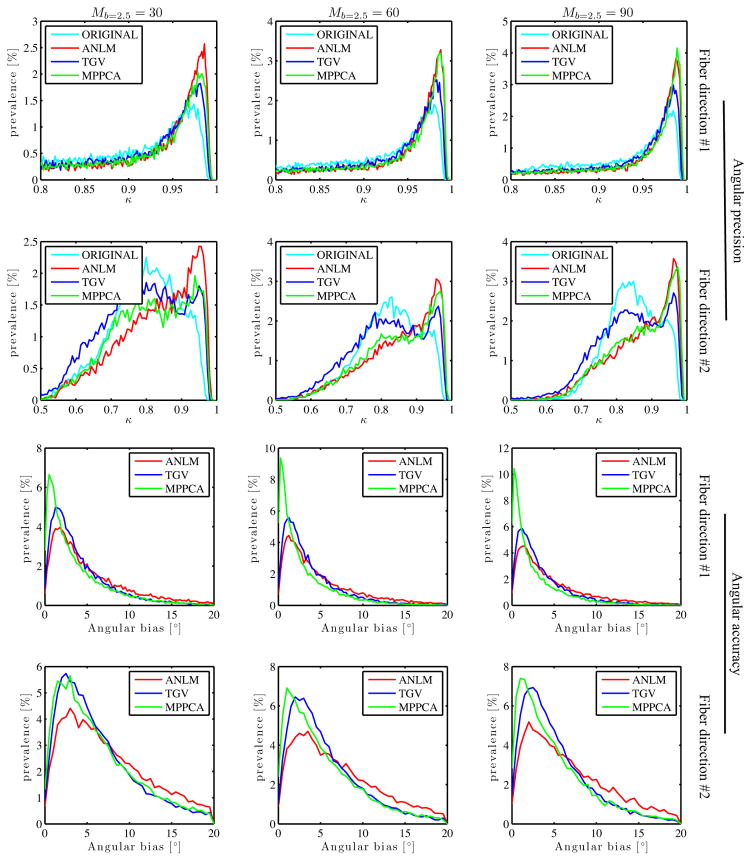
A similar bootstrapping approach is used to evaluate the effect on the estimation of diffusion directions using constrained spherical convolution. The distribution of angular precision, probed by the coherence metric κ (Eq. [13]), and the angular deviation from original data amongst white matter voxels is shown in Fig. 12. Again, for all evaluated M, ANLM, MPPCA, and – to a lesser degree – TGV improve the variability or dispersion in the primary and secondary diffusion directions. However, consistent with previous results, MPPCA outperforms all other methods in terms of accuracy. Indeed, MPPCA shows minimal angular deviation from the original data, whereas the deviations are significantly higher for TGV, and more so for ANLM.

Figure 12.

The effect of denoising on the angular precision, probed by a coherence metric κ, and the angular accuracy of the primary and secondary diffusion directions are shown as function of the number of measurements M and the denoising technique.

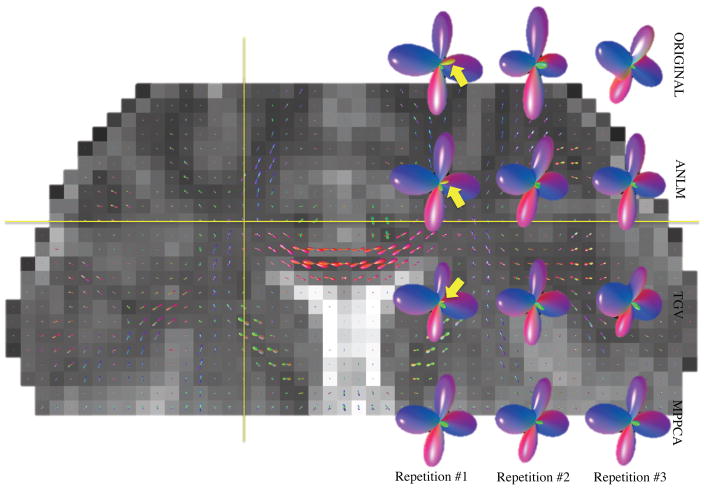
In Fig. 13, we show the fODF corresponding to a single voxel for each of the three repetitions (limited to M_b=2.5 = 60), with and without applying the different denoising techniques. In the particular voxel, the callosal commissure, superior longitudinal fasciculus, and corticospinal tract cross. This complex fiber crossing is assumed to be represented by a fODF with three distinct lobes. The success rate to detect the third lobe strongly depends on the method. MPPCA returns in 98% of the n = 100 bootstrap realizations exactly three distinct peaks. The success rate lowers to 65% and 48% for ANLM and TGV, respectively, whereas no denoising (ORIGINAL) results in a success rate of 70%. A spurious fourth peak (yellow arrows in Fig. 13) is detected in 2%, 30%, 52%, and 28% of the cases for MPPCA, ANLM, TGV, and ORIGINAL, respectively.

Figure 13.

Effect of denoising on the fiber ODF for a voxel with a three-fiber crossing (crosshair). Studying the three repetitions of the M_b=2.5 = 60 data subsets separately shows that MPPCA consistently improves the estimation of the third peak. Other methods show low coherence of the third direction and often a spurious fourth peak.

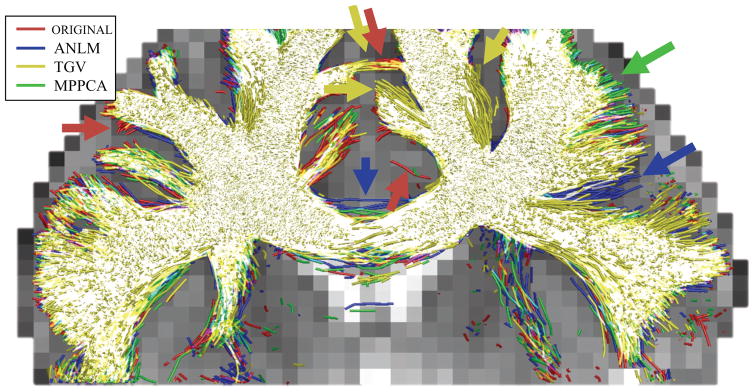
Finally, we performed probabilistic tractography on the denoised images corresponding to one of the repetitions (again restricted to M_b=2.5 = 60) to render digital reconstructions of the major fiber pathways as colorful tubes (see Fig. 14). (Jeurissen et al., 2011) Some obvious spurious fibers aside, all tractograms look perfectly plausible, yet very different, especially towards the cortical areas. Those differences reflect the differences in noise and signal patterns that depend on the used denoising technique (see Figs. 3–6, 10, and 11).

Figure 14.

Overlay of all tractograms derived from a single repetition of the M_b=2.5 = 60 data subset before and after denoising with the different techniques. Tractography was seeded in the corpus callosum. The cores of the major fiber bundles overlap well (white color). However, changing noise characteristics and possibly signal suppression introduced by ANLM and TGV have very different local and global effects on the tractogram that are often indistinguishable from anatomy (arrows) because of their plausible appearance.

Figure 3.

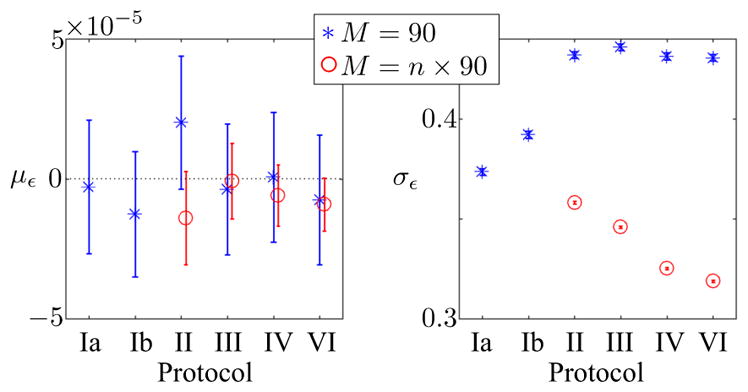
The 95% confidence intervals of the mean error (μ_ε, [%]) in the estimation of the noise-free signal for the different diffusion encoding schemes show that MPPCA lacks a significant bias in single- and n-shell protocols. The remaining noise standard deviation, normalized by σ, is significantly higher for the multi-shell protocols if M is kept constant (blue). This observation indicates that more principal components are needed to approximate the diffusion weighted signal as function of the b-value in a linear basis if M is spread across a few shells and, as such, P increases. Nonetheless, MPPCA boosts SNR without compromising the accuracy for all evaluated protocols. Moreover, analyzing multiple shells (M = n × 90; red) simultaneously when the number of directions per shell is fixed improves the performance of MPPCA because the increase in M is generally larger than the associated increase in P.

4. Discussion

4.1. Noise versus artifacts

In the literature, the term “noise” has been used to refer to different sources of undesired signal fluctuations. Here, we restrict the definition of noise to the random signal fluctuations induced by the motion of electrons or ions, i.e. the thermal noise (Johnson, 1928; Nyquist, 1928). The collection of spatially and temporally varying image distortions, such as cardiac pulsation and motion, often referred to as physiological noise (Chang et al., 2005) are imaging artifacts. Clearly distinguishing between “noise” and “artifacts” is important to interpret the performance of image denoising techniques.

The ideal denoising technique is selective in the sense that it suppresses the local signal fluctuations rooted in thermal noise, not from other origins such as fine anatomical detail, motion, or Gibbs ringing. By studying residual maps, we demonstrated that the proposed denoising technique, MPPCA, outperforms ANLM and TGV in that respect. Although all evaluated techniques showed show improved precision in the estimation of diffusion model parameters, MPPCA was the only technique that did not compromise the accuracy. The reduced accuracy originates from a low-pass filtering component present in the competing methods, causing image blur and partial voluming.

4.2. Noise reduction, not removal

Despite its popularity, the term “denoising” might be misleading, as it can be misinterpreted as full noise suppression or removal. However, noise reduction is the highest achievable goal. No single technique can make a complete separation of signal and noise. Neither can PCA. Indeed, noise corrupts all M principal components and not only those M̃ components that are nullified during the procedure. The noise corruption of the eigenvectors and eigenvalues of the remaining P components cannot be undone. Consequently, the standard deviation of the residuals is systematically lower than the estimated noise standard deviation (see Fig. 7). Basically, the noise variance reduction primarily scales with P/min(M, N). M is typically the maximum number of DW images in the data, where N needs to be set by the user. We suggest to choose N > M. However, in case of spatially varying noise, it might be beneficial to select a sliding window with N ≳ M. Note that simulations and experiments showed that P, and as such, the performance of MPPCA depends on the diffusion encoding protocol. However, both single- and multi-shell strategies showed significant increase in SNR without loss in accuracy. Moreover, the redundancy (M − P) is expected to increase when analyzing multiple shells simultaneously.

4.3. Targeted post-processing

The accuracy and precision of diffusion parameter estimation will be affected by the presence of imaging artifacts. Although artifacts such as Gibbs ringing (Veraart et al., 2015) often result in spurious local signal oscillations, our denoising technique will not detect or remove them. Despite the convenience of a brute force technique, e.g. smoothing or total variation minimization (Block et al., 2008; Veraart et al., 2015; Perrone et al., 2015), that might deal with different types of unwanted fluctuations simultaneously, we here advocate the use of targeted artifact correction techniques for improved accuracy and specificity. Other examples of targeted image processing tools are the Gibbs correction framework of Kellner et al. (2015) or FSL’s TOPUP and EDDY for EPI and eddy current distortion corrections, respectively (Smith et al., 2004; Sotiropoulos et al., 2013; Glasser et al., 2013). Note, however, that denoising should be applied as the first step of the processing pipeline because data interpolation or smoothing will change the noise characteristics on which MPPCA relies.

4.4. Rician signal bias

The SNR dependent difference between the expectation value of a Rician – or more generally, a noncentral χ – distributed value and its underlying noise-free value causes inaccuracies in the estimation of the diffusion parameters. Since the SNR of the dMRI signals depends on factors such as diffusion gradient direction, b-value, diffusivity, and diffusion anisotropy, the so-called noise bias is omnipresent in quantitative dMRI. Indeed, many noise-related artifacts have been discussed earlier (Jones and Basser, 2004; Veraart et al., 2013a, 2011a,b). MPPCA returns an estimate of the expectation value of the signal and, as such, the denoised signal needs to be further corrected for the well known noise bias. Because MPPCA outputs the noise level as well (Veraart et al., 2016), the correction can easily be done by using the methods of moments, often referred to as Koay’s inversion technique (Koay and Basser, 2006). Note that in our experiments, we omitted this step to avoid interference of the signal-dependent correction with the residual analysis. However, our simulations demonstrated very high accuracy of MPPCA in combination with the inversion technique resulting in a bias of only 0.01%. Theoretically, the SNR-dependency of the variance of a Rician distributed variable might violate the assumption of having a constant noise level within the sliding window or across the DW images. This potential pitfall is expected to be a theoretical instead of a practical concern as it was not detected in our experiments, which included high b-valued data.

4.5. Computation time and code sharing

Compared to our previous work on the use of Marchenko-Pastur distribution for noise map estimation, we revised and sped up our algorithm for the simultaneous denoising and noise map estimation (Veraart et al., 2016). The histogram fitting routine is replaced here by a non-iterative technique that exploits the knowledge that the omitted noise variance must be well explained by universal properties from random matrix theory. By doing so, we lost the dependency on binning of the eigenspectrum and, more importantly, we highly reduced the computational expense. Denoising of a clinical whole brain dMRI data set can now be done in a few minutes on a single-core computer, which is an order of magnitude faster than the previous approach. However, no significant differences in terms of accuracy or precision between both approached have been observed. The code is publicly available as part of the open-source MRtrix framework (command: dwidenoise; http://www.mrtrix.org).

4.6. Beyond dMRI

Noise analysis using random matrix theory has previously been explored in the context of finance (Laloux et al., 1999), wireless communication systems (Ahmed et al., 2014), cardiac MRI (Ding et al., 2010), DCE-MRI (Jahani et al., 2013), and fMRI (Sengupta and Mitra, 1999). However, this work is the first to demonstrate the power of random matrix theory and a highly computationally efficient algorithm in the context of the denoising of dMRI data. Note that despite our focus on a few commonly used diffusion metrics throughout this work, similar conclusions will apply for all diffusion parameters, both empirical and from biophysical models, because noise variance is a signal property that will propagate to all metrics derived from it. For example, we demonstrated that denoising, not to mention signal suppression by competing denoising tools, has local and global effects on the tractogram that are often indistinguishable from anatomy. Hence, we would advocate evaluating the accuracy of post-processing tools at the signal level using analysis of residuals, instead of studying their accumulated effect on the tracts, especially because the ground truth is typically missing. Furthermore, due to the unfavorable fitting landscapes of many microstructural models, denoising might be even more important in more complex models of diffusion (Jelescu et al., 2016).

5. Conclusion

We propose a fast and accurate denoising technique that reduces signal fluctuations solely rooted in thermal noise, not from other origins such as fine anatomical detail. The thermal noise-selective nature of the proposed technique is based on data redundancy in the PCA domain using universal properties of the eigenspectrum of random covariance matrices. The resulting images show highly enhanced SNR and enable improved precision in the estimation of diffusion model parameters whereas the accuracy is preserved.

Highlights.

• Denoising enhances the image quality for visual, quantitative, and statistical interpretation

• Random matrix theory enables data-driven threshold for PCA denoising

• The Marchenko-Pastur distribution is a universal signature of noise

• The technique suppresses signal fluctuations that solely originate in thermal noise

• Precision of diffusion parameter estimators increases without lowering accuracy