Estimating infectious disease transmission distances using the overall distribution of cases

Abstract

The average spatial distance between transmission-linked cases is a fundamental property of infectious disease dispersal. However, the distance between a case and their infector is rarely measurable. Contact-tracing investigations are resource intensive or even impossible, particularly when only a subset of cases are detected. Here, we developed an approach that uses onset dates, the generation time distribution and location information to estimate the mean transmission distance. We tested our method using outbreak simulations. We then applied it to the 2001 foot-and-mouth outbreak in Cumbria, UK, and compared our results to contact-tracing activities. In simulations with a true mean distance of 106m, the average mean distance estimated was 109m when cases were fully observed (95% range of 71–142). Estimates remained consistent with the true mean distance when only five percent of cases were observed, (average estimate of 128m, 95% range 87–165). Estimates were robust to spatial heterogeneity in the underlying population. We estimated that both the mean and the standard deviation of the transmission distance during the 2001 foot-and-mouth outbreak was 8.9km (95% CI: 8.4km-9.7km). Contact-tracing activities found similar values of 6.3km (5.2km-7.4km) and 11.2km (9.5km-12.8km), respectively. We were also able to capture the drop in mean transmission distance over the course of the outbreak. Our approach is applicable across diseases, robust to under-reporting and can inform interventions and surveillance.

Background

Characterizing the spatial patterns of disease transmission is crucial to our understanding of pathogen dispersal. Public health interventions implicitly target next generations of transmission through contact tracing and spatial targeting of quarantine, isolation or other control measures, though often with crude information about where pathogens will move in space. More information about where cases may arise in relation to identified cases could help target resources both for control and enhanced surveillance. Despite its usefulness, the geographical mean distances between the locations of cases in relation to the individuals that infected them, have been difficult to elucidate. We rarely observe infection pairs (i.e., who infected whom) in a transmission network. Where only a minority of cases are observed, analyses tend to be restricted to characterizing the spatial and temporal scales at which cases tend to occur together but the relationship between spatial clustering and transmission distance is complex (Bhoomiboonchoo et al., 2014; Grabowski et al., 2014; Lin et al., 2011; Morrison et al., 1998; Salje et al., 2015; 2012). Only where we have been able to observe the majority of cases in a transmission network or we have detailed epidemiological data on who infected whom, has estimation of mean transmission distances previously been possible (Assiri et al., 2013; Ferguson et al., 2001a; Keeling et al., 2004).

It is not surprising that we are rarely able to reconstruct transmission pathways for outbreaks. Directly estimating the distance between sequential cases requires both the identification of cases and their infectors. Such contact tracing efforts can be expensive and time-consuming. In some cases it may be impossible. Usually only a fraction of cases are detected. Not everyone infected will develop symptoms severe enough to be detected (e.g., most dengue cases are not severe enough to seek care), and even the best surveillance systems rarely identify 100% of symptomatic cases. Further, if there exists an intermediary vector or reservoir (such as the case of dengue, chikungunya or cholera), sequential cases in a transmission chain may never have been in contact with each other. Phylogeographic methods have been developed to estimate rates of viral movement across countries or continents under these conditions (Faye et al., 2015; Rabaa et al., 2013). However, these approaches have not yet been able to reliably capture micro-scale dynamics except in isolated settings such as hospital-based outbreaks (Cotten et al., 2013; Iles et al., 2014; Pybus et al., 2012; Rabaa et al., 2010), and may be impossible where genome mutation rates are particularly low or high relative to the generation time. Even where phylogenetic approaches can be used, it is likely to require potentially prohibitive labor-intensive sequencing of large numbers of pathogens throughout the course of an outbreak (Stack et al., 2010). Other fields have attempted to infer movement properties in poorly observed settings. Plant biology, for example, has developed methods to describe seed dispersal in situations where the source is unknown and thereby understand the relative importance of wind and animal movements in seed spread (Nathan and Muller-Landau, 2000). However, these methods have not been successfully applied to human disease spread.

Here, we present an approach to estimate the mean transmission distance in infectious disease processes using only the point locations of cases (e.g., place of residence), times at which individuals become symptomatic and the generation time distribution of the pathogen. The method is applicable in situations with full data as well as those where only a small proportion of infections are observed. We demonstrate the robustness of our approach using simulated data and then apply it to data from an outbreak of foot-and-mouth disease in the UK in 2001.

Methods

Distribution of distances between cases

In outbreaks originating from a single introduction into a community, a pair of cases occurring at time points t₁ and t₂ can be separated by a variable number of transmission events (denoted by θ, the number of infection events required to link a pair of cases) (Box 1 and Figure 1). For example, two cases occurring at the same time may have been infected by the same infectious individual (in which case θ =2) or alternatively, their most recent common ancestor (MRCA) may be two or more generations back (θ >2). The distance between sequential cases in a transmission chain (i.e. θ =1) can be characterized by a transmission kernel, which we define here as the probability density function of all transmission distances during an epidemic. If we assume a constant isotropic transmission kernel (i.e. one with no directional preference), that transmission events are independent of each other and each infected individual has a single infector (i.e., co-infections do not occur), the distance between pairs of cases will depend on the number of transmission events that separate them. However, without detailed genetic information on the infecting pathogen or contact tracing information, we are unlikely to be able to directly identify the number of transmission events that separate any two cases. We can, however, calculate the mean distance between all observed pairs of cases that occur at two time points ( ${\mu }_t^{\mathit{obs}}(t_1,t_2)$, the mean of the distribution represented by the solid black line in Figure 1).

Box 1. Overview of key terms.

Transmission linkage (θ) - The number of transmission events that link two cases (see example in Figure 1)

Transmission kernel - The probability distribution function of the distance between sequential cases in a transmission chain

Most recent common ancestor (MRCA) - The most recent infector that can link a pair of cases

Mean transmission distance (μ_k) - The mean of the transmission kernel

Standard deviation of transmission distance (σ_k) - The standard deviation of the transmission kernel

Mean distance between θ transmission-linked pairs (μ_a(θ,μ_k,σ_k)) - The mean distance between cases separated by θ transmission events where the transmission kernel has mean μ_k and standard deviation σ_k

Transmission-linkage weights (w(θ, t₁, t₂)) - The proportion of case pairs where one occurs at t₁ and the other at t₂ that are separated by θ transmission events

Mean distance between all pairs (μ_t(t₁, t₂, μ_k, σ_k)) - The mean distance separating all pairs of cases where one occurs at t₁ and the other at t₂ and the transmission kernel has mean μ_k and standard deviation σ_k

Observed mean distance between case-pairs (μ_t^obs(t₁ , t₂)) - The observed mean distance separating all pairs of cases where one occurs at t₁ and the other at t₂

Figure 1.

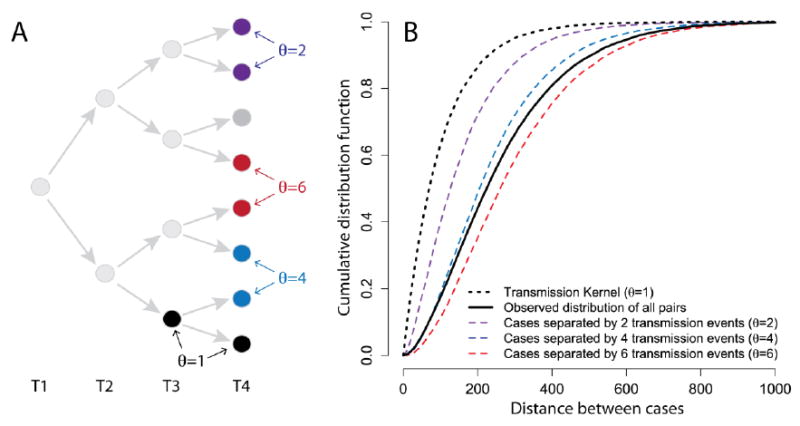
(A) Example transmission tree with (B) the cumulative distribution function for pairs of cases separated by different numbers of transmission events assuming a constant exponentially distributed transmission kernel with a mean of 100m.

If we know the proportion of case-pairs at two time points that are separated by each possible θ, we can estimate the mean distance between all case pairs as the weighted sum:

$${\mu }_t(t_1,t_2,{\mu }_k,{\sigma }_k)=\sum _{i}w(\theta =i,t_1,t_2)\cdot {\mu }_a(\theta =i,{\mu }_k,{\sigma }_k)$$ [1]

where μ_t(t₁, t₂, μ_k, σ_k) is the mean distance separating all pairs of cases where one occurs at t₁ and the other at t₂; μ_a (θ,μ_k, σ_k) is the mean distance between pairs of cases separated by θ transmission events where the transmission kernel has mean and μ_k standard deviation σ_k; and w (θ, t₁, t₂) are the weights representing the proportion of case pairs occurring at t₁ and t₂, respectively that are separated by θ transmission events. The variance of the distance between all case pairs can be similarly estimated (see Text S1).

We do not need to assume that the number of transmission events that separate a pair of cases infected at the same time is even (as would be the case if the generation time was of a fixed duration) or that individuals infected at the same time are from the same generation. Instead we can use information on the generation time distribution to calculate w (θ, t₁, t₂).

Estimation of weights

To estimate w (θ, t₁, t₂), we extended a method developed by Wallinga and Teunis that calculates the probability that a case occurring at time t₁ was infected by a case at time t₂ based on a known generation time distribution, g(x) and the number of cases occurring at each time point (Wallinga and Teunis, 2004). We produce an n × n matrix, where cell [i, j] represents the probability that a case i was infected by a case with the same time of disease onset as case j (the Wallinga-Teunis matrix) and n is the total number of cases. For each pair of cases, we can use the Wallinga-Teunis matrix to estimate the probability that they are separated by θ transmission events by multiplying together the cells of each unique chain (see Figure 2 for a worked example). This assumes that the generation times for all infections were independent of each other and that only the day of symptom onset affected the probability of case i infecting case j. We could compute the probability of every possible path linking two cells, however, this quickly becomes computationally intractable. Instead we sampled transmission trees by randomly choosing the infector for each case. To do this we take each case in turn and randomly drew its infector out of all the other cases, with the probability of any other case being the infector coming from the Wallinga-Teunis matrix (i.e. determined by the time between the cases and the generation time distribution). Note that we are not inferring that any of the other cases in the dataset is the true infector, instead, by assuming that the observed cases are a temporally representative subsample of all cases, we are drawing the time point of the infector (whether it was observed or not), rather than the infector itself. By re-estimating the tree for each simulation, we adjust for the probability of each transmission tree. Once we estimate a transmission tree we compute the number of transmission events required to link each pair of cases. Our estimate of w (θ, t₁, t₂) is the proportion of simulations in which a case occurring at time t₁ and a case occurring at t₂ are separated by θ transmission events:

$$\widehat{w}(\theta =i,t_1,t_2)=\frac{{\sum }_{k=1}^{N_{\mathit{sim}}}{\sum }_{i=1}^n{\sum }_{j=1}^n{\mathit{I}}_1(t_i=t_1,t_j=t_2,{\Theta }_{\mathit{ij}}=\theta )}{N_{\mathit{sim}}{\sum }_{i=1}^n{\sum }_{j=1}^n{\mathit{I}}_{\mathbf{2}}(t_i=t_1,t_j=t_2)}$$ [2]

where N_sim is the number of resamples; I₁ and I₂ are indicator functions and Θ_ij is the number of transmission events separating i and j in simulation k.

Figure 2.

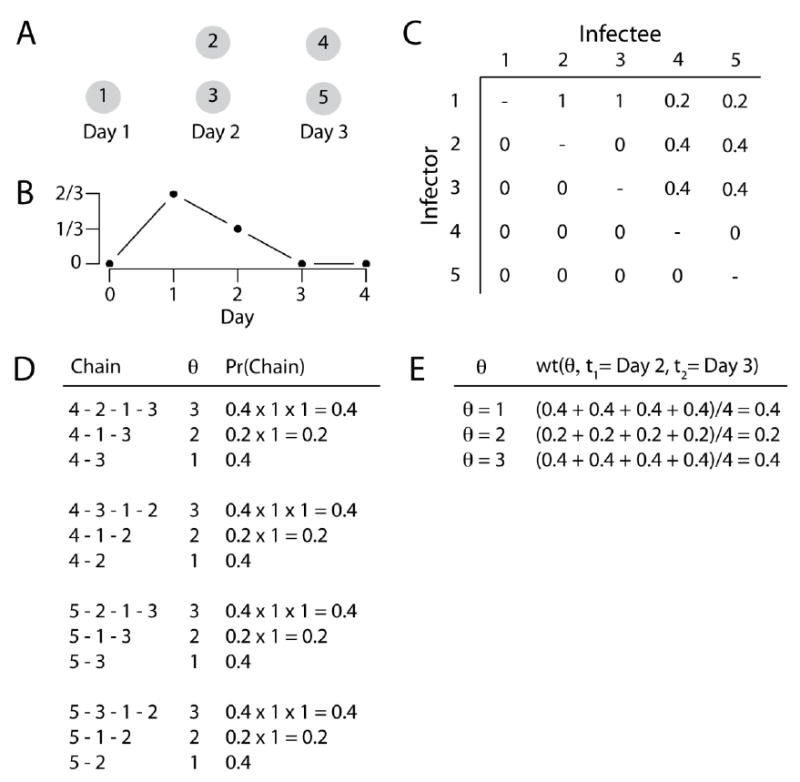
Example calculation of the weights from the Wallinga-Teunis matrix. Assume five cases occur over three days as set out in (A) and we know the generation time distribution (B) so that two thirds of sequential infections are a day apart and one third are two days apart. We can build a Wallinga-Teunis matrix (C) that sets out for each case the probability that a case occurring at each time point was its infector. The columns of the matrix have been normalized so that they add to one. (D) Sets out all possible pathways connecting a case at time 2 with a case at time 3, with the associated number of transmission events (θ) for that chain and the probability of that chain calculated from the Wallinga-Teunis matrix (chains with zero probability such as 4-5-2 have been excluded). (E) sets out the average probability for each θ from (D), which represents the weights used in the calculation of the transmission kernel.

Estimation of distance separating cases of known θ

For a transmission kernel with mean μ_k and standard deviation σ_k, we can approximate the mean squared dispersal distance between pairs of cases that are separated by θ transmission events (Bovet and Benhamou, 1988; Codling et al., 2008; Kareiva and Shigesada, 1983) as:

$${\mathit{ER}}^2(\theta ,{\mu }_k,{\sigma }_k)\approx {\mu }_k^2\cdot \theta \cdot \left(1+\frac{{\sigma }_k^2}{{\mu }_k^2}\right)$$ [3]

where ER²(θ, μ_k, σ_k) is the mean squared dispersal distance and represents the average squared distance between pairs of cases separated by θ transmission events. As transmissions occur in two-dimensional space, we cannot simply square root the mean squared dispersal distance to obtain the mean dispersal distance. Instead, under a condition of isotropic transmission, we use the central limit theorem to assume that cases separated by θ transmission events are approximately normally distributed with mean μ_α (θ, μ_k, σ_k) (Bovet and Benhamou, 1988; Codling et al., 2008; Kareiva and Shigesada, 1983).

$${\mu }_a(\theta ,{\mu }_k,{\sigma }_k)\approx 0.5\cdot \sqrt{\pi \cdot {\mathit{ER}}^2(\theta ,{\mu }_k,{\sigma }_k)}$$ [4]

Under a simplifying assumption that the mean and the standard deviation of the transmission kernel are the same, μ_a (θ, μ_k, σ_k) becomes:

$${\mu }_a(\theta ,{\mu }_k,{\sigma }_k)\approx 0.5\cdot {\mu }_k\sqrt{2\mathit{\pi \theta }}$$ [5]

These approximations work well across a wide range of θs (see Figure S1 for testing of θs between one and 25).

Using these estimates, we derived approximations for the mean of the distances separating all pairs of cases at two time points:

$${\mu }_t(t_1,t_2,{\mu }_k,{\sigma }_k={\mu }_k)\approx {\mu }_k\sum _{i}w(\theta =i,t_1,t_2)\cdot 0.5\cdot \sqrt{2\pi i}$$ [6]

An approximation for the variance of the distances separating all pairs of cases at two time points is set out in Text S1 of the supplementary materials.

Estimation of mean transmission distance

We can rearrange Equation 6 to give us a direct estimate of μ_k.

$${\widehat{\mu }}_k=\frac{2\cdot {\mu }_t^{\mathit{obs}}(t_1,t_2)}{{\sum }_i\widehat{w}(\theta =i,t_1,t_2)\cdot \sqrt{2\mathit{\pi i}}}$$ [7]

where ${\mu }_t^{\mathit{obs}}(t_1,t_2)$ is the observed mean distance between cases occurring at the two time points. A weighted average estimate across all combinations of t₁ and t₂ is then:

$${\widehat{\mu }}_k={\widehat{\sigma }}_k=\frac{1}{{\sum }_i{\sum }_j{n}_{\mathit{ij}}}{\sum }_i{\sum }_j\frac{2\cdot {\mu }_t^{\mathit{obs}}(t_1,t_2)\cdot n_{\mathit{ij}}}{{\sum }_k\widehat{w}(\theta =k,t_1,t_2)\cdot \sqrt{2\mathit{\pi k}}}$$ [8]

where n_ij is the number of case pairs where one case occurs at time i and one at time j.

Violation of σ_k = μ_k assumption

Assuming equal mean and standard deviation of the transmission kernel can be limiting. However, our approach provides estimates of the bounds of the mean transmission distance when they are not the same. When the standard deviation is greater than the mean, the lower bound of the mean transmission distance occurs when μ_k → 0 and σ_k ≫ μ_k. At this point ${\mu }_a(\theta ,{\mu }_k,{\sigma }_k)\to 0.5\cdot {\sigma }_k\cdot \sqrt{2\pi }$ and the standard deviation of the transmission kernel is:

$${\sigma }_k(t_1,t_2)=\frac{2\cdot {\mu }_t(t_1,t_2,{\mu }_k,{\sigma }_k)}{{\sum }_{i}w(\theta =i,t_1,t_2)\cdot \sqrt{\mathit{\pi i}}}$$ [9]

When the mean is greater than the standard deviation, the upper bound of the mean transmission distance is when μ_k ≫ σ_k and σ_k → 0. At this point ${\mu }_a(\theta ,{\mu }_k,{\sigma }_k)\to 0.5\cdot {\mu }_k\cdot \sqrt{2\pi }$ and the mean of the transmission kernel is:

$${\mu }_k(t_1,t_2)=\frac{2\cdot {\mu }_t(t_1,t_2,{\mu }_k,{\sigma }_k)}{{\sum }_{i}w(\theta =i,t_1,t_2)\cdot \sqrt{\mathit{\pi i}}}$$ [10]

which is equivalent to $\sqrt{2}$ times the value obtained under the assumption of equal mean and standard deviation of the transmission kernel. Thus we can use these formulations to place bounds on the transmission distance when the relationship of the mean and standard deviation are unknown. The behavior of our approach at different combinations of the mean and standard deviation of the transmission kernel is set out in Figure 3.

Figure 3.

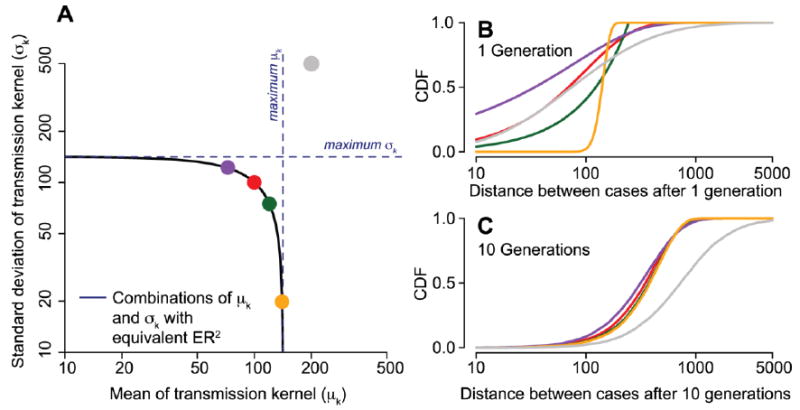
Transmission kernels with different means and standard deviations can produce point patterns with the same mean squared dispersal distance (ER²) and therefore are not distinguishable from each other in the presented approach. (A) Combinations of values with the same ER². (B) Cumulative distribution function of transmission kernels with exponential distribution with μ_k = σ_k =100m (red line in (B, C) and red dot in (A)), uniform distribution between 0 and 246m (green), gamma distribution with μ_k =80m and σ_k =117m (purple), Gaussian distribution with μ_k =140m and σ_k=20m (orange) and log-normal distribution with μ_k =200m and σ_k =500m (grey). Kernels with equivalent ER² in (A) generated points that had indistinguishable cumulative distribution functions after ten generations, whereas the kernel with an inconsistent ER² (in grey) had a different cumulative distribution function.

Violation of the central limit theorem

This approach relies on the central limit theorem, such that the form of the transmission kernel does not matter as long as it has a defined mean and standard deviation. Transmission kernel distributions that have long tails, such as particular power law distributions, violate this assumption. Occasional long-distance transmission events will bias the estimate of μ_k upwards. This can be problematic where occasional long-distance transmissions result in several foci of ongoing transmission. However, given that most outbreak investigations are bounded by some geographical area, the cases in the long tail of the transmission kernel may be unobserved. The estimated mean transmission distance in these circumstances would represent an estimate from transmission events within the study area.

Impact of population immunity and heterogeneous population structure

The spatial spread of a pathogen may be impacted by local immunity. As a greater proportion of the local population becomes infected and develops resistance, the pathogen will spread preferentially to susceptible populations, thereby potentially violating our assumption of isotropic transmission. Similarly, substantial spatial structure in the underlying population may result in violations in the assumption of isotropic transmission. In such settings transmissions may preferentially occur in areas of increased population where more susceptible individuals reside. The impact of local immunity and heterogeneous population structure on estimates of mean transmission distance is explored in a simulation study (see below).

Confidence intervals

We can use a bootstrapping approach to obtain uncertainty in the mean transmission distance estimate. In each bootstrap iteration, all the observed cases are resampled with replacement, and the mean transmission distance recalculated. This is then repeated many times (we conducted 500 iterations). Ninety-five percent confidence intervals can then be generated from the 2.5% and 97.5% quantiles from the resultant distribution. This would account for uncertainty in the observation process effectively accounting for the possibility that we are seeing only a sample of all cases.

Simulation study application

To assess the performance of our approach we simulated transmission chains on a population of 100,000 individuals. In each simulation we used a transmission kernel with a mean and standard deviation of 100m and generation time distribution with mean one week and standard deviation of 2 days. We ran different scenarios varying the functional form of the transmission kernel (either an exponential distribution or a log-normal distribution). In addition we explored the sensitivity of our results to large misspecification of the mean generation time: we estimated the mean transmission distance where we assumed a mean time of half a week between sequential infections (representing a 50% underestimate) and where we assumed a mean time of three weeks between sequential infections (representing a 50% overestimate). In each scenario, we assessed our ability to correctly identify the true mean transmission distance under conditions of partially observed data: for each simulation, we randomly deleted between 0% and 98% of cases before estimating the transmission distance (2000 simulations in all). We then fit a loess curve to compare the error in our estimate by the proportion of cases observed (Cleveland et al., 1992).

Where infection results in subsequent immunity of the host, pathogen spread may violate our assumption of isotropic movement as pathogens go in search of susceptible hosts. To explore the impact of immunity on our approach, we simulated epidemics where individuals became immune following infection. To allow appropriate comparison to situations without immunity, we also simulated epidemics without immunity but used a seasonally adjusted effective reproductive number to produce similar epidemic curves. In both the simulations with and without immunity, we estimated the mean transmission distance for all cases occurring up to the end of each epidemic week and compared it to the true mean distance.

The underlying spatial structure of the population may also impact our ability to estimate the mean transmission distance. We used the same simulation framework to explore the impact of having either moderate or high spatial structure in the underlying population. To simulate clustered populations we used a Matérn cluster process (Matérn, 1986). A Matérn cluster process works by initially placing a number of parent points at random throughout the study area (representing the center of each ‘community’). Daughter points (representing the location of each individual) are then placed at random within a set radius of each parent point. We used a constant population size of 316 individuals per community in each of 316 different communities spread across an area of 100km², resulting in a total population of 10,000. We used a community radius of 1000m for moderate spatial structure and a community radius of 100m for scenarios of high spatial structure (See Figure S2).

Occasional long-distance transmission events will result in long-tailed kernels that will violate our assumption of equal mean and standard deviation of the transmission kernel. To explore the impact of such transmission events we simulated epidemics where a proportion of transmission events occurred at random across the whole study area, irrespective of location. The remainder of transmission events following a base exponentially distributed kernel with a mean of 100m. We performed 1,000 simulations of outbreaks in unstructured populations as well as moderate and highly structured populations. The proportion of non-spatial transmission events for a particular simulation was drawn from a uniform distribution ranging from 0% to 10%. At the end of each simulation we compared the true mean transmission distance with the distance estimated using our approach.

Further details on the simulations can be found in the Text S2 of the supplementary materials

Application to 2001 outbreak of foot-and-mouth disease in Cumbria and Dumfriesshire, UK

Foot-and-mouth disease is a caused by a virus that is transmitted to livestock through contact of humans or other infected livestock. In 2001, a large outbreak of foot-and-mouth disease occurred in the UK (Ferguson et al., 2001a; Haydon et al., 2003). Foot-and-mouth disease causes large-scale economic loss for both farmers and the wider economy. The 2001 epidemic resulted in the culling of over four million animals and cost the UK national treasury 2.7 billion British Pounds (Davies, 2002). In particular, Cumbria and neighboring Dumfriesshire bore the brunt of the epidemic with 1,070 infected livestock (Figure 5). Intensive contact tracing was performed upon the discovery of any infected case and the location of the infector was identified where possible. The dates when infected animal were identified and the latitude and location of the infected farms were made available from the UK Food and Environment Research Agency. Where the source of the infection was known, its location was also provided.

Figure 5.

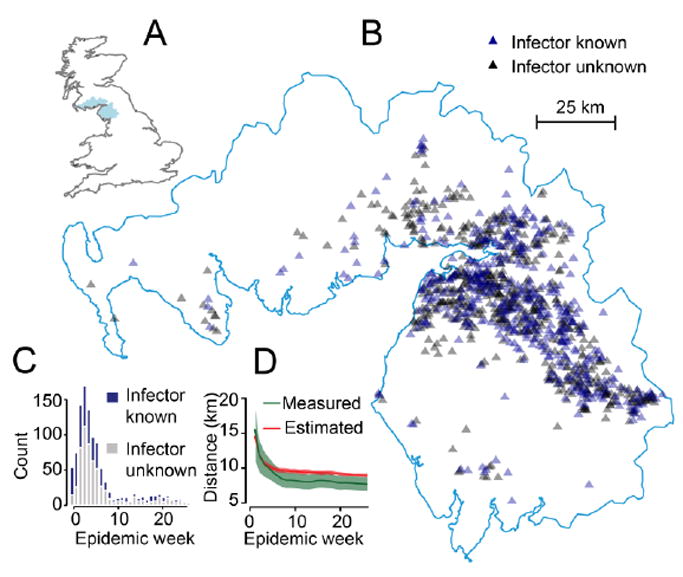
Outbreak of Foot and Mouth Disease in Cumbria, UK in 2001. (A) Location of Cumbria and Dumfriesshire in the UK. (B) Location of cases. (C) Epidemic curve by week. (D) Measured mean transmission distance from contact tracing activities (green) and estimated through our approach (red) for all cases up to each epidemic week with 95% confidence intervals.

We estimated the mean distance between sequential infected farms in this outbreak using initially only the cases where the location of the infector was known. We assumed that the generation time of foot-and-mouth disease was normally distributed with a mean of 6.1 days and a standard deviation of 4.6 days (Haydon et al., 2003). In addition, we estimated the mean transmission distance using all cases, including those where the location of the infector was unknown.

Results

Simulation study results

In simulations using an exponentially distributed transmission kernel, when all cases were observed our method estimated an average mean distance of 109m (95% range of estimates of 71m-142m) versus a true mean distance of 106m (resulting in a mean difference between the estimated and true transmission distance of 3m, 95% range of difference in estimates of (-)37m-36m) (Figure 4). Further, it recovered the true mean transmission distance when only subsets of cases were observed (Figure 4). Even when just five per cent of cases were observed, the method produced only a small over-estimate (mean difference of 22m, 95% range of (-)18m–59m). The results were virtually identical for a lognormal transmission kernel (mean difference of 6m, 95% range of (-)33m–42m). Misspecification of the true mean generation time resulted in small errors in the mean transmission distance estimates: a 50% overestimate of the time between infections resulted in a mean error of 30m ((-)18m–74m) whereas a 50% underestimate resulted in a mean error of -22m ((-)51m 6m). Simulations performed on clustered populations had similar performance to simulations in unclustered populations (mean error of 6m [(-)32m-46m] for moderate spatial structure and -14m [(-)31m-17m] for high spatial structure).

Figure 4.

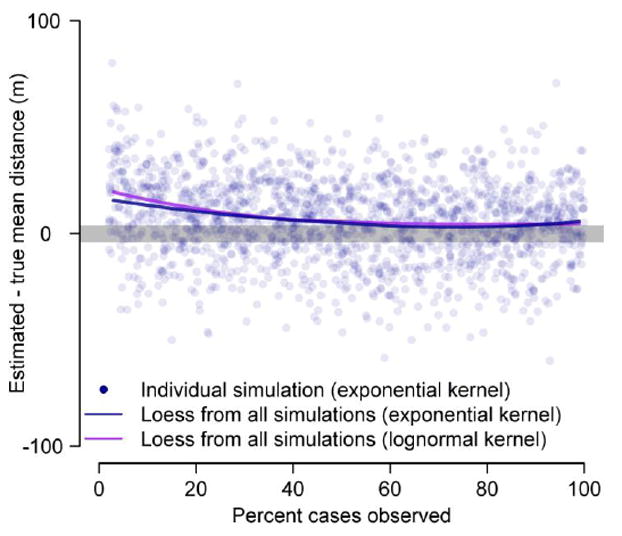
Estimates of mean transmission distance from simulated transmission chains where only a subset of cases are observed. The blue dots represent estimates from individual simulations with an exponential distributed transmission kernel. The lines represent loess curves from 2000 simulations.

The introduction of immunity into the simulations had an important impact on our ability to estimate the mean transmission distance (Figure S3). At the start of the simulated epidemics, when no immunity was present, our approach was able to correctly estimate the true mean transmission distance. However, as individuals became immune, successful infection events preferentially occurred away from the site of the source of the outbreak, violating our assumption of isotropic transmission. This resulted in a significantly biased estimate of the mean transmission distance. When 50% of the population was immune, we estimated a mean transmission distance of 410m versus a true mean transmission distance of 106m. This suggests that where immunity is driving the spatial spread of an outbreak, our approach would over-estimate the true mean transmission distance.

The introduction of occasional long-distance events resulted in an over estimate of the mean transmission distance due to the violation of the equal mean and standard deviation of the transmission kernel. In scenarios of outbreaks in unstructured populations where 2% of transmission events did not follow the base kernel and instead occurred in individuals drawn at random across the whole study population (irrespective of where they lived), resulted in an over-estimate of 193m ((-)77m-475m) (Figure S4). Scenarios with occasional long-distance events run in either moderately or highly clustered populations resulted in similar errors.

Application to 2001 outbreak of foot-and-mouth disease in Cumbria and Dumfriesshire, UK

Contact tracing activities identified the source of infection in 438 farms (41% of all infected farms in the region). From these activities, the mean distance between the infector farm and the infectee farm was measured at 6.3km (95% confidence interval of 5.2km-7.4km). These calculations exclude seven farms where the source was traced to outside the study area. The standard deviation of distances was 11.2km (95% confidence interval of 9.5km-12.8km).

We used our approach to estimate the mean distance between transmission related farms (without using contact tracing information). Using only farms where the infector was known (but excluding the seven farms where the source was known to be outside the study area) gave a mean transmission distance of 9.1km (95% confidence intervals of 8.4km-9.7km). Including the seven farms where the source was outside the study area gave a mean transmission distance of 9.2km. Using all case farms (irrespective if the infector had been identified or not) gave a mean transmission distance of 8.9km (95% confidence interval of 8.6km-9.3 km). These estimates are slightly greater than the 6.3km obtained from contact-tracing activities. This is consistent with the standard deviation of the transmission distance (estimated as 11.2km from contact-tracing) being greater than the mean and therefore in violation of the equal mean and standard deviation assumption. Importantly, the mean-squared dispersal distance was the same in both our estimate and the estimate from contact-tracing efforts (Figure 6). Note that the mean-squared dispersal distance is the same, even when the mean and the standard deviation of the kernel are different (see Equation 3). In addition, both the mean and the standard deviation of the transmission distance fall within the upper bounds for those values (12.6 km for both, see Figure 6A).

Figure 6.

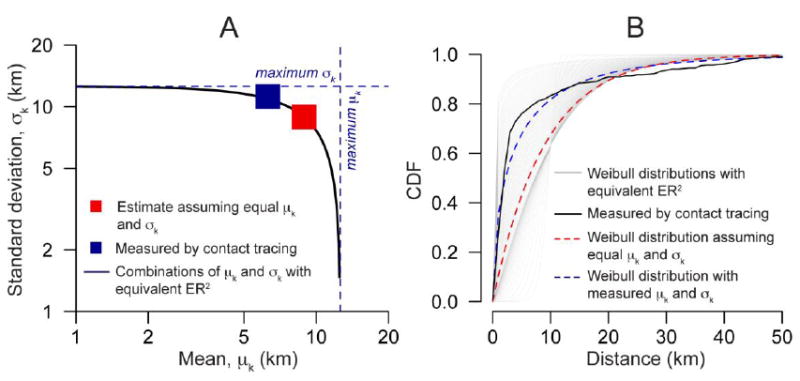
(A) Estimate of the mean transmission distance for foot-and-mouth disease in Cumbria in 2001 compared to estimates from contact tracing activities. (B) Weibull distributions with equivalent ER² from Equation 3 (black line in panel A).

Following the start of the outbreak, the UK government imposed restrictions on the movement of cattle and the culling of animals within 3km of infected farms (Ferguson et al., 2001b). We explored the evolution of the mean transmission distance over the course of the epidemic. We estimated the mean transmission distance of all cases that had occurred up to each week of the epidemic and compared that to the estimates from the contact tracing activities. We found that both the contact tracing activities and our approach showed a sharp reduction in the mean transmission distance over the course of the outbreak (Figure 5D). Cases up to week 3 had an estimated mean transmission distance of 15.5km (95% CI: 10.8-20.2km) from contact tracing activities and an estimated mean transmission distance of 14.5km (13.7-15.9km) using our approach. By week 10, this fell to 8.3km (7.0-9.5km) using contact tracing and 9.6km (9.2-10.1km) using our approach.

Discussion

Understanding the distance between sequential cases in a transmission chain is key to elucidating dispersal mechanisms and designing efficient intervention measures. However, characterizing transmission distances has been limited to date to cases where active investigation has identified putative transmissions using epidemiologic evidence or where a sufficient proportion of cases have been detected to allow inference of potential transmission pathways using mathematical modelling approaches (Ferguson et al., 2001b; Keeling et al., 2001; Neri et al., 2014; Ster and Ferguson, 2007). In cases where active investigations are not done and only a small proportion of cases are detected, estimating the mean transmission distance has not previously been possible. Through simulation, we demonstrated the robustness of our approach when only a minority of cases in an outbreak was observed. We then applied it to an outbreak of foot-and-mouth disease in Cumbria, one of the few occasions where intensive contact tracing was performed. We found our approach only slightly over-estimated the measured mean distance between transmission pairs. Importantly, the measured mean and standard deviation of the transmission distance were within our estimates of the upper bound of those values.

For the foot-and-mouth disease example, we were able to generate mean transmission distances that were consistent with the estimates from the contact tracing activities right from the start of the outbreak. Our approach also captured the subsequent reduction in the transmission distance during the course of the epidemic, presumably resulting from the restrictions placed on the movement of livestock. In addition, the government introduced the culling of animals, 3km around infected farms (Ferguson et al., 2001b). We could expect that this latter activity would act as an extreme form of herd immunity, which we found had the potential to substantially bias our estimates. Our ability to generate mean transmission distance estimates that were broadly consistent with that from contact tracing is therefore somewhat surprising. The 3km culling radius is far smaller than the mean transmission distance and was potentially too small to act as an effective herd immunity. In addition, it has been suggested that many cattle farms did not follow the culling strategy (Ferguson et al., 2001b). Our simulations incorporating immunity may also represent an extreme example, where infection events are continuously forced outwards through spatially dependent exhaustion of susceptibles. The approach may be less biased in scenarios where substantial pockets of susceptible individuals remain in all directions (i.e. the assumption of isotropy is not violated).

We are unable to differentiate between different functional forms of the transmission kernel, however, understanding the mean transmission distance provides a useful indicator of disease spread. In addition, we can identify a set of distributions with equal mean-squared dispersal distances within which the true transmission kernel may fall. For example, assuming the transmission kernel for the foot-and-mouth outbreak was Weibull distributed identifies a range of possible distributions, one of which is close to the one calculated from contact tracing (Figure 6B, see also Figure S5 of the supplementary materials for an example with a log-normal distribution).

We have found that our approach is robust to a number of departures from ideal conditions for our estimator. However, there are potential challenges that we have not addressed in this manuscript. Foot-and-mouth disease has a relatively short generation time. It is unclear how this approach would perform with diseases with much longer or highly variable generation times. Similarly, the generation time distribution may change during the course of an epidemic (Nishiura, 2010). However, we have shown through simulation that our approach is largely robust to such changes. Long-tailed transmission kernel distributions that result in occasional transmission events over very long distances would bias our results upwards. For example, occasional long-distance transmissions are known to have played an important role in the spread of foot-and-mouth disease across the UK. These epidemiologically-important events would not be captured using our approach. Finally, our method requires that all cases in an outbreak are part of the same transmission tree (even if the MRCA is several generations back). Where more than one transmission chain exists and we have no ability to differentiate between the different chains (such as in settings of sustained endemic transmission) we would not be able to use this approach. While we have applied our approach to the specific setting of infectious disease outbreaks, there may applications outside this field, where point patterns are generated through branching processes. There may also be extensions that allow the estimation of mean distances in three-dimensional space or where there exists a bias in the direction of movement.

Highlights.

• Knowing mean transmission distances in outbreaks can help target interventions

• We propose a method to estimate it that only uses data on where and when cases occur

• Simulations show its robustness to when only a small proportion of cases are observed

• The method captures the mean transmission distance in the 2001 UK foot and mouth outbreak