Selective association between cortical thickness and reference abilities in normal aging

Abstract

A previous study of reference abilities and cortical thickness reported that association between reference abilities and cortical thickness summarized over large ROIs suppressed was suppressed after controlling for mean cortical thickness and global cognition. In this manuscript, we showed that preserving detailed spatial patterns of cortical thickness can identify reference ability specific association besides the association explained by global cognition and mean cortical thickness. We identified associations between cortical thickness and 3 cognitive reference abilities after controlling for mean thickness, global cognition and linear chronological age: (1) memory, (2) perceptual speed, and (3) vocabulary. Global cognition was correlated with mean overall thickness, but also was found to have a regionally specific pattern of associations. Non-linear associations between cortical thickness and cognition were not observed, neither were non-linear age effects. Age-by-thickness interactions were also absent. This implies that all thickness-cognition relations and age associations are independent of age, and that consequently no age range is inherently special, since brain-behavioral findings are invariant across the whole age range.

Introduction

The association of cerebral atrophy with normal aging (Babakchanian et al., 2012; Chen, He, Rosa-Neto, Gong, & Evans, 2011; Fjell et al., 2009; Fjell et al., 2013; Thambisetty et al., 2010; Tisserand et al., 2002), and cognitive decline (Lemaitre et al., 2012; Sanchez-Benavides et al., 2010) has been consistently shown in studies using Magnetic Resonance Imaging (MRI). With the advent of large databases of high-quality data capturing brain structure, precise quantification of structure-function relationships in the brain is possible with unprecedented accuracy and precision. Until recently, structure-function relationships had been subject to prohibitive influences of statistical noise, making the discovery of fine-grained neural substrates of cognition all but impossible: low sample sizes impacted the quality of cognitive instruments and neural measures, which additionally often lacked sufficient spatial resolution. However, with the advent of the software packager FreeSurfer and large databases of high-quality data capturing brain structure, these analyses become more feasible.

Recently, there has been a particular focus on cortical thickness because FreeSurfer enables thickness estimation on the entire cortical ribbon with sub-millimeter resolution, usually at 10,000 to 100,000 locations (“vertices”). Fine-grained and robust thickness-cognition relationships are the crucial starting point for the enterprise of understanding how brain structure and brain activation give rise to behavior. Once thickness-cognition relationships are demonstrated and understood, one can both ascertain whether these relationships are mediated by brain activation, or whether brain activation contributes to behavior above and beyond the observed thickness-cognition relationship.

Since the relationships between cortical thickness and functional activation are not necessarily local, the best analytic strategy for a multimodal research program is multivariate on conceptual grounds, i.e. we are looking at pattern of correlations between different vertices, and these patterns might ultimately be linked to patterns of functional activation. Multivariate analysis is also the preferred strategy on statistical grounds since our number of variables (=vertices) exceeds the number of observations by 2 orders of magnitude, implying a large degree of redundancy and correlations across subjects between the vertices by necessity. Proceeding vertex-wise in a univariate manner without taking into account this large degree of redundancy would result in overly stringent false-positive corrections with a risk of false-negative findings.

On the side of cognition, a multivariate strategy with the simultaneous consideration of a broad base of cognitive outcomes is also advisable since we are interested in thickness effects that are common to all as well as particular to any individual cognitive outcome. In this paper we thus engaged in a 2-step procedure: first, we performed Principal Components Analysis on the thickness data to obtain component scores, which are subsequently used in a sparse multivariate regression with 4 cognitive measures as outcomes (episodic memory, fluid reasoning, perceptual speed, vocabulary). We looked at effects across the whole age range, as well as in age tertiles. We also considered non-linear effects of age on cognitive outcomes.

The current paper follows from, and can be contrasted with, a recent publication from our group (Salthouse et al., 2015) which examined similar thickness-cognition relations in a subset of the participants in this study. It used a coarser spatial resolution and considered 33 bilateral regions of interest. Remarkably, this investigation yielded few, if any, thickness-cognition relationships that were not accounted for by the general relationship between global cognition and mean thickness. The current paper was a direct extension of these analyses, with the purpose of testing whether finer spatial resolution could uncover more detailed and nuanced thickness-cognition relationships. Therefore we again included a general, global measure of cognition as a target of prediction, along the 4 specific cognitive abilities in order to ensure that any specific relationships of thickness patterns to cortical thickness were not simply accounted for by the relationship of mean thickness to global cognitive status.

Compared with the many studies investigating the relation of cortical thickness to cognitive performance in healthy and disease populations, our study brings the advantage of coverage across the whole adult lifespan with multivariate cognitive outcomes. The simultaneous consideration of multiple outcomes in a single analytic framework in the current study reduces collinearities and strengthens the specificity of any particular dependencies.

Method

Participants

Market-mailing procedures, flyers and by word of mouth were used in initial recruitment. In initial telephone screening, participants who met basic inclusion criteria (i.e., right handed, English speaking, no psychiatric or neurological disorders, and normal or corrected-to-normal vision) were further screened in person with structured medical, neurological, psychiatric, and neuropsychological evaluations to ensure that they had no neurological or psychiatric disease or cognitive impairment. Global cognitive functioning was assessed with the Mattis Dementia Rating Scale, on which a score of at least 135 was required for retention in the study. In addition, any performance on tests in the cognitive test battery that was indicative of mild cognitive impairment was grounds for exclusion. More detailed description about this study can be found in (Salthouse et al., 2015; Stern et al., 2014).

The study was approved by the Internal Review Board of the College of Physicians and Surgeons of Columbia University, and after the nature and risks of the study were explained, written informed consent was obtained from all participants prior to study participation. Participants were compensated for their participation in the study.

Cognitive Measures

As described in (Salthouse et al., 2015) twelve measures were selected from a battery of neuropsychological tests to assess cognitive functioning. Three memory measures were based on sub-scores of the Selective Reminding Task (SRT) (Buschke & Fuld, 1974): the long-term storage sub-score (SRT_LTS), continuous long-term retrieval (SRT_CLRT), and the number of words recalled on the last trial (SRT_Last). For perceptual speed, the Digit Symbol subtest from the Wechsler Adult Intelligence Scale - Revised (D. Wechsler, 1981) , Part A of the Trail Making Test, and the Color Naming component of the Stroop (Golden, 1978; Stroop, 1935) test were chosen. Fluid reasoning ability (GF) was assessed with scores on three different tests: WAIS III Block Design test, WAIS III Letter-Number Sequencing test, and WAIS III Matrix Reasoning test. Vocabulary was assessed with scores on the Vocabulary subtest from the WAIS III, the Wechsler Test of Adult Reading (WTAR) (David Wechsler, 2001), and the American National Adult Reading Test (AMNART) (Grober & Sliwinski, 1991).

MRI acquisition and Cortical Thickness Measures

MRI images were acquired in a 3.0T Philips Achieva Magnet using a standard quadrature head coil. A T1-weighted scout image was acquired to determine subject position. T1-weighted images of the whole brain were acquired for each subject with an MPRAGE sequence with 180 contiguous 1 mm thick axial slices using the following parameters: TR 6.5 ms, TE 3 ms; flip angle 8°, acquisition matrix 256×256 and 256 mm field of view. A neuroradiologist reviewed anatomical scans and any with potentially clinically significant findings, such as abnormal neural structure were removed from the sample prior to the current analysis. In sum, 322 participants were scanned and their MRI images were analyses. Cortical thickness was measured using the FreeSurfer analysis package (Version 5.1, http://surfer.nmr.mgh.harvard.edu/). In statistical analyses, 144, 618 vertices that were included after masking out colossal values.

Statistical Analyses

Demographics, cognitive and cortical thickness measures

For the global cognition measure, a principal component analysis of the twelve cognitive measures was performed. Global cognition was quantified as the projection on the first principal component. Each cognition measure was derived as sum of three cognitive measures as defined. The four cognition measures were orthogonalized with global cognition in the statistical analyses.

For cortical thickness measures, the principal component analysis on cortical thickness measures at 144, 618 vertices yielded 321 principal components and scores. The first 4 principal components explain 5.4% of total variation in the data, after removing the mean across-subjects vertex pattern.

Demographic information is reported with mean and standard deviation for continuous variables and percent for categorical variables. Spearman's rank order correlation analyses were performed to test association between demographic variables, mean cortical thickness and global cognition. Due to the missing values in the cognitive measure and covariates (age and education), n=297 subjects were included in the final analysis. The twelve cognitive measures were standardized by subtracting their means and then dividing by their standard deviations.

Linear and non-linear association between age and reference abilities

Previous studies (Thambisetty et al., 2010) have reported non-linear associations between age and cognition. For the five cognitive measures, we examined linear and nonlinear associations in two ways. First, we used nonlinear regression analysis with natural cubic splines (Hastie, 1990), and tested whether the nonlinear trend significantly improved model fit comparing to that of linear model using F-test (Wood, 2013).

Second, we divided the sample to three age groups using age tertiles (33 years and 63 years). We separately fitted linear regression models with cognitive measures as outcomes and age, age group membership, and their interactions as independent variables. Years of education was included as a covariate.

Sparse multivariate multiple regression analyses with covariance estimation

Classical multiple regression models regress a single response on p≥1 predictors. Multivariate multiple regression is a generalization of the classical multiple regression model to q>1 responses. The model can be expressed as

$$\mathrm{Y}=\mathrm{XB}+\mathrm{E}\text{with the covariance of error term}\Sigma ,$$

where Y is an n × q matrix where each row represents a q-dimensional response of a subject, X is an n × p matrix where each row represents a p-dimensional predictor of a subject, and B is a p × q matrix where each element represents association between a predictor and a response. Multivariate analysis is often more powerful, particularly when the responses are correlated, and can provide a way to understand the pattern of relations across separate response measures by addressing issues like how may dimensions of responses are important and how the predictors contribute to these responses.

The most typical estimate of B is the ordinary least squared (OLS) estimate. The Curds and Whey algorithm (Breiman & Friedman, 1997) refines the OLS by multiplying shrinkage matrix that reflects correlations between multivariate outcomes. One downside of this approach is the loss of interpretability of coefficients due to shrinkage matrix multiplication. An alternative method is to jointly estimate B and Ʃ with L₁ penalization to reduce dimensionality. This method is called sparse multivariate multiple regression analysis with covariance estimation (SMRCE) (Rothman, Levina, & Zhu, 2010). In SMRCE, the estimation can be achieved by minimizing the objective function:

$$\mathrm{Tr}[1∕\mathrm{n}{(\mathrm{Y}-\mathrm{XB})}^{\mathrm{T}}(\mathrm{Y}-\mathrm{XB})\Omega )]-\log \mid \Omega \mid +{\lambda }_1{\sum }_{j^{\prime }\ne j}\mid w_{j^{\prime }j}\mid +{\lambda }_2{\sum }_{j,k}\mid b_{jk}\mid ,$$

where w_j′j is an element of Ω = Ʃ⁻¹ and b_jk is an element of B. The algorithm has been implemented in MRCE R-package (http://cran.r-project.org/web/packages/MRCE/index.html). To select tuning parameters λ₁ and λ_2, 10-fold cross-validation was used. To account for nonlinear association, we added linear, quadratic and cubic polynomial terms for all the predictors as well as age. For the final model, 95% CIs were computed using bootstrapping.

Results

Demographics

Demographic characteristics of the participants are summarized in Table 1. The participants ranged from 20 to 79 years of age, and increased age was associated with lower levels of cognition and lower levels of mean cortical thickness. Years of education ranged from 9 to 24, and more education was associated with higher levels of cognition, but was not related to mean cortical thickness.

Table 1.

Descriptive Statistics (n=297) and correlations.

	mean	SD	Spearman's Correlation
			Education	Mean Thickness	Global Cognition
Age	48.56	18.42	0.15*	−0.64***	−0.50***
Education (yrs)	16.16	2.46	-	−0.06	0.27***
Mean Thickness	2.44	0.12	-	-	0.43***
Global Cognition	0.01	2.29	-	-	-
Sex (Female, %)	56.22

^*p<0.05

**p<0.01

^***p<0.001

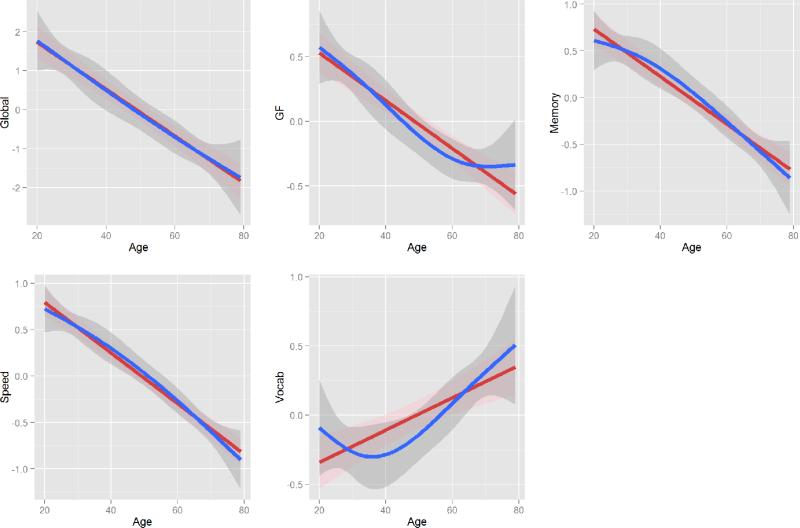
Linear vs. non-linear pattern in cognitive measures

Both linear and nonlinear models were significant (p's < 0.001) for the five cognitive measures. Although nonlinear patterns were observed in GF and Vocabulary, the model fits of the nonlinear models were not significantly better than linear models for all five cognitive measures at the significance level of 0.05 (Table 2) either with and without education as a covariate in the models.

Table 2.

Model Comparison (Linear VS. Nonlinear) with education adjusted.

p-values (F-test)	Unadjusted	Education adjusted
Global	0.9715	0.4158
GF	0.3142	0.6277
Memory	0.5422	0.2996
Speed	0.6244	0.2674
Vocab	0.1348	0.0667

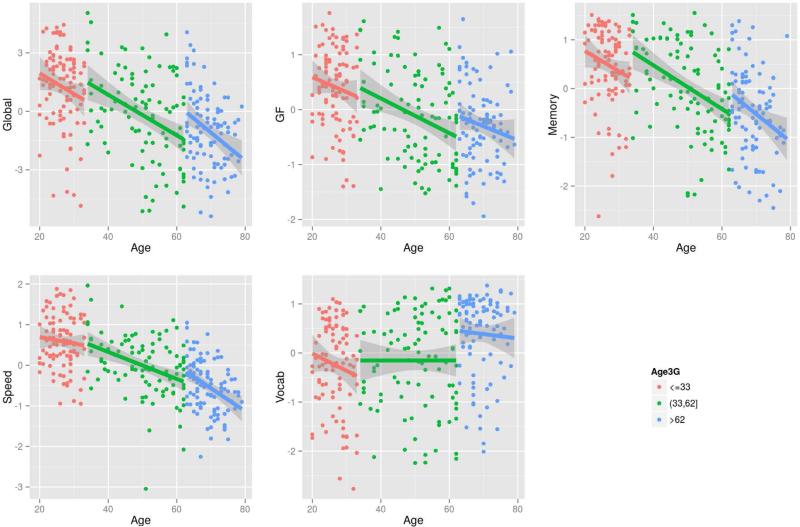
In addition, we tested whether the association between age and cognition differed by age groups. Using tertiles (33 and 62), we divided the sample into three groups (less and equal to 33, greater than 33 and less and equal to 62, greater than 62). With education adjusted, Vocab showed significant differences (Age by Age group interaction, F=3.4423, df=2, p=0.0333). In other models, there was no significant age X age group interaction.

Principal Component Analysis of Cortical thickness

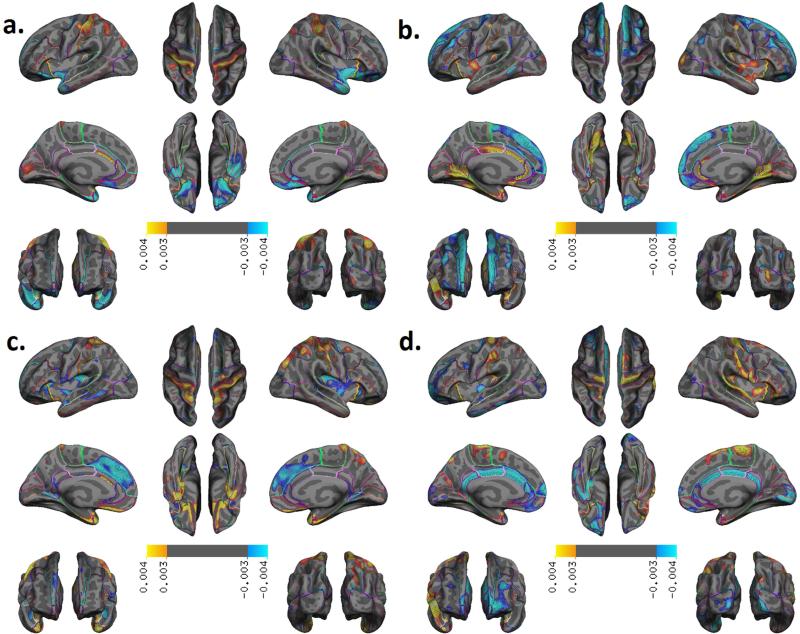
Principal components analysis (PCA) was applied to the thickness measures across vertices and 321 principal components (PCs) were derived. The first 4 principal components contained 5.4% of the aggregate variance of the data, with the first component yielding 1.7% of the variance in the data. The loadings of the point estimates of PCs1-4 are displayed in Figure 3. Loadings were normalized such that any PC had a Euclidean norm of 1, and we used a threshold of p<0.003 for visualization. For PC1 this means that loadings shown were larger and smaller than the 97%ile and 5%ile, respectively. For the other PCs we have the following lower- and upper-threshold percentile values: PC2 – [5, 95], PC3 – [6, 96], and PC4- [4, 95].

Figure 3.

Spatial Patterns of Cortical Thickness in the first four principal components. (a) PC1: post central gyrus (+), inferior temporal, olfactory, parahippocampal, Insula, frontal inferior orbital (−); (b) PC2: precuneus, paracentral (+) Medial superior frontal (−); (c) PC3: superior frontal (−), lingual (+); (d) PC4: isthmus, posterior and caudal anterior cingulate (−), precentral and superior temporal (+).

The first component (PC1) showed higher positive loadings in the post central area and negative loadings in the inferior temporal, frontal inferior orbital, olfactory, and parahippocampal area, and insula. The second component (PC2, 1.5 % variance of data) showed high positive loadings in the precuneus and paracentral area and negative loadings in the medial superior frontal area. The third component (PC3, 1.2 % variance of data) showed high positive loadings in the lingual area and negative loadings in the superior frontal area. The fourth component (PC4, 1.0 % variance of the data) showed high positive loadings in the precentral and superior temporal areas and negative loadings in the isthmus, posterior, and caudal anterior cingulate area.

Selective association between cognition and cortical thickness using SMRCE

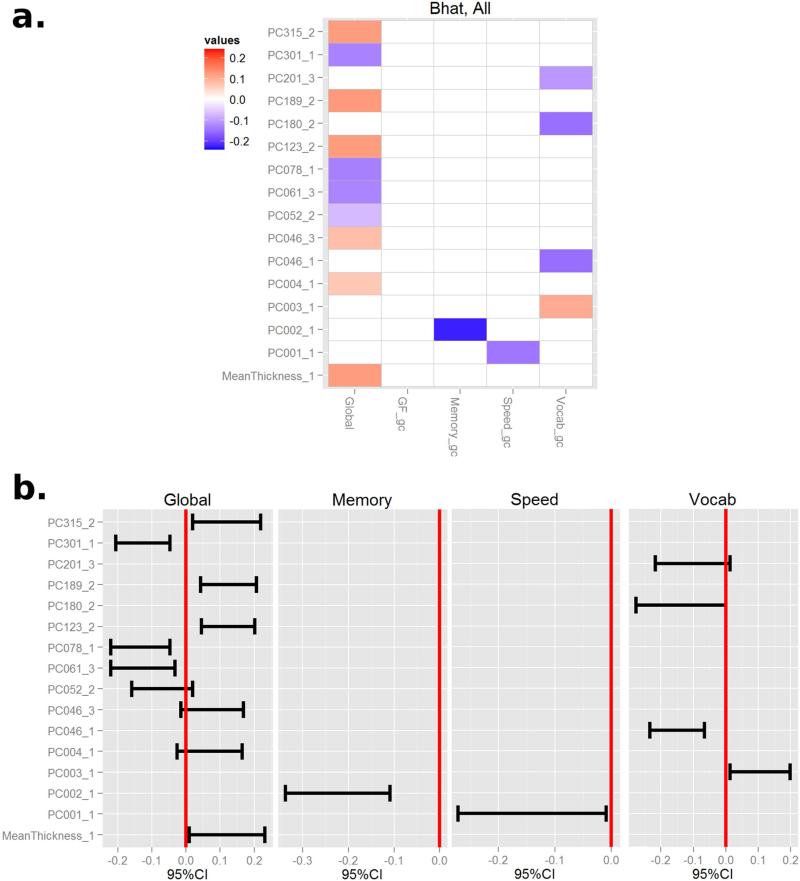
The SMRCE was applied to the 297 subjects’ data with 5 cognitive measures (global cognition, GF, Memory, Speed, and Vocab) as dependent variables, and linear, quadratic, and cubic polynomials of the 321 PCs as well as mean thickness, age and education as independent variables. We found a selective association patterns between cortical thickness and RAs. Figure 4 displays a heat map of the standardized coefficients of B. In the heat map, the columns represent outcomes (Global cognition and 4 RAs orthogonalized for global cognition), and the rows represent first, second and third order polynomials of PC scores and mean cortical thickness. Due to the dimensionality of the predictors, the non-zero coefficients that were associated with at least one of the cognitive measures were included in the heat map. In the red-blue scale, white corresponds to zero correlation, blue is a strong negative correlation and red is a strong positive correlation. There was no remaining correlation with GF after controlling for global cognition. Memory, speed and Vocab were selectively associated with PC2 (negative), PC1 (negative) and PC3 (positive), respectively. To derive 95% confidence intervals, bootstrapping was performed with 5000 repeats. Their 95% confidence intervals did not include zero.

Figure 4.

Standardized Coefficients and their 95% CIs obtained by bootstrapping (5000 repeats). The reference ability specific associations with cortical thickness PCs were stronger. There were no selective association with GF and PCs.

For clarity, we stress that all Principal Component contributions were considered in the sparse multivariate multiple regression, and the analysis was in no way restricted to the first 4 PCs. The regression produced a neat breakdown of associations for each of the 4 PCs separately (apart from fluid reasoning), but this is an empirical result of the analysis – it was not forced in any way apriori.

Discussion

Here we are interested in the association between spatial patterns in cortical thickness and cognitive outcomes measured in multiple domains. This is a multi-variate multiple regression regardless in which variables were considered as dependent variables. Although we are not testing causal relationship, it is very natural for us to treat cognitive outcomes as dependent variables to investigate RA-specific association patterns with cortical thickness. Since cortical thickness is measured over many vertices and the vertices are highly correlated with each other, it is not feasible to run regression utilizing all of the vertices. Instead, we used a principal component approach to optimally summarize the vertex data. In statistical literature, principal component regression and its variant such as partial least squares correlation and canonical correlation have often been used for neuroimaging data including morphologic MRI (Goldsmith, Bobb, Crainiceanu, Caffo, & Reich, 2011; Grellmann et al., 2015; Hibar et al., 2011; Karama et al., 2009; Liu & Calhoun, 2014). Our approach is a direct extension of this principal component regression to a multi-variate outcome with feature selection. As we already pointed out in the method section, the prediction can be improved by accounting for correlation between outcomes. To the best of our knowledge, this is one of the first attempt to use this approach for cortical thickness and cognition and thus it provides a unique contribution to the literature.

In this paper, we found selective associations between cortical thickness and cognitive reference abilities after controlling for mean thickness, global cognition and linear chronological age. The negative correlation between memory and PC2 indicates that cortical thickness was positively correlated with memory performance in medial superior frontal areas, while showing a negative correlation with cortical thickness in precuneus and para-central areas. Perceptual speed was negatively associated with PC1, implying a positive relationship between speed performance and cortical thickness in the inferior temporal, olfactory, parahippocampal, and inferior frontal orbital area and insula, while showing a negative relationship to cortical thickness in the postcentral gyrus. Lastly, the correlation between vocabulary and PC3 implies that better vocabulary ability was associated with higher thickness in the lingual area, but lower superior frontal thickness. Mean thickness was related to overall cognition, but did not relate to any individual reference abilities. We did not observe an association between fluid reasoning ability (Gf) and principal component scores. This possibly indicates that the association of cortical thickness and GF is fully explained by chronological age and global cognition.

Beyond the correlation with mean cortical thickness, global cognition also has its own signature correlation pattern in form of PC4, implying positive correlation with regional thickness in superior temporal and pre-central areas, and negative correlation with posterior and anterior cinguli.

We have shown that mean cortical thickness is positively associated with global cognition. The question we tested here is whether there is any further relationship between cortical thickness and cognition after controlling for (or residualizing out) mean thickness and global cognition. The PCs were obtained from a data array from which the mean pattern was removed; thus, the PCs describe relative, rather than absolute, effects. This is, in particular, important for negative correlations between regional cortical thickness attributable to a covariance pattern: it is unlikely that negative correlations would ever be found in the raw signal, since additional variance components which would occlude this negative correlation in the raw signal have been stripped away by the Principal Components decomposition. In the PCs, we did observe negative associations between thickness and cognition at some vertices. It is important to understand what these observations imply. These negative association arise because the sum of voxel loadings in every PC is forced to equal zero. These negative associations indicate that, within the context of this PC, better performance is associated with greater thickness at some vertices with co-varying lesser thickness at other vertices. This may hint at age-related thickness changes that occur in lockstep.

The proportion of variance accounted for by the first four principal components might be considered relatively low. However it would be helpful to know that variance is not an inferential statistic with absolute meaning (although it is commonly used this way in neuroimaging); rather, it has to be seen in the context of the number of variables and observations present in the data. For totally random IID noise, for instance, the variance spectrum and every PC would account for 1/297=0.3% of the variance in our data. The first 4 PCs account for much more variance than that, and this can be interpreted as representing as very significant variance concentration.

Non-linear associations between cortical thickness and cognition were not observed, or rather, the surviving effects were constituted by Principal Components of vanishing variance contribution, (PC 46 and lower). Non-linear age effects were not found in the SMRCE analyses, neither were age-by-thickness interactions. This means that all brain-behavioral effects and age associations are themselves independent of age. Future analyses with larger N might uncover age-effects in the thickness-cognition relationships, but in our current data no age range is inherently privileged and brain-behavioral findings are true for the whole age range.

We replicated prior accounts of the significant association of mean thickness and global cognition, and similarly found a lack of a significant association between reference abilities and mean cortical thickness as in our companion paper (Salthouse et al., 2015). In contrast to our companion paper, however, our approach found that cortical thickness patterns preserve reference-ability specific information.

A few other findings might be worth recalling: the three first Principal Component patters which showed these selective associations are mutually orthogonal and their pattern scores were correlated negatively with age (minimum R=−0.37, p<0.0001). Although these patterns capture thickness-cognition relationships beyond age, this still allows that the patterns themselves manifest an age relationship. The possible diagnostic potential of these 3 patterns can thus be tested in independent data by obtaining pattern scores on for any participant, and relating them to general cognitive-functioning variables. The thickness patterns also present an important point of departure for identifying mediators based on functional neuroimaging through which they act to produce behavior.

While our study can be seen as complementary to our recent companion paper, it is not a one-to-one extension that merely substitutes a finer resolution of surface vertices for coarser regions of interest; instead, some further analytic details were altered.

First, our companion paper (Salthouse et al., 2015) conducted a principal-axis factor analysis with a subsequent oblique rotation on 33 mean values of cortical surface ROIs to retain 5 factors. In the current paper there was no such dimensionality reduction up front; we performed a principal component analysis on the data from all vertices and retained all the PCs for the subsequent regression analysis. In contrast to our companion paper we used a principal component analysis with no rotation. Apart from the computational intractability of oblique rotations guided by considerations of topography for ~10⁵ vertices, there was no need for any rotation since we retained all 321 Principal Components (and any derived non-linear terms as independent variables), and let the sparsity constraint of SMRCE determine which contributions to shrink to zero. This execution is free of possibly arbitrary decisions on the part of the analyst. Interestingly this approach rendered main relations between cognition and cortical thickness in the first 4 Principal Components without a priori truncation and oblique rotation.

Second, the companion paper reported results separately with and without control of general factors, and with and without control of age. This multi-step procedure was shown mainly for illustrative purposes to demonstrate how the moderately large thickness-cognition relations apparent in traditional, univariate, analyses, can be substantially reduced when controlling relations between general factors and controlling the influence of age. Such illustration was not performed in the current study; we conducted a single analysis that controlled for both potential confounders, global intelligence and age in one shot. While our companion paper found few cognitive domain-specific relationships when controlling for both of these factors, we were able to identify PCs that were uniquely related to 3 of the four reference abilities.

Thus, despite minor differences in analytic procedures we feel that the current results differ from those in our previous article mainly because of the greater spatial resolution of the thickness measures. The previous, companion, article began with mean cortical thickness measures across large bilateral regions of interest, which were then summarized into five factors. This summarization within ROIs and across hemispheres is likely to aggregate vertices within one ROI which manifest a large degree of heterogeneity (and which, if subjected to separate ROI-wise PCA analyses, would show highly degenerate variance spectra). In contrast, in the current paper the principal component analysis was applied directly to the vertex data, without any intermediate summarization. Thus the resulting PCs can directly represent variations and patterns of cortical thickness at a much higher resolution; while in both cases a set of number of summary variables is used to examine relations with the cognitive measures, the PCs used in the current analysis more fully capture the spatial complexity of the cortical surface.

Another question is whether the advantage of greater spatial resolution is lost when the vertices measures are combined into a much smaller number of components prior to the analyses. Doesn't the PCA process effectively result in a decrease in spatial resolution? It is important to clarify that each PC captures a unique topography of vertices whose thicknesses are inter-correlated. Thus the spatial resolution is not lost, it is just parceled out across the set of PCs. Surprisingly, the first four PCs captured aspects of the variability across subjects in cortical thickness that were sufficient to predict most of our cognitive variables. The restriction to 4 PCs was the result of, rather than the input to, the SMRCE technique. Other outcomes (with contributions from multiple PCs which would have enabled different linear combinations) were perfectly conceivable too. In fact, although we noted some nonlinear contributions from other PCs for Vocabulary and Global Cognition, we focused our discussion and figures only on the first 4 PCs. This is because the contributions by these other PCs were much lower in the variance spectrum (PC 146 and beyond), and thus they could safely be ignored and our focus restricted to the first four PCs. However, restriction to considering just these PCs emerged naturally from our analytic framework and was not forced apriori in any way.

In conclusion, we can state that our study yielded robust and topographically distinct cortical thickness patterns underlying memory, perceptual speed, vocabulary, and general cognition, beyond a topographically non-specific relationship of mean thickness and general cognition Non-linear effects as well as age-moderation was not observed in our current study. Future work will address the gap in our understanding how thickness correlates of cognition generate behavior via the interplay with neural activation.

Besides, there is an expanding literature investigating structural covariance networks in healthy and pathological aging, including investigations of how age-related changes in specific covariance patterns progress in a disease-specific manner (Evans, 2013; Seeley, Crawford, Zhou, Miller, & Greicius, 2009; Spreng et al., 2014). The reference-ability specific association with the principal components can guide us to hypothesize reference-ability specific functional networks.

This study was carefully designed and conducted to avoid selection bias. The sample consisted of volunteers from the general population, with exclusion of individuals who scored below our threshold on the Mattis Dementia Rating Scale, as well as those who met criteria for MCI (i.e cognitive performance 1.5 standard deviations below the age-adjusted mean). These stringent criteria for normal cognition could have eliminated cognitively normal elders with lower levels of education. In the analysis, we examined the effect of education on the association between cortical thickness and reference abilities, and we did not find significant association with years of education, and the findings did not change by adjusting for education. In the future, more careful investigation and quantification of potential bias relative to the targeted population will be conducted statistical methods such as propensity matching might be considered to adjust for potential selection bias.

Figure 1.

Linear (red) and non-linear (blue) association between age and five cognitive outcomes. The 95% confidence intervals were depicted in pink and gray shades for linear and non-linear estimates, respectively.

Figure 2.

Age-Cognition by Age groups.

Highlights.

• We showed that preserving detailed spatial patterns of cortical thickness could allow us to identify reference ability-specific association with cortical thickness besides the association explained by global cognition and mean cortical thickness.

• Principal component analysis on cortical thickness evaluated at vertices revealed orthogonal spatial patterns.

• Multivariate multiple regression analysis showed selective association patterns between three reference abilities and principal components of cortical thickness even after controlling for global cognition and mean cortical thickness.

• Identified cortical thickness-cognition associations were mostly linear.

• Mean cortical thickness was highly associated with global cognition measure, but another regional pattern was also correlated with global cognition.

• Bootstrapped 95% confidence interval showed the found selective associations were stable.