Skip to main content
NCBI home page
Elsevier - PMC COVID-19 Collection logoLink to Elsevier - PMC COVID-19 Collection
. 2016 Oct 11;17:19–26. doi: 10.1016/j.epidem.2016.10.002

Data-driven outbreak forecasting with a simple nonlinear growth model

Joceline Lega 1,⁎, Heidi E Brown 1
PMCID: PMC5159251  NIHMSID: NIHMS824889  PMID: 27770752

Highlights

  • •

    We present EpiGro, a simple data-driven method to forecast the scope of an ongoing outbreak.

  • •

    We provide general hypotheses for expected model validity and also discuss model limitations.

  • •

    We propose an automated parameter estimation method that can be used for forecasting.

  • •

    We test our approach on 9 different outbreaks and show robustness over multiple systems and over noisy data sets.

  • •

    In the absence of other information or in conjunction with other models, EpiGro may be useful to public health responders.

Keywords: Infectious disease outbreaks, Mathematical model, Surge capacity, Chikungunya virus infection

Abstract

Recent events have thrown the spotlight on infectious disease outbreak response. We developed a data-driven method, EpiGro, which can be applied to cumulative case reports to estimate the order of magnitude of the duration, peak and ultimate size of an ongoing outbreak. It is based on a surprisingly simple mathematical property of many epidemiological data sets, does not require knowledge or estimation of disease transmission parameters, is robust to noise and to small data sets, and runs quickly due to its mathematical simplicity. Using data from historic and ongoing epidemics, we present the model. We also provide modeling considerations that justify this approach and discuss its limitations. In the absence of other information or in conjunction with other models, EpiGro may be useful to public health responders.

1. Introduction

As infectious diseases are identified for the first time or emerge in new populations, researchers increasingly use mathematical models to describe observed patterns and to plan and evaluate public health responses (Anderson and May, 1992, Grassly and Fraser, 2008, Keeling and Danon, 2009, Anderson et al., 2015). These models vary in complexity and scale, from simple compartmental models (Hethcote, 2000) to complex stochastic agent-based and metapopulation approaches that include external information like transportation networks (Rvachev and Longini, 1985, Hufnagel et al., 2004, Eubank et al., 2004, Ferguson et al., 2006, Balcan et al., 2010, Ajelli et al., 2010, Van den Broeck et al., 2011). The latter have been shown to efficiently capture the real-time spread of epidemics (Tizzoni et al., 2012), but often require large amounts of information. Key parameters need to be estimated from epidemiological data, which may be accomplished by maximum likelihood estimation (Ionides et al., 2006, Bretó et al., 2009, King et al., 2015) or data assimilation (Rhodes and Hollingsworth, 2009, Shaman and Karspeck, 2012). However, for newly emerging infections or when estimating the impact of bioterrorism events (Walden and Kaplan, 2004, Rotz and Hughes, 2004), such information may not always be available. Sometimes, the community is able to quickly compile and share epidemiological parameters, as was for instance the case for the devastating 2014/2015 Ebola outbreak (Van Kerkhove et al., 2015, Chowell et al., 2014). It is nevertheless expected that model choices reflect the balance between data availability and the needs of the public health community (Keeling and Danon, 2009). Moreover, since the accuracy of predictions depends heavily on modeling assumptions (Keeling and Danon, 2009, Wearing et al., 2005), it is also important to balance the need for detailed, realistic models against limitations in parameter information (May, 2004).

Knowing how many cases to expect, as well as when they will peak, before an outbreak has run its course is central to preparing a public health response (Flu Activity Forecasting Website Launched, 2016). Entire epidemiological curves can often be fitted with standard functions, such as for instance a logistic curve or the Richards model (Tjørve and Tjørve, 2010, Peleg and Corradini, 2011, Wang et al., 2012, Ma et al., 2014), but are only effective late into the outbreak. Conversely, time series approaches allow forecasting, but are considered accurate only for short-term prediction. For instance, using only case data and an autoregressive integrated moving average (ARIMA) model, researchers were able to forecast hospital bed utilization during the severe acute respiratory syndrome (SARS) outbreak in Singapore up to three days forward (Earnest et al., 2005). Additional information is usually required for longer forecasts (see e.g. 3-month dengue forecasting using climate data (Gharbi et al., 2011)), limiting the utility of such approaches for newly emerging diseases, when many associated risk factors are still unknown.

We identify a simple property common to the epidemiological curves of many outbreaks and explore the modeling implications of this finding. In particular, it allows us to describe the course of each outbreak in terms of a very simple model, whose two parameters can be extracted from epidemiological data. This is different from estimating disease transmission rates since, for instance, knowledge of the model discussed in this article is not sufficient to recover the parameters (e.g. R0) of a simulated epidemic that follows the SIR (Susceptible – Infected – Removed) dynamics. We present an automated parameter extraction method that allows us to explore the applicability of the method to a variety of different outbreaks and, more importantly, explain how the model may be used to forecast the scope of ongoing outbreaks, including those of some vector-borne diseases.

2. Methods

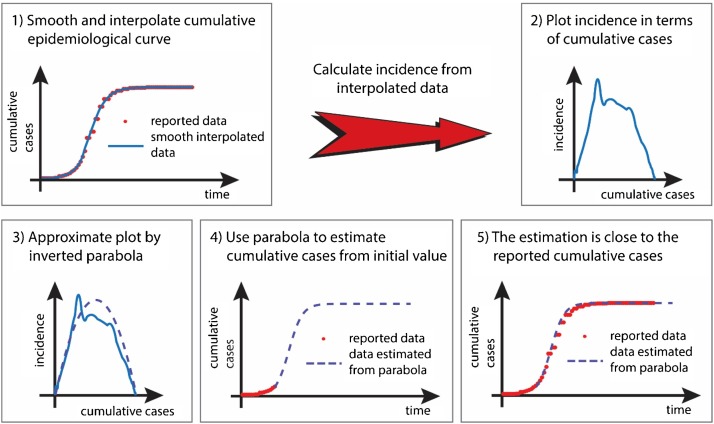
Our general methodology is described in Fig. 1 . Starting from reported epidemiological data, we consider the cumulative number of cases, C, and numerically produce a smooth interpolation of its evolution (panel 1). Data collection procedures for the examples discussed in this article are given in Technical Appendix 1 in Supplementary Material. We then use this smoothed data to estimate incidence, G, as described in Technical Appendix 2 (see Supplementary Material). The crucial point of our approach is that rather than plotting C as a function of time, we plot the estimated incidence G, as a function of cumulative cases, C, G(C) (panel 2). For many outbreaks, the graph of G as a function of C has a single “hump” and can, at first order, be approximated by an inverted parabola (panel 3). This inverted parabola, whose equation contains two parameters, defines a simple model for the evolution of the outbreak, which can be used to predict future number of cases given an initial condition (panel 4). We developed a method, detailed in Technical Appendix 3 in Supplementary Material, that automatically associates a parabola to available epidemiological data of one-wave outbreaks. It works on partial (for ongoing outbreaks) or full (for outbreaks that have completed their course) data sets and proceeds as follows: rather than attempting to estimate the parabola parameters from the cumulative epidemiological curve, we fit the graph of G(C) to its parabolic approximation and the graph of C(t) to its corresponding time course, simultaneously. Doing so therefore demands that the two unknown parameters describing the parabola be chosen to provide good approximations of two different (albeit related) plots. This approach is easily applicable to ongoing outbreaks for which limited data are available, and can therefore be used for forecasting.

Fig. 1.

Fig. 1

Open in a new tab

Sketch of the general methodology.

3. Results

3.1. Robustness over multiple systems

The proposed approach applies to one-wave outbreaks of multiple diseases and sizes, as illustrated in Fig. 2 and supported by our analysis of a variety of epidemiological curves (see additional Appendix figures). The model was tested in detail on nine one-wave outbreaks: 2014–15 chikungunya outbreaks in the Dominican Republic (Fig. 2A), Guadeloupe (Fig. A1), and Dominica (Fig. A2); 2014–15 Ebola outbreaks in Guinea (Fig. A3), Liberia (Fig. A4), and Sierra Leone (Fig. A5); 2008 outbreak of Salmonella SaintPaul in the US (Fig. A6); 2008 outbreak of gastroenteritis in Majorca (Fig. 2B); and 2009 outbreak of H1N1 in Canada (Fig. A7), as well as on one two-wave outbreak of pertussis (2011–12 in the state of Washington, US; Fig. 4). The parabolas plotted in the figures were selected using the automated parameter approximation method. Inspection of these plots reveals that they capture the time course of the cumulative number of cases fairly well (right panel of each figure and as depicted in panel 5 of the schematic of Fig. 1). For very noisy data (e.g. left panels of Figs. A3–5 for Ebola), the chosen parabola nicely interpolates through widely oscillating reported incidence data. The peak incidence (maximum of the blue solid curve on the left panel of each figure) is typically higher than the maximum M of each parabola (Figs. 2B, 4, A1–A5) and may not occur at the same value of the cumulative number of cases. The time frame for the peak of the outbreak (that is when the cumulative curve shown on the right panel of each figure is the steepest), as well as the duration of the entire outbreak (when incidence returns to values close to zero) are however reasonably well captured.

Fig. 2.

Fig. 2

Open in a new tab

Modeled and observed progression of single-wave outbreaks of different diseases and sizes. (A) 2014–15 chikungunya outbreak in the Dominican Republic. The parabolic approximation has a maximum M ≈ 46,540 cases/week and crosses the horizontal axis at C0 ≈ 539,227 cases. (B) small outbreak of gastroenteritis in Majorca, Spain. Model parameters are M ≈ 7.6 cases/day and C0 ≈ 71 cases.

Fig. 4.

Fig. 4

Open in a new tab

Modeled and observed progression of a two-wave outbreak. Same as Fig. 2, but for a pertussis outbreak in the state of Washington in 2012. Model parameters are M ≈ 30 cases/week and C0 ≈ 1491 cases for the first wave; the parabola modeling the second wave has a maximum M2 ≈ 155 cases/week and crosses the horizontal axis at C1 ≈ 674 cases and C2 ≈ 4233 cases.

For these reasons, we expect the parabolic model to describe general trends of one-wave outbreaks, such as order-of-magnitude estimates for their final number of cases, duration, and time frame of peak incidence. These statements are made more quantitative below.

A reason for the versatility of this approach is that the parabolic approximation is also “hidden” in the standard SIR model. Fig. 3 presents simulations of this model for small and large values of R0  > 1. The left panel of each row shows the time course of S, I, and R scaled to the total population N = S + I + R, and the right panel shows a numerical evaluation of the scaled incidence G/N as a function of scaled cumulative cases C/N (solid curve), together with two parabolic approximations P1 and P2. In the context of the SIR model, C = R + I is the total number of cases and its rate of change G = dC/dt is incidence. It is clear from these simulations that for both values of R0, the SIR model displays the one-hump behavior seen in the graphs of G(C) obtained from outbreak data, and the graph of G as a function of C is very close to an inverted parabola.

Fig. 3.

Fig. 3

Open in a new tab

Simulations of the SIR model for two values of R0 > 1. Top row: R0 = 1.25; bottom row: R0 = 10. Left: time course of S, I, and R scaled to the total population N. Right: scaled growth rate (incidence) G/N as a function of C/N (thick solid blue curve). Also shown are two parabolic approximations, P1 and P2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The two parabolic approximations P1 and P2 plotted in Fig. 3 cross the horizontal axis at C = 0 and C = C0, where C0 is the final number of cases in the model and can be numerically estimated by solving a transcendental equation (details are in Technical Appendix 4 in Supplementary Material). The maximum M1 of parabola P1 is a numerical evaluation of the maximum of G. The maximum M2 of parabola P2 is equal to γ C0 (R0-1)/4, based on a theoretical justification also provided in Technical Appendix 4 in Supplementary Material. Both parabolic approximations are very good, but P1, which estimates M from the data, gives a better fit than P2. The method proposed in this article proceeds in a similar way: it numerically estimates values of C0 and M that provide as good a parabolic fit of G as possible, given the available data.

The approach can be extended to multiple-wave outbreaks, in which case a parabola, or a piece thereof, is fit to each wave. The number of waves in any outbreak may easily be identified by plotting G as a function of C, where C, the cumulative number of reported cases, is known as a function of time. Fig. 4 provides an example of a two-wave outbreak, with incomplete data. In this case, the growth rate G is modeled as a piecewise parabolic function of C. Our approach predicts a total of 4232 cases by the end of the outbreak. An article published in 2014 (Bowden et al., 2014) mentions over 4900 cases reported by the end of 2012.

3.2. Robustness over noisy data sets

The fit of G to a parabola, or to pieces thereof, does not have to be perfect to produce good, order of magnitude estimates of the time evolution of the cumulative number of cases of an outbreak. In particular, fluctuations in G (incidence) do not change the overall one- or two-hump behavior of the curve. To make this statement more quantitative, we assessed whether adding a small amount of noise (see Technical Appendix 5 in Supplementary Material for noise generation) to the data significantly affected the outcome of the automated parameter estimation procedure. Specifically, we found that the standard deviation of the distribution of estimates for the duration, peak incidence, and final number of cases (these quantities are defined in Technical Appendix 6 in Supplementary Material) obtained from the parabolic model optimized for each outbreak, rescaled to their respective means, was typically of a few percent (<3% in all cases; see Supplementary Table A1). As a consequence, the parabolic fits can be performed without specific knowledge of the exact nature of the noise present in the data (recall that G represents incidence). A surge in G may reflect an actual increase in the number of reported cases, or an improvement in the way the disease is diagnosed, or possibly an increase in the number of reported cases due to “concern bias” (Doshi, 2009). Changes in G also occur when numbers of confirmed or suspected cases are retroactively updated by the relevant reporting agencies. Such fluctuations are typical of disease data and cannot be avoided.

3.3. Automated forecasting tool

We tested the implications of using the parabolic approximation for forecasting the peak, duration, and final number of cases of an ongoing outbreak. This was accomplished by applying the automated parameter extraction method to each outbreak and comparing predictions obtained from partial data sets to predictions obtained from the entire data set. Results on partial data sets for the nine one-wave outbreaks considered in this study indicate that the correct orders of magnitude for the peak, duration, and final number of cases, can be obtained with this method fairly early in each outbreak (Supplementary Table A2). Averaging over these outbreaks, which differ in size and in quality of reported data, we found that when 30% (resp. 50%) of the total cases had been reported, the automated procedure led to typical relative errors equal to 31% (resp. 19%) for the estimated time of peak incidence, 32% (resp. 21%) for the estimated duration, and 51% (resp. 27%) for the expected total number of cases of the outbreak (Table 1 ). This may sound like a large error, but the order of magnitude is correct.

Table 1.

Relative error using the automated parameter extraction procedure, calculated by averaging the absolute values of the relative errors reported in Supplementary Table A2.

Average Relative Error
Percentage of Reported Cases 10% 30% 50% 70%
Error on Predicted Peak 0.37 0.31 0.19 0.12
Error on Predicted Duration 0.52 0.32 0.21 0.12
Error on Predicted Number of Cases 0.84 0.51 0.27 0.15
Open in a new tab

The approach proposed in this article may therefore be useful for estimating the broad scope of emerging outbreaks and guide the public health response accordingly. For instance, in the case of Ebola in Sierra Leone, using data from the end of August to the end of October 2014, the method predicted that the outbreak would last 283 days and have more than 7000 cases. Fig. 5 illustrates how the automated approximation method revises its estimates as the epidemiological information becomes more complete.

Fig. 5.

Fig. 5

Open in a new tab

Same as Fig. 2, but for four intermediate stages of the 2014–15 chikungunya outbreak in the Dominican Republic. From left to right and top to bottom, the times of the estimates are at about 25, 35.5, 46, and 57 weeks into the outbreak. Data were available for 71 weeks.

3.4. Modeling implications

Similar to a parameterized SIR model capturing the average course of many infectious diseases, the approach presented in this article not surprisingly appears to apply to various outbreak data. Although we do not claim that all outbreaks follow the SIR model, we can nevertheless use this observation to infer the following general hypotheses for the validity of the method.

(i) The disease spreads relatively quickly, in a densely populated or well-connected area so that a macroscopic approach is likely to capture average trends.

(ii) The disease is new to the area, or immunity is transient and does not persist over a period of time longer than the duration between outbreaks, so that there initially is a large number of susceptible individuals.

The pertussis example shows that the approach may also work beyond these assumptions: the estimated vaccine coverage in Washington State two years before the outbreak was 70.6% among 13–17 year olds and 81.9% among 19–35 month olds (DeBolt et al., 2012). While pockets of the populations likely had lower immunity, this indicates that the population may not have been fully susceptible. Similarly, the Salmonella example suggests that when reported in aggregate, large food-borne outbreaks also have an epidemiological curve that has the parabolic property, even though there is no human-to-human transmission. We believe this effect is likely due to the combination of an initial “exponential-like” spread due to the transportation/restaurant network (in this example the outbreak was linked to salsa at Mexican style restaurants (Behravesh et al., 2011)), followed by a public health response that effectively limits further spread of the disease.

Similar macroscopic considerations can be extended to vector-borne diseases: if we denote by C(t) the total number of cases up to time t and by C0 the total population that will eventually be infected, the rate of change of the cumulative number of infected individuals is expected to be proportional to the product of two terms: the likelihood, assumed to be proportional to C/C0, that when a vector bites an individual, this person happens to be infected, and the number of remaining susceptible individuals C0  − C. Then G has the parabolic approximation G = dC/dt = κ (C/C0) (C0  − C), where the constant κ depends on the number of infected vectors and may be a slowly-varying function of time. We can therefore add the following hypothesis to the above list.

(iii) For a vector-borne disease, the vector is present and abundant in levels that support disease transmission, so that there is no need to model the dynamic of the vector population.

We used the approach described in this article for our solution to the 2014/15 Defense Advanced Research Projects Agency (DARPA) Forecasting Chikungunya Challenge and our model performed best (DARPA, 2014, CHIKV, 2015). Our forecasts for future cumulative numbers of cases are summarized in Fig. 6 , which provides an illustration of the effectiveness of the present methodology when applied to mosquito-borne diseases. Reported cumulative numbers of cases of chikungunya in 40 Pan American Health Organization (PAHO) countries from 09/01/2014 to 02/01/2015 are compared to one- to four-week forecasts obtained using this method. Even though errors are present, most of the points are close (in comparison to their distance from the origin) to the diagonal (the red line in each plot), indicating that the method provided good, order-of-magnitude predictions for the number of reported cases of chikungunya, even in early stages of the outbreak. In this case, parabolas were fit to the epidemiological data for each country by hand, by plotting graphs similar to those in Fig. 2. Because of the simplicity of the underlying parabolic model, estimates of outbreak magnitude were obtained in a few minutes on a standard CPU, comparable to those commonly found on handheld devices. Simplicity and speed are two primary advantages of the approach described in this article.

Fig. 6.

Fig. 6

Open in a new tab

Predicted vs. observed numbers of chikungunya cases in PAHO countries. Each data point (circle) depicts predicted (y-coordinate) and reported (x-coordinate) cumulative numbers of cases (confirmed + suspected + imported) on a given week, for a given country. The red lines have slope 1 and correspond to a perfect match between predicted and observed data. Predictions are monthly forecasts for numbers of cases 1, 2, 3, and 4 weeks ahead, made on 09/01/14, 10/01/14, 11/01/14, 12/01/14, 01/01/15, and 02/01/15. Left: 28 PAHO countries that experienced one-wave outbreaks. Right: 12 PAHO countries that experienced two-wave outbreaks. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

A parabolic approximation is often “hidden” in the epidemiological data of single-wave outbreaks and we have proposed a rationale for this observation, which is that such a property also holds for the SIR model. In this paper we built on that property and described a new tool, EpiGro, which performs well in forecasting the scope of an ongoing outbreak. We provided general hypotheses for when this approximation might be expected to be relevant, including its extension to vector-borne diseases. We also developed a method for automatically extracting parameters from epidemiological data, discussed its robustness, and explored its use for forecasting the duration, size, and time of peak incidence of an unfolding outbreak. The novelty of our approach is to simultaneously fit the available data to both incidence (plotted as a function of the cumulative number of cases) and cumulative number of cases (plotted as a function of time), rather than just fitting the observed number of cases, or attempting to estimate disease-specific transmission parameters from limited data. The only input necessary is the cumulative number of cases reported up to the time at which the forecast is made. While there is mounting evidence that a logistic model may be used for disease forecasting (Chowell et al., 2014, Pell et al., 2016), it is essential to have robust methods that identify optimal parameters. Technical Appendix 8 in Supplementary Material compares the present approach with a logistic fit of the cumulative epidemiological curve and illustrates similarities and differences between the two methods. Recent work (Pell et al., 2016) proposed to give more weight to recent data points in the calculation of the error to be minimized when fitting cumulative curves to solutions of the logistic equation, in order to improve the performance of a logistic fit. While the mathematics underlying the parabolic approximation is fairly simple, our results indicate that the present method can provide useful information on the order of magnitude of the scope of an outbreak, relatively early in its development, and that predictions generally improve as the disease unfolds and epidemiological data become more complete. Further work on the automated parameter estimation procedure is likely to lead to better outcomes, especially in the early stages of an outbreak. This however goes beyond the scope of the present article, whose main goal is to establish the presence of the parabolic behavior in outbreak data and to discuss the consequences of this observation, including its potential as a forecasting tool for emerging outbreaks.

From a modeling point of view, our main message is that for many single-wave outbreaks, including simulated deterministic outbreaks following the SIR model, the cumulative number of cases not surprisingly exhibits linear growth followed by quadratic nonlinear saturation and thus qualitatively behaves like a solution of the logistic equation (note that in that context C0, the total number of cases, represents the carrying capacity of the system and is typically denoted by K). The data-driven forecasting approach presented here builds on this realization and is able to quickly (in a few minutes on a standard CPU) provide order-of-magnitude estimates of the scope of an outbreak without knowledge of disease transmission information. In times of increasing model complexity, this reminds us that simple considerations may still be useful, especially in the absence of disease transmission parameters. We therefore suggest that the method discussed in this article could be included in the fleet of models that responders and planners use to rapidly address emerging infectious disease outbreaks.

Doing so would of course only address a small piece of the disease forecasting puzzle. Because the present approach is data-driven and macroscopic, it can only start making useful predictions once a significant number of cases have been reported. It also cannot capture the presence of local clusters which can affect the effective speed of disease transmission. However, if the goal is to describe the large-scale spread of an emerging disease at the macroscopic level, one could envision coupling this method to models for the prediction of disease arrival times in specific countries, as for instance described in (Brockmann and Helbing, 2013). Once the disease is predicted to arrive in a given location, one could use linear growth to estimate the initial number of cases and switch to the method proposed here after enough cases have been reported, in order to include nonlinear effects. Even though such a strategy may seem crude, it is likely to be fast, and based on the discussion presented in this article, it should be able to correctly predict the order of magnitude of many outbreaks.

Contributions

Order in list of authors reflects participation in this article. J.L. developed the model, ran the simulations, and wrote the technical appendices. J.L. and H.E.B interpreted and analyzed the results, wrote the article, and approved its contents for publication. Both authors declare no competing financial interests.

Article summary line

Using data from historic and recent epidemics, we present EpiGro, a simple data-driven method to forecast the scope of an ongoing outbreak.

Acknowledgments

We are grateful to Luigi Sedda for useful feedback on a previous version of this manuscript. Research reported in this publication was supported in part by the National Institute of Allergy and Infectious Diseases of the National Institutes of Health under Award Number K01AI101224. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Preliminary results from this study were presented at the DARPA Chikungunya Challenge Finale; May 12, 2015, Washington, DC, USA.

Biographies

Joceline Lega is a professor of mathematics at the University of Arizona with expertise in the modeling of nonlinear phenomena.

Heidi E. Brown is an assistant professor of epidemiology at the University of Arizona, College of Public Health. Her research focuses on vector-borne disease transmission dynamics.

Footnotes

Appendix A

Supplementary material associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.epidem.2016.10.002.

Appendix A. Supplementary Material

The following are Supplementary material to this article:

Technical Appendices
mmc1.pdf (235.2KB, pdf)
Supplementary Tables
mmc2.pdf (552.6KB, pdf)
Supplementary Figures A1–A7
mmc3.docx (1.4MB, docx)

References

  1. Ajelli M., Gonçalves B., Balcan D., Colizza V., Hu H., Ramasco J.J., Merler S., Vespignani A. Comparing large-scale computational approaches to epidemic modeling: agent-based versus structured metapopulation models. BMC Infect. Dis. 2010;10:190. doi: 10.1186/1471-2334-10-190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Anderson R.M., May R.M. Oxford University Press; 1992. Infectious Diseases of Humans: Dynamics and Control. [Google Scholar]
  3. Anderson R.M., Andreasen V., Bansal S., De Angelis D., Dye C., Eames K.T.D. Modeling infectious disease dynamics in the complex landscape of global health. Science. 2015;347:aaa4339. doi: 10.1126/science.aaa4339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Balcan D., Gonçalves B., Hu H., Ramasco J.J., Colizza V., Vespignani A. Modeling the spatial spread of infectious diseases: the global epidemic and mobility computational model. J. Comput. Sci. 2010;1:132–145. doi: 10.1016/j.jocs.2010.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Behravesh C.B., Mody R.K., Jungk J., Gaul L., Redd J.T., Chen S. 2008 Outbreak of salmonella saintpaul infections associated with raw produce. N. Engl. J. Med. 2011;364:918–927. doi: 10.1056/NEJMoa1005741. [DOI] [PubMed] [Google Scholar]
  6. Bowden K.E., Williams M.M., Cassiday P.K., Milton A., Pawloski L., Harrison M. Molecular epidemiology of the pertussis epidemic in Washington State in 2012. J. Clin. Microbiol. 2014;52:3549–3557. doi: 10.1128/JCM.01189-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bretó C., He D., Ionides E.L., King A.A. Time series analysis via mechanistic models. Ann. Appl. Stat. 2009;3:319–348. [Google Scholar]
  8. Brockmann D., Helbing D. The hidden geometry of complex, network-driven contagion phenomena. Science. 2013;342:1337–1342. doi: 10.1126/science.1245200. [DOI] [PubMed] [Google Scholar]
  9. CHIKV, Challenge Announces Winners . DARPA press release; 2015. Progress toward Forecasting the Spread of Infectious Diseases.http://www.darpa.mil/news-events/2015-05-27 [Google Scholar]
  10. Chowell G., Simonsen L., Viboud C., Kuang Y. Is West Africa approaching a catastrophic phase or is the Ebola epidemic slowing down? Different models yield different answers for Liberia. PLOS Curr. 2014 doi: 10.1371/currents.outbreaks.b4690859d91684da963dc40e00f3da81. Outbreaks. 2014 Nov 20. Edition 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. DARPA . 2014. Forecasting Chikungunya Challenge, Challenge Description on InnoCentive Site.https://www.innocentive.com/ar/challenge/9933617 [Google Scholar]
  12. DeBolt C., Tasslimi A., Bardi J., Leader B.T., Hiatt B., Quin X. Pertussis epidemic—Washington, 2012. MMWR. 2012;61:517–522. [Google Scholar]
  13. Doshi P. Calibrated response to emerging infections. BMJ. 2009;339:b3471. doi: 10.1136/bmj.b3471. [DOI] [PubMed] [Google Scholar]
  14. Earnest A., Chen M.I., Ng D., Sin L.Y. Using autoregressive integrated moving average (ARIMA) models to predict and monitor the number of beds occupied during a SARS outbreak in a tertiary hospital in Singapore. BMC Health Serv. Res. 2005;5:36. doi: 10.1186/1472-6963-5-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Eubank S., Guclu H., Anil Kumar V.S., Marathe M.V., Srinivasan A., Toroczkai Z., Wang N. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429:180–184. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
  16. Ferguson N.M., Cummings D.A., Fraser C., Cajka J.C., Cooley P.C., Burke D.S. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Flu Activity Forecasting Website Launched . 2016. CDC Launches New Website Featuring Flu Forecasts by External Researchers.http://www.cdc.gov/flu/news/flu-forecast-website-launched.htm [Google Scholar]
  18. Gharbi M., Quenel P., Gustave J., Cassadou S., La Ruche G., Girdary L., Marrama L. Time series analysis of dengue incidence in Guadeloupe, French West Indies: forecasting models using climate variables as predictors. BMC Infect. Dis. 2011;11:16. doi: 10.1186/1471-2334-11-166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Grassly N.C., Fraser C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol. 2008;6:477–487. doi: 10.1038/nrmicro1845. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42:599–653. [Google Scholar]
  21. Hufnagel L., Brockmann D., Geisel T. Forecast and control of epidemics in a globalized world. Proc. Natl. Acad. Sci. U. S. A. 2004;101:15124–15129. doi: 10.1073/pnas.0308344101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Ionides E.L., Bretó C., King A.A. Inference for nonlinear dynamical systems. Proc. Natl. Acad. Sci. U. S. A. 2006;103:18438–18443. doi: 10.1073/pnas.0603181103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Keeling M.J., Danon L. Mathematical modelling of infectious diseases. Br. Med. Bull. 2009;92:33–42. doi: 10.1093/bmb/ldp038. [DOI] [PubMed] [Google Scholar]
  24. King A.A., Domenech de Cellès M., Magpantay F.M.G., Rohani P. Avoidable errors in the modelling of outbreaks of emerging pathogens, with special reference to Ebola. Proc. R. Soc. B. 2015;282:20150347. doi: 10.1098/rspb.2015.0347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ma J., Dushoff J., Bolker B.M., Earn D.J.D. Estimating initial epidemic growth rates. Bull. Math. Biol. 2014;76:245–260. doi: 10.1007/s11538-013-9918-2. [DOI] [PubMed] [Google Scholar]
  26. May R.M. Uses and abuses of mathematics in biology. Science. 2004;303:790–793. doi: 10.1126/science.1094442. [DOI] [PubMed] [Google Scholar]
  27. Peleg M., Corradini M.G. Microbial growth curves: what the models tell us and what they cannot. Crit. Rev. Food Sci. Nutr. 2011;51:917–945. doi: 10.1080/10408398.2011.570463. [DOI] [PubMed] [Google Scholar]
  28. Pell B., Baez J., Phan T., Gao D., Chowell G., Patch Kuang Y. Models of EVD transmission dynamics. In: Chowell G., Hyman J.M., editors. Mathematical and Statistical Modeling for Emerging and Re-Emerging Infectious Diseases. Springer International Publishing; Switzerland: 2016. pp. 147–167. [Google Scholar]
  29. Rhodes C.J., Hollingsworth T.D. Variational data assimilation with epidemic models. J. Theor. Biol. 2009;258:591–602. doi: 10.1016/j.jtbi.2009.02.017. [DOI] [PubMed] [Google Scholar]
  30. Rotz L., Hughes J. Advances in detecting and responding to threats from bioterrorism and emerging infectious disease. Nature. 2004;10:S130–136. doi: 10.1038/nm1152. [DOI] [PubMed] [Google Scholar]
  31. Rvachev L.A., Longini I.M., Jr. A mathematical model for the global spread of influenza. Math. Biosci. 1985;75:3–22. [Google Scholar]
  32. Shaman J., Karspeck A. Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci. U. S. A. 2012;109:20425–20430. doi: 10.1073/pnas.1208772109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Tizzoni M., Bajardi P., Poletto C., Ramasco J.J., Balcan D., Gonçalves B. Real-time numerical forecast of global epidemic spreading: case study of 2009A/H1N1pdm. BMC Med. 2012;10:165. doi: 10.1186/1741-7015-10-165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tjørve E., Tjørve K.M.C. A unified approach to the Richards-model family for use in growth analyses: why we need only two model forms. J. Theor. Biol. 2010;267:417–425. doi: 10.1016/j.jtbi.2010.09.008. [DOI] [PubMed] [Google Scholar]
  35. Van Kerkhove M.D., Bento A.I., Mills H.L., Ferguson N.M., Donnelly C.A. A review of epidemiological parameters from Ebola outbreaks to inform early public health decisionmaking. Sci. Data. 2015;2:150019. doi: 10.1038/sdata.2015.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Van den Broeck W., Gioannin C., Gonçalves B., Quaggiotto M., Colizza V., Vespignani A. The GLEaMviz computational tool, a publicly available software to explore realistic epidemic spreading scenarios at the global scale. BMC Infect. Dis. 2011;11:37. doi: 10.1186/1471-2334-11-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Walden J., Kaplan E. Estimating time and size of bioterror attack. Emerg. Infect. Dis. 2004;10:1202–1205. doi: 10.3201/eid1007.030632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wang X.-S., Wu J., Yang Y. Richards model revisited: validation by and application to infection dynamics. J. Theor. Biol. 2012;313:12–19. doi: 10.1016/j.jtbi.2012.07.024. [DOI] [PubMed] [Google Scholar]
  39. Wearing H.L., Rohani P., Keeling M.J. Appropriate models for the management of infectious diseases. PLoS Med. 2005;2:e174. doi: 10.1371/journal.pmed.0020174. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Technical Appendices
mmc1.pdf (235.2KB, pdf)
Supplementary Tables
mmc2.pdf (552.6KB, pdf)
Supplementary Figures A1–A7
mmc3.docx (1.4MB, docx)

Articles from Epidemics are provided here courtesy of Elsevier

RESOURCES