Evaluation of the 2-(1-Hexyloxyethyl)-2-devinyl pyropheophorbide (HPPH) mediated photodynamic therapy by macroscopic singlet oxygen modeling

Abstract

Photodynamic therapy (PDT) is known as a non-invasive treatment modality that is based on photochemical reactions between oxygen, photosensitizer, and a special wavelength of light. However, a dosimetric predictor for PDT outcome is still elusive because current dosimetric quantities do not account for the differences in the PDT oxygen consumption rate for different fluence rates. In this study, we evaluate several dose metrics, total fluence, photobleaching ratio, PDT dose, and mean reacted singlet oxygen (mean [¹O₂]_rx) for predicting the PDT outcome and a clinically relevant tumor re-growth endpoint. For this reason, radiation-induced fibrosarcoma (RIF) mice tumors are treated with 2-(1-Hexyloxyethyl)-2-devinyl pyropheophorbide (HPPH) and different in-air fluences (30 J/cm², 50 J/cm², 135 J/cm², 250 J/cm², and 350 J/cm²) and in-air fluence rates (20, 50, 75, 150 mW/cm²). Explicit measurements of HPPH and oxygen concentration as well as tissue optical properties are performed pre- and post-treatment. Then, this information is incorporated into a macroscopic model to calculate the photobleaching, PDT dose, and mean [¹O₂]_rx. Changes in tumor volume are tracked following the treatment and compared with the dose metrics. The correlation demonstrates that mean [¹O₂]_rx serves as a better dosimetric quantity for predicting treatment outcome and a clinically relevant tumor re-growth endpoint.

Graphical Abstract

1. Introduction

Photodynamic therapy (PDT) is an emerging treatment modality that has received much attention in recent years due to its use to treat certain malignant and nonmalignant diseases [1–5]. PDT requires administration of a photosensitizer that localizes in tumor tissue and is subsequently excited by exposure to a specific wavelength of light [2, 3, 5, 6]. Following the absorption of light, the photosensitizer makes a transition from its ground state (singlet state) into a relatively long-lived electronically excited state (triplet state) via a short-lived excited singlet state. In type II PDT, which is the focus of this paper, the triplet can transfer its energy directly to oxygen (³O₂) to form singlet-state oxygen (¹O₂) [1, 2]. The massive production of ¹O₂ is thought to be the major cause of cytotoxicity and tumor lysis via reacting with the surrounding biological molecules [7, 8]. Because of the high reactivity and short half-life of ¹O₂, only cells that are proximal to the area of ¹O₂ production (areas of photosensitizer localization) are directly affected by PDT [5]. Therefore, PDT destroys the cancer in a way that causes significantly less harm to the body than by current treatments like chemotherapy and radiation [5, 9]. However, the lack of an accurate dosimetry quantity that accounts for intra- and inter-patient variability in all aspects of PDT dosimetry including photosensitizer concentration, tissue optical properties and oxygen concentration ([³O₂]) for evaluation of the treatment outcomes prevents the widespread clinical use of PDT.

Over the past few decades, there has been much investigation into the utility of using photosensitizer photobleaching and light fluence to guide the delivery of PDT and predict the tumor viability [10–12]. There is also an increasing body of evidence that suggests a PDT dose metric, which is calculated by the time integral of the product of local photosensitizer concentration and light fluence rate (φ), can predict PDT efficacy [13–16]. Under well-oxygenated conditions, it is generally accepted that PDT dose is the most well-defined biophysical dosimetry quantity and a good predictor of the treatment outcome [15, 17]. However, theoretical and experimental mice studies have shown that in tumors, which are frequently poorly oxygenated, small changes in φ or initial oxygenation ([³O₂]₀) may have large PDT effects [18]. It is known that high φ can create more severe hypoxia during illumination and result in less effective PDT. More recently, it has been suggested to account for ¹O₂ production based on the luminescent measurements of either ¹O₂ or sensitive assays for ¹O₂ detection during PDT to overcome the limitations of PDT dose [19–22]. However, the detection and interpretation of the ¹O₂ signals as well as the selection of luminescent assays that are non-toxic and safe for human and animal models are major obstacles to use this method for clinical applications [20, 23, 24]. Moreover, the phosphorescence emission arises from a transition of ³O₂ from its singlet state to its ground state. This process competes with the reaction of ¹O₂ with cellular and extracellular substrates, which leads to an increase in phosphorescence emission in conditions where substrates for ¹O₂ are not plentiful. An additional challenge is the weak and short lifetime of the luminescence signal of ¹O₂ due to its rapid reaction with the biological environment that prevents direct detection of ¹O₂ for clinical and interstitial applications [12, 21, 23, 24].

In this study, a macroscopic explicit dosimetry model is used, which predicts the amount of cumulative reacted ¹O₂ concentration ([¹O₂]_rx) on the basis of measurable quantities that contribute to the photodynamic effect [1, 17, 25–27]. The correlation of [¹O₂]_rx with outcomes of 2-(1-Hexyloxyethyl)-2-devinyl pyropheophorbide (HPPH)-mediated PDT is compared to fluence, photosensitizer photobleaching ratio, and PDT dose in a well-characterized mouse radiation-induced fibrosarcoma (RIF) tumor model. A tumor cure index (CI) assay is considered as the treatment outcome. It should be noted that the photobleaching ratio in this study is different from photobleaching-based implicit dosimetry. A range of excitation conditions including various exposure times, different in-air fluence rates (φ_air) and in-air fluences are used to induce different CI. Then, [¹O₂]_rx is calculated for different treatment conditions using the macroscopic model, based on the explicit dosimetry of the tissue optical properties, interstitial light distribution, photosensitizer concentration, and [O₂]₀.

2. Theory and method

2.1 Mouse tumor models for in vivo studies

RIF tumors were propagated on the shoulders of female C3H mice (~9 weeks old; NCI-Frederick, Maryland, United States) by the subcutaneous injection of a suspension of 1 × 10⁶ cells/ml. When the tumors reached ~3 mm in diameter and depth (~7 days after the injection of cells), the mice received 0.25 mg/kg HPPH via tail vein injection. Following the drug-light interval of 24 h, PDT was performed and the tissue oxygenation and HPPH concentration was measured prior to and post treatment (see Figure 1a). The mice were treated on a heated water pad under anesthesia in all studies (see Figure 1b). Animal husbandry was provided by the University of Pennsylvania Laboratory Animal Resources in Association for Assessment and Accreditation of Laboratory Animal Care (AALAC)-accredited facilities according to protocol (803929) approved by the University of Pennsylvania Institutional Animal Care and Use Committee (IACUC).

Figure 1.

(a) Multi-fiber spectroscopic contact probe for the measurement of the HPPH tumor uptake. (b) Experimental setup for superficial PDT of two mice at a time.

2.2 Measurements of the tissue oxygenation prior to and post PDT

For direct measurements of the tissue oxygen saturation of hemoglobin pO₂, the point measurements were made prior to and post PDT by using an OxyLitePro 2 Channel tissue pO₂ monitor (Optronix Ltd., Oxford, United Kingdom). Then, [³O₂] was calculated by multiplying the measured pO₂ with ³O₂ solubility in tissue, which is 1.295 µM/mmHg [28–30].

2.3 Measurements of the HPPH concentration prior to and post PDT

A custom-made multifiber spectroscopy probe with multiple source-detector separations (Figure 1a) was used to measure the HPPH concentration in each individual tumor, using surface fluorescence measurements. Fluorescence signals in tumors were obtained using an excitation light of 405 nm pre- and post-PDT. The raw fluorescence spectrum was fit to the basis spectrum of HPPH and auto-fluorescence in the absence of HPPH using singular value decomposition (SVD). The attenuation of HPPH fluorescence signal due to the light absorption and scattering by tissue was corrected by applying an empirical correction factor (CF) of the following form [16, 18, 31]:

$$\mathrm{C}\mathrm{F}=\frac{C_{01}+C_{02}{\mu }_s^{\prime }}{{\mu }_s^{\prime }}·\text{exp }[(b_1+b_2{\mu }_s^{\prime })·\sqrt{3{\mu }_a{\mu }_s^{\prime }}]$$ (1)

where C₀₁, C₀₂, b₁, and b₂ are constants (2.3, −0.10, 1.37, and −0.13 respectively) determined from fitting the fluorescence SVD for phantoms with different optical absorption coefficients, μ_a and optical reduced scattering coefficients, ${\mu }_s^{\prime }$. The correction factor is specific to the probe and semi-infinite geometry set-up used for the measurements.

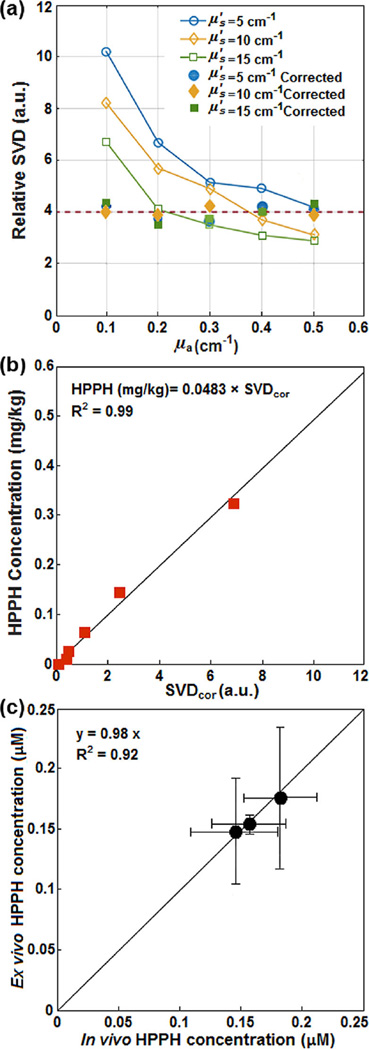
To obtain CF, a calibration curve was first determined between raw SVD and various HPPH concentrations ranging from 0–0.7 mg/kg (0–1.1 µM). Then a set of liquid phantoms were prepared with varying optical properties (μ_a = 0–0.6 cm⁻¹, ${\mu }_s^{\prime }=5–15{\text{ cm}}^{-1}$) and a constant HPPH concentration of 0.39 µM (0.25 mg/kg) using Intralipid (Fresenius Kabi, Uppsala, Sweden) as the scatterer and ink (Parker Quink, Newhaven, East Sussex, England) as the absorber. Optical properties of each phantom were measured and fluorescence spectra were obtained. SVD_cor obtained by applying CF to the raw SVD (SVD_cor = CF · SVD) from phantom experiments with the same HPPH concentration should have the same magnitude. Three separate phantoms with different concentrations of scatterers were used and fit with the equation above to produce a corrected SVD. Fluorescence measured in vivo from mice studies were corrected using Eq. (1), and absolute concentration of HPPH was obtained using the calibration curve between the SVD_cor and HPPH concentration in µM (see Figure 2a and b).

Figure 2.

(a) Fluorescence single value decomposition (SVD) amplitude for phantom experiments with different optical properties with the same HPPH concentration. (b) HPPH concentration (in mg/kg) versus corrected SVD (SVD_cor). (c) The in vivo measured photosensitizer concentration using the contact probe (based on fluorescence spectroscopy) versus ex vivo measured HPPH concentration. The solid lines in (b) and (c) are the linear fits (with intercept = 0) to the data with R² = 0.99 and 0.92, respectively.

To evaluate the accuracy of the in vivo HPPH concentrations, ex vivo measurements of the HPPH concentration were performed in another set of mice and compared with the in vivo measurements. Mice with tumors were administered HPPH at the same concentration as PDT-treated mice. After a 24 h drug-light interval, the tumors were excised and homogenized solutions of the tumors were prepared using Soluble (PerkinElmer, Waltham, Massachusetts, United States). The fluorescence of the homogenized sample was measured by a spectrofluorometer (FluoroMax-3; Jobin Yvon, Inc., Edison, New Jersey, United States) with an excitation at 405 nm and an emission range from 630 nm to 750 nm with an emission maximum at 667 nm. The photosensitizer concentration in the tissue was calculated based on the change in fluorescence resulting from the addition of a known amount of HPPH to each sample after its initial reading. As shown in Figure 2c, the in vivo measured HPPH concentration was correlated to ex vivo data using a linear fit (y = 0.98x with a goodness of fit of R² = 0.92) to examine their agreement. The error bars in Figure 2c are obtained from the standard deviation of multiple measurements made within the same sample: measurements in vivo using the fluorescence contact probe were made at 5 locations on the tumor surface (in 3 mice) at 1 mm steps. Ex vivo measurements were made with 5 samples (each roughly 50 mg in weight) from the same 3 mice.

2.4 In vivo PDT

PDT was performed by surface illumination of the tumors using a diode laser (B&W Tek, Newark, Delaware, United States) emitting an 8-Watt maximum power and 665 nm beam. As shown in Figure 1b, the light was delivered via a 140 µm-diameter optical fiber and the laser beam was collimated through a coupling lens on the end of the fiber to a 1 cm diameter beam spot over the tumor surface. A range of total in-air fluences (30 J/cm², 50 J/cm², 135 J/cm², 250 J/cm², and 350 J/cm²) including different φ_air (20 mW/cm², 50 mW/cm², 75 mW/cm², and 150 mW/cm²) and exposure times (from 333 to 7000 s) was used to induce different PDT outcome and assess the reciprocity between HPPH concentration and light dose. Two groups of tumor-bearing mice (i) with no HPPH and no excitation and (ii) with no HPPH but light illumination (φ_air = 150 mW/cm² and 2334 s exposure) were considered as controls.

2.5 Measurement of the cure index post-PDT

After PDT, width (a), length (b), and height (h) of the treated mice and controls were measured daily with slide calipers. Then, the tumor volumes (V) were calculated using V = π × a² × b/6 obtained from Refs. [7, 32]. The temporal changes of the tumor volumes were studied over 13 days (see Figure 3) and the tumor re-growth factor (k) was calculated by the best exponential fit (f (d) = e^k(d−1)) to the measured volumes over different days (d); k is the tumor re-growth factor [7]. CI was calculated from k for each treated group (k_{Treated group}) and k for the control (k_Control):

$$\mathrm{C}\mathrm{I}=1-\frac{k_{\text{Treated group}}}{k_{\text{Control}}}$$ (2)

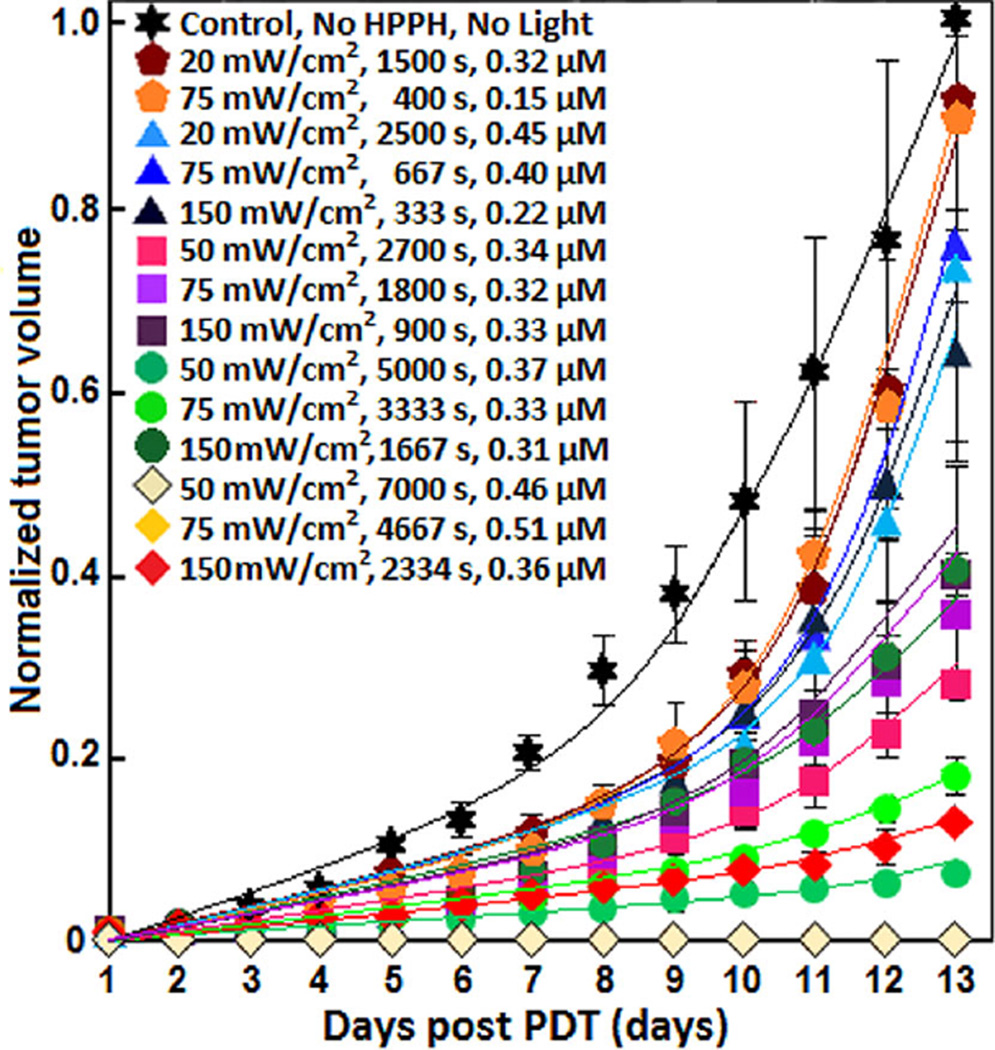
Figure 3.

Tumor re-growth versus days post treatment. Solid lines are the exponential fit (e^k(d−1)) to the data. The resulting tumor re-growth rate, k, are listed in Table 2.

2.6 Monte-Carlo simulation of the spatial distribution of φ in tumor

The diffusion theory is not valid for the simulation of the spatial distribution of φ in tissue when the lateral dimension of beam geometry becomes comparable to the mean-free-path of the photons or when the region of interest is near the air-tissue interface [33]. Therefore, the longitudinal distribution of φ for the 1 cm diameter field, μ_a = 0.6–1.0 cm⁻¹ and ${\mu }_s^{\prime }=8–11{\text{ cm}}^{-1}$ was determined using Monte-Carlo (MC) simulation (see Figure 4). Based on a previous study from our group, an empirical six-parameter (λ₁, λ₂, λ₃, b, C₂ and C₃) fitting equation was used to fit the MC data:

$$\phi /{\phi }_{\text{air}}=(1-b\cdot {\mathrm{e}}^{-{\lambda }_{1}d})(C_2{\mathrm{e}}^{-{\lambda }_{2}d}+C_3{\mathrm{e}}^{-{\lambda }_{3}d})$$ (3)

where, λ₁, λ₂, λ₃, b, C₂ and C₃ are a function of μ_a and ${\mu }_s^{\prime }$; a detailed derivation and explanation of each parameter can be found elsewhere [33].

Figure 4.

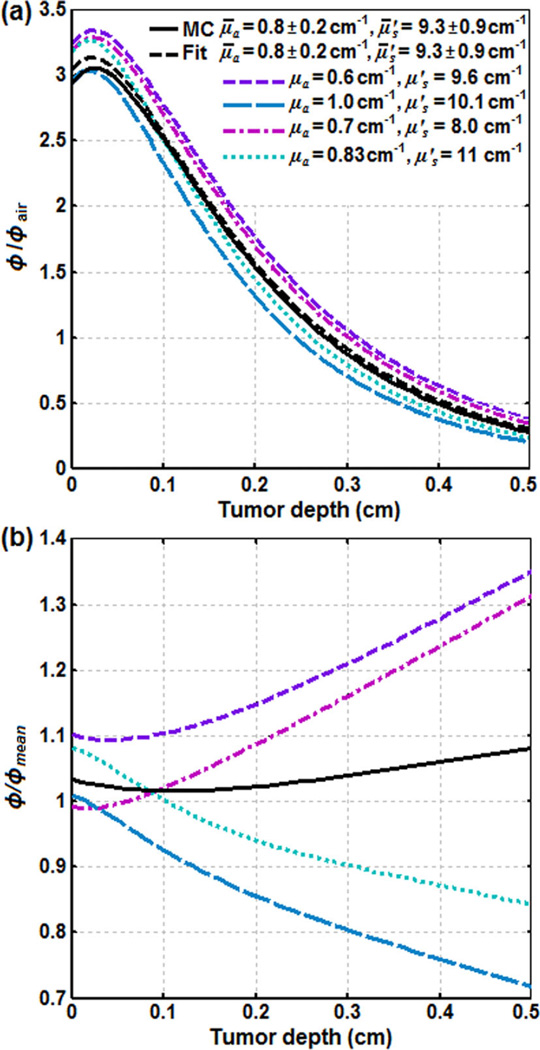
The distribution of fluence rate (φ) in tumor for a 1 cm collimated laser beam incident on the skin surface: (a) the ratio of φ and in-air fluence rate (φ_air) versus tumor depth, and (b) the ratio of φ for each condition and the mean fluence rate (φ_mean) versus tumor depth. MC and Fit are the simulations using Monte-Carlo and Eq. (3) for the mean tissue optical properties, μ̄_a = 0.8 ± 0.2 cm⁻¹ and ${\mu }_s^{\prime }=9.3\pm 0.9{\text{ cm}}^{-1}$, respectively.

These ranges of μ_a and ${\mu }_s^{\prime }$ were measured in our previous study [34] based on the monitoring of φ profile along a catheter inserted into the RIF tumors in 27 mice administered with the same amounts of HPPH [35]. Figure 4a and b present the ratio of φ and φ_air (φ/φ_air) and the ratio of φ and φ_mean (φ/φ_mean) versus tumor depth, respectively. φ_mean is the fluence rate calculated based on the Eq. (3) for the mean tissue optical properties, μ̄_a = 0.8 ± 0.2 cm⁻¹ and ${\overline{\mu }}_s^{\prime }=9.3\pm 0.9{\text{ cm}}^{-1}$ (the dashed black line). Figure 4 only presents φ/φ_air and φ/φ_mean calculated for the μ_a and ${\mu }_s^{\prime }$ with the highest deviation from μ̄_a and ${\overline{\mu }}_s^{\prime }$.

2.7 Macroscopic model for [¹O₂]_rx calculation

By simplifying and combining the energy transfer processes in PDT, a set of governing equations are produced, which describes the creation of [¹O₂]_rx [36, 37]. These equations are dependent on the three-dimensional distribution of the photosensitizer (S₀), [³O₂], φ and photosensitizer-specific reaction-rate parameters:

$$\frac{\mathrm{d}[S_0]}{\mathrm{d}t}+\left(\xi \sigma \frac{\phi ([S_0]+\delta )[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\right)[S_0]=0$$ (4)

$$\frac{\mathrm{d}[{}^3{\mathrm{O}}_2]}{\mathrm{d}t}+\left(\xi \frac{\phi [S_0]}{[{}^3{\mathrm{O}}_2]+\beta }\right)[{}^3{\mathrm{O}}_2]-g(1-\frac{[{}^3{\mathrm{O}}_2]}{{[{}^3{\mathrm{O}}_2]}_0})=0$$ (5)

$$\frac{\mathrm{d}{[{}^1{\mathrm{O}}_2]}_{\mathrm{r}\mathrm{x}}}{\mathrm{d}t}-\left(\xi \frac{\phi [S_0][{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\right)=0$$ (6)

where, [³O₂]₀ denotes the initial oxygen concentration and g represents the maximum oxygen supply rate to tissue. β represents the ratio of triplet state (T) phosphorescence to reaction between T and ³O₂. δ is the low concentration correction parameter and σ is the ratio of photobleaching to reaction between ¹O₂ and cellular targets. ξ is the initial oxygen consumption rate.

The distribution of φ was calculated for μ̄_a = 0.8 ± 0.1 cm⁻¹ and ${\overline{\mu }}_s^{\prime }=9.3\pm 0.9{\text{ cm}}^{-1}$ by using MC. Then, to obtain the corresponding temporal changes of [S₀], [³O₂] and [¹O₂]_rx, the information of φ distribution, the magnitude of β, ξ, δ, σ and the measured HPPH concentration (see Section 2.3) were passed to the time (t)-dependent differential Eqs. (4–6) for a given treatment time point. Determination of β, ξ, δ, σ, and g was done by a previous study involving partial treatment and determination of the necrosis radius of the tumor [34, 38]. The definitions and the magnitude of all parameters obtained for HPPH from the previous studies are given in Table 1. [¹O₂]_rx can change up to a maximum of 11% if the parameters are 10% over- or under-estimated (larger σ estimates smaller [¹O₂]_rx and larger g and ξ estimate larger [¹O₂]_rx).

Table 1.

Tissue optical properties, initial oxygen concentration and HPPH-specific reaction-rate parameters; some values are expressed as mean ± standard deviation.

Parameters	Definitions	Values	References
μa (cm−1)	Optical absorption coefficient	0.76 ± 0.10	[34]
${\mu }_s^{\prime }({\text{cm}}^{-1})$	Optical reduced scattering coefficient	9.32 ± 0.87	[34]
[3O2]0 (µM)	Initial tissue oxygen concentration	20.49 ± 2.38	[30]
g (µM/s)	Maximum oxygen supply rate	1.54 ± 0.90	[34]
ξ (cm−2 mW−1 s−1)	Initial oxygen consumption rate	(71.5 ± 38.3) × 10−3	[34]
σ (µM−1)	Ratio of photobleaching to reaction between 2O1 and cellular targets	(1.10 ± 5.8) × 10−5	[34]
δ (µM)	Low concentration correction	33	[11]
β (µM)	Ratio of phosphorescence to reaction between T and 3O2	11.9	[40]

All the calculations were performed using MAT-LAB R2013a (64-bit, Natick, Massachusetts, United States) software, which was run on an iMAC OSX version 10.9.5 (Processor 3.1 GHz Intel Core 17 and Memory 16 GB 1600 MHz DDR3). The detailed description of the model has been published previously [17, 29, 39].

2.8 Statistical analyses

To assess the consistency of the measurements, each individual experiment and treatment condition was independently carried out four times. Non-parametric Mann–Whitney tests were used to evaluate whether the re-growth rate of the tumors in each two groups of samples, control and treated mice, are significantly different from each other. Analyses were carried out using SPSS 14.0 software and the statistical significance was defined at p < 0.05 level (95% confidence level).

3. Results

In vivo HPPH-mediated PDT with five different in-air fluence including different φ_air and various exposure times was performed in the mouse models bearing RIF tumors. Explicit measurement of the tissue optical properties as well as the tissue oxygenation and photosensitizer concentration in tumor has been performed to rigorously quantify HPPH photobleaching, PDT dose, and [¹O₂]_rx. Table 2 summarizes all the measured and calculated quantities.

Table 2.

PDT dose, mean singlet oxygen concentration (Mean [¹O₂]_rx), tumor re-growth factor and cure index (CI) calculated for each PDT treatment condition.

In-air fluence (J/cm2)	φair (mW/cm2)	Timea (s)	Pre-HPPHb (µM)	Post-HPPHc (µM)	PDT dosed (µM J/cm2)	Mean [1O2]rx (µM)	k (1/days)	CI
30	20	1500	0.32 ± 0.20	0.24 ± 0.09	8.03 ± 5.10	0.34 ± 0.20	0.366 ± 0.012	0.04 ± 0.03
	75	400	0.15 ± 0.03	0.10 ± 0.04	3.77 ± 0.81	0.15 ± 0.03	0.372 ± 0.010	0.02 ± 0.03
50	20	2500	0.45 ± 0.07	0.30 ± 0.05	17.96 ± 2.66	0.67 ± 0.09	0.342 ± 0.013	0.10 ± 0.03
	75	667	0.40 ± 0.13	0.26 ± 0.09	16.10 ± 5.49	0.51 ± 0.13	0.365 ± 0.040	0.04 ± 0.09
	150	333	0.22 ± 0.13	0.14 ± 0.06	8.85 ± 5.37	0.28 ± 0.13	0.363 ± 0.044	0.04 ± 0.06
135	50	2700	0.34 ± 0.12	0.18 ± 0.05	30.43 ± 10.99	0.82 ± 0.28	0.292 ± 0.012	0.23 ± 0.03
	75	1800	0.32 ± 0.16	0.13 ± 0.10	28.82 ± 14.55	0.76 ± 0.36	0.318 ± 0.027	0.16 ± 0.07
	150	900	0.33 ± 0.18	0.14 ± 0.07	30.40 ± 19.23	0.72 ± 0.36	0.322 ± 0.042	0.15 ± 0.10
250	50	5000	0.37 ± 0.22	0.10 ± 0.02	48.52 ± 29.16	1.00 ± 0.58	0.186 ± 0.020	0.51 ± 0.05
	75	3333	0.33 ± 0.09	0.09 ± 0.04	43.64 ± 12.85	0.89 ± 0.25	0.245 ± 0.027	0.36 ± 0.07
	150	1667	0.31 ± 0.21	0.07 ± 0.01	42.22 ± 30.38	0.83 ± 0.55	0.298 ± 0.037	0.22 ± 0.11
350	50	7000	0.46 ± 0.10	0.10 ± 0.01	70.50 ± 16.49	1.25 ± 0.28	0.000 ± 0.000	1.00 ± 0.00
	75	4667	0.51 ± 0.13	0.08 ± 0.01	79.99 ± 27.52	1.39 ± 0.45	0.000 ± 0.000	1.00 ± 0.00
	150	2334	0.36 ± 0.17	0.06 ± 0.02	58.04 ± 29.38	0.98 ± 0.44	0.204 ± 0.017	0.46 ± 0.04
350	150	2334	0	0	0	0	0	0
0	0	0	0	0	0	0	0.380 ± 0.045	0

^aPDT exposure time

^bHPPH concentration prior to PDT

^cHPPH concentration after PDT

^dPDT dose is calculated by the time integral of the product of local photosensitizer concentration and light fluence rate (φ).

The measured spectra of tumor re-growth vs. different days post-PDT are shown in Figure 3 for the different initial HPPH concentration, delivered energy, φ_air, and exposure times. Based on the calculated statistical p-values varied from 0.001 to 0.043 using Mann–Whitney tests, all treatment conditions of 135 J/cm², 250 J/cm², and 350 J/cm² had significant control of the tumor re-growth after PDT as compared to the control mice. PDT with in-air fluence delivered at 30 J/cm² and 50 J/cm² did not significantly change the tumor re-growth rate as compared to the control mice; p-values varied from 0.244 to 0.671 using Mann-Whitney tests. CI was calculated from the Eq. (2) for each treated group. The total energy delivered at 135 J/cm² and 250 J/cm² showed partial response to treatment from 15 to 51%. CI was calculated to be 0.11 and 0.46 for the delivered energies of 50 J/cm² with 20 mW/cm² and 350 J/cm² with 150 mW/cm², respectively. As no tumor re-growth was seen for 350 J/cm² with 50 mW/cm² and 75 mW/cm² throughout the 13 day follow up, only the result for 50 mW/cm² has been presented in Figure 3. According to Figure 3, PDT using 135 J/cm², 250 J/cm², and 350 J/cm² at 50 mW/cm² was a more effective treatment than PDT administered with three times the φ_air at 150 mW/cm².

The light parameters and the measured initial HPPH concentrations were used to construct the fluence and φ effects on the photosensitizer photobleaching. The temporal changes of the HPPH concentration calculated from Eq. (4) vs. fluence at 3 mm tumor depth are shown in Figure 5a for each of the treatment conditions; fluence at 3 mm corresponds to the minimum light fluence encompassing the entire tumor with a depth of 3 mm. The calculated loss of HPPH via photobleaching (solid lines) is in agreement with those that has been measured experimentally post PDT (symbols). As shown in Figure 5b, the percentages of the photobleaching increase with increasing the total fluence and φ_air.

Figure 5.

(a) The temporal changes of the HPPH concentration versus fluence at 3 mm tumor depth for the different treatment conditions. The solid lines present the calculated changes of the photosensitizer concentration during the treatment. The symbols show the measured HPPH concentration post treatment. (b) The percentages of the HPPH photobleaching versus fluence at 3 mm tumor depth.

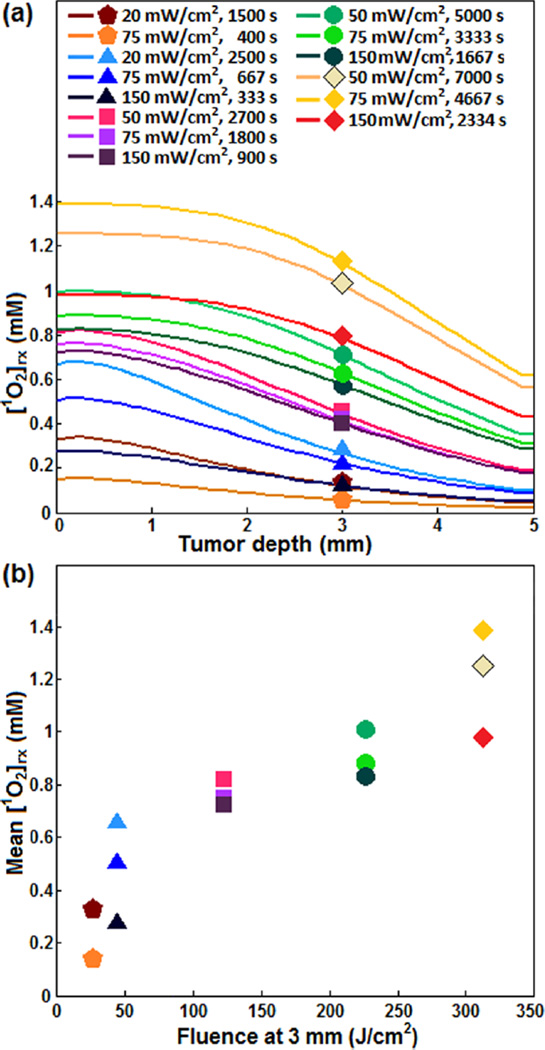
As the production of [¹O₂]_rx is critical for PDT, evaluating the distribution of [¹O₂]_rx in tumor during the treatment helps in the development and optimization of the treatment protocols. The experimentally derived photochemical parameters [34] and the initial concentration of HPPH and [³O₂]₀ were used to calculate the spatial distributions of [¹O₂]_rx in tumors during irradiation at several φ and exposure times; the result has been shown in Figure 6a. Figure 6b shows mean [¹O₂]_rx produced at a 3 mm depth inside the tumor (mean [¹O₂]_rx) versus the fluence at 3 mm; fluence at 3 mm corresponds to the minimum light encompassing the entire tumor. Although mean [¹O₂]_rx is strongly dependant on the fluence, different [¹O₂]_rx can be generated with the same fluence depending on φ_air.

Figure 6.

(a) The spatial distribution of reactive singlet oxygen ([¹O₂]_rx) in the RIF tumors calculated for different treatment conditions. (b) The calculated mean singlet oxygen (Mean [¹O₂]_rx) versus total fluence at 3 mm tumor depth.

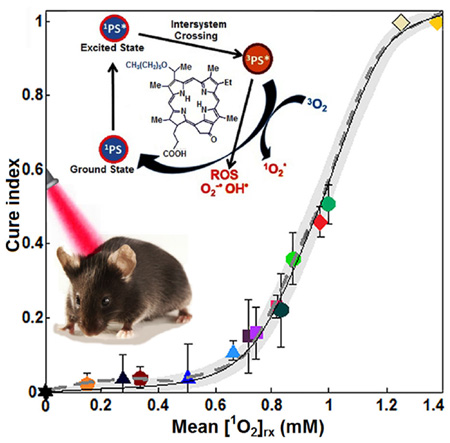
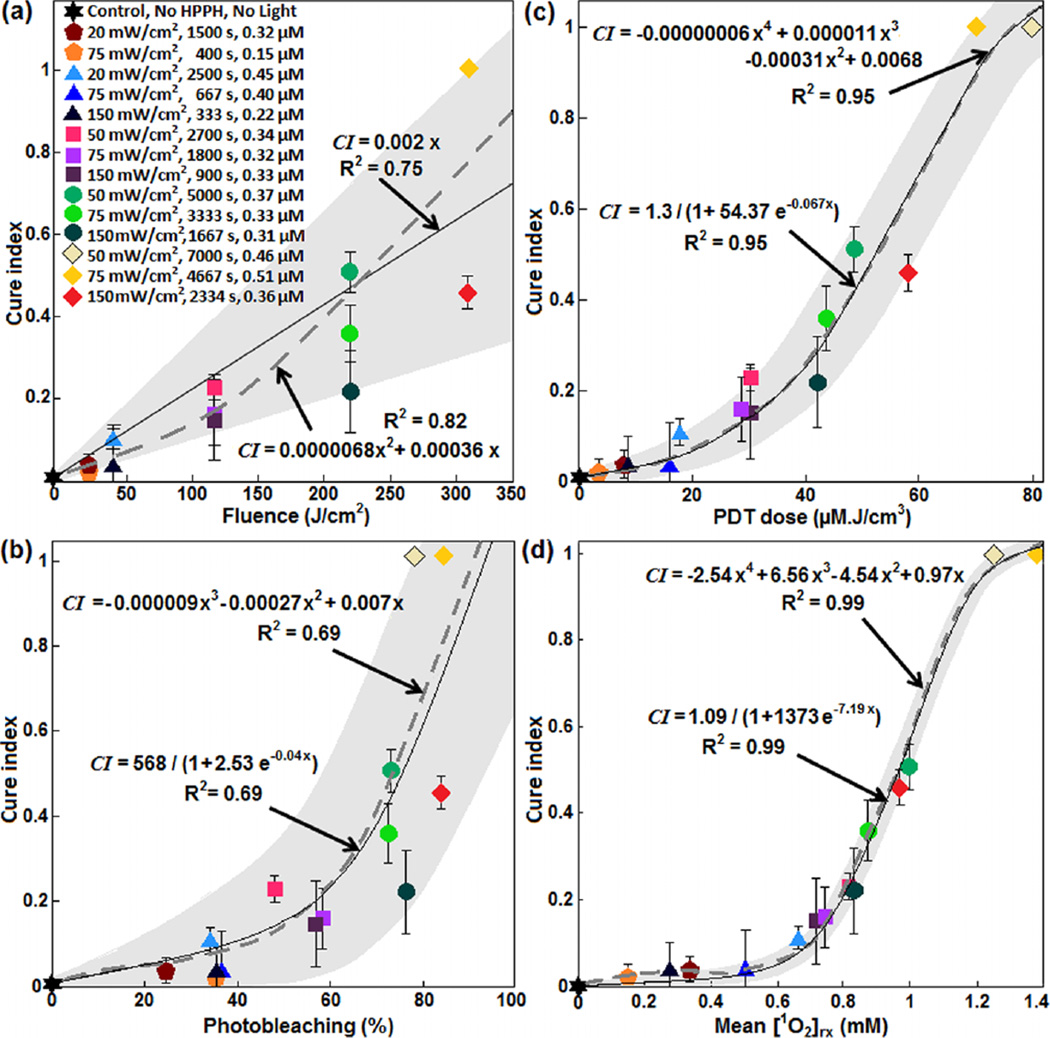
As shown in Figure 7, several dosimetric matrices, fluence, photobleaching (%), PDT dose, and mean [¹O₂]_rx were evaluated for predicting the treatment outcome. The mean CI from the four independent measurements was considered as the treatment outcome. Photobleaching was defined by the ratio of fluorescence intensity after PDT relative to that before PDT. PDT dose was calculated over the entire PDT interval for each group of mice, using the time integral of the products of φ at 3 mm tumor depth and local HPPH concentration. Then, CI was correlated to the fluence at 3 mm tumor depth, percentage of photobleaching, PDT dose and mean [¹O₂]_rx. The results have been shown in Figure 7a–d along with the best theoretical fit obtained from CI = 0.002x, CI = 568/(1 + 2.53 e^−0.04x), CI = 1.3/(1 + 54.37 e^−0.067x) and CI = 1.09/(1 + 1373 e^−7.19x) for fluence, percentages of photobleaching, PDT dose, and mean [¹O₂]_rx, respectively; the dashed line shows an independent polynomial fit. A comparison of the goodness of fit R² = 0.75, 0.69, 0.95 and 0.99 respectively for Figure 7a–c, and d and the corresponding upper and lower bounds of the fits (gray area) shows that mean [¹O₂]_rx serves as a better dosimetric quantity for predicting the treatment outcome and a clinically relevant tumor re-growth endpoint.

Figure 7.

(a) Fluence at 3 mm tumor depth, (b) measured photosensitizer photobleaching (%), (c) calculated PDT dose and (d) average singlet oxygen (mean [¹O₂]_rx) versus tumor cure index. The solid lines show the best fit to the data using functional forms CI = 0.002x, CI = 568/(1 + 2.53 e^−0.04x), CI = 1.3/(1 + 54.37 e^−0.067x) and CI = 1.09/(1 + 1373 e^−7.19x) for (a), (b), (c), and (d), respectively. The goodness of fit R² = 0.75, 0.69, 0.95 and 0.99 for (a), (b), (c) and (d), respectively. The gray area shows the upper and lower bounds of the fit with 95% confidence level. The dashed gray lines show an independent fit using polynomial curves.

4. Discussions

A series of preclinical explicit dosimetry including a range of φ and different light exposure times was performed on mice bearing RIF tumors to span a range of PDT outcomes and assess the reciprocity between HPPH concentration and light dose. Based on the finding of this study, the response of the RIF tumors to a given dose of PDT depends critically on the photosensitizer concentration as well as the total radiation energy and the φ at which the therapy is administered. Tumors of about the same size treated with identical doses of HPPH and irradiated with the identical energy exhibited different surviving fractions as φ_air was lowered. For the group of mice irradiated with energy delivered at 350 J/cm², 250 J/cm², and 135 J/cm², CI increased as the source strength was lowered from 150 mW/cm² to 50 mW/cm². For the group with a delivered energy of 50 J/cm² or 30 J/cm², CI also increased as φ_air was lowered from 150 mW/cm² to 20 mW/cm² and 75 mW/cm² to 20 mW/cm², respectively. This is in agreement with previously reported results showing that the reduced φ_air enhances the therapeutic response by extending the radius of ¹O₂ formation around a tumor capillary in multicell tumor spheroid models [41].

Several dosimetric matrices, fluence, photobleaching, PDT dose, and mean [¹O₂]_rx were evaluated as a means to estimate the outcomes of in vivo HPPH-mediated PDT; CI was considered as the treatment outcome. A comparison of the goodness of the fit and the corresponding upper and lower bounds of the fits (gray area) to the data have been presented in Figure 7. Figure 7a shows that, while fluence correlates with PDT outcome as a monotonic increasing curve, it exhibits large uncertainties as defined by the large bounds of the gray area as well as by the lower value of R² (~0.75 for linear fit and 0.82 for second-order polynomial fit). The inaccuracy of fluence alone for the prediction of PDT outcome has been reported, previously [10–12, 15, 32, 42]. Figure 7b shows that photobleaching, as defined by the ratio of fluorescence intensity after PDT relative to that before PDT, is not a better dosimetric quantity to correlate to PDT outcome compared to fluence, as evident by the lower value of R² (~0.69) and a still relatively large grey area indicating the bounds of the fit. The HPPH concentration (~0.15–0.51 µM) used clinically is much lower than δ (= 33 µM) and this may be a reason for the poor correlation of the photobleaching ratio and CI. In addition, photobleaching of the photosensitizer may also take place from non-oxygen dependant mechanisms [7, 8, 43, 44]. However, it must be considered that in photobleaching-based implicit dosimetry, a more sophisticated model than just bleaching fraction is used and the results of this paper does not mean that other methodologies of photobleaching-based implicit dosimetry is invalid. Figure 7c shows a better correlation of the PDT dose with CI with a higher value of R² (0.95) and a narrower band of gray area as compared to fluence and photobleaching ratio. Therefore, PDT dose allows for reduced subject variation and improved treatment evaluation as compared to the fluence and photobleaching. Although PDT dose accounts for both light dose and tissue photosensitizer levels, it does not account for the oxygen dependence of ¹O₂ quantum yield and thus overestimates [¹O₂]_rx in the presence of hypoxia. As a result, PDT dose does not account for the φ dependence of oxygen consumption. It is very interesting to observe that PDT dose starts to exhibit threshold dose behavior as it can be fit by a sigmoid function (S(x) = 1/(1 + e(−(x − x₀)/w₀)), where x₀ = 52.62 µM J/cm₂ and uncertainty, w₀ = 14.9 µM J/cm² (Figure 7c). This value can be converted to the absorbed dose by HPPH by multiplying by the extinction coefficient (ε = 0.108 µM⁻ cm⁻¹) which is 5.68 J/cm³. This value corresponds to 19 × 10¹⁸ photons/cm³ (by dividing the energy per photon hc/λ for λ = 665 nm). PDT dose threshold behavior has been reported in the literature and our PDT dose threshold for HPPH is smaller than that reported for aluminum chlorosulphonated phthalocyanine (AISPC 38 × 10¹⁸ photons/cm³), but is bigger than that reported for Photofrin (8.2 × 10¹⁸ photons/cm³) [41, 45, 46]. Figure 7d shows that mean [¹O₂]_rx correlates much better with CI than any other dosimetric matrices. This is the most important finding of our in vivo study since [¹O₂]_rx quantifies the total cumulative production of ¹O₂ that reacted with tissue. Mean [¹O₂]_rx is a good dose metric to combine the explicit dosimetry quantities for light fluence, photosensitizer concentration, and [³O₂]. According to the fitting equation CI = 1.09/(1 + 1373 e^−7.19x), the mean [¹O₂]_rx threshold concentration of x₀ = 0.98 mM and w₀ = 0.11 mM can be obtained. According to Table 1, PDT using 30 J/cm² and 50 J/cm² at 20 mW/cm² generated more [¹O₂]_rx as compared to the same fluence administered at higher fluence rates. PDT using 135 J/cm², 250 J/cm², and 350 J/cm² at 50 mW/cm² generated more [¹O₂]_rx than the three times larger φ_air administered at 150 mW/cm².

5. Conclusion

Based on the findings of this study, the response of the RIF tumor mice models to a given dose of PDT depends critically on the tissue oxygenation, photosensitizer uptake of the tumors as well as the total energy and φ at which the therapy is administered. Therefore, an accurate dosimetry quantity for evaluation of the treatment outcome should be able to account for all of these parameters. In this study we evaluated the efficacy and outcomes of different PDT regimens based on the calculation of the interstitial fluence, HPPH photobleaching, PDT dose and mean [¹O₂]_rx generated by individual PDT in RIF tumors. A correlation of the total fluence, photobleaching, PDT dose and mean [¹O₂]_rx with CI suggests that mean [¹O₂]_rx is the best dosimetric quantity for predicting the treatment outcome and a clinically relevant tumor re-growth endpoint. Although PDT dose is a better dosimetry quantity compared to fluence and photobleaching, the influence of [³O₂] is not completely taken into account when using PDT dose. We believe that the clinical application of PDT would be greatly facilitated by mean [¹O₂]_rx, which integrates the interactions between φ, tissue oxygenation, and photosensitizer distribution. Our results further suggest that tumors of about the same size treated with identical doses of HPPH and irradiated with the identical energy exhibited different surviving fractions as φ was increased. Therefore, φ effects must be considered as a possible source of treatment failure in PDT, and these effects should be considered in study designs that seek to compare responses among different tumor lines or photosensitizers.