An Acrobatic Substrate Metamorphosis Reveals a Requirement for Substrate Conformational Dynamics in Trypsin Proteolysis

Abstract

The molecular basis of enzyme catalytic power and specificity derives from dynamic interactions between enzyme and substrate during catalysis. Although considerable effort has been devoted to understanding how conformational dynamics within enzymes affect catalysis, the role of conformational dynamics within protein substrates has not been addressed. Here, we examine the importance of substrate dynamics in the cleavage of Kunitz-bovine pancreatic trypsin inhibitor protease inhibitors by mesotrypsin, finding that the varied conformational dynamics of structurally similar substrates can profoundly impact the rate of catalysis. A 1.4-Å crystal structure of a mesotrypsin-product complex formed with a rapidly cleaved substrate reveals a dramatic conformational change in the substrate upon proteolysis. By using long all-atom molecular dynamics simulations of acyl-enzyme intermediates with proteolysis rates spanning 3 orders of magnitude, we identify global and local dynamic features of substrates on the nanosecond-microsecond time scale that correlate with enzymatic rates and explain differential susceptibility to proteolysis. By integrating multiple enhanced sampling methods for molecular dynamics, we model a viable conformational pathway between substrate-like and product-like states, linking substrate dynamics on the nanosecond-microsecond time scale with large collective substrate motions on the much slower time scale of catalysis. Our findings implicate substrate flexibility as a critical determinant of catalysis.

Introduction

Protein function is determined by macromolecular geometry conferred by the folded state, as noted by Anfinsen nearly 40 years ago (1); however, recent years have brought fresh meaning to this paradigm with an increasing appreciation of the temporal dependence of protein structure. Proteins constantly sample varied conformational fluctuations about the time-averaged structures that we observe crystallographically or spectroscopically, and these conformational dynamics are in many cases closely coupled to protein function (2–4). Nowhere is this clearer than for enzymes, proteins evolved to accelerate biological chemical reactions. Varied examples have revealed that enzyme conformational dynamics can facilitate substrate binding, progression along the catalytic reaction coordinate, and product release (5–10). Most studies of protein dynamics in enzyme catalysis have naturally focused on conformational changes within the enzyme. However, for the many enzymes that catalyze reactions of protein substrates, an overlooked source of potentially relevant dynamics lies within the substrate.

Trypsins are serine proteases, a class of proteolytic enzymes that have been well characterized and used to dissect and understand catalysis, most often using short oligopeptide model substrates as proxies for natural protein substrates. Following formation of a noncovalent Michaelis complex, the catalytic mechanism proceeds through two sequential steps (Scheme 1) (11). In the first step, the enzyme serine nucleophile attacks the carbonyl of a substrate peptide bond, forming a covalent acyl-enzyme intermediate, and displacing the peptide product composed of residues C-terminal to the cleavage site (the “primed side” residues according to the nomenclature of Schechter and Berger (12)). In the second step, a nucleophilic water molecule hydrolyzes the acyl-enzyme, releasing the nonprimed side peptide product. Classic studies using unstructured oligopeptide substrates have shown substrate discrimination to occur at the acylation step; for specific peptide substrates, acylation is fast, and acyl-enzyme hydrolysis is rate-determining (13, 14). Much less is known about cleavage kinetics for structured protein substrates, but overall rates of catalysis are often several orders of magnitude slower than for oligopeptide substrates (15), suggesting that substrate structure may variably impede progression of the reaction pathway. Furthermore, modeling studies have implicated a requirement for local unfolding of a protein chain around the cleavage site to enable proteolysis (16). Thus, it seems plausible that substrate conformational dynamics (i.e. the dynamical behavior of a protein substrate during catalysis) may influence serine protease catalytic rates.

SCHEME 1.

An ideal model to examine protein substrate dynamics and their impact on proteolysis is provided by the canonical (Laskowski mechanism) serine protease inhibitors (17). These inhibitors are highly specific limited proteolysis substrates for their target enzymes, yet they differ from ordinary substrates in being bound many orders of magnitude more tightly and cleaved many orders of magnitude more slowly (18). They interact with an enzyme by mimicking an ideal substrate, using an exposed binding loop, which is complementary to the active site for recognition, and presenting a “reactive site” peptide bond for cleavage (19, 20). Intriguingly, short peptides that recapitulate the sequence surrounding the reactive site behave as ideal substrates, not inhibitors, and thus the slow cleavage and inhibitory nature of canonical inhibitors are conferred by structural context and perhaps consequent constraints on dynamics (21).

In studies using mesotrypsin, a trypsin isoform capable of more rapid proteolysis of canonical inhibitors compared with other trypsin family members (22–24), we have examined relative proteolytic susceptibility of a spectrum of closely related canonical inhibitors belonging to the Kunitz-BPTI⁴ family (15, 25, 26). The Kunitz domain, typified by BPTI, possesses a compact pear-shaped protein fold that is stabilized by a hydrophobic core and three conserved disulfide bonds (Fig. 1) (25). Surprisingly, despite close conservation of these structural features, different Kunitz family members vary widely in their rates of cleavage by mesotrypsin; human amyloid precursor protein inhibitor (APPI) and amyloid precursor-like protein 2 Kunitz domain (APLP2-KD) are cleaved nearly 3 orders of magnitude faster than BPTI, with substrate-like kinetics (Fig. 1) (15, 26). Mutagenesis experiments have demonstrated that sequence variation within the binding loops of these inhibitors does not fully account for their differential proteolysis rates; rather, sequence differences in the scaffold, far removed from the enzyme interface, have a profound effect on proteolysis (25). Furthermore, in a recent combinatorial protein engineering effort, we identified an APPI variant, APPI-3M, in which only three amino acid substitutions (Fig. 1A) produced a striking ∼100-fold reduction of the proteolysis rate, despite very minimal impact of the mutations on protein structure (Fig. 1B) (27). These differences in catalysis, not easily explained by sequence or static X-ray crystal structures, may be reflective of distinct protein dynamics within the Kunitz domains or at the enzyme interface.

FIGURE 1.

Homologous Kunitz domains differing in mesotrypsin cleavage rates. A, sequence alignment of select Kunitz domain substrates. The alignment highlights conserved residues in red, divergent residues in black, and engineered mutations for APPI-3M in cyan. Secondary structure elements are represented above the primary sequence by black arrows (β-strands) and red α-helix. Conserved disulfide linkages are indicated as dashed lines. The enzyme-binding loop is indicated below the sequence; P₁ and P₁′ residues, between which mesotrypsin cleaves, are underlined. B, APPI, APPI-3M engineered mutant, and BPTI all possess the characteristic Kunitz-BPTI family protein fold with compact 3D structure and three conserved disulfide linkages. P₁ and P₁′ residues flanking the scissile bond and Cys side chains are shown in stick representation. PDB codes: APPI, 3L33; APPI-3M, 5C67; BPTI, 2RA3. Rates of proteolysis for all four Kunitz domains by mesotrypsin are shown below.

In this work, we investigate the structure of the most rapidly cleaved natural Kunitz domain identified to date, APLP2-KD, in complex with mesotrypsin. Unlike prior solved Kunitz domain crystal structures, here APLP2-KD is trapped in a product-like complex, revealing a remarkable conformational transformation after cleavage. This snapshot reveals an unprecedented structural plasticity in the substrate that may be key to its comparatively rapid proteolysis, a hypothesis that we probe through both free (unbiased) and stepwise guided molecular dynamics (MD) simulations. Our results implicate conformational motions within the protein substrate as a determinant of proteolytic rates; this example shows that we must look beyond the enzyme to fully appreciate the importance of protein dynamics in enzyme catalysis.

Results

Crystal Structure of Mesotrypsin-APLP2-KD* Product-like Complex Reveals Acrobatic Conformational Change

To gain insight into the interaction between rapidly cleaved protein substrate APLP2-KD and mesotrypsin, we cocrystallized the substrate with the catalytically inactive mesotrypsin-S195A variant. The complex crystallized in the P2₁2₁2 space group with one copy of the dimeric complex in the asymmetric unit, and the structure was solved and refined to 1.4 Å resolution with the statistics described in Table 1. To our surprise, APLP2-KD in this complex displayed hydrolysis of the Arg-15–Ala-16 peptide bond. We will refer to this two-chain form of the substrate as APLP2-KD*, where the asterisk denotes a modified form of APLP2-KD cleaved at the reactive site bond (18). Clear electron density revealed the new C terminus of Arg-15, still positioned in the specificity pocket of the enzyme active site (Fig. 2A). However, as the result of a large conformational change in the Kunitz domain, primed side substrate residues 16 and 17 were disordered, whereas residue Met-18, for which only the backbone was visible, was now located >27 Å from Arg-15, near the opposite end of the molecule (Fig. 2B). Continuous electron density was observed throughout the rest of the protein substrate and throughout the mesotrypsin chain. As examination of the active site clearly showed distinct density for the mesotrypsin S195A inactivating mutation (Fig. 2A), it was initially unclear how the substrate reactive site bond had become hydrolyzed. Subsequent analysis of the enzyme preparation used for the crystallographic studies uncovered a small amount (∼0.1%) of enzymatic activity that could be quenched by serine-modifying inhibitor phenylmethylsulfonyl fluoride, revealing minor contamination with nonmutant active mesotrypsin (data not shown). Apparently, the trace amount of active mesotrypsin catalyzed complete limited proteolysis of APLP2-KD at the reactive site; the processed APLP2-KD* then bound to mesotrypsin-S195A, and this product-like complex preferentially crystallized out of solution.

TABLE 1.

X-ray data collection and refinement statistics

Data merged from two crystals were used for structure determination. Values from highest resolution shell are shown in parentheses. ND indicates CC½ for full dataset was not reported by HKL2000.

Mesotrypsin-APLP2-KD* complex
PDB code	5JBT
Data collection
Space group	P21212
Cell dimensions
a, b, c (Å)	99.01, 54.58, 56.60
α, β, γ (°)	90, 90, 90
Resolution (Å)	50–1.40 (1.42–1.40)
Rmerge	0.064 (0.231)
Rmeas	0.080 (0.278)
Rp.i.m.	0.021 (0.102)
CC½	ND (0.970)
I/σI	27.2 (6.76)
Completeness (%)	99.3 (99.8)
Redundancy	12.8 (7.3)
Refinement
Resolution (Å)	50–1.40
No. of reflections	57,667
Rwork/Rfree	16.3/19.9
No. of atoms
Protein	2125
Ligand/ion	5
Water	259
B-factors
Protein	19
Ligand/ion	35
Water	30
Ramachandran statistics
Favored (%)	98
Allowed (%)	2
Outliers (%)	0
r.m.s.d.
Bond lengths (Å)	0.0219
Bond angles (°)	2.0874

FIGURE 2.

Crystal structure of mesotrypsin-APLP2-KD* product-like complex reveals acrobatic conformational change. A, stick representation of the protein environment surrounding the active site of mesotrypsin-bound APLP2-KD*, with 2F_o − F_c map contoured at 2.0σ. Enzyme is shown in gray with catalytic triad residues Ala-195 (mutated from Ser), His-57, and Asp-102 in orange. APLP2-KD* nonprimed side residues are colored red and remain bound in the active site, including P₁ residue Arg-15, occupying the primary specificity subsite, which possesses a C-terminal carboxylate formed by cleavage of the scissile bond. Primed side substrate residues are absent from the active site. B, stick representation of the protein environment surrounding the new position of APLP2-KD* P₃′–P₅′ residues Met-18, Pro-19, and Arg-20 (yellow), with 2F_o − F_c map contoured at 1.2σ. P₁′–P₂′ residues Ala-16 and Va-l17 were not visible in density maps, presumably due to disorder. C, schematic representation of mesotrypsin-APLP2-KD* complex crystal structure (left) reveals a large conformational change undertaken by the substrate upon proteolysis; crystal structure of intact APPI complex with mesotrypsin (PDB code 3L33) is shown for comparison (right). A superposition of the two structures (intact APPI as a semi-transparent reference) highlights the acrobatic contortion of APLP2-KD* upon proteolysis, emphasizing the new conformational space occupied by the prime side residues (yellow β-strand), antiparallel β-hairpin, and α-helix.

Although subsequent extensive efforts to cocrystallize highly purified mesotrypsin-S195A with intact APLP2-KD were not successful, we are able to gain insight into the APLP2-KD* conformational change through comparisons with the structure of mesotrypsin bound to intact APLP2-KD homolog APPI (Protein Data Bank code 3L33) (25). Superposition reveals that although the enzyme is essentially static, the substrate has undergone a massive conformational change upon cleavage, in which the α-helix has rotated nearly 180° to the opposite side of the molecule, and the β-hairpin has become nearly inverted and traverses the center of the Kunitz domain (Fig. 2C). The conformational transformation has little impact on the substrate's nonprimed side residues 11–15, which remain firmly fixed at the enzyme interface with little deviation from their pre-cleavage positions. By contrast, the primed side substrate residues are evacuated from the enzyme active site cleft as a result of the conformational change.

Prior studies have suggested that dissociation of primed side residues from the enzyme active site may represent a common rate-limiting step during proteolysis of canonical inhibitors (20, 23, 28). While acyl-enzyme formation can proceed rapidly, inter- and intramolecular interactions that tether the primed side leaving group can favor peptide bond resynthesis over acyl-enzyme hydrolysis, slowing reaction progress (20, 28). The motions evidenced by the new crystal structure of cleaved APLP2-KD* appear to facilitate primed side residue dissociation from the enzyme, and thus might help to explain the more rapid proteolysis of this Kunitz domain compared with others. Notably, the only prior reported crystal structure of a post-cleavage Kunitz domain, cleaved BPTI* (where BPTI* is BPTI cleaved at the Lys-15–Ala-16 reactive-site bond) bound to rat anionic trypsin, revealed a native-like structure in which the P₁′–P₃′ residues were retained in the trypsin active site, poised for peptide bond resynthesis (29). As BPTI is proteolyzed orders of magnitude more slowly than APLP2-KD (Fig. 1), it would appear from these limited data that post-cleavage substrate dynamics may correlate with proteolysis rates. We reasoned that perhaps the conformation observed in the APLP2-KD* complex mimics a productive “open” conformation of the acyl-enzyme, required along the reaction trajectory, which promotes forward reaction progress by allowing water to enter the active site and hydrolyze the acyl-enzyme. Alternatively, the specific conformation stabilized by the crystal lattice may be merely reflective of globally increased substrate motions of APLP2-KD relative to BPTI that may accelerate proteolysis by acting at this or other steps along the reaction pathway.

Substrate Global Conformational Dynamics Correlate with Increasing Rates of Proteolysis

To gain further insight into the potential role of substrate dynamics in governing rates of proteolysis, we next employed free (unbiased) all-atom MD simulations for a series of mesotrypsin-Kunitz domain complexes. The complexes of APPI, APPI-3M, and BPTI with mesotrypsin span a broad range of known catalytic rates (Fig. 1), and for each there was an available experimental X-ray structure of the pre-cleavage Michaelis complex on which to base a starting model (23, 25, 27). Because acyl-enzyme hydrolysis and associated conformational changes have been previously postulated to limit catalytic rates (20, 23, 28), as starting points for simulations we modeled the acyl-enzymes that would be initially formed upon nucleophilic attack by mesotrypsin Ser-195, prior to any significant conformational changes involving primed side residue movement. After energy minimization, the initial positioning of the P₁′ residue in all acyl-enzyme models was consistent with the positioning of the P₁′ residue of cleaved BPTI* from the previously reported experimental structure (29). Because of the anticipated slow time scale of large substrate motions such as those evidenced in the APLP2-KD* complex, multiple long simulations (1000+ ns/replicate) were conducted for each acyl-enzyme, along with several 100–200-ns replicates for convergence. The results reported for free simulations are based on analyses of an aggregate of >20 μs of trajectory data.

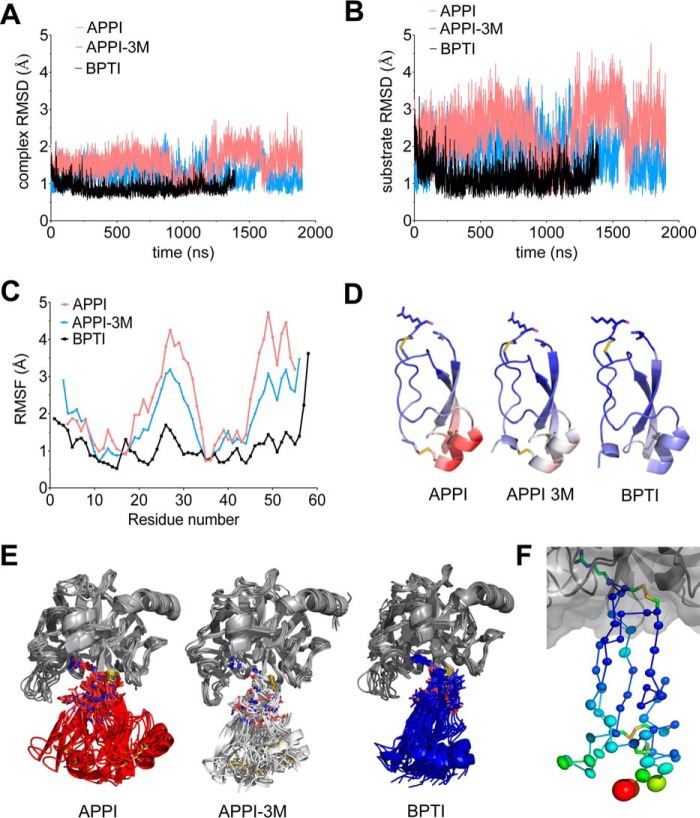
To evaluate differences among the complexes in the overall magnitude of global conformational dynamics, we aligned frames on backbone atoms and compared root-mean-square deviation (r.m.s.d.) plots of backbone atom deviation from average positions for all protein residues over the course of the simulations. We observed that the complex involving the more rapidly cleaved APPI substrate sampled a considerably wider range of global conformational states than the complexes with slower proteolyzed substrates APPI-3M or BPTI (Fig. 3A). These differences can be attributed largely to conformational fluctuations of the substrate chain, and comparisons based on r.m.s.d. calculations for the substrate backbone atoms only show yet greater differences in the range of conformational states sampled (Fig. 3B). The per residue root-mean-square fluctuation (RMSF) plots of the individual substrate chains display peak magnitudes that correlate with proteolysis rates observed biochemically; these plots also reveal which residues within each substrate demonstrate the greatest positional deviation over the duration of the simulation (Fig. 3C). By mapping the RMSF values onto the protein structures, we observed that the positional fluctuations of the largest magnitude were evidenced by the α-helix and β-turn regions of the substrate, distal to the point of contact with the enzyme (Fig. 3D). These observations could result from large local conformational fluctuations within these elements of the Kunitz domain secondary structure or, alternatively, from changes in orientation of the substrate at the enzyme interface, where the apparent magnitude of distal fluctuations might be amplified by their greater distance from a pivot point or hinge region. To distinguish between these possibilities, we superposed selected frames from each MD simulation representing a subset of structures with the greatest r.m.s.d. relative to the positional average (Fig. 3E). These superpositions confirm the second phenomenon; the substrates appear to undergo a rocking or swinging type of motion relative to the enzyme, resulting in large positional translations of residues at the base of the Kunitz domain, although the structural motifs within the domain remain comparatively rigid.

FIGURE 3.

Global substrate conformational dynamics correlate with increasing rates of proteolysis. A, r.m.s.d. plots calculated from the MD simulations utilizing backbone atoms (NC_αC) over all residues in the acyl-enzyme complexes reveal differential magnitude of global conformational dynamics. Amplitudes of backbone atom deviation from average positions vary following the pattern APPI > APPI-3M > BPTI, which coincides with the proteolytic susceptibility of these substrates from most to least rapidly cleaved by mesotrypsin. B, r.m.s.d. plots calculated for backbone atoms (NC_αC) of the substrate chain alone show the same trend as in A but with larger amplitudes of atomic deviation, showing that the global conformational dynamics of the complexes are largely driven by movements involving the substrates. C, RMSF plots from MD simulations analyzing substrate-only backbone atoms (NC_αC) per residue reflect the magnitude of positional fluctuations between residues of the different substrates. Peak heights of protein regions showing greatest fluctuations correlate with observed proteolytic rates (APPI > APPI-3M > BPTI). D, positional RMSF values from C are shown mapped onto the protein structure of each substrate. Blue-white-red spectrum indicates regions of low, intermediate, and high positional deviation. E, superpositions show a selection of mesotrypsin-substrate complexes representative of the global conformational deviations observed in the MD simulations. The largest displacements were manifested by the distal (bottom) regions of the substrates, due to alterations in the relative positioning of enzyme and substrate at the molecular interface. F, anisotropic displacement parameters of BPTI from a 1.3 Å anisotropically refined structure of a mesotrypsin-BPTI complex (3P95) reveal largest displacements at the base of BPTI and directional displacement tendencies consistent with the global motions captured by MD, as is most apparent for the β-turn residues at the lower left corner. Thermal motion for Cα atoms of BPTI is shown as thermal ellipsoids colored according to the equivalent isotropic B-factors ranging from blue (smallest) to red (largest).

To determine whether experimental evidence from high resolution crystal structures might corroborate the presence of such quasi-rigid body motions in trypsin complexes with intact Kunitz domains, we examined 3P95, a 1.3-Å structure of mesotrypsin bound to a BPTI variant (30), and 4Y0Y, a 1.25-Å structure of bovine trypsin bound to BPTI (31). Both structures were previously refined with full anisotropic treatment of atomic displacement parameters. From comparison of full anisotropic to TLS models and from Rosenfield analysis (32), we found evidence of quasi-rigid body motion of substrate and enzyme chains, although there did remain residual displacements unaccounted for by the rigid body treatment (data not shown). The BPTI molecules in these structures showed the greatest magnitude of displacements at the bottom of the Kunitz domain distal from the enzyme, and Cα thermal ellipsoids, especially in the β-turn region, show directional displacements consistent with the directional swinging captured in the unbiased MD simulations (shown for 3P95 in Fig. 3F; results with 4Y0Y were similar). These analyses offer experimental support for the types of global motion observed in our free MD simulations, albeit on a smaller scale constrained by the crystal lattice.

To gain insight into local dynamics of substrate residues nearer to the intermolecular interface that may propagate into these global conformational fluctuations, we next mined the MD data to extract temporal changes in substrate chain φ and ψ angles over the course of the simulations. These analyses (data not shown) revealed some of the greatest differences in backbone conformation dynamics between the substrates to be concentrated in the nonprimed side of the binding loop. Ramachandran plots of substrate residues Gly-12 and Pro-13 reveal substantial differences in the distribution of backbone conformations for these residues, coinciding with a much more diverse ensemble of distinct conformational states for Pro-13 and the Cys-14–Cys-38 disulfide bond in APPI compared with APPI-3M or BPTI (Fig. 4). We anticipate that greater flexibility in this region of the APPI binding loop likely contributes to the broader ensemble of global conformational states accessed by the APPI acyl-enzyme complex on the nanosecond-microsecond time scale (Fig. 3). The correlation between global substrate motion on the microsecond time scale and proteolysis rates occurring much more slowly suggests that fast substrate dynamics may represent an integral determinant of proteolytic susceptibility, perhaps by facilitating access to rarer conformational states such as that observed in the APLP2-KD* complex crystal structure.

FIGURE 4.

Local backbone dynamics of nonprimed substrate residues facilitate global dynamics. Ramachandran plots analyzing φ and ψ angle distributions over the course of MD simulations for substrate residues Gly-12 and Pro-13, the P₄ and P₃ residues, respectively, reveal distinctions between the different substrates that correlate with both global dynamics and proteolysis rates. Rapidly cleaved APPI (top row) shows a broader conformational distribution at Pro-13 and the Cys-14–Cys-38 disulfide bond. Slowly cleaved BPTI (bottom row) reveals different preferred backbone conformations for Gly-12 and Pro-13 and a tighter conformational distribution. APPI-3M (middle row), an APPI mutant with BPTI-like resistance to proteolysis, shows a shift in backbone conformation preferences and conformational distributions toward those manifest by BPTI. Structural representations on the right depict the wide range of conformations adopted by Pro-13 and the Cys-14–Cys-38 disulfide bond in APPI (pink), and the comparative rigidity of these residues in APPI-3M (blue) and BPTI (green). Ramachandran plots were generated in VMD, and structure figures were generated in PyMOL.

Substrate Primed Side Local Conformational Dynamics Do Not Correlate with Rates of Proteolysis

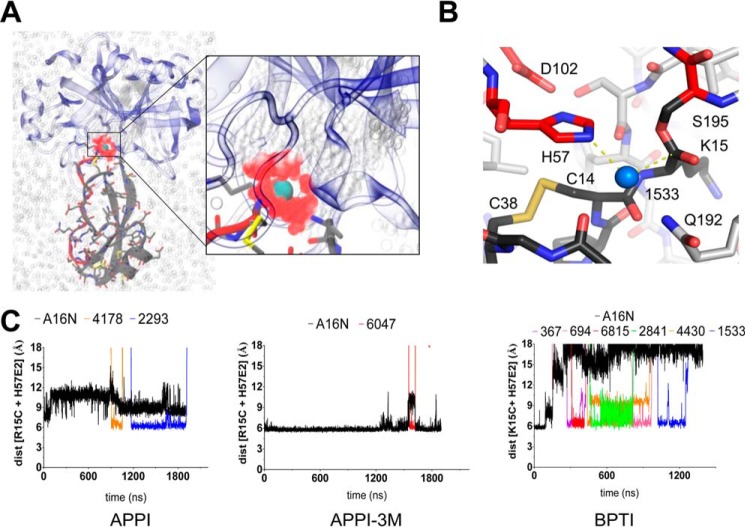
Because prior work has implicated the spatial retention of primed side leaving group residues by the acyl-enzyme as a likely feature contributing to the slow proteolysis of Kunitz domains and other canonical inhibitors (20, 23, 28, 29), we next examined the movements of P₁′ substrate residue Ala-16 throughout the MD simulations. Distance between Ala-16(N) and Arg/Lys-15(C), which is spatially fixed in the active site by the covalent acyl bond, was plotted as a unidimensional reporter of Ala-16 motion (Fig. 5A). Contrary to our expectations, the BPTI substrate showed the most dynamic Ala-16 behavior despite possessing the slowest cleavage rate. Furthermore, scatter plots examining global substrate r.m.s.d. (as measured in Fig. 3B) versus Ala-16 r.m.s.d. revealed that the local dynamics of primed side residues do not correlate in a consistent manner with the larger global motions (Fig. 5B). Thus, the impact of global dynamics on reaction rate does not appear to be mediated via any influence on the local motions of primed side residues on the nanosecond-microsecond time scale.

FIGURE 5.

Local dynamics of cleaved substrate primed side N terminus are independent of global dynamics and proteolysis rates. A, P₁′ residue Ala-16 motion is plotted as a function of distance between the terminal amine and P₁ residue Arg/Lys-15 carbonyl carbon over the duration of MD simulations for each substrate. Magnitude of Ala-16 movement (BPTI > APPI > APPI-3M) does not correlate with the biochemical proteolysis rates observed (APPI > APPI-3M > BPTI), suggesting that local Ala-16 dynamics do not strongly influence substrate proteolysis rates. B, scatter plots of Ala-16 local dynamics (x axis) from A versus global substrate dynamics (y axis) from Fig. 3B for the individual substrates illustrate the absence of consistent correlation between global and local primed side substrate motion. C, structural context of Ala-16 motion was examined in the BPTI simulation. The Ala-16 amine initial position is defined by close proximity to the Lys-15 carbonyl carbon (distance in black) and His-57(Nϵ2) (distance in gray). Local conformational motions over the duration of the simulation carry Ala-16 to a new position stabilized by H-bonds with His-57 and Tyr-59 carbonyl oxygens (distances in blue and red, respectively). Call-out boxes show representative structures illustrating the transition. D, unlike the large local motions observed for Ala-16 (plotted in black and gray as in C), the environment of P₃′ residue Ile-18 is little changed over the course of the BPTI simulation. H-bonding distance between backbone atoms of Ile-18 and Tyr-35 in the adjacent β-strand (gold and green) are maintained throughout the simulation, demonstrating that the BPTI scaffold structure is not perturbed by local Ala-16 dynamics. E, structural superposition of representative MD frames from the BPTI simulation illustrate how Ala-16 pivots and translates independently of larger scaffold motion.

Closer analysis of the simulation involving BPTI, in which Ala-16 was observed to migrate furthest from its initial position, provides additional insight into the nature of the primed side motion. As Ala-16 drifts from its initial position defined by key contacts with Lys-15 and His-57, it adopts an alternate position stabilized by contacts with the backbone carbonyls of His-57 and Tyr-59 (Fig. 5C). By contrast with the contacts defining the initial position of Ala-16, which are rapidly lost as the simulation proceeds, hydrogen bonds formed between backbone atoms of Ile-18 and Tyr-35 on the adjacent β-strand are maintained throughout the duration of the simulation, demonstrating scaffold integrity and stability (Fig. 5D). By superposing a series of frames illustrating the conformational shift in the primed side residues, we see that first Ala-16 rotates about ψ until the amine points away from the acyl bond, and then the residue translates to its new favored position; this shift requires adjustments only in residues 16–17, and it is not connected to global motions affecting the complex (Fig. 5E). Similar rotational motion was observed in the APPI simulation, but in this case the methyl side chain of Ala-16 remained in closer proximity to the acyl carbonyl bond.

Because MD simulations are conducted in a hydration box to recapitulate the native aqueous environment, they can provide information about the movement of water as well as protein atoms, enabling us to evaluate whether incursion of water into the active site could plausibly limit the catalytic rate. Previous structural studies have revealed the path taken by a hydrolytic water molecule during trypsin catalysis (14), and they have demonstrated through reconstruction of the reaction coordinate that the substrate P₁′ leaving group must be displaced prior to acyl-enzyme hydrolysis (29). To identify water molecules in the simulations that might meet geometric criteria to become “hydrolytic” waters, we initially searched for waters that moved to within 3.5 Å of the Lys/Arg-15 carbonyl carbon during the simulations, finding multiple waters in all simulations (shown for the APPI complex in Fig. 6A). To increase the stringency of the screen, we looked for waters that simultaneously approached within 3.5 Å of the Lys/Arg-15 carbonyl (the point of nucleophilic attack in the deacylation reaction) and the enzyme His-57(Nϵ2) (the activating base in the reaction) (Fig. 6B). We found water occupancy to be very common whenever the Ala-16(N) or methyl side chain drifted from the site; although some waters occupied a potentially hydrolytic position for only a few frames, others persisted with residence times of up to hundreds of nanoseconds (Fig. 6C). The simulations reveal facile incursion of water into the hydrolytic position on the nanosecond-microsecond time scale, whereas catalytic turnover of these substrates by mesotrypsin occurs on a time scale of seconds to minutes. Furthermore, local dynamics facilitated solvent access most effectively in the simulation involving the BPTI complex, the slowest cleaved among the three complexes evaluated. Together, these data argue against physical exclusion of water by the primed side leaving group residues as a determinant of proteolysis rates of these substrates by mesotrypsin.

FIGURE 6.

Incursion of potentially hydrolytic water molecules into the active site is not rate-limiting. A, solvent hydration box surrounding the mesotrypsin-APPI substrate complex is shown; zoom-in panel shows the Arg-15 carbonyl carbon (green sphere) with waters that satisfy the 3.5 Å distance criterion at any point throughout the duration of the simulation colored in red. B, representative structure is shown for a water (water 1533) that met geometric criteria for nucleophilic attack geometry, simultaneously approaching within 3.5 Å of the Lys-15 carbonyl C and mesotrypsin His-57(Nϵ2) in the BPTI acyl-enzyme simulation. C, distance versus time plots show entry and residence time for potential hydrolytic waters that met geometric criteria for 50 ns or longer in each simulation. Water O and Ala-16 N positions are plotted as summed distances of these atoms to (i) Lys/Arg-15 carbonyl C and (ii) His-57(Nϵ2).

One caveat to the above conclusion is that in the acyl-enzyme starting models for the simulations, Ala-16(N) was by default modeled in the fully protonated state, whereas in the course of the proteolytic reaction (Scheme 1), upon acyl-enzyme formation, the leaving group amine would initially be uncharged until equilibration with solvent. Potentially, the initially formed uncharged amine terminus might be retained more stably in the active site, shielded from charge equilibration, and demonstrate local dynamics distinct from a protonated N terminus. To confirm the robustness of our results and interpretation, we replicated all three long (∼2 μs) simulations for APPI-, APPI-3M, and BPTI-acyl-enzymes using new starting models in which the Ala-16 free amine termini remained uncharged. In general, the replicate simulations reconfirmed the greater magnitude of global conformational dynamics in the APPI acyl-enzyme relative to APPI-3M or BPTI (data not shown). As in the original simulations, for APPI and BPTI, Ala-16 rapidly drifted from its starting point to alternative positions further from the acyl bond, whereas in APPI-3M, Ala-16 remained in proximity to the acyl bond for the full 1800-ns simulation. Thus, irrespective of the charge state of the Ala-16 N terminus, the local dynamics surrounding this residue do not consistently correlate with substrate proteolysis rates. Our analyses support the interpretation that Ala-16 motions on the nanosecond-microsecond time scale are not connected to larger global motions affecting the complex and are most likely unrelated to the differential cleavage rates of these Kunitz family substrates.

Distinct Hydrogen Bond Does Not Govern Global Conformational Dynamics or Rates of Proteolysis

Despite the 100-fold faster rate of proteolysis of APPI relative to APPI-3M, and the corresponding striking differences in global conformational dynamics (Fig. 3), these substrates differ at only three amino acid residues (Fig. 1A), potentially enabling us to dissect the structural basis for dynamic and biochemical differences. Our previously solved crystal structure of APPI-3M in complex with mesotrypsin identified a specific hydrogen bond between the carbonyl of Val-34 and Thr-11(Oγ) (Fig. 7A) (27), also evident in structures of BPTI, but absent in the rapidly cleaved APPI, suggesting that this stabilizing contact might represent a determinant of proteolysis rates for these substrates. To test this hypothesis, we generated mutants of APPI-3M and BPTI with Thr-11 substituted with Val, a sterically similar residue that lacks the ability to form a hydrogen bond. We determined proteolytic cleavage rates by mesotrypsin using previously described HPLC assay methods (15, 23), and we also conducted long (1–2 μs) all atom acyl-enzyme MD simulations of these substrates with mesotrypsin. The enzyme kinetics experiments reveal that the hydrogen bond-null mutants are cleaved at similar rates as their hydrogen bonding counterparts (Fig. 7B), and the MD simulations likewise show conformational fluctuations that very closely mirror results with the corresponding nonmutant substrates (Fig. 7C). Although this hydrogen bond turns out not to be a significant stabilizing factor in controlling either the dynamics or the proteolytic susceptibility of the Kunitz domain substrates, the close concordance of biochemical and MD data provides further support for the robustness and relevance to catalysis of dynamic behaviors observed in the simulations. These data further support the premise that global substrate dynamics and reaction rates are integrally linked.

FIGURE 7.

Elimination of scaffold-stabilizing H-bond has minimal impact on cleavage rates and substrate dynamics. A, structural overlay shows enzyme-binding loops of APPI (pink, PDB code 3L33) and APPI-3M (blue, Protein Data Bank code 5C67) with engineered mutations shown in green and the H-bond formed in APPI-3M between Thr-11(Oγ) and Val-34 carbonyl O shown as a yellow dashed line. B, measured hydrolysis rates of native and H-bond-null mutants (APPI-3M-T11V and BPTI-T11V) are tabulated, showing average ± S.D. from independent experiments performed in triplicate. Similar hydrolysis rates were found for H-bond-null mutants and their H-bonding analogs, revealing that the presence of this H-bond does not strongly impact proteolysis rates. C, RMSF plots from MD simulations show per residue backbone atom (NC_αC) fluctuations from average positions for each substrate chain. Positional fluctuations of H-bond-null mutants very closely mirror those of their H-bonding analogs, showing that this H-bond has minimal impact on global substrate dynamics.

Molecular Dynamics Simulations with Complementary Biasing Approaches Recapitulate the Substrate Conformational Change upon Cleavage

Conformational dynamics observed in free MD simulations were primarily limited to rocking motions of substrate relative to enzyme (Fig. 3D) and localized excursions of substrate-primed side residues (Fig. 5); on the nanosecond-microsecond time scale, we observed no large reorganizations of substrate secondary structure such as were captured in the APLP2-KD* product-like complex crystal structure (Fig. 2). We anticipate that the large motions responsible for this divergent conformational state must occur on much longer time scales. Importantly, the time scale of proteolysis is also much slower (seconds or longer), and thus if proteolysis rates are limited by substrate conformational dynamics, as suggested by our correlative data, then it is these slower motions, controlling access to rarer conformational states, that would directly impact rates.

To gain insight into possible pathways of transition from a native-like substrate conformation to the APLP2-KD* form observed crystallographically, we again employed molecular modeling and MD simulations, using the mesotrypsin-APPI acyl-enzyme starting model. Because unbiased MD simulations over such long time scales (perhaps seconds of simulation) were unfeasibly costly in terms of computational time, we did not apply the canonical statistical mechanical ensembles, but rather we employed other user-defined biased ensembles to accelerate productive exploration of the most relevant conformational space. We individually evaluated a variety of enhanced sampling approaches with biased ensembles, including Maxwell's demon MD (MdMD) (33, 34), targeted MD (TMD) (35–37), replica-exchange MD (REX) (38–40), and steered MD (SMD) (41–43), for their capability to guide the substrate from initial to target (APLP2-KD*-like) conformation. Throughout the various strategies, we used Cα r.m.s.d. measurements between homologous residues of the APPI acyl-enzyme and a target acyl-enzyme model, based on the mesotrypsin-APLP2-KD* crystal structure, to gauge progress toward the conformational transition end point.

No single MD approach proved capable of completing the full conformational transition or of reducing r.m.s.d. by >50%, perhaps due to the complex changes in topology that require partial unfolding of the Kunitz domain. Ultimately, however, we were successful in modeling the complete transition by using a staged biasing protocol. Biasing methods first were ranked based on the r.m.s.d. shift accomplished by each as a stand-alone method, and then the methods were employed in sequence to sample excursions along possible pathways between the two states. The staged biasing protocol started with Maxwell's demon MD, progressed through targeted MD, replica-exchange MD, and finished with two stages of steered MD, the first applying steering forces throughout the entire structure, and the final stage applying forces only to a subset of homologous atoms within a specific loop (Fig. 8; supplemental Movie S1). Maxwell's demon MD quickly traversed >45% of the initial r.m.s.d. needed to reach the final conformation, during which time the primed side residues fully dissociated from the enzyme surface, and the α-helix swiveled to a new position. In targeted MD, the r.m.s.d. again narrowed considerably, as the β-turn became inverted and primed side residues reached the bottom of the substrate structure, distal to the enzyme interface. Further progress was next made during replica-exchange MD, in which the substrate residues that form the β-strands and β-turn motif (yellow and green in Fig. 8 and supplemental Movie S1) continued to sample a wide variety of loop conformations. However, a major barrier to progress appeared to have been reached, wherein this region of β-structure was stuck to the left of residues 5–14 (red as viewed in Fig. 8 and supplemental Movie S1); further progress would require the β-turn segment to pass above the α-helix and between the red and blue segments, in a maneuver that we dubbed “threading the needle.” This significant change in domain topology was hindered by the constraints of disulfide bonds linking Cys residues 5–55, 14–38, and 30–51. In the final stage of the protocol, steered MD identified a conformational pathway that traversed this change in topology by applying gentle directional forces to the backbone atoms of the two conflicting loops, greatly accelerating the discovery of a possible pathway between the two states, and a close approximation of the target structure was ultimately achieved (Fig. 8; supplemental Movie S1). Whereas the initial r.m.s.d. between analogous substrate residues in the starting model and target was greater than 25 Å, the final substrate coordinates in the simulation closed the gap to an r.m.s.d. of about 2 Å.

FIGURE 8.

Molecular dynamics simulations with complementary biasing approaches model the substrate conformational change upon cleavage. A staged biasing protocol, employing a mosaic of biasing ensembles, was used to model the structural reorganization of the substrate upon proteolysis from an initial native-like acyl-enzyme structure to a final target acyl-enzyme structure similar to the mesotrypsin-APLP2-KD* crystal structure. The r.m.s.d. plot shows the stepwise convergence of the structural model toward the target structure, as assessed by center of mass measurements from backbone atoms of homologous residues. Snapshots along the trajectory illustrate intermediate conformational excursions of the substrate at each stage of the complementary biasing protocol. The initial MdMD approach plateaued after traversing ∼45% of the r.m.s.d.; subsequent biasing approaches TMD, REX, and SMD achieved further stepwise progression toward the final state. Inset panel shows superpositions of initial model versus target structure (left) and final conformational state versus target structure (right), illustrating convergence over the staged biasing protocol from an initial r.m.s.d. for substrate of >25 Å to a final r.m.s.d. of ∼2 Å. Substrate target conformations are shown as semi-transparent schematics for reference.

Closer examination of local substrate motions involved in threading the needle revealed substantial conformational deviations in P₄ and P₃ residues Gly-12 and Pro-13, as the loop composed of residues 6–13 flexed outward and β-turn-β residues 22–30 passed through the circular opening (Fig. 9, A and B). Comparison of the nonprimed side binding loop dynamics in the simulations with the anisotropic displacement parameters from the APLP2-KD* crystal structure reveals certain similarities (Fig. 9C). We find experimental evidence for the side-to-side displacements of the Cys-38–Cys-14 disulfide bond, and for anisotropic displacements of Gly-12 and Pro-13 atoms that are suggestive, on a smaller scale, of the directional motions of these atoms in our simulations. This comparison offers experimental corroboration for the directional preferences of the binding loop dynamics predicted computationally. Notably, residues Gly-12 and Pro-13 also revealed differential dynamic tendencies between Kunitz domain substrates on the nanosecond-microsecond time scale in unbiased simulations, correlating with cleavage rates (Fig. 4). Plausibly, the greater flexibility of these residues on the fast time scale in more rapidly cleaved substrates may be permissive for energy barrier crossing to achieve rare conformational states, such as that found in the mesotrypsin-APLP2-KD* structure, on the slower time scale of catalysis.

FIGURE 9.

Local backbone dynamics of nonprimed substrate residues facilitate loop reorganization in conformational transition to APLP2-KD*-like structure. Coupled motions involving nonprimed side residues Gly-12 and Pro-13 coincide with threading the needle in the transition pathway identified by the staged biasing protocol. A, views of substrate from frames along staged biasing trajectory highlight the crossing of β-turn residues 24–27 (yellow) behind the loop composed of residues 6–13 (red/orange shades). Times indicated correspond to the relative time on the x axis from Fig. 8. B, superposition of frames from A highlights the large positional deviation of nonprimed side residues Gly-12 and Pro-13, as well as the Cys-14–Cys-38 disulfide bond. Colors are as shown in A: 112 ns, brick red; 115 ns, red; 119 ns, orange; 160 ns, light orange. C, anisotropic displacement parameters of APLP2* from the mesotrypsin-APLP2* complex (5JBT), viewed as thermal ellipsoids from a similar angle as the simulation frames in A and B, reveal anisotropic side-to-side displacement of the Cys-14–Cys-38 disulfide bond and of Gly-12 atoms, while atoms of the Pro-13 side chain show diffuse diagonal displacements, reminiscent of the dynamics captured in the conformational pathway modeled by steered MD (A and B).

Discussion

Many studies over the past 2 decades have demonstrated important roles of conformational dynamics in enzymatic processes, facilitating a better understanding of how enzymes operate (5–10). Enzyme mechanisms once perceived to be rate-limited purely by chemical steps have in some cases been shown to be controlled by a hierarchy of protein dynamics; protein sequence and structure dictate intrinsic fast dynamics, which in turn propagate to large collective motions controlling catalytic progress (4). In the classic example of adenylate kinase, Kern and co-workers (5) found that catalytic rate is determined by a slow lid-opening event, influenced by fast thermal fluctuations in hinge regions, thus linking dynamics across different time scales to catalysis (44). The impact on catalysis of conformational dynamics within protein substrates has not to our knowledge been previously explored, but it represents an additional potential mechanism by which protein dynamics may influence enzymatic rates. Here, we have used free MD simulations to study nanosecond-microsecond conformational dynamics of a series of mesotrypsin-substrate systems, finding that fast substrate dynamics, both globally and within a localized hinge region, correlate with proteolysis rates. We further have solved the crystal structure of a mesotrypsin-APLP2-KD* product-like complex, which reveals a surprising degree of conformational plasticity post-cleavage in this rapidly proteolyzed substrate. Using an MD-staged biasing protocol, we have succeeded in mapping one possible pathway of conformational transition from the substrate-like to product-like state. Intriguingly, we found that energy barrier crossings in this pathway appeared to be facilitated by local motions in the same nonprimed residue hinge region. Our results strongly suggest that substrate dynamics facilitate catalytic turnover in Kunitz domain proteolysis by mesotrypsin, and they hint at potential connections between fast (nanosecond-microsecond) substrate dynamics, slow sampling of rarer conformational states, and the time frame of catalysis (seconds and longer).

MD simulations offer a reliable computational approach for studying molecular motions on a spectrum of time scales, but they currently remain limited by the computation time required to model macromolecular systems on the millisecond and longer time scales of many biological processes (45). Impressive computational advances have led to characterization of the native-state dynamics of BPTI on the nanosecond-millisecond time scale (46) and to detailed elucidation of trypsin dynamics involved in binding to small molecule inhibitor benzamidine on the nanosecond-microsecond time scale (47, 48). Nevertheless, adequate sampling of our acyl-enzyme systems on the catalytic time scale of second to minutes remains out of reach to current free MD capabilities. To model such long time scale structural transitions, a variety of MD algorithms has been developed to enhance sampling capabilities and to accelerate the discovery of viable pathway excursions between two states (49). Here, we employed several enhanced sampling methods that took advantage of experimental data from our mesotrypsin-APLP2-KD* crystal structure, which revealed a large post-cleavage conformational change in the substrate. By integrating complementary biasing approaches, we succeeded in modeling these large collective motions in the substrate, which required the surmounting of high energy barriers and are anticipated to take place on the slow time scale of mesotrypsin proteolysis.

Proteolysis of Kunitz domains by mesotrypsin is slow compared with most enzymatic reactions (seconds to minutes) (15, 23, 26), and proteolysis of these substrates by other trypsins, toward which they act as inhibitors, is remarkably slower yet (days to years) (15, 23, 50). Constrained dynamics during cleavage of these and other canonical serine protease inhibitors have been linked to their relative proteolytic resistance (20, 51, 52). For cleavage of chymotrypsin inhibitor 2 by subtilisin, we found that acylation occurred rapidly (within milliseconds) but reversibly, leading to an equilibrium favoring the intact peptide bond, and that a later step presumed to be acyl-enzyme hydrolysis was rate-limiting (20, 28). Conservation of active site geometry across multiple families of serine proteases and canonical inhibitors suggested that this kinetic mechanism was likely to be conserved (20). Subsequent structural investigations of trypsin reaction intermediates and complexes with intact and cleaved Kunitz domains have allowed reconstruction of the reaction coordinate (14, 23, 29); these studies have lent support to the hypothesis that retention of primed side (leaving group) substrate residues in the active site promotes peptide bond resynthesis and slows acyl-enzyme hydrolysis. A crystal structure of a reactive site-cleaved inhibitor from another family of canonical/Laskowski mechanism inhibitors, in this case in an inhibitory complex with a metallopeptidase, likewise demonstrated retention of primed side residues in the active site (53), suggesting that this inhibitory mechanism for slowing catalytic turnover generalizes even beyond the serine proteases.

In light of this previous work, our present results from free MD simulations, showing lack of correlation between primed side substrate dynamics and cleavage rates (Fig. 5), along with facile incursion of water into the active site on the nanosecond time scale (Fig. 6), are somewhat surprising. Our results clearly implicate substrate dynamics in determining proteolysis rates, but the specific rate-determining step(s) and precise mechanism by which dynamics control rates are unclear. It may be that for the specific case of cleavage by mesotrypsin, the rate-determining step is shifted from deacylation to acylation; this would be consistent with evidence that mesotrypsin accelerates canonical inhibitor cleavage via mutations that disrupt primed side substrate interactions, facilitating acyl-enzyme hydrolysis (23, 24, 54). Alternatively, the energy landscape for cleavage of Kunitz domains may differ from that of chymotrypsin inhibitor 2, such that acylation should be reconsidered as a rate-determining step in cleavage of Kunitz domains more generally, as has been suggested by other computational studies (51, 52). It remains to be further explored how each step in the catalytic cycle may be impacted by the differential flexibility of Kunitz domains on the fast (nanosecond-microsecond) time scale and by consequent differential access to rare conformational states on the time scale of proteolysis.

The relevance of this study is not limited to cleavage of Kunitz domains or other canonical serine protease inhibitors but extends to other protease systems as well. Many proteases function not just in protein degradation but as regulators of proteome constituency and activity, through specific limited proteolysis. In this capacity, the natural substrates of these regulatory proteases are intact folded proteins, not the short peptides typically studied as laboratory models. A number of previous studies have examined structural context of substrate and cleavage site selection in limited proteolysis (55–58), but information is lacking about the corresponding local or global conformational dynamics of these substrates. We anticipate that, as we have found here, not only substrate structure but also intrinsic substrate dynamics may profoundly influence substrate specificity, not only by impacting molecular recognition but also by controlling rates of catalytic turnover. Support for this premise is found in the control of human cationic trypsinogen/trypsin autoproteolysis and cleavage by regulatory protease chymotrypsin C (59). In this example, zymogen activation serves as a conformational switch that alters both the kinetics and thermodynamics of proteolysis for two regulatory cleavage sites, most likely through alterations in global dynamics (59). Thus, to fully understand the role of protein conformational dynamics in proteolysis, or in other enzyme systems that act on protein substrates, we must look beyond the enzyme and consider also the role of substrate dynamics in catalysis.

Experimental Procedures

Protein Expression, Purification, and Site-directed Mutagenesis

Expression plasmids pPICZα-APLP2-KD (26), pPICZα-BPTI (60), and pPIC9K-APPI-3M (27) have been described previously. A mutation altering Thr-11 to Val in pPICZα-BPTI, to generate the construct for BPTI-T11V, was introduced using the QuikChange kit (Agilent Technologies) according to the manufacturer's protocol. A mutation altering Thr-11 to Val in pPIC9K-APPI-3M, to generate the construct for APPI-3M-T11V, was introduced by PCR assembly following previously described protocols (27). Mutated constructs were verified by DNA sequencing. Kunitz domain substrates APLP2-KD, BPTI-T11V, and APPI-3M-T11V were recombinantly expressed and purified from the methylotrophic yeast Pichia pastoris essentially according to our previously described protocols (25–27). Kunitz domain protein concentrations were determined by titration versus active site-titrated bovine trypsin (Sigma), as described previously (23). Mesotrypsin and catalytically inactive mutant mesotrypsin-S195A were expressed recombinantly as zymogen forms in Escherichia coli, isolated from inclusion bodies, refolded, purified, and proteolytically activated essentially as described previously (23, 24). Active mesotrypsin was quantified by titration with 4-nitrophenyl 4-guanidinobenzoate (23), whereas mesotrypsin-S195A was quantified by absorbance reading at 280 nm using a calculated extinction coefficient of 41,535 m⁻¹·cm⁻¹.

Kunitz Domain Hydrolysis Studies

The linear initial rates of depletion of intact APPI-3M-T11V and BPTI-T11V in time course studies with active mesotrypsin were quantified by HPLC to obtain approximations of k_cat, following previously published procedures (15, 23, 25, 27). Substrate concentrations were 30–50 μm, and enzyme concentrations were 1–2 μm. Values reported reflect average and standard deviation from three independent experiments.

Protein Crystallization, Data Collection, Structure Determination, and Refinement

APLP2-KD was mixed with mesotrypsin-S195A in an equimolar ratio at a total protein concentration of 2–4 mg/ml, mixed 1:1 (v/v) with reservoir solution, and crystallized via the hanging drop method over a reservoir containing 0.2 m ammonium sulfate, 0.1 m sodium cacodylate, and 30% PEG-8000 at room temperature. As described under “Results,” productive preparations of mesotrypsin-S195A were later found to contain contamination of ∼0.1% mol fraction of active mesotrypsin; pure preparations lacking such trace contamination did not produce crystals. Crystals were harvested, cryoprotected, and flash-cooled in liquid N₂. Native X-ray diffraction data were collected at 100 K at beamline X25, National Synchrotron Light Source, Brookhaven National Laboratory. Data were merged from two crystals, one of which diffracted to high resolution (1.4 Å) but had poor completeness in several shells due to ice rings, and the second of which diffracted to lower resolution but with better completeness. Data were merged and scaled using DENZO/SCALEPACK (61). Crystals belonged to the space group P2₁2₁2, with unit cell dimensions a = 99.01, b = 54.58, c = 56.60, α = β = γ = 90°, and contained one copy of the complex in the asymmetric unit. The structure was solved by molecular replacement using MOLREP in CCP4 (62), using as the search model the complex of human mesotrypsin with APPI (Protein Data Bank (PDB) 3L33). Free-R flags were assigned to a random 5% of reflections, and this test set was maintained throughout all stages of refinement. Refinement employed alternating cycles of manual rebuilding in COOT (63) and automated refinement using REFMAC (64). The APLP2-KD* chains required extensive manual rebuilding in COOT due conformational changes relative to the search model. At later stages of refinement, solvent molecules were added into peaks greater that 1σ and within acceptable hydrogen bonding distance from neighboring protein atoms, and full anisotropic treatment of atomic displacement parameters was employed. The quality of the final model was analyzed using wwPDB validation tools (65). The coordinates and structure factors have been submitted to the Worldwide Protein Data Bank under the accession code 5JBT. This and other structures with anisotropically refined thermal factors were analyzed by comparison of full anisotropic to TLS models and by Rosenfield analysis using the software ANISOANL within the CCP4 Suite (66). Structure figures were generated using PyMOL (Schrodinger, LLC), VMD (67), and UCSF Chimera (68).

Unbiased Molecular Dynamics Simulations

Initial structural models were generated using crystallographic structures of human mesotrypsin in complex with various Kunitz domain substrates (PDB codes): APPI (3L33) (25); APPI-3M (5C67) (27); and BPTI (2RA3) (23). Acyl-enzymes models were generated by manually breaking the reactive site residue 15–16 peptide bond of substrate, in silico mutation of Ala-195 of catalytically inactive mesotrypsin structures back to the native Ser-195, and formation of an acyl bond between Ser-195 and substrate residue 15. Placement of nonprimed side substrate residues and Ser-195 were modeled after trypsin acyl-enzyme crystal structures 2AGE and 2AGG (14), and placement of primed side substrate residues were modeled after trypsin-cleaved BPTI co-crystal structure 3FP7 (29). The structural models were built using the protein preparation wizard in Maestro to generate sterically relaxed structures and were further refined for the Amber force field within the YASARA refinement module (69–71). Each model consisted of ∼4103 atoms, including hydrogens. Final models were subjected to energy optimization with Polak-Ribière conjugate gradient with an R-dependent dielectric. Model conformations were validated with WHAT-IF and PROCHECK (71–73). Model manipulation was done with Maestro (Macromodel, version 9.8, Schrödinger, LLC, New York) or Visual Molecular Dynamics (VMD) (67).

MD simulations were conducted using methods we have previously described (33, 74, 75). Briefly, each mesotrypsin-substrate acyl-enzyme system was minimized with relaxed restraints using either Steepest Descent or Conjugate Gradient PR, equilibrated in solvent with physiological salt conditions, and then MD calculations were run for bursts of 100–200 ns or for production runs of >1000 ns. The protocol for refinement included the following steps: 1) simulated annealing with explicit water molecules and ions; 2) energy minimization; and 3) MD simulation for 500 ps to relax to the force field (both AMBER03 and Charmm were tested). Tables were generated for most optimal conformations. TIP3P water molecules were added around the protein at a depth of 15–18 Å from the edge of the molecule (76), producing a box with between 4.8 and 5.12 × 10⁴ atoms, including proteins, counter-ions, solvent ions, and solvent waters. Simulations were completed using the Amber force field with NAnoscale Molecular Dynamics 2 engine (NAMD2) for the equilibration and setup and then exported to Yasara for load-balancing runs on a Linux Beowulf cluster. Simulations were carried out using the particle mesh Ewald technique with repeating boundary conditions with a 9-Å nonbonded cutoff, using SHAKE with a 2-fs time step. A constant temperature of 300 K was maintained using the Berendsen weak-coupling algorithm with a time constant of 1.0 ps. Pre-equilibration was started with 10,000 steps of minimization followed by 10,000 ps of heating under MD, with the atomic positions of protein fixed. Then, two cycles of minimization (10,000 steps each) and heating (2000 ps) were carried out with restraints of 10 and 5 kcal/(mol·Å²) applied to all protein atoms. Next, 5000 steps of minimization were performed with solute restraints reduced by 1 kcal/(mol·Å²). Then, 1000 ps of unrestrained MD were carried out, and the system was slowly heated from 1 to 310 K. Equilibration was determined from a flattening of r.m.s.d. over time after an interval of >10 ns. The production MD runs were carried out with constant pressure boundary conditions (relaxation time of 1.0 ps). Our methods for equilibration and production run protocols are described in greater detail elsewhere (33, 74, 77, 78). Translational and rotational center-of-mass motions were initially removed, and periodically, simulations were interrupted to have the center-of-mass removed again by a subtraction of velocities to account for the “flying ice cube” effect (79). Following the simulation, the individual frames were superposed back to the origin to remove rotation and translation effects.

Molecular Dynamics Simulations with Biasing

The following methods were used individually, and later in succession, in attempts to explore excursions along conformational pathways leading from a native-like mesotrypsin-APPI acyl-enzyme to the APLP2-KD* conformation observed crystallographically: 1) MdMD (33, 34); 2) TMD (35–37); 3) REX (38–40); and 4) SMD (41–43). Throughout the various strategies, we used Cα r.m.s.d. measurements between homologous residues of the APPI acyl-enzyme and a target acyl-enzyme model, based on the mesotrypsin-APLP2-KD* crystal structure, to gauge progress toward the conformational transition end point.

MdMD

The MdMD algorithm has been previously described in detail (33, 34, 75). The algorithm runs a recursive series of short MD “sprints,” at the conclusion of each either saving the current system state or reverting to the last archived state based on the value of a global progress variable, in this case reduction in r.m.s.d. from the target structure. To prevent trapping in local landscape wells, we may vary the sampling time of the sprint and randomize velocities from a Boltzmann distribution. The MdMD algorithm produced the largest r.m.s.d. reduction among stand-alone biasing methods and was subsequently implemented to initiate the staged biasing approach as described under “Results.”

TMD

TMD is a well known algorithm for moving a structure between two identified states using harmonic potentials applied upon the gradient of the force field (35–37). We used this algorithm within NAMD2 to push our structure during the second stage of biasing between the initial acyl-enzyme complex toward the APLP2-KD* target structure. We used a double-sided TMD energy function with standard presets as shown in Equation 1,

$$U_{\text{TMD}}=\frac{1}{2}\frac{K}{N}{\left(\text{DRMS}\left(t\right)-\text{DRMS}\times \left(t\right)\right)}^2$$ (Eq. 1)

to apply an enthalpic “driver” between states, such that DRMS(t) is RMS1(2) − RMS2(t), where RMS1 is r.m.s.d. from structure 1 and RMS2 is r.m.s.d. from structure 2.

REX

REX is a versatile algorithm for moving a structure out of a trapped local energy saddle point or well into a higher energy landscape before settling (38–40). We used REX within NAMD2 with standard settings to search for alternative conformations, using the feature to allow our structure to refold into different energy landscapes for brief excursions in attempts to jump energy barriers.

SMD

SMD is a versatile algorithm for moving a structure through various conformations using a “virtual” applied force within the system (41–43). SMD allows structures to be pulled or guided between two alternative conformations. A classical example used SMD in the unfolding of titin to mimic single-molecule experiments (41). We used SMD within NAMD2 to allow our structure to refold through topological energy barriers to reorganize two tightly packed loops of APPI that otherwise would have required unfeasibly long time sampling to undergo the transient conformational changes required.

Author Contributions

O. K., T. R. C., and E. S. R. designed the research. O. K., D. F. P., I. C., R. D. H., and A. H. generated constructs and proteins. O. K., R. W., A. H., and I. C. performed biochemical experiments. O. K., R. W., A. H., I. C., N. P., and E. S. R. analyzed and interpreted biochemical experiments. R. W. and D. F. P. crystallized proteins. A. S. S. collected and processed diffraction data. O. K. and R. W. solved and refined the crystal structure. O. K. and E. S. R. analyzed and interpreted the crystal structure. O. K. and T. R. C. conducted MD simulations. O. K., T. R. C., and E. S. R. analyzed and interpreted MD data. O. K., T. R. C., and E. S. R. wrote the paper. All authors edited the manuscript and approved the final version.