Abstract
The importance of physical forces in biology is becoming more appreciated. Neisseria gonorrhoeae has become a paradigm for the study of physical forces in the bacterial world. Cycles of elongations and retractions of Type IV pili enables N. gonorrhoeae bacteria to exert forces on its environment, forces that play major roles in the life cycle of this pathogen. In order to better understand the role of these forces, there is a need to fully characterize them. Here, we present two different techniques, optical tweezers and Polyacrylamide MicroPillars (PoMPs), for measuring pilus retraction forces. Initially designed for N. gonorrhoeae, these assays can be readily modified to study other pilus-bearing bacteria including Neisseria meningitidis.
Keywords: Neisseria, Type IV pilus, Retraction force, Optical tweezer, PoMPs
1. Introduction
Type IV pili (Tfp) play a critical role in the life cycles of both Neisseria meningitidis and Neisseria gonorrhoeae, the two main pathogens of the Neisseria genus. These appendages are thin (6 nm in diameter) and long (up to 30 µm in length) dynamic polymers emanating from the surface of the bacteria. They are associated with a wide range of functions including DNA uptake, twitching motility, cell adhesion, and biofilm formation (1). An explanation for this wide spectrum of functions stems from the extraordinary diversity of Tfp filaments: the main subunit, pilin, can undergo high frequency antigenic variation, (2) harbors various post-translational modifications (3) and the filaments themselves possess different minor pilins (4). Alongside these chemical and genetic variabilities, force generation has also been implicated as another important function of Tfp biology.
During the last decade, the role of physical forces in biology has emerged as a central theme. From development to differentiation, from motility to signaling, physical forces modulate biological fates and the bacterial world is no exception (5–8). N. gonorrhoeae Tfp can undergo cycles of extension and retractions and they can generate force during retraction (9). A single Tfp fiber can exert forces of 100 picoNewtons (pN) (10) and bundles of 8–10 Tfp can be retracted in unison exerting forces of up to 1 nanoNewtons (nN) which can be maintained for hours (11). In the context of cellular infection, these forces elicit dramatic rearrangements in the cortex of eukaryotic cells (12) and have been shown to trigger cytoprotective pathways (13). The techniques designed to measure those forces in N. gonorrhoeae can readily be adapted to measure the force generation in N. meningitidis or other pili-bearing bacteria.
For this chapter, we present two complementary techniques to measure the forces generated by the retraction of pili. The first one utilizes optical tweezers and is geared toward the measurement of forces from a single bacterium. The second utilizes arrays of Polyacrylamide MicroPillars (PoMPs) and is geared toward the measurement of forces from multiple bacteria in “infection-like” conditions. The use of these techniques will increase our understanding of the role of physical forces in the biology of the pathogenic Neisseriae and other pilus-bearing bacteria.
2. Materials
2.1. Calibration of Optical Tweezers
A basic laser tweezers set-up with a fixed laser trap obtained from a 2 W neodymium-doped yttrium aluminum garnet neodymium (Nd:YAG) laser (14).
Carboxylated silica or latex beads (Polysciences or Bangs laboratories).
Eppendorf tubes.
Piezoelectric stage P-517 (Physik Instrumente).
#1 coverglass (Fisher Scientific).
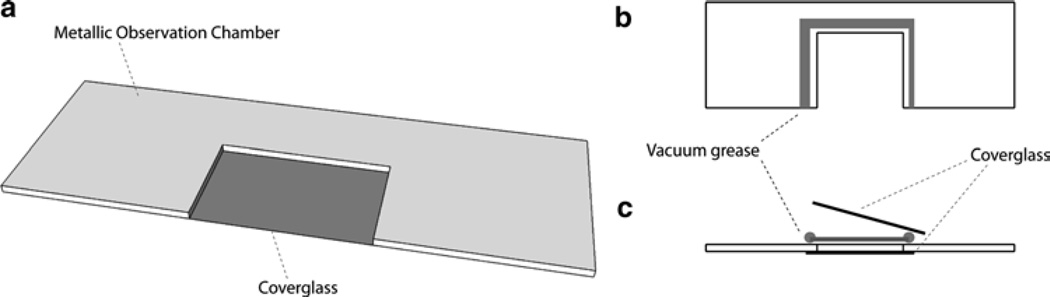
Observation chamber: a metallic slide with a 20 × 20 mm opening (15) (see Fig. 1).
Vacuum grease.
A computer with image analysis software, e.g., Image J (see Note 1).
Fig. 1.
Schematics of the observation chamber. (a) Schematic of an observation chamber with one coverglass at the bottom of it already in place. (b) Top view of an observation chamber with vacuum grease on the sides of the opening ready to be used to seal a coverglass on top. (c) Side view of an observation chamber with vacuum grease on the sides of the opening ready to be used to seal a coverglass on top. A coverglass is already at the bottom. After the liquid is added on the side, the chamber is sealed with more vacuum grease applied between the two coverglasses.
2.2. Optical Tweezers Assay
A basic laser tweezers set-up with a fixed laser trap obtained from a 2 W neodymium-doped yttrium aluminum garnet neodymium (Nd:YAG) laser (14).
Carboxylated Silica or latex beads (Polysciences or Bangs laboratories).
Agar plates to grow bacteria: use GCB-agar for pathogenic Neisseriae.
Dulbecco’s modified Eagle’s medium (DMEM).
Spectrophotometer.
Humidified incubator with 5% (v/v) CO2 for bacterial culture.
A computer with image analysis software, e.g., Image J (see Note 1).
2.3. Polyacrylamide MicroPillars Assay
The reagents and equipment listed below are required for the methods that describe activation of coverglasses, casting of PoMPs, coating of PoMPs, calibration of PoMPs using optical tweezers or magnetic tweezers, and PoMPs assays for measuring dynamic and static forces.
A silicon mould for the pillars, designed by usual photolithography techniques (see Note 2) (16, 17).
A plasma cleaner, e.g., PDC-32G (Harrick Plasma).
#1 coverglass.
0.1 M NaOH solution, prepared in distilled water.
Parafilm.
2 pairs of flat tipped tweezers, e.g., 2A model (SPI).
3-Aminopropyl-trimethoxysilane (Fluka).
70% (v/v) ethanol solution.
Solutions of 0.5% (v/v) and 4% (v/v) glutaraldehyde in phosphate buffered saline (PBS) pH 7.4.
Polyacrylamide solution 40% (Biorad) and bis-acrylamide solution 2% (Biorad). Mix to obtain the ratio of polyacrylamide and bis-acrylamide desired. For instance, to obtain 1 mL of 20% Acrylamide–1% bis-Acrylamide, combine 500 µL of both solutions.
10% (w/v) ammonium persulfate solution.
N,N,N′,N′-Tetramethylethylenediamine (TEMED).
Sulfo-SANPAH (Thermo Scientific).
50 mM HEPES buffer, pH 7.4.
Poly-l-Lysine solution: prepare a 30 µg/mL working concentration in PBS by diluting a stock solution of 1 mg/mL of Poly-l-Lysine hydrobromide (Sigma-Aldrich) (see Note 3).
Sterile tissue culture plates, 6-well.
An ultraviolet (UV) lamp: a germicidal lamp fitted within a laminar flow hood will suffice.
Piranha solution: mix three volumes of 1 M H2SO4 with one volume of 30% (v/v) hydrogen peroxide (H2O2).
Neodymium magnet (Applied Magnets).
Sewing needles: the size of the tip of the needle will control the size at which the magnetic gradient and thus the magnetic force is imposed (18).
Carboxylated magnetic beads, e.g., Dynabeads M270 carboxylic acid (Invitrogen Dynal).
Latex non-magnetic beads of a different diameter than the magnetic beads e.g., 1 µm beads (Polysciences or Bangs laboratories).
12 mL pipettes.
Pipettor tips.
3-Axis Micromanipulator e.g., Sutter instrument MP-285 (Sutter) (see Note 4).
Table-top centrifuge.
Dimethylpolysiloxane, with known viscosity of 12,500 cSt at 25°C (DPMS12M; Sigma-Aldrich).
An inverted microscope with a high magnification objective, preferably × 100 high numerical aperture.
A digital camera mounted on one of the ports of the microscope.
A computer with image analysis software e.g., Image J (see Note 1).
3. Methods
The principle behind optical tweezers is quite simple (19): when an intense light is focused on a point, the resulting three-dimensional gradient of electromagnetic energy will result in the ability to trap a dielectric object at that point. In other terms, if the light of a laser for example is concentrated in the focal plane of a microscope, all small transparent materials can be trapped. When the transparent object is exactly at the center of the concentrated light, no force is exerted on the object in the plane of focus. If the distance between the object and the center of the trap was to change, a restoring force would be exerted on the object. This force depends on several parameters including the shape, intensity, and wavelength of the focused light, the optical properties of both the object and the surrounding medium and the shape and size of the object. Formulae can be derived but calibration of the force is always preferred. We will assume that a basic optical tweezers set-up is readily available and outfitted with a fixed laser trap obtained from a 2 W neodymium-doped yttrium aluminum garnet neodymium (Nd:YAG) laser.
3.1. Calibration of Optical Tweezers
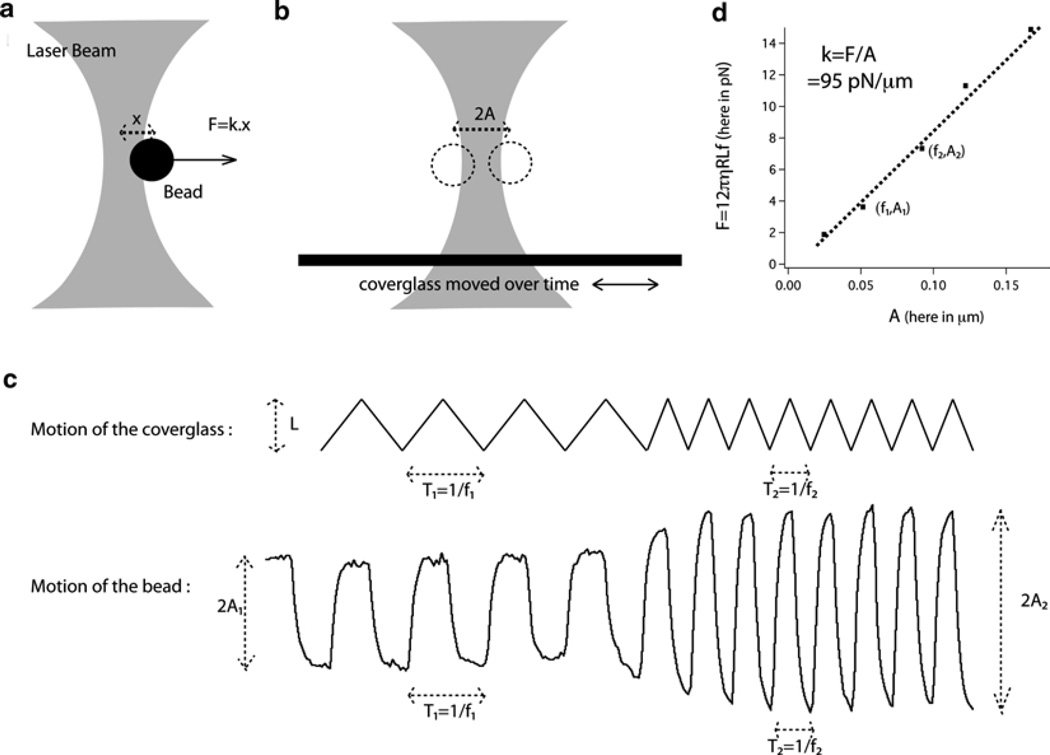
In order to be able to relate the displacement of the bead in the trap to a given force, the trap first needs to be calibrated. An easy and popular way to calibrate the trap is based on the fact that a bead of radius R moving in a medium of viscosity η at a speed v will be submitted to a force Fdrag = 6πηRv (20) (see Fig 2a, b). This method has the advantage of facile set-up, but other methods based on the analysis of the Brownian fluctuations of the bead exist and require more complicated set-up (20, 21). All the microscopy material is kept on an optical table.
Turn on the laser and ensure its stability by monitoring the output intensity over time. One hour of warming-up should be sufficient.
Prepare an observation chamber, which is a millimeter thick piece of aluminum with an opening of 20 × 20 mm with coverglasses on both sides maintained by vacuum grease (see Fig. 1) (15).
Place ~1 µL of the carboxylated silica or latex beads in 1 mL of distilled water. Add 0.2–1 µL of this bead suspension to 500 µL of water and place it into the observation chamber. Seal the chamber with vacuum grease (see Note 5 and Fig. 1).
Place the chamber on the piezoelectric stage. The beads should be spaced out far enough that you can trap an individual bead and move the stage by a full field of view without trapping other beads.
Measure the amplitude L of the movement of the stage by recording the motion of a bead stuck to the coverglass or another defect attached to the coverglass. The movement must be a periodic triangular signal so that the speed of the stage is constant during each half period. It is important to maximize L while utilizing a full field of view.
With the frequency of the signal set to zero, open the laser shutter to trap a single bead. Silica beads are easier to trap, whereas with latex beads, the bead must be as close as possible to the center of the trap when the shutter is opened.
Start recording a digital movie (see Note 6).
Slowly increase, by steps, the frequency of the signal (see Note 7). Each step should last at least ten periods of the current frequency. Figure 2c shows an example of two such steps.
Analyze the digital movie obtained using an implementation of cross-correlation algorithms (22) in your favorite image analysis software to retrieve the motion of the bead over time.
For each step, measure the frequency of the signal f and the maximum displacement in the trap A from the captured motion of the bead (see Fig. 2c). Assuming that the viscous drag force Fdrag = 12πηRLf and the elastic force Felas = kA are equal (see Note 8), the stiffness of the trap can be obtained as the slope of a graph representing force vs. A for all the frequency steps taken during the calibration (see Fig. 2d). As mentioned previously, the exact value to the trap’s stiffness will depend on several parameters such as the laser used, the exact optical set-up and the type of bead used, but as an approximate reference, a laser of a couple of watts will lead to stiffness of around 100 pN/µm for a silica bead of 1.5 µm diameter. Using latex beads will result in a trap approximately twice as stiff (see Notes 9 and 10).
Fig. 2.
Schematics of the optical tweezers assay. (a) Schematic of the optical tweezers. (b) Schematic of the two extreme positions of the bead during calibration. (c) Representation of the motion of the coverglass and the resulting motion of the bead at two different frequencies. Frequencies and amplitudes of the bead motion for each frequency can be measured on the trace of the bead motion. (d) An example of calibration of the trap: the slope of the graph of the viscous drag force vs. bead displacement gives the stiffness of the trap.
3.2. Optical Tweezers Assay
Once the trap has been calibrated, the beads and bacteria are now placed in close vicinity. The method described below for using pathogenic Neisseriae can be readily adapted to investigate other pilus-bearing pathogens.
Streak out Neisseria bacteria from frozen stocks, maintained in 20% (v/v) glycerol GCB broth at −80°C, onto GCB-agar plates and grow in a humidified incubator with 5% (v/v) CO2 for 16–20 h.
Suspend the bacteria at a concentration of ~108 bacteria/mL in DMEM by measuring the optical density (OD) at λ600 nm in a spectrophotometer (1.4 OD600 ~109 CFU/mL) (see Note 11).
Place ~1 µL of the carboxylated silica or latex beads in 1 mL of water. The choice of bead is paramount to ensure that they will adhere to the pilus (see Note 12).
Add 10 µL of the bacterial suspension and 1 µL of the bead suspension in 500 µL of DMEM and add this volume to an observation chamber. Allow the bacteria to settle for 30 min.
In the meantime, turn on the laser and allow it to stabilize.
Place the observation chamber under the microscope.
Locate a freely diffusing bead and trap the bead with the optical tweezers as described in step 6 of Subheading 3.1 (see Note 13).
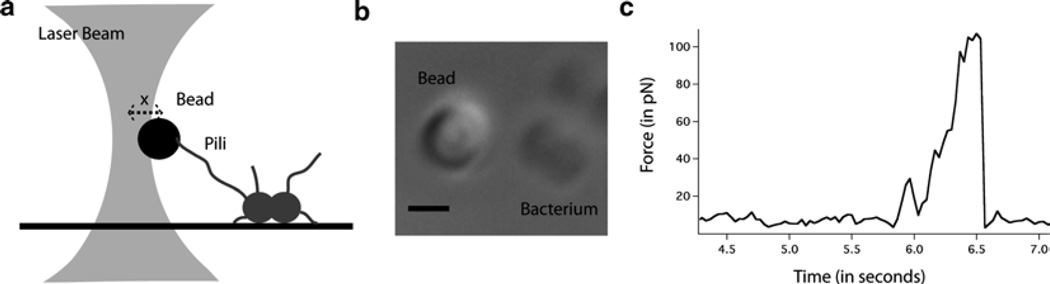
Bring the trapped bead in close vicinity to a bacterium tethered to the surface (see Fig. 3a, b). The distance between the two is commensurate with the length of the pilus being investigated, which is usually a few micrometer (see Note 14).
Start recording a digital movie (see Note 6).
Analyze the digital movie obtained using cross-correlation algorithms to retrieve the motion of the bead over time, as described in step 9 of Subheading 3.1.
The motion of the bead over time can be translated into the force exerted on the bead over time, now that the trap is calibrated (see Fig. 3c).
Fig. 3.
Use of the optical tweezers assay. (a) Attachment between a trapped bead and a pilus-bearing bacterium. (b) Optical microscopy image of the attachment event. The scale bar is 1 µm. (c) Example of the measurement of a pulling event using the optical tweezers assay.
3.3. Polyacrylamide MicoPillars Assay
Both N. gonorrhoeae and N. meningitidis infect mucosal epithelia primarily. Many bacteria also interact directly with biological or abiotic surfaces as communities, forming micro-colonies or biofilms. In this context, the optical tweezer-based assay cannot be used reliably to measure retraction forces in the more relevant in vivo “infection-like” conditions found within micro-colonies or biofilms. Recently, arrays of microscopic elastomeric pillars have been used to measure the forces exerted by eukaryotic cells on their environment (16, 23). In addition, previous methods based on the fabrication of substrate coated flexible gels have been extensively used to analyze the mechanical forces exerted by mammalian cells on their underlying support (24). The combination of these two techniques has permitted the manufacture of force measurement devices perfectly suited to analyze the retraction forces of Neisseria species and other pilus-bearing bacteria. The principle is to obtain a hexagonal array of identical micron-size elastomeric pillars. The motion of the pillars enables the measurement of the forces exerted by bacteria through retraction of their pili.
3.3.1. Activation of Coverglasses
Unless otherwise mentioned, all the following steps are performed on the bench.
Place a piece of Parafilm at the bottom of a flat clean glass dish.
Using tweezers, briefly pass the coverglasses through a flame and when cooled place them on the Parafilm. Prepare as many coverglasses as needed, as the activated coverglasses can be kept for up to a year.
With a pipette, add 0.1 M NaOH solution onto each coverglass. Add 1 mL to cover the entire surface of the coverglass and then remove the excess liquid with a pipette, leaving approximately 100–200 µL of the solution covering the full surface area of each coverglass.
Let the coverglasses dry at room temperature. Drying takes a few hours in a low humidity atmosphere, but overnight is usually recommended.
Add ~200 µL of 3-aminopropyl-trimethoxysilane on the top surface of each coverglass and incubate for 5 min at room temperature. This step should be done in a fume hood.
Slowly add water to immerse all of the coverglass(es) and incubate for 5 min at room temperature.
Use tweezers to remove the coverglasses individually and use a water squirt bottle to wash any residue from both sides. Keeping track of the activated side, put the coverglass on a rack immersed in water and agitate by slow rotation for 5 min.
Replace the water with a solution of 0.5% (v/v) glutaraldehyde in PBS. Ensure that all the coverglasses are immersed and incubate for 30 min at room temperature. This step should be done in a fume hood and the glutaraldehyde disposed of by following institutional health and safety recommendations.
Wash the coverglasses three times with water and dry overnight at room temperature.
The coverglasses, with their activated side maintained in an upward orientation, can be kept in Petri dishes sealed with Parafilm. Protected from dust, they can be used up to a year after preparation.
3.3.2. Casting of PoMPs
Take the desired number of activated coverglasses and place them in a clean plastic Petri dish with the activated side facing upward. The number chosen should be commensurate with the number of moulds to be used.
Prepare a sufficient volume of the polyacrylamide–bis-acrylamide solution at the concentration required (see Note 15). A volume of 15 µL is needed per coverglass.
Add 1/100th of the volume of 10% (w/v) ammonium persulfate and then 1/1,000th of the volume of TEMED to the acrylamide solution. Vortex for a few seconds.
Add 15 µL of the solution on top of each activated coverglass.
Using tweezers, delicately deposit the silicon mould with the holes facing the coverglass.
Allow the mixture to harden at room temperature, which usually takes from 15 to 45 min depending on the concentration of acrylamide and bis-acrylamide used. An easy way to follow the reticulation process is to prepare a greater volume of acrylamide solution and observe hardening of the remaining mixture after application to the coverglasses.
When the acrylamide gel has hardened, submerse the mould–gel–coverglass sandwich in 50 mM HEPES buffer, pH 7.4.
This step is critical and can be described as “shucking the mould.” Using two pairs of tweezers, or a pair of tweezers and a razor blade, use one pair of tweezers to hold the coverglass and slowly push one side of the second pair of tweezers or the razor blade between the coverglass and the mould. Be cautious in the application of force; the principal concern should be to go forward on the side of the mould. At some point during this process, the mould will be freed and the hydrogel micropillars on the coverglass will be exposed. These arrays of polyacrylamide micropillars over an activated coverglass are referred to as PoMPs.
Next, wash both sides of the mould with 70% (v/v) ethanol using a squirt bottle. Use a tissue to remove the excess ethanol and then dry the mould with clean air or preferably argon.
Store the mould in a plastic Petri dish sealed with Parafilm until next use.
Should some of the hydrogel remain stuck to the mould, apply a sufficient volume of 70% (v/v) ethanol to remove it. The hydrogel will turn white which will aid in identifying and removing all remaining gel. Use Kimwipes tissue to remove final traces. Finally, clean the mould using a plasma cleaner for 1 min, according to the manufacturer’s instructions. If traces of hydrogel still cannot be removed using this method, the mould can be immersed in Piranha solution for a few hours to remove any organic debris, then washed with ample water and dried with clean air or Argon and subsequently cleansed in a plasma cleaner.
3.3.3. Coating of PoMPs
Another advantage to using polyacrylamide is that the surface of the micropillars can be readily modified with functional groups for protein binding. For example, bifunctional chemicals such as SulfoSANPAH (25) can be used to activate the surface of the PoMPs to allow binding of virtually any protein.
Cover the PoMPs with 80 µL of a solution of 1 mM SulfoSANPAH in 50 mM HEPES buffer, pH 7.4 and place them under a UV lamp for 5 min. The distance between the UV lamp and the sample should be approximately 10–15 cm.
Aspirate the solution, add 80 µL of fresh 1 mM SulfoSANPAH in 50 mM HEPES buffer, pH 7.4 and repeat the UV treatment.
Wash the PoMPs once with 50 mM HEPES buffer, pH 7.4 and add on top of the PoMPs a solution of the protein to be covalently linked. For instance, coating with a solution of 30 µg/mL of polylysine in PBS is recommended for investigating the interactions of N. gonorrhoeae pili.
Place the PoMPs in an incubator at 37°C for 1 h and then wash three times with PBS prior to using them for calibration and force assays.
3.3.4. Calibration of PoMPs Using Optical Tweezers
As with using optical tweezers, there is a need to know what the relationship is between the displacement of each pillar and the force exerted on them. One method of achieving this would be to rely on the equation from elastic theory in a linear approximation, F = (3πEr4/4L3)x, where E is the Young modulus of the material, r the radius of the beam, L the length of the beam and x the displacement. However, this equation is totally valid only if the pillars are exactly cylindrical. Moreover, the high power dependence on both the radius and the length means that the value of both parameters must be measured very precisely. This is usually accomplished by scanning electron microscopy, but this technique is not suitable for samples composed of aqueous materials such as hydrogels as it involves dehydration of the samples, which is impossible for hydrogels. We therefore prefer to measure directly the relationship between force applied and displacement of the pillars. A calibration is necessary only once for each type of mould-polyacrylamide–bis-acrylamide combination that is used. A calibration of the pillars can be done using optical tweezers as follows:
Take the polylysine-coated PoMPs to be calibrated and mount them on an observation chamber.
Add ~1 µL of carboxylated silica or latex beads to 1 mL of water. Add 2–10 µL of these beads to the observation chamber.
Start recording a digital movie (see Note 6).
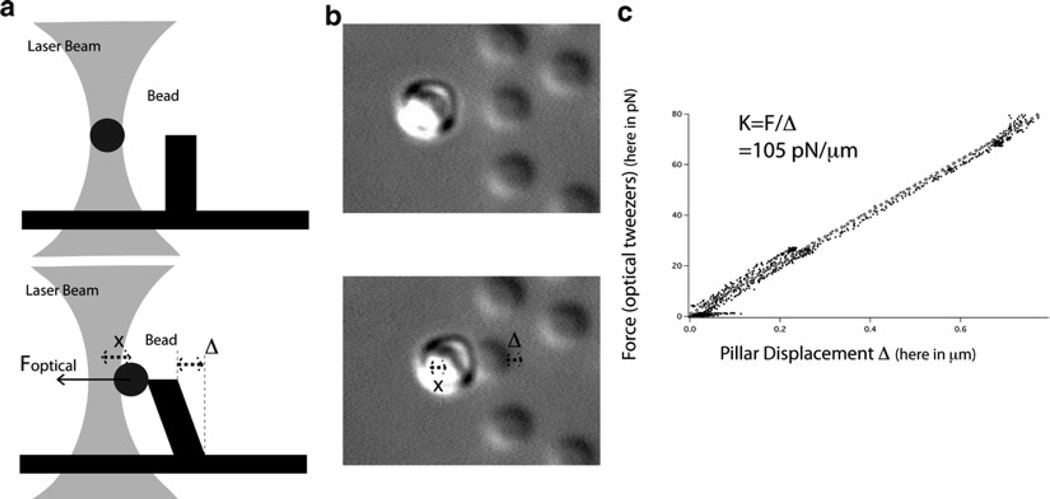
Trap a bead and bring the side of a pillar tip to it until contact. Slowly pull the pillar away from the bead (see Fig. 4a, b).
Analyze the digital movie as described in step 9 of Subheading 3.1 and track the positions of the bead, the pillar and a reference point in the field of view. From these positions, obtain the displacement x of the bead from the center of the trap, which will give the force exerted on the pillar as the trap is calibrated. Obtain also the displacement Δ of the pillar over time. The graph of force vs. Δ will enable the measurement of the stiffness of the pillar (see Fig. 4c).
Fig. 4.
Calibration of the pillars using optical tweezers. (a) Schematics of the calibration of the pillars using optical tweezers: at the beginning of the calibration when the bead is not in contact with the pillar and then in the middle of the calibration when force is exerted on the pillar. (b) Optical microscopy images of the calibration of the pillars using optical tweezers: at the beginning of the calibration when the bead is not in contact with the pillar and then in the middle of the calibration when force is exerted on the pillar. (c) An example of the calibration of the pillars with optical tweezers: the slope of the graph of the force of the optical tweezers vs. the displacement of the pillar gives the stiffness of the pillar.
3.3.5. Calibration of PoMPs Using Magnetic Tweezers
If optical tweezers are unavailable, an alternative method that is cheaper and easier to implement relies on the use of magnetic tweezers.
Attach a small cylindrical neodymium magnet to the end of a handle so that it can be mounted to a 3-axis micromanipulator.
Attach a sewing needle to the magnet in a fixed position. The needle will become magnetized and provide the small tip of the magnetic tweezers.
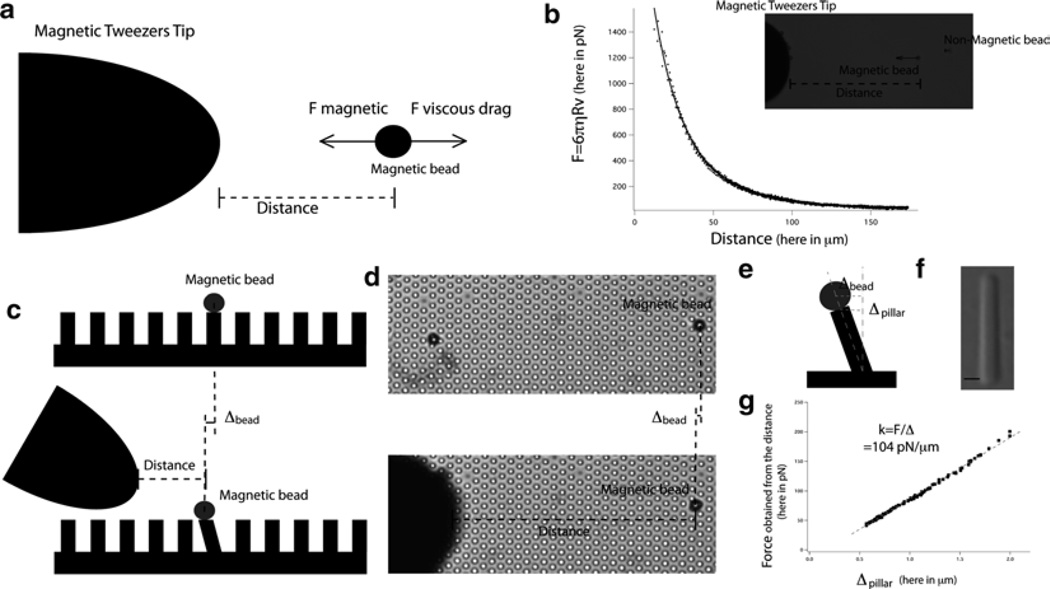
- Before calibrating the PoMPs, the magnetic tweezers first need to be calibrated. This is done once again by using the Stokes equation (Fdrag = 6πηRv) (see Fig. 5a, b).
- Add ~1 µL of magnetic beads as well as ~1 µL of nonmagnetic beads of a different diameter into separate Eppendorf tubes containing 100 µL of water.
- Remove all traces of water by using a magnet for the magnetic beads, or centrifugation at 13,000 × g for 5 min on a table-top centrifuge, for the non-magnetic beads.
- Add 300 µL of dimethylpolysiloxane, a medium of known viscosity (see Note 16).
- Stir well with a pipette tip to homogenize the mixture and incorporate the beads in the medium.
- Prepare a slide with a gasket a few millimeters high and add some of the viscous medium to it.
- Add a few droplets of both the magnetic and non-magnetic beads at the center of the gasket and mix again with a tip. A suspension of magnetic and non-magnetic beads in a viscous medium will be produced.
- Put the slide on a microscope stage and bring the tip into focus in the vicinity of the beads. Allow the system to settle for 10 min.
- Start recording a digital movie (see Note 6) and record the displacement of magnetic beads towards the tip.
- Analyze the digital movie as described in step 9 of Subheading 3.1 to determine the positions of the tip, magnetic beads, and non-magnetic beads.
- The movement of the non-magnetic beads enables the residual motion of the fluid itself to be tracked. The speed of the beads compared to the fluid can be computed and assuming that at all times the magnetic force and viscous drag force are equal, calibration of the magnetic tweezers will be obtained, i.e., the relationship between the distance between the bead and the tip and the force applied to the bead (see Fig. 5b).
Following calibration of the magnetic tweezers, the next step is to calibrate the PoMPs. Take the PoMPs, coated with polylysine as described in Subheading 3.3.3 and mount them onto an open observation chamber.
Make a dilute suspension of the carboxylated magnetic beads, e.g., 1 µL in 1 mL of water.
Add a few microliters of the suspension onto the pillars and wait for 20 min to allow most of the beads to settle before calibration can begin.
Select beads that are in contact with only a single pillar. These beads will be evenly surrounded by six pillars (see Fig. 5c, d).
Start recording a digital movie (see Note 6).
Bring the tip of the magnetic tweezers into focus and use the micromanipulator to change the force applied on the magnetic bead by slowly bringing the tip closer to the bead and then farther away. Repeat a couple of times.
Analyze the movie as described in step 9 of Subheading 3.1 to determine the position of the tip of the magnetic tweezers and the displacement of the bead.
The distance between the bead and the tip of the magnetic tweezers allows calculation of the force applied on the bead and the displacement. The stiffness of the pillar (force/displacement) can then be calculated, with one caveat. It is important to remember that the motion of the bead is followed, not the motion of the pillar. As such, the height of the pillar and the radius of the bead have to be measured in order to be able to calculate the stiffness of the pillar (see Fig. 5g). We will assume that the motion of the center of the pillar (ΔPillar) can be calculated as follows: ΔPillar = (L/(L + R))ΔBead where R is the radius of the bead and L the length of the pillar (see Fig. 5e). An accurate measurement of the length of the pillar can be done by mechanically disrupting the PoMPs and imaging the resulting free floating pillars (see Fig. 5f).
Fig. 5.
Calibration of the pillars using magnetic tweezers. (a) Schematic of the calibration of the magnetic tweezers. (b) An example of the calibration curve of the magnetic force exerted by the magnetic tweezers vs. distance and an optical microscopy image of the setup. (c) Schematic of the calibration of the pillars by the magnetic tweezers. (d) Optical microscopy images of the calibration of the pillars by the magnetic tweezers. (e) A schematic that explains the difference between the bead’s and pillar’s displacements. (f) Optical microscopy image of a pillar enabling accurate measurement of the pillar’s length. (g) An example of the calibration of the pillars with magnetic tweezers: the slope of the graph of the force of the magnetic tweezers vs. the displacement of the pillar gives the stiffness of the pillar.
3.3.6. PoMPs Assay
Once the PoMPs have been coated with polylysine or other protein of choice, the next step involves adding bacteria to the surface of the device at a known concentration. In order to mimic bacterial interactions with host cells, we recommend using the same surface density of bacteria to host cells that are used during infection assays. Depending on the type of data to be collected, the forces can be measured in two ways, termed dynamic or static force measurements (see Note 17).
- Dynamic PoMPs force measurements are made as follows:
- Mount the calibrated PoMPs onto an observation chamber.
- Suspend ~106 Neisseria bacteria in 500 µL of DMEM (see Note 11).
- Add this suspension to the observation chamber and put it under the microscope.
- Start recording a digital movie (see Note 6).
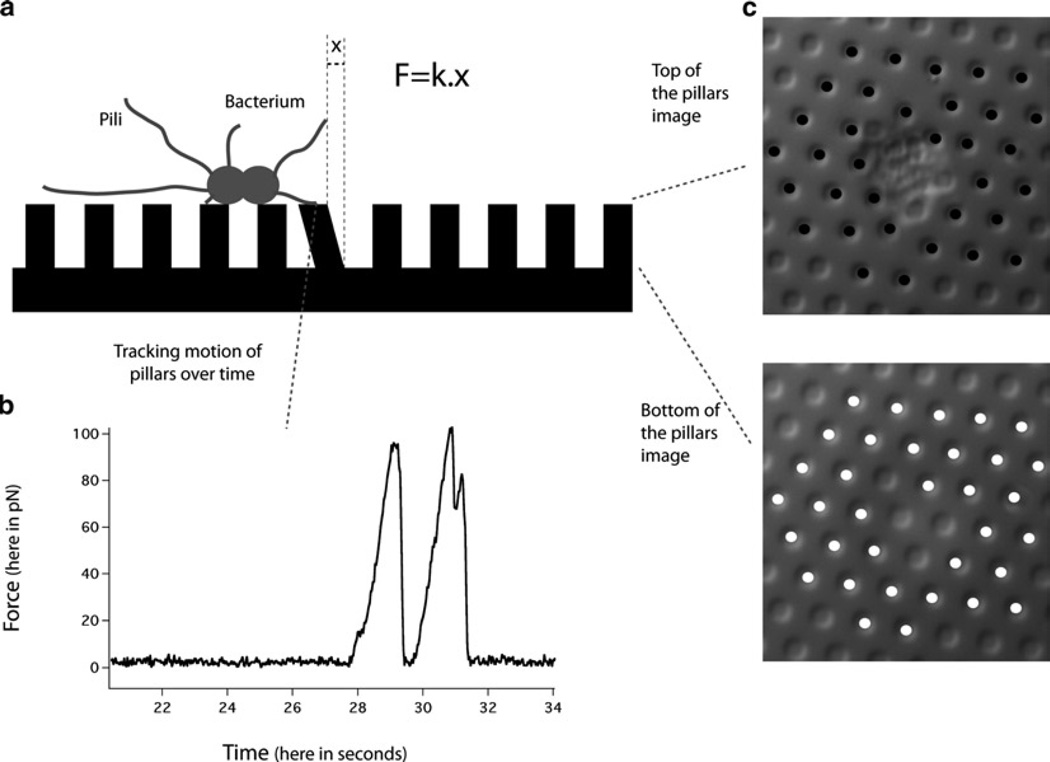
- Focus on the tip of the pillars.
- The motion of the pillars over time provides a measurement of the dynamic forces exerted by the bacteria on the pillars (see Fig. 6a, b).
- Static PoMPs force measurements are made as follows:
- Place the calibrated PoMPs into the well(s) of 6-well tissue culture plates.
- Suspend ~108 bacteria Neisseria bacteria in 2 mL of DMEM (see Note 11).
- Add the 2 mL of bacterial suspension onto the PoMPs and allow the bacteria to interact with the PoMPs over time.
- Fix the PoMPs with interacting bacteria by adding 2 mL of 4% (v/v) glutaraldehyde in PBS to the well for 1 h at room temperature.
- Transfer the fixed PoMPs to an observation chamber and take images under the microscope of both the tip and base of the pillars.
- The differences of position between the two images give the deflection of the pillars and thus the forces exerted by the bacteria, as the PoMPs are calibrated (see Fig. 6a, c). The differences of position between the two images can be obtained by using the implementation of cross-correlation algorithm as described in step 9 of Subheading 3.1 or by using a manual tracking software like the manual tracking plug-in from Image J (http://rsb.info.nih.gov/ij/plugins/manual-tracking.html).
Fig. 6.
The PoMPS assay. (a) Schematic of the PoMPs assay. (b) An example of a dynamic force measurement. (c) An example of a static force measurement.
Acknowledgments
N. B. and M. S. acknowledge the award of NIH grant AI079030. This work was also supported by the Agence Nationale de la Recherche(ANR)(ProgrammeBlanc2010SVSE5 “MECANOCAD”) and the CNRS (Program Prise de Risques “Interface physique, biologie et chimie”).
Footnotes
Other popular and powerful image analysis software programs are Matlab, Metamorph, Igor and IDL.
The moulds must be etched in silicon. Moulds made in SU8 resins or polymethylmethacrylate (PMMA) resin, which can be demoulded easily with PDMS, will not work for multiple demouldings with polyacrylamide. After the silicon mould has been made, it needs to be cleaned with Piranha solution for 2 h and then plasma cleaned in an air plasma cleaner for 1 min. After this treatment, the mould can be used repeatedly to obtain arrays of PoMPs on an activated coverglass. For use, the mould needs to be cut into pieces smaller than the coverglass and we recommend areas of 1 cm2.
Practically any protein can be used to coat the pillars. Trial and error with your protein of interest will be necessary to determine the concentration needed for the desired coating. When possible the use of fluorescently labeled protein helps in optimizing coating.
Other types of macromanipulators that can be used are the Burleigh PCS-5000, the Eppendorf Micromanipulator 5171 or the Injectman NI2.
The density of beads needs to be high enough that they will be found easily and low enough that no other bead is going to be trapped in the optical tweezers during the calibration.
The cost of both digital cameras and computer hard drives has dramatically decreased over recent years. A digital camera with capturing frequencies for at least part of their field of view, of 100 Hz or more is relatively inexpensive. The plethora of image analysis software available, e.g., Matlab, Metamorph, ImageJ, Igor, and IDL, combined with the availability of high computing power makes the use of recorded digital movies to analyze and to track microscopic movements a very attractive and affordable method. The implementation of cross-correlation algorithms (22) can lead to spatial resolution of less than 1/10th of a pixel, which is approximately 10–20 nm with the right magnification.
The frequency of the signal should not exceed a quarter of the recording frequency as this would hamper accurate analysis of the movie.
In order to make sure that the viscous drag force imposed on the bead is indeed equal to the elastic force of the optical trap, use only frequencies where a plateau in the bead displacement is attained at each half-cycle.
The viscous drag force equation (Stokes’s law) is valid only if the bead is far away from the surface. Thus, perform the calibration at a distance from the surface between 5 and 10 bead diameters. However, this will slightly alter the profile of the light and potentially affect the stiffness of the trap. If calibration must be done near the surface, correction formulae exist to account for the distance between the bead and the surface (26).
An important parameter to record when performing a calibration is the temperature of the sample. The viscosity of water varies from 10−3 kg/s m at 20°C to 0.65 × 10−3 kg/s m at 40°C and thus the viscosity reading inserted into the equation might change by more than 30%, depending on the temperature (25 or 37°C) at which calibration is done. Taking these parameters into account, this method typically leads to calibration of the trap with greater than 20% precision.
The nature of the buffer could change the value of the forces measured as it could affect the interaction of the pili with the beads or the interaction between pili. We recommend using the same buffer that is used for other biological assays for the bacteria of interest. For example, the buffer often used for studies of the interactions between human host cells and N. gonorrhoeae or N. meningitidis is DMEM and this medium would be recommended for all force measurements.
With the optical tweezers assay, it is important that the beads used will attach to the pili of interest. In the case of the pathogenic Neisseria, pili adhere to many different surfaces. The corrugated surface of the N. gonorrhoeae pili presents helical alternative patches of positively charged and negatively charged surfaces. This peculiar configuration explains why N. gonorrhoeae pili will strongly bind both to negative surfaces such as carboxylated beads or positive surfaces such as poly-l-lysine-coated beads. Depending on the physico-chemical properties of the pili on your bacteria of interest, different beads may need to be used. As a starting point, we recommend the use of carboxylated beads that are readily available from commercial sources. Beads covalently coated with poly-l-lysine or antibodies against pili are valuable reagents for force measurement assays.
Depending on the type of bead and the coating used, it is possible that the beads will sediment quickly and bind to the surface of the coverglass. In this case, you should use an open observation chamber where the beads can be added at varying times.
If the bacteria do not readily adhere to the bottom of the coverglass, a single bacterium can be easily isolated by allowing its interaction with larger beads (adherent to the surface of the coverglass). This will ensure that the bacteria do not move.
Linear elastic theory for a beam leads to the following equation for the relationship between force and displacement: F = (3πEr4/4L3)x where E is the Young modulus of the material, r the radius of the beam, L the length of the beam and x the displacement. From this equation, it is evident that the smaller the radius and the longer the beam, the softer the beam will be. However, if the geometrical parameters of the pillars can be adjusted to change their stiffness, there are still some technical constraints to take into account. With conventional approaches, the resolution of the features that can be patterned is around 1 µm, so the diameter for the pillars cannot be much smaller than this. Obtaining a ratio of length to radius greater than 20 is difficult and then demoulding becomes an issue. For this reason, we departed from the use of the widely popular PDMS (polydimethylsiloxane) polymer for moulding the features. The high Young modulus of the PDMS (~2 MPa) and the technological constraints mentioned above regarding the size and ratios of the features mean that PDMS pillars would have a stiffness too high to measure the lower forces that bacteria exerted, compared to eukaryotic cell forces. However, the use of polyacrylamide hydrogels considerably extends the flexibility of the micropillars system. Gels as soft as a 10% polyacrylamide – 0.1% bis-acrylamide and as stiff as 20% poly-acrylamide – 1% bis-acrylamide have been used. The constraints in the choice of the percentages are the following: too low percentage gels will prevent demoulding and too high percentages will lead to brittle and opaque gels. Pillars of a diameter of 1 and 7 µm in length have a stiffness of around 100 pN/µm when casted with a 20% polyacrylamide – 0.2% bis-acrylamide mix. Given the high dependence of the stiffness with the geometrical characteristic of the pillars this number may vary for different moulds, e.g., a 10% increase in the radius would lead to almost a 50% increase in the stiffness.
Any medium of known viscosity can be used, as long as the viscosity is high enough to enable recording. The medium recommended (dimethylpolysiloxane, with known viscosity of 12,500 cSt at 25°C) allows movies to be analyzed at 1 Hz with the recommended beads.
Both methods have advantages and disadvantages. In the dynamic method, all the pillars that are not released during image acquisition cannot have their force properly measured leading to a selection bias towards short-lived pulling events. However, all the dynamic information of the forces is available. In the static method, there is no dynamic information, but the longer-lived events can be recorded as well and more data can be collected for statistical analysis. It should also be noted that for the static method a number of pillars may be distorted during the demoulding process and thus care must be taken to avoid areas of the PoMPs that have pillars uniformly bent, as they are a tell-tale sign of a demoulding artifact rather than force generation. Depending on the data to be collected, add the bacteria at the desired concentration on top of the PoMPs and then either acquire a movie or fix and observe the differences in displacement of the pillars. Studies on the force generation of N. gonorrhoeae using the PoMPs technology led to the discovery that N. gonorrhoeae pili can bundle and exert pulling forces up to 1 nN. Such a technology can be used to study the retraction forces of N. meningitidis or other force-exerting bacteria. The ability to measure these forces may also be used to identify new bacterial phenotypes.
References
- 1.Mattick JS. Type IV pili and twitching motility. Ann Rev of Microbiol. 2002;56:289–314. doi: 10.1146/annurev.micro.56.012302.160938. [DOI] [PubMed] [Google Scholar]
- 2.Hagblom P, Segal E, Billyard E, et al. Intragenic recombination leads to pilus antigenic variation in Neisseria gonorrhoeae. Nature. 1985;315:156–158. doi: 10.1038/315156a0. [DOI] [PubMed] [Google Scholar]
- 3.Aas FE, Egge-Jacobsen W, Winther-Larsen HC, et al. Neisseria gonorrhoeae type IV pili undergo multisite, hierarchical modifications with phosphoethanolamine and phosphocholine requiring an enzyme structurally related to lipopolysaccharide phosphoethanolamine transferases. J Biol Chem. 2006;281:27712–27723. doi: 10.1074/jbc.M604324200. [DOI] [PubMed] [Google Scholar]
- 4.Brown DR, Helaine S, Carbonnelle E, et al. Systematic functional analysis reveals that a set of seven genes is involved in fine-tuning of the multiple functions mediated by Type IV Pili in Neisseria meningitidis. Infect Immun. 2010;78:3053–3063. doi: 10.1128/IAI.00099-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Farge E. Mechanical induction of twist in the Drosophila foregut/stomodeal primordium. Current Biol. 2003;13:1365–1377. doi: 10.1016/s0960-9822(03)00576-1. [DOI] [PubMed] [Google Scholar]
- 6.Gilbert PM, Havenstrite KL, Magnusson KEG, et al. Substrate elasticity regulates skeletal muscle stem cell self-renewal in culture. Science. 2010;329:1078–1081. doi: 10.1126/science.1191035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhang XH, Halvorsen K, Zhang CZ, et al. Mechanoenzymatic cleavage of the ultralarge vascular protein von Willebrand Factor. Science. 2009;324:1330–1334. doi: 10.1126/science.1170905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Engler AJ, Sen S, Sweeney HL, et al. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 9.Merz AJ, So M, Sheetz MP. Pilus retraction powers bacterial twitching motility. Nature. 2000;407:98–102. doi: 10.1038/35024105. [DOI] [PubMed] [Google Scholar]
- 10.Maier B, Potter L, So M, et al. Single pilus motor forces exceed 100 pN. Proc Nat Acad Sci USA. 2002;99:16012–16017. doi: 10.1073/pnas.242523299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Biais N, Ladoux B, Higashi D, et al. Cooperative retraction of bundled type IV pili enables nanonewton force generation. Plos Biol. 2008;6:907–913. doi: 10.1371/journal.pbio.0060087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Higashi DL, Zhang GH, Biais N, et al. Influence of type IV pilus retraction on the architecture of the Neisseria gonorrhoeae-infected cell cortex. Microbiol-SGM. 2009;155:4084–4092. doi: 10.1099/mic.0.032656-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Howie HL, Glogauer M, So M. The N.gonorrhoeae type IV pilus stimulates mechanosensitive pathways and cytoprotection through a pilT-dependent mechanism. Plos Biol. 2005;3:627–637. doi: 10.1371/journal.pbio.0030100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sterba Re, Sheetz MP. Basic laser tweezers. Meth Cell Biol. 1997;55:29–41. [PubMed] [Google Scholar]
- 15.McGee-Russell SM, Allen RD. Reversible stabilization of labile microtubules in the reticulopodial network of Allogromia. Adv Cell Molec Biol. 1971;1:153. [Google Scholar]
- 16.du Roure O, Saez A, Buguin A, et al. Force mapping in epithelial cell migration. Proc Nat Acad Sci USA. 2005;102:2390–2395. doi: 10.1073/pnas.0408482102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ghassemi S, Biais N, Maniura K, et al. Fabrication of elastomer pillar arrays with modulated stiffness for cellular force measurements. J Vac Sci Technol B. 2008;26:2549–2553. doi: 10.1116/1.3013424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tanase M, Biais N, Sheetz M. Magnetic tweezers in cell biology. Meth Cell Biol. 2007;83:473–493. doi: 10.1016/S0091-679X(07)83020-2. [DOI] [PubMed] [Google Scholar]
- 19.Ashkin A. Acceleration and trapping of particles by radiation pressure. Phys Rev Lett. 1970;24:156–&. [Google Scholar]
- 20.Simmons RM, Finer JT, Chu S, et al. Quantitative measurements of force and displacement using an optical trap. Biophys J. 1996;70:1813–1822. doi: 10.1016/S0006-3495(96)79746-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Clausen M, Koomey M, Maier B. Dynamics of Type IV Pili is controlled by switching between multiple states. Biophys J. 2009;96:1169–1177. doi: 10.1016/j.bpj.2008.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gelles J, Schnapp BJ, Sheetz MP. Tracking kinesin-driven movements with nanometre-scale precision. Nature. 1988;331:450–453. doi: 10.1038/331450a0. [DOI] [PubMed] [Google Scholar]
- 23.Tan JL, Tien J, Pirone DM, et al. Cells lying on a bed of microneedles: An approach to isolate mechanical force. Proc Nat Acad Sci USA. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang YL, Pelham RJ. Preparation of a flexible, porous polyacrylamide substrate for mechanical studies of cultured cells. Meth Enzymol. 1998;298:489–496. doi: 10.1016/s0076-6879(98)98041-7. [DOI] [PubMed] [Google Scholar]
- 25.Kandow CE, Georges PC, Janmey PA, et al. Polyacrylamidc hydrogels for cell mechanics: Steps toward optimization and alternative uses. Cell Mech. 2007;83:29–46. doi: 10.1016/S0091-679X(07)83002-0. [DOI] [PubMed] [Google Scholar]
- 26.Happel J, Brenner H. Low Reynolds number hydrodynamics with special applications to particulate media. Boston: Kluwer; 1983. [Google Scholar]