Genetics of Skeletal Evolution in Unusually Large Mice from Gough Island

Abstract

Organisms on islands often undergo rapid morphological evolution, providing a platform for understanding mechanisms of phenotypic change. Many examples of evolution on islands involve the vertebrate skeleton. Although the genetic basis of skeletal variation has been studied in laboratory strains, especially in the house mouse Mus musculus domesticus, the genetic determinants of skeletal evolution in natural populations remain poorly understood. We used house mice living on the remote Gough Island—the largest wild house mice on record—to understand the genetics of rapid skeletal evolution in nature. Compared to a mainland reference strain from the same subspecies (WSB/EiJ), the skeleton of Gough Island mice is considerably larger, with notable expansions of the pelvis and limbs. The Gough Island mouse skeleton also displays changes in shape, including elongations of the skull and the proximal vs. distal elements in the limbs. Quantitative trait locus (QTL) mapping in a large F₂ intercross between Gough Island mice and WSB/EiJ reveals hundreds of QTL that control skeletal dimensions measured at 5, 10, and/or 16 weeks of age. QTL exhibit modest, mostly additive effects, and Gough Island alleles are associated with larger skeletal size at most QTL. The QTL with the largest effects are found on a few chromosomes and affect suites of skeletal traits. Many of these loci also colocalize with QTL for body weight. The high degree of QTL colocalization is consistent with an important contribution of pleiotropy to skeletal evolution. Our results provide a rare portrait of the genetic basis of skeletal evolution in an island population and position the Gough Island mouse as a model system for understanding mechanisms of rapid evolution in nature.

POPULATIONS that colonize islands face a host of new environmental conditions, including changes in resource availability, predation risk, and competition (Losos and Ricklefs 2009). These shifts can stimulate the evolution of unusual or exaggerated traits over a short time scale. Insular populations of mammals are enriched for cases of rapid morphological evolution, especially in traits related to body size (Foster 1964; Grant 1999; Pergams and Ashley 2001; Beheregaray et al. 2004; Lomolino 2005; Thomas et al. 2009; Durst and Roth 2015). Comparing island populations with their mainland relatives is a powerful approach for understanding the genetic basis of evolutionary change.

Wild house mice offer a particularly useful system for revealing the mechanisms of rapid phenotypic evolution on islands. By virtue of their commensalism, house mice successfully colonized a diverse array of island environments (Bonhomme and Searle 2012). Insular house mice often display distinct skeletal morphologies. Presence–absence or meristic polymorphisms of bones in the skull, humerus, pelvis, and vertebrae (including the tail) have been documented (Berry 1964, 1986; Berry and Jakobson 1975a; Berry et al. 1978; Davis 1983; Pergams and Ashley 2001; Renaud and Auffray 2010). Divergence in body size (Berry and Jakobson 1975b; Berry et al. 1978b, 1979, 1981, 1987; Rowe-Rowe and Crafford 1992; Adler and Levins 1994; Jones et al. 2003; Lomolino 2005; Durst and Roth 2012, 2015; Russell 2012; Gray et al. 2015; Cuthbert et al. 2016) suggests evolutionary changes to the skeleton in other island populations. As the scaffold for the body plan, the skeleton enables movement, provides support for muscles, and protects internal organs (Pourquié 2009). Moreover, studying skeletal divergence can reveal the dynamics of multi-trait evolution. Functional, developmental, and genetic interactions among traits are expected to produce patterns of covariation across the skeleton (Lande 1980; Atchley and Hall 1991; Lynch and Walsh 1998). Depending on its structure, this “modularity” may facilitate or constrain evolution compared to predictions for single traits (Lande 1979; Schluter 1996; Klingenberg 2008; Parsons et al. 2012).

Although the genetic underpinnings of skeletal evolution in island mice are unknown, considerable research has been dedicated to dissecting genetic differences in the skeleton in laboratory mice. Quantitative trait loci (QTL) have been identified for hundreds of skeletal components related to size and growth differences among classical inbred strains and among strains descended from artificial selection experiments (Leamy et al. 1999; Vaughn et al. 1999; Huang et al. 2004; Lang et al. 2005; Kenney-Hunt et al. 2006, 2008; Norgard et al. 2008; Sanger et al. 2011; Carson et al. 2012), with evidence that some QTL affect multiple traits (Leamy et al. 2002; Ehrich et al. 2003; Schlosser and Wagner 2004; Wolf et al. 2005, 2006; Christians and Senger 2007; Kenney-Hunt et al. 2008; Pavlicev et al. 2008; Roseman et al. 2009). QTL responsible for local skeletal shape variation also have been discovered, with a special emphasis on the mandible (Atchley et al.1985a,b; Klingenberg and Leamy 2001; Klingenberg et al. 2003; Klingenberg 2004; Wagner et al. 2007; Leamy et al. 2008; Willmore et al. 2009). These findings from laboratory mice provide a rich comparative context for examining the genetic architecture of skeletal evolution in natural populations of house mice, which experience evolutionary dynamics distinct from those in laboratory conditions.

The largest known wild house mice in the world inhabit Gough Island, a remote volcanic island in the central South Atlantic Ocean (Rowe-Rowe and Crafford 1992). The massive evolutionary increase in body size of Gough Island mice—to become twice the weight of their mainland counterparts (Jones et al. 2003; Gray et al. 2015)—suggests a substantial expansion of the skeleton. House mice likely colonized Gough Island a few hundred generations ago (Gray et al. 2014), raising the prospect that morphological evolution has been accelerated. In this study, we use Gough Island mice to understand the genetic basis of rapid skeletal evolution in nature.

Materials and Methods

Gough Island and its mice

Gough Island is part of the United Kingdom Overseas Territory of Tristan da Cunha and is located approximately halfway between South America and South Africa in the South Atlantic Ocean (40° 19′S and 9° 55′W). Gough Island has an area of 65 km². Fifty mice, live trapped on Gough Island in September 2009, were transferred to Charmany Instructional Facility in the School of Veterinary Medicine at the University of Wisconsin–Madison. Four mice died and two litters consisting of five pups were born during transport from the island to the facility. Upon their arrival, 46 mice (25 female and 21 male) were used to establish a breeding colony.

Female and male mice were housed separately in microisolator cages with a maximum of four mice per cage. Ground corn cobs (1/8th inch; Waldschmidt and Sons, Madison, WI) were used as bedding; irradiated sunflower seeds (Harlan Laboratories, Madison, WI) and nesting material were provided for enrichment. The room was temperature controlled (68–72°F) and set on a 12-hr light/dark cycle. Water and rodent chow (Teklad Global 6% fat mouse/rat diet; Harlan Laboratories) was provided ad libitum. Mice were mated after 8 weeks of age. Breeding individuals were given additional enrichments and were fed breeder chow (Teklad Global 19% protein/9% fat; Harlan Laboratories) ad libitum. All mice were weaned between 3 and 4 weeks of age. Individual mice were toe tattooed (using sterile lancets and tattoo paste) at 1 week of age and ear punched at weaning for the purposes of identification. All mice were weighed to the nearest milligram, beginning 1 week after birth and ending at 16 weeks. After the Gough Island mice (subsequently abbreviated GI) arrived to the Charmany Instructional Facility, we performed a random-mating common garden experiment using the wild founders. This was done to determine that the large body size of the GI mice has a genetic basis and not due solely to environmental factors.

Intercross experiments

Several partially inbred lines of GI mice were created through full-sib mating for four filial generations, a procedure expected to reduce within-line heterozygosity by 60% (Silver 1995). To incorporate variation segregating among GI mice, two partially inbred GI lines were used for intercross experiments (denoted as crosses A and B). One pair of male and female siblings from each partially inbred line was crossed with WSB/EiJ (subsequently abbreviated as WSB; The Jackson Laboratory, Bar Harbor, ME) to generate four independent F₂ intercrosses (Supplemental Material, Figure S1). WSB was chosen because it is a wild-derived strain, has a body size typical of wild house mice, is fully inbred, belongs to the same subspecies as GI mice, has a sequenced genome (Keane et al. 2011), and is featured in the Collaborative Cross (Threadgill and Churchill 2012). A total of 1374 F₂ mice were generated: 497 from cross A (WSB × GI = 279 and GI × WSB = 218) and 877 from cross B (WSB × GI = 494 and GI × WSB = 383). From this F₂ population, 827 mice were used for all skeletal phenotyping and analyses: 367 from cross A (WSB × GI = 206 and GI × WSB = 161) and 460 from cross B (WSB × GI = 252 and GI × WSB = 208).

Phenotyping

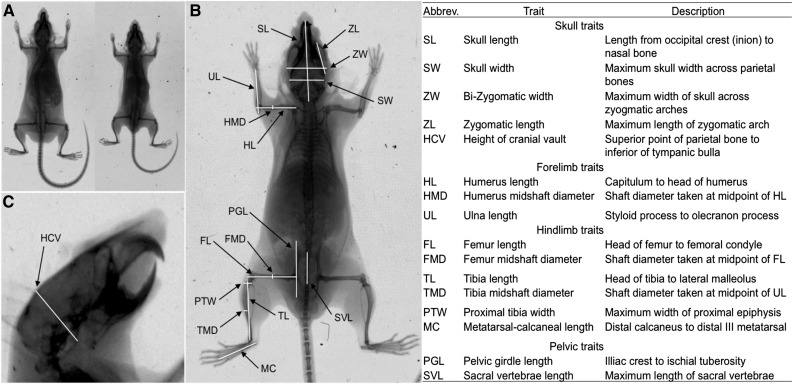
All mice were weighed to the nearest milligram every week, beginning 1 week after birth and ending at 16 weeks. Dual energy X-ray absorptiometry (DXA) was used to measure bone morphology. Digital X-ray images (Carestream Health DXS Pro 4000) were collected for 43 F₁ and 827 F₂ individuals and mice from the four parental strains of the cross. X-ray images were taken at three postnatal time points (5, 10, 16 weeks of age) for each animal. These time points were chosen to capture multiple episodes of growth throughout postnatal development. X-ray imaging at 5 and 10 weeks of age was performed using live animals. When individuals reached 16 weeks of age, they were either euthanized by CO₂ asphyxiation followed by imaging, or imaging was performed live followed by euthanasia (by decapitation). Liver samples were collected from all euthanized F₂ individuals and stored at −80°. For imaging of live mice, an anesthetic (50–100 mg/kg ketamine/0.5–1.0 mg/kg dexmedetomidine) was administered via intraperitoneal injection prior to X-ray imaging to allow for placement and X-ray exposure time. A dorsal and lateral X-ray image was taken of each individual. Skeletal dimensions were measured from the X-ray images using Carestream Molecular Imaging Software (Carestream Health). Measurements were chosen to capture axes of known variation across laboratory mouse strains and across species. A total of 16 measurements were used for phenotyping, including lengths and diameters of long bones, pelvis, and skull (see Figure 1).

Figure 1.

(A) An X-ray image illustrating the size comparison of a GI mouse (left) and a WSB mouse (right) at 16 weeks of age. (B) Locations of skeletal traits on an X-ray image taken from a dorsal view. (C) Location of the height of the cranial vault (HCV) on an X-ray image taken from a lateral view. The right panel lists the 16 skeletal traits measured, and includes names, acronyms, and descriptions of each trait.

Additional measurements were taken from the individual skeletal measurements to determine any changes in skeletal shape (described as nonproportional size changes), particularly of the limbs. These include forelimb-to-hindlimb ratios [intermembral index: (humerus length + radius length)/(femur length + tibia length) × 100], the ratio of distal and proximal elements of the hindlimb [crural index: (tibia length/femur length) × 100] and forelimb [brachial index: (radius length/humerus length) × 100], and the ratio of forelimb and hindlimb proximal elements [humerofemoral index: (humerus length/femur length) × 100]. Although no data were collected on the radius, ulna length was used as a substitute for the distal element of the forelimb.

Phenotypic distributions were inspected for extreme outliers. When it was concluded that outliers reflected reduced measurement accuracy caused by improper placement of animals during X-ray imaging or a lack of X-ray resolution, they were removed. These included six data points from the F₂ population [for sacral vertebrae length (SVL) at 5, 10, and 16 weeks, skull length (SL) at 5 weeks, skull width (SW) at 5 weeks, and SL at 10 weeks], one data point from the WSB population [zygomatic length (ZL) at 16 weeks), and three data points from the GI population [femur midshaft diameter (FMD) at 5 weeks, metatarsals and calcaneus length (MC) at 5 weeks, ZL at 10 weeks].

Genotyping

All mice were genotyped using the Mega Mouse Universal Genotyping Array (MegaMUGA, Geneseek, Lincoln, NE). The MegaMUGA is an Illumina array platform containing ∼77,800 markers. Most of these markers are single nucleotide polymorphisms (SNPs), although some are structural variants and transgenic markers. The markers are densely and relatively evenly spaced at 33 kb across the genome, found across all autosomes, sex chromosomes, and the mitochondria. This array was designed to maximize the number of informative markers for the Collaborative Cross (Aylor et al. 2011; Threadgill and Churchill 2012), the diversity outbred cross (Svenson et al. 2012), and wild house mouse populations (Churchill et al. 2004; Collaborative Cross Consortium 2012). The Collaborative Cross features eight parental strains, one of which is WSB. Liver tissue from all F₂’s and the parents of the cross were sent to Geneseek (NeoGene Corporation) for DNA extraction and genotyping. A total of 1536 samples were sent, including controls and samples from mice that died before reaching 16 weeks of age.

Multiple controls were used for DNA extraction and genotyping to identify technical and biological errors. Liver tissue was organized into 16 (96 well) plates in such a way as to minimize array batch effects on related sets of samples. Tissue from WSB was placed in identical wells on every plate to account for plate extraction effects. The four GI parental samples were replicated four times each across the 16 plates. Replicate samples of the first well of each plate were placed in a random well and run on different arrays.

We examined the genotypes for technical, biological, and data entry errors. We omitted markers that were not informative in the crosses and those with high levels of missing data. We removed a few individuals with high levels of missing data. We also removed a small number of individuals that had large numbers of Mendelian inconsistencies or mismatched sex, which were most likely unresolved sample mix-ups. Following these initial screens, the cleaned data included the four GI parents of the crosses, 70 F₁ individuals, 1346 F₂ individuals, and 33,191 markers. In all subsequent analyses, we focused on a subset of 11,833 markers that were fixed in the four GI parents and therefore segregated as in a standard F₂ intercross between inbred lines. We estimated intermarker genetic distances assuming a genotyping error rate of 0.2% and converted estimated recombination fractions to map distances with the Carter–Falconer map function (Carter and Falconer 1951).

Single-trait QTL analysis

Single-trait QTL analysis was performed using Haley–Knott regression (Haley and Knott 1992) on a 0.5-cM grid across the genome, as implemented in R/qtl (Broman and Sen 2009). Analysis was conducted separately for each of the 16 skeletal traits at 5, 10, and 16 weeks with sex, mother, and observer as additive covariates. Genome-wide significance thresholds were determined by permutation (Churchill and Doerge 1994), with adjustments for the X chromosome (Broman et al. 2006). Numbers of permutations were 47,840 and 946,400 for the autosomes and the X chromosome, respectively. A QTL was considered significant if its maximum LOD score met a 5% genome-wide significance threshold.

Additional single-trait scans were performed on F₂’s using two different methods to control for effects of body size on each skeletal trait: (1) by using relative skeletal sizes as our traits and (2) by treating body weight as an additive covariate in the model. Relative skeletal size was calculated by dividing each skeletal trait by the cube root of body weight for each individual (trait/body weight^1/3) and is referred to as the shape ratio (Mosimann 1970; Jungers et al.1995). The use of shape ratios accounts for the isometric component of body size, while maintaining allometric (size correlated) shape and nonallometric (size independent) shape. Alternatively, the treatment of body weight as a covariate accounts for both isometric shape and allometric shape, leaving nonallometric shape.

Genetic effects

QTL effects were measured using both additive and dominance effects. Additive effects were calculated as half the difference in genotype means between the GI and WSB homozygotes. Dominance effects were calculated as the difference between the genotypic mean of the GI/WSB heterozygote and the average genotypic mean of the GI and WSB homozygotes. To compare effects across traits and time points, additive effects were standardized by dividing by the phenotypic SD. Dominance effects were standardized by dividing the dominance effects by the additive effects (d/a). These ratios can be broken down into broad categories defined in Kenney-Hunt et al. (2006). Strong overdominant QTL are defined by having d/a ratios >2.5. A QTL is considered to be overdominant when d/a is between 1.5 and 2.5. GI is considered to be dominant to WSB when d/a is between 0.5 and 1.5. A QTL is considered codominant when d/a is between −0.5 and 0.5. WSB is considered to be dominant to GI when d/a is between −0.5 and −1.5. A QTL is considered to be underdominant when d/a is between −1.5 and −2.5. Strong underdominant QTL are defined by having d/a ratios less than −2.5.

Phenotypic correlations

Pearson product moment correlations were calculated for each pair of the 16 skeletal traits and body weight at 5, 10, and 16 weeks. Correlations of each trait with itself at different time points were also calculated. We observed significant trait correlations across the skeleton (see Results), raising the prospect that joint analysis of multiple traits could provide additional insights into genetic architecture. When traits are correlated, multi-trait mapping increases the power to detect QTL and increases the precision of estimated QTL location (Jiang and Zeng 1995; Knott and Haley 2000).

To form trait sets for multi-trait mapping, we fit the phenotypic correlations to models we developed (see Table S6) based on well-established knowledge of mouse developmental and functional processes, including temporal patterning of the prenatal skeleton (Shubin et al. 1997; Wellik and Capecchi 2003), germ layer and cell type origins (Morriss-Kay 2001; Jiang et al. 2002; Jeong et al. 2004; Gross and Hanken 2008; Yoshida et al. 2008), orthogonal patterning of skeletal axes (Wellik and Capecchi 2003; Carapuço et al. 2005), and effects of mechanical load on limb elements (Rauch 2005). Each model was composed of nonoverlapping sets of skeletal traits partitioned into hypothesized modules. The best-fitting model was selected using MINT (Márquez 2008), which calculates a goodness of fit statistic γ* that measures the similarity between expected and observed covariance matrices. Models were ranked based on their γ* value, and support for rankings was measured by jackknifing.

Joint mapping of multiple skeletal traits

In light of the correlations between skeletal dimensions across F₂s, we used two approaches to map QTL for sets of traits. First, we performed principal component analysis (PCA) on the full set of 16 measurements in the F₂ population using the prcomp function in R (Mardia et al. 1979; R Core Team 2016). Separate analyses were conducted for each time point (5, 10, and 16 weeks). We used single-trait QTL mapping to search for QTL for each of the 16 principal components; we report results for PC1 and PC2. QTL significance thresholds were established using permutation tests (1000 replicates and 18,736 replicates for the autosomes and the X chromosome, respectively).

We used multi-trait QTL analysis as a second method to identify loci that affect suites of traits, as implemented in R/qtlpvl (Tian and Broman 2015). Separate analyses were performed on trait sets delineated using two criteria: (1) overlapping 1.5 LOD intervals in single-trait QTL analyses (Figure 3 and Table S3) and (2) membership in the same modules of best-fitting models from MINT analyses of phenotypic correlations (Table S6). Multi-trait mapping used the same genotype probabilities, informative markers, and covariates used in single-trait QTL analyses. QTL significance thresholds were established using permutation tests (1000 replicates and 18,736 replicates for the autosomes and the X chromosome, respectively).

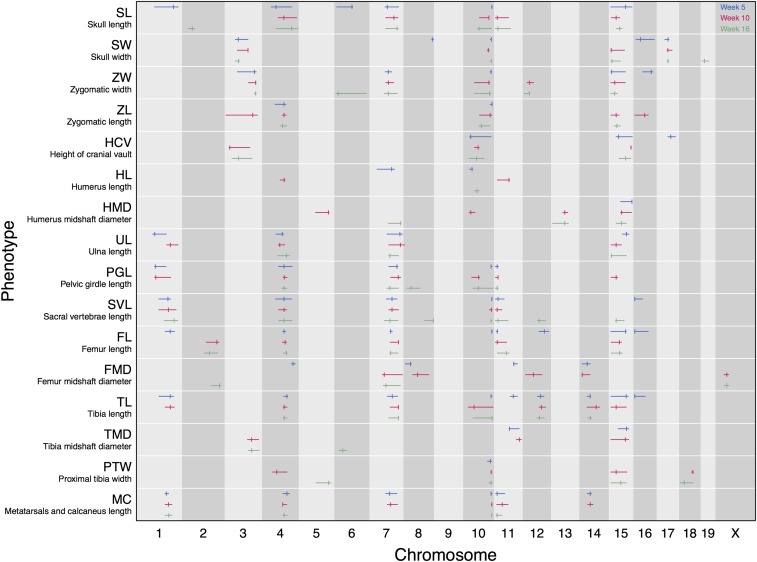
Figure 3.

Genomic intervals (in megabases) of all significant QTL for 16 skeletal measurements at 5 (in blue), 10 (in pink), and 16 (in green) weeks of age. Tick marks indicate the maximum LOD of the QTL. Confidence intervals are the 1.5 LOD intervals.

Tests for pleiotropy

To evaluate whether each QTL associated with multiple traits reflected the action of a single pleiotropic locus or two linked loci, we conducted a statistical test for pleiotropy, as implemented in R/qtlpvl (Tian and Broman 2015; Tian et al. 2016).The test was performed separately on two data sets: (1) QTL for skeletal traits from single-trait analyses and QTL for body weight from Gray et al. (2015) that have overlapping 1.5 LOD intervals and (2) QTL for traits within each module of the most supported models from MINT analyses. In this framework, the null hypothesis (H₀) is that one QTL controls all traits (pleiotropy) and the alternative hypothesis (H₁) is that two linked QTL control the traits (linkage), with each trait affected by one of the two QTL. Multi-trait QTL mapping was first performed under a single-QTL model, H₀. Then a two-dimensional scan over the chromosome was performed, with a two-QTL model, H₁, with each trait being affected by one or the other QTL. This involved an approximation in which, rather than consider all possible allocations of the traits to the two QTL, the traits were sorted based on their estimated QTL location, when considered individually, and then each possible cut point of this list was considered. Each possible cut point split the traits into two groups affected by the two different QTL. The test statistic LOD_2v1 was calculated by subtracting the LOD score of H₁ (maximizing over both QTL positions and the split of the traits into two groups) from the LOD score of H₀ (maximizing over QTL position). A P-value for the test of H₀ was calculated by a parametric bootstrap, with a large P-value indicating that the data are consistent with pleiotropy (H₀).

Data availability

All phenotype and genotype data from this study are available from the QTL Archive at the Jackson Laboratory, at http://qtlarchive.org.

Results

Phenotypic variation

GI mice have larger skeletons than WSB mice across postnatal development, with all but one trait (height of the cranial vault (HCV) at 16 weeks) showing significant expansions at all three time points (t-test; maximum P-value = 0.005; Figure 2 and Table S1). GI and WSB mice were raised in the same environment on a common diet; as a result, most differences should be genetic in origin. Averaging across traits, the GI skeleton is 14–15% (5 and 10 weeks of age) and 12% (at 16 weeks of age) larger than the WSB skeleton. Tibia midshaft diameter (TMD) shows the greatest proportional differences between GI and WSB (24% larger in female GI mice at 5 weeks of age and 22% larger in male GI mice at 10 weeks of age). Substantial divergence is also seen in the humerus and pelvis in females and in the humerus, pelvis, and femur in males (>17% larger in GI averaged across 5, 10, and 16 weeks of age).

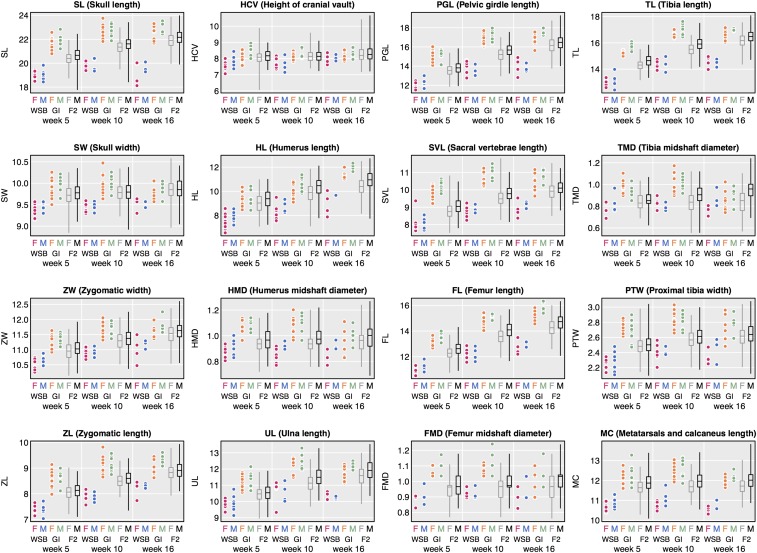
Figure 2.

Phenotypic distributions of 16 skeletal traits (in millimeters) for female (pink) and male (blue) WSB, female (orange) and male (green) GI, and female (gray) and male (black) F₂ animals at 5, 10, and 16 weeks of age. GI and WSB data are represented as scatter plots and F₂ data are represented with box plots.

Some of the skeletal differences between GI and WSB mice represent changes in shape. The width and depth of the skull show the smallest difference between GI and WSB, exhibiting only a 3–6% increase in GI mice, whereas the skull is 12–15% longer in GI mice. Both humerus and femur lengths show proportionally greater expansion in GI than their respective diameters late in postnatal development (Figure 2). Ratios of hindlimb-to-forelimb lengths (intermembral indices) and humerus-to-femur lengths (humerofemoral indices) are similar in GI and WSB mice. In contrast, brachial and crural indices are smaller in GI mice, indicating disproportionate expansion of proximal vs. distal limb elements relative to WSB (Table 1).

Table 1. Shape evolution in GI mice.

	F 5 wk		F 10 wk		F 16 wk		M 5 wk		M 10 wk		M 16 wk
Shape index	WSB	GI	WSB	GI	WSB	GI	WSB	GI	WSB	GI	WSB	GI
Intermembral index	72.3	72.0	70.9	70.6	70.6	70.6	73.0	71.3	72.5	71.7	72.4	73.9
Humerofemoral index	68.0	70.7	66.6	67.2	70.3	73.9	70.3	70.3	71.4	69.7	74.3	75.5
Crural index	118.8	117.4	117.3	112.6	114.6	108.2	118.0	116.5	117.6	112.5	111.2	107.0
Brachial index	132.5	121.5	131.6	123.3	115.6	104.1	126.4	119.4	121.0	118.8	106.0	102.4

Shape index values for GI and WSB mice for females (F) and males (M) at 5, 10, and 16 weeks of age. The intermembral index is the ratio of the forelimb to hindlimb [(HL + UL)/(FL + TL) × 100], the humerofemoral index is the ratio of proximal elements of the limb [(HL/FL) × 100], the crural index is the ratio of distal to proximal elements of the hindlimb [(TL/FL) × 100], and the brachial index is the ratio of distal to proximal elements of the forelimb [(UL/HL) × 100].

The majority of the skeleton increases in size across postnatal development in both GI and WSB mice (Table S2). More skeletal elements show significant increases in size between 5 and 10 weeks than between 10 and 16 weeks of age. In house mice, males are typically larger than females (Snell 1941). Although body weight and growth rate are sexually dimorphic in GI mice (Gray et al. 2015), not all GI skeletal elements show statistically significant differences in size between the sexes (see Figure 2). However, for all traits there are at least some small differences in the means between the sexes, with male averages exceeding female averages.

The trait means of the F₁ population from the GI and WSB intercross are closer to the GI means than the WSB means (data not shown). The trait means of the F₂ population from the GI and WSB intercross are intermediate compared to the parents (Figure 2). All 16 skeletal traits follow normal and continuous distributions (Figure S2). All but two skeletal traits [height of the cranial vault (HCV) at 5–10 weeks, metatarsal and calcaneus length (MC) at 10–16 weeks] in the F₂ population show significant increases in size over postnatal development (t-test; maximum P-value = 0.016).

Single-trait QTL mapping

A total of 208 QTL are identified across 16 skeletal traits and three time points (Figure 3 and Table S3). Multiple QTL are detected for all traits, with the exception of humerus midshaft diameter (HMD) and proximal tibia width (PTW) at 5 weeks of age. Nineteen of the 20 chromosomes contain at least one significant QTL for at least one time point. A large proportion of QTL for different traits colocalize, based on overlapping confidence intervals. Over half of all QTL are found on chromosomes 4, 7, 10, and 15, and span the entire skeleton, from skull to hindlimb. These highly colocalizing QTL are potentially pleiotropic and may act as global regulators of growth.

Effects of some QTL are restricted to specific regions of the skeleton (Figure 3), including the skull, femur, and other hindlimb elements. Numbers of QTL are similar across the three time points (69, 73, and 66 QTL at 5, 10, and 16 weeks of age, respectively). Although QTL on chromosomes 4, 7, 10, 11, and 15 are often found across all three time points, other QTL are mostly or entirely restricted to one time point. QTL on chromosomes 2, 5, 6, 13, 18, and X for hindlimb diameters (PTW, HMD, FMD) are not identified at early time points, suggesting these loci contribute to variation in size occurring later in postnatal development. In contrast, QTL on chromosome 16 (contributing to variation in skull widths and hindlimb lengths) disappear with age, suggesting these loci confer early growth differences between the two strains. There is a relative paucity of QTL for limb diameter traits, likely due in part to low repeatability. Because these traits are very small (<1 mm), they are more difficult to measure. Consistent with this idea, we observed higher standard deviations for limb diameter traits compared to longer measurements (data not shown).

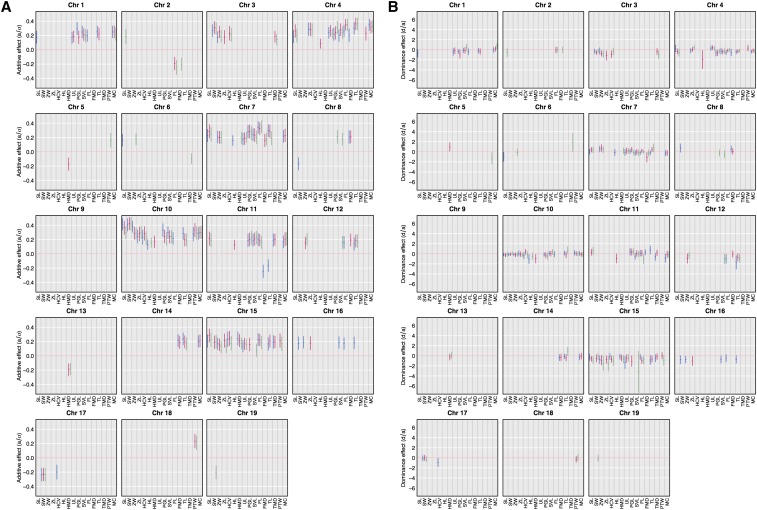
Standardized additive and dominance effects for all QTL are illustrated in Figure 4. Additive effects are small to moderate, ranging from 9 to 23% of the mean phenotypic differences between GI and WSB mice. The largest additive effect is 0.48 mm for skull width (SW) (chromosome 10 QTL at 10 weeks). Average values across traits of the standardized additive effect are also small: 0.23, 0.23, and 0.29 mm at 5, 10, and 16 weeks of age, respectively. The GI allele is associated with skeletal expansion at most QTL (93%); exceptions are primarily QTL for widths and diameters.

Figure 4.

Standardized (A) additive (a/σ) and (B) dominance (d/a) effects of skeletal trait QTL for 16 skeletal traits at 5 (in blue), 10 (in pink), and 16 (in green) weeks of age.

Inspection of standardized dominance values (d/a) reveals that the majority (63%) of QTL are codominant (d/a between −0.5 and 0.5). No QTL exhibit strong overdominance. The largest d/a ratio is 1.9 for the diameter of the tibia (TMD) QTL on chromosome 6 at 16 weeks of age; this is the only case of GI overdominance (d/a between 1.5 and 2.5). The GI allele is at least partially dominant (d/a between 0.5 and 1.5) at 6% of QTL. In contrast, WSB dominance (d/a between −0.5 and −1.5) is seen at 27% of the QTL. Only five QTL show values consistent with underdominance (d/a between −1.5 and −2.5) or strong underdominance (d/a < −2.5) of WSB alleles. The lowest d/a ratio (−3.2) is for the sacral vertebrae length (SVL) QTL on chromosome 15 at 16 weeks of age.

Accounting for body weight has disparate effects across QTL (Table S4). Many QTL are no longer significant, including loci on chromosomes 7, 10, 11, and 15. Some QTL are maintained, most of which map to chromosomes 4 and 14 and underlie pelvic and hindlimb traits. New QTL are identified in both weight-adjusted scans; many of these QTL also map to chromosome 14 and contribute to pelvic and hindlimb dimensions. Results depend on the method used to account for weight. QTL for skull and hindlimb traits on chromosome 7 are both maintained and acquired when shape ratios (trait/body weight^1/3) are used, but not when body weight is used as a covariate. QTL for skull and hindlimb traits on chromosomes 3 and 10 are maintained and acquired when body weight is used as a covariate, but not when shape ratios are used. Although there are some differences in results across the 5, 10, and 16 week time points, the overall patterns in the weight-adjusted scans remain similar, both in the traits involved and the chromosomal positions of QTL.

As a preliminary examination of epistasis, we tested for interactions among all pairs of single-trait QTL identified for each skeletal trait using the add.int function in R/qtl (Broman and Sen 2009). Out of the 430 tested QTL pairs, only 20 (5%) show a statistically significant interaction at the uncorrected P < 0.05 threshold, consistent with what we would expect based on chance alone.

Phenotypic correlations

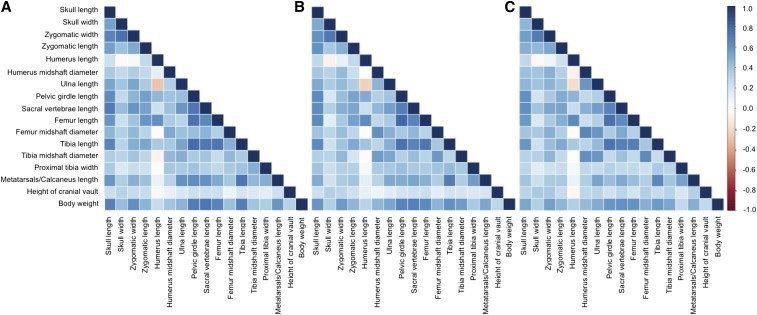
Most pairs of skeletal traits are positively correlated in the F₂s (Figure 5). High correlations are observed between measurements of the skull, pelvis, and hindlimb (absolute average Pearson’s r value = 0.54, 0.69, 0.62 at 5, 10, and 16 weeks, respectively; maximum P-value = 2.2e⁻¹⁶). Humerus length (HL) shows the most divergent pattern: weaker than average correlations with many traits and strong negative correlations with a few traits (absolute average Pearson’s r value across time points = 0.19; maximum P-value = 2.2e⁻¹⁶). Body weight is also highly correlated with all skeletal traits. Although correlation patterns are similar across the three time points, there are notable differences. The correlation between humerus length (HL) and the mid-shaft diameter of the humerus (HMD) changes during development, starting at 5 weeks as a positive correlation and ending at 16 weeks as a negative correlation (5 weeks: Pearson’s r = 0.11; P-value = 0.001; 10 weeks: Pearson’s r = −0.004; P-value = 0.875; 16 weeks: Pearson’s r = −0.08; P-value = 0.012). The correlation between the mid-shaft diameter of the femur (FMD) with both the mid-shaft diameter of the humerus (HMD) and ulna length (HL) increases during development. Intratrait correlations across pairs of time points are high and positive (Table S5). The earliest and latest time points (5 and 16 weeks) show a lower correlation compared to the correlations among consecutive time points.

Figure 5.

All pairwise phenotypic correlations among the 16 skeletal traits at 5 (A), 10 (B), and 16 (C) weeks of age. Values represent the Pearson product moment. A positive correlation is represented in blue, and a negative correlation is represented in red. The depth of color indicates the strength of the correlation.

Analyses of phenotypic correlations using MINT reveal evidence for modularity (nonrandom trait groupings) across the skeleton (Table S6). Overall, the null hypothesis of independence among traits fits the data poorly. Modules based on developmental timing (H₁) show the best fit at 5 and 10 weeks of age. In contrast, modules that separate the skeleton into axial and appendicular components (H₃) receive the most support at 16 weeks. Limb-specific analyses also support modularity. For models H₀–H₅, the limb length vs. diameter model (H₄) fits best for all three time points.

Principal component analysis

PC1 and PC2 collectively explain more than half of F₂ skeletal variation at each age (Figure S3A). Four QTL (on chromosomes 4, 7, 10, and 15) contribute to PC1 at all three time points. Two lines of evidence suggest that these loci are involved in global size expansion. First, they overlap with the QTL that affect the largest number of traits. Second, PC1 scores are highly positively correlated with body weight (Pearson’s r = 0.78; P < 0.0001), whereas PC2 scores are weakly correlated with body weight (r = −0.10; P = 0.003). A single QTL (on chromosome 4) contributes to PC2 across time points (Figure S3B). This locus overlaps with QTL that are maintained in analyses adjusted for body weight, suggesting that it contributes to the evolution of shape.

Multiple-trait QTL mapping

Multi-trait QTL mapping identifies QTL that are not found in single-trait mapping or principal component mapping, including loci that affect the skull, pelvis, and limb lengths (Table S7). Overall, LOD scores are higher and confidence intervals are narrower than in single-trait scans. Otherwise, multi-trait and single-trait analyses reveal similar genetic properties in terms of QTL colocalization across traits and temporal variation in QTL activity (Table S7 and Table S8).

Pleiotropy vs. linkage

All but one of the colocalizing skeletal QTL from single-trait analyses and body weight QTL from Gray et al. (2015) are consistent with pleiotropic models at 5 and 10 weeks of age (Table 2). Although additional QTL fit linkage models at 16 weeks, most QTL support pleiotropic models at this age as well. These results again suggest that colocalizing QTL are global regulators of growth rather than contributors to specific skeletal elements. Results for skeletal modules from multi-trait mapping are similar (Table S9). For whole-skeleton modules, pleiotropy is rejected for only 16 and 10% of QTL at 5 and 10 weeks of age, respectively (maximum P ≤ 0.03). Support for linkage is greater at 16 weeks of age (30%; maximum P ≤ 0.03). Limb-specific modules exhibit similar patterns (Table S9). These results raise the prospect that the majority of detected QTL control more than one trait within a given module. In cases where pleiotropy is rejected, it is possible to infer which traits are affected by each of the two linked QTL. For example, for the QTL on chromosome 4 for the hindlimb module at 5 weeks, a partitioning of limb length and diameter elements is inferred (Table S9).

Table 2. Tests of pleiotropy vs. close linkage.

Week	Chr	Traits with overlapping QTL	P	LOD	QTL 1 Pos	QTL 2 Pos	QTL 1 traits	QTL 2 traits
5	1	SL, UL, PGL, SVL, FL, TL, MC, BW	0.13	12.0	73.7
	3	SW, ZW, BW	0.52	6.3	58.3
	4	SL, ZL, UL, PGL, SVL, FL, FMD, TL, MC, BW	<0.01*	24.7	93.6	133.0	SL, ZL, UL, PGL, SVL, FL, TL, MC, BW	FMD
	7	SL, ZW, HL, UL, PGL, SVL, FL, TL, MC, BW	0.96	17.0	146.0
	10P	HCV, HL, BW	0.22	6.4	119.4
	10D	SL, SW, ZW, ZL, HCV, PGL, SVL, FL, TL, PTW, MC, BW	0.95	27.5	124.8
	11P	PGL, SVL, FL, MC, BW	0.23	8.1	19.3
	11D	FMD, TL, TMD, BW	0.19	16.8	96.5
	12	FL, TL, BW	0.16	5.5	75.6
	14	FMD, TL, MC, BW	0.87	7.9	71.9
	15	SL, ZW, HCV, HMD, UL, FL, TL, TMD, BW	0.81	11.6	48.7
	16	SL, ZW, SVL, FL, TL, BW	0.23	9.5	21.9
	17	SW, HCV, BW	0.86	5.6	49.8
10	1	UL, PGL, SVL, TL, MC, BW	0.07	6.9	159.6
	3	SW, ZW, ZL, HCV, TMD, BW	0.36	12.7	49.7
	4	SL, ZL, HL, UL, PGL, SVL, FL, TL, PTW, MC, BW	0.38	24.0	104.1
	7	SL, ZW, UL, PGL, SVL, FL, FMD, TL, MC, BW	0.25	14.9	95.4
	10	SL, SW, ZW, ZL, HCV, HMD, PGL, SVL, TL, PTW, MC, BW	0.97	26.5	120.8
	11	SL, HL, PGL, SVL, FL, MC, BW	0.06	6.8	19.3
	12	ZW, FMD, TL, BW	0.02*	8.7	27.7	79.8	ZW, FMD	TL, BW
	14	FMD, TL, MC, BW	0.06	6.0	40.0
	15	SL, SW, ZW, ZL, HCV, HMD, UL, PGL, FL, TL, TMD, PTW, BW	0.10	16.2	51.5
16	1	SVL, MC, BW	0.04*	6.1	136.2	170.1	MC	SVL, BW
	2	FL, FMD, BW	0.01*	10.4	120.7	161.3	FL, BW	FMD
	3	SW, HCV, BW	0.19	7.1	47.7
	4	SL, ZL, UL, PGL, SVL, FL, TL, MC, BW	<0.01*	32.2	86.5	105.0	UL, TL, BW	SL, ZL, PGL, SVL, FL, MC
	6	ZW, TMD, BW	0.03*	9.1	46.2	82.0	ZW, BW	TMD
	7	SL, ZW, HMD, UL, PGL, SVL, FL, FMD, TL, BW	0.34	16.9	95.4
	10	SL, SW, ZW, ZL, HCV, HL, PGL, SVL, TL, PTW, MC, BW	0.58	26.5	121.2
	11	SL, PGL, SVL, FL, MC, BW	0.66	7.6	16.8
	12	SVL, TL, BW	0.16	4.1	98.9
	15	SL, SW, ZW, ZL, HCV, HMD, UL, SVL, FL, PTW, BW	0.38	14.6	51.5

Tests for the rejection of pleiotropy (H₀) for sets of QTL for skeletal traits from single-trait analyses and QTL for body weight (from Gray et al. 2015) that have overlapping 1.5 LOD intervals. QTL positions (in megabases), LOD scores, and P-values (P) are provided for each set of QTL on a given chromosome (Chr). A large P-value indicates that the data are consistent with the pleiotropic model (H₀). An asterisk indicates statistical significance to reject pleiotropy (H₀), providing support for a model of close linkage. If linkage is supported, QTL 1 and QTL 2 positions, along with the partitioning of traits affected by each of the two linked QTL, are listed. Please see right panel in Figure 1 for the 16 skeletal traits measured, including names, acronyms, and descriptions of each trait.

Discussion

We uncovered pronounced skeletal evolution in GI mice. The entire GI skeleton expanded. Heterogeneity in the degree of expansion gave rise to anatomically local patterns of divergence, including a relatively longer and narrower skull and an elongation of proximal vs. distal elements of the limbs. Our genetic portrait of skeletal evolution in GI mice adds to a growing list of studies that reveal the genetic basis of rapid evolution in novel environments (Cresko et al. 2004; Shapiro et al. 2004; Colosimo et al. 2005; Abzhanov et al. 2006; Hoekstra et al. 2006; Pool and Aquadro 2007; Gray et al. 2015). We found QTL underlying global skeletal divergence. Over half of all QTL are located on only four chromosomes and contribute to variation in traits spanning the entire skeleton. In addition, we found QTL responsible for changes to specific elements.

The extensive colocalization of QTL for many traits raises the intriguing prospect that a modest number of genetic changes were responsible for the expansion of the GI mouse skeleton. Skeletal QTL on chromosomes 1, 4, 6–11, 15, and 16 colocalize with all but one of the QTL for body weight and growth rate discovered in the same cross (Gray et al. 2015), and colocalized loci show evidence of pleiotropy. This genetic architecture could facilitate morphological evolution across the body (Cheverud 1984; Roff 1997), with natural selection to increase body size generating correlated expansions of the skeleton. For example, pleiotropy has been hypothesized to enable rapid phenotypic divergence among dog breeds (Chase et al. 2002; Drake and Klingenberg 2010). At the same time, our inference of pleiotropy should be viewed with caution. The power to distinguish pleiotropy from linkage is constrained by mapping resolution, which is relatively low in an F₂ intercross.

By incorporating body weight into our genetic analyses, we were able to disentangle QTL effects on skeletal shape from QTL effects on overall body size. Skeletal QTL on chromosomes 7, 10, and 15 largely disappear after adjusting for body weight, suggesting that these loci act as global regulators of growth rather than affecting local skeletal traits. Allometric shifts in GI mice to a relatively long and narrow skull and to relatively elongated proximal limb elements are also captured by the genetic analysis using body weight as a covariate.

These alterations in skeletal size and shape may have functional consequences. The elongated skull—a feature that is atypical for house mice (Samuels 2009)—could indicate a shift toward a more specialized diet. Carnivores and insectivores sometimes exhibit an elongated rostrum (Samuels 2009), and GI mice eat birds and a variety of invertebrates (Jones et al. 2003). Changes in limb proportions are likely to affect locomotion. Mammalian species living in open habitats have relatively long femurs (Brown and Yalden 1973; Herrel et al. 2002), a characteristic that can facilitate running (Samuels and Van Valkenburgh 2008). Mice on Gough Island experience an open habitat compared to mainland mice, which primarily live in and around human structures. Functional and ecological studies will be required to test these hypotheses.

Some of the results highlight differences between the skull and postcranium. The most severe shape changes are found in the skull. Some QTL act only (chromosomes 17 and 19) or primarily (chromosomes 3 and 6) in the skull. Skull width and depth likely completed growth by 5 weeks of age; early growth differences between GI mice and WSB could be reflected in QTL specific to 5 weeks. An example is the chromosome 16 QTL that controls the width of the skull at 5 weeks, but is not detected at 10 and 16 weeks. The skull length measurement includes both the length of the braincase and the length of the face. Combining these early and late growing regions in one measurement might have reduced power to detect QTL. Measuring the craniofacial region with higher resolution is an important goal for future genetic studies of skeletal evolution in GI mice.

Evolution of the GI mouse skeleton appears to have been highly integrated. The similarity of phenotypic correlations across time points suggests that skeletal modules are largely determined by 5 weeks of age and that timing during prenatal development is a key component of inferred modules. For the whole skeleton, our results are consistent with processes observed in a variety of mammals, with skeletal development proceeding first along the proximal–distal axis, followed by development along the appendicular axis (Bronner et al. 2010). For limb traits, lengths appear to form distinct clusters from diameters. This pattern may also reflect developmental timing, since long bone lengths develop first at the epiphyseal plate with the addition of bone tissue, followed by thickening of bone via appositional growth (Pourquié 2009). Our results indicate that the joint consideration of suites of skeletal traits based on their phenotypic correlations and developmental origins leads to better connections between QTL and potential biological mechanisms.

Similar genetic studies in laboratory populations of house mice and in wild populations of other vertebrates provide illuminating comparisons to skeletal evolution in GI mice. The Large (LG) and Small (SM) strains of mice were artificially selected for body size, resulting in a >20 gram disparity in adult body mass (Goodale 1938, 1941; MacArthur 1944). Skeletal differences that arose as correlated responses to selection were mapped (Cheverud et al. 1996; Leamy et al. 1999; Vaughn et al. 1999; Klingenberg et al. 2001; Klingenberg and Leamy 2001; Kenney-Hunt et al. 2006, 2008; Norgard et al. 2008, 2011; Sanger et al. 2011). A subset of nine common measurements collected at the same age (10 weeks) enables comparison to our results, including skull (SW, ZW, and HCV), pelvic (SVL), forelimb (UL), and hindlimb (FL, TL) traits (Kenney-Hunt et al. 2008). Fourteen percent of QTL for seven of the nine traits from the LG × SM cross overlap with the GI × WSB cross. For example, QTL on chromosomes 3, 4, 7, 10, and 15 are identified in both crosses and exhibit similar additive and dominance effects. This sharing is disproportionately driven by loci that are pleiotropic. Although wide confidence intervals on QTL location raise caution in interpreting this pattern, it suggests that a small subset of the detected genetic changes could involve the same biological pathways, genes, and/or mutations. Distributions of standardized additive effects across all QTL (shared and unshared) are similar in the two studies, implying that artificial and natural selection acted on mutations with common properties. Nevertheless, the observation that most QTL locations appear to be distinct suggests that the evolution of large size in GI and LG mice mostly involved different genes.

The threespine stickleback, Gasterosteus aculeatus, a target of extensive genetic studies of skeletal evolution, also provides useful context for our findings. Sticklebacks that recently adapted to new freshwater environments diverged in skeletal morphology, including bony plate armor loss and pelvic reduction (Peichel et al. 2001; Shapiro et al. 2004). In contrast to skeletal evolution in GI mice, changes in both meristic traits (e.g., bony lateral plate number, gill raker number, and presence/absence of bony plates) and some continuous traits (e.g., spine length, pelvic size, and bony plate size) involve loci with substantial phenotypic effects (Peichel et al. 2001; Colosimo et al. 2004; Cresko et al. 2004; Shapiro et al. 2004; Berner et al. 2014). However, genetic studies of smaller components of stickleback morphology have found hundreds of QTL with small to moderate effects (Miller et al. 2014; Conte et al. 2015). Therefore, some skeletal traits in stickleback display genetic properties distinct from those observed in GI mice, but the breakdown of stickleback skeletal morphology into smaller components reveals a similar evolutionary trajectory involving many mutations of modest effect.

Finally, our results speak indirectly to the evolutionary causes of skeletal divergence in GI mice. Evolution of the skeleton was presumably rapid and occurred in a new environment, observations consistent with natural selection as a primary evolutionary mechanism. The finding that QTL alleles from GI mice increase skeletal size in almost all cases suggests that natural selection targeted the skeleton or a correlated trait (Orr 1998). Body weight and body condition of GI mice correlate with overwinter survival, and mice that prey upon nestling seabird chicks maintain higher body weights during the winter season (Cuthbert et al. 2016). These patterns raise the prospect that natural selection targeted overall body size in GI mice, driving substantial and rapid evolution of the skeleton.