EXPLORING THE REPRODUCIBILITY OF PROBABILISTIC CAUSAL MOLECULAR NETWORK MODELS

Abstract

Network reconstruction algorithms are increasingly being employed in biomedical and life sciences research to integrate large-scale, high-dimensional data informing on living systems. One particular class of probabilistic causal networks being applied to model the complexity and causal structure of biological data is Bayesian networks (BNs). BNs provide an elegant mathematical framework for not only inferring causal relationships among many different molecular and higher order phenotypes, but also for incorporating highly diverse priors that provide an efficient path for incorporating existing knowledge. While significant methodological developments have broadly enabled the application of BNs to generate and validate meaningful biological hypotheses, the reproducibility of BNs in this context has not been systematically explored. In this study, we aim to determine the criteria for generating reproducible BNs in the context of transcription-based regulatory networks. We utilize two unique tissues from independent datasets, whole blood from the GTEx Consortium and liver from the Stockholm-Tartu Atherosclerosis Reverse Network Engineering Team (STARNET) study. We evaluated the reproducibility of the BNs by creating networks on data subsampled at different levels from each cohort and comparing these networks to the BNs constructed using the complete data. To help validate our results, we used simulated networks at varying sample sizes. Our study indicates that reproducibility of BNs in biological research is an issue worthy of further consideration, especially in light of the many publications that now employ findings from such constructs without appropriate attention paid to reproducibility. We find that while edge-to-edge reproducibility is strongly dependent on sample size, identification of more highly connected key driver nodes in BNs can be carried out with high confidence across a range of sample sizes.

1. Introduction

Biological networks provide a graphical framework for organizing complex relationships among many thousands of variables in ways that can reveal coherent structures. These structures reveal knowledge and improve the understanding of molecular processes linked to higher order functioning of living systems. Vast arrays of data are being generated in numerous areas of biomedical research such as large-scale multi-‘omic’ studies across many cell types, comprehensive characterizations of microbiota living in and around us, advanced imaging data, and deep clinical characterizations of populations to name a few. This upsurge of big data has forced the life and biomedical sciences to rapidly turn to the use of network constructs. One such organizing framework for integrating data comes in the form of probabilistic network models that seek to capture the regulatory states of a system and their association to complex phenotypes such as disease. A particular class of probabilistic causal networks being applied to model the complexity and causal structure of biological data is Bayesian networks (BNs).

BNs are increasingly used in the field of genetics to describe and predict gene, metabolite, and protein level interactions. These networks are able to infer causal relationships among variables by employing mutual information or conditional independence measures based on Bayes Theorem. Since 2000 when this method was first applied to understand gene regulation¹, numerous studies have showcased the advantage of using such methods to uncover biological insights that are not easily captured through descriptive methods such as hierarchical clustering or coexpression network analysis. Whether predicting regulatory genetic drivers of complex phenotypes such as human diseases or enabling identification of novel drug target interactions and adverse side effects, BNs have helped uncover the individual genes and biological processes involved in a broad range of human conditions, including cancer, diabetes and obesity, asthma and COPD, cardiovascular disease, and Alzheimer’s disease^2–9. For example, BNs generated from ileal pediatric samples identified a causal gene resulting in a predictor for adult-onset inflammatory bowel disease¹⁰. As sample sizes increase, it can be envisioned that more groups will use BNs to predict individual response to treatment and it will enable fine-tuning for precision medicine¹¹.

Constructing a BN structure from data is an NP-hard problem with the complexity equaling O(nⁿ), where n is the number of nodes in the structure. Many heuristic approaches are applied in searching for an optimal structure from the given data. However, these heuristic methods may find many local sub-optimal structures with no guarantee of finding a global optimal structure. To achieve high accuracy BNs, especially with respect to edge direction, large sample sizes or “big data” are required^12,13. With the number of large datasets for which BN reconstruction algorithms could be applied growing at an exponential rate, the application of BN algorithms face a similar trend regarding the number of networks being constructed to derive data-driven hypotheses. However, assessing the reproducibility of BNs in the context of gene regulatory networks has not kept pace, with there being no studies to our knowledge systematically exploring this issue. Thus, we thought it crucial to test the conservation and reproducibility of BN constructions as a way to gain confidence in the methods currently used in the field. While significant work has been carried out to assess the construction methods that perform best across different types of biological data^14–16, these types of comparisons do not explicitly address the reproducibility of any given BN.

Perhaps among the gravest concerns in the field of biomedical research today is the lack of reproducibility. It is estimated that over $28 billion of research money, or roughly 50% of life-science research, is not reproducible¹⁷. The scientific method is rooted with principles of reproducibility giving credence to hypotheses only if they can withstand the scrutiny of many groups trying to reproduce them. In the current era of big data biology, the number of hypotheses generated in even a single publication can number in the hundreds (e.g., GWAS study on a complex trait). These hypotheses are difficult to validate across multiple groups, as the number of groups to rigorously pursue every hypothesis generated is limited. While intuition may argue that the large sample sizes and the robustness of the models may inherently address issues relating to reproducibility compared to traditional biological studies, recent claims indicate that about one quarter (25.5%) of studies not reproduced are due to data-analysis and reporting issues¹⁷. We therefore focused our study on the reproducibility of individual directed edges and key driver nodes of BNs, as these are generally considered targets for biological validation studies.

2. Study design

Two different gene expression datasets and a simulated dataset were used in this reproducibility study. The first gene expression dataset was obtained from the GTEx Consortium where RNA was extracted from multiple tissues from deceased, healthy individuals. Here, we used data from whole blood, which had a large sample size (N = 379)^18,19. The second gene expression dataset was comprised of atherosclerosis patients undergoing Coronary Artery Bypass Grafting (CABG) surgery, at which time multiple tissues were extracted and RNA sequenced from the Stockholm-Tartu Atherosclerosis Reverse Network Engineering Team (STARNET)²⁰ We chose to utilize the liver tissue (N=545), which contained the strongest eQTL signal²⁰, a prior in the BN reconstruction algorithm we employed that helps reduce the search space and resolve true causal relationships. By leveraging these real-world datasets, we are able to capture the complex correlation structures that derive from gene expression data measured in populations. RNA levels are high fidelity sensors of the state of the system and of technical noise, where the many different variance components (technical, genetic, micro- and macro-environment) form a complex covariance structure that is difficult to reproduce in simulated datasets. In addition, these two biological datasets represent not only two distinct tissues, but also reflect different states of disease and wellness (Table 1).

Table 1. Overview of datasets used.

This table provides details on the two datasets used in this study.

	GTEx	STARNET
Tissue	Whole Blood	Liver
Patient Status	Deceased - Healthy	Living - Undergoing CABG
# Samples	379	545
# Genes Used	455	385
Priors	cis eQTLs	cis eQTLs + Causal Inference Priors

To assess and compare networks in a thorough manner, we restricted attention to a subset of genes (N=465) that have been previously identified as highly informative for inflammatory diseases and associated with immune and inflammation response^{2,5,8,21–24}. By selecting this set of genes to use in the analysis, we reduced the computational time and cost required to generate each network.

In order to assess the reproducibility of BNs, we subsampled from the complete datasets to generate datasets reflecting different sample sizes under identical conditions. Towards this end, we subsampled the data in three ways: 1) a subsampling of 50% of the samples (referred to as the subsampled-50 networks), 2) a subsampling of 80% of the samples (referred to as the subsampled-80 networks), and 3) a subsampling of 90% of the samples (referred to as the subsampled-90 networks) (Fig 1). All subsampling divisions were replicated five times. The first scenario was intended to mimic the situation in which an initial study producing a BN is followed by an equivalent replication study producing a confirmatory BN, while the second and third scenarios represent incremental data releases, as happens in the context of large studies where data freezes are employed. The same process was used with the simulated dataset, however, here we were able to control the power and increased our sample size (N=1000) to the point of reaching near perfect reproducibility. For the simulated datasets, we subsampled at 50%, 80%, and 90%, with five replicates generated at each level. We also generated the simulated data at a subsampling of 10% to represent how data with limited noise is reproduced at a small sample size (N=100).

Figure 1. Schematic of the study design.

For all datasets, networks were generated using the Reconstructing Integrative Molecular Bayesian Networks (RIMBANet) algorithm^25,26 as the output has been validated extensively (see methods). When available, eQTL data as well as previous information regarding the causal association between several genes (nodes) in the network were used as structural priors^5,9,20,25,26. With BNs, the predominant method for assessing confidence of an edge is based on the posterior probability associated with that edge. This is computed either directly from the network model or is empirically estimated by generating a distribution of models and computing summary statistics across the networks comprising the distribution. We utilized the latter scenario where the posterior probability is approximated by computing the number of networks that contain a particular edge and dividing this number by the total number of networks generated. In this study, we considered nine different posterior probability thresholds (0.1 to 0.9 in 0.1 increments) to explore the reproducibility of edges across different confidence levels. Thus, for each dataset, we generated nine networks for the complete and each of the subsampled datasets.

3. Results

3.1. Exploring edge-to-edge reproducibility

Comparing BN’s is a multifaceted task in itself as they are complex representations of high-dimensional data. To provide a more intuitive comparison consistent with how BNs are used in practice in the life sciences and biomedical research spaces, we compared networks in two ways: 1) by evaluating the confidence levels of individual edges and 2) by evaluating the higher-level topology of the network.

Given the stochastic search employed in the BN construction process, we first compared five networks generated on the complete dataset (includes all samples) for each cohort to characterize the degree of variability. As depicted in Table 2, at a posterior probability of 0.1, both datasets have a mean edge overlap of 99%. While the edges with high confidence (at a posterior probability >0.9) are found on average 97% in other replicates in GTEx and 96% in STARNET, we observe that 100% of these edges are present in other replicates when the posterior probability is > 0.5.

Table 2. Overlap of five replications of complete BN.

For each posterior probability, all combinations of replicates were looked at to calculate the percentage overlap divided by the total edges of each replicate. Here we report the mean percentage and standard deviation.

Posterior Probability	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
GTEx	99% (± 0.008)	99% (± 0.008)	99% (± 0.007)	99% (± 0.008)	99% (± 0.008)	99% (± 0.006)	99% (± 0.004)	98% (± 0.01)	97% (± 0.02)
STARNET	99% (± 0.01)	99% (± 0.01)	99% (± 0.01)	99% (± 0.01)	98% (± 0.01)	99% (± 0.02)	99% (± 0.01)	98% (± 0.02)	96% (± 0.02)

As the stochasticity of the BN reconstruction process does not seem to affect the reproducibility of the BNs, we next calculated the Jaccard index with respect to all network pairs within a given subsampled set (Table 3). The Jaccard index is a measure commonly used when comparing sets, and ranges from 0, for completely unrelated sets, to 1, for highly similar sets. In our case, the edge counts between replicates are comparable when the number of samples and posterior probability are the same (see standard deviations in Table 4), thus the maximum Jaccard index should be close to 1 (complete reproducibility). The Jaccard index had a mean of 0.27 when comparing edges from the subsampled-50 networks across the different posterior probability thresholds within the replicates or to the complete network within each cohort (Table 3). Interestingly, the Jaccard index achieved values close to 0.5 for edges from the subsampled-90 networks (Table 3), which is very different from the values we saw when comparing the replicates of the complete networks (mean >0.95 in both at a posterior probability >0.1). These results suggest that even with 90% overlap of samples, the edge-set overlap can still be different, highlighting significant reproducibility issues even among highly comparable sample sets. The data suggests that statistical power in resolving network relationships may be primarily responsible for the lower than expected reproducibility, an issue that can be experimentally addressed by increasing the sample size.

Table 3. Jaccard index values.

We calculated the Jaccard index (intersection divided by union) for the edges found in the networks at each posterior probability threshold. We compared the subsampling networks to their respective replicates and to the complete BN at the same posterior probability threshold. Standard deviation ranges from 0.01–0.04 in all cases.

		GTEx		STARNET
Sub- sampling	Posterior Probability	To Other Replicate	To Complete	To Other Replicate	To Complete
	0.1	0.23	0.26	0.22	0.27
50%	0.5	0.23	0.26	0.21	0.27
	0.9	0.20	0.20	0.16	0.19
	0.1	0.34	0.40	0.37	0.43
80%	0.5	0.34	0.40	0.36	0.43
	0.9	0.29	0.33	0.26	0.35
	0.1	0.44	0.51	0.43	0.52
90%	0.5	0.43	0.53	0.43	0.52
	0.9	0.33	0.39	0.36	0.42
	0.1	0.98		0.97
Complete	0.5	0.98	---	0.97	---
	0.9	0.95		0.93

Table 4. Number of edges in each network.

We calculated the number of edges present in each subsampled network. Displayed are the mean and standard deviation for number of edges at select posterior probabilities.

	GTEx			STARNET			Simulation
Sub- sampling	0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9
10%	---	---	---	---	---	---	209 (± 4.637)	192 (± 3.391)	47.4 (± 5.030)
50%	297.8 (± 8.349)	257.2 (± 3.271)	89 (± 9.055)	291.4 (± 5.683)	262.4 (± 4.336)	113.6 (± 11.393)	345.2 (± 3.493)	329 (± 2.550)	149.8 (± 7.396)
80%	390.8 (± 5.586)	343.6 (± 5.459)	136.6 (± 5.459)	373.2 (± 8.349)	329.8 (± 2.775)	135 (± 8.337)	380.6 (± 4.722)	368.6 (± 1.342)	149 (± 4.000)
90%	414.4 (± 6.465)	365 (± 5.099)	135 (± 4.950)	395 (± 6.205)	350.6 (± 3.647)	144.6 (± 3.782)	385.2 (± 1.095)	373.8 (± 3.493)	185.4 (± 8.081)
Complete	441.6 (± 0.894)	388.4 (± 1.517)	138.2 (± 2.280)	396.8 (± 4.382)	364.2 (± 4.025)	151 (± 1.225)	393.2 (± 0.447)	379.8 (± 0.447)	189.8 (± 0.837)

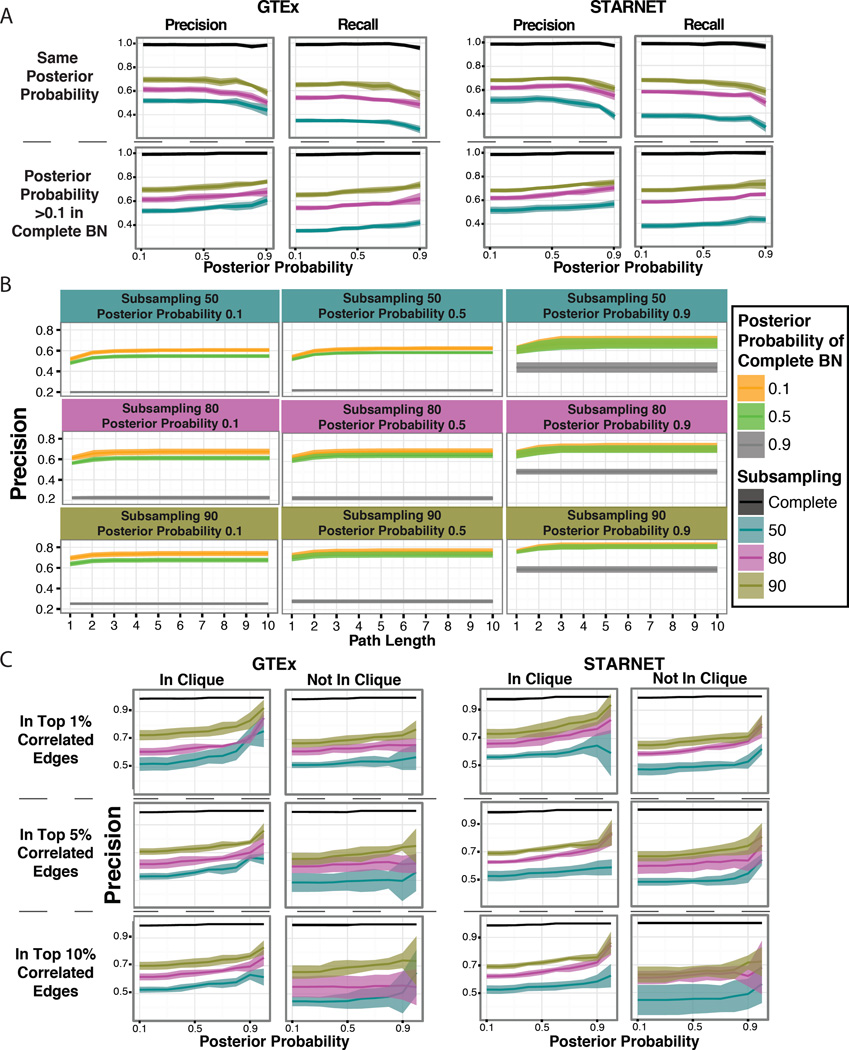
The number of edges in a BN is at least partially a function of power, given that as sample size increases, an increase in the number of edges in the BN is observed (Table 4). Thus, a more applicable measure for assessing reproducibility among networks is by looking at the number of overlapping edges between a subsampled network and the complete network, divided by the number of edges in the subsampled network. This measure relates to precision or positive predictive value, given here we accepted as truth the complete network (in the context of the simulated data, true and false positives are known with certainty). The flip side of precision is recall, or sensitivity, defined by dividing the overlap number of edges by the total number of edges in the complete network (Fig 2A).

Figure 2. Edge reproducibility rate.

In panel A, we compared the number of edges present in the complete BN to the subsampling network at the same posterior probability (top half) and by fixing the threshold for the subsampling networks but allowing any edge for the complete BN (posterior probability >0.1) as seen in the bottom half. In panel B, we show the results from the GTEx data as we allow for edges to be considered reproduced if there is a connection in the complete BN between those two nodes at a path length up to 10. In panel C, we illustrate the percision of edges depending on if the nodes are in the same correlation clique or not. For all panels coloring depicts the subsampling networks and the complete BN.

For both GTEx and STARNET, when comparing the subsampled and the complete network at the same posterior probability cutoff, we found that on average 44% of GTEx and 38% STARNETs’ most confident edges (posterior probability >0.9) in the subsampled-50 networks were reproduced, and this increases to 58% in GTEx and 61% in STARNET for the subsampled-90 networks (Fig 2A). We observed a trend of the precision increasing as the posterior probability increased to 0.4–0.5, but then observed a decrease as the confidence in the edges increased (Fig 2A). This is most likely due to a decrease in the number of edges in the BNs as the posterior probability increases (Table 4). We further evaluated the precision by relaxing the posterior probability for edges in the complete network to >0.1 (Fig 2A). In this case, on average 61% in GTEx and 57% in STARNET of the most confident edges (posterior probability >0.9) were reproduced in the subsampled-50 networks whereas for the subsampled-90 networks 76% in GTEx and 75% in STARNET were reproduced (Fig 2A).

The above definitions of precision at the edge level require the presence of the exact same edge, whereas causal relationships in one network may also be reflected in a different network via intermediary nodes. For example, in one network an edge might be present from A → B (path length=1) and in a second network it may appear as A→C→B, where there is a path from A to B, but via C (path length=2). We hypothesized that this may explain some portion of the edges that failed to reproduce. To test this, we further evaluated if two connected nodes from the subsampled networks were connected in the complete network within a path length of ten. For the GTEx BNs, we saw that in the subsampled-50 networks, the precision increased to an average rate of 67% (up from 61%) at a path length of five for the most confident edges (posterior probability >0.9), while in the subsampled-90 networks, the precision increased to an average rate of 81% (up from 76%) at a path length of three (similar results were seen for STARNET as well). The precision increased with both the path length and sample size (Fig 2B). It should be noted that after a path length of 3, the precision plateaus, providing confidence that increasing the path length further would not have added any new information in the context of our networks.

BNs reflect complex correlation structures or rich substructures in which the expectancy of certain nodes to be more or less connected may be contained within the network. Higher-order correlation structures have been informative for the underlying biology from large datasets^13,27. To explore whether the correlation structure of the data affected edge reproducibility, we examined whether genes in clique structures (groups of highly interconnected genes) were more or less likely to be reproduced, compared to the average precision of the network. For each data set, we computed the correlation matrix and took the top 1%, 5% and 10% most correlated values to build an undirected, correlation-based network. We focused on the most stringent correlation criteria to define edges, which was the top 1%. From these networks we were able to call all clique communities using the program COS (https://sourceforge.net/projects/cosparallel/). This enabled us to determine if both nodes of an edge were included in the same clique. We found that the precision was further improved in edges whose nodes were found in the same clique (Fig 2C). In the STARNET subsampled-90 networks, the most confident edges (posterior probability >0.9) present in a clique obtained using the top 1% correlated values had a mean precision measure of 85% compared to 71% for edges in which both nodes were not found in the same clique (whereas all edges had a mean precision of 75%). In the subsampled-50 networks, the edges in a clique had a precision rate of 65% versus 53% for edges comprised of nodes that did not both fall within the same clique (whereas all edges had a mean precision of 57%). The GTEx dataset provided similar results, showing that we were able to improve the precision of edges by incorporating correlation clique information.

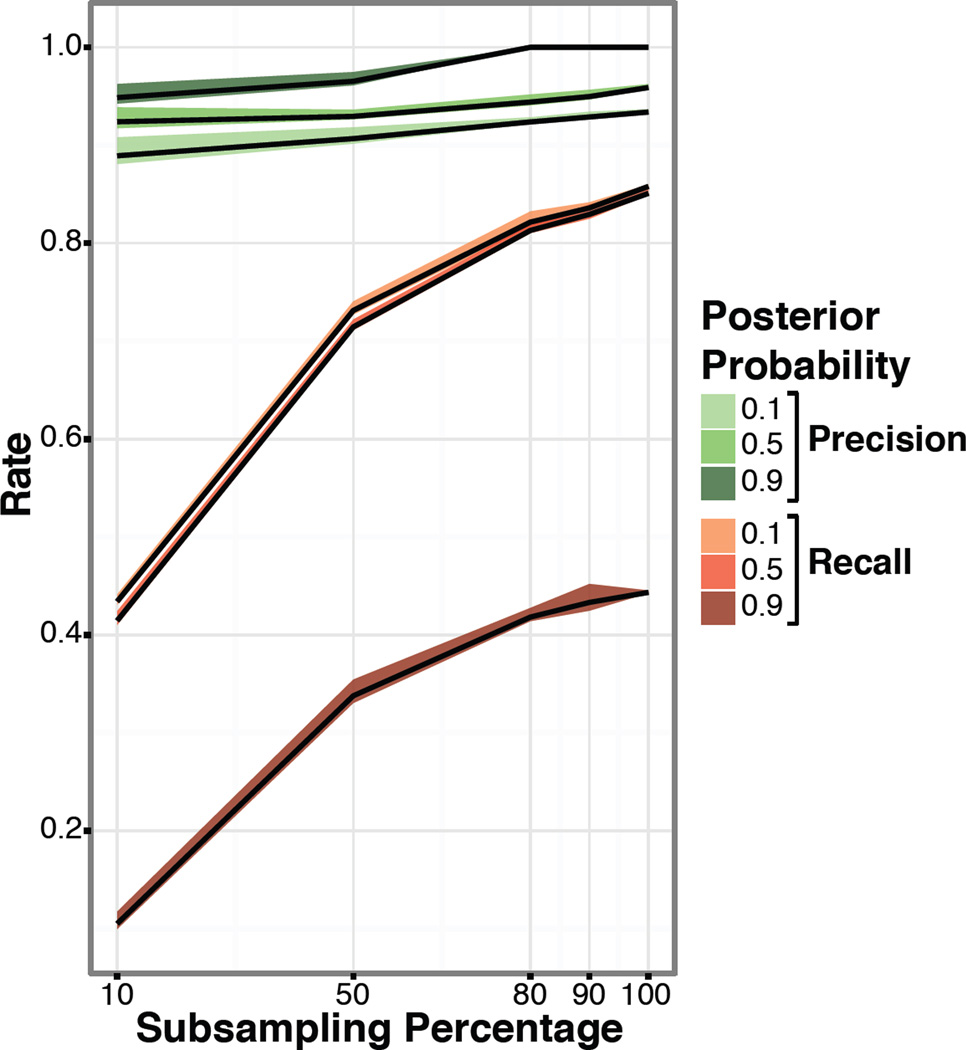
Precision and recall trends with the simulated datasets were similar to those observed in the biological datasets. This confirmed not only that our simulated data was reflective of the biological datasets, but also that by increasing sample size we could address the edge-level precision and improve recall (Fig 3). Thus, as larger datasets are generated, the issue of reproducibility of networks should be addressed.

Figure 3. Simulation data precision and recall.

We simulated a BN for 300 nodes, 1000 samples with discrete data and looked at the precision and recall for the subsampling at 10%, 50%, 80%, 90%, and 100%. The color scale represents the posterior probability threshold. We show the mean and standard deviation for the five replicates.

3.2. On the reproducibility of key driver nodes

Another important aspect of BNs is their higher order topology. Not all nodes in a BN are equivalent, but rather some are more connected having a substantial causal impact on many more nodes in the network (referred to here as key driver nodes, or KD nodes). One way to assess reproducibility of these types of important topological features is by examining the reproducibility of KDs. KD nodes are important and commonly inferred from networks as they help elucidate the regulatory states of complex systems, and are crucial from a diagnostic and drug discovery standpoint^2,5,28. Thus, we decided to assess the reproducibility of the detection of these types of nodes.

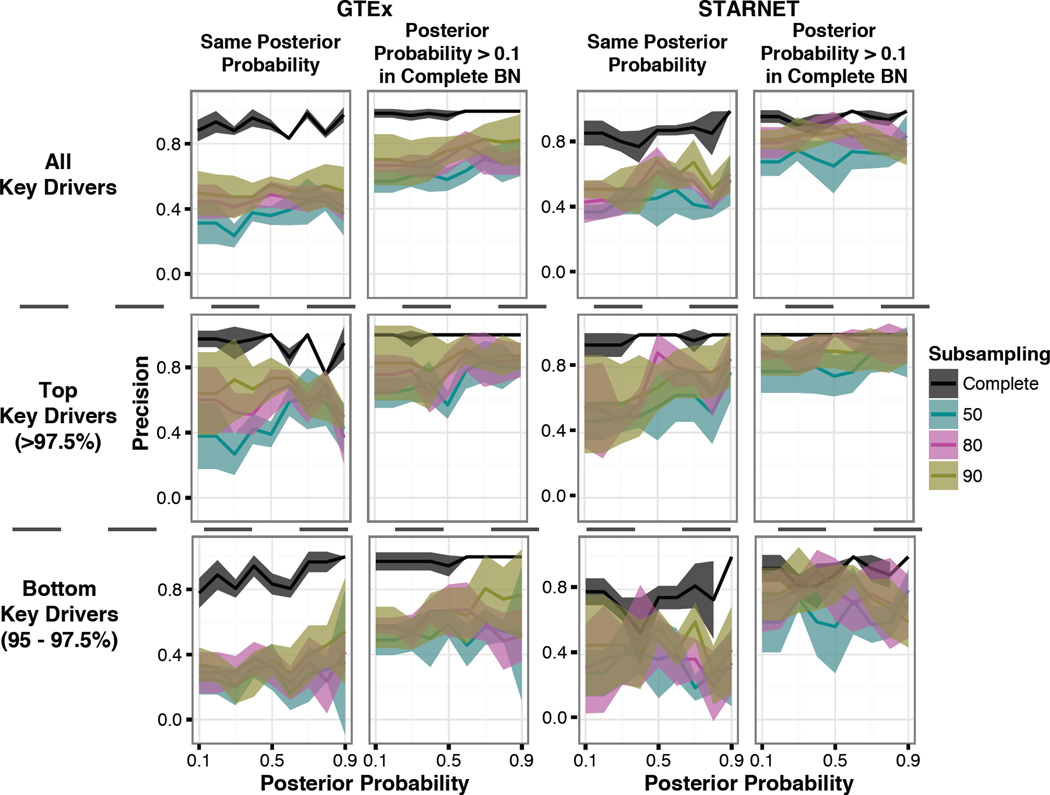
We calculated the KDs for each network built at each posterior probability threshold and assessed the precision of the KDs in the same manner applied to the edges (see methods). First, we evaluated the overlap of KDs between the complete and subsampled networks when they were built at the same fixed posterior probability. To see if a difference between the ranking of KDs and their precision could be measured, we defined the top KDs as being in the 97.5 – 100 percentile and bottom KDs as being in the 95 – 97.5 percentile. When evaluating the KDs of the network built from the most confident edges (posterior probability >0.9), we found that the top KDs from the subsampled-90 networks were reproduced at an average rate of only 49% while the bottom KDs were reproduced at an average rate of 54% in GTEx. In STARNET, the top KDs were reproduced at an average rate of 85% while the bottom KDs were reproduced at an average rate of 43% (Fig 4). To see if we could improve the reproducibility rate, we relaxed the threshold for the complete BN and allowed for the KD to be present at any posterior probability (similar to what was done with the edges). This drastically improved the reproducibility of the KDs. In GTEx, the top KDs from the subsampled-90 networks built on the most confident edges (posterior probability >0.9) were reproduced at an average rate of 87% while the bottom KDs were reproduced at an average rate of 77%. A similar evaluation of the STARNET results showed the top KDs were reproduced on average 93%, while the bottom KDs were reproduced at 60%. We saw in the subsampled-50 networks, at a posterior probability >0.5 that while the edge-overlap was on average 54% in GTEx and 53% in STARNET, the KD overlap was 58% in GTEx and 66% in STARNET. In the subsampled-90 networks, where the edge-overlap was on average 72% in GTEx and 71% in STARNET, the KD overlap increased to 76% in GTEx and 87% in STARNET. The KDs performed as well if not better than the edges, indicating that the KDs of BNs are more conserved than edges. Since the networks with fewer samples have fewer edges present, it could help explain why we see such low precision in the subsampled-50 networks. These results further support that a larger sample size, or increased power, will lead to more reproducible KDs.

Figure 4. Precision of key driver (KDs).

Precision is the % KDs of the subsampling network present in the complete BN (at either the same posterior probability threshold or at any). Left panel shows all KDs; Middle panel shows Top KDs (top 97.5% based on the weighted number of connections, see methods); Right panel, shows bottom KDs (95 – 97.5%). Mean and standard deviation for the five replicates are displayed, and color depicts subsampling.

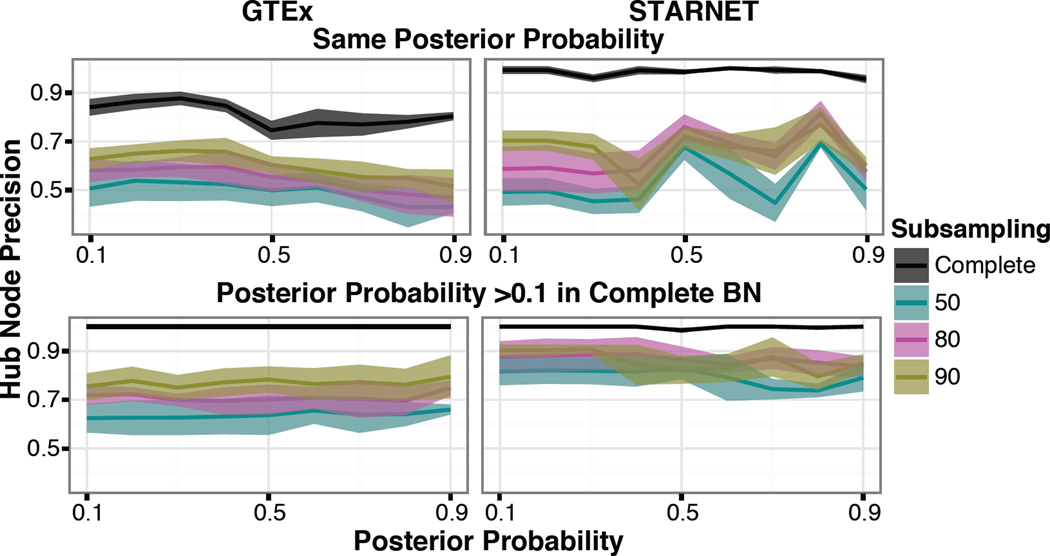
As the KDs take into account the shortest path to reach all nodes, we thought to additionally assess nodes with the highest number of first-degree downstream targets, hub nodes. These nodes have the most local and direct impact on other nodes. Here we took the top 10% of nodes based on their total number of out edges and applied the same analysis pipeline defined above for KDs. We found that when the posterior probability >0.1 for the complete network, the hub nodes were more reproduced in the subsampled networks, as can be seen by the subsampled-90 networks reaching an average rate of 78% in GTEx and 83% in STARNET at a posterior probability threshold of 0.5 (Fig 5). However, if we hold the posterior probabilities constant in both the complete and subsampled networks, the precision fluctuates in the GTEx dataset but appears to perform better in the STARNET dataset. This could be explained by the larger sample size of the STARNET dataset.

Figure 5. Hub nodes precision.

We define hub nodes as nodes in the 90^th percentile based on the number of first degree out edges. The top half illustrates the precision when the posterior probability is the same in both the subsampling and the complete BN. The bottom half illustrates the precision when the posterior probability in the subsampling network is fixed but the hub node in the complete BN can be at any posterior probability. The mean and standard deviation for the five replicates is displayed and color depicts subsampling.

4. Discussion

In this study on the reproducibility of BNs in the context of regulatory gene networks, while we found a high degree of reproducibility at the edge and key driver node levels, we also noted that a large proportion of edges and key driver nodes were not reproduced. Given the rate at which edges and key driver nodes did not reproduce in networks constructed from a moderate number of samples, caution should be exercised when interpreting specific features of a network. Validating hypotheses generated from networks is critical to ensure the accuracy of network predictions. However, we also observed that the lack of reproducibility might be attributed to power issues, which can be straightforwardly addressed by increasing sample sizes for network reconstructions. As obtaining large sample size is difficult and expensive, our results stress the need to assess the reproducibility of methods being deployed in the field. We must be aware of limitations so we can strive to improve them.

While we restricted attention to a coherent subset of several hundred genes to contain computational costs, we have observed similar trends in BNs built on 10,000 or more genes using the GTEx whole blood samples, suggesting that the subset of genes used was a good proxy for how larger networks of genes would behave. Ideally, we would have run our analysis on a completely validated BN from a biological dataset. However, at the time of this study, such a validated network was not available. Instead, we complemented our study of networks constructed from gene expression datasets with examination of simulated datasets containing discretized data for a comparable number of genes.

We used structural priors to generate the BNs, which could bias the structure of the resulting networks. However, we saw a decrease in precision and recall when priors were not used, further demonstrating the importance of high-confidence priors. We chose to include priors as this is typically done in practice today and their use has shown to increase accuracy of networks based on smaller sample sizes²⁶.

The reproducibility of KDs was of particular interest, given the role they play in current biological investigations of complex systems. KDs represent central information flow points in the network that are identified in disease studies as potential targets of therapeutic intervention or as features that may be critical as biomarkers of disease. We observed that KDs were more reproduced than edges. This suggests that while the edges may be less conserved due to nonlinear interactions or stochasticity, the overall structure of the network may still be well conserved, explaining the increased confidence in key driver node predictions. In particular, the top KDs, which are most connected and predicted to significantly impact network states, were reproduced at exceptionally high rates.

As biomedical and life sciences research gravitates toward network-based constructs, issues of reproducibility will come front and center. It is critical to characterize network reconstruction methods from the standpoint of what is required to lead to reproducible structures that in turn, lead to high-confidence hypotheses. Our analysis shows that well-powered Bayesian networks are highly reproducible. Since high power is not always possible to achieve because samples are scarce and assays are expensive, our results provide guidance on interpreting and using Bayesian networks. In cases of diminished power, it is critical to realize that key drivers, in particular the strongest key drivers, and hub nodes are more robustly reproduced than individual edges.

5. Methods

Bayesian Network Construction

RIMBANet was used to construct all Bayesian Networks^9,12,26. Continuous data was used for calculating partial priors, which are then used as priors in the network construction. Additional priors included genes that are cis eQTLs and the results from the causal inference test of cis gene → trans gene (for STARNET only)^20,29. For the eQTL priors, if a gene also has a strong eQTL associated with it in cis, such a gene can be considered as a parent node, given the genotype cannot be the effect of a gene expression change. The data was discretized into 3 states for each gene: high expression levels, low expression levels and unexpressed. This is done by first normalizing the values for each gene to ensure a normal distribution. Then, k-means clustering (k=3) is used with the option of dropping groups should there not be enough members to fill it to assign the values for each sample. In a case where there are only two clusters they would be classified as high and low³⁰. For the sake of quicker run times, when looking for the parents of each gene, the other genes were sorted by their mutual information and only the top 80% were considered as candidates. Also, the maximum number of parent nodes that were allowed for any given node was set to 3. After running successfully 1,000 reconstructions, the networks were pooled together. Finally, because a BN is a directed acyclic graph (DAG) by definition, the consensus network was obtained by searching for the shortest cycle and then the edge with the weakest weight (the smallest number of times it occurs in 1,000 reconstructions) was removed. This process was repeated until no cycles were present and the resulting network was a DAG.

Generation of Simulated Dataset

To generate the synthetic true network, we used the SynTRen software v1.2³¹. We extracted a subnetwork with 300 nodes from the background source network “DAG1_clean.sif” with default settings. We limited the node selection to 300 nodes to reduce the computational time required to generate all of the networks and to mimic the size of the biological datasets used in this study. Next, to generate the synthetic discretized data from the known network structure, we utilized Bayes Net Toolbox (BNT) for Matlab [https://code.google.com/archive/p/bnt/]. The conditional probability was customized so that we could discretize the data into three bins, similar to RIMBAnet. Given the configuration of parent node, the child nodes were skewed towards one of the three discretized states with a probability between 0.8 and 0.9, therefore, ensuring assignment to a given bin with high confidence.

Key Driver Node Detection

Key driver nodes (KDs) were detected by calculating the shortest downstream path length between each pair of nodes in the network. For each candidate key driver node, we took the inverse of path length between the candidate key driver node and every other node in the network. We then summed the inverse path lengths to obtain a final score per node. Based on this calculation, we defined nodes in the 95th percentile as KDs⁵. We define top KDs as nodes in the 97.5 – 100 percentile and bottom KDs as nodes in the 95 – 97.5 percentile. Code and data can be found at https://github.com/divara01/PSB2017_ReproducibilityOfBNs/ and http://research.mssm.edu/integrative-network-biology/Software.html