Statistical Methods for Analyzing Ancient DNA from Hominins

Abstract

In the past few years, the number of autosomal DNA sequences from human fossils has grown explosively and numerous partial or complete sequences are available from our closest relatives, Neanderthal and Denisovans. I review commonly used statistical methods applied to these sequences. These methods fall into three broad classes: methods for estimating levels of contamination, descriptive methods, and methods based on population genetic models. The latter two classes are largely methods developed for the analysis of present-day genomic data. When they are applied to ancient DNA (aDNA), they usually ignore the time dimension. A few methods, particularly those concerned with inferring something about selection or ancestor-descendant relationships, take explicit account of the ages of aDNA samples.

Although mitochondrial DNA (mtDNA) sequences have been obtained from human fossils since the 1980s and from Neanderthals since 1997, only since 2010 have nuclear DNA sequences been obtained in any abundance. A variety of statistical methods have been applied to hominin aDNA but only a few are widely used.

“Model free” methods

Some methods of analyzing aDNA data are purely descriptive. Principal components analysis (PCA) is the most commonly used. PCA assumes nothing about population genetics and is in that sense model free. Other methods (notably D- and F-statistics), make some assumptions about population genetics but do not yield estimates of population genetic parameters. They are used primarily to test for the occurrence of admixture. Other methods discussed later are based on population genetic models and estimate parameters of those models.

Principal components analysis

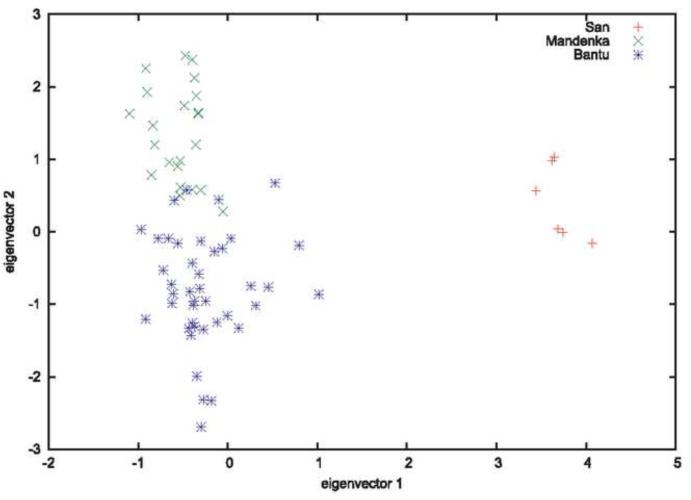
In population genetics, PCA is usually performed by finding the eigenvalues and eigenvectors of the matrix of covariances of allele frequencies between all pairs of individuals. [1] The highest order eigenvectors indicate the directions in the high dimensional allele-frequency space which account for most of the covariance. Often the individuals are plotted on the plane spanned by the first two eigenvectors. An example is shown in Figure 1. Relative distances in this space indicate their overall similarity. PCA is convenient because it is both easy to use and may provide a visually compelling result. For example, in an analysis of European populations, Novembre et al. [2] found a close correspondence between the geographic locations of individuals and their locations in principal components space.

Figure 1.

Example of principle components analysis. Plots of the first two eigenvectors for some African populations in the CEPH–HGDP dataset. (Figure 4 from reference [1]).

Ancient DNA sample are routinely combined with present-day samples in PCA. Usually the goal is to determine which present-day population an ancient sample is closest to. Drawing inferences about the relationship between the ancient and present-day samples requires additional assumptions. Skoglund et al. [3] showed that time differences in samples can be reflected in one of the principal component axes. Duforet-Frebourg and I [4] found that the sufficient migration between the time the ancient sample was taken and the present day can cause the ancient sample to not cluster with its present-day counterpart.

D-statistics

D-statistics are unusual in that they were first used with aDNA and have since been applied to present-day samples. They provided key evidence that Neanderthals and modern humans admixed. [5] D-statistics are computed for sets of four samples whose relationships are represented by a tree as shown in Figure 2. For analyzing Neanderthal admixture, H₁ and H₂ are two different present-day human genomes, N is the Neanderthal genome and C is the chimp genome. At each site, one nucleotide is chosen randomly from each genome and counts are made of sites at which both C and N differ and H₁ and H₂ differ. (H₁, H₂,N,C) is the percentage of sites at which N and H₂ share alleles. If there had been no admixture between N and both H₁ and H₂, then D(H₁, H₂,N,C) is expected to be 0. If there is admixture between N and H₂, then D will be positive.

Figure 2.

Illustration of population tree. In the application of D-statistics to Neanderthals, H₁ and H₂ were two different genomes from human populations (e. g. French and Yoruban), N was the Neanderthal, and C was the reference chimpanzee.

D provides a sensitive test for admixture because of the symmetry inherent in the population tree if there is no admixture. The symmetry takes account of incomplete lineage sorting provided the ancestral population has no geographic substructure. Furthermore, because sites are counted only if two copies of both alleles are seen, D is relatively insensitive to different levels of sequencing error in different genomes. [6] That is important because, if one of the genomes is from a fossil, its error rate is likely to be higher. In fact, in general it is unwise to assume the same error rate for sequences obtained in different laboratories using different sequencing platforms.. D does not directly estimate the admixture rate unless detailed assumptions are made about the branch lengths of the population tree, the time of admixture and the history of population sizes. [6]

F-statistics

F-statistics, which are closely related to D, were introduced by Patterson et al. [7]. Like D, F-statistics are used primarily to test for admixture. They are somewhat different from Wright’s F-statistics (F_IS, F_ST etc.) [8]. Here, the term F-statistics will be used only for those defined by Patterson et al. There are three F-statistics, denoted by F₂(P₁, P₂), F₃(P₁; P₂, P₃) and F₄((P₁, P₂,; P₃, P₄) where the P’s are the populations being compared. These statistics are designed to quantify the amount of genetic drift on different parts of a population tree. Because they focus on genetic drift and not mutation they assume that the all alleles are present in an ancestral population. That constraint is satisfied if all sites analyzed were determined to be polymorphic in a population that is an outgroup to those analyzed. For human populations, that condition cannot be satisfied in most cases. In practice, F-statistics are applied to both SNP array data and whole genome data without taking account of the effect of new mutations. Patterson et al. [7] found by simulation that in some cases, mutation does not affect conclusions drawn.

F₂ is defined to be the average across loci of (p₁ − p₂) where p₁ and p₂ are the frequencies of a diallelic SNP in P₁ and P₂. F₂ is additive along branches of a tree. F₂ measures the time separating P₁ and P₂ in units of the effective size of the intermediate population. Mutation will change this interpretation somewhat because the influx of variants by mutation depends on the history of population sizes, not merely the overall effective size.

F₃ (P₁;P₂,P₃) is the average of (p₁ − p₂)(p₁ − p₃) across sites. It will be positive for any three populations that have a tree-like history—for example H₁, H₂ and N in Figure 1—but it can be negative if P₁ is the product of admixture between P₂ and P₃. This statistic is often used as a test for admixture. F₄(P₁,P₂;P₃,P₄) is the average of (p₁ − p₂)(p₃ − p₄) across sites. It quantifies the covariance between the accumulated differences between P₁ and P₂ and between P₃ and P₄. If these two pairs do not share a branch of a population tree, then the covariance will be zero, a conclusion that is unaffected by incomplete lineage sorting. F₄(P₁,P₂;P₃,P₄) can be regarded as the numerator of D(P₁,P₂,P₃,P₄) . Using F₄ to test for admixture is equivalent to Cavalli-Sforza and Piazza’s [9] test of treeness.

Linkage disequilibrium and introgressed fragments

Admixture from one population to another results in the production of hybrid offspring that carry one parental chromosome from each population. Subsequent interbreeding and recombination break down introgressed chromosomes into shorter fragments. Several methods have used this process both to provide evidence of admixture and to estimate the time when admixture took place. There are two classes of methods. One uses the extent of linkage disequilibrium between pairs of sites. The method rolloff [7] is of this type. Sankararaman et al. [10] used a similar method to estimate the date of admixture from Neanderthals into human populations.

The other class of methods uses the lengths of fragments that derive from another population. These methods have been particularly useful for characterizing admixture from Neanderthals into humans because Neanderthal and humans differ sufficiently that identifying introgressed Neanderthal fragments is relatively easy. Several groups have taken this approach. [11-15]

Population genetic models

George Box’s dictum "All models are wrong but some are useful"[16] applies with special force in population genetics. It is hopeless to think that the complexity of human history can be represented by any model. Yet, the right model can capture the essential events that account for broad patterns in genomic data. Many computer-intensive methods have been developed to estimate model parameters, among others dadi [17], fastsimcoal2 [18], and G-PhoCS [19]. None of these widely used programs is tailored to aDNA. When they are used with ancient samples, the effective size in the branch leading to the ancient sample is reduced to reflect the shorter time available for genetic drift to act.

TreeMix

Pickrell and Pritchard [20] developed the program TreeMix to both test for whether a set of samples fits a population tree and, if they do not, which admixture events were mostly likely to have occurred. TreeMix has been widely applied to aDNA samples combined with present-day samples because, although it is model-based, it does not require an assumption-rich model. It begins by assuming that populations sampled have a history represented by a population tree. It then tests the tree hypothesis against alternative models that allow for admixture between different branches of the tree. It adds admixture events until the data are adequately explained. TreeMix achieves its computational speed by approximating the process of genetic drift by a Gaussian random walk.

Inferring the history of population sizes

The demographic history of a population determines the distribution of pairwise coalescence times in a population. This fact has been exploited by several programs that reconstruct the history of population size by estimating the coalescent time distribution. If a genome is sequenced to sufficient depth that heterozygotes can be identified with high confidence, even a single genomic sequence can be used. Li and Durbin [21] developed PSMC (for pairwise sequentially Markovian coalescent), a model that efficiently estimates past population sizes of a single population. Refinements of this type of method have been developed by Sheehan et al. [22] and Schiffels and Durbin [23]. PSMC is popular for the same reasons that TreeMix is. Although PSMC is based on a model of genetic drift, it makes few assumptions because it needs to model only the population ancestral to the population sampled.

Testing for direct ancestry

Rasmussen et al. [24] developed a test for direct ancestry of an aDNA sequence that is essentially model-free, even though it is presented in the context of coalescent theory. The test is especially convenient because it is applicable to pairs of sequences, one present-day and the other ancient. It is a likelihood ratio test of whether the length of the branch leading to the aDNA sequence is zero. If the branch is non-zero in length, then a maximum likelihood estimate of the relative branch lengths scaled by effective population sizes is obtained.

If aDNA samples are of different age are available, the method of projections [25] can be used to test whether those samples come from a lineage directly ancestral to a present-day population. [26]

Contamination

A major problem with analyzing hominin aDNA is contamination by present-day humans. Based only on the DNA sequences themselves, contaminating reads are difficult to distinguish from those endogenous to the source of the aDNA. For Neanderthals and Denisovans, the mtDNA sequences are sufficiently different that contaminating human mtDNA is easily detected. It is possible, however, that levels of mtDNA and nuclear DNA contamination differ. If the archaic individual was a female, the extent of contamination is indicated by the amount of Y-chromosome DNA detected. It is also possible to directly estimate the level of nuclear contamination from the presence of heterozygous aDNA sites [5,27].

Skoglund et al. [28] developed a method that uses the tendency of aDNA fragments to carry distinctive miscoding lesions to estimate the probability that each fragment is endogenous. Racimo et al. [29] took a different approach and used an explicit model of the archaic and present-day populations to jointly estimate the level of contamination of the archaic sample and the time of divergence of archaic and contaminating populations. Applying this method to different potentially contaminating populations allows identification of the source of contamination with some confidence.

Time sequence of samples

When aDNA is available from samples of different age, it is possible to approximate the changes in allele frequency of individual loci [30,31]. Several method have been developed both to test for selection and to estimate selection intensity. [32-35] As increasing numbers of aDNA is sequenced, more data will be available for the application of these methods. These methods all assume that the ancient and present-day DNA all come from the same population lineage, something that may be difficult to test for.

Branch shortening

An aDNA sequence is from a population lineage that is shorter than the lineage leading to any present-day sample. As a consequence, the aDNA sequence has had somewhat less time to accumulate mutations, a phenomenon called branch shortening. If the error rate in the aDNA sequence is low enough, branch shortening can be detected. In fact, detecting branch shortening is another way to verify that the aDNA sequence is endogenous. If the age of the fossil yielding the aDNA sequence is known, then the extent of branch shortening provides an estimate of mutation rates. Fu et al. [12] were able to estimate nuclear, Y-chromosome and mtDNA mutation rates using this method.

Discussion

Methods for analyzing aDNA data will flourish as more aDNA data become available. Methods will focus increasingly on whole-genome sequences. Although many methods for analyzing present-day sequences have been applied to aDNA, they do not take account of the additional complexity that aDNA creates. Sequence quality may be lower both because only low coverage may be obtained and because aDNA is subject to post-mortem modification. Furthermore, the age difference between ancient and present-day sequences may not be adequately taken account of. Analyzing aDNA gives access to a time dimension which had been previously been unseen. New methods will have to take better advantage of the ages of aDNA sequences.

One shortcoming of most analysis aDNA samples is shared by most current analysis of present-day samples. The starting point is a population tree, possibly with some admixture represented by connections among branches. This is convenient for modelers because samples are usually identified with named populations and most population genetics theory is developed in terms of randomly mating populations. Yet human populations are dispersed widely. True population distinctness may be rare even for island populations. The assumption of a population tree with or without admixture may be a reasonable starting point but little effort has been expended on testing the adequacy of that modeling framework. Unfortunately, accounting for the real geographic structure of gene flow and isolation-by-distance is difficult and taking account of spatial variation in population density adds to the difficulty. At present, we do not know what effect complexities in population structure might have on conclusions drawn from tree-based models. Future modelers will have to take up this challenge sooner or later.