Analysis of among-site variation in substitution patterns

Abstract

Substitution patterns among nucleotides are often assumed to be constant in phylogenetic analyses. Although variation in the average rate of substitution among sites is commonly accounted for, variation in the relative rates of specific types of substitution is not. Here, we review details of methodologies used for detecting and analyzing differences in substitution processes among predefined groups of sites. We describe how such analyses can be performed using existing phylogenetic tools, and discuss how new phylogenetic analysis tools we have recently developed can be used to provide more detailed and sensitive analyses, including study of the evolution of mutation and substitution processes. As an example we consider the mitochondrial genome, for which two types of transition deaminations (C⇒T and A⇒G) are strongly affected by single-strandedness during replication, resulting in a strand asymmetric mutation process. Since time spent single-stranded varies along the mitochondrial genome, their differential mutational response results in very different substitution patterns in different regions of the genome.

Introduction

Patterns of substitution among nucleotides are usually modeled as reversible processes that are constant among sites and over time. A common exception to this is the use of the gamma distribution to model variation in the average rate among sites (1), and non-reversible processes have been modeled, but lead to computational difficulties (2). Although reversible processes are computationally convenient, a strand-symmetric (not necessarily reversible) mutation model is a more natural model to assume if the mutation process is similar on the two complementary strands of double-stranded DNA. Strand-symmetric models, in which all substitution rates equal their complement (e.g., A⇒C = T⇒G) have only recently been used to model evolutionary processes (3), and strand asymmetry of specific types of substitution was systematically added to these strand-symmetric models to study substitution in mitochondrial DNA (mtDNA), in which a strand asymmetric replication process leads to strand asymmetry in the mutation and substitution processes. (As an aside, we refer to these models as “strand-symmetric” to avoid confusion with models that incorporate symmetric substitution matrices). Also peculiar to mitochondrial genomes due to their unusual replication process is that the strength of the asymmetries in mutation and substitution processes depends heavily on location in the genome (4); Cytochrome oxidase subunit I (COI) has the least asymmetry, whereas Cytochrome B (Cyt-b) has the most.

Phylogenetic programs are not generally designed to account for substitution processes that vary among sites, except for variation in average rate, and few are designed to incorporate simple non-reversible models that are strand-symmetric or nearly strand-symmetric. Thus, the easiest approach to study variation among sites is to divide sites into categories and evaluate the significance of rate differences among those categories (examples of possible categories are gene type, codon position, amino acid or redundancy class conservation, or position along the genome). This is the approach used in Faith and Pollock (4), and the methodology is described in detail below. An important consideration in such an approach is the density of the phylogeny relating the sequences being evaluated; as the site categories become small, there must be large numbers of well-distributed taxa in order to get meaningful estimates of substitution parameters for each group. The amount of divergence along the phylogeny can also be important, since too much divergence may also lead to imprecise and inaccurate parameter estimates.

Another important consideration is that the phylogeny should not generally be re-estimated for each category. This is true for practical reasons (estimating phylogenies takes time, and may be prohibitive for large numbers of groups), and for analytical reasons (there is a reduced amount of data in small clusters of sites, so phylogenies may be inaccurately estimated; it is better to focus the power of the smaller datasets on estimating only the substitution rates). For simplicity, the examples discussed use a single phylogeny estimated from the entire dataset, but there is nothing to prevent use of, for example, a posterior distribution of phylogenies taken from a Bayesian analysis program (e.g., Mr.Bayes; (5)). As long as the phylogeny is approximately correct, it is not believed to make a large difference in estimating model parameters (6, 7), but it may be useful to evaluate this assumption further in the future.

We usually evaluated support for alternative nested models based on the classic nested model approach, in which support is measured by the difference in log likelihoods (Δln L) between the models. In this approach, the likelihood, L, was calculated as the probability of the data, D, given a model, M, and its parameters, Θ, that is, L = P(D|M, Θ), and the parameter values used were the maximum likelihood estimators (MLEs), the parameter values that have the highest probability of producing the observed data. Significance was determined by assuming that 2ΔlnL was distributed as 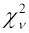, the chi square distribution, where ν is the number of degrees of freedom, equal to the difference in free parameters between the models (8). In cases where the chi square assumption is in doubt (e.g., (9)), the distribution of 2ΔlnL under the null model can be simulated, but this is not described here. We have sometimes also used the conceptually different and perhaps more logically consistent information-based approach (10, 11), in which models are viewed as being approximations to some unknown but presumably complicated true mechanism, and the best model is the one with minimal distance to the true mechanism, after correction for bias introduced by the number of parameters. Here, we discuss only the likelihood ratio results.

In our studies on vertebrate mitochondrial genomes, the most clear-cut differences among sites and among genomes were due to variation in rates of transitions, apparently due to hydrolytic deamination. In this system, the predominant deaminations are from adenine (A) to hypoxantine (H), resulting in a substitution to guanine (G) after replication, and from cytosine (C) to thymine (T). These mutations are strongly affected by variation in the time spent single-stranded during replication (4, 12, 13), but respond differently to time spent single-stranded. While C⇒T mutations occur at much higher rates in the single-stranded state (14-16), C⇒T substitutions rapidly reach an asymptotic maximum, whereas A⇒G substitutions increase approximately linearly with increase in time spent single-stranded (4).

The observation of a linear increase in a particular kind of substitution is particularly useful, since it provides a simple prior hypothesis for linking differences in substitution rates to time spent single-stranded that can be related to a single biological process (rate of polymerization). Such a prior hypothesis allows for the development of specialized methods with greater power to resolve differences among species or groups of species. Furthermore, with this prior hypothesis, and since transitions are the dominant mutation (fastest rate), one can gain some information even from individual genomes by looking at the equilibrium ratios of purines (A/G) or pyrimidines (C/T) to evaluate the response to single-strandedness. Custom-designed Bayesian methodologies that incorporate change in mutation processes along the genome allow more detailed and sensitive analyses, including study of the evolution of mutation and substitution processes (17, 18).

Materials

All analyses discussed used genes extracted from complete mitochondrial genomes from 42 vertebrates (4) or 16 primates plus two near outgroups (18). Gene sequences for all available vertebrate mitochondrial genomes were aligned using ClustalW (19) and stored in a MySQL database, from which datasets of interest were extracted. Phylogenetic trees were determined using the neighbor-joining algorithm on maximum likelihood distances for all protein-coding regions combined, which were calculated under the general time reversible model in PAUP* (20). Partly because there is so much data involved, we did not find that different reconstruction methods made much difference, nor did re-optimizing branch lengths using maximum likelihood. Phylogenetic trees (topology and branch lengths) were not modified in further analyses to focus statistical power on differentiating relative substitution rates (see discussion in introduction).

Datasets were subdivided by gene and by codon position, and most analyses were performed on 3^rd codon positions, which have many synonymous sites (sites that allow nucleotide substitutions without amino acid replacements). Some datasets consisted of only sites that coded for four-fold redundant or two-fold redundant 3^rd codon positions throughout all taxa in the alignment.

For each genome, it is necessary to know the location of the origin of light strand replication (O_L ) and the orientation of the heavy strand origin of replication (O_H ). For most vertebrates, O_H is located in the large intergenic region sometimes called the D-loop because of an RNA triplex structure that forms and is visible under an electron microscope, and which also contains the origins of light and heavy strand transcription. The O_L is usually located between the asparagine and cytosine tRNAs, about two-thirds of the way around the genome from the O_H in the direction of heavy strand replication. It is often detectable as an unusually large (for mitochondria) intergenic region that can be predicted to form a helix-loop-helix structure. In a number of vertebrates this intergenic region and structure have gone missing, however, most notably in the birds; in other work we are using our method to detect such missing origins, but in the present study organisms with ambiguously identified origins were not included. The predicted time spent single stranded at site i in species m ( 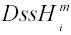) is calculated as

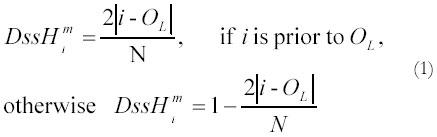
where N is the length of the genome, and “prior” means the site i is reached before the O_L in the process of replicating the heavy strand, and |i - O_L | is the number of nucleotides separating i and O_L (regardless of the site numbering system). Time units in this case are the (unknown) amount of time taken to replicate one genome length. When a set of sites was further partitioned according to 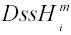, sites were divided into a given number of partitions (e.g., 20) with as close to equal numbers in each partition as possible. 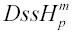was the average 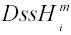for all sites, i, in partition p; if the partition was for an alignment, then 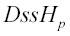was the average 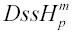over all species, m. To create partitions with extremely short or long time spent single-stranded (low or high 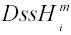we used the 70 sites with the lowest and highest .

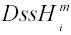Methods

Estimating model parameters

For any given dataset, we converted the alignment and the phylogenetic tree (with branch lengths) to Nexus format, opened it in PAUP* (20), and ran likelihood analyses that did not modify the topology or branch lengths. A detailed example protocol for this is given below. The model usually used for analyses was the general time reversible (GTR) model (21). For a model with fewer parameters and more sensitive evaluation of transition / transversion rate ratios, the HKY model (22), which incorporates nucleotide frequencies but only one rate parameter for all transversions and another rate parameter for all transitions, was also used. These analyses can also be done using PAML (23), and PAML is necessary for analyzing non-reversible models, but the “unrestricted” model in PAML has many more free parameters than the GTR model, and perhaps because of this over-parameterization it gave ambiguous results. PAUP* also has the benefit of a more intuitive interface with the option of batch file command input, so here we focus only on the methodology using PAUP*. Output from PAUP* can easily be imported into standard software programs for graphing purposes.

In one instance (4), a dataset consisting of the most slowly evolving sites was created by running (in PAUP*) a GTR model with rate variation among sites modeled according to a discretized gamma distribution with 100 rate categories. The posterior probability P_ij that each site j is in each rate category i was output using PAUP*’s lscores command (using ‘categlikes’ and ‘sitelikes’ options; see Protocol section) in an empirical Bayes approach, and the rate estimate for each site (PP_j ) was calculated as 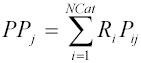, where R_i is the mean rate for category i.

Likelihood ratio tests

Maximum likelihood (ML) values calculated from PAUP* or other programs were compared between nested models. To determine whether two partitions had evolved under significantly different sets of substitution parameters, the comparison was between the sum of the separately estimated ML values for the two partitions and the ML value for the two partitions calculated as if they were one. To evaluate the degree to which individual sites supported one set of parameter values versus another (e.g., the ML parameter values for the extreme low and extreme high 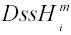conditions), analyses were run with both sets of fixed model parameters in addition to fixed topology and branch lengths, and the likelihood of the sequence data at each site was output using the ‘lscores’ (‘sitelikes’ option) command. The two sets of site-specific likelihood values were imported into a standard database program, and relative support for the two models at each site, i, was measured as the difference in natural log-likelihood values at that site, ΔlnL _i .

Analysis of nucleotide frequencies

Given the expectation of a linear relationship between nucleotide frequency ratios (e.g., G/A) and time spent single-stranded, the likelihood of a specific linear relationship (i.e., a specified slope and intercept) can be calculated for a sequence, S, from any set of species with the same linear relationship (and ignoring phylogenetic relationships), as

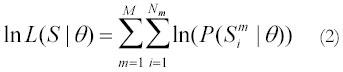
where θ are the parameters of the model (the slope and intercept), M is the number of species, N_m is the number of sites under consideration for species m that have one of the two nucleotides being considered (e.g., G or A), and is 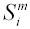the sequence at site i from species m. For example, if 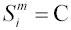, and dropping the site and species subscripts for simplicity, then 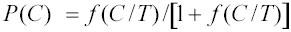, where 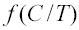is determined by the predicted time spent single stranded at site i based on the slope and intercept parameters (θ). ML values and Bayesian posterior distributions were evaluated with programs written in C by sampling the posterior probability space using the Metropolis-Hastings Monte Carlo algorithm and assuming uninformative prior distributions, P(θ)=1. The significance of different slopes and intercepts among species were evaluated using likelihood ratio tests as described above, except the comparisons were between separate or joint analysis of entire genomes, rather than individual genes or genome subsets. Clustering of species by slope and intercept was also evaluated using mixture models (Raina et al., in review), but the details are sufficiently complex that it is not warranted to describe them here.

Incorporating variable models at each site into phylogenetic analysis

Although data partitioning and analysis of nucleotide frequencies in individual genomes are useful strategies to identify variation in substitution patterns across sites and over time, both approaches are somewhat unsatisfactory. The data partitioning approach requires prior discrete categorization of the data, meaning that continuous change is not directly incorporated and that inefficiencies may result if the categorizations are not ideal. The analysis of nucleotide frequencies assumes that equilibrium has been reached, and ignores phylogenetic relationships, thus overestimating confidence in the accuracy of results for joint estimates of multiple species. To allow more rapid calculation of complex models, we have developed a Bayesian approach using augmented data at internal nodes, and assuming no more than two substitutions per site per branch (17, 18, 24-26). We also used a posterior predictive approach (24) for quickly evaluating extremely complex models in which the substitution matrix varied among all the sites (17). This is a statistically efficient way to analyze a variety of complex models, since it is much easier to calculate the likelihoods of complex models if states at all internal nodes are known. Although the details of these models are complex and are being published elsewhere (17), it is useful to compare the outlines of these approaches to the methods described in detail here.

Hidden Markov Models

In the implementation of a linearly dependent phylogenetic model, a single type of substitution varies along the genome according to 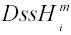. There is a strand symmetric “base” model (3), and this is augmented by the variable asymmetric substitution component. The strand symmetric model is not necessarily reversible, and has fewer free parameters than the GTR model. As before, the posterior probability space for the base model parameters as well as the variable strand asymmetric component was explored using Markov chain Monte Carlo techniques.

To allow for a non-linear response to time spent single-stranded, we also implemented a model in which the strand asymmetric substitution component at each site was related to the previous site by a simple hidden Markov model. The hidden Markov component was constant among sites, such that the probability of the strand asymmetric component at a site was a normally distributed random variable with mean equal to the previous site, and variance estimated as a free parameter depending on the distance to the previous site. This allows us to build complexity into models at each site with relatively little computational effort.

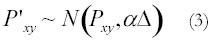
where Δ = difference in DssH’s of subsequent sites, P_xy = probability of substitution from state x to state y in site l, N = normally distributed, 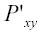= probability of substitution from state x to state y in site l+1.

Results

By applying the techniques described in this manuscript, we were able to evaluate differences along the genome in relative rates of substitutions between different nucleotides (4, 18). Since various aspects of the substitution gradients (e.g. slope, initiation point, saturation level) may well reflect important biological components of the replication process (e.g., rate of polymerization, initiation of replication, and single-stranded binding protein affinity, respectively), it is biologically important to obtain better analysis of these gradients and their evolution (4). The basic approach taken in Faith and Pollock (4), that of selecting sets of sites that are behaving as neutrally as possible, and as similar to each other as possible, worked well. Results in some cases were very consistent (e.g., increase in a single substitution type, A⇒G, fell on a straight line that was similar between redundancy classes) despite that the relative rates were clearly different, both among sites in a set (one has to assume that the linear increase continues within each gene) and over time. There are different slopes and intercepts between certain groups of primates, a sampling of which are shown in Table 1. Many of the slopes and intercepts have non-overlapping credible intervals (Table 1); a full analysis of the significance of these differences will be described elsewhere (Raina et al., in review), and preliminary analysis also indicates that there are other large differences among the vertebrates used in the Faith and Pollock (4) study (data not shown). Selection is another factor that is unlikely to have disrupted the analysis, but may have created further differences in substitution processes among sites, including some degree of dinucleotide or codon bias.

The dangers of over-parameterization relative to the size of the dataset should always be considered, and reduction of data to overly small clusters of sites should be avoided. In Faith and Pollock (4), the datasets for the phylogenetic analyses were no smaller than the sizes of the genes, and the smaller genes were not considered. For other datasets with greater genomic biodiversity (heavier taxonomic sampling), it may be feasible to evaluate much smaller sets of nucleotides; the tradeoff is in the high variance of parameter estimates with the smaller data sets. The model itself is also an important consideration with regards to over-parameterization; for example, the most general non-reversible model may have parameters that are difficult to resolve or identify precisely, and this may make interpretation difficult. We also found that the transition / transversion ratio was more clearly interpretable with an HKY model than with the GTR.

Discussion

The “divide and conquer” approach can produce new ways to interpret the data, and ideas for more appropriate complex models. Such models, if they can be incorporated, will make better use of the data, and improvements in analytical power will result. Thus, incorporating a linear model of change in one type of substitution directly into the likelihood calculations allows for more precise analysis of this type of change without so much over-parameterization (Fig. 1). The use of a hidden Markov model relating substitution rates between sites confirms the “divide and conquer” analysis by showing an approximately linear increase in A⇒G substitutions with DssH, although a linear increase is not part of the underlying model (Fig. 1). The increased power is apparent in the C⇒T substitutions, for which a sharp initial increase can be seen, followed by a long plateau. The basic shape of this curve was predicted in Faith and Pollock (4) based on plausibility and limited evidence, but is confirmed by this analysis. In Faith and Pollock (4), the difference in support at individual sites, ΔlnL_i , was used only to confirm the linear trend, but in other instances it may be very useful to graphically identify sites that are mis-classified.

Fig. 1. Substitution response profiles vs. DssH.

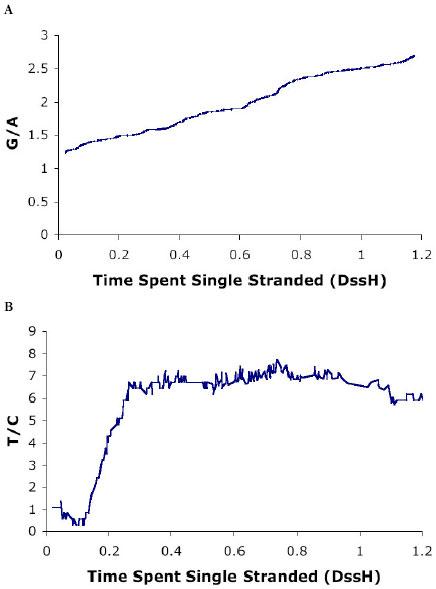
(a) G/A (A⇒G/ G⇒A) and (b) T/C (C⇒T/ T⇒C) response profile for the primate dataset. The posterior probability of the expected substitution rate ratio at every four-fold redundant (a) or two-fold redundant pyrimidine (b) site is shown. Results were obtained using a hidden Markov model for correlation of the A⇒G or C⇒T rates between adjacent sites, while the remaining substitution probabilities were held constant. The unit of time spent single-stranded is the (unknown) amount of time taken to replicate one genome length.

Appendix

Protocols

Equipment

Necessary equipment includes in-house perl scripts, PAUP* 4.0, PAML 3.1, MySQL relational database, and ClustalW v1.8.

Method

1. Dataset (alignments & phylogenetic tree reconstruction) preparation:

ClustalW was used to create alignments for each homologous gene set and concatenated using in-house Perl scripts. The vertebrate mitochondrial genetic code was used to parse out 3^rd codon positions for four-fold redundant (4x) codons, two-fold redundant purines (2xR) and two-fold redundant pyrimidines (2xY). The following examples demonstrate the parsing procedure:

2. Model parameters and Site-Specific support

Gamma-distributed ML parameter estimates were obtained using the existing phylogeny and the GTR model. Using these new model parameters, a neighbor-joining tree was recalculated. ML model parameters (GTR without gamma) were also estimated for two extremes, 4x sites with 70 lowest DssH values and those with highest 70 values. These ML estimates were obtained using PAUP* commands (see below) and were kept constant to calculate the likelihood of each site under the two models. Sample PAUP* commands used for that purpose are as follows: the relative model support for each site was evaluated by calculating the difference between the log-likelihoods (ΔLnL) of the two models. Likelihood results were also calculated from the joint analysis that assumes that both the extremes evolve under the same model. Twice this ΔLnL statistic has an expected distribution of χ² with nine degrees of freedom (the number of parameters added by including a second model). A large difference in the likelihoods indicates that the two extremes evolve differently.

3. Estimating base frequencies for calculating skews and substitution rates

PAML v3.1 can be used to estimate base frequencies and substitution rates from a fixed topology by fixing constraints such as branch lengths, etc., under the GTR model and empirical base frequencies. Similar analyses can be performed using a non-reversible model by setting the parameter ‘model’ to 9. The following script demonstrates the step-by-step method.

4. Confirmation of saturation of G⇒A substitutions

A GTR-γ model was run with 100 different rate categories, and posterior rate probabilities were calculated for each 4x site. The graphical version of PAUP* outputs the mean rate R_i for each category i when the ‘rates’ parameter is set to “gamma” under the ‘Options’ menu, and the shape parameter α and the number of categories are specified.

Table 1. Maximum likelihood values & 95% CI for slope and intercepts of C⇒T and A⇒G gradients in sample of primates and an outgroup, C. variegates.

Species	-ML	C⇒T Slope	Intercept	-ML	A⇒G Slope	Intercept
Homo sapiens1	574.51	-0.10 (-0.16, -0.04)	0.20 (0.16, 0.26)	1275.61	0.86 (0.23, 1.56)	2.20 (1.77, 2.71)
Pongo pygmaeus pygmaeus1	532.06	-0.10 (-0.15, -0.05)	0.19 (0.15, 0.24)	1189.91	1.54 (0.50, 2.54)	2.42 (1.85, 3.16)
Papio hamadryas1	629.60	-0.11 (-0.17, -0.05)	0.23 (0.18, 0.28)	1284.19	1.59 (0.96, 2.18)	1.45 (1.13, 1.83)
Colobus guereza2	603.77	-0.06 (-0.12, 0.01)	0.17 (0.12, 0.23)	1425.30	0.53 (0.20, 0.90)	1.10 (0.89, 1.35)
Trachypithecus obscurus2	556.39	-0.04 (-0.09, 0.02)	0.15 (0.11, 0.19)	1469.87	0.42 (0.19, 0.63)	0.70 (0.57, 0.85)
Cebus albifrons2	503.50	-0.10 (-0.14, -0.05)	0.16 (0.12, 0.20)	1405.69	0.34 (0.09, 0.64)	0.95 (0.74, 1.14)
Lemur catta2	381.70	-0.03 (-0.06, 0.00)	0.08 (0.06, 0.11)	1408.20	0.61 (0.36, 0.88)	0.69 (0.54, 0.87)
Cynocephalus variegates1	657.06	-0.12 (-0.19, -0.07)	0.24 (0.19, 0.29)	1269.62	1.13 (0.58, 1.66)	1.55 (1.22, 1.96)
1,2 indicate high and low, respectively, for the G/A response clusters. 95% CIs are in parentheses below numbers.