Abstract
BACKGROUND CONTEXT
The lumbar facet capsular ligament (FCL) is a posterior spinal ligament with a complex structure and kinematic profile. The FCL has a curved geometry, multiple attachment sites, and preferentially aligned collagen fiber bundles on the posterior surface that are innervated with mechanoreceptive nerve endings. Spinal flexion induces three-dimensional (3D) deformations, requiring the FCL to maintain significant tensile and shear loads. Previous works aimed to study 3D facet joint kinematics during flexion, but to our knowledge none have reported localized FCL surface deformations likely created by this complex structure.
PURPOSE
The purpose of this study was to elucidate local deformations of both the posterior and anterior surfaces of the lumbar FCL to understand the distribution and magnitude of in-plane and through-plane deformations, including the prevalence of shear.
STUDY DESIGN/SETTING
The FCL anterior and posterior surface deformations were quantified through creation of a finite element model simulating facet joint flexion using a realistic geometry, physiological kinematics, and fitted constitutive material.
METHODS
Geometry was obtained from the micro-CT data of a healthy L3–L4 facet joint capsule (n=1); kinematics were extracted from sagittal plane fluoroscopic data of healthy volunteers (n=10) performing flexion; and average material properties were determined from planar biaxial extension tests of L4–L5 FCLs (n=6). All analyses were performed with the non-linear finite element solver, FEBio. A grid of equally spaced 3×3 nodes on the posterior surface identified regional differences within the strain fields and was used to create comparisons against previously published experimental data. This study was funded by the National Institutes of Health and the authors have no disclosures.
RESULTS
Inhomogeneous in-plane and through-plane shear deformations were prominent through the middle body of the FCL on both surfaces. Anterior surface deformations were more pronounced because of the small width of the joint space, whereas posterior surface deformations were more diffuse because the larger area increased deformability. We speculate these areas of large deformation may provide this proprioceptive system with an excellent measure of spinal motion.
CONCLUSIONS
We found that in-plane and through-plane shear deformations are widely present in finite element simulations of a lumbar FCL during flexion. Importantly, we conclude that future studies of the FCL must consider the effects of both shear and tensile deformations.
Keywords: Deformation, FEBio, Finite element, Kinematics, Mechanics, Modeling, Motion segment, Spine, Zygapophyseal joint
Introduction
The facet joints comprise the posterior aspect of the three-joint complex that is the spinal motion segment (Fig. 1, Left). The facet joint consists of two rigid articular facets, one from each adjacent vertebra, and is encased by the fibrous facet capsular ligament (FCL) on the posterior aspect (Fig. 1, Middle) and the ligamentum flavum on the anterior aspect. The articular facets and the FCL function both to guide and to restrict spinal motion. Additionally, the FCL retains the lubricating synovial fluid within the articular cartilage-lined joint space.
Fig. 1.
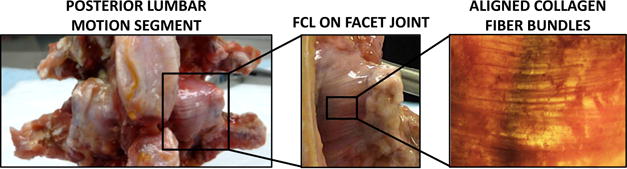
Lumbar facet joint location and morphology. (Left) On the lumbar motion segment, two facet joints flank the spinous processes on the posterior aspect of the spine. (Middle) The facet capsular ligament (FCL) spans between two rigid articular facets from adjacent vertebrae creating the joint. (Right) The posterior aspect of the FCL consists of highly aligned collagen fibers bundles that preferentially align between the articular facets, whereas the anterior aspect (not pictured) is rich with elastin-like fibers.
All FCLs along the spinal column contain two distinct materials that transition through the ligament thickness [1]. Specifically to the lumbar FCL, the posterior surface (viewed from the posterior aspect and facing out from the joint space) consists of highly aligned collagen fiber bundles that preferentially align between the rigid articular facets (Fig. 1, Right). The anterior surface (anterior aspect), which interacts with the synovial fluid within the joint space, is rich with unorganized elastin fibers [1]. The FCL has a convex curvature because it follows the geometry of the articular facets, and because it is a capsule it has multiple insertion sites across the facet joint. Articular facet kinematics drive FCL deformations that occur during all spinal motions (flexion and extension, lateral bending, and axial rotation), and which may be quite complex [1]. Additionally, the contained synovial fluid constantly pressurizes the FCL. Therefore, the elaborate structure compounded with the kinematic response gives rise to complicated three-dimensional (3D) deformations in vivo.
Three-dimensional deformations of the lumbar spine during flexion have been studied previously by applying rigid body kinematics to 3D models. Cheng et al. [2] developed a registration process that morphs 3D vertebral bodies to image frames of two-dimensional (2D) fluoroscopic data of human lumbar flexion and extension. With these subject-specific models, they compared in-plane and out-of-plane vertebral rotations of healthy individuals with those with either low back pain or degeneration, but they did not evaluate facet joint rotation per se. With regard to the facet joint, Kozanek et al. [3] created subject-specific 3D models using magnetic resonance and dual fluoroscopic imaging to measure the range of facet joint displacement and rotation at the end points of lumbar spine motion. They did not, however, attempt to describe the soft tissue deformations of the lumbar FCL.
Other studies have aimed to extract the 3D soft tissue deformations of the lumbar FCL in an isolated spine. Ianuzzi et al. [4] applied horizontal displacements to the T12 vertebra of fresh cadaveric lumbar spines (T12–S1, S1 potted) to simulate flexion, extension, and lateral bending (left and right). A grid of infrared markers placed on the surface of each FCL was optically tracked during the applied deformations. One principal strain was calculated to represent the entire FCL surface at four displacements within a series, but the regional variations in strain across the FCL were not reported. A previous study from our group [5] aimed to quantify lumbar FCL deformations by optically tracking structural characteristics inherent to the FCL over the course of static bending. Although our previous work extracted 3D FCL deformations, we were only able to characterize the deformation of a portion of the capsule. Additionally, the deformations across the FCL emulated flexion but were not indicative of true flexion because the rotation was not applied over the intervertebral discs. Thus, there exists a gap in the literature involving quantification of the full 3D deformations of the lumbar FCL during physiological spine motions.
Realistic finite element models of the joint can provide complementary analysis when properly informed by experimental data [6–13]. To construct a finite element model of the lumbar FCL, three pieces of information are necessary: geometry, boundary conditions, and material properties. Fig. 2 shows schematically how these inputs were obtained. Previously, our group published continuous in vivo vertebral kinematics during flexion and extension to quantify intervertebral margin strains [14], similar to data obtained by others [15,16]. From this data set, the facet joint motion was extrapolated from vertebral kinematics on sagittal plane. Furthermore, we previously characterized the instantaneous material properties of healthy cadaveric L4–L5 FCLs using a hyperelastic model with two fiber distributions (Claeson et al., submitted). To our knowledge, accurate tissue geometry for the lumbar FCL has not been published previously, but it can be obtained via micro-CT (μ-CT) (cf. [17]). Thus, the necessary information is now available to undertake a computational analysis of lumbar FCL motion.
Fig. 2.

Schematic showing the method by which the three inputs to the finite element facet capsular ligament model were obtained.
Structurally and kinematically, the FCL is a complex tissue whose structure and functional responsibilities change with location along the spinal column [18,19]. The differences are dramatic when comparing the articular facets [20] of the cervical, thoracic, and lumbar spine, but even within a given region there is considerable variation [21,22]. In this study, rather than attempt to model the entire spine or even the entire lumbar spine, we focused specifically on flexion of the L3–L4 joint because flexion evokes a large intervertebral angle and facet joint strain [4] compared with other segmental motions. Furthermore, L3–L4 has a high prevalence of severe degenerative disc disease and degenerative facet disease in elderly populations [23] and can be a cause of chronic low back pain.
The goal of the current study was to identify the continuous deformation of the L3–L4 FCL during flexion and extension by means of a realistic finite element model.
Materials and methods
Geometry acquisition through micro-CT
Specimen preparation
A healthy cadaveric spine was obtained through the University of Minnesota’s Anatomy Bequest Program. One right L3–L4 cadaveric facet joint capsule was resected from the motion segment (Fig. 3A) for imaging via μ-CT. All four structures of the joint capsule were present: FCL, ligamentum flavum, superior articular facet (SAF), and inferior articular facet (IAF). Posterior musculature, loose connective tissues, and the thin membrane were removed from the capsule. The capsule exterior was visually free of signs of degeneration (eg, enthesophytes). Two coats of radiopaque paint (MICROFIL Silicone Rubber Injection Compound, Flow Tech Inc, Carver, MA, USA) were applied to the capsule to form a thick layer over the posterior FCL surface (Fig. 3B). The radiopaque paint served to define the exterior boundaries of the radiolucent ligament.
Fig. 3.
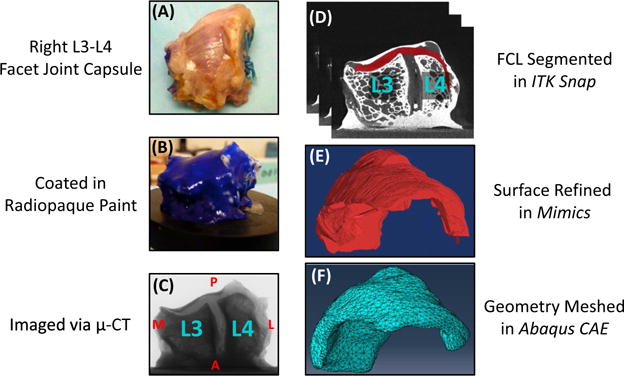
Constructing a finite element mesh of the lumbar facet capsular ligament. (A) A visually healthy, right facet joint capsule was resected from an L3– L4 motion segment. (B) The capsule was coated in radiopaque paint to aid in defining the exterior ligamentous boundary. (C) The capsule was imaged via μ-CT and was oriented as pictured. A: anterior; P: posterior; M: medial; L: lateral. (D) The resulting DICOM stack was imported into ITK-Snap, and the ligament was segmented from the rest of the capsular structures. Note the white posterior boundary was created by the radiopaque paint, and the locations of the articular facets of the L3 and L4 vertebrae. (E) The three-dimensional segmentation was imported into Mimics to refine the surface, and (F) the refined geometry was meshed with Abaqus/CAE.
Image acquisition
The painted FCL was placed on a custom stage, which fits securely into the housing area of the μ-CT scanner (XT H 225 Industrial CT Scanning, Nikon Metrology Inc, Brighton, MI, USA). The specimen rotated through 360°, whereas the μ-CT scanner sampled at 46.5 frames/mm, giving a voxel resolution of 21.5 μm. Fig. 3C shows the orientation of the facet joint, where the top of the image is posterior (P), the bottom is anterior (A), the left is medial (M), and the right is lateral (L).
Model geometry
Image stacks were saved as DICOM files and imported into ITK-Snap [24] for manual segmentation of the FCL from the rest of the capsule structures (Fig. 3D). The surface reconstruction was exported as an STL file and imported into Mimics (Materialise NV, Leuven, Belgium) for editing (Fig. 3E). In Mimics, the FCL was refined with the wrap tool; gap spacing and smallest detail were both set to 2% of the capsule length to smoothen the small irregularities on the tissue surface. After conversion to a parasolid in SOLIDWORKS, the refined FCL geometry was meshed in Abaqus/CAE with 24,236 10-node tetrahedral elements (Fig. 3F). The solid mesh was exported as an INP file and imported into PreView, the preprocessing module of FEBio [25]. The surface elements of the mesh were partitioned into three regions (Fig. 4, Top): (1) those connected to the superior vertebra (L3), (2) those connected to the inferior vertebra (L4), and (3) those free from either bone. The thickness of the FCL segmentation was approximately 3 mm at the joint space.
Fig. 4.
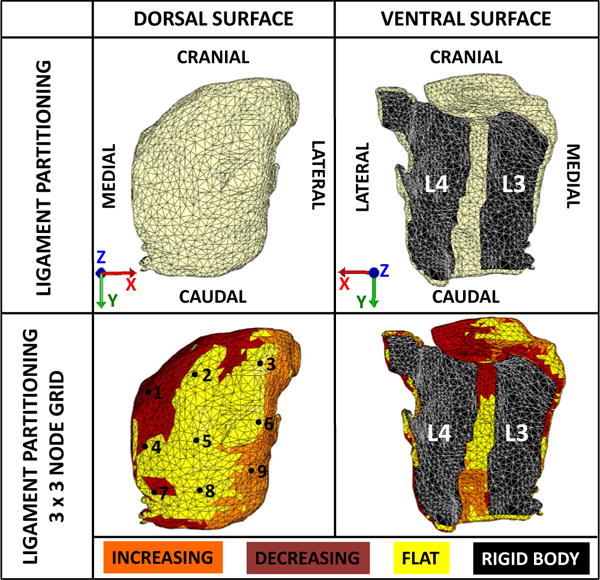
Partitioning the finite element mesh. (Top) The mesh was partitioned to reflect the attachments of the superior (L3) and inferior (L4) articular facets. The ligament was defined by an eight-parameter hyperelastic strain energy density function and the articular facets were defined by rigid bodies. Boundary conditions obtained from the subject-specific fluoroscopic data were applied to the model based on the global coordinate axes. (Bottom) The strain energy density function that defined the ligament region was warped to the curvature of the FE model based on the z-component (nz) of the normal vectors of each surface element. The ligament partition was further divided into three regions, which are flat (nz=0.079), increasing (nz=0.57), and decreasing (nz=−0.61) curvatures, where nz=0 would describe a planar surface. A 3×3 grid of nodes was selected on the posterior surface of the FE model to quantify regional ligament deformations.
Material model specification
Material model and model parameters
Three material definitions were used in the model. The attachment sites to the articular facets were specified to be rigid. The FCL itself was defined with an eight-parameter hyperelastic strain energy density function within FEBio. The model included a neo-Hookean ground matrix (Equation [1]) with two embedded fiber families described by an exponential strain energy density function (Equation [2]) and a 2D von Mises distribution of fiber orientation (Equation [3]).
| (1) |
| (2) |
| (3) |
In Equation (1), C1 is the neo-Hookean material coefficient, Ĩ1 is the first invariant of the deviatoric right Cauchy-Green deformation tensor, J is the determinant of the deformation gradient tensor, and K is the bulk modulus. In Equation (2), ξ is a measure of fiber modulus at small strain, α is the coefficient of the exponential argument, and β is the power of the exponential argument (ξ > 0, α ≥ 0, β ≥ 2). Finally, Equation (3) gives an orthotropic 2D distribution, in which (n1, n2, n3) are the components of the fiber direction vector n, b is a concentration parameter (b > 0), and I0 is the modified Bessel function of the first kind and order 0. The material parameters were specified by optimizing the parameters C1,α,β,ξ,θ1,θ2,b1, and b2 to fit experimentally obtained normal and shear reaction forces from displacement-controlled planar equibiaxial extension tests of healthy, cadaveric L4–L5 FCLs (n=6; Claeson et al., submitted). Optimized parameters were fitted separately for the six samples (sensitivity analysis described in Claeson et al., submitted), and then averaged to produce the following representative parameter set: C1=0.018±0.011 MPa, α =0.73±0.29, β =2.57±0.29, ξ =3.64±2.25 MPa, θ1=−22.39±8.63°, θ2=2.51±24.45°, b1=16.51±16.03.and b2=2.11±1.08. The FCL, as a viscoelastic tissue, exhibits rate-dependent loading as shown by Mattucci et al. [26]. Because of the relative low rate and long duration of our previous testing, however, the data were fitted by a hyperelastic model ignoring the viscoelastic effects.
Converting planar sample parameters to a three-dimensional tissue
The material model above was fitted to a planar model and needed to be adapted to fit the curvature of the in situ FCL geometry. Fibers in the FEBio model were mapped to the 3D shape in elements with a face on the tissue surface by first computing the surface normal to the element and then rotating the model fiber vectors so that they lay in a plane parallel to the surface. The X direction was defined as the medial-lateral direction. Fibers in non-surface elements were aligned parallel to those in the nearest surface element, which we considered an acceptable approximation because of the relative thinness of the tissue. Surface normal vectors were calculated for every external element face of the FCL model, and three partitions were created based on the component value: flat (|nz|>0.85), increasing curvature (|nz|<0.85) and (nx>0), and decreasing curvature (|nz|<0.85) and (nx<0) Average curvature within each group was applied to the fiber direction (Fig. 4, Bottom). Elements that were initially partitioned as rigid attachments retained their original definitions as rigid bodies. All elements were assumed to have the same material properties except for the rotation of the fibers.
Joint kinematics in spinal flexion
Sagittal plane motion during flexion
Kinematics of L3–L4 motion segments were extracted from the left sagittal fluoroscopic data of 10 healthy individuals during voluntary flexion. Further information on the fluoroscopic data sets and extraction of vertebral motion is given in Nagel et al. [14]. Because facet joint kinematics during flexion cannot be measured directly on the sagittal plane fluoroscopic images, vertebral body motion at the posterior disc margin was used to define facet joint motion by treating the vertebrae as rigid bodies. We note that posterior margin vertebral body motion does not fully represent FCL kinematics because of the effect of soft tissue (eg, ligamentum flavum) motion on the FCL. The left lateral kinematics obtained were mirrored to mimic the kinematics of a right facet joint. The analysis of the sagittal plane fluoroscopy data yielded subject-specific kinematics (n=10) to be used as inputs to the finite element model of a right FCL. Each of the 10 sets of kinematics was used to simulate vertebral motion.
Application of boundary conditions and prescribed motion
Global coordinates are defined with the right lateral as +X, inferior as +Y, and anterior as +Z (Fig. 4, Top). A negative rotation about the +X axis (−RX) occurred during flexion. In general, flexion-induced anterior displacement (+uZ), superior displacement (−uY), and sagittal plane rotation (−RX) for both vertebrae, which L3 rotating and displacing farther than L4 as the joint flexed (Table 1). All displacements and rotations were prescribed to the respective rigid articular facets to simulate relative rotation of the vertebral bodies. Anterior and superior displacements were prescribed for the IAF of L3, and all displacements were held fixed on the SAF of L4. Only sagittal plane rotation was permitted for both articular facets, and no contact occurred between the two articular facets as a function of the prescribed kinematics. The simulation began from an unloaded neutral position, the orientation in which the representative facet capsule was imaged via μ-CT.The ligament surface remained free, and during the simulation it deformed in response to displacements applied to the rigid articular facets. The simulation was performed under the assumption of quasistatic equilibrium, consistent with the hyperelastic material model.
Table 1.
Prescribed subject-specific L3 and L4 articular facet sagittal plane rotations
| Subject | Prescribed L3 rotation (°) | Prescribed L4 rotation (°) | Relative rotation (°) |
|---|---|---|---|
| 1A | 38.7 | 33.5 | 5.1 |
| O1 | 29.5 | 25.8 | 3.7 |
| O2 | 30.7 | 24.9 | 5.8 |
| O3 | 26.8 | 20.8 | 6.0 |
| O5 | 36.4 | 30.4 | 6.1 |
| O7 | 28.8 | 20.6 | 8.1 |
| O10 | 44.2 | 33.8 | 10.5 |
| O11 | 21.9 | 19.1 | 2.8 |
| O13 | 39.2 | 36.7 | 2.5 |
| O36 | 21.3 | 12.2 | 9.1 |
Verification and validation are important considerations in any modeling study. The FEBio software suite is well established and has been used to create finite element models of the intervertebral disc [27], glenohumeral capsule [28], and patellar ligament [29], among other biological tissues, so no additional verification of code function was deemed necessary. The model was validated by comparison with the strain versus flexion data of Ianuzzi et al. [4].
Data analysis
Postprocessing of the finite element data
An equally spaced 3×3 grid of posterior surface nodes (shown in Fig. 4, Bottom) was used to identify the regional differences within the strain field and to identify points for further analysis. The IAF, joint space, and SAF were traversed by three vertical nodes each, and the three nodes spanned from superior to inferior. This grid of points thus represented all of the major regions within the FCL. The values of the strain components at these points were tabulated and examined to determine the characteristics of the different regions.
In addition, the invariants I4 and I6 of the right Cauchy-Green tensor C were calculated for the two fiber families, where I4 represented the stretch in the primary fiber family and I6 represented the stretch through the secondary fiber family. I4 and I6 were calculated by Equations (4) and (5).
| (4) |
| (5) |
where n(1) is the dominant fiber family and n(2) is the secondary fiber family.
Comparison with Ianuzzi et al. [4]
Ianuzzi et al. calculated the first and second principal strains for vertebral motion in cadaveric lumbar spine subjected to an imposed displacement at T12 by tracking the motion of a 3×3 grid of markers on the FCL surface. To compare our results with Ianuzzi et al.’s, the 3×3 grid of nodes described above was analyzed to calculate tissue strains following their method. Nodal positions in 3D were extracted from the initial state and then at sequential states corresponding to −0.43°, −1.12°, −1.90°, and −2.54° of relative IVD rotation during flexion, matching the average relative L3–L4 rotation reported by Ianuzzi et al. The deformation gradient tensor was calculated as a best fit of the deformation of the nine-node grid. Following Ianuzzi et al.’s convention, the first principal strain was defined as the largest positive principal strain value, and the second principal strain was defined as the largest negative principal strain value.
Results
Anterior surface motion during simulated flexion
Anterior surface strain patterns at maximum flexion vary across the ligamentous surface and are generated directly from the displacement of the articular facets. Fig. 5 depicts the anterior surface strains for a representative simulation. Large strain values only accumulate in the ligamentous region that spans the joint space; the lateral rigid bodies (L3 and L4) do not carry strain. Ezz and EYY are the largest tensile and compressive strains, respectively, and occur out of necessity to conserve mass. The net effect of prescribed motion creates compression in the YY direction, and the ZZ direction thickens because motion in this direction is not constrained. Of note, these strain fields are oriented at an oblique angle, indicating the presence of shear. Furthermore, in-plane shear (XY) strains are pronounced and result from the inferior displacement of the L3 articular facet (black arrow) and fixed motion in the XX direction.
Fig. 5.
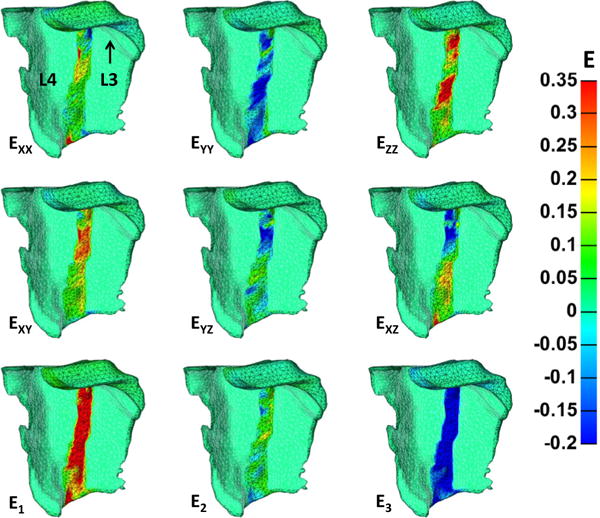
Anterior surface strains of a representative simulation at maximum flexion. Areas of zero strain with the indistinct mesh were partitioned as the rigid bodies of L3 and L4, and thus should not accrue strain. The largest tensile and compressive strains were ZZ and YY, respectively, and occurred because of articular facet motion and the need to conserve volume. Tensile in-plane shear (XY) strains are pronounced and also occur from the prescribed deformation. For reference, the deformation applied to L3 is upward displacement, displacement toward the reader, and rotation toward the reader.
Stresses on the anterior FCL surface occur largely as a result of the FCL’s structure and material definitions. Fig. 6 shows the Cauchy stresses for the same representative sample at maximum flexion. Again, only the ligament over the joint space exhibits a stress contour. The two fiber families of the model were prescribed on the XY plane, and accordingly σXX, σYY, and σXY exhibited the largest tensile stresses. As with the anterior strains, the stress field is oblique, indicating the presence of strain. Furthermore, through-thickness stresses, which are perpendicular to the fiber alignment, were smaller in value.
Fig. 6.
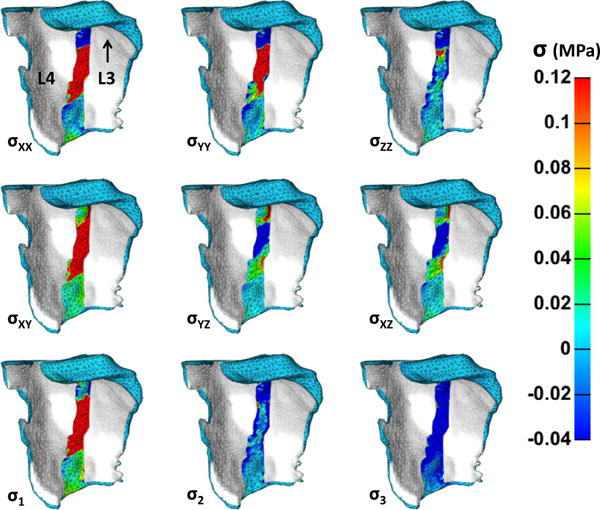
Anterior surface Cauchy stresses of the representative simulation at maximum flexion. Areas with the indistinct mesh were partitioned as the rigid bodies of L3 and L4, and thus should not accrue stress. Anterior surface tensile stresses occur in the direction of fiber family orientation, primarily in the XX, YY, and XY directions. Stresses are high because of the small joint space width. The through-plane shear stresses were also prominent with rotations in the opposite direction. For reference, the deformation applied to L3 is upward displacement, displacement toward the reader, and rotation toward the reader.
Posterior surface motion during simulated flexion
Posterior surface strains at maximum flexion varied greatly across the surface of the lumbar FCL. Strain values averaged across all simulations for the grid of nine surface nodes (Fig. 4, Bottom) are displayed in Table 2, along with the primary (I4) and secondary fiber stretch (I6). Nodes 2, 5, and 8 align vertically through the middle body of the capsule (over the joint space) and exhibit the highest strain values. The remaining nodes lie on the ligamentous surface that attaches anteriorly to the rigid articular faces. Although these nodes do carry some strain, it is small in comparison with those over the joint space. The center node (node 5) exhibits the largest stretches in both the primary (16%) and secondary (12%) fiber directions. Fig. 7 shows the posterior surface strains for the representative simulation and provides evidence to the findings above. Following with anterior surface, strains occur largely on the plane and in the area over the joint space. The strains, however, are more diffuse because the increased ligamentous area is more deformable Ezz is the largest middle-body tensile strain, with values ranging from 15% to 35% strain, leaving EYY as the largest compressive middle-body strain to conserve volume. Through-thickness (YZ) shear arises because motion is imposed only on the anterior surface.
Table 2.
Mean strain (%) at nine nodes spanning the posterior facet capsular ligament surface at maximum flexion
| (%) | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Node 1 | Node 7 | Node 8 |
|---|---|---|---|---|---|---|---|---|---|
| EXX | 0.20 | −11. | −0.046 | −0.018 | 5.2 | −0.0087 | −0.00037 | −3.2 | 0.17 |
| EYY | −0.65 | 6.3 | 0.0057 | 0.11 | −13. | 0.0069 | 0.0014 | 1.2 | −0.61 |
| EZZ | 0.61 | 13. | 0.040 | −0.084 | 16. | 0.0020 | −0.00097 | 20. | 0.60 |
| EXY | −0.53 | 11. | −0.022 | −0.16 | 7.5 | 0.00071 | 0.0018 | 13. | −0.69 |
| EYZ | −0.087 | −2.1 | 0.0019 | 0.17 | −8.7 | 0.00010 | −0.00086 | 5.5 | 0.34 |
| EXZ | −2.3 | 4.8 | −0.018 | −0.19 | 2.2 | −0.014 | −0.0017 | 9.6 | 2.0 |
| E1 | 2.8 | 16. | 0.050 | 0.45 | 19. | 0.024 | 0.0071 | 37. | 2.6 |
| E2 | −0.55 | 10. | 0.012 | −0.12 | 7.8 | 0.0029 | −0.00034 | 1.1 | −0.24 |
| E3 | −2.1 | −18. | −0.062 | −0.33 | −18. | −0.027 | −0.0067 | −20. | −2.2 |
| I4 | 0.96 | 1.0 | 1.0 | 1.0 | 1.2 | 1.0 | 1.0 | 1.2 | 0.96 |
| I6 | 0.97 | 0.82 | 1.0 | 1.0 | 1.1 | 1.0 | 1.0 | 0.99 | 0.97 |
The central column of nodes (2, 5, 8) exhibited by far the largest strains.
Fig. 7.
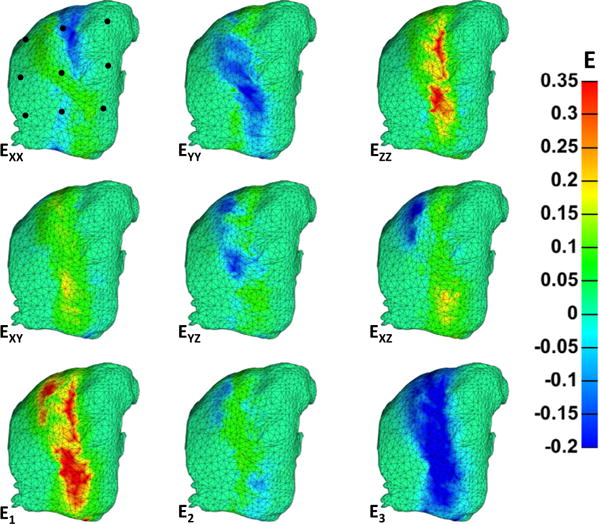
Posterior surface strains of the representative simulation at maximum flexion. The lateral edges of the mesh did not accumulate much strain, likely because of their anterior attachment to the rigid articular facets. The largest compressive (EYY) and tensile (EZZ) strains followed with the anterior surface strains, although these strains are more diffuse because the posterior surface ligament is more deformable. In-plane (XY) and through-plane (YZ, XZ) shear strains are also present but again more diffuse.
Posterior surface stresses are inhomogeneous, as witnessed with posterior surface strain, across the surface of the capsule at maximum flexion. Table 3 presents the mean Cauchy stresses across all simulations at maximum flexion at each of the nine nodes within the specified grid (Fig. 4, Bottom). The largest stresses are found at nodes 2, 5, and 8, which align vertically spanning the middle body (joint space). The Cauchy stress inhomogeneity at the posterior surface can be viewed in Fig. 8 for the representative sample. The lateral portions of the mesh, in general, do not carry much stress because they lie posterior to the rigid bodies. Posterior surface stresses are less pronounced than anterior surface stresses and are found primarily on the XX and XY planes. The decreased stress values likely occurred because of the larger ligamentous area over which the fiber families could reorganize before acquiring tension.
Table 3.
Mean calculated Cauchy stress (kPa) at each nine nodes spanning the posterior facet capsular ligament surface at maximum flexion
| (kPa) | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Node 7 | Node 8 | Node 9 |
|---|---|---|---|---|---|---|---|---|---|
| σXX | 1.6 | −30. | −0.038 | 0.14 | 33. | 0.014 | 0.0098 | 69. | 0.55 |
| σYY | 0.94 | −11. | 0.00026 | 0.29 | −19. | 0.026 | 0.011 | 68. | 0.031 |
| σZZ | 1.8 | −8.1 | 0.021 | 0.011 | −1.1 | 0.022 | 0.0099 | 0.19 | 0.52 |
| σXY | −0.76 | 9.6 | −0.018 | −0.17 | 45. | −0.0015 | 0.00081 | 91. | −0.15 |
| σYZ | 0.13 | −0.34 | 0.0062 | −0.082 | −5.5 | −0.00048 | −0.0011 | 14. | 0.42 |
| σXZ | −1.5 | −0.49 | −0.0091 | −0.12 | −1.5 | −0.0099 | −0.0016 | 15. | 1.5 |
| σ1 | 3.4 | −2.4 | 0.030 | 0.47 | 60. | 0.038 | 0.015 | 180 | 2.2 |
| σ2 | 1.0 | −12. | 0.0033 | 0.062 | −0.95 | 0.023 | 0.0099 | −8.6 | 0.16 |
| σ3 | −0.082 | −34. | −0.050 | −0.085 | −46. | 0.0016 | 0.0053 | −36. | −1.3 |
Fig. 8.
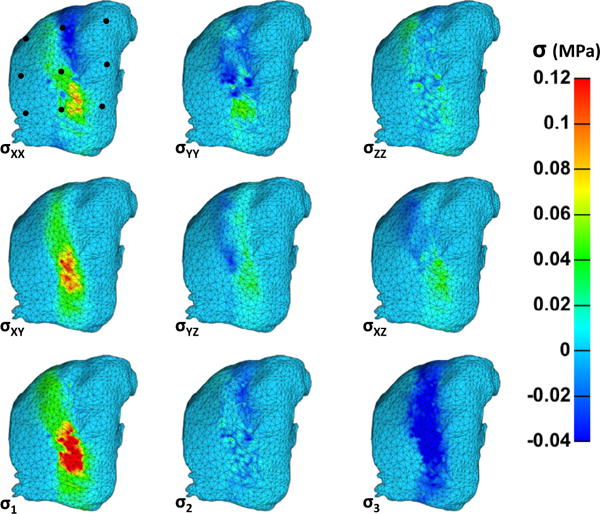
Posterior surface Cauchy stresses of the representative simulation at maximum flexion. The lateral edges of the mesh across all directions did not register much stress, likely due to their anterior attachment to the rigid articular facets. Posterior surface stresses are reduced from the anterior stresses because fibers are free to deform and rotate before acquiring stress. The largest stresses (σXX, and σXY) occurred in the primary direction of the two defined fiber families.
Presence of shear during simulated flexion
In-plane and through-plane shear deformations are present on both the anterior and posterior surfaces of the FCL at maximum simulated flexion. Shear strains (EXY, EYZ, and EXZ), generated by the relative rotation and displacement of the rigid articular facets, are of greater magnitude on the anterior surface than the posterior surface. Through-thickness XZ shear strains are unique in that two isolated areas of high magnitude strain exist with opposite rotation directions. Large XY and YZ shear strains are found in the same area, but shear in opposite directions. In-plane (XY) stresses are tensile, whereas through-plane (YZ, XZ) stresses are compressive, because tensile stresses are supported by the two fiber families oriented on the XY plane. Compressive stresses through the thickness, following with the strains, both shear in the opposite direction of the in-plane stresses.
Comparison to Ianuzzi et al. [4]
First (E1) and second (E2) principal strains averaged over the posterior capsule surface were comparable with those reported by Ianuzzi et al. Both data sets (bounded by 95% confidence intervals) are plotted for four instances of relative L3–L4 vertebral rotation in Fig. 9. The value of E1 in the simulations fell within the lower confidence bounds of the Ianuzzi et al. data for all relative rotation instances except for the maximum relative rotation. The values of E2 within the simulations nearly overlapped the E2 values given by Ianuzzi et al. The simulations gave a magnitude of E1 that was slightly smaller than that of E2 at each point, but the difference was not significant (p=.76 based on a paired t test).
Fig. 9.
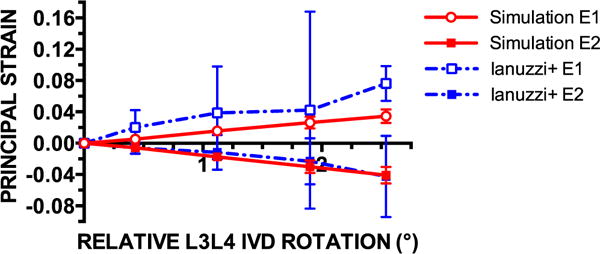
Mean first (E1) and second (E2) principal strains in finite element simulations (n=10) of facet joint flexion in healthy subjects were comparable with the principal strains recorded in a cadaver flexion study (n=7) by Ianuzzi et al. [4]. Mean values are bounded by 95% confidence intervals for all data sets. The relative rotation of adjacent vertebrae according to the defined coordinate system is negative, but the absolute value is displayed. The definitions of E1 and E2 followed the definition of Ianuzzi et al., where E1 was the largest positive value and E2 was the negative value of the largest magnitude of the eigenvalues in 3D. In the simulations, the magnitude of E2 was slightly larger than E1 at each point, but not significantly different.
Discussion
An anatomically and kinematically realistic finite element model of the lumbar facet joint during flexion elucidated the existence of in-plane (XY) and through-plane (YZ, XZ) shear deformations on the anterior and posterior surfaces of the FCL. The magnitudes of stress and strain were largest across the ligamentous surface between the attachments to the articular facets (ie, over the joint space). The largest tensile strains were found in the ZZ direction, resulting from ligament thickening to maintain constant mass. Conversely, the largest tensile Cauchy stresses appeared as in-plane shear (XY) stresses because of the prescribed fiber distributions aligned on the XY plane. Thus, the largest tensile strains were a function of unconstrained motion and the largest tensile stresses were a function of fiber direction.
The mean surface principal strains in our simulations were directly comparable with those observed experimentally by Ianuzzi et al. [4]. Experimental constraints limited Ianuzzi et al. to consider only mean surface strains, whereas the present study was also able to capture the inhomogeneity among regions. In Fig. 5, we see a wide distribution of E1, ranging roughly from 0% to 35%, whereas the average surface E1 was calculated at 6.40%. Calculating average surface principal strains understates the complexity of the resulting deformation field (including the presence of shear) in a tissue that has complex kinematics, a complicated geometry, and a distinct fiber alignment.
Previously, the parameters of the constitutive material for the FCL were optimized to fit both normal and shear force data obtained from displacement-controlled planar biaxial tests of healthy L4–L5 cadaveric FCLs (n=6, Claeson et al., submitted). Model parameters identified two distinct fiber populations, one running primarily superior-lateral to inferior-medial, and the other roughly lateral to medial with small variation among samples. A sensitivity analysis of the parameter values showed that the model determined the angles of the two fiber populations with high confidence. Here we extended the validation to 3D by comparing our data with those of Ianuzzi et al. [4], who calculated E1 and E2 by placing a 3×3 grid of surface markers on the posterior FCL during flexion of cadaveric lumbar spines. The E1 and E2 output from our finite element simulations were within the 95% confidence bounds of their data.
The structure and geometry of the FCL create inhomogeneity in the stress and strain fields. The highest density of elements at maximum stress and strain values occurred at the anterior ligament surface that spanned the joint space. The anterior region of a human lumbar FCL is elastin-rich [1]. The inherent extensibility of elastin could aid to mitigate stresses in this area, and a neo-Hookean material, instead of a distribution of stiff fiber families, may better represent this region. Because our constitutive data came from planar tests (Claeson et al., submitted), it was impossible to identify any through-thickness variation in material properties. The two-layer structure of the FCL could be of particular significance in relation to the through-thickness (YZ) shear strain and stress because of the proximity of the elastin-rich anterior layer to the bone surface. Additionally, the deformation in this region is strongly dependent on the width of the joint space; a larger space between the rotating and displacing articular facets would reduce the magnitude of stress and strain. Thus, because the size of the facet joint (and its joint space) varies widely between individuals [30], the deformations calculated here could change if the current subject-specific kinematics (n=10) were input into their respective subject-specific models instead of a single, general model.
The facet joints of the spinal column have various, location-dependent geometries and orientations that both facilitate and restrict different types of spinal motions. Cervical facet joints are oriented roughly parallel to the coronal plane [31,32], providing resistance to flexion and shear, but allowing rotation [33]. The thoracic facet joints are also oriented on the coronal plane [20,21] but are unique in that they share articular surfaces with the ribs at each level. The facet and costovertebral joints both add stability to the thoracic region, but the costovertebral joints provide added protection against flexion [34]. Conversely, the lumbar facet joints are aligned roughly with the sagittal plane [21,22], allowing substantial shear while limiting axial rotation [33]. Within each region of the spine, the specific angle of the facet joint with respect to the dominant plane of orientation varies slightly at each level to facilitate the specific kinematic responsibility of that level. For example, the facet joint orientations of the upper cervical vertebrae (occipital—C2) provide a greater range of motion in axial rotation than the lower cervical levels [35]. Thus, the data on L3–L4 FCL deformation provided here cannot describe FCL deformations at other spinal levels because twisting, lateral bending, and combined motions impose quite different motions on the vertebrae, and consequently on the FCL. Nevertheless, it is expected that the broad effects seen here, including in-plane and especially through-plane shear of the ligament, would arise during most spinal motions because of the curved geometry of the facet joint.
Abnormal and degenerated lumbar facet joints have altered kinematic function and thus altered load distributions. Lumbar facet joint tropism is found in 20% to 40% of the general population [33,36] and is identified by an asymmetry of facet joint angle with respect to the sagittal plane. Furthermore, abnormalities in the facet joint arise from remodeling due to aging and degeneration. Articular facet hypertrophy, articular cartilage thinning, laxity of FCL, and joint calcification (including osteophytes and enthesophytes) all affect normal facet joint mechanics [37]. Osteophytes commonly form [38] within the joint space of degenerated FCLs to restabilize the facet joint [39] and reduce relative motion [40,41]. Large stresses in this joint space area, as predicted by our simulations, could trigger the onset of osteophyte formation. Enthesophytes, bony protrusions occurring on the surface at the insertion points of ligament, are also present in degenerated FCLs [38,42]. Our study aimed to simulate the response of healthy FCLs during flexion; therefore, structural abnormalities and facet joint degeneration are not accounted for here. It can be hypothesized that the resulting magnitude of stress and strain through the FCL in flexion would be reduced if ossification of the joint limited range of motion.
Better understanding of the deformation of the lumbar FCL is important in elucidating the mechanisms by which facet joints can become painful, a prevalent and expensive diagnosis. Facet joint pain is a subset of chronic low back pain, but there is inconclusive evidence pertaining to adequate diagnosis and treatment (Cohen, 2007). In spite of—or perhaps because of—the lack of a clear picture of how facet pain arises, the number of facet joint interventions increased by a factor of 546% from 1997 to 2006 in the US Medicare population, and the resulting expenditures increased from over $229 million in 2002 to upward of $511 million by 2006 [43]. Pain is likely to occur from altered spine kinematics due to structural remodeling of the joint (degeneration) or from joint overuse and overloading (injury). For example, microinjury may occur after sustained and repetitive lumbar flexion, which increases facet joint range of motion and thus FCL strain [44]. The perception of pain is likely to emanate from the FCL itself because human cervical, thoracic, and lumbar FCLs are densely innervated with proprioceptive, nociceptive, and mechanoreceptive nerve endings [45–49]. Vandenabeele et al. [49] and McLain and Pickar [47] published images of the nerve fibers and endings within the lumbar FCL, but to our knowledge a schematic of innervation location has not been reported. Based on our findings, the middle body of the FCL would be a logical location for position- and pain-sensing nerve endings because of the large and readily occurring stress and strain values, at least in the case of lumbar flexion. This study, exposing the inhomogeneous deformation profile of a healthy lumbar FCL during flexion, can be used as a basis for future studies to discern the changes in FCL mechanics for painful or degenerated facet joints.
Conclusions
We found that in-plane and through-plane shear deformations are widely present in finite element simulations of a lumbar FCL during flexion. We speculate that the large strains, particularly in the region of the FCL above or near the joint space, could provide the proprioceptive system an excellent measure of spinal motion, and that the resulting stresses could play a role in osteophyte or enthesophyte formation. These ideas must be investigated further, both experimentally and theoretically, before any strong conclusions can be drawn, but our results suggest possible avenues for further exploration of lumbar FCL mechanobiology. Clearly, any such study should consider shear as well as tensile deformation.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health (T32 AR050938 and U01 EB016638). We thank Dr Alex Fok at the University of Minnesota Dental School for the use of the micro-CT. Additionally, the assistance of the FEBio staff is gratefully acknowledged.
Author disclosures: AAC: Nothing to disclose. VHB: Grant: NIH (H, Paid to the institution, U01-EB016638), pertaining to submitted manuscript; Support for Travel to Meetings for the Study or Other Purposes: NIH (H, Paid to the institution, U01-EB016638), pertaining to submitted manuscript; Trips/Travel: NIH (H, Paid to the institution, U01-EB016638), outside the submitted work; Grant: NIH (H, Paid to the institution, U01-EB016638), outside the submitted work; Fellowship Support: NIH (C, T32_AR050938), outside the submitted work.
Footnotes
FDA device/drug status: Not applicable.
The disclosure key can be found on the Table of Contents and at www.TheSpineJournalOnline.com.
Supplementary material
Supplementary material related to this article can be found at doi:10.1016/j.spinee.2016.08.014.
References
- 1.Yamashita T, Minaki Y, Ozaktay AC, Cavanaugh JM, King AI. A morphological study of the fibrous capsule of the human lumbar facet joint. Spine. 1996;21:538–43. doi: 10.1097/00007632-199603010-00002. [DOI] [PubMed] [Google Scholar]
- 2.Cheng JS, Carr CB, Wong C, Sharma A, Mahfouz MR, Komistek RD. Altered spinal motion in low back pain associated with lumbar strain and spondylosis. Evid Based Spine Care J. 2013;4:6–12. doi: 10.1055/s-0033-1341640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kozanek M, Wang S, Passias PG, Xia Q, Li G, Bono CM, et al. Range of motion and orientation of the lumbar facet joints in vivo. Spine. 2009;34:E689–96. doi: 10.1097/BRS.0b013e3181ab4456. [DOI] [PubMed] [Google Scholar]
- 4.Ianuzzi A, Little JS, Chiu JB, Baitner A, Kawchuk G, Khalsa PS. Human lumbar facet joint capsule strains: I. During physiological motions. Spine J. 2004;4:141–52. doi: 10.1016/j.spinee.2003.07.008. [DOI] [PubMed] [Google Scholar]
- 5.Claeson AA, Yeh YJ, Black AJ, Akkin T, Barocas VH. Marker-free tracking of facet capsule motion using polarization-sensitive optical coherence tomography. Ann Biomed Eng. 2015;43:2953–66. doi: 10.1007/s10439-015-1349-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bloemker KH, Guess TM, Maletsky L, Dodd K. Computational knee ligament modeling using experimentally determined zero-load lengths. Open Biomed Eng J. 2012;6:33–41. doi: 10.2174/1874230001206010033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ellis BJ, Debski RE, Moore SM, McMahon PJ, Weiss JA. Methodology and sensitivity studies for finite element modeling of the inferior glenohumeral ligament complex. J Biomech. 2007;40:603–12. doi: 10.1016/j.jbiomech.2006.01.024. [DOI] [PubMed] [Google Scholar]
- 8.Gardiner JC, Weiss JA. Subject-specific finite element analysis of the human medial collateral ligament during valgus knee loading. J Orthop Res. 2003;21:1098–106. doi: 10.1016/S0736-0266(03)00113-X. [DOI] [PubMed] [Google Scholar]
- 9.Guess TM, Stylianou A. Simulation of anterior cruciate ligament deficiency in a musculoskeletal model with anatomical knees. Open Biomed Eng J. 2012;6:23–32. doi: 10.2174/1874230001206010023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kia M, Stylianou AP, Guess TM. Evaluation of a musculoskeletal model with prosthetic knee through six experimental gait trials. Med Eng Phys. 2014;36:335–44. doi: 10.1016/j.medengphy.2013.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Moore SM, McMahon PJ, Debski RE. Bi-directional mechanical properties of the axillary pouch of the glenohumeral capsule: implications for modeling and surgical repair. J Biomech Eng. 2004;126:284–8. doi: 10.1115/1.1695574. [DOI] [PubMed] [Google Scholar]
- 12.Moore SM, Ellis B, Weiss JA, McMahon PJ, Debski RE. The glenohumeral capsule should be evaluated as a sheet of fibrous tissue: a validated finite element model. Ann Biomed Eng. 2010;38:66–76. doi: 10.1007/s10439-009-9834-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Song Y, Debski RE, Musahl V, Thomas M, Woo SL. A three-dimensional finite element model of the human anterior cruciate ligament: a computational analysis with experimental validation. J Biomech. 2004;37:383–90. doi: 10.1016/s0021-9290(03)00261-6. [DOI] [PubMed] [Google Scholar]
- 14.Nagel TM, Zitnay JL, Barocas VH, Nuckley DJ. Quantification of continuous in vivo flexion-extension kinematics and intervertebral strains. Eur Spine J. 2014;23:754–61. doi: 10.1007/s00586-014-3195-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pearcy MJ, Tibrewal SB. Lumbar intervertebral disc and ligament deformations measured in vivo. Clin Orthop Relat Res. 1984;191:281–6. [PubMed] [Google Scholar]
- 16.Takayanagi K, Takahashi K, Yamagata M, Moriya H, Kitahara H, Tamaki T. Using cineradiography for continuous dynamic-motion analysis of the lumbar spine. Spine. 2001;26:1858–65. doi: 10.1097/00007632-200109010-00008. [DOI] [PubMed] [Google Scholar]
- 17.Jaumard NV, Leung J, Gokhale AJ, Guarino BB, Welch WC, Winkelstein BA. Relevant anatomic and morphological measurements of the rat spine: considerations for rodent models of human spine trauma. Spine. 2015;40:E1084–92. doi: 10.1097/BRS.0000000000001021. [DOI] [PubMed] [Google Scholar]
- 18.Van Schaik JP, Verbiest H, Van Schaik FD. The orientation of laminae and facet joints in the lower lumbar spine. Spine. 1985;10:59–63. doi: 10.1097/00007632-198501000-00009. [DOI] [PubMed] [Google Scholar]
- 19.Yoganandan N, Knowles SA, Maiman DJ, Pintar FA. Anatomic study of the morphology of human cervical facet joint. Spine. 2003;28:2317–23. doi: 10.1097/01.BRS.0000085356.89103.A5. [DOI] [PubMed] [Google Scholar]
- 20.Panjabi MM. Articular facets of the human spine. Quantitative three-dimensional anatomy. Spine. 1993;18:1298. doi: 10.1097/00007632-199308000-00009. [DOI] [PubMed] [Google Scholar]
- 21.Masharawi Y, Rothschild B, Dar G, Peleg S, Robinson D, Been E, et al. Facet orientation in the thoracolumbar spine: three-dimensional anatomic and biomechanical analysis. Spine. 2004;29:1755–63. doi: 10.1097/01.brs.0000134575.04084.ef. [DOI] [PubMed] [Google Scholar]
- 22.Taylor JR, Twomey LT. Age changes in lumbar zygapophyseal joints. Observations on structure and function. Spine. 1986;11:739–45. doi: 10.1097/00007632-198609000-00014. [DOI] [PubMed] [Google Scholar]
- 23.Hicks GE, Morone N, Weiner DK. Degenerative lumbar disc and facet disease in older adults: prevalence and clinical correlates. Spine. 2009;34:1301–6. doi: 10.1097/BRS.0b013e3181a18263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, et al. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31:1116–28. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- 25.Maas SA, Ellis BJ, Ateshian GA, Weiss JA. FEBio: finite elements for biomechanics. J Biomech Eng. 2012;134:011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mattucci SF, Moulton JA, Chandrashekar N, Cronin DS. Strain rate dependent properties of younger human cervical spine ligaments. J Mech Behav Biomed Mater. 2012;10:216–26. doi: 10.1016/j.jmbbm.2012.02.004. [DOI] [PubMed] [Google Scholar]
- 27.Jacobs NT, Cortes DH, Peloquin JM, Vresilovic EJ, Elliott DM. Validation and application of an intervertebral disc finite element model utilizing independently constructed tissue-level constitutive formulations that are nonlinear, anisotropic, and time-dependent. J Biomech. 2014;47:2540–6. doi: 10.1016/j.jbiomech.2014.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Drury NJ, Ellis BJ, Weiss JA, McMahon PJ, Debski RE. Finding consistent strain distributions in the glenohumeral capsule between two subjects: implications for development of physical examinations. J Biomech. 2011;44:607–13. doi: 10.1016/j.jbiomech.2010.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Latypova A, Arami A, Becce F, Jolles-Haeberli B, Aminian K, Pioletti DP, et al. A patient-specific model of total knee arthroplasty to estimate patellar strain: a case study. Clin Biomech (Bristol, Avon) 2016;32:212–19. doi: 10.1016/j.clinbiomech.2015.11.008. [DOI] [PubMed] [Google Scholar]
- 30.Simon P, Espinoza Orias AA, Andersson GB, An HS, Inoue N. In vivo topographic analysis of lumbar facet joint space width distribution in healthy and symptomatic subjects. Spine. 2012;37:1058–64. doi: 10.1097/BRS.0b013e3182552ec9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bogduk N, Mercer S. Biomechanics of the cervical spine. I: normal kinematics. Clin Biomech (Bristol, Avon) 2000;15:633–48. doi: 10.1016/s0268-0033(00)00034-6. [DOI] [PubMed] [Google Scholar]
- 32.Milne N. The role of zygapophysial joint orientation and uncinate processes in controlling motion in the cervical spine. J Anat. 1991;178:189–201. [PMC free article] [PubMed] [Google Scholar]
- 33.Bogduk N. Clinical anatomy of the lumbar spine. 3rd. Melbourne: Churchill Livingstone; 1997. pp. 13–25. [Google Scholar]
- 34.White AA, III, Panjabi MM. Clinical biomechanics of the spine. Philadelphia: J.B. Lippincott Co; 1990. [Google Scholar]
- 35.Mimura M, Moriya H, Watanabe T, Takahashi K, Yamagata M, Tamaki T. Three-dimensional motion analysis of the cervical spine with special reference to the axial rotation. Spine. 1989;14:1135–9. doi: 10.1097/00007632-198911000-00001. [DOI] [PubMed] [Google Scholar]
- 36.Murtagh FR, Paulsen RD, Rechtine GR. The role and incidence of facet tropism in lumbar spine degenerative disc disease. J Spinal Disord. 1991;4:86–9. [PubMed] [Google Scholar]
- 37.Carrera GF, Haughton VM, Syvertsen A, Williams AL. Computed tomography of the lumbar facet joints. Radiology. 1980;134:145–8. doi: 10.1148/radiology.134.1.7350594. [DOI] [PubMed] [Google Scholar]
- 38.Boszczyk BM, Boszczyk AA, Korge A, Grillhosl A, Boos WD, Putz R, et al. Immunohistochemical analysis of the extracellular matrix in the posterior capsule of the zygapophysial joints in patients with degenerative L4-5 motion segment instability. J Neurosurg. 2003;99:27–33. doi: 10.3171/spi.2003.99.1.0027. [DOI] [PubMed] [Google Scholar]
- 39.Izzo R, Guarnieri G, Guglielmi G, Muto M. Biomechanics of the spine. Part II: spinal instability. Eur J Radiol. 2013;82:127–38. doi: 10.1016/j.ejrad.2012.07.023. [DOI] [PubMed] [Google Scholar]
- 40.Fujiwara A, Lim TH, An HS, Tanaka N, Jeon CH, Andersson GB, et al. The effect of disc degeneration and facet joint osteoarthritis on the segmental flexibility of the lumbar spine. Spine. 2000;25:3036–44. doi: 10.1097/00007632-200012010-00011. [DOI] [PubMed] [Google Scholar]
- 41.Tischer T, Aktas T, Milz S, Putz RV. Detailed pathological changes of human lumbar facet joints L1–L5 in elderly individuals. Eur Spine J. 2006;15:308–15. doi: 10.1007/s00586-005-0958-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.de Vlam K, Mielants H, Verstaete KL, Veys EM. The zygapophyseal joint determines morphology of the enthesophyte. J Rheumatol. 2000;27:1732–9. [PubMed] [Google Scholar]
- 43.Manchikanti L, Pampati V, Singh V, Boswell MV, Smith HS, Hirsh JA. Explosive growth of facet joint interventions in the Medicare population in the United States: a comparative evaluation of 1997, 2002, and 2006 data. BMC Health Serv Res. 2010;10:84. doi: 10.1186/1472-6963-10-84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Little JS, Khalsa PS. Human lumbar spine creep during cyclic and static flexion: creep rate, biomechanics, and facet joint capsule strain. Ann Biomed Eng. 2005;33:391–401. doi: 10.1007/s10439-005-1742-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Johnson GM. The sensory and sympathetic nerve supply within the cervical spine: review of recent observations. Man Ther. 2004;9:71–6. doi: 10.1016/S1356-689X(03)00093-6. [DOI] [PubMed] [Google Scholar]
- 46.Kallakuri S. Innervation of cervical ventral facet joint capsule: histological evidence. World J Orthop. 2012;3:10. doi: 10.5312/wjo.v3.i2.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.McLain RF, Pickar JG. Mechanoreceptor endings in human thoracic and lumbar facet joints. Spine. 1998;23:168–73. doi: 10.1097/00007632-199801150-00004. [DOI] [PubMed] [Google Scholar]
- 48.Suseki K, Takahashi Y, Takahashi K, Chiba T, Tanaka K, Morinaga T, et al. Innervation of the lumbar facet joints. Origins and functions. Spine. 1997;22:477–85. doi: 10.1097/00007632-199703010-00003. [DOI] [PubMed] [Google Scholar]
- 49.Vandenabeele F, Creemers J, Lambrichts I, Lippens P, Jans M. Encapsulated Ruffini-like endings in human lumbar facet joints. J Anat. 1997;191(pt 4):571–83. doi: 10.1046/j.1469-7580.1997.19140571.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


