Microfluidic glucose stimulation reveals limited coordination of intracellular Ca²⁺ activity oscillations in pancreatic islets

Abstract

The pancreatic islet is a functional microorgan involved in maintaining normoglycemia through regulated secretion of insulin and other hormones. Extracellular glucose stimulates insulin secretion from islet β cells through an increase in redox state, which can be measured by NAD(P)H autofluorescence. Glucose concentrations over ≈7 mM generate synchronous oscillations in β cell intracellular Ca²⁺ concentration ([Ca²⁺]_i), which lead to pulsatile insulin secretion. Prevailing models assume that the pancreatic islet acts as a functional syncytium, and the whole islet [Ca²⁺]_i response has been modeled in terms of islet bursting and pacemaker models. To test these models, we developed a microfluidic device capable of partially stimulating an islet, while allowing observation of the NAD(P)H and [Ca²⁺]_i responses. We show that β cell [Ca²⁺]_i oscillations occur only within regions stimulated with more than ≈6.6 mM glucose. Furthermore, we show that tolbutamide, an antagonist of the ATP-sensitive K⁺ channel, allows these oscillations to travel farther into the nonstimulated regions of the islet. Our approach shows that the extent of Ca²⁺ propagation across the islet depends on a delicate interaction between the degree of coupling and the extent of ATP-sensitive K⁺-channel activation and illustrates an experimental paradigm that will have utility for many other biological systems.

Pancreatic islet β cells sense extracellular glucose through changes in cellular redox potential, which can be assayed by measuring NAD(P)H autofluorescence intensity (1, 2). A rise in extracellular glucose causes a cascade of events, including increased cellular [ATP]/[ADP] ratio, closure of ATP-sensitive K⁺ (K_ATP) channels, and plasma membrane depolarization (3). Membrane depolarization results in Ca²⁺ influx through voltage-gated membrane channels, which in turn leads to insulin release.

Pancreatic islets are 100–200 μm in diameter and comprise 1,000–10,000 cells (≈85% of which are β cells) (4). When exposed to glucose concentrations over ≈7 mM, islets exhibit synchronous oscillations in β cell intracellular Ca²⁺ concentration ([Ca²⁺]_i), which cause pulses of insulin secretion (5, 6). The synchronous [Ca²⁺]_i response initiated by glucose initially led to the hypothesis that the islet acts as a functional syncytium (7–9). The observation of phase shifts in these [Ca²⁺]_i oscillations added to this model to include β cell heterogeneity (10, 11). These prevailing models suggest that propagating [Ca²⁺]_i waves within the islet are initiated by pacemaker β cells with low glucose stimulation thresholds (10, 11). These pacemaker cells then elicit a response from nonstimulated cells. Alternatively, islet [Ca²⁺]_i response has been described in terms of a bursting model (12, 13). In the context of this model, glucose induces closure of the K_ATP channel, resulting in depolarization of the β cell membranes to approximately –50 mV. Superimposed on this K_ATP-dependent response are periodic bursts of voltage (–40 mV) and Ca²⁺ influx (13). This model further suggests that β cell heterogeneity is averaged out by extensive cell–cell coupling, resulting in an entrained response. Regardless of the model used to describe islet [Ca²⁺]_i response, the extent of electrical coupling within the islet is still poorly understood. Studies have shown that the β cell NAD(P)H response within an islet is proportional to the level of the rate-limiting enzyme glucokinase, which indicates a lack of metabolic coupling (14).

Coordination of the glucose-stimulated β cell response may occur via electrical coupling through gap junction mediated diffusion of small molecules (8, 15), secretion of K⁺ into the intracellular space (16, 17), and/or purinergic receptor signaling (18). Driving a [Ca²⁺]_i signal across cells requires these coupling mechanisms to induce plasma membrane depolarization or release of Ca²⁺ from internal stores in nonstimulated cells. To test the degree of electrical coupling, we designed and built a novel microfluidic device that allows graded glucose stimulation of the islet while permitting simultaneous observation of the NAD(P)H and [Ca²⁺]_i responses. By using this device we show that the β cells of an islet are sufficiently coupled to synchronize the [Ca²⁺]_i response within glucose-stimulated regions. However, the β cells within an islet are not coupled to the extent that allows a glucose-stimulated [Ca²⁺]_i response to be transmitted into neighboring nonstimulated cells.

Methods

Microfluidic Device. Devices were fabricated by using the elastomer polydimethylsiloxane as described in ref. 19. Briefly, a two-part elastomer (Sylgard 184, Dow–Corning) was allowed to cure on a positive relief master made from photopolymerizable epoxy resin (SU-8-2100, Microchem, Newton, MA).

The cured mold was removed from the master, and access holes were cored through the elastomer polydimethylsiloxane at all port locations. Reagent wells were cored out by using a cork-borer. The elastomer polydimethylsiloxane mold was then irreversibly bonded to a 24-× 50-mm cover glass (VWR Scientific) by using an oxygen plasma treatment (Harrick Scientific, Ossining, NY). Tygon tubing (Cole–Palmer) was inserted directly into the cored-out port holes.

The device design comprises six ports: one for loading the islet, one for removing used islets, one for actuating the moveable wall, two for reagent reservoirs, and one for reagent waste. The gap joining the two channels was flat on one side and ellipsoidal on the other, being 100 μm wide at the left and right openings and 150 μm wide in the middle. The width of the holding region was 300 μm. The channel height throughout the device was ≈100 μm.

Pancreatic Islet Isolation and Treatment. Pancreatic islets were isolated from 6- to 12-week-old C57BL/6 male mice as described in refs. 20 and 21 by using collagenase digestion (Roche). Before use, the islets were incubated overnight in RPMI medium 1640 containing 11 mM glucose in a humidified environment at 37°C and 5% CO₂. Islets were suspended in imaging medium (125 mM NaCl/5.7 mM KCl/2.5 mM CaCl₂/1.2 mM MgCl₂/10 mM Hepes, 7.4 pH) containing 2 mM glucose and loaded with 4 μM Fluo-4 AM (Molecular Probes) at room temperature for 1 h. During imaging, islets were kept in a heated, humidified chamber on the microscope stage (Zeiss) and allowed to equilibrate in the device for 10 min. The treatments were pipetted (100 μl) into the appropriate reagent well. The reagent outlet fluid height was adjusted so that a flow rate of ≈10 μl·min^–1 in each fluid channel was established within the device. Wells were refilled as necessary to prevent them from running dry. Islets were allowed to equilibrate with each treatment for 10 min before imaging.

Confocal Imaging. One- and two-photon microscopy was performed on a LSM 510 microscope (Zeiss) with a 20 × 0.75 NA Fluar objective lens (Zeiss). The device was held on the microscope in a temperature-controlled stage (Zeiss) for imaging at 37°C. Fluo-4 and 2-(N-(7-nitrobenz-2-oxa-1,3-diazol-4-yl)amino)-2-deoxyglucose (2-NBDG, Molecular Probes) were imaged by using the 488-nm laser line and the long-pass 505 emission filter. The Fluo-4 label, found on the periphery of the islet, was imaged by positioning the microscope focal plane on the bottom layer of cells (in contact with the glass coverslip). NAD(P)H was imaged by using a 710-nm mode-locked Ti:Saph laser (≈3.5 mW at the sample) and fluorescence collection through a nondescanned detector with a custom 380- to 550-nm filter (Chroma Technology, Rockingham, VT) (1, 2). NAD(P)H was imaged during the experiments by focusing on a plane near the center of the islet that avoided fluorescence contribution from the Fluo-4 [Ca²⁺]_i dye. Sulforhodamine B (Molecular Probes) was imaged by using the 543-nm laser line and a long-pass 560 emission filter. Sulforhodamine B (0.2 μM) was used as a tracer in the 11 mM glucose streams to detect any leakage. Islets that did not sufficiently plug the hole between the two fluid streams were discarded. NAD(P)H concentrations were determined by imaging a standard curve in deep-well images, as described in refs. 22 and 23.

All images were analyzed by using metamorph 5.0 (Universal Imaging, Downington, PA). For [Ca²⁺]_i analysis, individual cells in the islets were outlined and their intensities versus time were plotted. From these plots, the relative intensity change (F/F₀) and frequencies were calculated.

Results

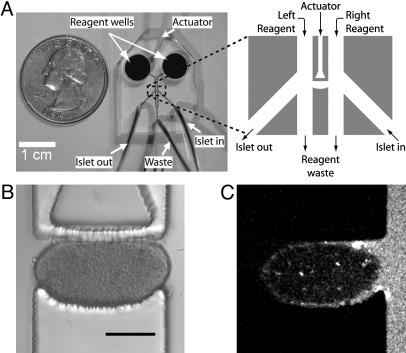
We developed a microfluidic device that traps and holds a pancreatic islet between two separate fluid streams (Fig. 1). Two large wells are used to deliver reagents to the appropriate microchannel (Fig. 1 A). The islet holding area is comprised of one semiellipsoidal wall and one movable wall (Fig. 1B). The adjustable wall is actuated by changing the hydraulic pressure within the actuator channel by means of an external water-filled syringe to accommodate a variety of islet sizes. When trapped in the holding area, the islet gently presses against the coverslip, walls, and ceiling of the device. The device allows switching of the separate solutions on either side of the islet (<1 min) by changing the solutions contained in the larger wells. In each experiment, leakage around the islet was assayed with a hydrophilic fluorescent dye (0.2 μM sulforhodamine B) in one stream of the device (Fig. 1C). Islets that allowed leakage of the dye into the other fluid stream were discarded.

Fig. 1.

The microfluidic device used to treat pancreatic islets with two separate fluid streams. (A) The microfluidic device comprises an actuator channel, islet in and out channels, two reagent channels, and a reagent waste channel. Tubing is connected to all channels except the two reagent channels, where larger wells are used to facilitate loading by means of a pipette. (B) Islets are loaded by closing the waste channel and by using pressure-driven flow from the “in” channel. The top wall can be actuated to minimize leakage for different islet sizes. This actuation does not cause a NAD(P)H rise or [Ca²⁺]_i oscillations in the absence of glucose stimulation. (C) Leakage is actively monitored during experiments by observing sulforhodamine B fluorescence from one channel. If no leakage is present, sulforhodamine B will remain in its channel. (Scale bar, 150 μm.)

To assess whether islet response was perturbed when trapped in this device, we observed the NAD(P)H and [Ca²⁺]_i dye responses. Initial device designs that strained or pinched the islet induced rises in NAD(P)H and [Ca²⁺]_i in the stressed regions. Islets trapped in the present device displayed uniform NAD(P)H and [Ca²⁺]_i intensities. In particular, no significant differences in these parameters were observed at the contact points within the device or when the fluid streams flowed past the islet. Increasing both streams to 11 mM glucose induced NAD(P)H and [Ca²⁺]_i responses that are quantitatively similar to those measured from cultured islets not confined in the device. These data indicate that the islet response is not significantly perturbed when trapped in the device.

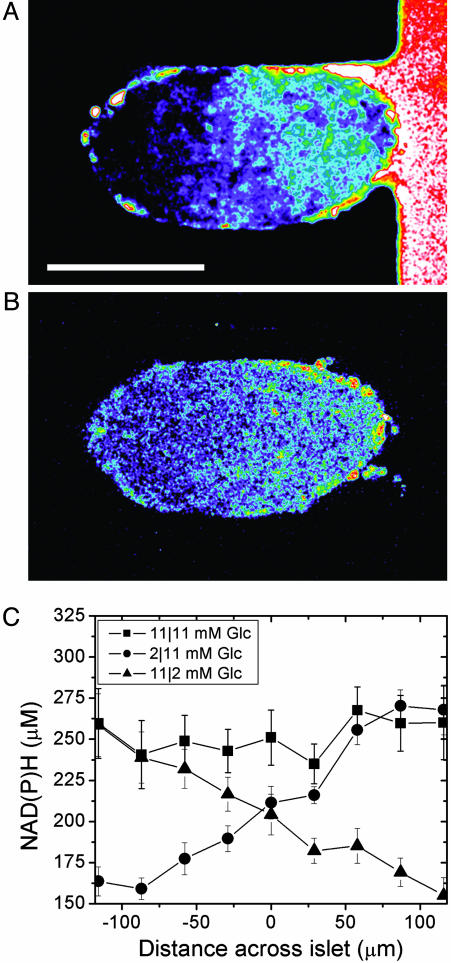
To characterize the glucose stimulation profile across a trapped islet, we measured both glucose penetration and NAD(P)H response. The islet shown in Fig. 2A was exposed to 2-NBDG, a fluorescent glucose analog, in the right stream of the device. This analog is transported into β cells through glucose transporter-2 and can be used to track glucose uptake and diffusion directly (24). A linear gradient of 2-NBDG intensity formed across the islet (Fig. 2 A), with an average slope of 0.43 ± 0.1% change in intensity per micrometer (n = 3; distances across islet diameters were normalized to 230 μm). The NAD(P)H response from these islets was observed when treated with nonstimulatory (2 mM) and stimulatory (11 mM) glucose concentrations in the left and right streams, respectively (Fig. 2B). Islets treated in this manner demonstrated a gradient in NAD(P)H intensity, with the brightest intensity on the stimulated (right) side. Similar to 2-NBDG, the NAD(P)H gradient had a slope of 0.46 ± 0.4% change in intensity per micrometer (n = 3 islets; distances across islet diameters were normalized to 230 μm). This graded NAD(P)H response confirms that the metabolic response (i.e., NADPH signal) of β cells is proportional to the local glucose concentration, as we have seen in isolated mouse islets (14). The average NAD(P)H concentration profile was measured from islets treated with combinations of solutions that contained either 2 or 11 mM glucose to achieve either full stimulation (11/11 mM in the left/right streams) or graded stimulation (2/11 or 11/2 mM in the left/right streams) (Fig. 2C). Full stimulation resulted in a relatively uniform NAD(P)H concentration (≈260 μM, 11/11 mM glucose), which is consistent with values obtained from freshly isolated islets (1). Unstimulated (2/2 mM glucose) cells had a uniformly low NAD(P)H concentration (≈160 μM). Regardless of orientation (11/2 or 2/11 mM glucose), graded stimulation resulted in an NAD(P)H gradient with the brightest intensity on the 11 mM side. The NAD(P)H concentrations observed at the edges of the islet reflected the local glucose concentration in the closer stream irrespective whether the two streams had the same or different (i.e., graded stimulation) glucose concentrations. The NAD(P)H dose–response curve is sigmoid in shape for isolated pancreatic islets over a wide range of glucose concentrations. However, between 2 and 11 mM glucose, the NAD(P)H response is relatively linear. These data indicate that stimulation from both sides of the islet (11/11 mM glucose) results in uniform stimulation across the islet, but that we can induce a linear stimulation gradient by placing 2 and 11 mM glucose in the separate fluid streams. Plotting the NAD(P)H concentration versus the expected glucose concentration across the islet results in a slope of 12.5 ± 0.6 μM NAD(P)H per mM glucose (n = 16). This plot and the equivalent plot for 2-NBDG were each used to calculate the glucose concentration at arbitrary points within the islet.

Fig. 2.

Glucose stimulation in the microfluidic device. The data shown were collected after 10 min of exposure to the indicated treatments. (A) A representative islet after exposure to 2-NBDG in the right stream. There was an increase in 2-NBDG on the right side of the islet because of its exposure to 2-NBDG in the right channel. (Scale bar, 150 μm.) (B) The same islet exposed simultaneously to 2 and 11 mM glucose shows a gradient in NAD(P)H levels, indicating a heterogeneous metabolic response. (C) The NAD(P)H concentrations across an islet exposed to 11/11, 2/11, and 11/2 mM glucose on the left/right side.

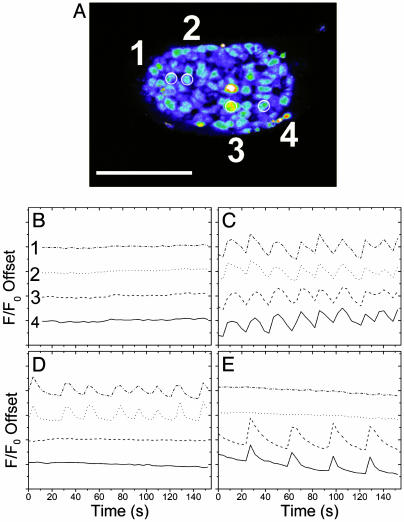
To determine the degree of electronic coupling between β cells, we imaged these same pancreatic islets by using a Ca²⁺-sensitive dye, Fluo-4. An image collected from a typical islet (from n = 8) is shown in Fig. 3A with four cells outlined, two on each half of the islet. The relative intensities (offset) are plotted from these four cells (Fig. 3 B–E; see also Movies 1–8, which are published as supporting information on the PNAS web site). Nonstimulatory glucose resulted in a flat [Ca²⁺]_i response from β cells (Fig. 3B). In contrast, stimulation on both sides of the islet caused the β cells to oscillate synchronously (Fig. 3C), as shown for the four cells outlined in Fig. 3A. The frequency of synchronous oscillations was 2.74 ± 0.11 min^–1 (n = 8), which is consistent with the known islet β cell response to 11 mM glucose (25). Creating a glucose gradient across an islet induced synchronous oscillations only on the stimulated half of the islet (Fig. 3 D, traces 1 and 2, and E, traces 3 and 4). These cells had a similar average frequency as those observed during full glucose-stimulation (2.50 ± 0.17 min^–1, n = 8). In contrast, the cells in the nonstimulated half of the islet did not oscillate. Therefore, β cells are not sufficiently electrically coupled to allow transmission of the glucose-stimulated [Ca²⁺]_i response into nonstimulated portions of the islet. It should be noted that in five of the eight islets studied, some α cells were found to oscillate asynchronously at 2 mM glucose stimulation with a significantly slower frequency (26). However, the α cells did not oscillate at 11 mM glucose, so they were discarded for analysis of the β cell behavior.

Fig. 3.

Ca²⁺ oscillations in a device-trapped pancreatic islet. Islets were loaded with Fluo-4 before being trapped in the device. (A) A representative islet with four cells circled for comparison between the four glucose treatments. (Scale bar, 150 μm.) (B–E) Relative offset intensities (F/F₀) from the outlined cells treated with 2/2(B), 11/11 (C), 11/2(D), or 2/11 (E) (left/right) mM glucose.

By using the data from islets stimulated with graded glucose, we determined the lowest local glucose concentration that sustained synchronous β cell [Ca²⁺]_i oscillations. The last synchronous oscillations were observed 129 ± 8 μm from the 11 mM glucose edge (n = 8). From this distance, the local glucose concentration was calculated from the 2-NBDG plot to be 6.6 ± 0.4 mM. Alternatively, the NAD(P)H concentration at this distance (210 ± 21 μM) and the observed slope of 12.5 ± 0.6 μM NAD(P)H per mM glucose indicates that the local glucose concentration experienced by the last oscillating β cell was 6.6 ± 0.7 mM. These two numbers are both in good agreement with the reported oscillation threshold for normal islets at 7 mM (5, 6). These data indicate that the oscillations are unable to move into tissue experiencing less than ≈7 mM glucose, even when it is likely that closely neighboring cells likely have a significant fraction of closed K_ATP.

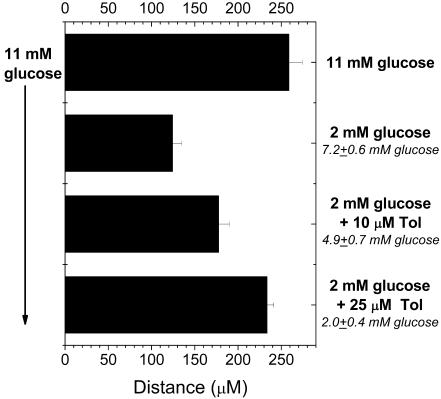
We artificially created a glucose gradient across the islet with this device. In the context of the bursting model (12, 13), this glucose gradient results in a varied open probability for K_ATP across the islet. The membrane potential of β cells experiencing low glucose stimulation is effectively clamped by open K_ATP channels. To determine whether releasing the K_ATP clamp allowed [Ca²⁺]_i oscillations to travel farther into nonstimulated portions of the islet, we used various amounts of a K_ATP channel antagonist (tolbutamide). Shown in Fig. 4 (see Movies 1–8) are the distances that oscillations were observed from the edge of the islet in the 11 mM glucose fluid stream (Fig. 4, left side of bar graph) toward the “test” fluid stream (Fig. 4, right side of bar graph). The test stream contained 11 mM glucose, 2 mM glucose, 2 mM glucose plus 10 μM tolbutamide, or 2 mM glucose plus 25 μM tolbutamide. With 11 mM glucose in the test stream, oscillations occurred across the islet (259 ± 15 μm) with a frequency of 2.61 ± 0.26 min^–1 (n = 8). When 2 mM glucose was placed in the test stream, oscillations again occurred in only part of the tissue with a similar frequency (2.59 ± 0.24 min^–1, n = 11). The NAD(P)H response at the last oscillation was used to determine an effective glucose stimulation of 7.2 ± 0.6 mM glucose, which is similar to our previous glucose gradient studies (6.6 ± 0.7 mM glucose). Placing 2 mM glucose plus 10 μM tolbutamide in test stream resulted in oscillations in regions above 4.9 ± 0.7 mM glucose stimulation (n = 6). These oscillations always originated on the 11 mM glucose stimulation side, consistent with initiation by glucose rather than the tolbutamide, and had a slightly lower frequency (2.38 ± 0.22 min^–1) across the islet. Placing 2 mM glucose plus 25 μM tolbutamide into the test stream drew the oscillations essentially across the islet (2.0 ± 0.4 mM effective glucose stimulation, n = 9). These oscillations also originated from the side of the islet exposed to the 11 mM glucose fluid stream but had a significantly lower frequency (1.61 ± 0.09 min^–1). Placing 50 or 100 μM tolbutamide in the test stream resulted in oscillations across the islet that were much faster in frequency and did not appear to have a consistent origin from the 11 mM glucose fluid stream (data not shown). These oscillations were interpreted to indicate that high concentrations of tolbutamide effectively overpowered the 11 mM glucose effect and as such were not analyzed further.

Fig. 4.

Penetration depth of synchronous [Ca²⁺]_i oscillations. Islets were treated with 11 mM glucose in one fluid stream of the microfluidic device (shown on left side of bar graph) while treatments were varied in the other stream (shown on right side of bar graph in bold). These treatments included 11 mM glucose (n = 8), 2 mM glucose (n = 11), 2 mM glucose plus 10 μM tolbutamide (Tol) (n = 6), and 2 mM glucose plus 25 μM tolbutamide (n = 9), with n representing the number of individual islets used for each measurement. Also shown on the right side of the bar graph (italicized) is the average glucose concentration observed at the specified distance of penetration, as based on the NAD(P)H response.

Glucagon-like peptide 1 (GLP-1) has multiple actions in β cells, including raising glucose-dependent Ca²⁺ influx (27). It has also been established that various gap junctions have increased conductance with raised cAMP, as is caused by GLP-1 stimulation (28). To see whether raising Ca²⁺ current with GLP-1 can overcome the K_ATP channel control of membrane potential, we measured the depth to which the oscillations were observed to travel down the glucose gradient (2 and 11 mM glucose) after 0, 10, and 30 min of 10 nM GLP-1 (7–36). GLP-1 (7–36) caused a significant increase in the oscillation frequency without a significant change in penetration depth (n = 5 islets, data not shown). These data are consistent with a significant control by K_ATP channels even in the presence of increased Ca²⁺ response in the stimulated cells. Although this method has not directly addressed this issue, it is also possible that glucose stimulation modulates gap junction conductance. This modulation could cause limited transmittance into nonstimulated islet regions.

Discussion

The glucose gradient that we created across the islet, as indicated by the diffusion of 2-NBDG and NAD(P)H response, resulted in a metabolic response proportional to the local glucose environment. This result confirms our previous studies, which showed that β cells are not metabolically coupled (14). However, this work also shows that β cells within an islet are not sufficiently coupled to allow an initiated [Ca²⁺]_i response to propagate into regions where the glucose concentration is below the oscillation threshold. The β cells are effectively coupled to coordinate the [Ca²⁺]_i response within regions above this threshold (>6.6 mM). This result indicates that islets do not contain pacemaker cells that set the threshold of the whole islet response. Furthermore, initiation and coordination of the [Ca²⁺]_i response are controlled by two different mechanisms. Therefore, it is necessary that islet response be understood in terms of the local glucose environment that each cell experiences.

Cell–cell transmittance of the Ca²⁺ response is likely a balance between the strength of coupling to initiate the response and the strength of the K_ATP channels to maintain membrane polarization. Our data are consistent with a significant control of this balance by the K_ATP channels. At the extremes of the islet, experiencing 2 and 11 mM glucose, it is likely that a significant fraction of K_ATP channels are open and closed, respectively. Because the device creates a gradient of glucose stimulation, the cells in the middle of the islet have varying fractions of open and closed channels. The strength of K_ATP channel conductance is proportional to the fraction of open channels. Because the neighbor of the last oscillating cell is experiencing only slightly less glucose stimulation (≈6 mM), it is likely that this neighboring cell has only a small number of open K_ATP, yet it still resists the coupling force to depolarize. This cell is also coupled to other cells that are experiencing even less glucose, therefore providing additional resistance to depolarization. The fact that we see a sharp cutoff as to where the oscillations stop in the islet indicates that the amount of coupling force is insufficient to overcome even a small number of open K_ATP channels. Oscillations penetrate further into nonstimulated cells when the K_ATP channel strength is further lowered with tolbutamide. These oscillations are slower than those observed with full or graded glucose simulation, suggesting that the frequency is dictated by the average glucose concentration experienced by the oscillating regions of the tissue. Furthermore, increasing the coupling pressure with GLP-1 was unable to push the oscillations deeper into nonstimulated regions of the islet. Interpreted within the bursting models, these data indicate that oscillations occur in regions with only a significant fraction of closed K_ATP channels.

The microfluidic device developed here offers advantages over other approaches for the study of tissue physiology. The device requires minimal fluid flow to treat the sides of the tissue with well defined stimulation. Also, the short distance between the reagent wells and the holding area enables rapid change of the solutions without significant tissue stress. The microfluidic device has the potential to facilitate studies on β cell communication in pancreatic islets. For instance, examining wave propagation during treatments that block gap junctions or deplete endoplasmic reticulum Ca²⁺ stores can easily be imaged to examine their roles in intracellular communication. Perhaps most importantly, the use of this experimental paradigm can be envisioned generally for many different studies of tissue physiology.