Abstract
Taxol and tau are two ligands that stabilize the microtubule (MT) lattice. Taxol is an anti-mitotic drug that binds β tubulin in the MT interior. Tau is a MT-associated protein that binds both α and β tubulin on the MT exterior. Both Taxol and tau reduce MT dynamics and promote tubulin polymerization. Tau alone also acts to bundle, stiffen, and space MTs. A structural study recently suggested that Taxol and tau may interact by binding to the same site. Using fluorescence recovery after photobleaching, we find that tau induces Taxol to bind MTs cooperatively depending on the tau concentration. We develop a model that correctly fits the data in the absence of tau, yields the equilibrium dissociation constant of ≈2 μM, and determines the escape rate of Taxol through one pore to be 1.7 × 103 (M·s)–1. Extension of the model yields a measure of Taxol cooperativity with a Hill coefficient of at least 15 when tau is present at a 1:1 molar ratio with tubulin.
Because of their essential role in cell division, microtubules (MTs) are a major target for antimitotic cancer therapeutics such as paclitaxel (Taxol) (for reviews, see refs. 1 and 2). Taxol stabilizes the intrinsically labile MT polymer, promotes MT assembly, and suppresses MT dynamics (3–5), possibly by strengthening lateral contacts between tubulin dimers (6, 7). In addition, Taxol affects MT structure by decreasing protofilament number (8) and increasing MT flexibility (9, 10). The Taxol-binding site has been localized to the luminal face of β tubulin and is accessible through 2-nm pores in the MT wall (11–13).
In postmitotic differentiated neuronal cells, MTs form a major component of axons and dendrites and are thus essential for nervous system development and function. In this context, MT dynamics and functions are regulated by MT-associated proteins (MAPs) such as tau (14). In vitro, as well as in vivo, tau stabilizes and promotes MT assembly, as well as stiffens, bundles, and spaces MTs (9, 14–21). Tau is a natively unstructured protein that is localized primarily to neuronal cell bodies and axons (15, 22). Tau expression is important for the establishment of normal axonal morphology and function (23–26). Furthermore, pathological tau function is implicated in the etiology of neurodegenerative diseases, such as Alzheimer's disease, Pick's disease, and frontotemporal dementia with Parkinsonism linked to chromosome 17 (27).
In the central nervous system, as a result of alternative splicing of two N-terminal exons and one C-terminal exon, tau is expressed as six major isoforms. Structurally, tau consists of two major “domains.” The N terminus, or “projection domain,” is involved in bundling and spacing MTs (18, 19). The C terminus, the “MT-binding domain,” is composed of either three or four repeated motifs. This region binds to the exterior of preassembled MTs (28–31).
A recent, intriguing cryoelectron microscopy study found that the MT-binding region can bind inside the MT lumen near the Taxol-binding site (32). Before this report, tau had been thought to bind exclusively to the MT exterior (29–33). The MT stabilizing properties of Taxol were exploited in biochemical studies of tau structure and function because they were thought to act independently. The work of Kar et al. (32), however, suggests that the two ligands may compete for the same binding site.
Here we report biochemical evidence for an interaction between tau and Taxol using fluorescence recovery after photobleaching (FRAP). When we used a fluorescently labeled tau, we found that the macroscopic tau off-rate is not affected by Taxol. However, FRAP measurements on a fluorescently labeled Taxol reveal that tau induces Taxol to bind MTs cooperatively in a tau concentration-dependent manner. We present a model for Taxol binding that fits the low tau concentration data well, yielding an accurate Taxol binding affinity and estimating the escape rate for Taxol through a pore. Expanding the model allows an estimation of Taxol cooperativity at high tau concentration.
Materials and Methods
Tubulin and Reagents. Unless otherwise stated, all MT samples were prepared by incubating 10 μl of 5 mg/ml bovine brain tubulin (Cytoskeleton) for 20 min at 37°C in GPEM-dex buffer (1 mM GTP/100 mM Pipes/1 mM EGTA/2 mM MgSO4/4 mg/ml 110-kDa dextran). Dextran in solution helps stabilize MTs because of macromolecular crowding (34). Taxol (Sigma) and BODIPY 564/570 Taxol (Molecular Probes), called botax, were stored in DMSO at 2 mM and 100 μM, respectively. Before addition to MTs, Taxol and botax were diluted into GPEM-dex to a final concentration of ≤10% DMSO. It should be noted that botax is less soluble (≤30 μM in 10% DMSO) than unlabeled Taxol (≤50 μM in 10% DMSO).
Tau Purification and Acrylodan Labeling. Recombinant full-length adult human four-repeat, 2N tau (441 aa) was overexpressed in Escherichia coli by using the pET vector expression system (Novagen) and purified as described (29). Tau protein concentration was determined by fractionation on a SDS/8% PAGE, followed by Coomassie blue staining relative to a tau standard curve calibrated by mass spectrometry (35). Purified tau was labeled to maximum stoichiometry with acrylodan (Molecular Probes), which modifies two endogenous cysteine residues (Cys-291 and Cys-322) as described (36).
Determination of Taxol KD. The equilibrium dissociation constant, KD, for botax binding to MTs in the presence and absence of tau was measured by using the fluorimetry method of Li et al. (37) with the minor difference of using SDS/PAGE densitometry to determine the amount of tubulin protein in the pellets (see Supporting Text, which is published as supporting information on the PNAS web site).
The botax KD was determined by plotting the fraction of filled Taxol sites, 〈f〉 = [Tax]bound/[tubulin]MT, called the fill ratio, as a function of the free Taxol concentration in solution, [Tax]free. The data were fit with the theoretical form for the fill ratio of a reversible binding reaction
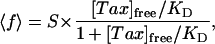 |
[1] |
where S, the maximum stoichiometry of botax binding to the MTs, and KD are parameters of the fit (13, 37, 38).
Fluorescent Tau Samples. Three types of samples with acrylodan-labeled tau were made to test the effects of MT assembly conditions on the tau dissociation rate: (i) tubulin (5 mg/ml) was polymerized in the absence of Taxol and tau for 20 min at 37°C. The MTs were then equilibrated with equimolar amounts of tau (1:1 molar ratio tau/tubulin). (ii) Tubulin (5 mg/ml) was polymerized in the absence of Taxol and tau for 20 min at 37°C. The MTs were equilibrated with 50 μM unlabeled Taxol before being equilibrated with equimolar tau. (iii) Tubulin (5 mg/ml) was polymerized in the presence of equimolar tau for 2 h at room temperature. All equilibrations were performed for 20 min at 37°C.
Fluorescent Taxol Samples. MT samples were prepared with botax at various final concentrations (5 nM to 10 μM) and with varying molar ratios of tau to tubulin (0, 1:50, 1:10, 1:1) using a method similar to Ross and Fygenson (13). Briefly, 5 mg/ml tubulin in GPEM-dex buffer was incubated for 20 min at 37°C. Botax was added (20 nM to 30 μM) to achieve the desired free botax concentration, accounting for the fraction of botax that binds to the MTs (13), and the sample was equilibrated for 20 min at 37°C. Tau was added to a final molar ratio with tubulin of 1:50, 1:10, or 1:1, and the sample was equilibrated for another 20 min at 37°C before being inserted into the flow cell.
The botax concentration in solution was measured in situ by comparing the fluorescence intensity of the background to a set of standards (13). We were limited to [Tax]free ≤ 10 μM by the insolubility of botax and the detrimental effects of high DMSO concentrations on MTs (39). Samples with the highest Taxol concentrations were made with 25% botax and 75% unlabeled Taxol to keep the DMSO concentration below 10%. Botax exhibits a 40-fold increase in fluorescence upon binding to MTs. This increases the signal-to-noise ratio and is essential to observing only the binding reaction.
Fluorescence Recovery Measurements. The experimental procedures used here were the same as in a previous study (13). Briefly, samples were inserted into a flow cell, and the MTs were bundled and aligned by flow around Sephadex beads fixed to the slide. The flow cells were made with extra Sephadex beads (particle size 40–120 μm, Sigma) to confine tau-coated MT bundles. Differential interference contrast microscopy and epifluorescence imaging were performed on an inverted microscope. FRAP movie data were recorded digitally without compression by using a cooled charged-coupled device (CCD) camera triggering a shutter. Exposure to bleaching light was controlled to prevent photodamage, as determined in ref. 13.
Data Analysis. FRAP data were analyzed as described (13). Briefly, intensity profiles of fluorescent bundles were taken from each video frame and were fit with Gaussians after subtracting a baseline to eliminate permanent background variations. For botax samples, the Gaussian amplitude was plotted against time and fit to an exponential of the form
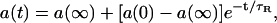 |
[2] |
where a(∞) is the amplitude at infinite time, a(0) is the amplitude of the first Gaussian captured after the bleach, and τR is the characteristic recovery time for fluorescence. For acrylodan tau samples, the Gaussian amplitude was plotted against time and fit to a biexponential of the form
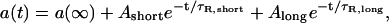 |
[3] |
where Ashort is the amplitude of the shorter recovery time scale, τR,short, and Along is the amplitude of the longer recovery time scale, τR,long.
Results
Tau Spaces MTs. Full-length, four-repeat tau was observed separating flow-bundled MTs in real time by using differential interference contrast and fluorescence microscopy (Fig. 1E). MTs labeled with 3.3 μM botax were bundled around Sephadex beads by flow (Fig. 1 A and B). After 30 min, unlabeled tau with botax in solution was injected into the flow cell at a final concentration of 23 μM tubulin, 23 μM tau, and 3.3 μM botax. Bundles midway along the flow path were observed as tau diffused into the field of view.
Fig. 1.
MTs were fluorescently labeled with botax and flow-aligned into densely packed bundles around a Sephadex bead. Panels present images of the same bundle as viewed by differential interference contrast (A and C) and fluorescence (B and D) before (A and B) and after (C and D) unlabeled tau diffused into the area. (E) Image of tau infiltrating a bundle. To the left of the tau front (arrow), tau has bound and spaced the MTs.
Upon tau binding, densely packed bundles of MTs disperse and become sparse (Fig. 1 C and D). This process is complete within 15 min. The experiment was repeated with a three-repeat, short tau isoform lacking one binding repeat (31 aa) and two N-terminal inserts (29 aa each). Short tau was unable to disperse the tightly bundled MTs (data not shown). Previous work has demonstrated that the size of the N terminus changes the spacing between MTs in vivo (18, 19), but is unknown whether the N terminus spaces the MTs by acting as a polymer brush or by mediating the structural conformation of tau.
Tau Off-Rate Is Unaffected by Taxol. MTs saturated with acrylodan-labeled, full-length tau (1:1 molar ratio with tubulin) were concentrated and aligned between closely spaced Sephadex beads by flow. The macroscopic rate for acrylodan tau dissociation from MTs was observed by using FRAP.
The resulting recovery curves were best fit by a biexponential (Eq. 3 and Fig. 2). To determine whether the short recovery time could be attributed to unbound tau diffusing in solution, a control experiment was performed by using an inert, fluorescein-labeled dextran (Molecular Probes) of comparable size diffusing around tau-coated MTs (data not shown). Dextran recovery was complete within 500 sec, consistent with the short recovery time observed for acrylodan-tau. The long recovery time observed in the tau experiments, 2,548 ± 568 sec, was not present in the dextran samples. We attribute this recovery time to dissociation of bound tau from the MTs. This time is therefore the inverse of koff, implying koff = 0.00039 sec–1 or, equivalently, that 1 tau dissociates every 42 min.
Fig. 2.
Representative biexponential fluorescence recovery curve for acrylodan-labeled four-repeat tau (circles). Recovery curves for all types of samples overlap this data. The fit (dashed line) yields a short time constant, ≈80 sec, corresponding to diffusion of unbound tau around the MTs or fast dissociation of loosely bound tau. The long time constant, ≈2,500 sec, corresponds to the characteristic dissociation time for tau.
The measurement was repeated for three different MT assembly conditions: (i) MTs polymerized in the absence of Taxol and tau, bound with tau alone; (ii) MTs polymerized in the absence of Taxol and tau, equilibrated with Taxol before binding tau; and (iii) MTs polymerized in the presence of tau alone. Identical recovery curves were measured for all assembly conditions, indicating that the tau dissociation rate is independent of the order of tau binding and the presence of Taxol.
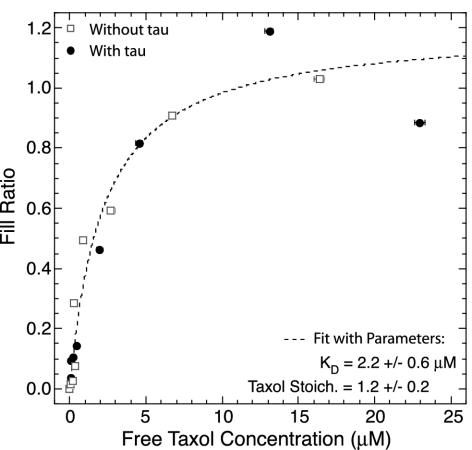
Botax KD Is Unaffected by Tau. The extent of botax binding to MTs was measured in the absence and presence of tau at equimolar concentrations by using fluorimetry. The equilibrium dissociation constant was determined by plotting the fill ratio against free botax concentration (Eq. 1 and Fig. 3). The two data sets overlap, indicating that tau has no effect on the equilibrium binding of botax. The average KD is 2.2 ± 0.6 μM (SE, n = 3), and the maximum stiochiometry is S = 1.2 ± 0.2, as plotted (Fig. 3, dashed line). These values are similar to those found by others for GDP MTs (37, 40).
Fig. 3.
Representative fill ratio curves for botax binding to MTs in the presence (filled circles) and absence (open squares) of tau. The two curves overlap, indicating that tau does not affect the equilibrium binding of botax. The dashed line curve is the average fit(n = 3) curve with fit parameters given.
There was no indication of the high-affinity Taxol site on GTP MTs reported elsewhere (37, 41). It may be that botax does not bind to the Taxol site in the GTP conformation as tightly as other Taxol derivatives. Another possiblity is that, because the MTs were polymerized without Taxol, they have GDP at most of their exchangeable sites because of hydrolysis, thus making the high-affinity KD undetectable.
Taxol Cooperativity Depends on Tau Concentration. FRAP was performed on MTs bound with varying amounts of botax. The fluorescence recovery curves were always simple exponential decays (Eq. 2), and the Gaussian intensity profiles showed little spreading, indicating that a chemical reaction process was being observed instead of a diffusive one (13).
The characteristic recovery time, τR, is the inverse of the macroscopic koff, which is slower than the microscopic koff because of Taxol rebinding. The probability of rebinding depends on the fraction of open binding sites, 〈ξ〉 = 1 – 〈f〉, which is varied by changing Taxol concentration (Eq. 1). Less Taxol in solution causes 〈ξ〉 to increase, leading to more rebinding and a longer τR (13).
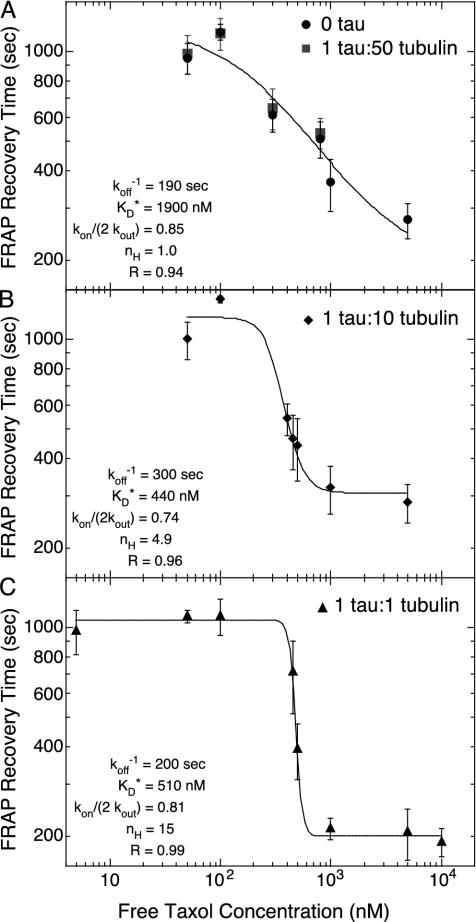
The molar ratio of tau to tubulin greatly affects the shape of the τR curve plotted against free Taxol concentration (Fig. 4). We tested molar ratios of 0, 1:50, 1:10, and 1:1 tau/tubulin. The 0 and 1:50 data sets were indistinguishable and are plotted together (Fig. 4A). All three plots have similar limits at low and high Taxol concentrations, ≈1,300 sec and 200 sec, respectively (Fig. 4). In the high Taxol limit, the probability of rebinding is small and τR approaches the microscopic koff.
Fig. 4.
Recovery time, τR, as a function of free Taxol concentration for tau to tubulin molar ratios of 0 and 1:50 (A), 1:10 (B), and 1:1 (C) with fit parameters from the model with a Hill coefficient to estimate the cooperativity. (A) At low tau concentrations, the model fits well without cooperativity nH = 1. (B) At intermediate tau concentration, τR becomes more sensitive to Taxol concentration with nH = 4.9. (C) At saturating amounts of tau, Taxol appears very cooperative with nH = 15. Fit parameters for each curve are listed inside the plot.
The main difference between the data sets is the sensitivity to Taxol concentration, as measured by the Hill coefficient, nH, of the sigmoidal recovery time curve. Sensitivity increases with increasing tau concentration (Fig. 4). At the lowest tau concentrations, the characteristic times for Taxol FRAP were similar to those reported previously (13) and fit well to a sigmoid with a Hill coefficient, nH = 1 (Fig. 4A). At 1:10 tau/tubulin, τR is more sensitive to the Taxol concentration in the range 100 nM to 1 μM, with nH = 5 (Fig. 4B). Ata1:1tau/tubulin ratio, τR is very sensitive to Taxol concentration between 300 nM and 1 μM, having nH = 15 (Fig. 4C). For both the 1:10 and 1:1 data sets, the recovery time is less responsive to changes in the Taxol concentration at low and high Taxol concentrations. This delay in the onset of response is characteristic for a system displaying “ultrasensitivity” or “cooperativity” (42).
Model. Our FRAP experiments probe the kinetics of Taxol binding to MTs. In these experiments, we observe little spreading of the Gaussian intensity profiles, indicating that Taxol is not diffusing along the MTs, but rather is passing through pores in the MT wall. The resulting recovery curve (Eq. 2) is an exponential decay, further supporting the conclusion that we are observing dissociation instead of diffusion. The recovery time, τR, varies with the free Taxol concentration, presumably because it is a function of the fraction of filled binding sites, 〈f〉. To fully understand how the fill ratio affects τR, we develop a mean-field binding reaction model to compare to our results.
Because the Gaussian intensity profiles maintain a constant width, the model is dominated by the binding and rebinding of Taxol to a single site. The diffusion of Taxol is fast, D ≈ 10–6 cm2/s, so we assume that the interior of the MT reaches equilibrium much faster than 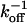 . This assumption implies that the concentration of free bleached Taxol in the MT interior, nb(x), is caused entirely by the dissociation of bleached molecules from the Taxol-binding sites.
. This assumption implies that the concentration of free bleached Taxol in the MT interior, nb(x), is caused entirely by the dissociation of bleached molecules from the Taxol-binding sites.
To find the fraction of bleached Taxols that rebind, we solve a diffusion equation subject to the boundary conditions of escaping at the walls and rebinding to sites
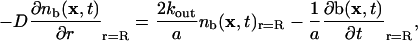 |
[4] |
where D is the diffusion coefficient in the MT interior, R is the inner diameter of the MT, and a is the area of the unit cell of the MT lattice. We introduce kout to represent the rate of Taxol passage through one pore in the MT wall. Because there are two pores per dimer, the escape rate per dimer is 2kout. This pore exchange rate depends on the physical characteristics of the pores and Taxol molecules, and has units of (M·s)–1. We assume that, once a bleached Taxol molecule escapes through a pore, it never returns. The last term corresponds to the rebinding of bleached molecules where b(x, t) is the average dimensionless occupation number, which is equal to the probability that the site at x is filled with a bleached Taxol at time t.
Although it is possible to solve for nb(x, t) exactly in terms of ∂b(x, t)/∂t, it is most useful to consider the limit of times longer than the time for diffusion across the lumen, R2/D. We further assume that 2kout is fast enough that bleached Taxols escape through the pores before they diffuse along the MT. This assumption is consistent with the observation that the bleached spot does not increase in width. Under these assumptions, we specialize to the case of a homogeneous distribution of Taxol molecules along the length of the tube. Although this is not necessary to solve the problem, it simplifies the resulting solution. In this limit, the concentration of bleached Taxols can be expressed as
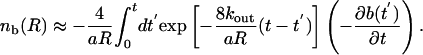 |
[5] |
Note that 2/aR = Ns/V, where Ns is the number of binding sites and V is the volume of the lumen. Therefore, kout is multiplied by the effective density of pores in the MT wall.
We can now write a simple reaction equation for the binding site with a bleached Taxol molecule:
 |
[6] |
where 〈ξ 〉 is the probability that a single site is empty. Thus, we write
 |
[7] |
the average fraction of empty sites as determined by equilibrium chemical kinetics.
In the homogeneous limit, the variables depend only on time, and Eq. 6 can be readily solved by using a Laplace transform. If we are interested in the long time limit, however, it is convenient to make the ansatz b = b(0)e–st. We find that, when t » (8kout/(aR) – s)–1, the rate s is given by
 |
[8] |
Thus, as long as the exchange rate of Taxol through the MT pores is fast enough, the decay profile should be approximately exponential with a decay constant given by Eq. 8. In the limit that 8kout/(aR) is the fastest rate in the problem, we find the approximate recovery time from Eq. 8 becomes
 |
[9] |
which is directly comparable to our experimental results. When t « (8kout/(aR) – s)–1, the model predicts deviations from purely exponential decay, but our observations occur at long times. This result can also be derived by using a more complicated Master equation (see Supporting Text) where the binding of both the bleached and unbleached molecules are kept explicit, suggesting that the mean-field result is exact within our approximations.
Discussion
Fluorescence recovery was used to measure the effect of tau on the macroscopic off-rate of Taxol. It was found that tau induces Taxol to bind cooperatively in a tau concentration-dependent manner (Fig. 4). To our knowledge, this is the first time cooperativity has been observed in the Taxol–MT system.
Tau Dissociation Agrees with Empirical Evidence. FRAP was used to measure the macroscopic dissociation rate of acrylodan-tau from MT bundles. Under these conditions, dissociation was slow (koff = 3.9 × 10–4 sec–1), and independent of the presence of Taxol or tau during assembly. The measured off-rate is consistent with empirical observations that tau remains associated with tubulin through multiple cycles of polymerization and depolymerization (14), but it is longer than expected considering the moderate binding affinity (KD = 10–100 nM) previously reported for tau (43, 44).
A recent, stopped-flow study using acrylodan-labeled tau measured the binding rate constants of tau (36). MTs were polymerized in the presence of acrylodan-labeled tau and unlabeled tau was introduced to the sample to chase the acrylodan tau off the MTs. A fraction of acrylodan-tau was mobile and replaced by unlabeled tau with a fast off-rate of koff = 2.5 sec–1. The remaining fraction was immobile and remained bound for >30 min (36). This result is consistent with our measurement of tau dissociation, which found both fast and slow rates. A fast dissociation rate would be indistinguishable from diffusion of unbound tau in our experiments, whereas the slow dissociation rate of over 30 min would be easily visualized.
Our results showed that tau dissociation was independent of conditions during MT polymerization. This is different from the study by Makrides et al. (36), which found tau bound to preassembled MTs did not display an immobile fraction. The difference may be due to the nature of tau binding at high concentrations. Stop-flow techniques are performed with low concentrations of tau and tubulin, where MT bundling is unlikely. At higher concentrations of tubulin and tau, like those used here, tau binding rates reflect complicated tau–tau interactions such as lattice parking problems (45) and oligimerization (31, 44). In particular, MT-bound tau may oligomerize to form cross-bridges between neighboring MTs (33). Although we could not directly observe crossbridging in our FRAP experiments, we did observe the dispersing of tightly packed MTs as tau bound (Fig. 1), which may indicate that cross-bridges were forming. Unlike the dilute conditions of other studies, the bundles in our experiments better resemble the crowded conditions found in axons. This finding implies that the slow off-rate measured here may be physiologically relevant.
Taxol Binding Model Fits Experiment. We present a model that describes how the mobility of Taxol, characterized by the fluorescence recovery time, is a function of the fraction of unoccupied Taxol binding sites, 〈ξ〉. The model accounts for Taxol rebinding multiple times as well as escape through pores in the MT wall.
For 0 and 1:50 tau/tubulin ratios, Eq. 9 fits the data well (Fig. 4A). In the limit of saturating Taxol concentrations, the data yield an estimate of koff = 5.0 ± 0.25 × 10–3 sec–1. Fitting the data to Eq. 9 reveals KD = 1.9 ± 0.50 μM, which is the same as the KD measured by using fluorimetry, 2.2 ± 0.60 μM. We can compute kon = koff/KD = 2,800 ± 820 (M·s)–1.
From this fit, we deduce that Taxol passes through the MT wall faster than it binds to the Taxol site because kon/2kout = 0.85 ± 0.014. Given the kon computed above, kout = 1,700 ± 1,000 (M·s)–1. This rate characterizes the passage of Taxol through one pore and is equal and opposite to kin, implying that Taxol enters through one pore slower than the association rate for Taxol. Because there are two pores per dimer, Taxol is able to traverse quickly to bind.
The rate of Taxol passage through the pores is especially interesting because Taxol binds quickly to MTs. Structural studies have shown the pores to be large enough (1.5 nm × 2.5 nm) to allow Taxol (≈1 nm) to pass (11, 12), but it has been suggested that the association rate of Taxol measured by using stopped-flow techniques is too fast to be explained by the pores (38, 46). A recent study by Diaz et al. (47) examined Taxol-binding kinetics to gluteraldehyde cross-linked MTs in the presence and absence of exterior-bound MAPs. They suggest that the binding occurs in two steps: the first is a concentration-dependent association, the second is concentration-independent exchange. This suggestion implies that Taxol binds to an exterior site first and then moves into its interior binding site. This proposed scheme of Taxol binding is so different from ours that the binding rate constants are not comparable. In addition, the Taxol-binding site had a higher affinity (KD = 38 nM) in their study, suggesting that their MTs were fixed with GTP at the exchangeable nucleotide-binding sites.
At low Taxol concentration, τR approaches the limit of 1/(1 – kon/2kout). Extrapolating from the fit, this limit is 1,300 sec. Because each binding event lasts ≈200 sec, we deduce that, when most sites are open, Taxol molecules rebind an average of 6.5 times. This is an upper bound on the average number of rebinding events Taxol experiences before escaping the MT lumen. The high and low Taxol limits are the same for all three tau concentrations, implying that tau has no effect on the Taxol dissociation rate or the number of rebinding events.
For the 1:10 and 1:1 tau/tubulin samples, Eq. 9 is a poor fit to the data. To reflect the greater sensitivity displayed in these data, we can modify the on rate to kon 〈ξn 〉, where 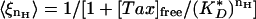 , where nH is the Hill coefficient, and
, where nH is the Hill coefficient, and 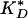 is the effective dissociation constant. These phenomenological parameters serve to quantify the degree of cooperativity observed in the data. The adjusted functional form fits the data well, with Hill coefficients of nH = 4.9 and nH = 15 for the 1:10 and 1:1 samples, respectively (Fig. 4 B and C).
is the effective dissociation constant. These phenomenological parameters serve to quantify the degree of cooperativity observed in the data. The adjusted functional form fits the data well, with Hill coefficients of nH = 4.9 and nH = 15 for the 1:10 and 1:1 samples, respectively (Fig. 4 B and C).
At a 1:1 molar ratio of tau/tubulin, MTs should be saturated with tau. Any effect of tau on mobility through the pore (e.g., altered pore size) would be reflected in the value of kon/2kout. The similarity of this fit parameter across all data sets suggests that tau does not block the pores and has very little effect on the binding and unbinding rates of Taxol. This finding is consistent with the results of Diaz et al. (47), who also find that tau does not affect the Taxol on rate and probably does not block the pores.
How tau induces Taxol to bind cooperatively is unknown, but we can place several constraints on possible mechanisms: (i) the apparent cooperativity depends on the amount of tau bound to the MTs, (ii) the recovery times at high and low Taxol concentration are unchanged, and (iii) the maximum cooperativity has a Hill coefficient of at least 15.
We note that our measurement of the Taxol KD does not show cooperative behavior in the presence or absence of tau. This discrepancy may be due to the dilute final concentrations of tubulin (4.5 μM) and tau (4.5 μM) at which the fluorometry experiments were performed. Because induced cooperativity depends on the tau concentration and crowding increases local tubulin and tau concentrations, it is likely that a crowded environment would enhance the cooperativity. Next, we consider three possible mechanisms for the Taxol cooperativity.
Tau May Bind Cooperatively and Competitively to the Taxol-Binding Site. The work of Kar et al. (32) shows that tau and Taxol can compete for the same binding site. We must consider whether competition between Taxol and tau could lead to cooperative Taxol binding. If Taxol and tau are competing for a single site, the total number of available sites would be reduced. This type of competition would shift the recovery time curves, but is insufficient to cause cooperativity. However, if tau binds cooperatively with low affinity to several Taxol binding sites at once, competition could lead to the appearance of cooperativity in Taxol binding. In this case, Taxol will be momentarily excluded from multiple sites. After the tau cooperatively dissociates, Taxol molecules will bind to the recently vacated sites and appear cooperative.
One weakness of this mechanism is that tau binding to the MT interior has only been observed when tau is present during MT assembly (32, 36). Competition studies observed that MTs polymerized in the presence of both Taxol and tau showed that increasing concentrations of Taxol decrease the amount of tau that pellets with MTs (32). In our experiments, MTs were assembled with neither Taxol nor tau, equilibrated with Taxol, and finally equilibrated with tau. Such conditions are reported to preclude the binding of tau to the interior site (30, 32). Additionally, we saw no decrease in fluorescence as tau bound to and dispersed tightly bundled, botax-labeled MTs (Fig. 1), suggesting that botax was not being displaced by tau.
Tau May Bind to Reduce the Fraction of Open Taxol-Binding Sites. Another competition scheme would be if tau binding to the exterior site causes a conformational change in the dimer that forbids Taxol binding. Exterior tau binding has been shown to be cooperative by a recent atomic force microscopy study (31) that observed tau binding as a ring of oligomers encircling the exterior of Taxol-stabilized MTs. The oligomer ring would affect Taxol sites on 12–15 protofilaments around the MTs, consistent with our measured maximum Hill coefficient of 15. Correlations between bound tau and Taxol result in an effective communication between neighboring Taxol sites because the tau can affect multiple binding sites at once. This type of competition, mediated through dynamic binding, is unlikely to cause cooperativity because tau has a 42-min dissociation rate, thus the tau will be “frozen” to the MTs over the time scales seen in the Taxol FRAP experiments.
The mechanisms discussed above are dynamic, but there is an equilibrium method by which exterior-bound tau could affect the Taxol binding. If Taxol and tau are competing for open dimers, the equilibrium rate equations for each will be coupled. Thus, the amount of tau bound will be affected by the amount of Taxol bound, and vice versa. This will ultimately cause changes to the empty fraction of Taxol-binding sites in such a way as to make the Taxol appear cooperative, even if it is not. When tau is added to botax-labeled MTs, we observe the tau to space MTs, indicating that tau is binding; however, we see no decrease in the overall intensity of fluorescence (Fig. 1), implying that tau does not displace Taxol. The intensity level did not change for >1 h, when we were presumably at equilibrium, making this equilibrium mechanism unlikely.
Tau May Induce Nearest-Neighbor Interactions Among Taxol. Exterior tau binding could cause a conformational change in tubulin that turns on an interaction between neighboring dimers. Unlike the conformational change discussed in the previous section, a nearest neighbor interaction could enhance binding for a site once a neighboring site is occupied. Enhanced binding is the exact prerequisite for cooperativity. Such conformational changes have been proposed to explain how tau stabilizes the MT lattice (21, 31, 48).
To calculate equilibrium expectation values, a cooperative lattice of binding sites can be modeled by using an Ising model (42) with nearest-neighbor interactions. In an Ising model, a site is either occupied or unoccupied, and the binding energy for that site depends on whether adjacent sites are occupied or unoccupied. Even with only nearest-neighbor interactions in one dimension, the fill ratio can show an arbitrarily sharp sigmoidal transition with Taxol concentration from mostly unoccupied to mostly occupied depending on the strength of the interaction (42).
If we assume that the off-rate is constant, as indicated in the data, the Taxol on-rate will depend on the number of adjacent occupied sites. Hence, the on-rate will display a sharp transition, also.
Conclusions
Our study reveals many interesting facts about tau binding to MTs. The short tau isoform is unable to space apart tightly bundled MTs, suggesting that the N-terminal inserts of tau might be a polymer brush or have structure. The dissociation rate for acrylodan tau is 1 tau per 42 min for crowded conditions, like those in the axon. Most striking, crowded conditions and high concentrations of bound tau lead to the appearance of cooperative binding of Taxol to MTs. The observed cooperativity could be caused by competition between Taxol and tau for the same site or to a conformational change in the tubulin dimer by which tau binding induces nearest-neighbor interactions. Because many MAPs have a similar C-terminal binding domain, it would be interesting to repeat this experiment with other MAPs and their isoforms, as well as dementia-linked tau mutants.
Supplementary Material
Acknowledgments
We thank Stu Feinstein, MaryAnn Jordan, Fyl Pincus, and Jacque Prost for helpful insights, and John Lew (University of California, Santa Barbara) for the gift of tau. This work was supported in part by the National Science Foundation Faculty Early Career Development (CAREER) Program Award BIO99-85493 and by Materials Research Science and Engineering Center Award DMR00-80034, and in part by an Alfred P. Sloan Foundation Fellowship (to D.K.F.). C.D.S. was supported by National Science Foundation Grant Division of Materials Research Grant 02-03755.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: MT, microtubule; MAP, MT-associated protein; FRAP, fluorescence recovery after photobleaching.
References
- 1.Jordan, M. A. (2002) Curr. Med. Chem. Anti-Cancer Agents 2, 1–17. [DOI] [PubMed] [Google Scholar]
- 2.Abal, M., Andreau, J. M. & Barasoain, I. (2003) Curr. Cancer Drug Targets 3, 193–203. [DOI] [PubMed] [Google Scholar]
- 3.Schiff, P. B., Fant, J. & Horwitz, S. B. (1979) Nature 277, 665–667. [DOI] [PubMed] [Google Scholar]
- 4.Kumar, N. (1981) J. Biol. Chem. 256, 10435–10441. [PubMed] [Google Scholar]
- 5.Howard, W. D. & Timasheff, S. N. (1988) J. Biol. Chem. 263, 1342–1346. [PubMed] [Google Scholar]
- 6.Nogales, E., Wittaker, M., Milligan, R. A. & Downing, K. H. (1999) Cell 96, 79–88. [DOI] [PubMed] [Google Scholar]
- 7.Downing, K. H. & Nogales, E. (1998) Curr. Opin. Struct. Biol. 8, 785–791. [DOI] [PubMed] [Google Scholar]
- 8.Diaz, J. F., Valpuesta, J. M., Chacon, P., Diakun, G. & Andreu, J. M. (1998) J. Biol. Chem. 273, 33803–33810. [DOI] [PubMed] [Google Scholar]
- 9.Dye, R. B., Fink, S. P. & Williams, R. C., Jr. (1993) J. Biol. Chem. 268, 6847–6850. [PubMed] [Google Scholar]
- 10.Felgner, H., Frank, R. & Schliwa, M. (1996) J. Cell Sci. 109, 509–516. [DOI] [PubMed] [Google Scholar]
- 11.Li, H., DeRosier, D. J., Nicholson, W. V., Nogales, E. & Downing, K. H. (2002) Structure (London) 10, 1317–1328. [DOI] [PubMed] [Google Scholar]
- 12.Meurer-Grob, P., Kasparian, J. & Wade, R. H. (2001) Biochemistry 40, 8000–8008. [DOI] [PubMed] [Google Scholar]
- 13.Ross, J. L. & Fygenson, D. K. (2003) Biophys. J. 84, 3959–3967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Weingarten, M. D., Lockwood, A. H., Hwo, S. Y. & Kirschner, M. W. (1975) Proc. Natl. Acad. Sci. USA 72, 1858–1862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cleveland, D. W., Hwo, S. Y. & Kirschner, M. W. (1977) J. Mol. Biol. 116, 227–247. [DOI] [PubMed] [Google Scholar]
- 16.Fellous, A., Francon, J., Lennon, A. M. & Nunez, J. (1977) Eur. J. Biochem. 78, 167–174. [DOI] [PubMed] [Google Scholar]
- 17.Kanai, Y., Chen, J. G. & Hirokawa, N. (1992) EMBO J. 11, 3953–3961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen, J., Kanai, Y., Cowan, N. J. & Hirokawa, N. (1992) Nature 260, 674–676. [DOI] [PubMed] [Google Scholar]
- 19.Frappier, T. F., Georgieff, I. S., Brown, K. & Shelanski, M. L. (1994) J. Neurochem. 63, 2288–2294. [DOI] [PubMed] [Google Scholar]
- 20.Brandt, R. & Lee, G. (1994) Cell Motil. Cytoskeleton 28, 143–154. [DOI] [PubMed] [Google Scholar]
- 21.Panda, D., Goode, B. L., Feinstein, S. C. & Wilson, L. (1995) Biochemistry 34, 11117–11127. [DOI] [PubMed] [Google Scholar]
- 22.Binder, L. I., Frankfurter, A. & Rebhun, L. I. (1985) J. Cell Biol. 101, 1371–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Drubin, D. G., Feinstein, S. C., Shooter, E. M. & Kirschner, M. W. (1985) J. Cell Biol. 101, 1700–1807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Caceres, A. & Kosik, K. S. (1990) Nature 343, 461–463. [DOI] [PubMed] [Google Scholar]
- 25.Esmaeli-Azad, B., McCarty, J. H. & Feinstein, S. C. (1994) J. Cell Sci. 107, 869–879. [DOI] [PubMed] [Google Scholar]
- 26.Liu, C. W., Lee, G. & Jay, D. G. (1999) Cell Motil. Cytoskeleton 43, 232–242. [DOI] [PubMed] [Google Scholar]
- 27.Lee, V. M., Goedert, M. & Trojanowski, J. Q. (2001) Annu. Rev. Neurosci. 24, 1121–1159. [DOI] [PubMed] [Google Scholar]
- 28.Goode, B. L., Denis, P. E., Panda, D., Radeke, M. J., Miller, H. P., Wilson, L. & Feinstein, S. C. (1997) Mol. Biol. Cell 8, 353–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chau, M. F., Radeke, M. J., de Ines, C., Barasoain, I., Kohlstaedt, L. A. & Feinstein, S. C. (1998) Biochemistry 37, 17692–17703. [DOI] [PubMed] [Google Scholar]
- 30.Al-Bassam, J., Ozer, R. S., Safer, D., Halpain, S. & Milligan, R. A. (2002) J. Cell Biol. 157, 1187–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Makrides, V., Shen, T. E., Bhatia, R., Smith, B. L., Thimm, J., Lal, R. & Feinstein, S. C. (2003) J. Biol. Chem. 278, 33298–33304. [DOI] [PubMed] [Google Scholar]
- 32.Kar, S., Fan, J., Smith, M. J., Goedert, M. & Amos, L. A. (2003) EMBO J. 22, 70–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hirokawa, N., Shiomura, Y. & Okabe, S. (1988) J. Cell Biol. 107, 1449–1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rivas, G., Fernandez, J. A. & Minton, A. P. (1999) Biochemistry 38, 9379–9388. [DOI] [PubMed] [Google Scholar]
- 35.Panda, D., Samuel, J. C., Massie, M. Feinstein, S. C. & Wilson, L. (2003) Proc. Natl. Acad. Sci. USA 100, 9548–9553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Makrides, V., Massie, M., Feinstein, S. C. & Lew, J. (2004) Proc. Natl. Acad. Sci. USA 101, 6746–6751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Li, Y. K., Edsall, R., Jagtap, P. G., Kingston, D. G. I. & Bane, S. (2000) Biochemistry 39, 616–623. [DOI] [PubMed] [Google Scholar]
- 38.Odde, D. (1998) Eur. Biophys. J. 27, 514–520. [DOI] [PubMed] [Google Scholar]
- 39.Robinson, J. & Engelborghs, Y. (1982) J. Biol. Chem. 257, 5367–5371. [PubMed] [Google Scholar]
- 40.Derry, W. B., Wilson, L. & Jordan, M. A. (1995) Biochemistry 34, 2203–2211. [DOI] [PubMed] [Google Scholar]
- 41.Caplow, M., Shanks, J. & Ruhlen, R. (1994) J. Biol. Chem. 269, 23399–23402. [PubMed] [Google Scholar]
- 42.Hill, T. L. (1985) Cooperativity Theory in Biochemistry (Springer, New York).
- 43.Hong, M., Zhukareva, V., Vogelsberg-Ragaglia, V., Wszolek, Z., Reed, L., Miller, B. I., Geschwind, D. H., Bird, T. D., McKeel, D., Goate, A., et al. (1998) Science 282, 1914–1917. [DOI] [PubMed] [Google Scholar]
- 44.Ackmann, M., Wiech, H. & Mandelkow, E. (2000) J. Biol. Chem. 275, 30335–30343. [DOI] [PubMed] [Google Scholar]
- 45.Frey, E. & Vilfan, A. (2002) Chem. Phys. 284, 287–310. [Google Scholar]
- 46.Diaz, J. F., Strobe, R., Engelborghs, Y., Souto, A. A. & Andreu, J. M. (2000) J. Biol. Chem. 275, 26265–26276. [DOI] [PubMed] [Google Scholar]
- 47.Diaz, J. F., Barasoain, I. & Andreu, J. M. (2003) J. Biol. Chem. 278, 8407–8419. [DOI] [PubMed] [Google Scholar]
- 48.Goode, B. L. & Feinstein, S. C. (1994) J. Cell Biol. 124, 769–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.