Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Dec 8.
Published in final edited form as: J Biomech. 2016 Nov 3;49(16):4090–4097. doi: 10.1016/j.jbiomech.2016.10.051

Ex vivo loading of trussed implants for spine fusion induces heterogeneous strains consistent with homeostatic bone mechanobiology

Jason P Caffrey a, Esther Cory a, Van W Wong a, Koichi Masuda b, Albert C Chen a, Jessee P Hunt c, Timothy M Ganey d, Robert L Sah a,b,e,*
PMCID: PMC5164966  NIHMSID: NIHMS828889  PMID: 27836500

Abstract

A truss structure was recently introduced as an interbody fusion cage. As a truss system, some of the connected elements may be in a state of compression and others in tension. This study aimed to quantify both the mean and variance of strut strains in such an implant when loaded in a simulated fusion condition with vertebral body or contoured plastic loading platens ex vivo. Cages were each instrumented with 78 fiducial spheres, loaded between platens (vertebral body or contoured plastic), imaged using high resolution micro-CT, and analyzed for deformation and strain of each of the 221 struts. With repeated loading of a cage by vertebral platens, the distribution (variance, indicated by SD) of strut strains widened from 50 N control (4 ± 114 με, mean ± SD) to 1000 N (−23 ± 273 με) and 2000 N (−48 ± 414 με), and between 1000 N and 2000 N. With similar loading of multiple cages, the strain distribution at 2000 N (23 ± 389 με) increased from 50 N control. With repeated loading by contoured plastic platens, induced strains at 2000 N had a distribution similar to that induced by vertebral platens (84 ± 426 με). In all studies, cages exhibited increases in strut strain amplitude when loaded from 50 N to 1000 N or 2000 N. Correspondingly, at 2000 N, 59–64% of struts exhibited strain amplitudes consistent with mechanobiologically-regulated bone homeostasis. At 2000 N, vertically-oriented struts exhibited deformation of −2.87 ± 2.04 μm and strain of −199 ± 133 με, indicating overall cage compression. Thus, using an ex vivo 3-D experimental biomechanical analysis method, a truss implant can have strains induced by physiological loading that are heterogeneous and of amplitudes consistent with mechanobiological bone homeostasis.

Keywords: Lumbar spine, Interbody fusion, Experimental mechanics, Strain, Micro-computed tomography

1. Introduction

Lumbar spine interbody fusion implants, or cages, are used clinically to induce vertebral fusion as a treatment for degenerative disc disease (Weiner and Fraser, 1998; Zdeblick and Phillips, 2003). These cages provide mechanical support between vertebrae and are typically composed of polyether ether ketone (PEEK) or metal, such as titanium. Cages can be implanted by several surgical approaches (Blumenthal and Ohnmeiss, 2003), including anterior lumbar interbody fusion (ALIF) and posterior lumbar interbody fusion (PLIF). There are currently over 400 interbody fusion devices with FDA 510(k) approval (U.S. Food and Drug Administration, 2016), of which most are purposed for the lumbar spine region. Many cages are designed for usage with biologics (Agarwal et al., 2009; Bishop et al., 1996; Burkus et al., 2002a), such as native or synthetic bone grafts, or growth factors including bone morphogenetic protein (BMP).

Bone formation and remodeling involve mechanobiology, a complex process by which mechanical loads influence the osteogenic biological response (Cowin and Hegedus, 1976; Frost, 2003; Mow and Huiskes, 2004; Oftadeh et al., 2015; Turner, 1998). With controlled loading in vitro or in vivo, strain amplitudes up to ~200 με (microstrain, 10−6 strain) result in net bone resorption, ~200–1500 με preserve bone homeostasis, and > 1500 με promote bone formation (Akhter et al., 1998; Burger et al., 1992; Cullen et al., 2001; Duncan and Turner, 1995). Such mechanobiological strain regimes may be useful to facilitate bone ingrowth into fusion devices (Reid et al., 2011). The lack of bone formation within and around a cage may lead to cage subsidence after implantation and negatively affect fusion outcome (Blumenthal and Ohnmeiss, 2003; Reid et al., 2011). Many orthopaedic devices are designed to minimize the effects of stress shielding, in which low post-implant bone tissue strains lead to resorption (Kanayama et al., 2000). The trussed spine cage is designed to facilitate mechanobiological ingrowth of bone tissue by means of its structural and material properties. Cage functionality has been described by effects on range of motion ex vivo, while clinical effectiveness is evaluated by patient outcome measures and fusion rate (Burkus et al., 2002b; Fogel et al., 2014). Intrinsic cage mechanical function has been assessed experimentally for overall structural properties and theoretically by finite element modeling (Adam et al., 2003; Bevill and Keaveny, 2009; Choi et al., 2013; Fogel et al., 2014). Local mechanical properties of trabecular bone and other tissues have been quantified in vitro (Keaveny et al., 2001; Muller, 2009; Nagaraja et al., 2005; Suffoletto et al., 2006). However, loading-induced local deformations and strains of spine fusion implants has not previously been quantified.

With the advent of 3-D printing for implants, cages with internal architectures have been introduced. Additive manufacturing have been leveraged to enable fabrication of cages with an open-space trussed architecture. Such a cage design may distribute load throughout the cage, allow lateral and axial communication, and provide space for bone growth and fusion (Kiapour et al., 2011). In engineering, truss structures are comprised of linear elements (struts) that are connected at joints (vertices). In response to applied loads, struts are considered to be in either tension (positive) or compression (negative), with a truss in static equilibrium having a sum of forces equal to zero. Increased loads result in higher magnitude strut forces in both tension (more positive) and compression (more negative), but the net force sum remains zero. As a truss system, we hypothesized that, when subjected to physiological load, some of the connected elements of a trussed cage are in a state of compression and others in tension, with a portion in a strain range that is supportive of bone being in a state of mechanobiological homeostasis (Duncan and Turner, 1995). We expect that for all the struts in a cage, increased applied load will lead to increased variability of strut deformations/strains (force), with little change to the overall deformation and strain mean (~zero), consistent with a truss structure.

Image-based tracking of intrinsic or affixed markers allows experimental estimation of local strains. More traditional experimental methods elucidate overall implant deformation and strain with platen-to-platen displacement transducers or extensometers, or local strains with mounted strain gauges. These approaches would yield only overall deformation and be difficult to affix to individual and internal struts. Imaging with x-ray or fluoroscopy are often employed to determine the position of spine cages (Burkus et al., 2002a; Nayak et al., 2013). Such imaging methods, along with image analyses such as texture analysis, can delineate bone deformation in vitro to a resolution of 1.23 μm and strain of 300 με during physiological loading (Bay et al., 1999a, 1999b). With marker-based tracking, high contrast markers are affixed to a structure and the movement of marker positions is assessed with imaging. Such approaches have used extrinsic markers, such as implanted cardiac beads, and intrinsic markers, as with fluorescence microscopy to determine depth-dependent properties of articular cartilage (Schinagl et al., 1997; Zerhouni et al., 1988). In gait analysis, externally-mounted fiducials are used to assess regional motion in 3-D using multiple high-speed cameras (Davis et al., 1991; Whittle, 1996). Such image-based methods could be similarly applied to assess the mechanics of structures such as spine cages.

For orthopaedic biomechanics analysis, 3-D imaging modalities such as μCT, CT, or MRI have begun to be used (Meisel et al., 2008; Williams et al., 2005). Marker tracking by μCT imaging is emerging as a powerful method for precisely determining position of markers, or fiducials (Gortchacow et al., 2011). Image analysis of fiducial centroid position typically allows localization at sub-voxel resolution due to the contribution of partial-volume effects at the marker surface (Penney et al., 1998; Van Sint Jan et al., 2002). Regional femoral stem micro-motion has been quantified by tracking affixed markers using μCT (Gortchacow et al., 2011). For 3-D printed truss cages, the thin, roughened titanium material composition facilitates x-ray or (μ)CT analysis of internal cage structure. The overall objective of this study was to quantify the local strut-associated strains of cages loaded between vertebral body or contoured plastic platens ex vivo after placement of markers, with a particular emphasis on strain distribution, described by both variance and mean.

2. Methods

2.1. Study design

For four 4WEB ALIF cages (#1-#4), strut deformation and strain were determined for (1) a single cage (#1) loaded repeatedly with vertebral platens, (2) multiple cages (#2 and #3) loaded with vertebral platens, and (3) a single cage (#4) loaded with contoured plastic platens (Table 1).

Table 1.

Study groups for each aim for unloaded and loaded cages with single-cage repeated trials (n) or multiple cages (N).

Study Platens Load [N] n N
1 Vertebral 50
1000
2000		 3
3
3		 1
1
1
2 Vertebral 50
2000		 1
1		 2
2
3 Plastic 50
2000		 2
2		 1
1
Open in a new tab

2.1.1. Study 1: intra-cage response to repeated loading by vertebral platens

To quantify the distribution of strain between struts, and strain reproducibility, for a given cage loaded with vertebral platens, repeated measures (n=3) of a single cage subjected to 50 N, 1000 N, and 2000 N were made. Strain distribution variance, indicative of increased number of struts in compression (negative) and tension (positive), was compared to 50 N control for 1000 N and 2000 N loads using Levene's tests (median). Comparisons of repeated 50 N load vertebral platen control were also made to quantify the sensitivity of strain detection.

2.1.2. Study 2: inter-cage response to loading by vertebral platens

Subsequently, to quantify the reproducibility of load-induced strain between cages, two other cages were tested individually, at 50 N and 2000 N by vertebral platens and compared to 50 N control. Strain variance was compared to 50 N control at 2000 N using Levene's test.

2.1.3. Study 3: intra-cage response to repeated loading by plastic platens

To determine the extent and reproducibility of load-induced strain response to contoured plastic platens, a single cage was loaded repeatedly (n=2) to 50 N and 2000 N. Strain variance at 2000 N was compared with 50 N control and that for study 1, 2000 N by Levene's tests.

For all studies, strut deformation, strain amplitude, and corresponding percentage of struts exhibiting strains within the combined mechanobiological homeostasis+formation (≥200 με) ranges were described statistically for each experimental group, and also compared between groups by 1-way ANOVA with post-hoc Tukey tests. Also, mean strain was compared with value 0 between all groups. Strut deformation and strain data are reported as mean ± SD calculated in two ways, by assessing (1) the distribution for struts within each trial/cage (indicated as trial/cage-averaged) to quantify the distribution of deformation and strain internal to individual cages, or (2) the average of all struts within each trial/cage (indicated as strut-averaged) to quantify the variation between trials/cages. In each study, deformation and strain are reported as the distribution, vertical strut distribution, and amplitudes. All groups were tested for normality by the Kolmogorov-Smirnov test. The significance threshold for all statistics was set to α=0.05. Statistics were performed using Excel (v2013, Microsoft, Redmond, WA, USA) and SPSS (v22, IBM, Armonk, NY, USA).

2.2. Sample preparation

Anterior lumbar interbody fusion (ALIF) cage implants and platens (vertebral body or contoured plastic) were prepared for mechanical loading. ALIF spine implants were provided by 4WEB Medical. The implants had a trussed design (40 mm × 27 mm × 16 mm, L×W×H) with roughened titanium struts (1.25 mm diameter). Zirconia spheres (0.5 mm diameter) were attached using cyanoacrylate at each vertex (intersection of multiple truss struts) to serve as fiducial markers (66 total) (Fig. 1). Additional spheres (n=12) were placed at the center of some struts, and used to validate the linearity of displacement and thus consistency of strain along a single strut (data not shown). Human vertebral bodies (L4 and L5) from one cadaveric donor (51 year old female) were obtained from a tissue bank (University of Miami) and stored at −80 °C. The vertebral bodies were prepared to simulate a fusion condition by excising the L4-L5 intervertebral disc, cutting with an oscillating saw parallel to the endplates and then a rongeur. Plastic platens comprised of polysulfone (an autoclaveable inert plastic) were designed to mimic the vertebral bodies and contoured to provide a counter-surface match to the cages. The prepared vertebral bodies or contoured plastic served as loading platens, superior and inferior to the cage.

Fig. 1.

Fig. 1

Open in a new tab

Structure of 4WEB ALIF cage with affixed fiducial sphere markers. 3-D microCT volume model of implant (gray) with fiducials attached (red) in (A) posterior, (B) right anterior oblique, and (C) left anterior oblique views. (D) Posterior view photo. Right and Left sides are indicated by “R” and “L”, respectively. Red dots in (A-C) represent attached fiducials. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2.1. Mechanical loading

Compressive loads were applied ex vivo to cages between loading platens via a custom μCT-compatible compression device with in-line load monitoring. The stand-alone cage was inserted anteriorly without graft material between the vertebral or plastic platens, and the platen-cage-platen complex was loaded. This loading device was designed to fit within a μCT scanner bed and apply compressive loads without interfering with the x-ray transmission paths. A swivel plate allowed for 3 rotational degrees of freedom at one vertebral body to allow the natural conformation of the platen to the cage (Fig. 2). For samples using donor vertebral body platens, the bone-cage-bone complex was sealed in a fluid-tight bag with phosphate-buffered saline within to maintain high humidity. Compressive loads of 50 N, 1000 N, or 2000 N were applied via the platens to the implant, allowing 10 min of relaxation to equilibrium, as determined by the in-line load cell (9000 N capacity), prior to imaging. Load levels were selected to represent physiological amplitudes (Nachemson, 1975; Schultz et al., 1982). The 50 N load was applied to maintain the cage between the loading platens. Between trials, 30 min was allowed for relaxation, during which time, the sample and loading apparatus were disassembled and reassembled.

Fig. 2.

Fig. 2

Open in a new tab

Cage loading configuration. (A) Schematic. Photos with (B) vertebral body and (C) plastic platens. Swivel plate allows superior platen to conform to implant lordosis. Arrow indicates direction of force [F] application. Red dots in (A) represent attached fiducials.

2.3. Imaging and analysis

High resolution 3-D images were acquired for each load level and processed to determine location of fiducials. The loaded implant was imaged on a micro-Computed Tomography scanner (Skyscan 1076, Bruker-microCT, Kontich, Belgium) with (9 μm)3 voxel size, applying an electrical potential of 100 kVp and current of 100 μA, using a 0.038 mm copper+0.5 mm aluminum filter. A beam-hardening correction algorithm was applied prior to image reconstruction. Images were reconstructed and thresholded (85–255 grayscale values) to segment the radiopaque spheres as fiducials. Image processing included removal of speckles <40,000 voxels and Gaussian filtering (radius = 10, CTAn, Bruker-microCT, Kontich, Belgium) to remove noise and improve fiducial sphericity and reproducibility. Automated individual object 3-D analysis was performed to calculate fiducial 3-D centroids (CTAn).

Control studies confirmed that a sub-voxel resolution of ~1 μm was achieved for detecting load-induced bead displacement. A spring was fitted with radiopaque beads, similar to the cage, with five beads spaced regularly across the length of the spring (38 mm), and subjected to 0, 10 μm, and 20 μm of overall compression. After each compression, the sample was imaged by μCT at (9 μm)3 voxel resolution, and bead centroids determined by image processing as described above. The position of one outer bead was used as the coordinate origin, and the other was used to determine the extent of spring compression (relative to the 0 state). Assuming a linear spring, the centroid positions of the central 3 beads were compared to those predicted from the two outer beads. For N=3 spheres, deviation of the spheres from the predicted position in the x, y, and z image axes were 0.6 ± 0.4 μm, 0.5 ± 0.3 μm, and 1.0 ± 0.5 μm, respectively, averaged over two trials (mean ± SD). The variability in each measure represents ~1/10 voxel resolution for centroid determination, which is expected due to partial volume effects (Verhulp et al., 2004). Thus for the average strut length of ~10 mm, the z-directed strain resolution was 1 μm/10mm=100 με.

2.4. Data reduction/calculations

Deformation, engineering strain, and deformation and strain amplitudes were calculated for each truss strut using pairs of fiducials in an automated fashion using software implemented in MATLAB 2012b (MathWorks, Natick, MA, USA). Fiducial centroids were registered between pairs of scans via 3-D linear transformation (translation and rotation). Using 3-D centroids, struts were automatically defined as pairwise combinations of fiducials, which matched the 221 struts on each cage. A portion of the anterior face of the cage had an instrumentation attachment plate, and connected struts (n=12) were not analyzed. In each of study 1 and the vertebral platen control study, two peripheral fiducials were observed on μCT to make direct contact with the loading platen; thus, the 15 associated struts were excluded from analysis. Strut lengths were calculated for each strut in each trial as the scalar linear distances between sphere pairs in the 50N load conditions (9.0 ± 2.2 mm, N=221). Deformation was calculated between pairs of scans as the scalar change in length of each strut from 50 N initial load to 50 N, 1000 N, or 2000 N final load. Engineering strain (negative in compression, positive in tension) was calculated for each strut as the deformation divided by the initial strut length at 50 N. Deformation and strain amplitudes were taken as the absolute values (magnitude) of deformation and strain, respectively. Vertical cage deformation and strain were calculated by averaging values for central axially-oriented struts (N=10).

3. Results

In all studies (described in detail below), cages subjected to 1000 N or 2000 N load exhibited strut strain distribution variances and amplitudes higher than those of 50 N controls. Strain distribution variance for 1000 N and 2000 N, and amplitude for 2000 N, was greater than that of 50 N controls in all studies, and those for 2000 N were greater than for 1000 N in study 1 (p < 0.05, all pairs). Correspondingly, percentages of strut strain amplitudes in the combined homeostasis+formation (≥200 με) ranges for 2000 N loads were greater than those for 50 N controls (p < 0.05, all pairs). Normality testing on strut-averaged strain showed normally distributed strains for 50 N vertebral (p=0.20) and plastic platen (p=0.20) controls, and 2000 N groups for studies 1 (p=0.20), 2 (p=0.06), and 3 (p=0.20). Study 1, 1000 N and study 3, 2000 N trended towards normality (p < 0.05). Thus, application of 2000 N by either vertebral or plastic platens caused strain distribution to broaden and strain amplitude to increase compared to 50 N controls.

3.1. Study 1: intra-cage response to repeated loading by vertebral platens

3.1.1. Strain distribution

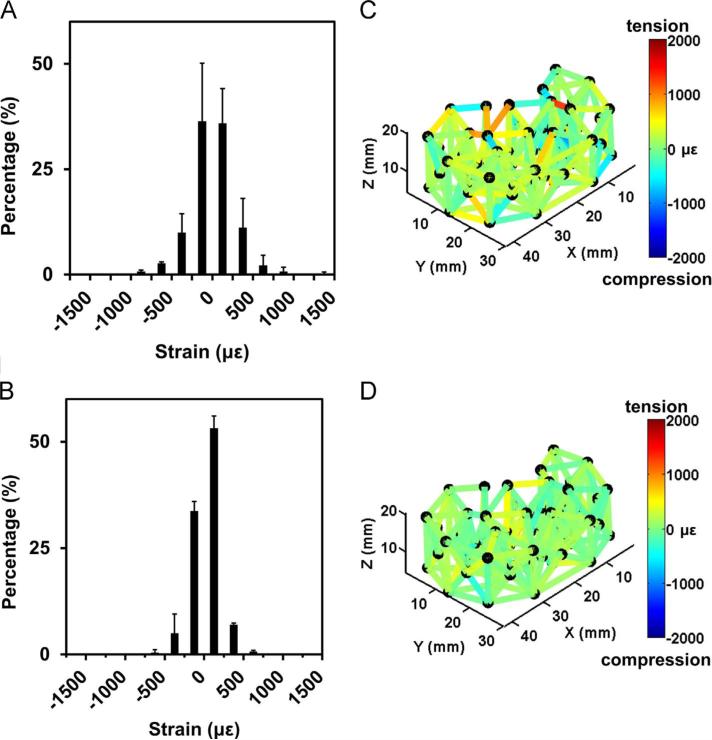
In repeated measures of cage #1, physiological loads of 1000 N and 2000 N, applied with vertebral platens, caused a distribution of strut strains with both positive (tension) and negative (compression) values (Table 2, Fig. 3). Trial-averaged (n=3) strain of all struts showed distribution (variance, indicated by SD) that widened from 50 N control (4 ± 114 με) to 1000 N (−23 ± 273 με) and 2000 N (−48 ± 414 με), and between 1000 N and 2000 N (Table 2, p < 0.05, all pairs). Although strain variance increased (larger positive values and more negative values about the mean), the means of the strain distributions were not different from zero for both 1000 N (p=0.99) and 2000 N (p=0.94). Vertical (central axially-oriented struts, N=10) strut-averaged deformation was 0.17 ± 0.60 μm and −1.87 ± 0.82 μm for 1000 N and 2000 N load, respectively, and the corresponding vertical strain was 12 ± 39 με and −124 ± 52 με (Table 3).

Table 2.

Deformation and strain of all struts. For deformation (ΔL) and strain (ε) of struts in each control and loaded group, mean, SDs (variation between trials/cages) of averaged strut values, and SDs (variation between the struts within trial/cage) of average trial/cage values.

Study Platens Load [N] Mean
 SD, Strut
 SD, Trial/Cage
ΔL [μm] ε [με] ΔL [μm] ε [με] n ΔL [μm] ε [με] n
Control Vertebral 50 0.04 4 0.96 99 2 0.95 114 206
1 Vertebral 1000 −0.19 −23 0.33 35 3 2.29 273 206
1 Vertebral 2000 −0.40 −48 0.17 27 3 3.48 414 206
2 Vertebral 2000 0.33 23 0.93 107 2 3.45 389 221
Control Plastic 50 0.34 38 0.21 25 2 1.12 127 221
3 Plastic 2000 0.79 84 0.03 2 2 3.59 426 221
Open in a new tab
Fig. 3.

Fig. 3

Open in a new tab

Intra-cage strain distribution for repeated loading by vertebral platens (study 1). Histograms of strain for all struts in repeated (A) 1000 N and (B) 2000 N measures. Representative trial strain colormaps for (C) 1000 N and (D) 2000 N shown on cage layout. Error bars represent SD (n=3). Positive strain values indicate tension and negative strain values indicate compression.

Table 3.

Deformation and strain of vertical struts. Forde formation (ΔL) and strain (ε) of vertical struts (N = 10), mean, SDs of averaged strut values, and SDs of average trial/cage values.

Study Platens Load [N] Mean
 SD, Strut
 SD, Trial/Cage
ΔL [μm] ε [με] ΔL [μm] ε [με] n ΔL [μm] ε [με] n
Control Vertebral 50 −0.62 −41 0.19 14 2 0.75 49 206
1 Vertebral 1000 0.17 12 0.60 39 3 2.09 148 206
1 Vertebral 2000 −1.87 −124 0.82 52 3 3.51 238 206
2 Vertebral 2000 −2.87 −199 2.04 133 2 3.80 264 221
Control Plastic 50 1.00 66 0.32 20 2 0.44 30 221
3 Plastic 2000 −3.30 −224 0.64 41 2 4.30 295 221
Open in a new tab

3.1.2. Strain amplitude and mechanobiological ranges

Strut-averaged strain amplitude also increased with load, from 193 ± 33 με at 50 N to 355 ± 35 με at 2000 N (p < 0.05), with that from 50 N to 1000 N, 251 ± 10 με, not reaching significance (p=0.306, Table A.1).

These strain amplitudes corresponded to 49% and 64% homeostasis (200–1500 με) and 0% and 1% formation (> 1500 με) for 1000 N and 2000 N load, respectively. Percentages of strut strain amplitudes in the combined homeostasis+formation (≥200 με) ranges for 2000 N were greater than those for 50 N (p < 0.05), but not significantly for 1000 N (p=0.08).

3.1.3. Vertebral platen control

Under repeated 50 N tare load, comparison of image datasets yielded strut strain indicative of noise, i.e. relatively small and symmetrically distributed. Repeated trial-averaged (n=2) deformation and strain distribution was normally distributed (p=0.20, Fig. 4A, C) with small strut-averaged strain amplitudes of 193 ± 33 με, respectively (Table 2), consistent with control loading study, considering the z-direction displacement resolution (~100 με) of two beads. Strain amplitudes corresponded to 37% homeostasis and 0% formation. This baseline measurement for noise indicates that deformation and strain could be assessed with high sensitivity.

Fig. 4.

Fig. 4

Open in a new tab

Intra-cage strain distribution for controls. Histogram of strain for all struts for (A) vertebral platen and (B) plastic platen controls. Representative trial strain colormaps shown on cage layout for (C) vertebral platen and (D) plastic platen controls. Error bars represent SD (n=2). Positive strain values indicate tension and negative strain values indicate compression.

3.2. Study 2: inter-cage response to loading by vertebral platens

3.2.1. Strain distribution

The strain distribution at 2000 N was similar for two additional cages (#2 and #3, Table 2, Fig. 5). Relative to strain distribution at 50 N, strain at 2000 N, 23 ± 389 με, increased in variance (p < 0.05) but not in mean (p=0.99). Vertical strut-averaged deformation and strain distribution was 2.87 ± 2.04 μm and 199 ± 133 με, respectively (Table 3).

Fig. 5.

Fig. 5

Open in a new tab

Inter-cage strain distribution for loading by vertebral platens (study 2). (A) Histogram of strain for all struts in multiple cage 2000 N measures. (B) Representative cage strain colormap shown on cage layout. Error bars represent SD (N=2). Positive strain values indicate tension and negative strain values indicate compression.

3.2.2. Strain amplitude and mechanobiological ranges

Corresponding strut-averaged strain amplitude also increased consistently between cages, from 193 ± 33 με at 50 N to 337 ± 48 με at 2000 N (p < 0.05, Table A.1). These strain amplitudes corresponded to 59% homeostasis and 1% formation. Percentages of strut strain amplitudes in the combined homeostasis+formation ranges was greater for 2000 N than 50 N control (p < 0.05).

3.3. Study 3: intra-cage response to repeated loading by plastic Platens

3.3.1. Strain distribution

Repeated loading of cage #4 at 2000 N with plastic platens induced strains with a distribution similar to those induced by vertebral body platens (Table 2, Fig. 6). Trial-averaged (n=2) strain of all struts showed widened distribution (increased variance), from 50 N control (38 ± 127 με) to 2000 N (84 ± 426 με, p < 0.05). Strain variance was similar to that of study 1 for 2000 N (p=0.92). Also similar to study 1, the means of the strain distributions were not different from zero at 2000 N (p=0.71). Vertical strut-averaged deformation and strain distribution was −3.30 ± 0.64 μm and 224 ± 41 με, respectively (Table 3). Using the vertical strut deformations of the loaded cage (study 3), the apparent stiffness and effective modulus of the cage under axial compression were 618,000 ± 118,000 N/mm and 12.4 ± 2.4 MPa, respectively.

Fig. 6.

Fig. 6

Open in a new tab

Intra-cage strain distribution for repeated loading by plastic platens (study 3). (A) Histogram of strain for all struts in repeated 2000 N measures. (B) Representative trial strain colormap shown on cage layout. Error bars represent SD (n=2). Positive strain values indicate tension and negative strain values indicate compression.

3.3.2. Strain amplitude and mechanobiological ranges

Strut-averaged strain amplitude also increased with load from 50 N control (193 ± 33 με) to 2000 N (336 ± 1 με, p < 0.05, Table A.1). Compared with donor vertebral body platens (study 2, 2000 N), strut-averaged strain amplitudes were not significantly different (p=0.97). Strain amplitudes corresponded to 59% homeostasis and 0% formation for 2000 N load. Percentages of strut strain amplitudes in the combined homeostasis+formation ranges for 2000 N were greater than those for 50 N control (p < 0.05). Thus, loading with plastic platens produced strains similar to those induced by loading with vertebral bodies as platens.

3.3.3. Plastic platen control

For repeated 50 N plastic platen control, trial-averaged (n=2) strain distribution was normally distributed (p=0.20, Fig. 4B, D) with strut-averaged strain amplitudes of 132 ± 14 με, respectively, similar to vertebral platens (p=0.33, Table A.1). Corresponding percentages of strain amplitudes in mechanobiological ranges were 21% homeostasis and 0% formation.

4. Discussion

In the present study, local deformations and strains were quantified for ex vivo loaded trussed ALIF cages using μCT to track affixed fiducials. Struts exhibited a strain distribution with approximately equal numbers of struts in compression as tension and centered about zero. Vertical loaded strains, as determined by central axially-oriented struts, showed mainly compressive responses. Repeated compression of a single cage between vertebral platens exhibited deformation and strain amplitudes that increased with physiological load. Loading of multiple cages with vertebral platens indicated comparable strain responses, as did repeated loading with contoured plastic platens.

The study design and approach involved a number of tradeoffs. Cage loading was axial compression, simulating the primary loading applied to the spine; more complex loading conditions, such as bending, torsion, and shear, were not analyzed. Static loading was selected rather than dynamic loading to facilitate imaging and analysis. Since the cage material (titanium) behaves elastically, the static loading response is likely representative of the dynamic response (Welsch et al., 1993). Strain was calculated as engineering strain from end-to-end strut deformation and length, and assumed to be represent simple compression/tension. Shear, torsion, and bending strains were not assessed.

There was a substantial variation in the deformation of individual struts between trials, although the overall distribution of strut deformation and strain was consistent, with roughly equal number of struts in compression and tension within each trial. Variation between trials for individual struts is likely due to the sensitivity of local strut mechanics to the end-loading conditions of the platens, similar to that recognized for biomechanical testing of trabecular bone (Keaveny et al., 1997). The strain distribution was consistent with a truss in static equilibrium, which has net zero load (some negative, some positive) within the structure. Non-linear overall load-displacement/strain relationships are likely due to complex loading condition between the cage and platens. The present study was conducted in an ex vivo configuration, as it is likely that the resolution with 2-D fluoroscopic techniques would be insufficient to assess implant deformation and strain in vivo.

The results of the present study extend previous experimental mechanical analysis of interbody fusion cages that address the overall behavior of the vertebral-cage complex or large spine segments (Coe et al., 1989; Nayak et al., 2013; Rapoff et al., 1997; Wang et al., 2014). Previous experimental biomechanical studies of cages measure platen-to-platen deformation and thus describe relative changes in construct rotational or flexural stiffness, but not the actual mechanical properties or behavior of the cage. Such measures are likely to reflect the test setup and vertebrae, which are not mechanically rigid and typically more compliant than the cage materials. Compressive failure loads, reported to be 3000–6000 N, are well above the loads applied in the present study (Jost et al., 1998; Wang et al., 2014). There do not appear to be any other reports of localized cage deformation or strain in a simulated implant condition, as assessed in the present study.

The amplitudes of cage strut strains, determined in the present study, are in the range of those mediating mechanobiological homeostasis of bone. Loading up to 1500 με induced a five-fold increase in bone formation in rat tibiae (Cullen et al., 2001). In the present study, for various load conditions, ~60% of struts exhibited strain amplitudes consistent with mechanically-induced mechanobiological homeostasis (200–1500 με), whereas a small percentage (up to ~1%) were consistent with formation (> 1500 με) (Duncan and Turner, 1995; Frost, 2003). Induced fluid flow may transduce and amplify the solid strain to higher effective mechanoregulatory signals in the implant (Zhao et al., 2015). In the post-implant fusion situation, such strain and mechanobiology may be highly relevant to the osteogenic biological response. Bone ingrowth through the cage would likely alter the mechanical environment over time, sharing load transmission with the cage.

The 3-D printed nature of the trussed cages facilitates their design for operation in a targeted mechanobiological response regime. While the present study analyzed and quantified macroscopic strut deformation and strain, microstructural factors may also affect implant performance. Surface roughness, asperities, texture, and charge may modulate local interactions with cells, and subsequent responses, including formation of oriented trabeculae. The similar response of vertebral and contoured plastic platens facilitates future in vitro studies of cage mechanobiology, with the latter eliminating the complexity of effects on cage-attached cells of components in post-mortem bone.

In conclusion, the present study provides the first quantification of localized strains throughout a cage structure when subjected to physiological loads. The mechanical testing approach contributes to an emerging paradigm in the experimental analyses of the mechanical behavior of complex implant structures, combining mechanical loading, imaging such as μCT, and image analysis. Loaded strut strain amplitudes were largely consistent with mechanobiological homeostasis of bone, which may be an important property for interbody fusion. Loading with contoured plastic platens produced similar results as vertebral body platens, which may be useful for mechanobiology experiments. Further studies are needed to investigate modulation of strain, effective modulus, and mechanobiological cellular response through cage design.

Supplementary Material

Suppl 1

Acknowledgments

This work was supported by 4WEB Medical (RLS) and the National Science Foundation Graduate Research Fellowship under Grant no DGE-1144086 (JPC). Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

Footnotes

Appendix A. Supporting information

Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.jbiomech.2016.10.051.

References

  1. Adam C, Pearcy M, McCombe P. Stress analysis of interbody fusion–finite element modelling of intervertebral implant and vertebral body. Clin. Biomech. 2003;18:265–272. doi: 10.1016/s0268-0033(03)00022-6. [DOI] [PubMed] [Google Scholar]
  2. Agarwal R, Williams K, Umscheid CA, Welch WC. Osteoinductive bone graft substitutes for lumbar fusion: a systematic review. J. Neurosurg. Spine. 2009;11:729–740. doi: 10.3171/2009.6.SPINE08669. [DOI] [PubMed] [Google Scholar]
  3. Akhter MP, Cullen DM, Pedersen EA, Kimmel DB, Recker RR. Bone response to in vivo mechanical loading in two breeds of mice. Calcif. Tissue Int. 1998;63:442–449. doi: 10.1007/s002239900554. [DOI] [PubMed] [Google Scholar]
  4. Bay BK, Smith TS, Fyhrie DP, Saad M. Digital volume correlation: three-dimensional strain mapping using X-ray tomography. Exp. Mech. 1999a;39:217–226. [Google Scholar]
  5. Bay BK, Yerby SA, McLain RF, Toh E. Measurement of strain distributions within vertebral body sections by texture corrleation. Spine. 1999b;24:10–17. doi: 10.1097/00007632-199901010-00004. [DOI] [PubMed] [Google Scholar]
  6. Bevill G, Keaveny TM. Trabecular bone strength predictions using finite element analysis of micro-scale images at limited spatial resolution. Bone. 2009;44:579–584. doi: 10.1016/j.bone.2008.11.020. [DOI] [PubMed] [Google Scholar]
  7. Bishop RC, Moore KA, Hadley MN. Anterior cervical interbody fusion using autogeneic and allogeneic bone graft substrate: a prospective comparative analysis. J. Neurosurg. 1996;85:206–210. doi: 10.3171/jns.1996.85.2.0206. [DOI] [PubMed] [Google Scholar]
  8. Blumenthal SL, Ohnmeiss DD. Intervertebral cages for degenerative spinal diseases. Spine J. 2003;3:301–309. doi: 10.1016/s1529-9430(03)00004-4. [DOI] [PubMed] [Google Scholar]
  9. Burger EH, Klein-Nulend J, Veldhuijzen JP. Mechanical stress and osteo-genesis in vitro. J. Bone Miner. Res. 1992;7S2:397–401. doi: 10.1002/jbmr.5650071406. [DOI] [PubMed] [Google Scholar]
  10. Burkus JK, Gornet MF, Dickman CA, Zdeblick TA. Anterior lumbar interbody fusion using rhBMP-2 with tapered interbody cages. J. Spinal Disord. Tech. 2002a;15:337–349. doi: 10.1097/00024720-200210000-00001. [DOI] [PubMed] [Google Scholar]
  11. Burkus JK, Transfeldt EE, Kitchel SH, Watkins RG, Balderston RA. Clinical and radiographic outcomes of anterior lumbar interbody fusion using recombinant human bone morphogenetic protein-2. Spine. 2002b;27:2396–2408. doi: 10.1097/00007632-200211010-00015. [DOI] [PubMed] [Google Scholar]
  12. Choi KC, Ryu KS, Lee SH, Kim YH, Lee SJ, Park CK. Biomechanical comparison of anterior lumbar interbody fusion: stand-alone interbody cage versus interbody cage with pedicle screw fixation – a finite element analysis. BMC Musculoskelet. Disord. 2013;14:220–229. doi: 10.1186/1471-2474-14-220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Coe JD, Warden KE, Sutterlin CE, 3rd, McAfee PC. Biomechanical evaluation of cervical spinal stabilization methods in a human cadaveric model. Spine. 1989;14:1122–1131. doi: 10.1097/00007632-198910000-00016. [DOI] [PubMed] [Google Scholar]
  14. Cowin SC, Hegedus DM. Bone remodeling I: a theory of adaptive elasticity. J. Elast. 1976;6:313–325. [Google Scholar]
  15. Cullen DM, Smith RT, Akhter MP. Bone-loading response varies with strain magnitude and cycle number. J. Appl. Physiol. 2001;91:1971–1976. doi: 10.1152/jappl.2001.91.5.1971. [DOI] [PubMed] [Google Scholar]
  16. Davis RB, III, Ounpuu S, Tyburski D, Gage JR. A gait analysis collection and reduction technique. Hum. Mov. Sci. 1991;10:575–587. [Google Scholar]
  17. Duncan RL, Turner CH. Mechanotransduction and the functional response of bone to mechanical strain. Calcif. Tissue Int. 1995;57:344–358. doi: 10.1007/BF00302070. [DOI] [PubMed] [Google Scholar]
  18. Fogel GR, Parikh RD, Ryu SI, Turner AW. Biomechanics of lateral lumbar interbody fusion constructs with lateral and posterior plate fixation: laboratory investigation. J. Neurosurg. Spine. 2014;20:291–297. doi: 10.3171/2013.11.SPINE13617. [DOI] [PubMed] [Google Scholar]
  19. Frost HM. Bone's mechanostat: a 2003 update. Anat. Rec. A. 2003;275:1081–1101. doi: 10.1002/ar.a.10119. [DOI] [PubMed] [Google Scholar]
  20. Gortchacow M, Wettstein M, Pioletti DP, Terrier A. A new technique to measure micromotion distribution around a cementless femoral stem. J. Biomech. 2011;44:557–560. doi: 10.1016/j.jbiomech.2010.09.023. [DOI] [PubMed] [Google Scholar]
  21. Jost B, Cripton PA, Lund T, Oxland TR, Lippuner K, Jaeger P, Nolte LP. Compressive strength of interbody cages in the lumbar spine: the effect of cage shape, posterior instrumentation and bone density. Eur. Spine J. 1998;7:132–141. doi: 10.1007/s005860050043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kanayama M, Cunningham BW, Haggerty CJ, Abumi K, Kaneda K, McAfee PC. In vitro biomechanical investigation of the stability and stress-shielding effect of lumbar interbody fusion devices. J. Neurosurg. 2000;93:259–265. doi: 10.3171/spi.2000.93.2.0259. [DOI] [PubMed] [Google Scholar]
  23. Keaveny TM, Pinilla TP, Crawford RP, Kopperdahl DL, Lou A. Systematic and random errors in compression testing of trabecular bone. J. Orthop. Res. 1997;15:101–110. doi: 10.1002/jor.1100150115. [DOI] [PubMed] [Google Scholar]
  24. Keaveny TM, Morgan EF, Niebur GL, Yeh OC. Biomechanics of trabecular bone. Annu. Rev. Biomed. Eng. 2001;3:307–333. doi: 10.1146/annurev.bioeng.3.1.307. [DOI] [PubMed] [Google Scholar]
  25. Kiapour A, Vijay G, Ferrara L, Hunt J. Subsidence evaluation of 4-WEB, a novel cross strut based, interbody cage design.. International Society for the Study of the Lumbar Spine (ISSLS); Gothenburg, Sweden. 2011. [Google Scholar]
  26. Meisel HJ, Schnoring M, Hohaus C, Minkus Y, Beier A, Ganey T, Mansmann U. Posterior lumbar interbody fusion using rhBMP-2. Eur. Spine J. 2008;17:1735–1744. doi: 10.1007/s00586-008-0799-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mow VC, Huiskes R. Basic Orthopaedic Biomechanics and Mechano-Biology. 3rd ed. Lippincott Williams & Wilkins; Philadelphia: 2004. p. 736. [Google Scholar]
  28. Muller R. Hierarchical microimaging of bone structure and function. Nat. Rev. Rheumatol. 2009;5:373–381. doi: 10.1038/nrrheum.2009.107. [DOI] [PubMed] [Google Scholar]
  29. Nachemson A. Towards a better understanding of low-back pain: a review of the mechanics of the lumbar disc. Rheumatol. Rehabil. 1975;14:129–143. doi: 10.1093/rheumatology/14.3.129. [DOI] [PubMed] [Google Scholar]
  30. Nagaraja S, Couse TL, Guldberg RE. Trabecular bone microdamage and microstructural stresses under uniaxial compression. J. Biomech. 2005;38:707–716. doi: 10.1016/j.jbiomech.2004.05.013. [DOI] [PubMed] [Google Scholar]
  31. Nayak AN, Gutierrez S, Billys JB, Santoni BG, Castellvi AE. Biomechanics of lateral plate and pedicle screw constructs in lumbar spines instrumented at two levels with laterally placed interbody cages. Spine J. 2013;13:1331–1338. doi: 10.1016/j.spinee.2013.03.048. [DOI] [PubMed] [Google Scholar]
  32. Oftadeh R, Perez-Viloria M, Villa-Camacho JC, Vaziri A, Nazarian A. Biomechanics and mechanobiology of trabecular bone: a review. J. Biomech. Eng. 2015;137:010802. doi: 10.1115/1.4029176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Penney GP, Weese J, Little JA, Desmedt P, Hill DL, Hawkes DJ. A comparison of similarity measures for use in 2-D-3-D medical image registration. IEEE Trans. Med. Imaging. 1998;17:586–595. doi: 10.1109/42.730403. [DOI] [PubMed] [Google Scholar]
  34. Rapoff AJ, Ghanayem AJ, Zdeblick TA. Biomechanical comparison of posterior lumbar interbody fusion cages. Spine. 1997;22:2375–2379. doi: 10.1097/00007632-199710150-00010. [DOI] [PubMed] [Google Scholar]
  35. Reid JJ, Johnson JS, Wang JC. Challenges to bone formation in spinal fusion. J. Biomech. 2011;44:213–220. doi: 10.1016/j.jbiomech.2010.10.021. [DOI] [PubMed] [Google Scholar]
  36. Schinagl RM, Gurskis D, Chen AC, Sah RL. Depth-dependent confined compression modulus of full-thickness bovine articular cartilage. J. Orthop. Res. 1997;15:499–506. doi: 10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]
  37. Schultz AB, Andersson GB, Haderspeck K, Ortengren R, Nordin M, Bjork R. Analysis and measurement of lumbar trunk loads in tasks involving bends and twists. J. Biomech. 1982;15:669–675. doi: 10.1016/0021-9290(82)90021-5. [DOI] [PubMed] [Google Scholar]
  38. Suffoletto MS, Dohi K, Cannesson M, Saba S, Gorcsan J., 3rd Novel speckle-tracking radial strain from routine black-and-white echocardiographic images to quantify dyssynchrony and predict response to cardiac resynchronization therapy. Circulation. 2006;113:960–968. doi: 10.1161/CIRCULATIONAHA.105.571455. [DOI] [PubMed] [Google Scholar]
  39. Turner CH. Three rules for bone adaptation to a mechanical stimuli. Bone. 1998;23:399–407. doi: 10.1016/s8756-3282(98)00118-5. [DOI] [PubMed] [Google Scholar]
  40. U.S. Food, and Drug Administration [14 Sept];510(k) Database. 2016 [Google Scholar]
  41. Van Sint Jan S, Salvia P, Hilal I, Sholukha V, Rooze M, Clapworthy G. Registration of 6-DOFs electrogoniometry and CT medical imaging for 3D joint modeling. J. Biomech. 2002;35:1475–1484. doi: 10.1016/s0021-9290(02)00074-x. [DOI] [PubMed] [Google Scholar]
  42. Verhulp E, van Rietbergen B, Huiskes R. A three-dimensional digital image correlation technique for strain measurements in microstructures. J. Biomech. 2004;37:1313–1320. doi: 10.1016/j.jbiomech.2003.12.036. [DOI] [PubMed] [Google Scholar]
  43. Wang L, Huang H, Zhang Z, Zhang L, Li J. Biomechanical evaluation of a novel autogenous bone interbody fusion cage for posterior lumbar interbody fusion in a cadaveric model. Spine. 2014;39:E684–692. doi: 10.1097/BRS.0000000000000291. [DOI] [PubMed] [Google Scholar]
  44. Weiner BK, Fraser RD. Lumbar interbody cages. Spine. 1998;23:634–640. doi: 10.1097/00007632-199803010-00020. [DOI] [PubMed] [Google Scholar]
  45. Welsch G, Boyer R, Collings E. Materials Properties Handbook: Titanium Alloys. ASM International; 1993. [Google Scholar]
  46. Whittle MW. Clinical gait analysis: a review. Hum. Mov. Sci. 1996;15:369–387. [Google Scholar]
  47. Williams AL, Gornet MF, Burkus JK. CT evaluation of lumbar interbody fusion: current concepts. Am. J. Neuroradiol. 2005;26:2057–2066. [PMC free article] [PubMed] [Google Scholar]
  48. Zdeblick TA, Phillips FM. Interbody cage devices. Spine. 2003;28:S2–S7. doi: 10.1097/01.BRS.0000076841.93570.78. [DOI] [PubMed] [Google Scholar]
  49. Zerhouni EA, Parish DM, Rogers WJ, Yang A, Shapiro EP. Human heart: tagging with MR imaging–a method for noninvasive assessment of myocardial motion. Radiology. 1988;169:59–63. doi: 10.1148/radiology.169.1.3420283. [DOI] [PubMed] [Google Scholar]
  50. Zhao F, Vaughan TJ, McNamara LM. Multiscale fluid-structure interaction modelling to determine the mechanical stimulation of bone cells in a tissue engineered scaffold. Biomech. Model. Mechanobiol. 2015;14:231–243. doi: 10.1007/s10237-014-0599-z. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Suppl 1
NIHMS828889-supplement-Suppl_1.docx (27.6KB, docx)

RESOURCES