Mechanosensory function of microvilli of the kidney proximal tubule

Abstract

Normal variations in glomerular filtration induce proportional changes in proximal tubule Na⁺ reabsorption. This “glomerulotubular balance” derives from flow dependence of Na⁺ uptake across luminal cell membranes; however, the underlying physical mechanism is unknown. Our hypothesis is that flow-dependent reabsorption is an autoregulatory mechanism that is independent of neural and hormonal systems. It is signaled by the hydrodynamic torque (bending moment) on epithelial microvilli. Such signals need to be transmitted to the terminal web to modulate Na⁺-H⁺-exchange activity. To investigate this hypothesis, we examined Na⁺ transport and tubular diameter in response to different flow rates during the microperfusion of isolated S₂ proximal tubules from mouse kidneys. The data were analyzed by using a mathematical model to estimate the microvillous torque as function of flow. In this model, increases in luminal diameter have the effect of blunting the impact of flow velocity on microvillous shear stress and, thus, microvillous torque. We found that variations in microvillous torque produce nearly identical fractional changes in Na⁺ reabsorption. Furthermore, the flow-dependent Na⁺ transport is increased by increasing luminal fluid viscosity, diminished in Na⁺-H⁺ exchanger isoform 3 knockout mice, and abolished by nontoxic disruption of the actin cytoskeleton. These data support our hypothesis that the “brush-border” microvilli serve a mechanosensory function in which fluid dynamic torque is transmitted to the actin cytoskeleton and modulates Na⁺ absorption in kidney proximal tubules.

In mammalian kidneys, urine formation is initiated by filtration of a massive volume of plasma at the glomerulus to yield renal tubular fluid. This filtrate courses along the kidney tubules, where most of the fluid and electrolytes are transported back into the plasma, leaving waste solutes within the luminal fluid destined to become urine. The glomerular-filtration rate is not constant, however, and variations in circulatory demands can result in several-fold variation in the formation of tubular fluid. The capacity of the proximal renal tubule to alter its transport activity in proportion to the filtered volume is critical to the survival of the organism. Indeed, in rats, there is a nearly perfect glomerulotubular balance, so that despite large perturbations in filtration, reliably two-thirds of the filtered water is reabsorbed by the proximal tubule (1). Because water reabsorption is driven by Na⁺ transport, a prerequisite for precise glomerulotubular balance is that luminal fluid flow modulates proximal tubule epithelial cell Na⁺ reabsorption. This flow effect has been termed “perfusion-absorption balance” (2, 3) and has been demonstrated in microperfusion studies in rats (4-8). In mammalian kidneys, the primary pathway for proximal Na⁺ transport is into the cell through the Na⁺-H⁺ exchanger isoform 3 (NHE-3) within the luminal cell membrane and out across the peritubular cell membrane via the Na⁺, K⁺-ATPase. For these two transporters in series, the entry step is rate-limiting, and thus, the flux variations must be mediated by changes in the activity of NHE-3 (9).

The mechanism by which a perturbation of luminal fluid flow could be translated into a change in reabsorptive flux has been elusive. Early attention focused on the microanatomy of the luminal membrane, which is configured as a regular hexagonal array of densely packed microvilli of uniform height (the “brush border,” which has been identified by light microscopy) (10). At one time, the proximal-tubule brush border was considered to be a possible unstirred layer; however, calculations indicated that there was unlikely to be significant convective stirring within this pile (11). Moreover, the diffusion barrier between the bulk luminal fluid and the cell membrane was unlikely to hinder Na⁺-H⁺ exchange (12). Two studies suggested that increases in axial-flow velocity recruited new transporters into the luminal membrane. Preisig (13) examined recovery of cellular pH from an acute acid load in vivo (ammonium pulse) and found that increases in luminal flow rate enhanced NHE-3 activity. Maddox et al. (14) subjected rats to acute changes in vascular volume to obtain hydropenic, euvolemic, and volume-expanded groups, with respective grouping according to decreased, normal, and increased glomerular-filtration rate. When brush-border membrane vesicles were prepared from each of these groups and Na⁺-H⁺ kinetics were assessed, it was found that the maximum flux velocities stratified in parallel with the glomerular-filtration rate.

Ultimately, perfusion-absorption balance must derive from an afferent sensor of fluid flow rate in series with a cascade of effector steps, which activate luminal transporters or insert new membrane transporters. Model calculations led Guo et al. (15) to propose that the proximal tubule microvilli are that sensor. In this role, their regularity in height and spacing appeared to be advantageous because the bending deformation of the microvilli would be both small and uniform. In this model, it was proposed that the critical component was the actin cytoskeleton, which is abundant within and beneath the brush border (10). The model given in Guo et al. (15) described how the actin-filament bundle that is the central core of the microvillus deforms under hydrodynamic loading. The proposed role for the microvilli is that they cannot only sense fluid drag forces, but they can also amplify these forces through their mechanical lever arm as they are transferred to the intracellular cytoskeleton at the terminal web, where the actin-filament bundle within the microvillus attaches at its roots to the main cell body. To serve the hypothesized function, the microvilli should be relatively stiff structures that are able to transmit the torque (bending moment), without significant bending, because of the hydrodynamic drag acting on the their tips (16). In this scheme of signal transduction, specific interaction between the proximal-tubule cytoskeleton and the luminal membrane NHE-3 is a critical feature. In this regard, at least one such connecting molecule has been identified, namely, ezrin, which is a kinase-anchoring protein that links NHE-3 and the actin cytoskeleton (17).

The aim of this article is to provide evidence that establishes the mechanosensory function of proximal tubule microvilli. Experimental preparation consisted of the S₂ segment of mouse proximal tubule, which was dissected and perfused in vitro to eliminate confounding neurohumoral factors as well as changes within the peritubular environment. When the perfusion rate of the tubule is varied, there are changes in both luminal fluid velocity and tubule diameter, and both velocity and diameter are incorporated into a model for calculating the drag and torque on the microvilli. Here, we show that variations in microvillous torque are proportional to changes in volume reabsorption, key evidence in support of the mechanosensory hypothesis. These changes depend on NHE-3 and are abolished by nontoxic disruption of the actin cytoskeleton.

Methods

Black C57/6J mice, which were purchased from The Jackson Laboratory, were used for studying flow-dependent proximal-tubule transport. Breeding pairs of NHE-3 knockout mice were obtained from Gary Shull's laboratory (University of Cincinnati) (18). Homozygous wild-type (NHE^+/+) and null (NHE-3^-/-) mice were obtained by breeding heterozygotes. Ages of null (NHE-3^-/-) animals were matched with their wild-type controls.

All animals were maintained on a normal diet and tap-water until the day of the experiment. The mice were anesthetized by i.p. injection of 50 mg of pentobarbital per kg of body weight. Kidneys were then removed and cut in coronal slices. Individual tubules were dissected in cooled (4°C) Hanks' solution containing 137 mM NaCl, 5 mM KCl, 0.8 mM MgSO₄, 0.33 mM Na₂HPO₄, 1 mM MgCl₂, 10 mM Tris·(hydroxymethyl)amino-methane hydrochloride, 0.25 mM CaCl₂, 2 mM glutamine, and 2 mM L-lactic acid. Proximal tubules (S₂) were perfused with an ultrafiltrate-like solution at perfusion rates of 5, 10, 15, 20, and 25 nl/min. The perfusion rates were adjusted by changing the gravity of the reservoir connected to the perfusion pipette and were measured by using constant-bore glass capillary tubes. The solution for luminal perfusion contained 125 mM NaCl, 22 mM NaHCO₃, 1 mM CaCl₂, 1.2 mM MgSO₄, 2 mM glutamine, 2 mM lactic acid, 10.5 mM glucose, 5 mM KCl, and 1.2 mM phosphoric acid. The bath medium contained 101 mM NaCl, 22 mM NaHCO₃, 1 mM CaCl₂, 1.2 mM MgSO₄, 2 mM glutamine, 2 mM lactic acid, 10.5 mM glucose, 5 mM KCl, 1.2 mM phosphoric acid, 32.5 mM Hepes, and 5 g/dl albumin. All solutions were bubbled with 95% O₂/5% CO₂ and had a pH of 7.4. The osmolalities of the bath and perfusate were adjusted to 300 mosmol of KgH₂O by the addition of either H₂O or NaCl. The extensively dialyzed (methoxy-³H)inulin was added to the perfusate at a concentration of 30 μCi/ml (1 Ci = 37 GBq) as a volume marker. Proximal tubules (S₂) that were isolated from mouse kidney were perfused at 37-38°C in a 1.2-ml temperature-controlled chamber. Bath fluid was changed continuously at a rate of 0.5 ml/min to maintain the constancy of pH and bath osmolality during the experiment (19). The first period of collection began after an equilibration time of 30-60 min. For each experimental period, three timed collections of tubular fluid were made. The volume of the perfusate and collected samples were measured in a fixed-volume collection pipette, and ³H-inulin concentrations in those samples were determined in an LS5801 liquid scintillation counter (Beckman Coulter). The rate of net fluid reabsorption (J_v) was calculated according to the ³H-inulin-concentration changes between the original and collected fluid according to the following equation: J_v = V_o - V_L, where V_L is the measured rate of fluid collection, V_o = V_L (IN_L/IN_o), and IN_L/IN_o is the ratio of radioactive inulin in collected and perfusion fluid, respectively. The rates of fluid absorption were expressed per mm of the proximal tubule.

Tubular inner diameters were measured from the center of the tubule under the different perfusion rates and recorded by using a charge-coupled device (CCD) video camera. Three measurements were made from each flow rate, and the means of those volumes were calculated.

Dextran-80 and cytochalasin D were purchased from Sigma. Control and experimental groups were studied under identical experimental conditions. Data are presented as means ± SE. Student's t test was used to compare control and experimental groups. ANOVA and Dunnett's test were used for comparison of several experimental groups with a control group. The difference between the mean values of an experimental group and a control group was considered significant at P < 0.05.

Results

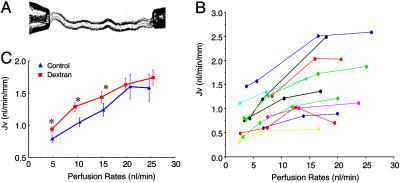
Because the proximal tubule absorbs Na⁺ isosmotically, fluid transport rates are used widely as a surrogate for Na⁺ absorption. Accordingly, ³H-inulin was added to the luminal perfusate as a volume marker, and fluid reabsorption was calculated by ³H-inulin-concentration changes between the original and collected fluid (20). First, the flow-dependent proximal tubule transport was examined under the control condition in individual tubules. As shown in Fig. 1A, mouse S₂ segments were isolated and perfused with NaHCO₃^- Ringer's solution at the perfusion rates of 2.5-25 nl/min, and fluid absorption (J_V) was measured. These data, which are summarized in Fig. 1B, show flow-dependent Na⁺ absorption from 11 proximal tubules that were isolated and perfused from 11 mouse kidneys in vitro. Each line represents J_v at three or more perfusion rates in the same tubule. Although the baseline reabsorption rates varied depending on tubule conditions, a significant increase in transport in response to increased flow rates was observed in all perfused tubules. The strong stimulation was observed by increasing the flow rate from 10 to 15 nl/min; and the maximal transport activities were reached at the perfusion rate of 20 nl/min. Increasing flow rates further from 20 to 25 nl/min did not further stimulate J_v. Second, the mean of J_v was examined at perfusion rates of 5, 10, 15, 20, and 25 nl/min, and data are shown Fig. 1C (control group). These data include the results from Fig. 1B, with three or more pefusion rates from each tubule, and results of J_v from 13 additional tubules for which data were obtained at only two perfusion rates (data not shown in Fig. 1B). Our results show that J_v increased significantly from 0.79 ± 0.05, to 1.05 ± 0.07, 1.24 ± 0.10, 1.60 ± 0.19, and 1.58 ± 0.21 nl·min^-1·mm^-1 when the perfusion rate increased from 5 nl/min to 10, 15, 20, and 25 nl/min, demonstrating that increased tubular perfusion rate enhances Na⁺ absorption in mouse proximal tubules. These observations of flow-dependent transport suggest a flow-responsive element within the brush border.

Fig. 1.

Effects of tubular flow rate on volume transport (J_v) in isolated proximal tubules of mouse kidney. (A) Photograph taken from an experiment showing that an isolated proximal tubule held with perfusion (right) and collecting (left) pipettes under the microscopy. (B) Flow-dependent proximal-tubule transport. Each line represents J_v under different perfusion rates from the same tubule. Results from a total of 11 proximal tubules were isolated and perfused from 11 mice kidneys in vitro. Three to four values of J_v were measured under different perfusion rates from each tubule. Data from 13 additional tubules were obtained at only two perfusion rates (data not shown). (C) Flow-dependent proximal-tubule transport in control (blue) and (3.6-fold) increased viscosity by using dextran-80 (red). The flow-dependent transport curve was shifted to the left by addition of dextran-80. ^*, P < 0.05, compared with controls.

Hydrodynamic drag and torque on the microvilli can be increased by increasing the tubular flow rate or by increasing the fluid viscosity without changing the flow rate. Accordingly, we evaluated whether Na⁺ absorption is altered by increasing the viscosity of the tubular perfusion solution. The flow-dependent transport activities were examined at the same perfusion rates of 5, 10, 15, 20, and 25 nl/min as the control, and viscosity increased 3.6-fold by addition of dextran-80 (0.075g/dl) to the tubule perfusate (21). Changing the viscosity did not change the maximal absorption rate, yet the absorption rate increased significantly at perfusion rates of 5, 10, 15, and 20 nl/min, and the flow-dependent transport curve was shifted to the left. The results shown in Fig. 1C indicate that increasing the axial flow rate stimulated Na⁺ absorption in mouse proximal tubules in vitro under conditions of normal and increased viscosity by dextran-80.

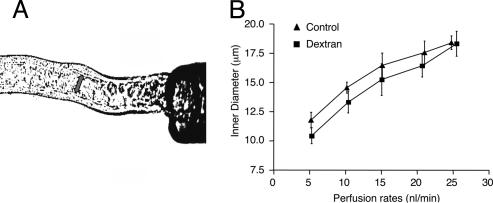
Our previous fluid shear-stress model (15) for predicting microvillous torque suggested that the nonlinearity in the J_v vs. perfusion curves in Fig. 1C might be due in part to flow-dependent changes in tubule diameter. A change in tubule diameter would not only affect the magnitude of the fluid shear stress acting on the microvilli tips, but it would also cause ultrastructural changes in the microvilli distribution within the brush border, as observed by Maunsbach et al. (22). We have examined the effect of increasing flow on tubule inner diameter (Fig. 2). The proximal tubules were perfused in vitro at perfusion rates of 5, 10, 15, 20, and 25 nl/min under the conditions of absence and presence of dextran-80. A 50% increase is observed in inner diameter between the low and high perfusion rate in both groups, and the response is nonlinear. Because the shear stress at the brush-border edge is inversely proportional to the diameter cubed (for a given axial flow) in Poiseuille flow, these large changes in diameter can have a profound effect on the fluid shear stress acting on the microvilli tips and, hence, the torque that they experience. This cubic dependence implies that increases in luminal diameter will blunt the flow-dependent increase in microvillous torque. It is possible that such diameter changes may have played a role in the inability of previous investigators to discern flow-dependent transport in vitro.

Fig. 2.

Effects of tubular flow rate on inner tubular diameters in the absence and presence of dextran-80. (A) Photograph taken from an experiment showing the measurement of inner diameters. (B) Changes of tubular inner diameters in response to perfusion rate in the absence (▴) and presence (▪) of dextran-80. Inner diameters were increased significantly when the perfusion rate was enhanced from 5 nl/min to 10, 15, 20, and 25 nl/min in both groups. There was no significant difference between control and dextran groups.

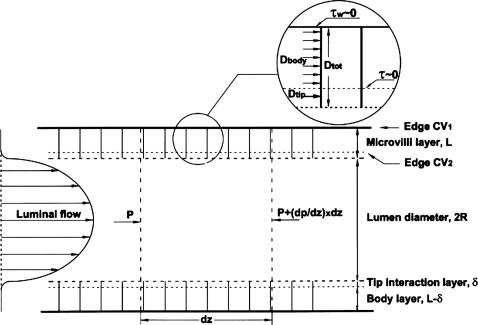
Guo et al. (15) developed a theoretical model in which the detailed velocity distribution throughout the brush border is used to determine the fluid drag and torque distribution on each microvillus. This model does not allow us to determine easily how the drag and torque on the microvilli change with flow and diameter because it requires that we determine the detailed flow around each microvillus as their spacing changes in response to tubule diameter changes. To analyze our experimental results, we present a simpler global model in which the detailed geometry of the microvilli and their spacing is not needed. This global model is independent of the detailed velocity profiles derived in Guo et al., except that it utilizes the following two important conceptual simplifications. (i) The flow at the edge of the brush border is confined to a thin-tip-interaction layer of thickness δ <150 nm, where the velocity decays rapidly from its value at the brush-border edge to its value in the interior, and (ii) the velocity within the main body of the brush border, which occupies ≈95% of the brush border thickness, L, is nearly uniform and driven by the local axial-pressure gradient in the tubule and not the fluid shear stress in the tubule lumen. Guo et al. show that the slip velocity at the brush-border edge is only ≈1/400 of the tubule center-line velocity, and the uniform flow in the main body of the brush border is again 1/400 of this edge velocity, making it a nearly stagnant flow that is five orders of magnitude smaller than the velocity in the lumen. These vastly different velocity scales enable us to separate the drag and torque on each microvillus into the following two components: a uniform drag, D_body, acting over the main body L - δ of the microvillus, and a tip drag, D_tip, acting in the thin interaction layer of thickness δ. The corresponding components for the torque are T_body and T_tip. Furthermore, the shear stress acting at both the base of the tip-interaction layer and the base of the microvilli are negligible because the flow within the body of the brush border is negligible.

By using the above simplifications, one can define two distinct control volumes in Fig. 3 and apply a local force balance per unit of tubule length. For the first control volume, we consider a unit length of the entire interior of the proximal tubule (tubule lumen plus brush border). A force balance requires that the drag force D_totN, where D_tot is the drag on the entire microvillus and N is the number of microvilli per unit of tubule length, be balanced by the force due to the pressure gradient dP/dz per unit of length acting over the entire interior cross-section whose radius is R + L, where R is the radius of the tubule lumen without the brush border.

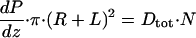1

Fig. 3.

Control volumes 1 and 2 (CV₁ and CV₂) used to obtain the drag forces D_body and D_tip on each microvillus. Control volumes used in Eqs. 1 and 2 are shown. CV₁ contains the entire tubule lumen including complete brush-border microvilli layer, whereas CV₂ contains the tubule lumen and only the tip-interaction layer of the brush-border microvilli. The fluid shear stress τ_w at the base of CV₁ and τ at the base of CV₂ are both negligible.

Note that in Eq. 1, the shear force on the apical membrane of the epithelial cell vanishes because the wall shear stress is negligible.

To determine the drag due to only the microvilli tips, D_tip, we consider a second cylindrical control volume whose radius is R + δ. A similar force balance to that used in writing Eq. 1. requires that:

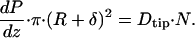2

As noted previously, the shear force at the cylindrical side wall of this second control volume also vanishes because it is at the base of the tip-interaction layer, where the fluid shear is negligible. The drag force only on the body of the microvillus, D_body, is the difference between the drag in Eqs. 1 and 2.

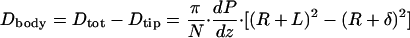3

The total torque on each microvillus, T_tot, is the sum of the tip T_tip and body T_body torques. The detailed solutions in Guo et al. (2000) show that of the total drag on a 2.5-μm microvillus, 74% appears within 150 nm of the brush-border edge and is due to the fluid shear stress in the tip-interaction layer, whereas the remainder is due to the viscous loss in the interior of the brush border. Because δ << L or R, the lever arm for the drag force on the tip is approximately the total length L of the microvilli. However, because the drag force on the main body of the microvillus acts uniformly along its length because the flow in the interior is uniform, this drag acts as if it were applied approximately at the center of the microvillus. Thus,

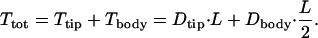4

By substituting Eqs. 2 and 3 into Eq. 4, one obtains,

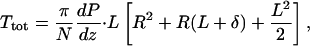5

where terms of order δ² have been neglected.

Because the axial water flow in the brush border contributes very little to total flux, the total local perfusion rate Q, which satisfies Poiseuille's law, is given by the flux in the lumen,

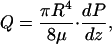6

where μ is the viscosity of the fluid. The local axial-pressure gradient, dP/dz, can now be written in terms of Q by using Eq. 6, and this result can be substituted into Eq. 5, yielding the following:

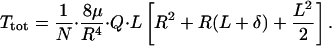7

Eq. 7 is an expression for the total torque on the microvillus in terms of Q, R, μ, and microvillus geometry N and L.

It is difficult to evaluate Eq. 7 in absolute terms unless N is measured experimentally by using electron microscopy. However, in our perfusion experiments, the length of the tubule segment is fixed, and therefore, N does not change as the tubule diameter increases with flow. Only the spacing of the microvilli along the tubule cross-section changes. Thus, one can take the ratio of the torques on the microvillus at any two perfusion rates, and N will cancel out. If we take r as a convenient reference state, we obtain the ratio of the total torque at any perfusion rate and diameter relative to the reference state r as follows:

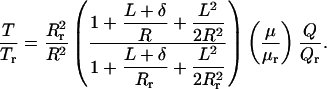8

Eq. 8 is the critical relationship that enables us to relate reabsorption J_v to torque and compare theory and experiment. There are two subtle points in the derivation of Eq. 8. Because of the reabsorption, there is a radial pressure gradient in the brush border, but it can be shown that dP/dz will be nearly constant across the brush border if reabsorption per unit of length is uniform or slowly varying. We also assume that when a tubule expands at constant length, the spacing of the microvilli changes but their length L remains the same.

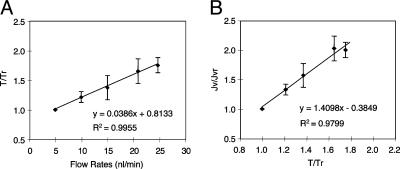
By using Eq. 8, the change in torque T at any perfusion rate Q to any reference perfusion rate Q_r can be related if the relative change in the tubule diameter 2R for that measured Q is also known. This relationship is shown in Fig. 4A for the flow-diameter measurements that are shown in Fig. 2. In this calculation, we assume that L = 2.5 μm, δ = 150 nm, and μ = μ_r because the viscosity is unchanged. Furthermore, because Fig. 1C provides the measured relationship between J_v and Q, Eq. 8 or Fig. 4A can be used to plot the relationship between J_v and T. This relationship is shown in Fig. 4B, where both J_v and T are scaled by their values at the reference perfusion rate Q_r at 5 nl/min. This observed relationship between J_v and T is almost perfectly linear, suggesting that the flow-dependent changes of transport activity are modulated directly by the changes in microvillous torque.

Fig. 4.

Analysis of the changes of transport activity and total torque in response to increased perfusion rates. (A) The relationship between increasing perfusion rates and changes in torque. T, total torque of the microvilli (body and tip); Tr, reference value of the total torque at the perfusion rate of 5 nl/min; T/Tr, ratio of total torque at related perfusion rates of 10, 15, 20, and 25 nl/min to the reference value at a perfusion rate of 5 nl/min. (B) The proximal-tubule transport activity corresponding to changes of torque. The data of T/Tr and J_v/J_vr were obtained from the calculation at perfusion rates of 5, 10, 15, 20, and 25 nl/min. The relationship between the changes of torque and changes of transport activity are proportional.

It is striking that the changes in tubule diameter in response to Q provide a linear relationship between T and Q (microvilli function as a linear transducer) when the relationships between Q and R and between T and R are both nonlinear. Note that there are two competing nonlinear effects. As Q increases, it causes R to increase, which decreases the torque T because the fluid shear acting on the microvilli tips decreases as the tubule diameter expands. This decrease in torque, deriving from tubule distention, offsets the increase in T that results from the increase in Q. Note that the increase in T is less than a factor of two over a 5-fold increase in Q, as shown in Fig. 4A.

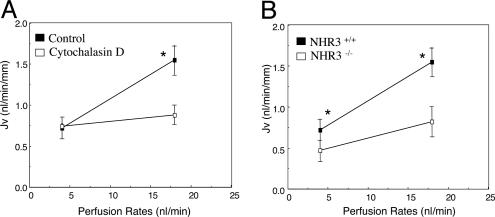
These changes in microvillous torque in response to axial flow need to be transmitted to the terminal web, where the actin-filament bundle within the microvillus attaches at its roots to the main cell body. We hypothesize that this force on the cytoskeleton leads to an alteration of transport activity by modulation of membrane-bound NHE-3. To examine this hypothesis, the effects of cytochalasin D, an actin cytoskeleton inhibitor (23), on flow-dependent proximal-tubule transport was studied. As shown in Fig. 5A, addition of 3 μM cytochalasin D did not change the baseline J_v at low flow rate, but it abolished the flow-stimulated increase in J_v (1.56 vs. 0.76 in control and 0.94 vs. 0.81 nl·min^-1·mm^-1 in the cytochalasin group at perfusion rates of 20 and 5 nl/min, respectively). These results indicated that 3 μM cytochalasin D has no toxicity to cells but inhibits actin cytoskeletal signaling, which is critical to the flow-stimulated Na⁺ transport in the proximal tubule. Because NHE-3 is the major ion transporter that is responsible for absorption of 50-60% of the filtered Na⁺ and HCO₃^- in the proximal tubule (24, 25), we examined flow-dependent Na⁺ absorption in NHE-3 knockout mice. Fig. 5B shows a summary of the data from the NHE-3 knockout mice. In addition to the significant reduction of baseline J_v at low flow rate, as reported (18, 25), the increased flow-stimulated transport activities were reduced by 56% in NHE-3 null mice compared with the wild type. The slope of the flow-dependent change in J_v is significantly different between the NHE-3 null mice and control (0.023 ± 0.008 vs. 0.056 ± 0.017, P < 0.05). In addition, the absolute changes and the percentage changes from lower and higher flow rates were also diminished significantly in NHE-3 null mice. These results suggested that NHE-3 activity can be stimulated by increasing axial flow. Although 44% of the flow stimulated increase in J_v is still retained because of increased axial flow, this increment of J_v must be mediated by NHE-3-independent Na⁺ transport mechanisms, such as Na⁺/glucose-cotransport, and/or a para-cellular Na⁺ transport pathway. In contrast, cytochalasin D abolished the increment of transport activity due to enhanced flow, consistent with our hypothesis that the transduction of signals from brush border to terminal web via the actin cytoskeleton is essential for the modulation of all Na⁺ transport mechanisms regulated by axial flow in proximal tubules.

Fig. 5.

Role of cytoskeleton and NHE-3 on flow-dependent proximal-tubule transport. (A) Effect of cytochalasin D on flow-dependent proximal-tubule transport. The J_v was measured at low and high perfusion rates in the absence and presence of 3 μM cytochalasin D in the luminal perfusion solution. Cytochalasin D abolished the increment of J_v due to enhanced perfusion rate. ^*, P < 0.05, compared with controls. (B) Flow-dependent proximal-tubule transport in wild-type and NHE-3 knockout mice. J_v was measured at low and high perfusion rates in wild-type and NHE-3 knockout mice, respectively. In addition to the significant reduction of baseline J_v, the increase of flow-stimulated J_v was diminished significantly in NHE-3 knockout mice compared with wild-type mice. ^*, P < 0.05, compared with controls.

Four tables for the experimental data presented in Figs. 1C, 2B, and 5 are presented in Tables 1-4, which are published as supporting information the PNAS web site.

Discussion

The primary hypothesis of this study is that flow-dependence of kidney proximal tubule Na⁺ reabsorption is signaled by the hydrodynamic torque on epithelial microvilli. The experimental model has been the isolated perfused proximal tubule of the mouse, and our results are the first demonstration of flow-dependence in the in vitro setting. The advantage of this preparation is not only the obvious constancy of the peritubular environment, but also elimination of the possibility of unspecified filterable factors that may modulate epithelial cell function (5). With the first description of the technique of in vitro perfusion, using proximal tubules from rabbit kidney, Burg and Orloff (20) had sought to reproduce the perfusion-absorption balance that had been observed in the intact rat kidney. However, they found no flow-dependent reabsorption and concluded that glomerulotubular balance was “not an intrinsic property of the proximal tubule”. In subsequent work, flow-dependent Na⁺ reabsorption has never been found in rabbit tubules by any investigators, and it has been an open question as to whether this difference between rat and rabbit tubules truly required an intact kidney or was a species difference. The experimental findings described in this article clearly establish the mouse tubule, as suitable for the study of flow-dependent transport, and the analysis offers a possible explanation for its absence in the rabbit. With reference to Eq. 7, the total torque on the microvilli varies directly with luminal perfusion and inversely with luminal area. Obviously, this functional relationship implies that measurements of luminal diameter are critical to assessing changes in hydrodynamic forces and torques, but it also means that when perfusion rate is increased, relatively small amounts of tubular distention will suffice to nullify any increase in torque. If isolated mouse proximal tubules are less distensible than rabbit tubules (and, thus, more like rat tubules encased in vivo), then changes in perfusion would be expected to produce changes in hydrodynamic force on the microvilli. With the aid of Eq. 8, these diameter changes also explain why a 5-fold increase in flow in the control in Fig. 1C results in only a 2-fold increase in reabsorption. Burg and Orloff (20) had observed that in rabbit proximal tubule a 3-fold increase in perfusion rate produced a 37% increase in volume reabsorption, which was not statistically significant (Table 2 in ref. 20). However, this finding occurred in association with a 41% increase in tubule diameter. Application of Eq. 8 to their data (by using our values of L and δ) predicts a 43% increase (rather than a 3-fold increase) in torque and, thus, a comparable change in fluid reabsorption.

These findings support the role of microvillous torque as the afferent signal to modulate proximal-tubule Na⁺ reabsorption in response to changes in luminal flow. Evidence that the signal is not flow per se is provided by the impact of dextran added to the perfusate to increase viscosity. This maneuver increased the hydrodynamic force on the microvilli, and Na⁺ reabsorption increased at all but the highest luminal perfusion rates. When Na⁺ reabsorption (with the control perfusate) is plotted as a function of the estimated microvillous torque, the relation is strikingly linear, with no suggestion of a transport maximum. Such linearity of reabsorption, over a broad range of delivery rates, has been a consistent finding in studies of HCO₃^- transport in the proximal tubules of rat kidneys (6, 26, 27). Note, however, that in the dextran perfusions, the effect of microvillous torque on reabsorption is not linear (3.6-fold torque increase in viscosity resulting in a 1.2-fold increase in reabsorption). In the dextran perfusions, there were obvious toxic changes in the cell, such as swelling and the appearance of vacuoles, and there was not an easy way to explain their effect on transport.

In contrast to the mechanosensory function of microvilli proposed for the proximal nephron, flow-dependent transport in the distal nephron has recently been attributed to renal epithelial cilia (28). Subsequently, Liu et al. (29) demonstrated that flow-dependent increases in [Ca²⁺]_i occur in both principal cells with apical cilia and intercalated cells with apical microvilli or microplicae that lack cilia, suggesting that these intercalated cell projections also serve a mechanosensory function. Although the linear dependence of reabsorption on microvillous torque is reassuring, this issue is difficult to resolve with certainty because of the positive correlation of hydrodynamic drag on both microvilli and cilia. Our data show that increased torques on the microvilli produced a stimulation of Na⁺ transport, whereas the torques on the cilia should lead to a decrease in absorption because the bending of the cilia causes an increase in intracellular Ca²⁺ through stretch-activated ion channels (28). The increased intracellular Ca²⁺ will produce an inhibition of Na⁺ and HCO₃^- absorption in proximal tubules (30). It is not known whether these two competing effects could provide part of the feedback mechanisms for reduction of transport activity when axial flow rates far exceed the physiological range.

Increasing luminal flow in the proximal tubule in rats has been found to enhance the luminal-membrane density of the Na⁺/H⁺ transporter, a finding in brush-border membrane vesicles (14) and also in direct examination of pH recovery by the intact cell (13). Consistent with these observations, we found that perfusion-absorption balance is reduced significantly in NHE-3-deficient mice. What this study adds to existing knowledge is the finding that nontoxic doses of cytochalasin abolish the flow-dependent increase in Na⁺ reabsorption. This finding supports the model assumption that the actin cytoskeleton is a key mediator for transduction of the hydrodynamic force on microvilli to the change in NHE-3 density within the luminal cell membrane. The range of membrane proteins that respond to this hydrodyamic force and biochemical signals that affect this traffic remain as important objectives for future investigation.