Cycling antibiotics may not be good for your health

Save for the career opportunities for those who study it, from a human perspective antibiotic resistance is not a good thing. People are dying or remaining ill for longer with bacterial infections that, if not for resistance, would have been readily cured by antibiotics (1, 2). Despite well intentioned calls for the more prudent use of these drugs the overall tide of ever-increasing frequencies of resistant pathogens and number of antibiotics to which they are resistant has not abated (3). The only slowing that has taken place is the pace at which antibiotics with new targets are entering the market (4, 5).

As bad a problem as antibiotic resistance is in open communities, it is all that graver in hospitals and their intensive care units (ICUs), where infections are more likely to be lethal. The success of most of the oft-touted advances of medical intervention requires effective antibiotics to prevent and treat infections. Hospitals are dangerous places to be—especially if you are sick, but even if not. In recent years in the United States there have been ≈2 million hospital-acquired (nosocomial) infections resulting in some 90,000 deaths (6) with comparable (or sometimes lower) rates in Europe (7). To be sure, many of these patients were severely compromised and would have succumbed to these infections even if the bacteria responsible were susceptible to the treating antibiotic(s). However, it is clear that resistance contributes to a substantial fraction of deaths due to nosocomial infections as well as greater morbidity and longer periods of hospitalization and costs to those who survive (8, 9).

Antibiotic resistance in hospitals is particularly tragic because it is a problem with at least partial solutions. In theory (10, 11), the frequencies of resistant bacteria in hospitals can be reduced by (i) reducing antibiotic use, (ii) controlling the spread of bacteria, (iii) using antibiotics for which there is no resistance, (iv) increasing the rate of turnover of patients, and (v) restricting the input of patients and health-care workers carrying resistant nosocomial pathogens. Moreover, in hospitals the control efforts should lead to substantial reductions in the frequency of resistance in months rather than the years or decades predicted for open communities (10, 12).

These predictions, which were generated with the aid of mathematical models, have been at least partially supported by real-life observations. A nationwide program of active surveillance for methicillin-resistant Staphylococcus aureus (MRSA) that included the implementation of strict barrier precautions for MRSA-colonized patients, temporarily furloughing colonized health-care workers, and closing contaminated hospital wards has been successful in maintaining low levels of MRSA infections in hospitals in The Netherlands, despite high levels in surrounding countries (13). This successful strategy is anticipated by models (10, 14) that also predict conditions that could lead to its failure (14). The roles of different infection control procedures in limiting resistance predicted with models (15) has to a fair extent been confirmed (16).

Resistance to single antibiotics would be higher with cycling than with mixing.

Clearly, antibiotics are the driving force responsible for ascent and persistence of resistance in hospitals, and efforts should be made to reduce their use. Unfortunately, for medical reasons as well as social and economic forces, policies to reduce the total level of antibiotic use in hospitals are difficult to implement. Also, in recent years an increasing amount of attention has been given to controlling resistance by modulating the pattern of use of different antibiotics rather than reducing the quantities used. These efforts have met at least short-term success. For example, in the course of a year, a switch from cephalosporins to cabanapenems reduced the incidence of cephalosporin-resistant Gram-negative infections in a hospital. Not unanticipatedly, this decline in the frequency of cephalosporin resistance was countered by an increase of carbanepenem resistance, an observation that was characterized as “squeezing the balloon” (17, 18).

Could the air be let out of this balloon; can the overall frequency of resistance be reduced by shorter-term and more repetitive changes of the antibiotics being used, “cycling”? In this issue of PNAS, Bergstrom et al. (19) suggest that it cannot. Using a simple mathematical model of the epidemiology of antibiotic treatment and resistance in hospitals, they evaluate the efficacy of cycling two antibiotics, relative to their simultaneous application, “mixing.” Their analysis predicts that over broad conditions the overall frequency of resistance to single antibiotics would be higher with cycling than with mixing.

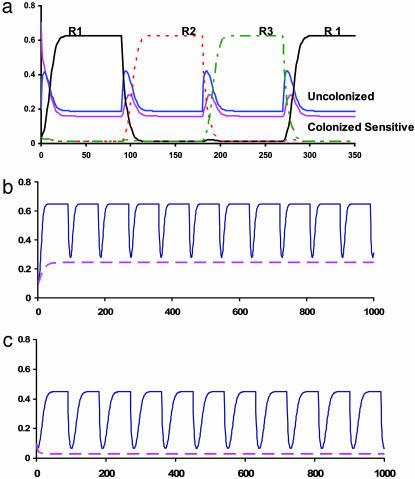
The results of a numerical solution (computer simulation) of a simple extension of the model of Bergstrom et al. (19) for three rather than two antibiotics and single drug-resistant states generalize their prediction (Fig. 1b). This extension predicts that the more antibiotics used the better; with mixing three antibiotics the anticipated equilibrium frequency of patients carrying resistant bacteria is 0.24 rather than 0.39 for two. These simulations also illustrate the earlier points: reducing the input of patients carrying resistant bacteria and improving infection control can substantially reduce the level of resistance (Fig. 1c).

Fig. 1.

Simulation results with a three-antibiotic–three-resistant states extension of the model in figure 1 of Bergstrom et al. (19). (a) Changes in the frequencies of the different patient states with antibiotic cycling every 90 days: β = 1, c = 0, γ = 0.03, m = 0.07, m₁ = m₂ = m₃ = 0.033333, τ₁ + τ₂ + τ₃ = 0.5, μ = 0.10, σ = 0.25, and α = 0.80. R1, resistant to antibiotic 1; etc. (b) Fraction of patients carrying resistant bacteria: cycling (α = 0.80) solid line and mixing (α = 0) broken line; parameters as in a. (c) Fraction of patients carrying resistant bacteria with cycling (α = 0.80) and mixing (α = 0) with reduced rates of input of patients carrying resistant bacteria m₁ = m₂ = m₃ = 0.01 and improved infection control, β = 0.50. The rest of the parameters are the same as those in a. Copies of the Berkeley madonna program used for this simulation can be obtained from www.eclf.net.

Why is mixing better than cycling in reducing the level of resistance? One important contribution of the Bergstrom et al. article (19) is a general explanation for this seemingly counterintuitive result that should be of interest to ecologists and evolutionary biologists, for whom antibiotics are of concern only to sick people and physicians. A more restricted and less abstract way to think about this process is to consider what happens when all colonized patients are treated and there is no transmission of bacteria between them. With mixing two antibiotics and two single-drug-resistant states, all patients colonized with bacteria susceptible to both antibiotics and half of those with bacteria resistant to one would be cleared by treatment as well as spontaneously. With three antibiotics and three resistant states, treatment would clear two-thirds of the patients colonized with resistant bacteria. With cycling at any given time only one antibiotic would clear an ever-declining fraction of patients colonized with bacteria susceptible to its action, and the colonized population would become increasingly dominated by patients carrying bacteria resistant to the prevailing antibiotic (Fig. 1a). As the cycling period decreases, less time is spent with population dominated by patients with bacteria resistant to the treating antibiotic and, as Bergstrom et al. show, the average frequency of resistance with cycling approaches that of mixed use.

The results of Bergstrom et al. (19) also suggest that cycling need not always be worse than mixing. If resistance is acquired by horizontal transfer of genes or accessory elements the likelihood of hosts' acquiring resistance to both antibiotics can be less with cycling than mixing. However, because of the higher overall frequencies of resistance to single antibiotics, if acquired resistance to both antibiotics is through mutation, cycling is once again worse than mixing.

One of the messages of Bergstrom et al. (19), like that of other theoretical studies of infectious disease (20, 21), is the utility of mathematical models for the design of intervention protocols. While hand-waving may provide exercise, yak-yak may sound nice, and gut feelings can be pleasant, it is not possible to precisely define the processes involved and generate the quantitative predictions needed with purely intuitive arguments. Neither Bergstrom et al. nor we are advocating mathematical models as alternatives to careful empirical studies of the efficacy of different antibiotic use protocols (or other interventions), but rather we advocate their use as tools to design treatment regimes and to interpret the results of empirical studies of their application. Bergstrom et al. make a number of predictions about antibiotic use that can be evaluated by prospective studies monitoring of the frequencies and transmission of resistant and susceptible bacteria in hospitals or ICUs.

Not only have Bergstrom et al. (19) advanced the theory of the epidemiology of antibiotic use in hospitals, but their article has also set the stage for additional modeling and empirical studies. How would the situation change if (i) patients were treated with antibiotics to which their colonizing bacteria are known to be susceptible, (ii) individual patients are sequentially or simultaneously treated with different antibiotics, (iii) there is a flow of patients between different units of the hospital or other high-antibiotic-use institution such as a nursing home, or (iv) nonabsorbable antibiotics were used to eradicate all bacteria that could potentially become resistant? What are the effects of different antibiotic use protocols on the magnitude and duration of morbidity and rate of mortality of nosocomial infections? These and other questions about the epidemiology of antibiotic treatment and resistance in hospitals and the world beyond are amenable to and make for some delicious modeling. Career opportunities for some could be for the good of many.