Anticorrelated motions as a driving force in enzyme catalysis: The dehydrogenase reaction

Abstract

Molecular dynamics and cross-correlation analysis of the horse liver alcohol dehydrogenase HLADH·NAD⁺·PhCH₂O^– complex has established anticorrelated motions between the NAD⁺-binding domain and other portions of the enzyme. Four pairs of anticorrelated interactions are (i and ii) cofactor-binding domain: C^α of V292 and the CG1 of V203 with C7 of PhCH₂O^–; (iii) cofactor-binding domain: amide carbonyl oxygen of I318 with amide N of H67; and (iv) cofactor domain: C^α of T178 with carbonyl oxygen of L141. The average distances between pairs are 9.2 Å for i, 8.2 Å for ii, 14.7 Å for iii, and 18.2 Å for iv. The motions of i and ii are most important in the ≈0.5 Å pushing of C4 of NAD⁺ toward C7 of PhCH₂O^– to form push near-attack conformer (NACs). The motions of iv are less so, and those of iii are not important. Seventy-five quantum mechanics/molecular mechanics calculations of the energies of reaction were carried out without structural restrictions from different stages of the molecular dynamics trajectory. Of the 71 conformations, the 29 fulfilling NAC criteria were associated with the lowest energies of activation. Thus, anticorrelated motions from the NAD⁺-binding domain by way of the neighboring V292 and V203 have a pushing motion, which moves the C4 of NAD⁺ toward the H–C7 of the substrate. Longer-range anticorrelated motions involving the cofactor-binding domain have no or very little influence on NAC formation.

Apresent issue concerns the occurrence of rate-promoting vibrations, which assist in lowering barrier height in enzyme catalysis (1–5). A related issue addressed here is the question of whether certain thermal Brownian motions of an enzyme–substrate complex (E·S) participate in lowering the energy barrier of activation (6) by creating the most reactive ground-state conformations [near-attack conformers (NACs) (7)]. One such possibility is that ground-state conformations, which lead directly to the lowest energy-transition state (NACs), are formed with assistance of anticorrelated motions of residues proximal to the active site.

From Eq. 1, the free energy of activation is equal to the sum of the standard free energies for formation of reactive E·NAC conformers (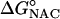) plus the activation energy (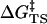) for conversion of E·NAC to E·TS as shown in Eq. 2.

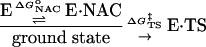[1]

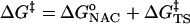[2]

We report here the findings of a study of correlated and anticorrelated motions of an E·S complex, the role of certain anticorrelated motions in the formation of E·NAC, as well as the demonstration that reactions that pass through E·NAC follow a kinetically favored trajectory. The reaction of interest is the oxidation of a primary alcohol by horse liver alcohol dehydrogenase (HLADH·NAD⁺). The computational tools used have been molecular dynamics (MD) simulations, cross-correlation analysis, and quantum mechanics (QM)/molecular mechanics (MM).

HLADH (EC 1.1.1.1) (8) consists of two subunits of identical composition in which a 12-stranded β-sheet makes up the central core (9). Each subunit binds a molecule of NAD⁺ and a Zn²⁺ at the active site and an additional Zn²⁺, which is structural. Alcohol oxidation by NAD⁺ involves first the proton dissociation of RCH₂OH followed by transfer of a hydride equivalent from RCH₂O^– to NAD⁺ (Eq. 3).

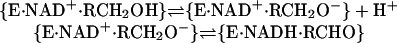[3]

In an earlier study we carried out MD simulations (10) for 1–2 ns the structures of HLADH·NAD⁺·PhCH₂OH, HLADH·NAD⁺·PhCH₂O^–, and HLADH·NADH·PhCHO using one subunit covered by a 32-Å-radius pool of transferable intermolecular potential three-point water molecules. By doing so we were able to derive an ensemble of dynamic conformations for the reactive HLADH·NAD⁺·PhCH₂O^– species, define the paths of H⁺ transfer to water, and established the presence of a water channel, which facilitates proton shuttling (10). We reported that the Michaels complex assumed the conformation of a reactive conformer [NAC (7)] 60% of the time. We defined the NAC as a conformer in which the distances between the transferring of an H^– equivalent from C7 of PhCH₂O^– and acceptor C4 of NAD⁺ are ≤3.0 Å (3.9 Å for the heavy atoms C7 and C4) and the angles of C7–H–NC4 range from 132° to 180°. Concurrently, an investigation from Karplus and coworkers (11) appeared in which the kinetic features, the adiabatic potential barrier heights, the rate constants (including quantum mechanical effects such as tunneling), and potential of mean force of the HLADH·NAD⁺·PhCH₂O^– species were described by use of self-consistent charge density functional tight-binding QM/MM implemented in charmm.

Quite recently, we reported 10-ns MD simulation of the reactive HLADH·NAD⁺·PhCH₂O^– species and the correlated (motions in the same directions) and anticorrelated (motions toward each other) collective domain motions within the protein structure (12). We now describe the anticorrelated motions of protein-entity pairs with the relative motions of PhCH₂O^– substrate and NAD⁺ cofactor. The energy barriers of reaction were determined for the MD-generated conformations of HLADH·NAD⁺·PhCH₂O^– by use of QM/MM analysis. We observed that proximal motions correlated with reactant motions are of importance in NAC formation, and the generated NACs have the kinetic advantage of being on a direct path to the lowest energy-barrier height. Such reactive conformations generated by a pushing movement of the protein are push NACs (13). Computational studies leading to the proposal that formation of reactive conformations in the dehydrogenase enzymes occur by protein motions pushing reactants together was put forward first by Schwartz and coworkers (13).

Methods

Dynamics Procedure. Classic MD simulations to 10 ns and cross-correlation analysis and methods have been reported (12). Visualization and manipulation of these structures was performed by using midasplus (University of California, San Francisco).

QM/MM Method and Conditions. Seventy-one snap shots from MD trajectories with 100-ps intervals were used as starting structures for QM [at the Austin model 1 (AM1) level] and MM calculations of the minimum reaction-energy path (14, 15). The energy profile was calculated along the reaction coordinates for the hydride to cross over the energy barrier. The snap shots chosen are well dispersed in time to assure that the calculated structures represent a diverse set of enzyme, substrate, and cofactor conformations. The QM/MM module of charmm 27 (16, 17) was used for the energy calculation. In our approach, the substrate and the pyridine ring of the cofactor were partitioned to be treated quantum mechanically. The remainder of the partitioned system is represented by charmm MM force field with empirical potential and fixed charges. A sphere with a radius of 20 Å around the transferred hydride of the structures was included for the QM/MM calculations. This sphere includes most of the subunit one residues and a small portion of the subunit two residues that are close to the reaction site of the subunit one. The link-atom method (18, 19) was applied to connect QM and MM portions of structure. The link atom is treated quantum mechanically and serves to saturate the unsatisfied valence of the QM atom. The atoms in the MM region are allowed to move in response to hydride transferring. The distances between the transferred hydride and the acceptor carbon, NC4 of NAD⁺, and between the hydride and donor carbon, C7 of RCH₂O^–, are systematically decreased and increased, respectively. Energy minimization was performed at each step until the C7–H bond was broken and the H–C4 bond formed. The height of the energy barrier is defined as the difference between the highest energy value in the reaction coordinate and the energy value at the starting points. The distances the hydride was moved between each step ranged from 0.05 to 0.1 Å (20). The energy minimization was performed at each point by using the adoptedbasis Newton–Raphson minimization routine in charmm. The tolerance in energy gradient was set to 0.1 kcal/(mol·Å) (14). We then calculate, from the energy-barrier heights described above, the thermally averaged effective hydride-transfer barrier following the analytical barrier-distributions approach (15) (Eqs. 4 and 5).

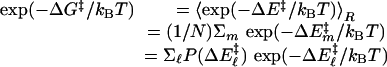[4]

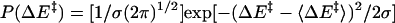[5]

In Eq. 4, the subscript R represents the ensemble average taken over N conformations calculated, ΔE^‡ represents energy-barrier heights, and P(ΔE^‡) is the probability distribution of calculated barrier heights. In Eq. 5, σ is the variance of energy-barrier distribution, and 〈ΔE^‡〉 is the average value of the energy barriers.

Results

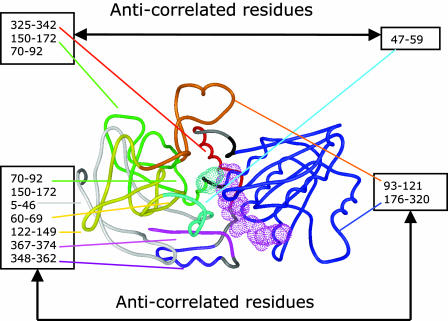
Fig. 1 shows the color-coded cross-correlation map of the HLADH·NAD⁺·PhCH₂O^–. The NAD⁺ and PhCH₂O^– are shown by pink and cyan dotted surfaces, respectively. Different anticorrelated regions are color-coded for easy viewing. Residues 176–320 (dark blue), indicating the cofactor-binding domain, and 93–121 (orange) are correlated. Residues 176–320 (dark blue) and 93–121 (orange) are anticorrelated with residues 5–46 (light gray), 60–69, and 122–149 (yellow), 70–92 and 150–172 (green), 348–362 (purple), and 367–374 (pink). Residues 47–59 (cyan) are anticorrelated with residues 70–92 and 150–172 (green) and 325–342 (red). The overall picture is that the blue-, orange-, and cyan-colored regions are moving toward or away from the rest of the protein: the light-gray, green, yellow, red, purple, and pink regions.

Fig. 1.

Anticorrelated motions mapped onto the monomer structure. NAD⁺ and PhCH₂O^– are shown by pink and cyan dotted surfaces, respectively. The regions of the anticorrelated motions are assigned and labeled.

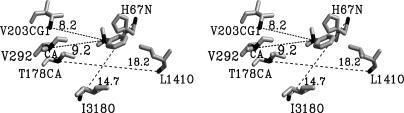
The anticorrelated motions of the NAD⁺-binding domain and the pushing together of reactants were determined by examination of cross-correlation coefficients (12) and distance histograms. We chose to examine anticorrelated interactions of V292, V203, I318, and T178 residues of the NAD⁺-binding domain. The interactions of these residues are shown in stereo in Fig. 2. As can be seen, the distances separating the anticorrelated pairs are CG1 of V203···C7 of PhCh₂O^– (8.2 Å), C^α of V292···C7 of PhCh₂O^– (9.2 Å), amide carbonyl oxygen of I318···amide N of H67 (14.7 Å), and amide carbonyl oxygen of L141···C^α of T178 (18.2 Å). That the magnitude of the motions V203···C7 (1.5 Å), I318···H67 (1.6 Å), and T178···L141 (1.75 Å, with the major subdomain of the conformation, shown in Fig. 3D) are closely related as may be expected of a domain movement. The V292···C7 motion (0.95 Å, with the major subdomain of the conformation, shown in Fig. 3A) is less. Both V292 and V203 residues are situated on the face of the NAD⁺ pyridine ring distal to the substrate (data not shown). Thus, movement of one or both of these residues toward the substrate would be expected to push the NAD⁺ pyridine ring toward the substrate.

Fig. 2.

The geometric placement of chosen anticorrelated pairs in the HLADH·NAD⁺·PhCH₂O^– complex. The view angle of the stereo structure shown is a flip-over from Fig. 1.

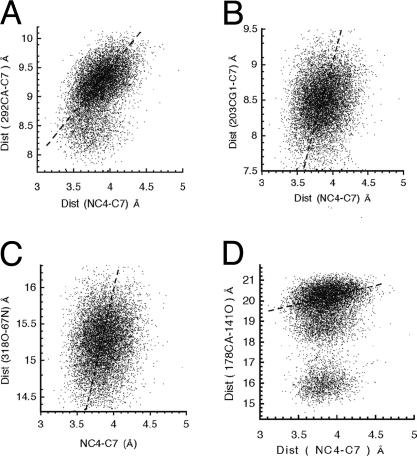
Fig. 3.

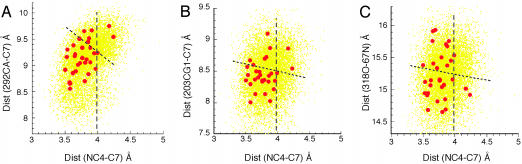
Distance histograms for four anticorrelated pairs. Histograms of the distances between C7 of PhCH₂O^– and NC4 of NAD⁺ plotted vs. the distances between C^α of V292 and C7 of PhCH₂O^– (A), the distances between CG1 of V203 and C7 of PhCH₂O^– (B), the distances between the carbonyl oxygen of I318 and the nitrogen of H67 (C), and the distances between the carbonyl oxygen of L141 and the C^α of T178 (D). Slopes of the dashed lines are calculated directly from x–y coordinates. In three dimensions, the motion of L141 toward T178 is seen to create three different protein conformations without change in the distances separating reactants.

In Fig. 3, the histograms of the distances between C7 of PhCH₂O^– and NC4 of NAD⁺ are plotted vs. the distances between C^α of V292 and C7 of PhCH₂O^– (Fig. 3A), the distances between CG1 of V203 and C7 of PhCH₂O^– (Fig. 3B), the distances between the carbonyl oxygen of I318 and the nitrogen of H67 (Fig. 3C), and the distances between the carbonyl oxygen of L141 and the C^α of T178 (Fig. 3D). The 9,500 points on each plot represent distance distributions derived from the conformer coordinates obtained from the 95,000 observations at equally spaced times during the MD simulations. The dashed lines in the distance-distribution plots of Fig. 3 represent the ratio (correlation slopes) of distances of movements of the anticorrelated pair compared to simultaneous movement of NC4 of the NAD⁺ toward C7 of PhCH₂O^–. The correlation slopes are 1.9 in Fig. 3A (major subdomain), 3.3 in Fig. 3B, 3.6 in Fig. 3C, and 5.0 in Fig. 3D (major subdomain).

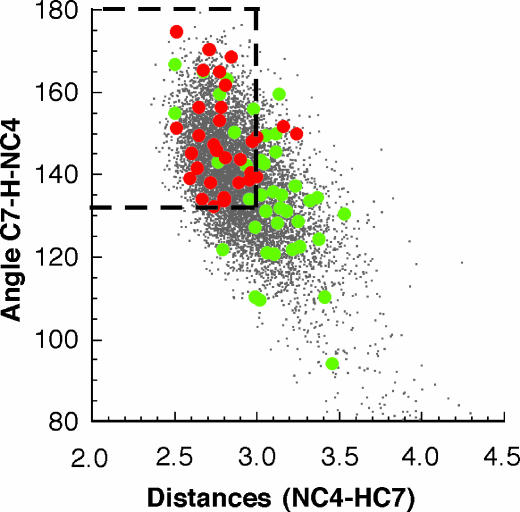
Seventy-one snapshots of coordinates of HLADH·NAD⁺· PhCH₂O^– were picked from the MD simulations at time intervals of 100 ps as starting ground states for AM1/MM minimum reaction-energy path calculations using the QM/MM module of charmm 27. The AM1/MM-calculated energy-barrier heights for all conformers range from 19 to 50 kcal/mol. Reactions exhibiting the lowest values of energy-barrier heights among the 71 structures examined are projected as red dots on the histogram plot of the distances C7 of PhCH₂O^–···NC4 of NAD⁺ vs. the angle C7–H···NC4 (Fig. 4). Inspection of Fig. 4 shows that the most reactive conformations are located in the area of the distance distribution of conformations by the inserted box, which defines (5) the NACs. This finding provides evidence that for the HLADH catalysis, anticorrelated motions of the protein generate NAC formation and NACs are associated with the most favorable values of energy barriers. To compare our results to those of Thorpe and Brooks (15), we used the analytical barrier-distributions approach (15) and estimated the thermally averaged effective hydride-transfer barrier to be 18.4 kcal/mol. It is generally appreciated that AM1-calculated values of energy barriers overestimate the barrier heights in comparison with ab initio and density functional results (21). By inclusion of the quantum-mechanical corrections to the vibration energy (21) (≈2.8 kcal/mol) to the calculated hydride-transfer barrier height, our calculated energy value (15.6 kcal/mol) may be compared to the experimentally simulated tunneling value of ≈16 kcal/mol (22, 23).

Fig. 4.

The histogram plot of the distances C7 of PhCH₂O^–···NC4 of NAD⁺ vs. the angles C7–H···NC4; reactions exhibiting the lowest values of energy-barrier heights are projected as red dots. The higher values of energy-barrier heights are represented as green dots. The most reactive conformations are located in the area of the distribution of conformations by the inserted box, which defines (5) the NACs.

Data points in Fig. 5 A–C are duplicates of those shown in Fig. 3 A–C with the addition of the recognition of the conformers with lowest energies of reaction. The vertical line marks the distance between heavy atoms when C4···H–C7 is at van der Waals distance. In Fig. 5, 29 of the 31 conformations of lowest energies are to the left of the vertical line with heavy atoms C4···C7 distances <3.9 Å, which, along with a favorable angle, is the requirement used in the NAC definition. The line across the “waist” of the distance distributions divides the populations into two equal bodies. Those conformations, which are characterized as having the distance between C4 and C7 ≤ 3.9 Å are to the left of the vertical line. Of these conformations, the ones that arise with the closing distances between an anticorrelated pair are below the line, which separates the distance distribution into two equal parts; that is to say that push NACs are to be found in the lower-left quadrant. Examination of Fig. 5 establishes that NAC formation takes place as interacting pairs come together. The anticorrelated motions of the amide carbonyl oxygen of I318 and amide N of H67 (Fig. 5C) are seen to have very little pushing effect in the direction of NAC formation.

Fig. 5.

The lowest values of energy-barrier heights are projected as red dots on the distance histograms of Fig. 3. Data points in A–C are duplicates of those shown in Fig. 3 A–C with the addition of the recognition of the conformers with the lowest energies of reaction. Reactions exhibiting the lowest values of energy-barrier heights are projected as red dots on the histograms of the distances between C7 of PhCH₂O^– and NC4 of NAD⁺ plotted vs. the distances between C^α of V292 and C7 of PhCH₂O^– (A), the distances between CG1 of V203 and C7 of PhCH₂O^– (B), and the distances between the carbonyl oxygen of I318 and the nitrogen of H67 (C).

Discussion

Early QM/MM studies of acetylcholine esterase (14) and dihydrofolate reductase (15) found that the conformation fluctuation of entire protein and reactant lead to significant differences in the calculated reaction-energy barrier for the various conformers. A combination of 10-ns MD simulation of the dynamics structures of the HLADH·NAD⁺·PhCH₂O^– complex and cross-correlation identification of anticorrelated pairs at the active site and use of unrestrained QM/MM calculations of energies of reaction from randomly chosen ground-state conformation has established that (i) those conformations in which the reactant atoms (C4 of NAD⁺ and H–C7 of PhCH₂O^–) are at van der Waals distance and angle of approach between 132° and 180° are associated with the most favorable energies of reaction; (ii) these conformations (NACs) are created by the anticorrelated pushing motions between CG1 of V203 and C^α of V292 toward C7 of PhCh₂O^–, which spans 8.2 and 9.2 Å average distances, respectively; and (iii) the anticorrelated interactions at longer distances [amide carbonyl oxygen of I18 and amid N of H67(14.7 Å) and the anticorrelated pair of amide carbonyl oxygen of L141 and C^α of T178 (18.2 Å)] are not directly in the direction required for a pushing effect and have very little influence on NAC formation.

The enzyme residues V292 and V203 were shown to be of particular importance in the early kinetic isotope-effects studies of HLADH and mutants in the laboratories of Klinman and coworkers (5, 24) and Rubach and Plapp (22). Comparison of the MD-derived close-contact distances (CCDs) between NAD⁺ and PhCH₂O^– in wild type (V203) and mutant (V203L, V203A, and V203G) in HLADH·NAD⁺·PhCH₂OH complexes has been carried out (25). A linear relationship was found (Eq. 6) between the experimental (24) free energies of activation and the NAD⁺ pyridine ring C4 to PhCh₂O^– C7 CCDs.

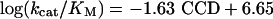[6]

Thus, restriction of distance between reactants facilitates quantum mechanical tunneling. This distance has now been shown with the HLADH·NAD⁺·PhCH₂O^– complex to be diminished by anticorrelation motions, which create push NACs.

Some 10 years ago, Almarsson and Bruice (26) carried out MD studies of enzymatic substrate reductions with NAD(P)H. Attention was drawn to the positioning of bulky substituents at the NAD(P)H cofactor surface distal to the substrate {dogfish muscle lactate dehydrogenase I249 and V136 [PDB ID code 1LDM (27)]; dihydrofolate dehydrogenase F103 [PDB ID code 3DFR (28)]; malate dehydrogenase A245 and L157 [PDB ID code 4MDH (29)]; and glyceraldehydes 3-P dehydrogenase I12 and Y317 [PDB ID code 1GPD (30)]}. They noted that the steric demand of the bulky distal substituents induces the formation of one of two quasi-boat conformers of NAD(P)H in which the axial H of NAD(P)H is pointed to the substrate carbonyl carbon and at times at van der Waals distance. The quasi-boat conformation contributes to the energetic advantage of enzymatic catalysis and is required geometry along the pathway to the transition state (21). Recently, an ab initio electronic-structure calculation (31) for NADH in the enzyme TDP-d-glucose dehydrogenase has shown that the hydride donor ability of NADH is influenced by the degree of bending in the dihydronicotinamide ring, and in this enzyme complex, the ring is profoundly puckered.

Conclusions

This and previous studies of nicotinamide dehydrogenases (10, 12, 22–26) have established the importance, to the free energy of activation, of a substituent adjacent to the face of the NAD⁺ or NADH nicotinamide ring and distal to the substrate. It has now been shown with HLADH·NAD⁺·PhCH₂O^– that anticorrelated motions of the V292 of the cofactor-binding domain, in particular, and V203 with motions of the substrate push cofactor C4 and substrate H–C7 into position to create reactive ground-state conformations (NACs). Additionally, the ground-state NAC species have been shown to be associated with the transition states of lowest energy. In summary, anticorrelated interactions at the surface of the active site push the NAD⁺ toward the substrate creating push NACs, which are associated with the lowest energies of reaction.