Changes in connectivity profiles define functionally distinct regions in human medial frontal cortex

Abstract

A fundamental issue in neuroscience is the relation between structure and function. However, gross landmarks do not correspond well to microstructural borders and cytoarchitecture cannot be visualized in a living brain used for functional studies. Here, we used diffusion-weighted and functional MRI to test structure-function relations directly. Distinct neocortical regions were defined as volumes having similar connectivity profiles and borders identified where connectivity changed. Without using prior information, we found an abrupt profile change where the border between supplementary motor area (SMA) and pre-SMA is expected. Consistent with this anatomical assignment, putative SMA and pre-SMA connected to motor and prefrontal regions, respectively. Excellent spatial correlations were found between volumes defined by using connectivity alone and volumes activated during tasks designed to involve SMA or pre-SMA selectively. This finding demonstrates a strong relationship between structure and function in medial frontal cortex and offers a strategy for testing such correspondences elsewhere in the brain.

Since early attempts to parcellate human and nonhuman cortex into structurally distinct subdivisions, the hypothesis that structural borders correspond to functional borders has been widely held (1-3). However, this hypothesis has been tested only rarely. Structural features such as sulci and gyri are commonly used to define anatomical regions in functional imaging, neurophysiology, and lesion studies, yet they have only a limited correspondence to more fine-grained structural organization such as cytoarchitecture (4-6). Microstructural borders based, for example, on measurements of cyto-, myelo-, or receptor architecture (7-9), can only be defined post mortem, and the methodological demands of such studies preclude investigation of the regional functional specializations in the same animals. Detailed testing of the relationship between these anatomically-based measures and function based on comparisons between subjects is limited by the apparently substantial interindividual variations in microstructural anatomical boundaries (4-6).

A structural feature that has not previously been used to define areal boundaries in the human neocortex is connectivity to other brain regions. Whereas features such as cytoarchitecture, myeloarchitecture, and receptor distributions distinguish the processing capabilities of a region, connectional anatomy constrains the nature of the information available to a region and the influence that it can exert over other regions in a distributed network. Therefore, not only does structural variation reflect functional organization, but local structural organization also determines local functional specialization. Data on brain connectivity in macaque monkeys show that cytoarchitectonically and functionally distinct regions of prefrontal cortex have distinct connectivity “fingerprints” (10). Differences in connectivity that parallel differences in cytoarchitecture have been used to define subdivisions in macaque cortex within regions previously thought to be homogenous (11).

Previously, we have shown that the human thalamus can be subdivided by using noninvasive diffusion imaging data on the basis of its connectivity to specific cortical targets (12). However, this approach was limited by the need to define potentially connected cortical target regions a priori. Here, we develop a fundamentally different strategy for inferring structural parcellation from diffusion data that allows “blind” discrimination of regions with different patterns of connection. Probabilistic diffusion tractography is used to derive connectivity profiles for points along cortical regions of interest. By calculating the cross-correlation between these profiles, it is possible to define regions with similar connections and to identify points where connectivity profiles change.

Our focus here is the medial frontal cortex. In the macaque monkey, the medial part of the homologue of Brodmann's area 6 consists of two cytoarchitectonically distinct regions: F3, or supplementary motor area (SMA) proper, and F6, or pre-SMA (2, 13). These two regions exhibit different functional responses (14-16) and have distinct connections (17, 18). The precise anatomical homologues of SMA and pre-SMA in humans are not clear as different studies have identified two (19) or three (20) cytoarchitectonically distinct regions within human area 6. A recent diffusion tensor imaging study in humans showed that regions presumed to correspond to SMA and pre-SMA have distinct connectivity with the striatum (21). There is consistent evidence for a functional distinction, at least between anterior and posterior parts of human medial area 6, because functional imaging studies have found differential involvement of these regions in tasks engaging distinct cognitive or motor domains (22-24). Whereas the arcuate sulcus corresponds with the border between SMA and pre-SMA in macaque (14, 16), there is no local landmark that differentiates functionally defined SMA and pre-SMA in the human brain (25); the vertical line from the anterior commissure provides the best approximation (19). Here, we use diffusion tractography methods and functional MRI (fMRI) to test directly whether boundaries defined by differences in connectivity can discriminate between functionally defined SMA and pre-SMA in humans.

Methods

Data Acquisition. Diffusion-weighted, blood oxygenation level-dependent (BOLD) fMRI, and T1-weighted images were acquired in nine healthy subjects (ages 24-35 years, five male) on a 1.5 T Siemens Sonata MR scanner with maximum gradient strength of 40 mT·m^-1. All subjects gave informed written consent in accordance with ethical approval from the Oxford Research Ethics Committee.

Diffusion-weighted data were acquired by using echo planar imaging (72 × 2 mm thick axial slices, matrix size 128 × 104, field of view 256 × 208 mm², giving a voxel size of 2 × 2 × 2 mm). The diffusion weighting was isotropically distributed along 60 directions by using a b value of 1,000 s·mm^-2. For each set of diffusion-weighted data, 5 vol with no diffusion weighting were acquired at points throughout the acquisition. Three sets of diffusion-weighted data were acquired for subsequent averaging to improve signal-to-noise ratio. The total scan time for the diffusion-weighted imaging (DWI) protocol was 45 min.

BOLD fMRI data were acquired by using echo planar imaging (20 × 5 mm thick axial slices positioned from the top of the brain, matrix size 128 × 128, field of view 256 × 256 mm², giving a voxel size of 2 × 2 × 5 mm, repetition time = 2.5 s, 341 vol, echo time = 45 ms, and flip angle = 90°).

Subjects practiced the fMRI tasks before entering the scanner. Blocks (30-s duration) of rest (i) alternated with blocks of finger tapping (ii) or serial subtraction (counting backward in threes) (iii) in an ABACACAB cycle repeated 3.5 times. The current task was indicated by the word “rest,” “move,” or “count” displayed on a projection screen at the foot of the scanner bed viewed via a mirror. During move blocks, subjects pressed buttons with the fingers of their right hand in a repeating 1234321 sequence at a frequency of ≈4 Hz. During count blocks, subjects counted covertly backwards in threes from a three-digit reference number displayed on the screen for 2 s before the start of the counting block. To ensure task compliance, at the end of each counting block a red screen instructed subjects to report the number they had reached by pressing buttons with their index figure to indicate tens and middle finger to indicate units (e.g., 47 = index finger button four times and middle finger button seven times). The total scan time for the fMRI protocol was ≈15 min.

A T1-weighted anatomical image was acquired by using a flash sequence (repetition time = 12 ms, echo time = 5.65 ms, and flip angle = 19°, with elliptical sampling of kspace, giving a voxel size of 1 × 1 × 1 mm in 5 min and 5 sec).

DWI Analysis. Diffusion data were corrected for eddy currents and head motion by using affine registration to a reference volume (26). Data from the three acquisitions were averaged to improve the signal-to-noise ratio. Probability distributions on fiber direction were calculated at each voxel by using described methods (27). Probabilistic tractography was then performed from voxels within specified seed masks (12, 27).

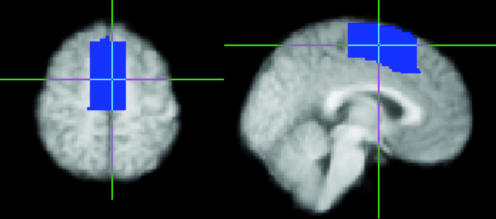
A medial frontal cortex mask was defined on the group average T1-weighted image by using the program fslview, which can be accessed at www.fmrib.ox.ac.uk/fsl (Fig. 1). The mask included gray matter on the medial wall and extended from y = -22 to y = 30 [Montreal Neurological Institute (MNI) coordinates] and from a short distance above the cingulate sulcus (as visible on the average brain) to the dorsal surface of the brain. Two single-slice masks were used for initial parcellation: an axial slice (MNI Z = 58) and a sagittal slice (MNI X = -2). These masks were transformed into the space of each subject's diffusion data by using the program flirt (26). For each subject, probabilistic tractography was run from all voxels in this seed mask (12, 27). During tractography, knowledge of location was maintained in three spaces: Seed space (MNI), the space of the original DWI data, and a low-resolution (5 × 5 × 5 mm³) space. All diffusion information used in tractography was sampled on the original diffusion imaging grid. Probabilities of connection from each seed voxel (at 2 × 2 × 2 mm³ resolution) to every other voxel in the low-resolution brain (at 5 × 5 × 5 mm³) were binarized and stored in a matrix, A, of dimensions (number of seed voxels × number of voxels in the rest of the brain). The connectivity profiles were binned at this lower resolution for reasons of data storage. The cross correlation matrix of A was computed, resulting in a symmetric matrix, B, of dimensions (number of seeds × number of seeds) in which the (i,j)th element value is the correlation between the connectivity profile of seed i and the connectivity profile of seed j. The nodes in B were permuted by using a spectral reordering algorithm (Supporting Text, which is published as supporting information on the PNAS web site, ref. 28, and D.J.H., unpublished work) that finds the reordering that minimizes the sum of element values multiplied by the squared distance of that element from the diagonal, hence forcing large values toward the diagonal. If the data contains clusters (representing seed voxels with similar connectivity), then these clusters will be apparent in the reordered matrix and break points between clusters will represent locations where connectivity patterns change. Clusters were identified by eye as groups of elements that were strongly correlated with each other and weakly correlated with the rest of the matrix. Elements that did not clearly belong to a single cluster were left unclassified.

Fig. 1.

Medial frontal cortex mask shown in axial (Left, Z = 58) and sagittal (Right, X = -2) view. The vertical line indicates Y = 0 (vertical line from the anterior commissure). These two slices are used for the initial, single-slice parcellations of medial frontal cortex.

Population maps of resulting clusters in brain space were derived by binarizing clusters corresponding to putative SMA (most posterior cluster) and pre-SMA (most anterior cluster) for each subject and averaging these binarized clusters across subjects so that voxel values in the population maps indicated the proportion of subjects in whom a cluster was present at that point.

Diffusion image analysis was carried out on an Intel 2.4-GHz processor. Approximate processing times were as follows: Fitting local diffusion parameters at each brain voxel, 24 h per subject; probabilistic tractography, 10 s per voxel; and reordering a cross-correlation matrix of 400 × 400, 90 min (for larger matrices, time scales at approximately N³).

fMRI Analysis. fMRI data were analyzed by using programs contained in the fmrib software library, which can be accessed at www.fmrib.ox.ac.uk/fsl. The following preprocessing steps were applied: motion correction by using the program mcflirt, removal of nonbrain structures by using the program BET (29), spatial smoothing by using a Gaussian kernel of full width at half maximum of 3 mm, mean-based intensity normalization of all volumes by the same factor, temporal high-pass filtering by using Gaussian-weighted least-squares fitting with a filter of σ = 57.5 s. Time series statistical analysis was carried out by using the program film with local autocorrelation correction (30). Z (Gaussianized T) statistic images were thresholded by using Gaussian Random Field theory-based maximum height thresholding with a corrected significance threshold of P = 0.01. Registration to standard space was carried out by using the program flirt (26).

Assessing Structure-Function Correspondence. For each subject, voxels that were suprathreshold for either functional task and were contained within the anatomically defined medial frontal volume of interest defined a seed mask for further connectivity analyses. Cross-correlation connectivity matrices for these voxels were derived, reordered, and mapped back onto the brain as before to define putative SMA and pre-SMA for each subject. Centers of gravity of fMRI activation clusters and of connectivity-defined clusters were found and the distances between connectivity- and functionally-defined clusters were compared by using paired Student t tests. To characterize the connections of SMA and pre-SMA, the connectivity distributions for all voxels within each region were found for each subject. These profiles were then averaged across subjects and were mapped onto the average T1-weighted brain in standard space.

Results

For each subject, DWI data were used to perform probabilistic tractography (12, 27) from voxels within medial frontal “seed” masks. Probabilities of connection from each seed voxel to every other brain voxel were binarized and stored in a matrix, A, whose cross correlation matrix, B, was found. Elements in matrix B therefore express the correlation in connectivity profile between medial frontal seed points. The nodes in matrix B were permuted by using a spectral reordering algorithm (Supporting Text, ref. 28, and D.J.H., unpublished work) that forces large values toward the diagonal. If the data contain clusters (representing seed voxels with similar connectivity), then these clusters will be apparent in the reordered matrix and break points between clusters will represent locations where connectivity patterns change. Note that if such structure is not present in the original data then the reordered matrix will not have a clustered organization.

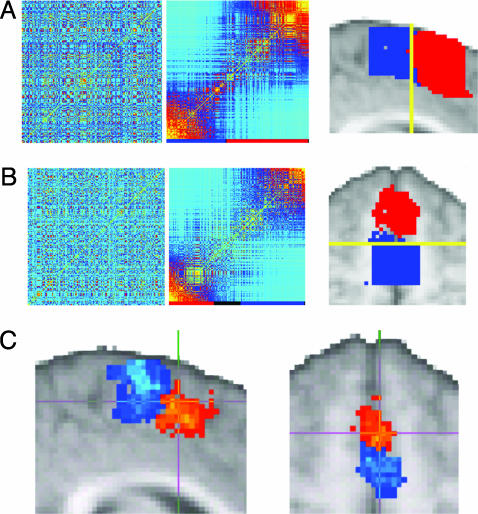
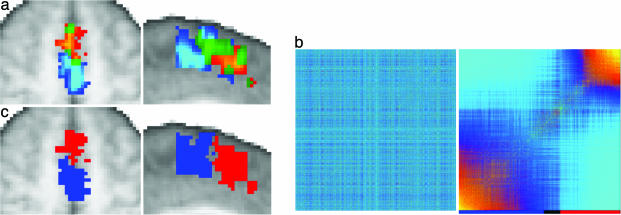
Connectivity-Based Division of Medial Frontal Cortex. We first defined single-slice orthogonal seed masks on the medial frontal cortex in the axial (MNI Z = 58) or sagittal (MNI X = -2) plane on the group average T1-weighted image (Fig. 1). These masks were registered to each subject's DWI data for generation of connectivity matrices. Reordered connectivity cross-correlation matrices contained clearly identifiable clusters in all subjects (Fig. 2, and Figs. 6 and 7, which are published as supporting information on the PNAS web site). Note that such structure will only be apparent in the reordered matrices if there is clustered organization in the data. The reordered matrices were divided into two or three clusters. When these clusters were mapped back onto the brain they corresponded to discrete regions situated along the anterior-posterior axis of the medial frontal cortex (Figs. 2, 6, and 7). The border between the most anterior and most posterior cluster was located close to the vertical line extending from the anterior commissure (Y = 0), suggesting that the regions correspond to SMA and pre-SMA. To test this hypothesis directly, we compared subregions defined on the basis of connectivity to functional activation sites during tasks designed to involve SMA or pre-SMA selectively.

Fig. 2.

Connectivity-based parcellation of medial frontal cortex. (a and b) Result of parcellating a sagittal (a) and axial (b) slice in a single subject. Original (Left) and reordered (Center) cross-correlation matrices are shown. The clusters identified in the reordered matrices are indicated by the colored bar below the matrices. Black regions on the color bar represent elements that did not clearly belong to one cluster and were therefore unclassified. (Right) The images show the clusters mapped onto the brain by using the same color scheme as the color bar. For all subjects, clusters were present in the reordered matrices and were mapped onto discrete regions distributed along a posterior-anterior axis. The yellow line indicates Y = 0. For individual subject data see Supporting Text.(c) Population probability maps for putative SMA (red to yellow) and pre-SMA (blue to turquoise) shown for single sagittal (Left) and axial (Right) slices. Population maps have been thresholded to only include voxels where a cluster was present in four or more subjects (of nine). Green voxels represent overlap between SMA and pre-SMA. The crosshairs are positioned at Y = 0.

Medial Wall fMRI Activations. We acquired BOLD fMRI data while subjects performed blocks of finger tapping or serial subtraction (counting backwards in threes) alternating with rest. These two functional tasks were selected because previous studies have shown that finger tapping activates the SMA (24), whereas serial subtraction activates the pre-SMA (31, 32) in the superior medial frontal cortex. Both tasks activated the superior medial frontal cortex in all subjects (Fig. 3a, and Fig. 8, which is published as supporting information on the PNAS web site). In some subjects, there was overlap between activated clusters for the two tasks. In all subjects, medial wall activations during finger tapping were more posterior and superior than those during serial subtraction, as anticipated if finger tapping involves the SMA and serial subtraction involves the pre-SMA.

Fig. 3.

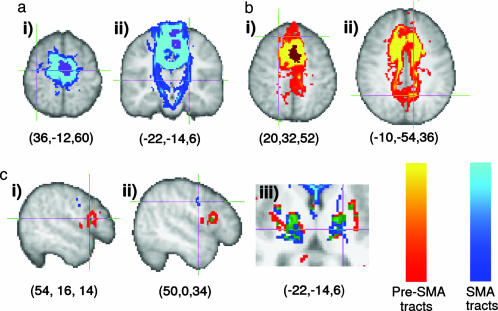
Testing structure-function correspondence. (a) Activation for a single subject during serial subtraction (red to yellow) and finger tapping (blue to turquoise). Voxels activated during both tasks are green. (b) Original (Left) and reordered (Right) connectivity cross-correlation matrix for all medial frontal voxels activated in either task for this subject. The reordered matrix was divided into two clusters (indicated by the colored bar). (c) When mapped onto the brain, the border between the connectivity-defined clusters corresponds closely to the boundary between the functionally activated volumes. Note that although clusters are shown for example slices in a and c, the matrices in b include all voxels from the 3D volume that was activated by either task and fell within the anatomically defined medial frontal mask. The matrices in this case are therefore typically much larger than the single-slice matrices shown in Fig. 2. For data from all subjects see Supporting Text.

Testing Structure-Function Correspondence. Medial superior frontal voxels activated in either task were entered into a connectivity analysis for each individual subject. For all subjects, the resulting reordered cross-correlation matrices contained clusters of similar connectivity that were defined by an investigator blind to the fMRI results (Fig. 3b). In all nine subjects, two connectivity clusters were identified, and in two of nine subjects, an additional, smaller cluster was found between the other two (see Fig. 8). When the clusters were mapped back onto the brain, they appeared as distinct regions along medial frontal cortex and the anterior and posterior connectivity clusters corresponded closely to the activated SMA and pre-SMA volumes during fMRI (Figs. 3 a and c and 8).

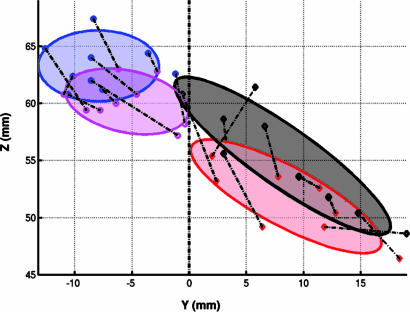
The centers of gravity for superior medial frontal counting-related activations (pre-SMA) colocalized with the centers of the most anterior connectivity-defined clusters, whereas the centers of movement-related activations (SMA) colocalized with the most posterior connectivity-defined clusters (Fig. 4). For all subjects, the center of the most posterior connectivity cluster was closer to functionally defined SMA (median distance = 2.23 mm, and range = 0.42-5.30) compared with pre-SMA (median distance = 8.02 mm, and range = 4.53-13.29) (P = 0.002), whereas for all subjects the center of the anterior connectivity cluster was closer to functionally defined pre-SMA (median distance = 3.07 mm, and range = 1.5-5.42) than SMA (median distance = 9.13 mm, and range = 3.47-13.17); (P = 0.002).

Fig. 4.

Colocalization of structurally and functionally defined clusters for all subjects. Each point represents the center of gravity of an fMRI activation or connectivity-defined cluster for a single subject. Centers of activation during finger tapping (magenta) colocalize with connectivity-defined SMA (blue), whereas centers of activation during serial subtraction (black) colocalize with centers of connectivity-defined pre-SMA (red). Ellipses represent 85% confi-dence intervals. Dashed lines connect points from the same individual.

Connections from SMA and pre-SMA Regions. The finding that regions corresponding to SMA and pre-SMA form distinct clusters in the reordered cross-correlation matrices reflects their different connectivity profiles. To characterize the connectivity profile of each area, we mapped the connectivity distributions from all voxels within putative SMA or pre-SMA for each subject onto the average T1-weighted brain template. These distributions were then averaged across all subjects (Fig. 5). As predicted from literature from nonhuman primates (17, 18, 33-37), connections from SMA were found to the corticospinal tract, precentral gyrus, and ventrolateral thalamus (Fig. 5 a and c), whereas connections from pre-SMA were found to the superior frontal gyrus, medial parietal cortex, inferior frontal cortex, and anterior thalamus (Fig. 5 b and c). Consistent with a recent DWI study in humans (21), pathways from SMA connected to more posterior sites in the putamen than those from pre-SMA. More unexpectedly, connections were seen from SMA to orbitofrontal cortex (data not shown) and from pre-SMA to the external capsule/insula (Fig. 5c). Although there is evidence for a weak orbitofrontal connection from SMA in macaque (38), consistent with its presence here in humans, it also is possible that the orbitofrontal and insula connections originated from superior parts of the cingulate sulcus (35, 39) included in the medial frontal seed mask. The borders between SMA/pre-SMA and the cingulate motor areas are difficult to define and the anatomy of this region is highly variable between subjects (9, 40). The inferior border of our medial frontal mask was located a short distance above the cingulate sulcus on the group average anatomical image, corresponding to Z = 50 at its most caudal end, Z = 46 at the level of the vertical line from the anterior commissure, and Z = 38 at its most rostral end. The connection from SMA to orbitofrontal cortex was more commonly seen in subjects in whom putative SMA extended below the level of Z = 48. Similarly, the connection from pre-SMA to external capsule/insula was most commonly seen in subjects in whom pre-SMA extended below the level of Z = 40.

Fig. 5.

Connections from putative SMA and pre-SMA. (a) The population map of putative SMA (thresholded at more than four subjects) is purple. The group connectivity distribution ranges from blue to turquoise. Connections from putative SMA tended to go to the precentral gyrus [crosshairs in ai and the corticospinal tract (aii)]. (b) The population map for putative pre-SMA (more than four subjects) is brown. The group connectivity distribution from putative pre-SMA ranges from red to yellow. Connections from pre-SMA tended to go to the prefrontal cortex [crosshairs in bi show a termination point in the superior frontal gyrus) and medial parietal cortex (bii)]. (c) Group connectivity distributions from pre-SMA and SMA are rendered together for comparison (ci and cii). Connections from pre-SMA terminated in inferior frontal gyrus. In the precentral gyrus, connections from SMA terminated in caudal parts of the gyrus, corresponding to motor and premotor cortices, whereas pre-SMA connections terminated in more rostral, inferior parts of precentral gyrus (ciii). In the thalamus, connections from SMA traveled through the ventrolateral part of the thalamus and the adjacent internal capsule, whereas those from pre-SMA traveled through more anterior parts of the thalamus. Green regions in C represent overlap between connectivity distributions from SMA and pre-SMA. Coordinates given below each brain slice indicate the location of the crosshairs in MNI coordinates.

Discussion

By using a generalizable method for discriminating between gray matter regions based on differences in connectivity, we identified a sharp change in connectivity profile along the superior medial frontal cortex. The specific connectivity of the more posterior region to motor and premotor cortex and the corticospinal tract and of the more anterior region to the inferior frontal gyrus, medial parietal, and superior frontal cortex suggested anatomical homology to SMA and pre-SMA in the macaque brain (17, 18, 33-36). There was an excellent correspondence between these regions defined by connectivity and those identified as SMA or pre-SMA by functional criteria. These results therefore directly establish a close relationship between connectional anatomy and function in the superior medial frontal cortex and add further support to the general principle that variations in connectivity reflect functional specialization (10).

The strategy we present here provides an approach to in vivo investigation of human brain organization. Previously, the only structural boundaries easily measurable in vivo were features such as gyri and sulci that do not correspond well to microstructural borders (4, 6). Conventionally defined microstructural borders based on measures such as cyto-, myelo-, and receptor architecture can only be assessed post mortem. Although recent high-resolution MRI studies have shown some promise for detection of prominent myeloarchitectonic boundaries in specific regions of visual cortex (41, 42), it is not clear whether the approach will be more generally useful in regions with less distinct differences in myeloarchitecture. However, changes in connectivity characterize differences between many different brain regions (10, 11, 17) and could therefore provide a basis for defining microstructural boundaries much more generally.

Diffusion imaging data previously has been used to parcellate subcortical gray matter on the basis of remote connectivity (12) or local diffusion properties (43). For example, classification of thalamic voxels according to the cortical target with which they showed the highest probability of connection resulted in clusters that we proposed correspond to thalamic nuclei or nuclear groups (12, 44). The approach presented here represents a fundamentally different strategy for using connectivity information to parcellate gray matter. First, it does not rely on prior knowledge of what constitute meaningful divisions in connectivity targets. The regions in the medial frontal cortex were detected by using changes in connectivity profiles alone without the need for prior knowledge of what those profiles are. Having detected a change in connectivity, we were able in this case to trace the connections of the two defined regions to their major targets to characterize the different spatial distributions of connectivity profiles. This procedure allowed the areas to be related to homologous regions in the macaque brain. However, accurate and complete tracing to all final targets is not essential simply for discrimination of connectionally distinct regions. This finding is particularly important when tracing distributions from regions of cerebral cortex where low starting anisotropy and the presence of fiber crossing and complexity can make longer distance tractography difficult. However, the accuracy of the underlying tractography process will be reflected in the sensitivity of the approach proposed here. The inclusion of more sophisticated tracking techniques that attempt to model and trace through areas of complex fiber architecture would enable the detection of connectional differences that are invisible to the tracking methods used to drive the results in this paper. In addition, localized image artifacts could lead to spurious differences in connectivity profiles, and therefore, improvements in data quality and artifact reduction will further increase confidence and sensitivity.

The ability to assess borders of connectivity-defined cortical regions noninvasively allows for the individual variation and basis of brain structure to be addressed in another way. It already is known that there is substantial variability in both structural (4, 6, 40) and functional (45, 46) brain anatomy between individuals, but a more complete description demands analysis of substantially greater numbers of individuals than can be studied conveniently by using classical histological methods post mortem. However, there are limits to the information that can be provided by diffusion tractography not only due to limitations in current technology such as the difficulty of tracking in the presence of complex fiber architecture (47, 48) but also due to fundamental limitations of diffusion imaging data. For example, it is not possible to differentiate between anterograde and retrograde connections or to determine whether a connection is direct or indirect. Therefore, classical approaches to identifying connections and defining histology remain crucially important for gaining a full understanding of cortical anatomy.

Clusters in the reordered connectivity matrices were identified by eye and were manually defined in the present study. In the case of connectivity data from the superior medial frontal cortex, matrices could be clearly divided in this way into two or three clusters after reordering (see Figs. 6-8). However, it would be desirable to objectively determine both the number of clusters and the location of break points in reordered matrices. This determination will become increasingly important as the approach is applied to larger cortical volumes. There are a number of established techniques for data clustering, some of which have been successfully applied for example to brain data, for example, to objectively define cytoarchitectonic borders in human cortex (49). Future work will be needed to explore the suitability of such techniques for objectively identifying clusters in connectivity data.

Definition of connectional and functional boundaries in the same brain allows direct testing of structure-function relationships. Previous studies (50, 51) have extrapolated from population maps of cortical areas based on cytoarchitecture in one group of subjects to functionally defined regions of cortex in another group to infer relations between structure and function. A general limitation of this strategy is the uncertain interpretation of group correlations arising from interindividual variations in both the structural and functional borders. Determining whether variations in functional anatomy reflect variations in structural anatomy within an individual has previously been limited by the difficulty of measuring both structural and functional anatomy in the same subject. The potentially generalizable methods described here allow the connectional anatomy of the neocortex to be related both to gross anatomical features and to functional activation patterns within individuals and over relatively large populations.