Vaccination and the theory of games

Abstract

Voluntary vaccination policies for childhood diseases present parents with a subtle challenge: if a sufficient proportion of the population is already immune, either naturally or by vaccination, then even the slightest risk associated with vaccination will outweigh the risk from infection. As a result, individual self-interest might preclude complete eradication of a vaccine-preventable disease. We show that a formal game theoretical analysis of this problem leads to new insights that help to explain human decision-making with respect to vaccination. Increases in perceived vaccine risk will tend to induce larger declines in vaccine uptake for pathogens that cause more secondary infections (such as measles and pertussis). After a vaccine scare, even if perceived vaccine risk is greatly reduced, it will be relatively difficult to restore prescare vaccine coverage levels.

The history of vaccination policy includes numerous bouts of public resistance, often in the form of vaccine scares (1-4). In the United Kingdom, for example, a pertussis vaccine scare in the 1970s caused a decline in the level of vaccine coverage, resulting in substantial increases in morbidity and mortality from whooping cough (4). Currently, measles-mumps-rubella vaccine uptake is declining in the United Kingdom, with mounting concern that widespread outbreaks of measles may recur (5).

In deciding whether to vaccinate their children, parents consider the risk of morbidity from vaccination, the probability that their child will become infected, and the risk of morbidity from such an infection. The decisions of individual parents are indirectly influenced by the decisions of all other parents, because the sum of these decisions yields the vaccine coverage levels in the population and hence the course of epidemics.

Game theory (6-9) attempts to predict individual behavior in such a setting, where the payoff to strategies chosen by individuals depends on the strategies adopted by others in the population. Here, we integrate epidemic modeling (10) into a game theoretical framework to analyze population behavior under voluntary vaccination policies for childhood diseases. This approach allows us to quantify how risk perception influences expected vaccine uptake and coverage levels and what role is played by the epidemiological characteristics of the pathogens.

The Vaccination Game

Description of Game. For simplicity, we imagine that all individuals are provided with the same information and use this information in the same way to assess risks. An individual's strategy is the probability P that s/he will choose to vaccinate. The vaccine uptake level in the population is the proportion of newborns who will be vaccinated and hence is the mean of all strategies adopted by individuals in the population. We ignore any delay between changes in vaccine uptake and corresponding changes in overall vaccine coverage in the population; consequently, if no disease-related or vaccine-related mortality occurs, then the proportion of the population vaccinated, p, will be equal to the vaccine uptake level.

The payoff to an individual will be greater when morbidity risk (probability of adverse consequences) is lower. We use r_v and r_i to denote the morbidity risks from vaccination and infection, respectively, and π_p to denote the probability that an unvaccinated individual will eventually be infected if the vaccine coverage level in the population is p. With this notation, the payoff is -r_v to a vaccinated individual and -r_iπ_p to an unvaccinated individual. Thus, the strategy of vaccinating with probability P yields expected payoff

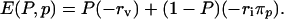[1]

In the context of vaccination, parents act according to perceived morbidity risks, which may differ significantly from actual morbidity risks (3, 11). Consequently, we interpret r_i and r_v as the perceived morbidity risks from infection and vaccination and E(P, p) as the perceived payoff. The game is unchanged if we scale the payoff function by a constant. Therefore, we can eliminate one of the parameters, leaving only the relative risk, r = r_v/r_i. Thus, we can write

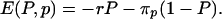[2]

Characterization of Nash Equilibria. We now seek to identify which strategies are likely to be adopted. If most of the population adopts strategy P, and individuals that adopt any other strategy Q always obtain a lower payoff than those adopting P, then P is said to be a Nash equilibrium. In contrast, if most individuals adopt strategy Q, but individuals adopting a strategy that is closer than Q to P obtain a higher payoff than those adopting Q (and those adopting a strategy further from P obtain a lower payoff), and if this is true for any Q ≠ P, then P is said to be convergently stable. If P is a Nash equilibrium, and everyone is currently playing P, then no one should change strategy. If P is convergently stable, then regardless of what strategy is most common in the population, individuals should start to play strategies closer to P, and ultimately adopt P. It is generally expected that a strategy observed in a real population (12) must be a convergently stable Nash equilibrium (CSNE).

Suppose that a proportion ε of the population vaccinates with probability P and the remainder vaccinate with probability Q. Because we ignore any difference between vaccine uptake, εP + (1 - ε)Q, and overall vaccine coverage in the population, p, we can always write

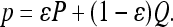[3]

The payoff to individuals playing P is, therefore,

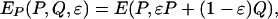[4]

whereas the payoff to individuals playing Q is

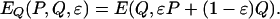[5]

The payoff gain to an individual playing P in such a population is

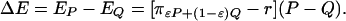[6]

The payoff gain ΔE is a measure of the incentive for an individual to change strategies from Q to P. For any given relative risk, r, there is a unique strategy P = P^*, such that ΔE is strictly positive for all strategies Q ≠ P^* and all proportions ε, where 0 ≤ ε < 1 (see Appendix for a proof). The special case of this fact for small proportions playing Q (ε near 1) implies that P^* is a Nash equilibrium. We also show in Appendix that, if neither P nor Q is equal to the Nash equilibrium P^*, but P is closer than Q to P^*, then ΔE > 0, implying that P^* is convergently stable and hence a CSNE.

The unique CSNE in this vaccination game is easily found (see Appendix). If the vaccine is perceived to be sufficiently risky (r ≥ π₀) then the CSNE is “never vaccinate” (P^* = 0). In contrast, if r < π₀, then the CSNE is “vaccinate with nonzero probability P^*” (0 < P^* < 1). In the latter case, the CSNE is said to be mixed (as opposed to the pure strategies P = 0 and P = 1).

Incorporation of an Epidemic Model

To make more precise predictions, we must specify the infection probability π_p. For this, we need an epidemiological model. We use a standard three-compartment model in which individuals are either susceptible to the disease (S), infectious (I), or recovered to a state of lifelong immunity (R). This SIR model, and variants thereof, are widely used in modeling childhood diseases (10, 13). The model is specified by the rates of change of the proportions of the population in each compartment.

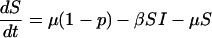[7]

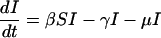[8]

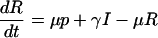[9]

Here, μ is the mean birth and death rate, β is the mean transmission rate, 1/γ is the mean infectious period, and p is the vaccine uptake level (assuming, for simplicity, that individuals are never infected before being vaccinated). Once a dynamical steady state is reached, the vaccine coverage level in the population will equal the uptake level. Because we shall focus on the steady-state solution of the model, our notation p for vaccine uptake is consistent with our notation in the game theoretical analysis (compare Eq. 3).

The third equation in the SIR model above is superfluous because S + I + R = 1. The remaining two equations can be written in a convenient, dimensionless form,

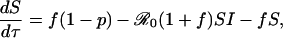[10]

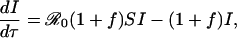[11]

where τ = t/γ is time measured in units of the mean infectious period, f = μ/γ is the infectious period as a fraction of mean lifetime, and 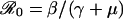is the basic reproductive ratio (the average number of secondary cases produced by a typical primary case in a fully susceptible population). For childhood diseases, f < 0.001 and 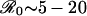(e.g., ref. 10).

The predictions of the SIR model depend on the critical coverage level that eliminates the disease from the population (10), p_crit, which itself is a function of .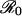

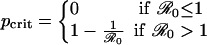[12]

If p ≥ p_crit, then the system converges to the disease-free state (Ŝ, Î) = (1 - p, 0), whereas if p < p_crit, it converges to a stable endemic state given by

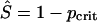[13]

and

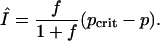[14]

Because S and I are constant in this situation, the probability that an unvaccinated individual eventually becomes infected can be expressed, using Eqs. 10-14, as the proportion of susceptible individuals becoming infected versus dying in any unit time,

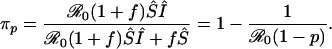[15]

(Note that the parameter f does not appear in this expression for π_p, so the CSNE will not depend on the birth rate or the infectious period of the disease.) The condition r < π₀, which yields a mixed CSNE, can therefore be written

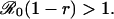[16]

The value of the mixed CSNE P^*, obtained by solving the equation r = π_P^* for P^*, is

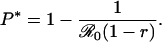[17]

Results and Discussion

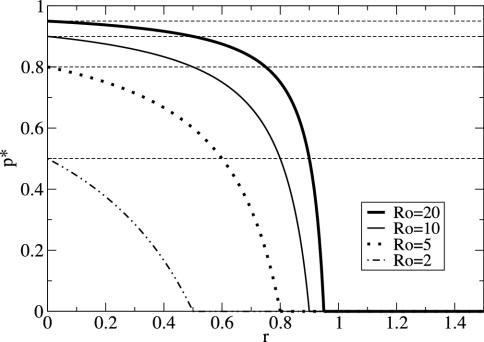
For any perceived relative risk r > 0, the expected vaccine uptake is less than the eradication threshold, i.e., P^* < p_crit (Fig. 1). This finding formalizes an argument that has previously been made qualitatively (8, 14); namely, it is impossible to eradicate a disease through voluntary vaccination when individuals act according to their own interests. In situations where vaccination is perceived to be more risky than contracting the disease (r > 1), one would expect, even without the aid of a model, that no parents would vaccinate their children. Our game theoretical analysis shows that, in fact, the threshold in perceived relative risk beyond which all parents should cease vaccinating depends on 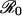. In particular, parents can be expected to play a pure nonvaccinator strategy if r > π₀, i.e., if

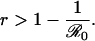[18]

Fig. 1.

Vaccine coverage p^* at the CSNE versus relative risk r, from Eq. 17, for various values of 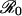. Dashed horizontal lines demarcate the critical coverage level p_crit that eliminates the disease from the population (Eq. 12). In the limit of very large 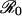, the plot of p^* versus r approaches a step function with a step at r = 1 (Eq. 17).

For childhood diseases, this relative-risk threshold is close to 1, but for diseases with relatively small 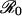, the threshold could be substantially smaller.

With knowledge of the perceived relative risk, r, we can thus predict vaccine coverage levels under voluntary policies. However, risk perception (and hence the value of r) can change over time in response to a variety of factors, such as media coverage and the activities of antivaccination groups (3, 11, 15, 16, ¶). Under normal circumstances, the relative risk is perceived to be very low (typically much lower than the relative-risk threshold, r ≪ π₀ < 1). During a vaccine scare, the perceived risk of vaccination will rise (by definition) and hence relative risk will increase to some new level r′> r. Note that a reduction in the perceived risk of morbidity from natural infection has the same effect. In either case, the qualitative nature of our predictions depends on whether the new risk ratio exceeds the relative-risk threshold; if r < r′ ≪ π₀, then behavioral changes will be relatively minor during a scare, whereas if r ≪ π₀ < r′, then dramatic changes in vaccine uptake can occur (see Table 1 and Fig. 2).

Table 1. Payoff gain ΔE (Eq. 6) to an individual adopting the new CSNE P′ (associated with perceived relative risk r′) when a proportion ε of the population does the same, and the remainder play the strategy P (which is the CSNE associated with relative risk r).

Case	Payoff gain, ΔE	ΔP
r < π0, r′ < π0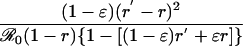
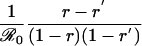r < π0, r′ > π0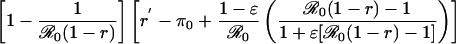
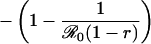r > π0, r′ < π0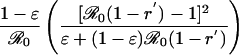
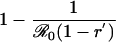r > π0, r′ > π0	0	0

π0 is the probability that an individual will eventually become infected if nobody is vaccinated (compare Eq. 15). To see that ΔE is always strictly positive if 0 ≤ ε < 1, note that r < π0 if and only if 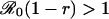(compare Eq. 16). The third column of the table shows ΔP = P′ - P, the change in the population's vaccine uptake after the change in risk perception. When both r and r′ exceed π0, the CSNE is the same before and after the change in risk perception (P′ = P = 0).

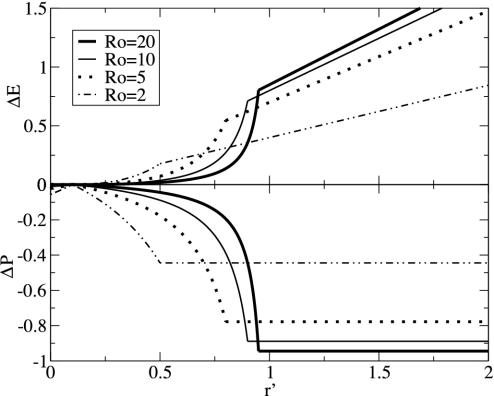
Fig. 2.

Analysis of vaccine scares: payoff gain, ΔE, and change in vaccine uptake, ΔP, after a shift in risk perception from r < π₀ to r′ (see Table 1). For this figure, r = 0.1 and the proportion of individuals currently adopting the new CSNE is ε = 0 (corresponding to the start of a vaccine scare); the shapes of the curves are qualitatively similar for other values of r and ε.

Several lines of evidence suggest that it is likely that r′ > π₀ during a vaccine scare. Many parents currently have concerns about the safety of the measles-mumps-rubella vaccine (17, 18) and other vaccines (19), and many parents (in developed countries) believe that diseases such as measles and whooping cough are essentially harmless (20). (Together, these observations indicate that r′ > 1 for measles, mumps, and rubella at present in the United Kingdom.) Targeted surveys show that among subscribers to a parenting magazine (21) and among inhabitants of specific areas in the United Kingdom (22), a significant proportion of parents believe vaccines entail more risk than the diseases against which they protect (r′ > 1) and this perception is correlated with not vaccinating (21).

When r ≪ π₀ < r′, the degree to which a vaccine scare is likely to have an impact on vaccination behavior depends sensitively on the value of 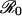. The payoff gain ΔE that measures the incentive to switch from the previous CSNE P (associated with r ≪ π₀) to the new CSNE P′ (associated with r′ > π₀) is always larger for diseases with larger 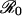. Consequently, we would expect individuals to be convinced more rapidly to change their vaccination behavior in the face of a vaccine scare for measles or whooping cough (for which 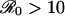) than for less transmissible infections. In general, for a given increase in risk perception, we expect precipitous reductions in vaccine uptake to be more common for diseases with higher .

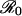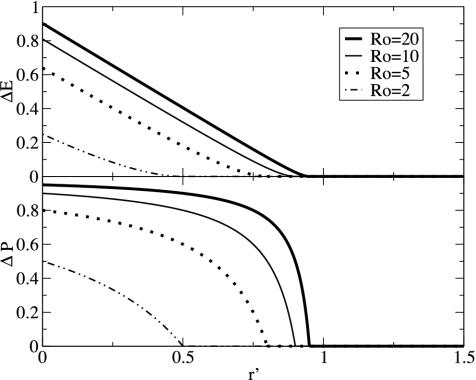
If 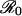is large, individuals are also likely to be more responsive to any reductions in the perceived relative risk of vaccination that occur after a vaccine scare (Fig. 3 and Table 1). Such reductions in r might result from media coverage of a few severe cases of disease (which are more likely as vaccine uptake drops and disease incidence rises). More importantly, education programs that aim to increase public confidence in vaccines after a scare are likely to be most effective for precisely the vaccines for which scares have the greatest impact.

Fig. 3.

Analysis of public education programs to counteract vaccine scares: payoff gain, ΔE, and change in vaccine uptake, ΔP, after a shift in risk perception from r > π₀ to r′. As in Fig. 2, ε = 0 here. The results are independent of r (because the CSNE is always P = 0 when r > π₀). The shapes of the curves are qualitatively similar for other values of ε, but the maximum of ΔE goes to zero as ε increases to 1.

Unfortunately, the effectiveness of education programs is constrained in a way that vaccine scares are not. During a vaccine scare, the payoff gain ΔE is given by the expression in the second row of Table 1; this expression is bounded below by a positive number for all ε (even for ε = 1), so the incentive not to vaccinate remains substantial even as the vaccine coverage approaches zero. In contrast, during successful education programs to combat a vaccine scare, risk perception will shift from r > π₀ to r′ < π₀, and the proportion of the population vaccinated will climb to the new CSNE level as more and more individuals are vaccinated. In this case, the payoff gain for adopting the new CSNE is given by the third row of Table 1, which implies (regardless of 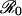) that ΔE → 0 as ε → 1; this means that the incentive to vaccinate diminishes as the vaccine coverage approaches the new CSNE level. We conclude that, in general, it will be relatively easy to induce a drop in vaccine uptake during a scare, but relatively difficult to restore uptake levels afterward. This prediction is consistent with the history of the pertussis vaccination scare during the 1970s in Britain (23), for which vaccine uptake dropped much more quickly than it later recovered after the scare. All else being equal, we anticipate that when the current measles-mumps-rubella scare in Britain is over, vaccine uptake will rise more slowly than it declined.

We have demonstrated previously that game theory can be a useful tool for evaluating schemes to prepare for the potential reintroduction of a pathogen that has been eradicated globally through mass vaccination (9). Here, we have investigated the feedback between individual vaccination decisions and population-level processes that determine vaccine uptake and herd immunity for an endemic disease, bearing in mind that vaccination decisions are strongly influenced by incorrect risk perception (11, ¶). Because our goal has been to elucidate the most fundamental issues, we have focused on the simplest possible epidemiological model appropriate for childhood diseases and have assumed implicitly that transient dynamics (13), seasonal forcing (13, 24), and stochasticity (13, 25) all have negligible effects. We have also ignored variance in risk perception and any effects of risk perception spreading nonhomogeneously through social networks. All these features of real systems merit further investigation.

Appendix

The probability π_p that an individual eventually becomes infected must decrease strictly with the proportion p of the population that is vaccinated, until p reaches the eradication threshold, 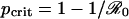. Thus, the maximum of π_p occurs for p = 0 and for p ≥ p_crit, π_p = 0.

Nash Equilibrium. If r ≥ π₀, then r > π_p for all p > 0, so for any ε ∈ [0,1) in Eq. 6, ΔE > 0 for all Q ≠ P if and only if P = 0. Thus, P^* = 0 is the unique Nash equilibrium. If r < π₀, then there exists a unique p^* ∈ (0, p_crit), such that π_p - r > 0 if p < p^*, π_p^* = r and π_p - r < 0 if p > p^*. For any Q < P, we have p = εP + (1 - ε)Q < P for all ε ∈ [0,1) and, similarly, for any Q > P we have p > P for all ε ∈ [0,1). Therefore, in this case where r < π₀, for any ε ∈ [0,1) in Eq. 6, ΔE > 0 for all Q ≠ P if and only if P = p^*. Thus, the Nash equilibrium P^* is the unique solution of the equation π_P^* = r.

Convergent Stability. Given relative risk r, let P^* denote the associated Nash equilibrium. Suppose a proportion ε of the population plays a strategy P (not necessarily equal to P^*) while the remainder play Q ≠ P. We must show, for ε ≪ 1, that if Q < P ≤ P^*or P^* ≤ P < Q, then individuals playing P obtain a higher payoff than those playing Q, i.e., ΔE > 0 in Eq. 6. In fact, this is true for any ε ∈ [0,1) and follows immediately because π_p decreases with p and π_P^* = r. If Q < P ≤ P^*, then π_εP+(1-ε)Q - r > 0, whereas if P^* ≤ P < Q, then π_εP+(1-ε)Q - r < 0. Hence, in either case, ΔE > 0 in Eq. 6.