Time-domain diffuse correlation spectroscopy

Abstract

Physiological monitoring of oxygen delivery to the brain has great significance for improving the management of patients at risk for brain injury. Diffuse correlation spectroscopy (DCS) is a rapidly growing optical technology able to non-invasively assess the blood flow index (BFi) at the bedside. The current limitations of DCS are the contamination introduced by extracerebral tissue and the need to know the tissue’s optical properties to correctly quantify the BFi. To overcome these limitations, we have developed a new technology for time-resolved diffuse correlation spectroscopy. By operating DCS in the time domain (TD-DCS), we are able to simultaneously acquire the temporal point-spread function to quantify tissue optical properties and the autocorrelation function to quantify the BFi. More importantly, by applying time-gated strategies to the DCS autocorrelation functions, we are able to differentiate between short and long photon paths through the tissue and determine the BFi for different depths. Here, we present the novel device and we report the first experiments in tissue-like phantoms and in rodents. The TD-DCS method opens many possibilities for improved non-invasive monitoring of oxygen delivery in humans.

1. INTRODUCTION

Cerebral blood flow (CBF) is normally under tight physiological control to ensure adequate delivery of oxygen and glucose to the brain and maintain neuronal function and structural integrity. However, cerebral autoregulation is often impaired in patients suffering from common conditions such as shock, stroke, cerebral edema, or traumatic brain injury, or those under anesthesia or mechanical ventilation. When cerebral autoregulatory capacity is diminished, CBF fluctuates extensively over time and the brain is at significant risk for injury from inappropriately low or high perfusion. While CBF management is an essential element of neurointensive critical care, none of the currently available tools provides a convenient, continuous, and reliable bedside measure of cerebral blood flow [1].

Near-infrared spectroscopy (NIRS) provides non-invasive and continuous measures of the attenuation of light propagating through the brain cortex and estimates the cerebral blood volume (CBV) and cerebral hemoglobin oxygenation (SO₂). However, neither SO₂ nor CBV are good substitutes for the CBF. Hemoglobin oxygenation depends on both perfusion and consumption and cannot disentangle changes in the flow and oxygen metabolism [2,3]. The use of CBV as a surrogate of CBF is based on the Grubb relationship [4], which fails during fast dynamic changes [5] and with disease [6,7] or altered physiology [8,9]. NIRS can also estimate CBF from manipulations of expired oxygen [10] or boluses of injected dyes like indocyanine green [11], but these methods are more invasive and cannot provide continuous monitoring.

A direct and more robust way to optically measure microvascular blood flow is provided by diffuse correlation spectroscopy (DCS) [12,13]. In DCS, the tissue of interest is illuminated by coherent near-infrared light, which causes a speckle interference pattern to form after the light multiply scatters through the tissue. Dynamic scattering of the light by moving red blood cells causes the speckle pattern to fluctuate rapidly. These fluctuations are typically detected 2 to 3 cm away from the source and quantified by measuring the temporal intensity autocorrelation curve of a single speckle [13,14]. The decay of the autocorrelation curve is fitted with the solution of the correlation diffusion equation to obtain an index of blood flow (BFi) in units of cm²/s. Although the units of BFi are not the conventional units of ml/min/100 g tissue for perfusion, the BFi is reliably proportional to the absolute flow, as demonstrated in simulations and validation studies against “gold-standard” measurements, such as arterial spin-labeled MRI [15–17], fluorescent microspheres [18], bolus tracking time-domain NIRS [19], and phase-encoded velocity mapping MRI [20]. Diffuse correlation spectroscopy is mostly sensitive to flows in the capillaries and small vessels [21], making it a potentially better measure of tissue perfusion than methods such as ultrasound, which measure blood velocity in large supply vessels. Moreover, unlike laser Doppler flowmetry, which is limited to measurement depths of at most a millimeter, with DCS, like with NIRS, it is possible to estimate blood flow in the human cerebral cortex from a sensor placed on the scalp.

While these advantages make DCS nearly ideal for performing non-invasive, transcranial measurements of cerebral blood flow, quantification of the cerebral blood flow index (CBFi) is limited by low cerebral sensitivity and susceptible to inter- and intra-subject variability from differences in the optical properties of tissue. While DCS inherently has greater sensitivity to the brain than NIRS by virtue of the greater weight given to higher blood flow and the preferential weight given to longer path-length photons [22], the confounding contribution of extracranial scalp and skull layers cannot be neglected. For example, different pressures applied to the probe on the scalp can alter the superficial blood flow and contaminate the CBFi estimates [23]. Furthermore, the tissue-reduced scattering coefficient ( ${\mu }_s^{\prime }$) is an important parameter for the quantification of CBFi, but it is not constant across individuals or even anatomical locations. A 20% error in the scattering coefficient leads to a 20% error in the measured CBFi estimates [24], as predicted theoretically [13]. Variations from extracranial sources or optical tissue properties reduce the statistical power of the DCS measurements and hamper the ability to develop clinical thresholds for abnormal CBFi.

We have developed a novel method, time-domain diffuse correlation spectroscopy (TD-DCS), to address both of these limitations directly (Fig. 1). By employing a novel long coherence pulsed laser, we measure the photon time of flight (TOF) through the tissue and the DCS fluctuation dynamics simultaneously. By moving the DCS operation from continuous wave (CW) to the time domain, we exploit the many advantages of time-resolved reflectance spectroscopy (TRS), where a train of ultra-fast laser pulses is used to measure the TOF through the tissue and their distribution, the so-called temporal point-spread function (TPSF) [25–27]. This enables us, for the first time to our knowledge, to employ the time-gating strategies [28–30] used in TRS for DCS blood flow measurements and to realize improvements that are not possible when the two techniques are performed independently [31].

Fig. 1.

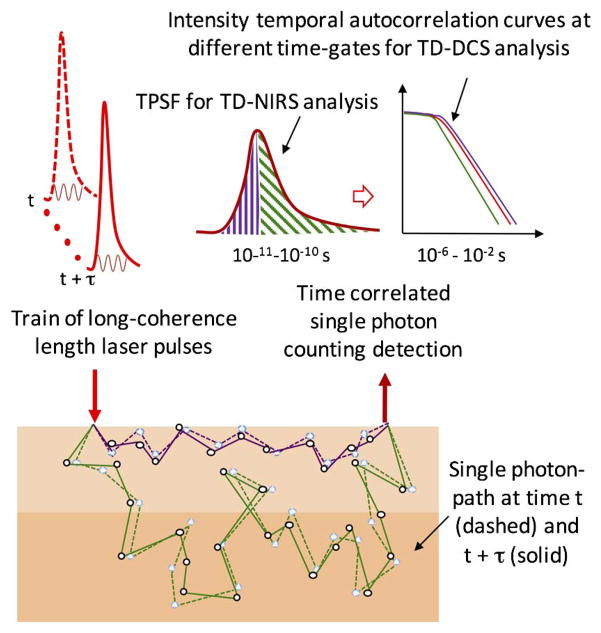
Conceptual illustration of time-resolved diffuse correlation spectroscopy. TD-DCS uses trains of long-coherence-length laser pulses to measure both TOFs and path length-dependent autocorrelation functions at the detector for improved determination of blood flow. The figure illustrates two different photon paths (purple and green) in highly scattering media for the light pulse at time t (dashed line) and at time t + τ (solid line). On average, light traveling in more superficial layers (purple paths) has a shorter TOF than light traversing deeper (green paths) into the tissue (time differences on the 10–100 ps time scale). The difference in the paths at t and t + τ is due to the motion of the red blood cells, which causes flow-dependent fluctuations in the detected intensity on the 10–1000 ns timescale. Time-tagging photons’ TOF (ps) and absolute arrival (ns) allows multiple analyses to be performed from the same data stream. In particular, photons can be separated by TOF into those traveling shorter (purple) or longer (green) paths through the tissue, enabling the calculation of the DCS correlation function from photons traveling to different depths in the tissue.

In our approach, time-correlated single-photon counting (TCSPC) is used to time-tag each detected photon with two values, the TOF from the source to the detector to obtain the TPSF, and the absolute arrival time to calculate the temporal autocorrelation function for DCS. By evaluating the correlation functions over different time gates of the TPSF, TD-DCS is able to differentiate between early and late arriving photons and evaluate the BFi at different depths within the tissue. Since the time gates are calculated from the TOF tag on every detected photon, multiple time gates are applied in parallel, which maximizes the utilization of the detected photons. Monte Carlo simulations of time-gated intensity autocorrelation functions under realistic conditions demonstrate an 80% improvement in cerebral sensitivity. Furthermore, the actual tissue optical scattering and absorption coefficients are also determined from the TPSF, improving the reliability of absolute CBFi comparisons within and between subjects.

We have constructed a TD-DCS prototype and performed measurements on liquid phantoms, which mimic human optical properties, and on small animals, demonstrating that our approach has the potential to be rapidly translated to humans and into a clinically viable, non-invasive, comprehensive cerebral hemodynamic monitoring method with significant advantages over the existing methods.

2. METHODS

A. Prototype TD-DCS

Since TRS and DCS are both photon-counting techniques with similar requirements for photon detection rates, a unified detection pathway common to both modalities is readily feasible. However, contradictory requirements for generating DCS correlation and TRS time-of-flight signals complicate efforts to combine the two techniques simultaneously. Typically, DCS is performed with a CW laser of a coherence length longer than the difference between the longest and shortest paths through the tissue to ensure the photons interfere fully at the detector. TRS typically utilizes ultra-fast illumination pulses of durations as short as picoseconds to minimize the convolution of the TOFs with the impulse response function of the device. However, the effective coherence length of these ultra-fast pulses is too short for the photons to remain correlated at the detector. We demonstrate theoretically and experimentally that both conditions can be relaxed by using pulses of tens to hundreds of picoseconds in width, which are sufficiently short for TRS measurements while maintaining a sufficient coherence length for DCS measurements. In particular, exploiting the recent advances in laser sources, detectors, and electronics, we have found practical solutions that enabled us to build the first TD-DCS device (Fig. 2) and, for the first time to our knowledge, to obtain the synergistic benefits achieved only when the TRS and DCS modalities are performed simultaneously.

Fig. 2.

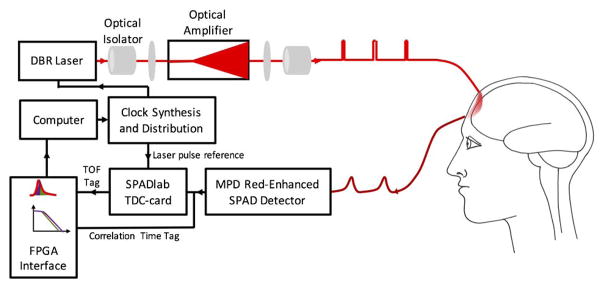
Schematic diagram of the novel TD-DCS device. We modified an 852 nm DBR laser to provide 150 ps pulses. We used an electrically pumped taper diode amplifier to amplify the peak optical power of the laser while maintaining its coherence length. Amplification enables adequate detected photon flux through the tissue. New red-enhanced SPAD detectors are used to detect photons with high sensitivity and time resolution. Custom TDCs are used to determine the TOF for the photons through the tissue. Finally, we built a custom FPGA board to collect the TOF tag from the TDC and merged it with the absolute arrival time used to calculate the correlation functions.

The key element of the new device is a picosecond pulsed laser source with a high peak power. Such a laser is not readily available commercially, but requires modifying commercial components. We developed a TD-DCS light source based on a two-stage laser master oscillator and amplifier (MOPA) configuration [32,33]. As a seed laser for the amplifier, we used a monolithic distributed Bragg reflector (DBR) laser at 852 nm with a CW coherence length of 10 m and 280 mW average optical power (PH852DBR280TS, Photodigm, Inc.). Optical pulses of durations ranging from 65 to 185 ps are created by electrically gain switching the seed laser using a picosecond pulsed laser driver (T165-9, Highland Technology, Inc.). We amplified the peak optical power to 2 W via stimulated emission from an electrically pumped taper diode amplifier (m2k-TA-0850-3000-DHP, m2k-laser GmbH). The wave vectors of the seed laser photons are exactly cloned by stimulated emission, so the amplifier output preserves the coherence and pulse properties of the source. A low seed power is used to avoid mode hopping or distortion of the pulse. To maximize the illumination duty cycle, we used repetition rates of 150 MHz, a rate at which the 4–5 ns-long TPSFs do not overlap. Using pulse durations of 150 ps, the average power is up to 50 mW, similar to those used in conventional DCS, and it is safe for human use when appropriately diffused over an area larger than 1 mm², according to the ANSI standard.

Other key features of this device include a new class of red-enhanced single-photon avalanche diode (SPAD) detectors [34,35] (PDM-R-FC, SPADlab, Politecnico di Milano and MPD Srl), which combine the high-temporal resolution (nominally 60 ps FWHM) needed for time gating with the high photon detection probability in the near-infrared necessary for penetrating centimeters of tissue. Each detector is paired with a time-to-digital converter (TDC) to measure the TOF by time-correlated single-photon counting (TCSPC) using custom TDC-cards [36] (SPADlab, Politecnico di Milano) with 20 ps RMS precision and conversion rates in excess of 5 MHz. Finally, we have built a custom field-programmable gate array (FPGA) board to pair the TDC result with photon arrival times from a counter inside the FPGA locked to the laser clock. Each detected photon is time tagged by two values: a fine resolution value for the time of flight from source to detector for the TPSF, and a coarse resolution value for the absolute arrival time to calculate the temporal correlation functions for DCS. We adopted the time-tagging strategy for DCS from fluctuation correlation spectroscopy, which enables time-gated separation of a single photon stream by fluorescence lifetime into separate autocorrelation functions [37,38]. For maximum flexibility in the analysis, the time gating and autocorrelations are currently not implemented in the FPGA, but are instead performed with software after the photon events are transferred from the FPGA.

B. Theoretical Considerations

Boas et al. [12] showed that the decay of the intensity autocorrelation function could be described by a correlation diffuse equation that is similar to the regular photon diffusion equation but replaces the traditional absorption coefficient (μ_a) with a dynamic absorption coefficient. That is, in the traditional photon diffusion equation, μ_a is replaced with the dynamic absorption term ${\mu }_a+2{\mu }_s^{\prime }{D}_B{k}_o^2\tau$ to obtain the correlation diffusion equation, where ${\mu }_s^{\prime }$ is the reduced scattering coefficient, D_B is the Brownian diffusion coefficient acting as an index of blood flow, k_o = 2πn/λ is the wavenumber of light, and τ is the correlation time. Thus, the solution of the time domain-correlation diffusion equation can be obtained from the traditional TD-NIRS solution by making this replacement. For a semi-infinite medium, the TD-DCS solution for the field temporal autocorrelation function, G₁, is thus

$$\begin{array}{l}{G}_1(\rho ,z=0,t)\\ =c{\left(\frac{3{\mu }_s^{\prime }}{4\pi ct}\right)}^{3/2}exp[-({\mu }_a+2{\mu }_s^{\prime }{D}_B{k}_o^2\tau )ct]exp\left(-\frac{3{\mu }_s^{\prime }{\rho }^2}{4ct}\right)\\ \times \left[exp\left(-\frac{3{\mu }_s^{\prime }{z}_o^2}{4ct}\right)-exp\left(-\frac{3{\mu }_s^{\prime }{(z_o+2z_b)}^2}{4ct}\right)\right],\end{array}$$ (1)

where t is the arrival time of the photons with respect to the laser pulse at t = 0, and ρ is the source-detector separation.

The normalized field temporal autocorrelation function is obtained by dividing G₁(τ) by G₁(τ = 0). By doing so, we obtain the path length-dependent normalized field temporal autocorrelation function,

$$g_{1s}(\tau ,s)=exp(-2{\mu }_s^{\prime }{D}_B{k}_o^{2}s\tau ),$$ (2)

where we have replaced the transit time of light through the tissue, t, with the path length of light through the tissue, s. This is an important equation as it indicates that the decay rate of the field temporal autocorrelation function increases linearly with the photon path length. This makes sense, as the decay rate increases with the number of dynamic scattering events and the number of dynamic scattering events increases linearly with the photon path length, as has been detailed extensively in the past [39–41]. Another important result of this equation is that the path length-dependent decay of g_1s(τ; s) is independent of the absorption coefficient of the medium.

For historical completeness, we note that g _1s(τ; s) was originally derived by first principles [39] and extended to CW-DCS by integrating over the distribution of detected photon path lengths, i.e.

$$g_1(\tau )=\int \mathrm{d}sP(s)g_{1s}(\tau ,s).$$ (3)

For light diffusion through a highly scattering medium, P(s) is given by the solution of the time-domain photon diffusion equation. For a semi-infinite medium, the solution of Eq. (3) would be equal to the solution of the correlation diffusion equation for CW-DCS given by Eq. (1).

Experimentally, with TD-DCS, we measure the path length-dependent normalized intensity autocorrelation function (g_2s), which is related to g_1s by

$$g_{2s}(\tau ,s)=1+\beta g_{1s}^2(\tau ,s),$$ (4)

where β accounts for the loss of coherence due to the spatial and temporal coherence of the detected light.

C. Photon Budget/SNR Considerations

The competing operational requirements of TRS and DCS are a challenge for sustaining a suitable detected photon flux for an acceptable signal-to-noise ratio (SNR). TRS requires short-pulsed illumination with maximum repetition rates limited by the duration of the TPSF to frequencies of up to 100–200 MHz, which decreases the measurement duty cycle by a factor of 50 with respect to CW-DCS operation. DCS requires small detection apertures similar in size to a single laser speckle, a requirement typically enforced by detection through single-mode fibers. The 5 μm mode field diameters of the single-mode DCS detector fibers are an order of magnitude smaller than the 50 μm core diameters of the graded-index multimode fibers typically used for TRS detection and have a corresponding smaller photon detection efficiency. In our approach, these factors are compensated by employing a pulsed light source with an average power two orders of magnitude greater than that typically used for TRS [42], and single-photon counting detectors highly sensitive to the near-infrared.

The effective detected photon flux is further reduced as a consequence of the time-gating scheme, which increases the sensitivity of the measurement to the deeper layers of the tissue. The increase in sensitivity is achieved by considering only the fraction of the detected photons that have traveled the longest distances through the tissue. This is performed by time gating the signals such that only late arriving photons in the TPSF are included in the calculation of the DCS correlation function. Since the unwanted photons outside of the gate are excluded, the flux contributing to the blood flow signal is reduced. In principle, the reduction in SNR from the reduced flux through a late gate can be overcome by decreasing the source-detector separation until the flux through the gate matches the level of the CW signal obtained at the original separation distance. The increase in sensitivity from the delayed time gate should be greater than the loss incurred from the shorter separation, yielding a net improvement in sensitivity with no loss in SNR. This strategy has been successfully employed for the null separation method in time-domain near-infrared spectroscopy (TD-NIRS) [28,43]. We have extended this concept to TD-DCS and demonstrated, with Monte Carlo simulations, that when the source-detector separation is reduced to 1 cm, a time gate starting at 1.5 ns maintains the same flux through the gate as a CW flux with a 3 cm separation. Under these conditions, not only do we maintain the same flux, we almost double the TD-NIRS and TD-DCS sensitivity to the brain compared to CW (See Supplement 1, Fig. S1). The Monte Carlo simulations suggest gated TD-DCS is feasible from the photon budget viewpoint and show, for the first time to our knowledge, that we can achieve greater sensitivity to the brain than to the scalp in human adults using DCS.

The signal-to-noise ratio for a DCS measurement is not only determined by the detected photon flux, but also depends on the amplitude of the correlation curve at zero correlation time τ = 0. Any reduction of this amplitude, known as β, results in a corresponding reduction in the SNR in the determination of the decay rate of the correlation function. β is largely determined by the maximum coherence of the light arriving at the detectors. The short illumination pulse required for TD-DCS reduces the coherence length of the source compared to the CW case. For a pulsed source, the greatest coherence length for a given pulse duration occurs when the optical pulse is transform limited. Transform-limited pulses represent the upper bound for the coherence length, given in this case by the product of the pulse temporal width and the speed of light. In practice, chirping and other phase artifacts in the pulse can reduce the coherence length below this limit. When the coherence length of DCS illumination is less than the difference between the longest and shortest photon path lengths through the tissue, β is reduced, as interference is diminished between photons with path-length differences greater than the coherence length. The dependency of β on the coherence for short-coherence CW illumination has been derived by Bellini [44] with a theory that we apply to short laser pulses and time gates. Bellini predicts that the contributions of photons to the correlation function are modulated by a Gaussian envelope with a width set by the coherence length. Photons with TOFs outside this envelope diminish the amplitude of the correlation function and should not be included in the gate. Furthermore, as predicted by Bellini, β depends on the distribution of path lengths within the gate, and further decreasing the gate width below the coherence length further decreases the path-length distribution and increases β. Hence, to maximize β, the gate duration should be smaller than the coherence length, and multiple time gates of shorter durations are preferred for TD-DCS rather than a single large monolithic time gate. Although each individual narrow gate has a lower β and photon flux than in the CW regime, fitting many gates simultaneously improves the SNR in the estimate of the blood flow index, since the photons in all of the gates are used in the estimation. Based on these considerations, we find that utilizing narrow time gates allows us to optimize the analysis of the TD-DCS measurements.

3. RESULTS

A. Measurements of β in Homogeneous Phantoms

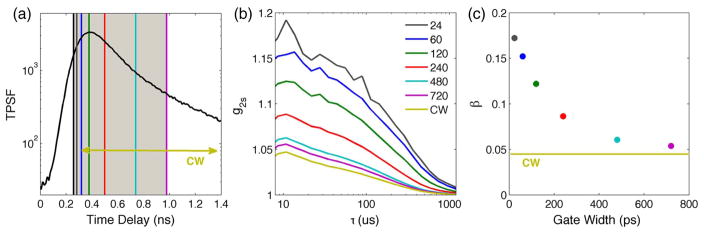
We experimentally show with measurements in a homogeneous turbid phantom the dependence of β on the time gate width and demonstrate that β increases when we decrease the time gate width below the coherence length of the pulsed laser (Fig. 3). When the measured path length-dependent normalized intensity temporal autocorrelation function (g_2s) [Eq. (4)] is calculated using every detected photon, regardless of the TOF, the result is equivalent to a CW measurement with a low coherence source. However, as the width of the time gate is decreased, β increases as the differences in path lengths of the photons arriving through the gate decrease with respect to the coherence length, and we obtain a path length-resolved estimate of the BFi.

Fig. 3.

TD-DCS measurements on a diluted milk phantom to demonstrate the β dependence on the time gate width. (a) TPSF with superimposed gates of different widths all starting right before the peak at t = 250 ps. The gate labeled CW is 3000 ps wide. (b) Measured path length-dependent normalized intensity temporal autocorrelation functions for the corresponding gates. (c) The correlation amplitude β as a function of the gate width for the corresponding gates. β increases with narrower time gates, as predicted by Bellini [44].

B. Measurement of Brownian Motion from the Path-Length-Dependent Correlation Function in a Homogeneous Phantom

By using short-duration time gates, the gated correlation curve is simply described by the path length-dependent normalized field temporal autocorrelation function g _1S without convolution over the path-length distribution needed in CW-DCS [39–41] [see Eqs. (2) and (3)]. Diffusion theory predicts that the decay rate of g_1S depends linearly on the path length of the light with the zero decay rate at the zero path length. We experimentally verified this in a homogeneous turbid phantom (Fig. 4). The x-intercept of the decay rate versus the path length corresponds to t_O, the temporal offset of the laser pulses in the experiment, and the slope is proportional to the product of the reduced scattering coefficient ( ${\mu }_s^{\prime }$) and the Brownian diffusion coefficient (D_B ). With TD-DCS, as the reduced scattering coefficient can be estimated from the TPSF, D_B can be obtained from the decay rate of individual path length-dependent autocorrelation functions or from the slope of the decay rate versus the path length.

Fig. 4.

Linear dependence of the decay rate of g_1S on the light path length in a homogeneous turbid phantom. (a) TPSF with superimposed twelve gates of fixed widths (48 ps) starting at different time delays. (b) Measured path length-dependent normalized field autocorrelation functions for the corresponding gates. (c) Slope of the field autocorrelation functions at the 12 gates as a function of the path length (i.e. time delay · speed of light in water). The small gray symbols correspond to g _1s slopes for overlapping gates 48 ps wide shifted 12 ps each. The linear fit is done considering all of the slopes, the intercept is t_o, and the slope is proportional to $D_B·{\mu }_s^{\prime }$. The resulting D_B is 1.0e⁻⁶ mm2/s, in close agreement with the D_B measured using a CW-DCS system (0.85e⁻⁶ mm²/s).

C. Measurements of Cerebral Blood Flow in Rats Under Hypercapnic Challenge

Transcranial measurements were performed in vivo on two anesthetized rats under mechanical ventilation with a source-to-detector separation of 5 mm. These experiments provide the opportunity to measure blood flow in a layered tissue. Correlation curves were calculated for narrow-width time gates around the peak of the TPSF [Fig. 5(a)]. In contrast to the homogeneous phantom, the decay rate of the path length-dependent correlation functions in the rats showed two regimes [Fig. 5(b)]. The decay rate for early arriving photons versus the path length exhibits a slower slope than later arriving photons. Assuming the effective scattering coefficient remains constant over the two regimes, the change in slope can be interpreted as different flows, with short path length photons reporting slower flow from the scalp and long path length photons reporting a faster flow from the brain. By analyzing the longer path length photons, the sensitivity of the blood flow measurement to the brain is increased. With CW-DCS, both short and long path lengths contribute to the detected signal and the discrimination of the cerebral signal is more challenging. In fact, multi-distance measurements and two-layer models requiring knowledge of the thickness of the superficial layer are needed to accurately separate superficial from deep signals for CW-DCS [45,46].

Fig. 5.

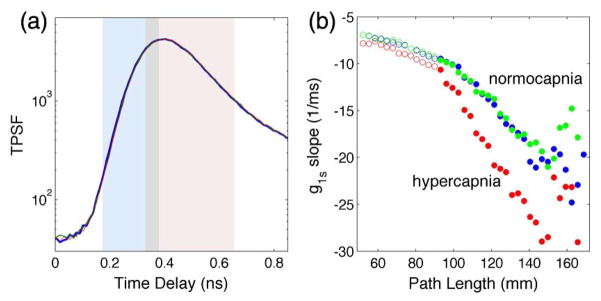
TD-DCS measures on a rat during two periods of normocapnia (blue and green lines) and hypercapnia (red line). (a) TPSF measured during normocapnia (blue and green) and hypercapnia. The curves are overlapping, suggesting negligible changes in tissue scattering and absorption with hypercapnia (red). The shaded areas span the range of the 37 gates 48 ps wide shifted 12 ps each. The gray shaded area indicates the gate at the border between the early (light blue) and late (pink) gates. (b) Slope of the field autocorrelation functions for the 37 gates as a function of the path length during normocapnia (blue and green symbols) and hypercapnia (red symbols). The open circles correspond to the 13 early gates; the closed circles correspond to the 24 late gates. The decay rate is much higher for late gates, and assuming a constant scattering coefficient across tissue layers, by using Eq. (2), we find the BF is three times higher in the brain than in the scalp and skull. When comparing the normocapnia and hypercapnia periods, the decay rate for early gates does not change significantly; instead, the decay rate for late gates increases with hypercapnia.

To investigate the sensitivity of the measurement to cerebral blood flow, we modulated the cerebral blood flow with a hypercapnic challenge of inspired CO₂. CO₂ differentially increases blood flow in the brain without increasing blood flow in the peripheral circulation [47]. Following an increase in end-tidal CO₂ from 35 to 45 mmHg, we verified that the slope of the path length-dependent decay rate for short path lengths did not change, while it increased for longer path lengths. The measured 55% increase in CBFi is consistent with the expected increase due to this hypercapnic challenge.

4. DISCUSSION AND CONCLUSION

We have introduced a novel method for simultaneous TD-NIRS and DCS measurements that synergistically exploits TD photon TOFs to calculate time-gated DCS correlation functions. Time gates for the correlation functions are implemented in parallel using TCSPC, enabling the use of narrow time gates without sacrificing photon efficiency. The width of the time gates has a larger influence in TD-DCS than in TD-NIRS, since the TD-DCS signal depends not only on the magnitude of the detected light, but also on its coherence. We show that narrow time gates of durations less than the duration of the laser pulse increase the amplitude of the correlation functions, which is essential for overcoming the loss in SNR due to the intrinsically lower coherence of a pulsed source. Furthermore, the narrow time gates result in a direct measurement of the path length-dependent correlation functions, which are obscured by a convolution with the path length distribution in conventional CW-DCS methods. The decay rates of path length-dependent correlation functions are independent of the optical absorption coefficient of the media, which has the potential to reduce uncertainty in the estimation of blood flow. Prior demonstrations of path length-resolved DCS relied on the selection of individual path lengths by nonlinear optics [41] or interferometry [48], limiting throughput and applicability for transcranial human measurements. Here, we have taken the novel approach of exploiting the path length-dependent correlation functions to improve the sensitivity of transcranial blood flow measurements to the brain by distinguishing the contributions from short and long paths. We overcame the conflicting requirements for pulse duration in TD-NIRS and DCS and designed and constructed a new pulsed MOPA source with sufficient coherence and power for DCS.

We have demonstrated that TD-DCS measurements are practical in live animals with a method feasible for human use. TD-DCS studies in human subjects will be possible once the device meets the electrical and optical safety standards for human use. In particular, safety interlocks must be devised for the two-stage source to the prevent release of the full optical power of the amplifier in the event of a rare catastrophic failure. With the performance characteristics of the current device, we estimate cerebral blood flow can adequately be measured in humans from 20 to 30 s of data acquisition.

The current system includes only one color source and two detectors, but it can be easily extended to multiple sources and multiple detectors. With additional sources of different colors, the TPSF measured with TD-DCS will provide quantification of oxygenated and deoxygenated hemoglobin concentrations and hemoglobin oxygenation, which, when combined with blood flow, will enable the estimation of oxygen consumption. Multiple detectors can be used to perform multi-distance measures or to increase SNR. Importantly, we will be able to exploit the large amount of independent information measured by this method and solve the global nonlinear optimization problem to improve accuracy in determining cerebral hemoglobin oxygenation, flow, and metabolism.