Significance
Understanding the principles governing self-assembly remains an important problem in statistical mechanics. We find, surprisingly, that general design principles for this challenging problem can be obtained by applying ideas from the field of stochastic thermodynamics to nonequilibrium self-assembly problems. Our central results constrain the set of possible configurations achievable under a nonequilibrium drive.
Keywords: self-assembly, nonequilibrium self-assembly, pattern formation, stochastic thermodynamics, second law of thermodynamics
Abstract
We consider an important class of self-assembly problems, and using the formalism of stochastic thermodynamics, we derive a set of design principles for growing controlled assemblies far from equilibrium. The design principles constrain the set of configurations that can be obtained under nonequilibrium conditions. Our central result provides intuition for how equilibrium self-assembly landscapes are modified under finite nonequilibrium drive.
The fields of colloidal and nanoscale self-assembly have seen dramatic progress in the last few years. Indeed experimental and theoretical work has elucidated design principles for the assembly of complex 3D structures (1–4). Most of these advances, however, are based on an equilibrium thermodynamic framework: the target configuration minimizes a thermodynamic free energy (5). Understanding the principles governing self-assembly and organization in far-from equilibrium systems remains one of the central challenges of nonequilibrium statistical mechanics (6–13). In this report, we show that design principles can be derived for a broad class of nonequilibrium driven self-assembly processes. Our central result constrains the set of possible configurations that can be achieved under a nonequilibrium drive.
Imagine a self-assembly process in which interactions among the various monomers are described by a set of energies . The ratio of association and dissociation rates is set by a combination of interaction energies and chemical potentials of the monomers. This generic setup is sufficient to describe many self-assembly processes. Examples include growth of crystals from solution by nucleation (9), growth dynamics of cell walls (14), growth of multicomponent assemblies (4), and growth dynamics of biological polymers and filaments (15). The chemical potential controls the growth of the assembly. If the chemical potential is tuned to a coexistence value such that the assembly grows at an infinitesimally slow rate, then the configuration of the assembly can be predicted by computing the equilibrium partition function and free energy appropriate to the set of interaction energies.
For values of the chemical potentials more favorable than the coexistence chemical potential, the assembly grows at a nonzero rate. In such instances, the growing assembly might not have sufficient time to relax to values characteristic of the equilibrium partition function (9, 16, 17). Defects are accumulated as the assembly grows at a nonzero rate. The time taken for a defect to anneal increases rapidly with distance from the interface of the growing configuration. Due to the resulting kinetically trapped states, the crystal can assume configurations very different from those representative of the equilibrium state (9, 16, 17).
By applying the second law of thermodynamics and the formalism of stochastic thermodynamics, we derive a surprising thermodynamic relation that is applicable to the above mentioned kinetic processes. This relation provides constraints on the configurations that are achievable in a nonequilibrium self-assembly process,
| [1] |
Here, is the size of the assembly at some instant of time, is the average rate of the growth of the assembly, is the variance of growth rate fluctuations, is probability distribution associated with a configuration in the growing assembly, is the equilibrium probability distribution obtained when the assembly is grown at an infinitesimally slow rate, and is the relative entropy between distributions and . The relative entropy is a measure of distinguishability between distributions and and is zero only when the two distributions are identical and is nonzero otherwise. We have assumed that the chemical potential of each monomer is the same and exceeds the equilibrium coexistence value by (i.e., the concentrations of monomers in solution exceeds the equilibrium concentration required for assembly). The chemical potential difference provides the nonequilibrium driving force for self-assembly.
An alternative and presumably more practical formulation of the central result is in terms of interaction energies. Imagine that we wish to generate compositions and structures in the growing assembly that are characteristic of a Hamiltonian different from the Hamiltonian governing the interactions between species . The central result places a bound on the minimum required excess chemical potential required to achieve such an assembly,
| [2] |
Here, is the free energy of particle system described by the Hamiltonian . The free energies differences can either be computed directly from simulations or estimated using an analytical framework.
Hence, given a chemical potential drive, Eqs. 1 and 2 constrain the set of allowed nonequilibrium structures found in the assembly. Alternately, given a target distribution or a target effective Hamiltonian , the central result sets a bound on the minimum chemical potential driving force required to achieve the assembly. If the chemical potentials of the monomers can be varied, in Eqs. 1 and 2 is replaced by an average, . The bound can be used to variationally optimize nonequilibrium driving forces that result in configurations characteristic of a desired effective energy landscape.
Thermodynamic Bounds for Nonequilibrium Self-Assembly
We now outline the derivation of the central result. This derivation is based on a generalization of the framework introduced in ref. 15. We begin by invoking one of the central results of stochastic thermodynamics (15, 18, 19) for a system in contact with a heat bath,
| [3] |
where is the entropy of the system, and is the entropy due to energy exchange between the system and environment. Eq. 3 is simply a statement of the second law of thermodynamics.
The growing self-assembling structure will be the thermodynamic system for the purposes of this report. The system is allowed to exchange material and energy with the environment. Let denote the probability distribution associated with the observing a system size and a microscopic configuration at a particular instant of time. The entropy of the system is given by configuration
| [4] |
where is the Boltzmann constant.
To proceed, we decompose the distribution as , where and are both normalized probability distributions. In performing the decomposition, we have assumed that the system has reached a steady state and that distribution of compositional fluctuations for a given system size and that is independent of the time . This decomposition is the main assumption behind our theoretical approach. With this assumption, we can associate an effective energy function with the distribution , . This definition of the effective energy function is simply a statistical construct (analogous to a potential of mean force). The energy function does not control the dynamics of the system. This effective energy function can have a form very different from that of the interactions specified by the interaction Hamiltonian .
Using this decomposition and the total average entropy production rate in a self-assembly process, can be written as
| [5] |
A closer investigation reveals that .*
Hence, to have a growing assembly with a distribution of compositional fluctuations characteristic of the energy function , the chemical potential difference must at least exceed ,
| [6] |
A simple algebraic manipulation allows us to rewrite Eq. 6 as Eq. 1. When the chemical potentials of the monomers contributing to the assembly are unequal, is replaced by the average excess chemical potential for the growing assembly, .
The structure of Eq. 6 is reminiscent of the variational Gibbs–Bogoliubov–Feynman inequality generalized for nonequilibrium systems. As such, Eq. 6 can be applied to obtain bounds on optimal nonequilibrium driving forces that can maximize the yield of desired configurations. Finally, our central results show how the average entropy production rate in a self-assembly process is coupled to the compositional fluctuations in the self-assembled system. Recent work by Barato and coworkers (20, 21, 22) has demonstrated that the entropy production rate bounds the fluctuations of various dynamical currents generated in a nonequilibrium processes. In the next section, using a model system, we demonstrate that the bound imposed by the entropy production rate on cumulants of fluctuations of the growth rate of the assembly lead to a set of tighter design principles,
| [7] |
where denotes the average rate of growth of the assembly, denotes the variance in the growth rate of the assembly.
We will now illustrate the result on two space-filling, lattice-based model systems. In each example, the distribution of compositional fluctuations in the growing assembly is modified when the assembly is grown at a nonzero rate. Our bound acts as a design principle and provides intuition into how the equilibrium landscape of compositional fluctuations is modified under a nonequilibrium drive. We emphasize that although these examples focus on distributions of compositional fluctuations, our central results are valid more generally and also apply to statistics of structural fluctuations (9). We choose the lattice-based models as examples because they are analytically tractable and serve to illustrate the utility of Eqs. 6 and 7.
Exactly Solved Model of Nonequilibrium Polymer Assembly
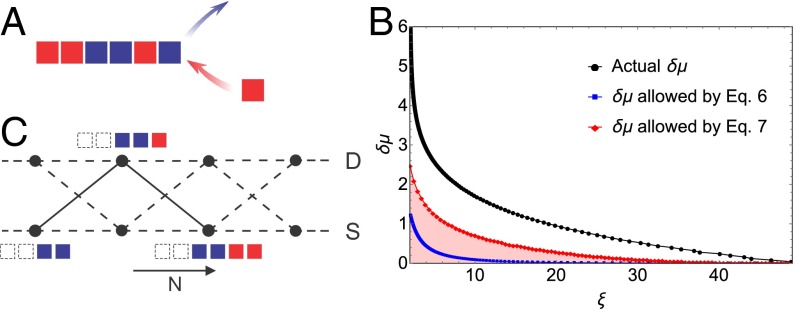
As our first example, we will consider a model of 1D polymer assembly (Fig. 1A). For simplicity, the system that we are studying will contain two types of monomers with equal concentrations. In scenarios where the polymer is nucleated from a solution, the concentration of monomers or their chemical potential provides the nonequilibrium driving force for the assembly. We allow only nearest-neighbor interactions between the monomers in the assembly. If the average length of pure monomer domains in a polymer at equilibrium is , our results impose a constraint on the excess chemical potential required to achieve assemblies in which the average length of pure monomer domains is (SI Appendix),
| [8] |
where is the excess chemical potential, and we have assumed that the two monomers have the same chemical potential. The compositions in such an assembly differ from those obtained close to equilibrium (), when the polymer grows at an infinitesimally slow rate. Our thermodynamic bound does not depend on the kinetic model chosen. Furthermore, as discussed previously, in cases with unequal chemical potentials, Eq. 8 can be generalized by simply replacing with the average excess chemical potential.
Fig. 1.
Application of the bounds to 1D fiber growth model. (A) Schematic of the 1D polymer growth process. The polymer is assembled from a bath composed of two monomer types (red and blue). (B) Schematic of the effective Markov state model. This Markov state model resolves the nature of terminal bond in the self-assembled system (vertical rungs), bond between like monomers and bond between unlike monomers, and the number of particles in the self-assembled system (horizontal axis). The rates of transitions between the mesoscopic states resolved in this effective model depend on the composition of the assembly and are described in SI Appendix. We demonstrate that this effective model captures the dynamics and compositional fluctuations of the self-assembly process. (C) Comparison between the lower bounds of obtained from Eqs. 6 and 7 and the value of obtained from simulations. The equilibrium domain length, , for this plot is 50. The red shaded region represents the region that is disallowed by Eq. 7. Our thermodynamic bounds are valid and, in spite of their minimal nature, do reasonable job of predicting the compositional fluctuations in the assembly.
We theoretically verify the bound for the polymer assembly problem by mapping the dynamics of the self-assembly process onto an effective Markov state model (Fig. 1B). This effective model resolves the terminal bond in the self-assembled system (vertical rungs) and the number of particles in the self-assembled system (horizontal axis). The details of the various transition rates between the mesoscopic states are provided in SI Appendix, in which we also demonstrate that the Markov state caricature accurately describes the dynamics and compositional fluctuations of the self-assembly process. Furthermore, we demonstrate that the expression for the entropy production rate, computed from this Markov state caricature indeed equals
| [9] |
where is defined in Eq. 8. This calculation verifies the thermodynamic bound and its underlying assumptions for the 1D polymer-assembly model.
The Markov state caricature allows us to map the self-assembly process onto the dynamics of a random walker on a graph. In SI Appendix, we verify that the effective mean field Markov state caricature manages to reasonably describe even the second cumulant of fluctuations in the growth rate. Barato and coworkers (20, 21, 22) have recently demonstrated that fluctuations of various dynamical currents in such Markov state process are bound by the entropy production rate. As demonstrated in SI Appendix, we adapt these bounds to show that
| [10] |
where is the average growth rate of the polymer, and is the variance of the growth rate.
In Fig. 1C, we demonstrate the two thermodynamic bounds in Eqs. 8 and 10 for a particular kinetic model of polymer growth (23). Including information from higher-order cumulants does indeed strengthen the bound. These demonstrations prove the theoretical validity and effectiveness of our bound and pave the way for applications to more complex systems.
Specifically, for systems with more than two monomer types or for monomers with longer ranged interactions, it is more convenient to express in terms of the actual and effective interaction Hamiltonians. Although effective, Markov state caricatures for such systems can be complex and analytically intractable, our thermodynamic bounds are easily accessible and provide very useful intuition for the compositional fluctuations of the nonequilibrium assembly. We now demonstrate these ideas by considering a 2D analog of the fiber growth process described above (ref. 24 and Fig. 2A).
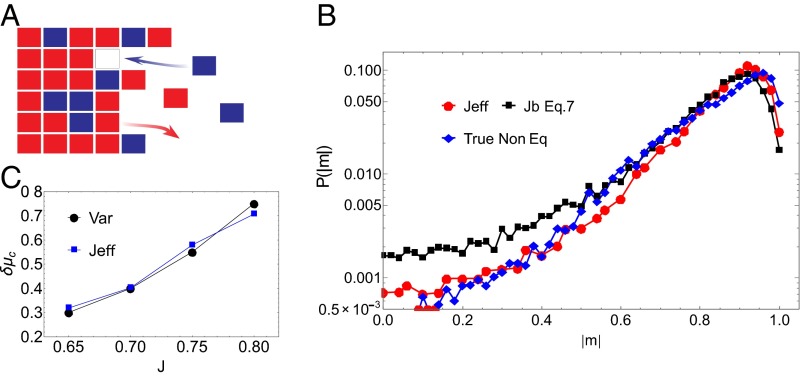
Fig. 2.
Application of the bounds to the nonequilibrium 2D growth process. (A) We assemble a 2D configuration from a monomer bath containing red and blue blocks. The energy of interaction between similar monomers is , whereas that between dissimilar monomers is . As discussed in the main text, when the assembly is grown at equilibrium, the statistics of compositional fluctuations in the assembly are equivalent to that of an Ising magnet with coupling constant . (B) We compare the value of critical driving force obtained by computing using the Onsager solution, as described in the main text, with that obtained by computing the variance of magnetization fluctuations as described in ref. 24. The agreement between the two estimates confirms that the system has anomalously large fluctuations at the nonequilibrium critical driving force we identify. (C) We calculate the probability of magnetization from the nonequilibrium simulations and compare it with distribution obtained by sampling an Ising model at and from Eq. 7. These data were obtained for and . The system grows rapidly for these parameters as evidenced by the value of computed for these parameters. We expect the system to be far from linear response. The close agreement between the distribution predicted by and the nonequilibrium distribution, even far from the mean, suggest that our theoretical bound indeed accurately captures the fluctuations in this nonequilibrium system.
Nonequilibrium 2D Self-Assembly Process
As a natural generalization of the 1D polymer model, we imagine a 2D assembly growing at one end as described in Fig. 2A. This model was first introduced in ref. 24. We again imagine two monomer types with interactions between like monomers set by the energy scale and interactions between unlike monomers set by the energy scale . The details of the kinetic model are described in Methods. When the chemical potential is set to the intensive equilibrium free energy of the assembly, , the assembly does not grow on average. Assigning spin to the red monomers and spin to the blue monomers, the statistics of the compositional fluctuations in the equilibrium assembly are equivalent to that of an Ising model with coupling constant . We will work in regimes where the coupling constant is above the critical coupling constant of the Ising model, .
We are interested in the statistics of compositional fluctuations because the growth rate of the assembly is tuned by changing the chemical potential. In ref. 24, Whitelam et al. demonstrated that by tuning the chemical potential driving force, this system can be positioned at a nonequilibrium critical point even though the coupling constant is higher than . Given these nontrivial thermodynamic properties, this nonequilibrium 2D model system is ideal for illustrating how our bounds can be effective even in conditions with large correlation lengths. Specifically, we will demonstrate that our bounds, in particular in Eq. 7, can capture the renormalization of the coupling constant due to the nonequilibrium driving force with surprising accuracy. This bound works even close to the nonequilibrium critical point.
We begin by assuming that the compositional fluctuations in the growing assembly can be described by an effective nearest-neighbor coupling constant . We performed simulations in which we extracted the value of as a function of the excess chemical potential by analyzing compositional fluctuations in the growing assembly. We computed the average magnetization inside the growing assembly and used the Onsager solution for the 2D Ising model to extract . As the increases, the decreases and will eventually reach the critical value of the 2D Ising model. To confirm that the value of the critical driving force, computed using the Onsager method above is indeed the same one as the critical driving force discovered in ref. 24, we also determine following the method described in ref. 24. We computed the variance of magnetization fluctuations as a function of and identify as the point at which the variance of magnetization fluctuations shows a pronounced peak indicating anomalously large correlation lengths. In Fig. 2B, we compare the estimate of obtained using both the procedures and find that they match, which implies that the nonequilibrium critical point that we identity by studying the average magnetization does indeed have large correlation lengths.
In Fig. 2C, we calculate the probability of magnetization from a nonequilibrium system simulated at and . The system grows rapidly for these parameters, as evidenced by the value of computed for these parameters (Fig. 3). We expect the system to be far from linear response for these parameters. We compare the nonequilibrium magnetization distribution to the distributions obtained by sampling magnetization fluctuations in an equilibrium Ising model with coupling constant . The agreement between the nonequilibrium distribution and distribution corresponding to again confirms that our method for extracting accurately captures magnetization fluctuations in the system.
Fig. 3.
Comparison between from the simulations and from Eqs. 6 and 7 for different values of : (A), (B), (C), and (D).
Next, using Eq. 7, we compute the bound for these parameters. We compare the nonequilibrium distribution to the distribution obtained by sampling an Ising model at . The close agreement between the observed and predicted probability distributions, even far from the mean, suggests that our theoretical bound indeed accurately captures the fluctuations in this nonequilibrium system. To the best of our knowledge, we are not aware of any other thermodynamic theory that is able to make such detailed predictions.
In Fig. 3, we plot and for various values of the coupling constant and various values of the driving force . We computed the bounds from both Eqs. 6 and 7. The bound obtained from Eq. 6 does a reasonable job of predicting the effective coupling constant for low nonequilibrium driving forces. Including information about higher order cumulants using Eq. 7 again improves the bound and provides a close to accurate estimate of the effective coupling constant . Near equilibrium, the starts to coincide with the , as expected. For intermediate values of the driving force, the bounds start to deviate away from the effective value predicted by simulations. Strikingly, the agreement between the bound predicted by Eq. 7 and the effective value improve dramatically close to the critical regime when the nonequilibrium driving forces are substantial. We anticipate that this improved agreement might be due to the nature of entropy production fluctuations. In particular, the bound in Eq. 7 is saturated when the underlying entropy productions fluctuations in the system are Gaussian, even if the nonequilibrium driving forces are high (20). Recent work has found that the distribution of entropy production in an Ising model with a time dependent magnetic field is Gaussian to a good approximation even close to criticality (25). Further studies need to be performed to verify the Gaussian hypothesis in our system. This will be a topic of future work.
The close agreement between the bounds predicted by theory and the effective value computed from simulations, even in the critical regime, is surprising given the minimal nature of our theory. The results illustrate the utility of our central relations as design principles for nonequilibrium self-assembly.
Applications and Conclusion
Using the framework of stochastic thermodynamics and physically justified approximations, we have put forward a general predictive framework for nonequilibrium self-assembly. Our central results, Eqs. 6 and 7, are built around a simple and intuitive expression for entropy production in nonequilibrium self-assembly process. This expression relates compositional fluctuations in the self-assembled system to the chemical potential excess driving the assembly process. Given a set of programmed interactions between monomers and configurations specified by the energy function , our central result constrains the set of allowed configurations that can be obtained under a nonequilibrium drive. A unique feature of our result is its thermodynamic character: the bound does not depend on the details of the kinetic model chosen. Many recent theoretical and experimental studies have postulated that nonequilibrium protocols can potentially be used to overcome bottlenecks and enhance the yield of desired self-assembled configurations (26). Our framework is ideally suited to verify these postulates and explore connections between energy consumption and improved yield of target configurations.
We anticipate that our results will find important applications in studies of crystal nucleation (17), self-assembly of metal organic frameworks (27), nonequilibrium roughening transitions, and the synthesis of nanocrystals using DNA and other biopolymers as building materials. In all these instances, the assembly process can occur far from equilibrium depending on the effective chemical potentials imposed. Coarse-grained interaction energies or force fields are available that parametrize and describe the equilibrium structures in the above mentioned problems (3). These force fields play the role of defined in this work. Motivated by the results from the nonequilibrium 2D Ising model where our bounds were able to predict how the compositional fluctuations were modified by the nonequilibrium drive with surprising accuracy, even close to the nonequilibrium critical point, we expect that our results can identify the nonequilibrium driving forces required to generate configurations characteristic of a different interaction Hamiltonian .
We do note that both the examples used in this report to illustrate our results are based on space-filling lattice models, whereas the proposed applications detailed in the paragraph above have both compositional and structural fluctuations. Nonetheless, encouraged by the performance of our bounds in the nonequilibrium Ising model, we anticipate our results will be useful in above mentioned applications involving both compositional and structural fluctuations. Indeed, we expect that our results will be similarly applicable to nonequilibrium generalization of Ising models with structural fluctuations (28). These so-called elastic Ising models exhibit structural and compositional phase transitions and have been used in studies of structural transitions in alloys.
A mismatch of chemical potentials provides the nonequilibrium driving force in Eq. 6. Our results also apply to nonequilibrium error-correction mechanisms for biopolymer assembly in which the assembly process is driven by consumption of energy rich ATP/GTP molecules. In such instances, the term is replaced by the appropriate average energy consumption rate. In these biophysical applications, the nonequilibrium driving force generates configurations that posses correlations greater than those in equilibrium. Although such fibers are not achievable with the kinetic protocols described above, the thermodynamic nature of our bounds allows their application to these biophysical error correction mechanisms. Indeed, Sartori et al. (29) have recently derived a similar bound for a specific model of kinetic proofreading. Our general thermodynamic bounds, particularly that in Eq. 7, can elucidate the tradeoffs between speed accuracy and energy consumption in such nonequilibrium biochemical replication processes.
Methods
In our 1D polymer growth simulation, we consider a polymer growing in a bath containing two types of monomer. The concentrations of both types are equal to c. The chemical potential is related to the concentration c by the relation: . The nearest-neighbor monomers are allowed to interact with energy if they are the same and with energy if they are different. We perform kinetic Monte Carlo simulations in which monomers are added to the polymer with the rate c (or ). Monomers are allowed to dissociate from the polymer with the rate (i here can be either s or d), which depends solely on the composition of the fiber. is set to 1. We use to denote the probability that a particular bond in the assembly is between two like monomers. It is related to the correlation length by .
The simulations for the nonequilibrium 2D assembly problem follow the same rules as in the 1D case. However, we used the standard Metropolis Monte Carlo algorithms for the 2D case. We also impose constraints on the Ising model so that there are no bubbles inside the assembly and so that the size of the maximum overhang is restricted to three cells. The results of the 2D Ising model are similar and can be found in SI Appendix.
For the purposes of computing the effective coupling constant , we labeled the red particles as spin up and blue particles as spin down . We then computed the average per unit magnetization in the growing assembly and used the Onsager solution to extract the value of . This procedure is only valid for .
Supplementary Material
Acknowledgments
We gratefully acknowledge useful discussions with Dmitri Talapin and David Limmer and support from The University of Chicago.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. M.P.B. is a Guest Editor invited by the Editorial Board.
*The proof for this statement is simple once we realize that . Using Jensen’s inequality, we obtain the bound on .
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1609983113/-/DCSupplemental.
References
- 1.Ke Y, Ong LL, Shih WM, Yin P. Three-dimensional structures self-assembled from DNA bricks. Science. 2012;338:1177–1183. doi: 10.1126/science.1227268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jones MR, Seeman NC, Mirkin CA. Programmable materials and the nature of the DNA bond. Science. 2015;347:1260901. doi: 10.1126/science.1260901. [DOI] [PubMed] [Google Scholar]
- 3.Reinhardt A, Frenkel D. Numerical evidence for nucleated self-assembly of DNA brick structures. Phys Rev Lett. 2014;112:238103. doi: 10.1103/PhysRevLett.112.238103. [DOI] [PubMed] [Google Scholar]
- 4.Hedges LO, Mannige RV, Whitelam S. Growth of equilibrium structures built from a large number of distinct component types. Soft matter. 2014;10:6404–6416. doi: 10.1039/c4sm01021c. [DOI] [PubMed] [Google Scholar]
- 5.Hormoz S, Brenner MP. Design principles for self-assembly with short-range interactions. Proc Natl Acad Sci USA. 2011;108:5193–5198. doi: 10.1073/pnas.1014094108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Weber SC, Brangwynne CP. Getting RNA and protein in phase. Cell. 2012;149:1188–1191. doi: 10.1016/j.cell.2012.05.022. [DOI] [PubMed] [Google Scholar]
- 7.Mann S. Self-assembly and transformation of hybrid nano-objects and nanostructures under equilibrium and non-equilibrium conditions. Nat Mater. 2009;8:781–792. doi: 10.1038/nmat2496. [DOI] [PubMed] [Google Scholar]
- 8.Whitelam S, Jack RL. The statistical mechanics of dynamic pathways to self-assembly. Annu Rev Phys Chem. 2014;66:143–163. doi: 10.1146/annurev-physchem-040214-121215. [DOI] [PubMed] [Google Scholar]
- 9.Sanz E, Valeriani C, Frenkel D, Dijkstra M. Evidence for out-of-equilibrium crystal nucleation in suspensions of oppositely charged colloids. Phys Rev Lett. 2007;99:055501. doi: 10.1103/PhysRevLett.99.055501. [DOI] [PubMed] [Google Scholar]
- 10.Rabani E, Reichman DR, Geissler PL, Brus LE. Drying-mediated self-assembly of nanoparticles. Nature. 2003;426:271–274. doi: 10.1038/nature02087. [DOI] [PubMed] [Google Scholar]
- 11.Ursell TS, et al. Rod-like bacterial shape is maintained by feedback between cell curvature and cytoskeletal localization. Proc Natl Acad Sci USA. 2014;111:E1025–E1034. doi: 10.1073/pnas.1317174111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Levandovsky A, Zandi R. Nonequilibirum assembly, retroviruses, and conical structures. Phys Rev Lett. 2009;102:198102. doi: 10.1103/PhysRevLett.102.198102. [DOI] [PubMed] [Google Scholar]
- 13.Hagan MF, Chandler D. Dynamic pathways for viral capsid assembly. Biophys J. 2006;91:42–54. doi: 10.1529/biophysj.105.076851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jiang H, Si F, Margolin W, Sun SX. Mechanical control of bacterial cell shape. Biophys J. 2011;101:327–335. doi: 10.1016/j.bpj.2011.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Andrieux D, Gaspard P. Nonequilibrium generation of information in copolymerization processes. Proc Natl Acad Sci USA. 2008;105:9516–9521. doi: 10.1073/pnas.0802049105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kim AJ, Scarlett R, Biancaniello PL, Sinno T, Crocker JC. Probing interfacial equilibration in microsphere crystals formed by DNA-directed assembly. Nat Mater. 2009;8:52–55. doi: 10.1038/nmat2338. [DOI] [PubMed] [Google Scholar]
- 17.Auer S, Frenkel D. Suppression of crystal nucleation in polydisperse colloids due to increase of the surface free energy. Nature. 2001;413:711–713. doi: 10.1038/35099513. [DOI] [PubMed] [Google Scholar]
- 18.Esposito M, Van den Broeck C. Three faces of the second law. I. Master equation formulation. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82:011143. doi: 10.1103/PhysRevE.82.011143. [DOI] [PubMed] [Google Scholar]
- 19.Schnakenberg J. Network theory of microscopic and macroscopic behavior of master equation systems. Rev Mod Phys. 1976;48:571. [Google Scholar]
- 20.Barato AC, Seifert U. Thermodynamic uncertainty relation for biomolecular processes. Phys Rev Lett. 2015;114:158101. doi: 10.1103/PhysRevLett.114.158101. [DOI] [PubMed] [Google Scholar]
- 21.Pietzonka P, Barato AC, Seifert U. Universal bounds on current fluctuations. Phys Rev E. 2016;93:052145. doi: 10.1103/PhysRevE.93.052145. [DOI] [PubMed] [Google Scholar]
- 22.Gingrich TR, Horowitz JM, Perunov N, England JL. Dissipation bounds all steady-state current fluctuations. Phys Rev Lett. 2016;116:120601. doi: 10.1103/PhysRevLett.116.120601. [DOI] [PubMed] [Google Scholar]
- 23.Whitelam S, Schulman R, Hedges L. Self-assembly of multicomponent structures in and out of equilibrium. Phys Rev Lett. 2012;109:265506. doi: 10.1103/PhysRevLett.109.265506. [DOI] [PubMed] [Google Scholar]
- 24.Whitelam S, Hedges LO, Schmit JD. Self-assembly at a nonequilibrium critical point. Phys Rev Lett. 2014;112:155504. doi: 10.1103/PhysRevLett.112.155504. [DOI] [PubMed] [Google Scholar]
- 25.Gingrich TR, Rotskoff GM, Crooks GE, Geissler PL. Near-optimal protocols in complex nonequilibrium transformations. Proc Natl Acad Sci USA. 2016;113:10263–10268. doi: 10.1073/pnas.1606273113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.England JL. Dissipative adaptation in driven self-assembly. Nat Nanotechnol. 2015;10:919–923. doi: 10.1038/nnano.2015.250. [DOI] [PubMed] [Google Scholar]
- 27.Sue ACH, et al. Heterogeneity of functional groups in a metal–organic framework displays magic number ratios. Proc Natl Acad Sci USA. 2015;112:5591–5596. doi: 10.1073/pnas.1416417112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shokef Y, Souslov A, Lubensky TC. Order by disorder in the antiferromagnetic Ising model on an elastic triangular lattice. Proc Natl Acad Sci USA. 2011;108:11804–11809. doi: 10.1073/pnas.1014915108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sartori P, Pigolotti S. Thermodynamics of error correction. Phys Rev X. 2015;5:041039. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.