Significance
The magnitude and timing of Antarctic temperature change through the last deglaciation reveal key aspects of Earth’s climate system. Prior attempts to reconstruct this history relied on isotopic indicators without absolute calibration. To overcome this limitation, we combined isotopic data with measurements of in situ temperatures along a 3.4-km-deep borehole. Deglacial warming in Antarctica was two to three times larger than the contemporaneous global temperature change, quantifying the extent to which feedback processes amplify global changes in polar regions, a key prediction of climate models. Warming progressed earlier in Antarctica than in the Northern Hemisphere but coincident with glacier recession in southern mountain ranges, a manifestation of changing oceanic heat transport, insolation, and atmospheric CO2 that can further test models.
Keywords: climate, paleoclimate, Antarctica, glaciology, temperature
Abstract
The most recent glacial to interglacial transition constitutes a remarkable natural experiment for learning how Earth’s climate responds to various forcings, including a rise in atmospheric CO2. This transition has left a direct thermal remnant in the polar ice sheets, where the exceptional purity and continual accumulation of ice permit analyses not possible in other settings. For Antarctica, the deglacial warming has previously been constrained only by the water isotopic composition in ice cores, without an absolute thermometric assessment of the isotopes’ sensitivity to temperature. To overcome this limitation, we measured temperatures in a deep borehole and analyzed them together with ice-core data to reconstruct the surface temperature history of West Antarctica. The deglacial warming was C, approximately two to three times the global average, in agreement with theoretical expectations for Antarctic amplification of planetary temperature changes. Consistent with evidence from glacier retreat in Southern Hemisphere mountain ranges, the Antarctic warming was mostly completed by 15 kyBP, several millennia earlier than in the Northern Hemisphere. These results constrain the role of variable oceanic heat transport between hemispheres during deglaciation and quantitatively bound the direct influence of global climate forcings on Antarctic temperature. Although climate models perform well on average in this context, some recent syntheses of deglacial climate history have underestimated Antarctic warming and the models with lowest sensitivity can be discounted.
From the Last Glacial Maximum (LGM) around 21 ka to the middle of the Holocene, increased greenhouse gas concentrations and reduced reflectivities of the surface and atmosphere directly increased the uptake of energy to Earth’s climate system by about 7 (1–3) and warmed the surface by 3–6 on average (4–7). Although contributing little to this global average because of the comparatively small area involved, the warming in polar regions holds particular interest. In addition to driving changes of ice sheets, permafrost, and hydrology and modulating oceanic and atmospheric circulations, polar warming partly controlled both the evolution of surface reflectivity and the transfer of carbon dioxide from ocean to atmosphere and hence the climate forcing itself. Further, reconstructions of polar warming during deglaciation permit quantification of one key prediction of climate theory—that feedback processes amplify temperature changes in polar regions relative to the global average (4, 8, 9), a phenomenon referred to as polar amplification. Arctic data reveal a warming three to four times the global average based on a wide variety of indicators (6), including combined analyses of ice-core data and borehole temperatures (10, 11). Limited available constraints suggest a smaller but still amplified Antarctic warming, roughly 1.5 to 2.5 times greater than the global average (6, 12). This Antarctic estimate, however, derives from the isotopic composition of ice measured in cores. The scaling between ice isotopic composition and temperature depends on a great many factors (section 15.5 in ref. 13), such as the seasonal timing of snowfall and rate-dependent fractionations in clouds, that remain poorly known and are expected to vary with time. Moreover, the low accumulation rates at East Antarctic core sites have precluded convincing quantifications of the isotopic thermometers using independent information from borehole temperatures, the most direct legacy of past climate. One Antarctic study used such information (14), but the small accumulation rate at the site meant that diffusive heat transport greatly dominated advection, rendering the method imprecise.
Here we present a reconstruction of West Antarctic temperature history from the site of the West Antarctic Ice Sheet Divide ice core (WDC) (15, 16). This site is uniquely suitable for analyses using borehole temperatures, given the combination of thick ice and high snow accumulation rate, together with the wealth of information provided by the 68-ky core record. Elsewhere, similarly favorable conditions prevail only in central Greenland (10).
Reconstruction
We measured temperatures in the 3.4-km-deep WDC borehole (Materials and Methods). The temperature profile reveals a direct thermal remnant of the deglacial transition and subsequent Holocene temperature changes (Fig. 1).
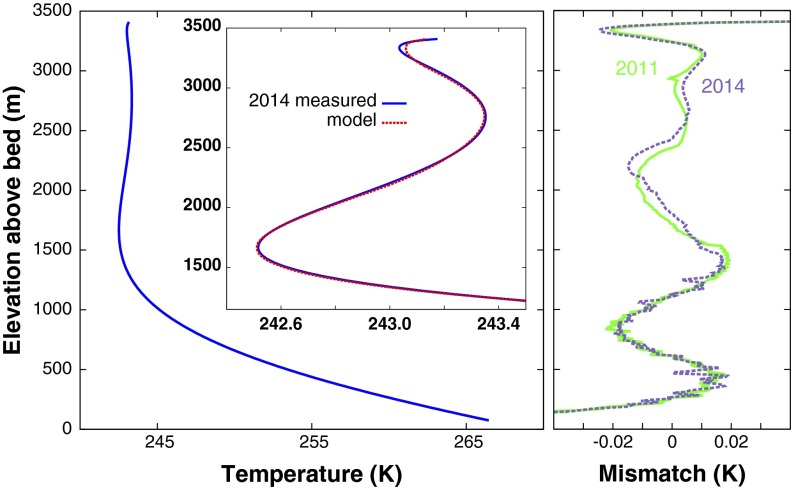
Fig. 1.
Observed and modeled temperatures in the WAIS Divide borehole. (Left) Ice temperature profile observed in 2014. At this scale the model and measurements are indistinguishable, as are the profiles measured in 2011 and 2014. Left Inset expands the upper portion and compares the model to the 2014 observation. The cold region centered around 1,700 m is a remnant of the last glacial climate. (Right) Difference between observed temperatures and optimal models (model minus observed), for both the 2011 and 2014 measurements.
Because of diffusive smoothing, borehole temperatures contain information about only long-term averages of climatic temperatures (SI Reconstruction Strategy). Our analysis therefore incorporates two additional sources of thermometric information from the core: the deuterium isotopic composition of ice () and the nitrogen isotopic composition of trapped gas () (SI Ice-Isotopic Data and SI Nitrogen-Isotopic Data and Fig. S1). Although not perfect thermometers, isotopic data provide a constraint based on temperature-dependent physical processes, and their use avoids a priori assumptions about climate variability that are otherwise required for interpreting borehole temperatures. The temperature () dependence of arises from atmospheric distillation processes (17) and, despite potential complexities, is usually treated as a linear relationship: . Due to gravitational settling of heavy gases, measures the thickness of firn (18, 19), the 50- to 120-m-deep porous layer of consolidated snow that blankets the ice-sheet surface. Firn densification proceeds at a rate dependent on both temperature and loading, so firn thickness depends on both temperature and accumulation rate (20, 21). Higher temperatures and slower accumulation both produce thinner firn, reducing .
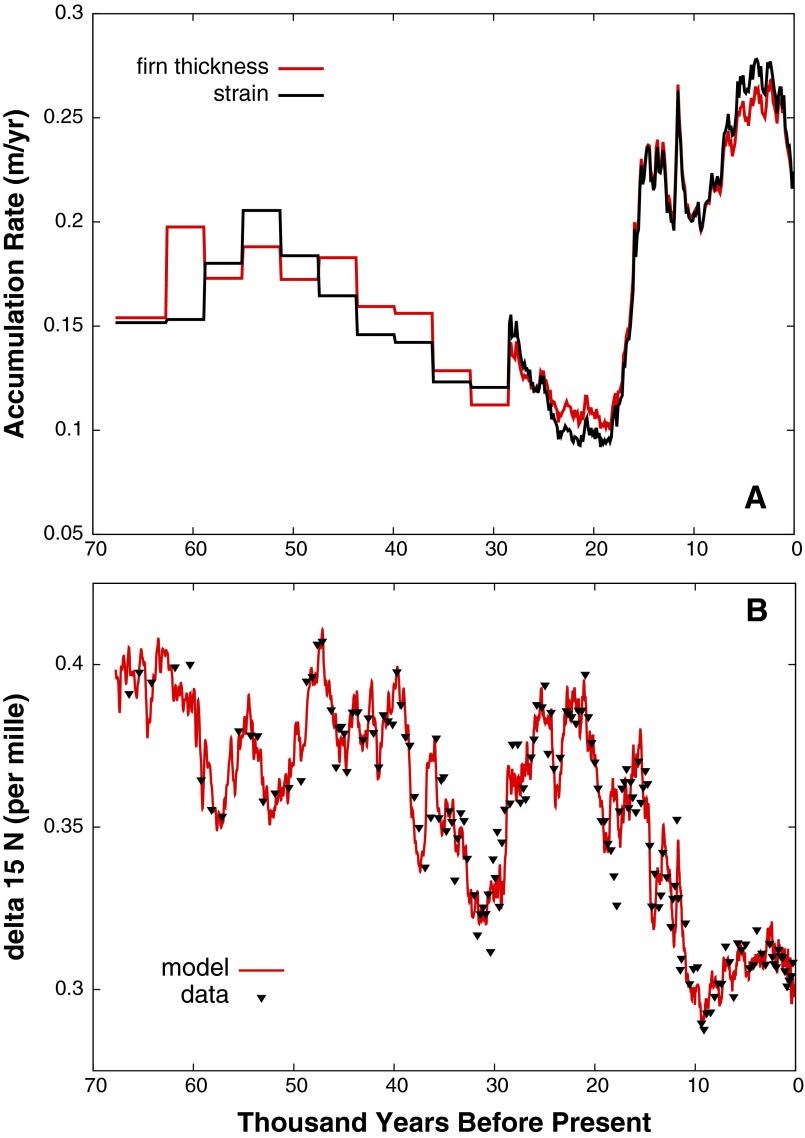
Fig. S1.
(A) Comparison of accumulation rates derived by correcting observed layer thicknesses for strain (black) and by using the reconstructed temperature and data together with the firn densification model (red). Both curves are for the optimized Eq. 2 (main text) plus perturbations. Versions for the optimized model without perturbations are nearly identical. (B) Comparison of data with model for the same case (16, 47).
To determine the surface temperature history , we optimized the match between temperatures measured in the borehole and those calculated with a numerical model of heat transfer driven by various scenarios as a boundary condition (Materials and Methods and SI Calculation of Temperatures vs. Depth). To start, we filtered the deuterium ice-isotopic record () to remove high-frequency variability. Using the time derivative of this filtered history (), we then optimized the temperature variation (relative to modern) given by
| [1] |
where the coefficient takes three values (Table S1), one for each of the three major periods of isotopic change (deglacial, early to mid-Holocene, and late Holocene). Fig. 2A shows the result. This calibrated is then used without further adjustments in subsequent optimizations of
| [2] |
in which the free parameters are three coefficients and a constant , the modern temperature. This relation introduces three basis functions , with ranges that reflect the broadest pattern of variations seen in the observed temperature–depth profile. They allow for adjustments to reconstructed average temperatures of the late glacial period, early Holocene, and mid- to late Holocene (SI Basis Functions and Fig. S2). Magnitudes are within in the final reconstruction.
Table S1.
Isotopic sensitivity parameters for optimized model
The interval 0–0.2 ka uses results from a shallow borehole (52).
The larger value includes a correction for seawater composition.
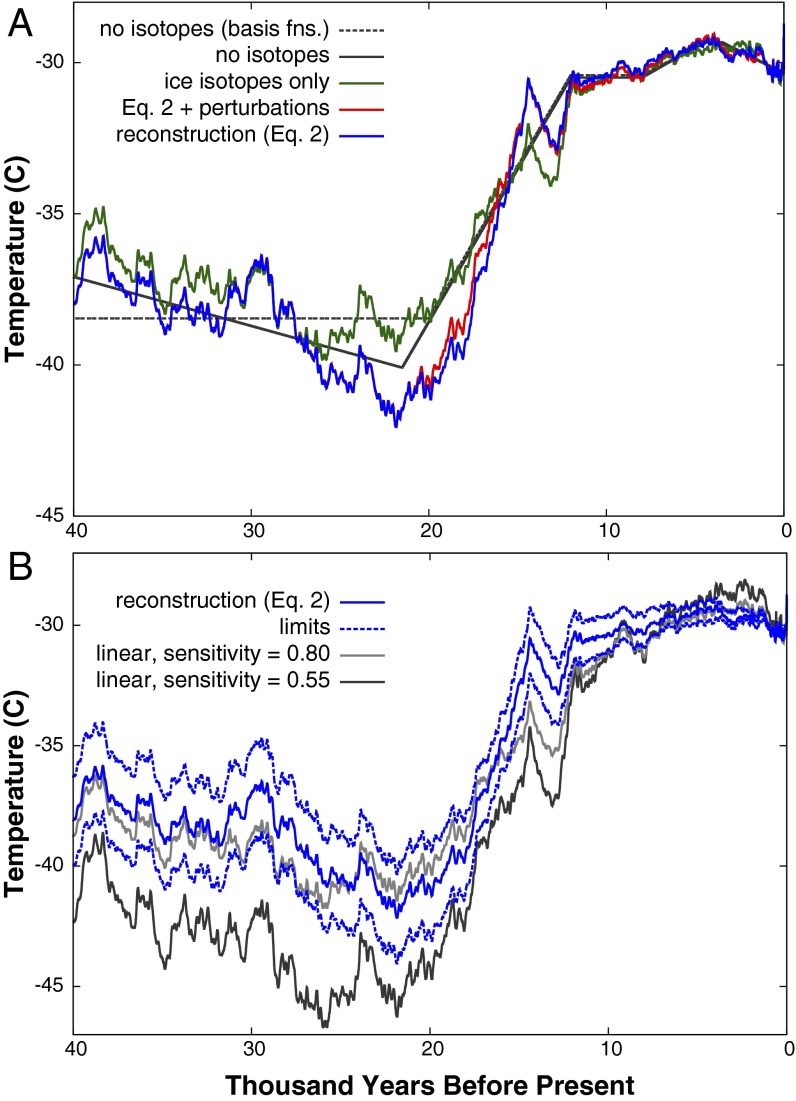
Fig. 2.
Optimal West Antarctic Divide surface temperature reconstructions. The blue curve, our optimal reconstruction using Eq. 2 without random perturbations, is identical in A and B. (A) Eq. 1 (green), Eq. 2 (blue), and Eq. 2 plus random perturbations (red). Also shown are calibrated basis functions without isotopes (dashed black) and the same with prescribed cooling before 21 ka (solid black). (B) Our final reconstruction [Eq. 2 (blue)] and model-dependent limits as defined in SI Calculation of Limits and Tolerance (dashed blue), together with linearly scaled ice-isotope curves with sensitivities = 0.55‰ and 0.80‰ (gray).
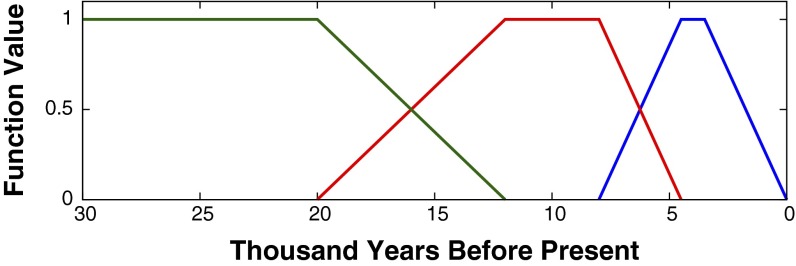
Fig. S2.
Standard versions of the basis functions introduced in main text Eq. 2 and used in final optimized reconstructions. In sensitivity tests, the ages of vertex points for these functions were shifted through ranges as described herein.
To incorporate data, the temperature history can be adjusted further by an amount determined by densification physics to reconcile the accumulation rate histories derived two independent ways (Materials and Methods and SI Firn Thickness Model and Use of Nitrogen Isotope Data): one from and using a model for the evolving firn density and thickness and a second one from the ice core’s observed annual layer thicknesses, corrected for strain using glaciological parameters determined in the optimization of Eq. 2. The multiplier ranges between 0 and 1, allowing us to control the relative importance of ice and gas isotopic records. It safeguards against possible problems with the nitrogen isotope method; the accuracy of as a thermometer is not well established, especially given imperfections of firn densification models and irregularities of the gas-trapping process at the firn base. We examined reconstructions with various values and used borehole temperatures to identify the range of admissible scenarios (SI Calculation of Limits and Tolerance).
Our final reconstruction (Fig. 2) uses for all but the late Holocene (Materials and Methods and SI Firn Thickness Model and Use of Nitrogen Isotope Data, The Coefficient ω) and gives a match between model and observed temperature profiles with a root-mean-square error of 1.47 cK (Table S2). This is an excellent match considering the total range of the temperature profile (Fig. 1), but still larger than the 0.8-cK tolerance defined by uncertainties in the measurement and in glaciological variables (SI Calculation of Limits and Tolerance). To assess how much of the remaining mismatch could be eliminated without altering the broad patterns implied by and , we introduced a random perturbation term to Eq. 2 before optimization (SI Reconstruction Strategy) and tested various scenarios. The best one reduced the rms error to 1.11 cK. Fig. 1 illustrates its match between model and observed temperature–depth profiles. This improvement is not large enough to negate the model without perturbations and regardless is achieved without any significant changes in the reconstructed temperature (Fig. 2A). In contrast, the optimized Eq. 1 using ice isotopes alone can be firmly rejected, as can optimized basis functions without isotopes (Fig. 2A and Table S2). Table S2 summarizes metrics of model performance for all stages of the analysis. We note that using instead of in Eq. 2 significantly improves model performance, providing evidence that the firn-thickness proxy serves as a thermometer despite potential complexities in the controls on firn structure and gas transport.
Table S2.
RMS mismatch of optimal models (cK)
The true total uncertainty of reconstructed temperatures is difficult to define, given that borehole temperatures preserve only long-term averages of the climatic forcing and given the possible nonthermal influences on the isotopic proxies providing higher-frequency information. Within the context of our reconstruction strategy, however, we can define limits by accounting for sources of uncertainty in input variables and arbitrary model choices (Table S4). The limits (Fig. 2B) are the quadrature sum of 2 uncertainties arising from model parameters and methodological choices, as summarized in Materials and Methods and SI Calculation of Limits and Tolerance.
Table S4.
Contributions to limits on reconstructed temperatures
| Variable | 2 variation | LGM temperature deviation, °C |
| Thickness history | 400 m, no deglacial increase | 1.3 |
| Depth–age scale | 3.6% at 20 ka; 5% at 40 ka | 0.6 |
| Thermal conductivity | 2% | 0.5 |
| Basal temperature | 1 °C | 0.16 |
| Strain parameters and | 0.6 and 0.1 | 0.12 |
| Depth of sensor | 1 m/km | 0.02 |
| Drilling disturbance | 4 mK | 0.01 |
| 2D effects | 0.5 |
Perspective on the utility of our reconstruction can be gained by comparison with temperature histories derived from the traditional method of treating temperatures as a single linear function of ice-isotopic data (, with constant dependent on whether refers to deuterium (D) or oxygen-18 content, such that ). Estimates of from studies of temporal and spatial covariation of and in Antarctica range from 0.4‰ to 1.0 (22, 23), corresponding to approximately 5.5 of uncertainty in the LGM temperature at West Antarctic Ice Sheet Divide, three times the uncertainty of our reconstruction. Estimates of from temporal covariations, presumably the most relevant for climate reconstruction, average (24), whereas the continent-wide spatial covariation gives (22, 25). Fig. 2B plots these two cases in comparison with our reconstruction. The LGM temperature given by the temporal sensitivity is too cold, whereas, surprisingly, the spatial one matches our reconstruction well. Both, however, are too cold in the second half of the deglaciation, 15–9 ka. That the comparative warmth of this interval emerges strongly from the borehole temperature data is apparent from both the range of our optimal reconstruction (Fig. 2B) and the shape of the simple nonisotopic models (Fig. 2A).
SI Reconstruction Strategy
This section summarizes the reconstruction strategy following the presentation in the main text, but with added details and comments.
To determine the surface temperature history , we optimized the match between temperatures measured in the borehole and those calculated with a numerical model of heat transfer driven by various scenarios as a boundary condition. To start, we filtered the deuterium ice-isotopic record () to remove high-frequency variability. Using the time derivative of this filtered history (), we then optimized the temperature variation (relative to modern) given by
| [S1] |
where the coefficient takes three values (Table S1), one for each of the three major periods of isotopic change (deglacial, early to mid-Holocene, and late Holocene). For the most recent period 0–0.2 ka we do not calibrate but instead add and adjust a trend whose shape follows the temperature reconstruction of Orsi et al. (52) derived from analysis of a neighboring shallow borehole.
Fig. 2A (main text) shows the result. This calibrated is used in all subsequent stages of the analysis, without further adjustments. Next we introduced three basis functions with ranges , so that
| [S2] |
and optimized the coefficients and the constant , the modern temperature. The basis functions reflect the broadest pattern of variations seen in the observed temperature–depth profile and allow for adjustments to average temperatures of the late glacial period, early Holocene, and mid- to late Holocene (Fig. S2). If matched perfectly the true temperature history, then we would here find . In fact, nonzero are found to improve the model performance significantly (Table S2), indicating that the of ice does not always preserve a linear signal of the long-term evolution of surface temperatures. On the other hand, an optimization of the basis functions without isotopes performs significantly worse than the isotopes alone (Table S2, top entry); the isotopes do record important information about past temperatures.
Uncertainty in how the measured temperature matches ice temperature at a given depth is approximately 0.5 cK, but additional unknowns in the model raise the tolerance to 0.8 cK (SI Calculation of Limits and Tolerance section). Any models with rms mismatch differing by less than this amount should be regarded as equivalent, whereas models performing worse by this amount or better compared with the final optimized reconstruction are rejected.
Fig. 2A (main text) also shows the history derived from basis functions without isotopic inputs, along with an optimized version prescribing a cooling before the LGM. Note that it would be a mistake to regard these nonisotopic models as better representations of the borehole temperature information. The borehole temperatures do discriminate between different histories containing a wide range of frequency contents, and these nonisotopic versions can be rejected, as can Eq. S1. The “long-term averages” of climatic temperatures preserved in the borehole temperature signal are millennia in the Holocene and tens of millennia in the glacial, but uneven weighting in the averages and the simultaneous constraint provided by the measurements at different depths increase the discriminatory power.
The gas-isotope data provide a test of the estimated using Eq. S2 and an opportunity for improvements. The history of accumulation rate () can be derived in two independent ways, one from and , using a model for the evolving firn density and thickness, and a second one from the ice core’s observed annual layer thicknesses, corrected for strain using parameters (total ice thickness, basal melt rate) determined in the optimization of Eq. S2. Discrepancies between the two versions of can in principle be eliminated by adjusting the temperature history by an amount determined by densification physics. Thus, we write
| [S3] |
where ranges between 0 and 1. This coefficient safeguards against possible problems with the method; the accuracy of as a thermometer is not well established, especially given imperfections of firn densification models and irregularities of the gas-trapping process at the firn base. We examined reconstructions with various values and used borehole temperatures to identify the range of admissible scenarios.
Including the term in Eq. S3 with for all but the late Holocene reduces the rms error of the optimized model temperature profile to 1.47 cK (Table S2). This is an excellent match considering the total range of the observed temperature profile (Fig. 1, main text), but still larger than the 0.8-cK tolerance defined by uncertainties in the measurement and glaciological variables. To assess how much of the remaining mismatch could be eliminated without altering the broad patterns implied by and , we introduced a random perturbation term to Eq. S3 before optimization. The magnitude of perturbations was restricted to one-half the difference between the optimized Eq. S3 scenario and its multimillennial average. Of 60 random scenarios we tested, the best one reduced the rms error to 1.11 cK. This improvement (rms error reduced by 0.36 cK) is not large enough to negate the model without perturbations and regardless is achieved without any significant changes in the reconstructed temperature: less than 0.8 °C warmer during deglaciation and less than 0.05 °C warmer at the LGM (Fig. 2A, main text).
Fig. 1 (main text) illustrates the match between model and observed temperature–depth profiles for this best-performing case. Regardless of whether the final perturbations are included, the reconstructed temperature history provides an excellent match to the constraints provided by measured borehole temperatures, ice-core layer thicknesses, and isotopes. Table S2 summarizes metrics of model performance for all stages of the analysis.
SI Ice-Isotopic Data
The of ice was measured by laser spectroscopy at the University of Washington as described in Steig et al. (24), and the associated data have been published previously (15, 16, 24). Use of rather than in our calculations makes no discernible difference because scales linearly with . The data are reported as per mille deviations from Vienna Standard Mean Ocean Water (VSMOW), normalized to the VSMOW-Standard Light Antarctic Precipitation standard water scale. The precision of the measurements is better than 0.8%.
SI Nitrogen-Isotopic Data
The of trapped in the ice was measured at Scripps Institution of Oceanography, University of California. Air was extracted from 12-g ice samples, using a melt–refreeze technique, and collected in stainless steel tubes at liquid-He temperature. was analyzed using conventional dual-inlet isotope ratio mass spectrometry (IRMS) on a Thermo Finnigan Delta V mass spectrometer. Results were normalized to La Jolla (CA) air, and routine analytical corrections were applied (55, 56). The data and model fits were reported previously by Buizert et al. (47) and are shown in Fig. S1.
SI Calculation of Temperatures vs. Depth
We use the control volume method (49) to solve the energy balance equation on a grid of 200 nodes in the ice and 25 nodes in subjacent bedrock. Grid spacing is smaller near the surface and increases with depth. The grid is rewritten by interpolation to allow for changes of ice thickness. The Kelvin temperature evolves with time and elevation above bed according to
| [S4] |
where is density, is the temperature-dependent heat capacity, is the vertical velocity, is the temperature-dependent thermal conductivity, and are the source terms. The latter are calculated from the rate of work of ice deformation and firn compaction and are of minor significance. Equations for thermal parameters are those of Yen’s compilation (57), but with thermal conductivity multiplied by a factor so that . We use to conform with recent measurements (58), but vary it from 1.00 to 1.04 in sensitivity tests.
Advection is of primary importance because ice accumulates, deforms, and flows downward. The age vs. depth relation for the core (SI Age–Depth Relation and Layer Thicknesses section) provides a tight constraint on the net vertical displacement of layers, making calculated temperatures only weakly sensitive to uncertain details of our flow model. The vertical velocity (negative in the ice sheet because of downward flow) depends on basal melt rate and vertical normal strain rate ,
| [S5] |
| [S6] |
for ice-equivalent accumulation rate and ice thickness . The history of can take any specified form (see below). The history of derives from the ice core’s measured annual layer thicknesses ,
| [S7] |
where indicates the depth following the layer through time. With the addition of a correction for densification near the ice surface (the density as a function of depth below the surface is assumed invariant over time), the vertical strain rate follows a Dansgaard–Johnsen model: uniform in the upper part of the ice sheet and varying linearly below a kink height specified by parameter (varied in sensitivity tests),
| [S8] |
| [S9] |
The requirement that Eqs. S5 and S6 match at the surface fixes the value for . Parameter defines how the strain rate at the bed compares to the strain rate in the upper fraction of the ice thickness. is sometimes referred to as the “sliding parameter” but this label misleads; the fraction of ice motion due to sliding can change with distance along a flowline, and such a gradient allows to take values less than or greater than unity. In our optimized models we use , because this value allows inferred from ice strain to match that inferred from in the deepest layers (ages in excess of 45 ka). A value implies that the fraction of motion due to sliding increases along the flowline. Whether this is true or not upstream of the WAIS Divide is unknown. Fortunately, the parameter has little influence on our temperature reconstruction, because the optimization adjusts basal melt rate . Using a larger value for is largely compensated in the temperature profile throughout most of the ice thickness by a smaller value for . Reducing from 1.3 to 0.7, for example, causes the optimized LGM temperature to decrease by only 0.08 °C.
As an initial condition, we set the profile at 120 ka, the starting time of model calculations, equal to the modern observed temperature–depth profile.
SI Basis Functions
The three basis functions ( in Eq. 2, main text) are simple, are piecewise linear, and range from zero to unity (Fig. S2). The and center on 4 ka and 10 ka, respectively, the approximate age equivalents of the depths of the two prominent extrema in the borehole temperature profile (Fig. 1, main text). The extends through the LGM. In the standard case, is defined by vertex values (0, 1, 1, 0) at ages of (0, 3.5, 4.5, 8) ka, whereas for calculations of limits the vertex ages range as (0–2.5, 2–5.5, 4–6, 6–9) ka. Ranges for vertex ages of are (4–8, 8–12, 12–, 15–) ka. For , the ages of the (0, 1) vertices range as (12–15, 15–) ka.
SI Firn Thickness Model and Use of Nitrogen Isotope Data
Calculation of .
Given simultaneous histories and , we calculated the firn density profile from the empirical model of Herron and Langway (20), recast to use overburden load as a driving variable as in refs. 28 and 47. Equations of the densification models are given in appendix A of ref. 47. The density profile, in turn, is used to calculate of gas at the depth of trapping by combining the barometric equation (section 15.3 of ref. 13 and ref. 18), an estimate of thermal fractionation due to temperature gradients (19), and a small convective-zone thickness offset. The calculated for current climate matches the observed modern value at the WAIS Divide.
Calculation of .
Starting with derived from observed ice-core layer thicknesses and the strain model derived with the preliminary optimized , we calculated , using the model summarized in the previous paragraph. Comparison with measured then defined an adjustment to , by calculating the derivative of mismatch between model and measured with respect to perturbations of and shooting for a perfect match by linear extrapolation. This process was iterated until measured and modeled agreed as well as possible in terms of rms error, thus defining a new adjusted accumulation rate history .
The temperature-history correction was then calculated as a function of the ratio of the adjusted accumulation rate to the original accumulation rate from strain-corrected layer thicknesses. This function describes the coupled dependence of on temperature and accumulation rate according to firn density models and the barometric equation and has been calibrated against modern-day observations at various sites (figure S1 of ref. 28). We used a simple approximation of the relationship, appropriate for the range of temperatures and accumulation rates at the WAIS Divide,
| [s10] |
in which the constant for temperature change in Kelvins. The entire process was iterated several times to achieve an optimal match against all constraints. Fig. S1A compares the optimized model’s two histories of accumulation rate, one estimated from ice strain and the other from reconstructed temperatures via .
We also repeated analyses with two alternative firn densification models (21, 54) and found that they performed not as well as Herron and Langway’s with respect to the borehole temperature match after optimization. The versions that produced an acceptable fit to the borehole temperatures corresponded to surface temperature histories well within the range of uncertainty defined using the Herron–Langway model. Details about use of the alternative densification models are provided in ref. 47.
Note that for most of the optimizations in this study, the density profile was assumed to be in equilibrium with the instantaneous values of and (a quasi-steady state). Only for the final optimizations of Eq. 2 (main text) with and without perturbations, and for the three different densification models, was the densification model run in fully time-dependent mode.
The Coefficient .
The following method was used to define in Eq. 2 of the main text for the nominal optimized models. Considering only the portion of the record with climate similar to modern (12 ka and younger), we perturbed in discrete intervals to assess whether, upon optimization, model performance improves or degrades by adjusting in the direction indicated by . Improvement was found for all but the latest Holocene, so we took for 3.5–12 ka but for ka. (In the late Holocene, the reconstruction is already tightly constrained by the combination of ice isotopes and borehole temperatures.) All possibilities in the 0–1 range are included subsequently in tests to define limits on the temperature history.
After iterative optimizations of Eq. 2 (main text) and experiments with for the -ka period, we found that in mid-Holocene there remains a difference of 0.015 between the two reconstructions of (Fig. S1A), implying that the thermometer does not entirely agree with the borehole temperatures. We assume this is a deficiency of the former and therefore do not force the match between versions to be better than 0.015 in the pre-Holocene. (There is no reason to expect it to perform better in LGM conditions than in the Holocene when conditions are similar to the present, whereas the cost of allowing a better match of is a greater deviation of from the ice isotopes. The borehole temperatures average over too great a length at LGM to choose.) This means that decreases to 0.5 for the LGM and prior in our standard case.
SI Calculation of Limits and Tolerance
Sensitivity tests reveal seven principal sources of uncertainty with nontrivial effects on reconstructed LGM temperature (ranked in descending order of importance): the ice thickness history, the depth–age scale, the temperature dependence of thermal conductivity of ice, the basal temperature (equivalent to the local melting point of ice), the depth of the borehole temperature sensor, and the residual thermal disturbance from drilling. Setting each of these to maximum and minimum plausible values and reoptimizing define limits on reconstructed temperatures (Table S4). Adding all of these individual contributions in quadrature then defines the range due to uncertain inputs.
In this exercise it was also found that choosing the right combination of values for these uncertain quantities could improve the rms borehole temperature mismatch by 0.3 cK. In combination with the 0.5-cK uncertainty of the direct temperature measurement, this indicates that any reconstructed temperature history that provides an rms mismatch within 0.8 cK of the mismatch for the standard optimal model should be regarded as equally viable. We produced a set of alternative optimized reconstructions by four processes: introducing random perturbations to Eq. 2 (main text) as described previously; varying the duration and timing of the basis functions in Eq. S3; varying the coefficient of in Eq. S3; and defining as weighted averages , where and are, respectively, the standard optimal model (Eq. S3) and the calibrated ice-isotope model (Eq. S1), and ranges from 0 to 1. From this entire set of optimized reconstructions, we accepted as viable those that met three criteria: (i) borehole temperature rms mismatch no worse than 0.8 cK compared with the standard model; (ii) accumulation rates calculated using nitrogen isotopes and strain match over the period 0–30 ka to within an rms difference of 1.36 , twice the rms difference for the standard model; and (iii) model values, averaged in 1-ka windows, never trend outside the range of measured points in the Holocene. Considered together, at every age the viable reconstructions span a range of temperatures. We identify the maximum and minimum values as uncertainty related to methodological choices.
Our temperature model used in all optimizations is one-dimensional. This enables large numbers of computations and is appropriate because the surface elevation and temperature vary little upstream of the WDC site. The accumulation rate, however, increases upstream by 0.12 in 30 km, and thus the vertical velocity field and temperature pattern are 2D. This variation is mostly accounted for automatically in our analysis because it is already embodied in the observed depth–age relation and hence in reconstructed accumulation rates, model velocities, and vertical heat advection. To examine the importance of residual 2D effects, we used a 2D flowline heat and ice flow model (62, 63) to calculate the depth–age and depth–temperature relations at the WDC site. Using these as inputs to the one-dimensional model and optimization, we compared temperature reconstructions for cases in which the upstream accumulation rate was either uniform or increasing as observed. LGM temperatures differed by as much as 0.5 °C for a variety of cases in which the imposed temperature history was not specified purely from the isotopic data. Such discrepancies represent another source of uncertainty on our reconstructed temperatures, and we treat this as a uniformly distributed random variable in the interval (−0.5, 0.5) °C, which contributes a 2 to the limits shown in Fig. 2B (main text).
SI Influence of Elevation and Thickness Changes on Interpretation of Reconstructed Temperatures
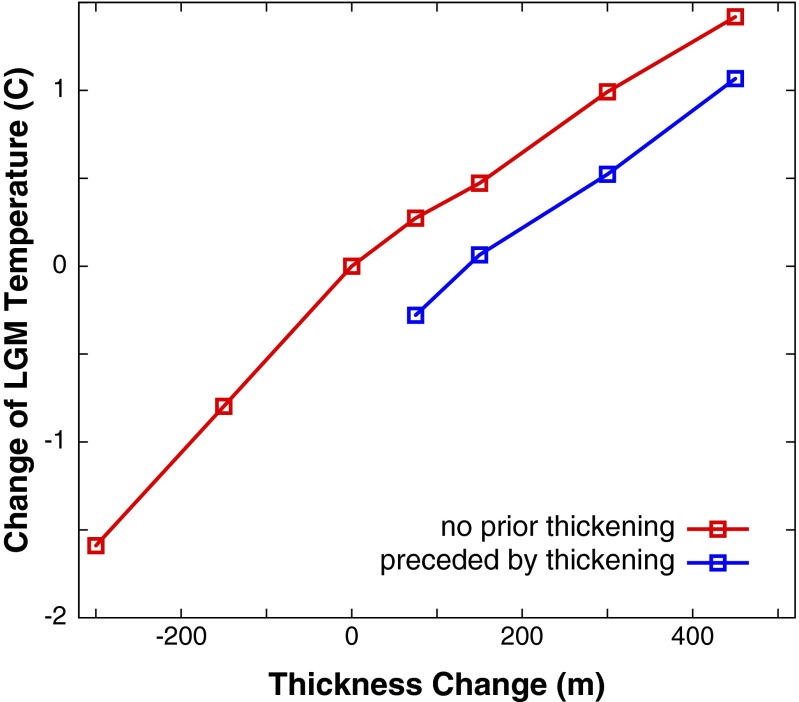
Our reconstruction is of temperature at the ice-sheet surface. Some aspects of the deglacial and Holocene temperature variations likely arise from changes of surface elevation via the atmospheric lapse rate, rather than from climate change connected to forcings and transports. This effect would warm the surface climate by about 0.7–1.0 °C per 100 m of subsidence. Further, the history of ice thickness influences our reconstructed surface temperature directly; thinning is associated with increased vertical ice velocity, which shifts reconstructed LGM temperatures to warmer values. Although the sensitivity depends importantly on the sequence and timing of thickness changes, a 130-m thinning from late glacial to mid-Holocene (or 100 m of surface subsidence after isostatic adjustment) raises the reconstructed LGM temperature by between roughly 0 °C and 0.3 °C, depending on the magnitude of preceding deglacial thickening. The lapse rate effect is thus the larger one.
Following the LGM, the dominant glaciological process would have been thickening ice and a rising surface due to greatly increased accumulation rate, proceeding more rapidly at the higher-accumulation WAIS Divide than at the drier East Antarctic sites (64). In contrast, the rise of sea level between 18 kyBP and 8 kyBP imposed a relative elevation drop of about 140 m. And, during the Holocene, retreat of grounded ice in the Ross Sea (65) caused thinning and surface lowering. Geological evidence constraining this history is sparse. Cosmogenic exposure-age dates on nunataks at the margin of the ice sheet (64, 66) indicate the interior of the WAIS was thicker at 10 kyBP than present by 100 m. The elevation histories from numerical full ice-sheet model simulations disagree by a few hundred meters despite use of similar climate histories. The model with the best treatment of ice dynamics of the grounded ice sheet (31, 59) yields thickness changes 50 m from the LGM to present. Another recent model yields LGM thickness and elevation of 360 m and 260 m greater than present (60), although this has been calibrated to target an assumed thickness increase of 200 m. Two earlier models produced LGM thicknesses a few hundred meters thinner (30) and 100 m thicker (29) than present. All such simulations show significantly smaller elevation and thickness changes than suggested by the ICE-5G and ICE-6G glacial isostatic adjustment model scenarios commonly used in climate modeling experiments (67), which are almost certainly incompatible with both geological and ice-dynamical constraints.
None of the ice-sheet models driven by climate records show more than 300 m of thinning at the WAIS Divide in the past 15 ky (29–31). A change of this magnitude, if preceded by thickening due to the known accumulation increase, warms our reconstructed LGM temperature by . For this reason, the limits of our LGM temperatures shown in Fig. 2B (main text) include a term of this magnitude. Given the other factors contributing to uncertainty, this range expansion is also equivalent to a 2 temperature variation arising from 400-m thinning without prior thickening, an unlikely case.
The preceding applies to the surface temperature reconstruction. For interpretations of constant-elevation climate, the larger lapse-rate effect must be included. As an outside case, suppose the ice at the WAIS Divide was 500 m thicker and the surface 400 m higher at LGM. Adjusting our constant-thickness LGM-to-late Holocene optimized temperature change of 11.3 with a reconstruction effect and a +2.8–4 °C lapse rate effect would give a constant-elevation temperature change of only . A more likely scenario of 200 m thickening when accumulation rises after the LGM, followed by 300 m of thinning to the mid-Holocene, would imply a reconstruction effect and (assuming isostatic adjustment) a +0.5–0.7 °C lapse rate effect, giving a constant-elevation temperature change of , which overlaps the range of surface temperatures shown in Fig. 2B. The difference between these cases illustrates that elevation changes could have a large influence on the interpretation of our temperature history. On the other hand, glaciological reasoning, ice sheet model simulations, and geological constraints all suggest that modest elevation changes are more likely, indicating that a smaller or possibly even negligible correction between surface temperature and constant-elevation temperature is more appropriate. In addition, the surface temperature difference between the LGM and the late Holocene is not much larger than that between the LGM and the early Holocene (Table S3), so elevation changes occurring after 10 kyBP have little effect on inferred deglacial warming. But if future evidence establishes that large ice-sheet changes occurred in the pre-Holocene, our interpretations related to constant-elevation climate will have to be revised.
Table S3.
Principal features of reconstructed temperature ( °C)
| Climatic variable | Minimum | Optimal | Maximum |
| Average LGM (20–23 ka) temperature | -43.1 | -41.2 | -39.4 |
| LGM to late Holocene (0–3 ka) | 9.6 | 11.3 | 13.2 |
| LGM to early Holocene (10–11.5 ka) | 9.1 | 10.7 | 12.4 |
| Fraction of warming completed by 15 ka | 0.72 | 0.77 | 0.82 |
Discussion
Our surface temperature reconstruction (Fig. 2B) indicates that the surface in central West Antarctica was colder during the LGM (average from 20 ka to 23 ka) than in the late Holocene by (2) (Table S3), whereas the net warming from the LGM to the middle Holocene thermal maximum (3–6 ka at this site) was perhaps as large as 13.7 . Cited estimates for the deglacial warming at locations in East Antarctica are smaller, from 7 to 9.3 at the ice-core sites Vostok, Dronning Maud Land, Talos Dome, Dome F, and Dome C (6, 12, 26). It is possible that there exists a real regional difference from West Antarctica, where the climate is more strongly influenced by the proximal ocean (24, 27), but these values all derive from assumptions about the sensitivity of ice isotopes to climatic temperature, a method known to be inaccurate in Greenland (10, 28).
Influence of Elevation and Thickness Changes.
Our reconstruction is of temperature at the ice-sheet surface. Some aspects of the deglacial and Holocene temperature variations likely arise from changes of surface elevation via the atmospheric lapse rate. Further, the history of ice thickness influences our reconstructed surface temperature directly; thinning is associated with increased vertical ice velocity, which would shift reconstructed LGM temperatures to warmer values (SI Influence of Elevation and Thickness Changes on Interpretation of Reconstructed Temperatures and Fig. S3). A plausible upper-limit case of 300 m thinning at WAIS Divide in the last 15 ky (29–31), preceded by thickening due to the known deglacial accumulation increase, warms our reconstructed LGM surface temperature by . For this reason, the limits of our LGM temperatures shown in Fig. 2B have been expanded by this magnitude. Including the lapse rate effect from such a thinning (adjusted for isostasy) would imply a constant-elevation temperature change from LGM to Holocene of (SI Influence of Elevation and Thickness Changes on Interpretation of Reconstructed Temperatures), which overlaps the range of surface temperatures shown in Fig. 2B. Glaciological reasoning, ice-sheet model simulations, and geological constraints all suggest that smaller elevation changes are more likely, indicating that a smaller or possibly even negligible correction between surface temperature and constant-elevation temperature is more appropriate.
Fig. S3.
Change of reconstructed LGM temperature as a function of specified thickness history. The standard case in this plot refers to constant thickness. If the thickness perturbation is constant before 12 ka and then decreases to zero at 5 ka, the optimized temperature (main text Eq. 2) changes by the amount shown in red, as a function of the thickness at ages 12 ka. If, in addition, thickness increases by 200 m from 18 ka to 13 ka, the optimized temperature changes as shown in blue.
Climatic Implications.
Climate models predict that global temperature changes are amplified in the polar regions by feedback processes involving atmospheric moisture transport, soil moisture, heat exchange through sea ice, and the dependence of longwave emissions and lapse rate on surface temperature, and by factors controlling surface albedo: sea ice, ice sheets, snow, and vegetation (4, 8, 9, 32). All of these operate in the Arctic, but the much smaller land area reduces or eliminates some of them in the Antarctic. Averaging results from various climate model simulations of the LGM (21 ka) gives a global average cooling relative to late Holocene of 4.4 compared with an Antarctic (south of 80 ) mean of (4). Our result for West Antarctica lies in the middle of the models’ rather broad range and implies that Antarctic amplification through the deglacial climate transition was a factor of 2–3. A smaller contrast is expected in comparisons focused on mid-latitude sites. In the interval 18–15 ka, we find that West Antarctica warmed by about 7 , compared with about 4 indicated by glacier retreat in New Zealand (33).
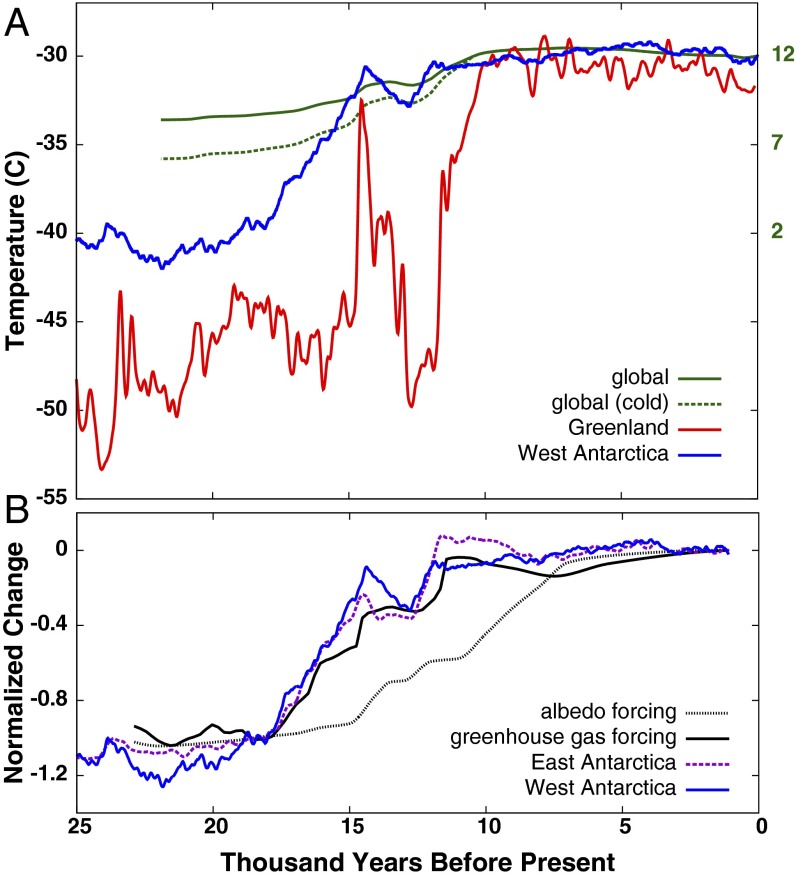
Fig. 3A illustrates how our West Antarctic history compares to estimated global-averaged temperature based on proxy records interpreted in a model context (6, 34). Some estimates of the global temperature depression at LGM are as small as 3.6 , whereas others are as large as 5.8 (6, 7), and the two global curves in Fig. 3A are scaled to match this range. Note that the only proxies contributing to the estimated global temperature history (6) from latitudes poleward of 55 are the isotopes from the four East Antarctic ice cores. Our results imply this might be a source of bias, most likely an underestimate of temperature change at high latitudes.
Fig. 3.
Comparisons of temperature histories and forcings. (A) This study’s optimal West Antarctic Divide surface temperature history (blue and left axis) from Eq. 2, central Greenland temperature history (red and left axis) from ref. 10, and global-average temperature from studies of the deglacial period (6) and the Holocene (34) with an LGM temperature 3.6 below modern (solid green and right axis) and scaled at ages greater than 11 ka to reach the colder LGM (−5.8 ) implied by ref. 7 (dashed green and right axis). The best-constrained studies yield an LGM temperature between these (5). (B) Various histories of forcings and temperatures (to facilitate comparisons of relative timing, the histories are all scaled to range from zero to unity between 18.5 ka and 1 ka, times of nearly identical annually integrated insolation at ): optimal West Antarctic Divide surface temperature (solid blue), average of East Antarctic ice cores (26) (dashed purple), methane and carbon dioxide greenhouse gas climate forcing (46) (solid black), and ice-sheet area albedo forcing calculated as sea-level change raised to the power 0.8 according to the average relationship between ice-sheet area and volume (section 8.10.3 in ref. 13) (dotted black).
A recent synthesis of climate sensitivities estimated from paleoclimate data (35) concluded that a doubling of atmospheric would increase global temperature by 2.2–4.8 (68% probability), values similar to or slightly higher than ones derived by other techniques. Those paleoclimate studies using Antarctic data have likely underestimated the temperature change in response to the well-constrained change in and thus underestimated climate sensitivity. In particular, the analysis producing the lowest estimated sensitivity in the compilation (36, 37) (a bit larger than 2.2 ) predicted an Antarctic LGM cooling smaller than even estimates from the East Antarctic isotopic proxies. Our reconstruction affirms that this is an underprediction. Antarctica accounts for a small fraction of global area and hence does not contribute much directly to climate sensitivity estimates, but the discrepancy may indicate too-weak feedbacks in some of the models used to assimilate proxy data.
A noteworthy aspect of our reconstruction is that by 15 ka, the millennial-averaged temperature had risen to within 2.5 of its late Holocene value (Fig. 2). The fraction of deglacial warming accomplished by this time was most likely 0.77 (Table S3). Such early warming of West Antarctica is consistent with inferences from retreat of glaciers in Southern Hemisphere mountain ranges. Extensive retreat occurred between 18 ka and 14.5 ka in Patagonia (38), with the Patagonian ice cap attaining near-present dimensions by 15.5 ka (39). Glaciers in the New Zealand Alps largely completed their major retreat by 15.7 ka (40). Thus, our temperature reconstruction and glacial geologic proxies both confirm a significant inference from isotopic records (6, 26, 41) that the high latitudes of the Southern Hemisphere experienced much of their warming millennia before the Arctic. At 15 ka Greenland had warmed by perhaps 5 (Fig. 3A), or less than 30% of the deglacial total (10), and did not maintain interglacial temperatures until around 11 ka, four millennia later than in West Antarctica.
Global climate evolution of the last deglaciation is regarded as the superposition of two modes (41): a global warming following radiative forcing and an interhemispheric redistribution of heat following variations in cross-equatorial heat transport by the Atlantic Meridional Overturning Circulation. Reduced Atlantic heat transport between 19 ka and 14.7 ka (Heinrich Stadial 1) cooled Greenland and contributed to the early Antarctic warming. Climate model experiments suggest that this contribution amounted to no more than a few degrees (42), however, and other factors such as increased insolation and associated sea ice feedbacks were probably important (15, 43). How these processes combined to produce the comparatively large inferred warming remains uncertain and offers a potentially illuminating target for further model studies.
In the period of early warming, 18.5–15 ka, increasing annually integrated insolation and reduced northward oceanic heat transport account for a climate forcing of 1 to a few watts per meter specific to the Southern Hemisphere (SI Climate Forcings During Deglaciation). This can be compared with the global forcings governing the difference between planetary temperatures of the LGM and Holocene. Taken together, decreasing ice-sheet extent (hence reduced albedo) and increasing greenhouse gas concentrations ( and ) account for about 90% of the direct global-averaged climate forcing, with respective magnitudes of 2.9 and 2.2 (2). Fig. 3B plots histories of these two forcings. Antarctic warming leads the greenhouse gas forcing through the deglaciation, and the fractional increases (Fig. 3B) put an upper limit on the contribution of the gases to Antarctic warming between 18.5 ka and 15 ka of 65%. The magnitude of the gas forcing by 15 ka was 1 , equal to or somewhat smaller than the forcing from combined insolation and reduced ocean transport. Given this similarity, the observation that could account for roughly half of the warming is consistent with normative estimates of its climatic impact.
Fig. 3B also shows strong similarities between our West Antarctic temperature history and a composite of the ice-isotopic records from interior East Antarctica (26), although the latter covaries yet more closely with the greenhouse forcing. In the Holocene, a maximum at around 4 ka appears in both parts of the continent, with a West Antarctic magnitude of 0.6–1.2 warmer than the last millennium (0–1 ka). Differences at other times might record changes of elevation, sea ice, or other factors. The West Antarctic warming just before 18 ka, attributed previously to insolation driving Southern Ocean warming and sea ice retreat to which East Antarctic isotopes are less sensitive (15), appears in Chile as glacier advance and in New Zealand as glacier retreat punctuated by readvances that left moraines (33, 44). These glaciers are thought to respond to Southern Ocean temperatures as well (45).
SI Climate Forcings During Deglaciation
At present the ocean transfers heat northward across the equator at a rate of about 1 PW (68). This amounts to an effective climate forcing throughout the Southern Hemisphere of approximately −4 . In the reduced transport period (which culminated between 17 ka and 14.5 ka), the contribution to Antarctic warming would have been substantially less than 4 , because the background circulation was weaker in the glacial climate, the transport did not cease entirely, and atmospheric heat exchange partly compensates (69–71). Another contributor to West Antarctic warming was annually integrated insolation, which increased steadily through the deglacial period in the Southern Hemisphere. The increase between 18.5 ka and 15 ka, specifically, was 2.5 at the periphery of Antarctica. The high albedo of the inland ice sheet (0.8) and moderate albedo of surrounding ocean regions (0.5) reduce the climate forcing to less than 1 . The combined forcing from ocean transport and insolation changes was thus not much larger than 1 . Other factors that might influence warming over the ice sheet include changes in the efficacy of atmospheric transport of heat and moisture and changes of winds at the Southern Ocean surface that alter sea surface temperatures around the continent. Such processes could be responding to variations of tropical climate or of ice-sheet topography in either hemisphere, for example.
These hemisphere-specific forcings can be compared with the global forcings governing the difference between planetary temperatures of the LGM and Holocene. Taken together, decreasing ice-sheet extent (hence reduced albedo) and increasing greenhouse gas concentrations ( and ) account for about 90% of the direct global-averaged climate forcing, with respective magnitudes of 2.9 and 2.2 (2). (The very important variations of water vapor, snow cover, and sea ice constitute feedbacks rather than direct forcings.) Fig. 3B plots histories of these two forcings. To facilitate comparisons of relative timing, the histories are all scaled to range from zero to unity between 18.5 ka and 1 ka, times of nearly identical annually integrated insolation at . The ice-sheet albedo effect is concentrated in the Northern Hemisphere (72), and indeed this largest forcing appears to contribute little directly to the early deglacial changes in Antarctica. The Northern Hemisphere ice sheets probably instigated changes in the oceanic heat transport and sea ice through releases of meltwater and orographic effects on winds (73, 74), but the primary albedo forcing can be discounted; its magnitude by 15 ka was only 0.3 . Antarctic temperature covaries much more strongly with the greenhouse gas forcing (41) (Fig. 3B, main text). Part of this correspondence likely arises because the climate warming itself and associated influences on Southern Ocean winds, sea ice, and currents drove the release of and its atmospheric increase (75), and part arises because of the feedback from the increasing greenhouse effect. Antarctic warming leads the greenhouse gas forcing through the deglaciation, and the fractional increases (Fig. 3B, main text) put an upper limit on the contribution of the gases to Antarctic warming between 18.5 ka and 15 ka of 65%. The magnitude of the gas forcing by 15 ka was 1 , compared with a forcing of 1 to a few from combined insolation and reduced ocean transport. Thus, given this similarity, the observation that could account for roughly half of the warming is consistent with normative estimates of its climatic impact.
Conclusion
The temperature reconstruction reported here provides information about the thermal state of firn and ice through time at the West Antarctic Divide site, an essential input to studies of the depth–age relationship, interhemispheric climate phasing, history, and covariation of temperature with accumulation (16, 47, 48). Of greatest immediate interest, however, is our demonstration that the global deglacial temperature change was amplified by a factor of 2–3 in the Antarctic, that Antarctic warming was largely achieved by 15 ka in coherence with records from Southern Hemisphere mountain ranges, and that climate models of the deglaciation perform well on average, but that the ones with lowest sensitivity can be discounted. The early warming of the Southern Hemisphere, which our study helps to quantify, arose from combined effects of reduced northward oceanic heat transport, increased insolation, and increasing atmospheric . Quantitative simulation of this phenomenon could provide an illuminating challenge for model studies.
Materials and Methods
Calculation of Temperatures as a Function of Depth.
We used the control-volume method (49) to solve the one-dimensional time-dependent energy balance equation accounting for conduction, advection, and sources (SI Calculation of Temperatures vs. Depth).
Optimization.
Singular value decomposition was used to find parameter values that minimized the squared mismatch of modeled and measured temperatures. Every such optimization involved free parameters related to surface temperature variations plus three additional free parameters: the modern mean surface temperature, the present ice thickness (known to be in the range 3,450–3,470 m), and the rate of basal melt. The latter accounts for the geothermal heat flux, which is not an independent parameter. The number of simultaneous free parameters in all optimizations (Eqs. 1 and 2) remains constant (six).
Measurement of Borehole Temperatures.
Temperatures in the fluid-filled WDC borehole were logged during December 2011 and again during December 2014, using the US Geological Survey Polar Temperature Logging System (PTLS) (50, 51) (SI Measurement of Borehole Temperatures). Combined uncertainties in assessing temperatures in the surrounding ice are 5.3 mK for the fluid-filled portion of the borehole (depths m). Above 96 m we used the temperature profile previously measured in a neighboring air-filled hole (52), shifted uniformly to match the values determined by the more accurate PTLS measurements.
Ice-Core Data.
Measurements of of ice and 15N of trapped were by laser spectroscopy and mass spectrometry, respectively (15, 47) (SI Ice-Isotopic Data and SI Nitrogen-Isotopic Data). The age–depth relation and annual layer thicknesses were determined by identifying and counting annual layers back to 31 ka and by cross-correlations of gas records prior to this time (16, 47, 53) (SI Age–Depth Relation and Layer Thicknesses).
Firn Thickness Model and Use of Nitrogen Isotope Data.
SI Firn Thickness Model and Use of Nitrogen Isotope Data provides more information.
Calculation of δ15 N(t).
Given simultaneous histories of accumulation rate () and , we calculated firn density profiles using an empirical model (20), recast to use overburden load as a driving variable as in refs. 28 and 47. The density profile, in turn, is used to calculate δ 15N(t) of gas at the depth of trapping, accounting for gravitational settling, thermal fractionation, and near-surface convective mixing with the atmosphere. The calculated δ 15N for current climate matches the observed modern value.
Calculation of .
We first calculated δ 15N(t) using an initial derived from observed ice-core layer thicknesses and the strain model associated with an initial optimized . Comparison with measured δ 15N(t) then defined an adjustment to . This process was iterated until measured and modeled δ 15 N(t) agreed as well as possible (Fig. S1), following the method described in refs. 28 and 47. The temperature-history correction was then calculated as a function of the ratio of the adjusted to the initial . This function describes the coupled dependence of δ 15N on temperature and accumulation rate according to firn density models and the barometric equation and has been calibrated against modern-day observations and various sites. The entire process was iterated several times. Fig. S1 illustrates the close match between the optimized model’s two histories of accumulation rate, one estimated from ice strain and the other from reconstructed temperatures via δ 15N. We also repeated analyses with two alternative firn densification models (21, 54).
The coefficient ω in Eq. 2.
As a function of age our optimized model uses for ka, for 3.5–12 ka, and for ka (see SI Firn Thickness Model and Use of Nitrogen Isotope Data, The Coefficient ω for explanation). Alternative variations of are used in defining limits on the temperature history.
Calculation of ±2α Limits on Reconstructed Temperature.
We perturbed uncertain input variables and recalculated optimal temperature histories. The most important variables proved to be the ice thickness history, depth–age scale, and thermal conductivity of ice (SI Calculation of Limits and Tolerance). In addition, we used such recalculations to assess the impact of altering choices about model strategy, including the shape and timing of basis functions and values of the coefficient , both in Eq. 2. Finally, we assessed the uncertainty arising from upstream variations of flow and temperature by comparing results from our one-dimensional model with those from a 2D model. The limits shown in Fig. 2B derive from quadrature sums of all these effects.
Data Availability.
All data are available online through the U.S. Antarctic Program Data Center (http://www.usap-data.org/).
SI Measurement of Borehole Temperatures
Temperatures in the fluid-filled WDC borehole were logged during December 2011 and again during December 2014, using the USGS PTLS. With the PTLS, a thermistor probe is lowered into the borehole at a constant rate while the sensor’s resistance and depth are continuously recorded. The resistance is later converted to temperature, using a special calibration function. Instrumental noise and temperature fluctuations due to borehole fluid convection are then removed using a wavelet analysis, and a deconvolution is performed to account for the finite response time of the probe. A full description of the measurement system, measurement uncertainties, and data processing techniques is available (50, 51). Uncertainties primarily arise from three sources: temperature-sensor calibration uncertainties and measurement-circuit drift, thermal fluctuations within the borehole due to convection of the borehole fluid, and the thermal disturbance caused by drilling processes. Except for the extreme ends of the borehole, the standard uncertainties due to these sources are less than 3.3 mK, 1.25 mK, and 4 mK, respectively. The quadrature sum provides a combined uncertainty of 5.3 mK for the temperature measurements in the fluid-filled portion (depths m) of the borehole. Above 96 m we used the temperature profile previously measured in a neighboring air-filled hole (52), shifted uniformly to match the values determined by the more accurate PTLS measurements.
SI Age–Depth Relation and Layer Thicknesses
The age–depth relation and annual layer thicknesses were determined by identifying and counting annual layers back to 31 ka and by cross-correlations of gas records prior to this time (16, 47, 53). The former is completely independent of the reconstructed temperatures, whereas the latter uses them in the calculation of age offset between gas and ice. The 2 uncertainty on age offset at ages greater than 31 ka is less than y. Optimizations using an age scale stretched or compressed by this amount change the reconstructed LGM temperature by a trivial amount, about ±0.05 °C. The range of our reconstructed temperature history (Fig. 2B, main text) includes the effects of stretching and compressing the age scale by 2 ky at 40 ka.
SI Comment on the Use of Nitrogen Isotopes
Our use of the firn-thickness proxy in the reconstruction ( in Eq. S3) is a unique application of a variable whose temperature dependence reflects a somewhat complex physical process. We emphasize that the optimization is still performed by use of the borehole temperatures alone. The improved model performance when Eq. S3 replaces Eq. S2 (Table S2) arises because the three main features of (the mid-Holocene maximum, the warmer late glacial, and the colder LGM) are all favored independently by the borehole measurements. More precisely, if we exclude the most recent 2.5 ka when the prior model is already tightly constrained, then assigning a value in Eq. S3, meaning that is included in accordance with theory, improves the borehole temperature match even though the optimization uses the same number of free parameters. This behavior provides evidence that the firn-thickness proxy serves as a thermometer despite potential complexities in the controls on firn structure and gas transport. The number of simultaneous free parameters in all optimizations (Eqs. S1–S3) remains constant (six).
SI Principal Features of Reconstructed West Antarctic Temperature
Table S3 summarizes key quantitative features of our reconstruction.
SI Thickness History
The forms of thickness histories used in optimizations are motivated by several considerations: (i) The doubling of accumulation rate between 18 ka and 15 ka would have caused thickening of a few hundred meters, (ii) retreat of the ice margins would have caused subsequent thinning, (iii) glacial geologic evidence indicates 100 m of thinning since 10 ka, (iv) the correspondence of East and West Antarctic temperatures from 8 ka to the present indicates no significant elevation changes in this period, and (v) full ice-sheet model simulations yield LGM thicknesses relative to present ranging from about −200 m to +360 m.
Our standard model scenario specifies 150 m of thickening between 18 ka and 15 ka followed by 50 m of thinning. In comparison, holding the thickness constant changes the reconstructed LGM temperature by +0.18 °C. Specifying a constant thickness before 12 ka, followed by thinning until 5 ka, changes the reconstructed LGM temperature by −1.59 °C to +1.42 °C as the initial thickness relative to modern ranges from −300 m to +450 m (Fig. S3). Including a 200-m increase between 18 ka and 13 ka, before the 12-ka to 5-ka thinning, reduces the LGM temperature by 0.5 °C compared with the previous case. Using thickness histories calculated for the WDC site in specific ice-sheet model simulations yields the following changes to LGM temperature: −0.085 °C [model of Pollard et al. (59)], +0.55 °C [model of Golledge et al. (60)], and +0.74 °C [model of Pollard and DeConto (29)].
Acknowledgments
We are deeply indebted to many participants in the WDC project and especially thank K. Taylor, E. J. Brook, and J. W. C. White. The helpful comments of two anonymous referees are gratefully acknowledged. This work is funded through the US National Science Foundation Grants 0539232, 0537661 (to K.M.C.), 0537930, 1043092 (to E.J.S.), 1043518 (to C.B.), 0944199, 0944197, 0440666 (to E.D.W.), 0539578, 1043528, 1338832 (to R.B.A.), and 0538657 (to J.P.S.) and National Aeronautics and Space Administration Grant NNX12AB74G (to M.K.). We gratefully acknowledge additional support from the Martin Family Foundation (K.M.C.), the USGS Climate and Land Use Change Program (G.D.C.), and National Oceanic and Atmospheric Administration Climate and Global Change Fellowships (C.B.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1609132113/-/DCSupplemental.
References
- 1.Hansen J, et al. Climate sensitivity: Analysis of feedback mechanisms. Geophys Monogr. 1984;29:130–163. [Google Scholar]
- 2.Hewitt CD, Mitchell JFB. Radiative forcing and response of a GCM to ice age boundary conditions: Cloud feedback and climate sensitivity. Clim Dynam. 1997;13:821–834. [Google Scholar]
- 3.Claquin T, et al. Radiative forcing of climate by ice-age atmospheric dust. Clim Dynam. 2003;20:193–202. [Google Scholar]
- 4.Masson-Delmotte V. Information from paleoclimate archives. In: Stocker TF, et al., editors. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. 2013. pp. 383–464. [Google Scholar]
- 5.Annan JD, Hargreaves JC. A new global reconstruction of temperature changes at the last glacial maximum. Clim Past. 2013;9:367–376. [Google Scholar]
- 6.Shakun JD. Global warming preceded by increasing carbon dioxide concentrations during the last deglaciation. Nature. 2012;484:49–55. doi: 10.1038/nature10915. [DOI] [PubMed] [Google Scholar]
- 7.von Deimling TS, Ganopolski A, Held S, Rahmstorf S. How cold was the last glacial maximum? Geophys Res Lett. 2006;33:L14709. [Google Scholar]
- 8.Pithan F, Mauritsen T. Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nat Geosci. 2014;7:181–184. [Google Scholar]
- 9.Graversen RG, Langen PL, Mauritsen T. Polar amplification in CCSM4: Contributions from the lapse rate and surface albedo feedbacks. J Clim. 2014;27:4433–4450. [Google Scholar]
- 10.Cuffey KM. Large arctic temperature change at the Wisconsin-Holocene glacial transition. Science. 1995;270:455–458. [Google Scholar]
- 11.Dahl-Jensen D. Past temperatures directly from the Greenland ice sheet. Science. 1998;282:268–271. doi: 10.1126/science.282.5387.268. [DOI] [PubMed] [Google Scholar]
- 12.Masson-Delmotte V. A comparison of the present and last interglacial periods in six Antarctic ice cores. Clim Past. 2011;7:397–423. [Google Scholar]
- 13.Cuffey K, Paterson W. The Physics of Glaciers. 4th Ed Elsevier; Burlington, MA: 2010. [Google Scholar]
- 14.Salamatin AN, et al. Ice core age dating and paleothermometer calibration based on isotope and temperature profiles from deep boreholes at Vostok Station (East Antarctica) J Geophys Res. 1998;103(D8):8963–8978. [Google Scholar]
- 15.WAIS Divide Project Members Onset of deglacial warming in West Antarctica driven by local orbital forcing. Nature. 2013;500:440–444. doi: 10.1038/nature12376. [DOI] [PubMed] [Google Scholar]
- 16.WAIS Divide Project Members Precise interpolar phasing of abrupt climate change during the last ice age. Nature. 2015;520:661–665. doi: 10.1038/nature14401. [DOI] [PubMed] [Google Scholar]
- 17.Kavanaugh JL, Cuffey KM. Space and time variation of δ 18O and in Antarctic precipitation revisited. Global Biogeochem Cy. 2003;17(1017):1–14. [Google Scholar]
- 18.Sowers T, Bender M, Raynaud D, Korotkevich Y. δ 15N of in air trapped in polar ice: A tracer of gas transport in the firn and a possible constraint on ice age-gas age differences. J Geophys Res. 1992;97(D14):15683–15697. [Google Scholar]
- 19.Severinghaus JP, Grachev A, Battle M. Thermal fractionation of air in polar firn by seasonal temperature gradients. Geochem Geophys Geosyst 2001 [Google Scholar]
- 20.Herron M, Langway C. Firn densification: An empirical model. J Glaciol. 1980;25:373–385. [Google Scholar]
- 21.Goujon C, Barnola J-M, Ritz C. Modeling the densification of polar firn including heat diffusion: Application to close-off characteristics and gas isotopic fractionation for Antarctica and Greenland sites. J Geophys Res. 2003;108(D24):4792. [Google Scholar]
- 22.Schneider DP, Steig EJ, Van Ommen T. High-resolution ice-core stable-isotopic records from Antarctica: Towards interannual climate reconstruction. Ann Glaciol. 2005;41:63–70. [Google Scholar]
- 23.Jouzel J, et al. Magnitude of isotope/temperature scaling for interpretation of central Antarctic ice cores. J Geophys Res. 2003;108(D12):4361. [Google Scholar]
- 24.Steig EJ, et al. Recent climate and ice-sheet changes in West Antarctica compared with the past 2,000 years. Nat Geosci. 2013;6:372–375. [Google Scholar]
- 25.Zwally HJ, Giovinetto M, Craven M, Morgan V, Goodwin I. Areal distribution of the oxygen-isotope ratio in Antarctica: Comparison of results based on field and remotely sensed data. Ann Glaciol. 1998;27:583–590. [Google Scholar]
- 26.Parrenin F, et al. Synchronous change of atmospheric and Antarctic temperature during the last deglacial warming. Science. 2013;339:1060–1063. doi: 10.1126/science.1226368. [DOI] [PubMed] [Google Scholar]
- 27.Nicolas JP, Bromwich DH. Climate of West Antarctica and influence of marine air intrusions. J Clim. 2011;24:49–67. [Google Scholar]
- 28.Buizert C, et al. Greenland temperature response to climate forcing during the last deglaciation. Science. 2014;345:1177–1180. doi: 10.1126/science.1254961. [DOI] [PubMed] [Google Scholar]
- 29.Pollard D, DeConto RM. Modelling West Antarctic ice sheet growth and collapse through the past five million years. Nature. 2009;458:329–332. doi: 10.1038/nature07809. [DOI] [PubMed] [Google Scholar]
- 30.Golledge NR, Fogwill CJ, Mackintosh AN, Buckley KM. Dynamics of the last glacial maximum Antarctic ice-sheet and its response to ocean forcing. Proc Nat Acad Sci USA. 2012;109:16052–16056. doi: 10.1073/pnas.1205385109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.DeConto RM, Pollard D. Contribution of Antarctica to past and future sea-level rise. Nature. 2016;531:591–597. doi: 10.1038/nature17145. [DOI] [PubMed] [Google Scholar]
- 32.Walsh JE. Intensified warming of the arctic: Causes and impacts on middle latitudes. Global Planet Change. 2014;117:52–63. [Google Scholar]
- 33.Putnam AE, et al. Warming and glacier recession in the Rakaia valley, Southern Alps of New Zealand, during Heinrich Stadial 1. Earth Planet Sci Lett. 2013;382:98–110. [Google Scholar]
- 34.Marcott SA, Shakun JD, Clark PU, Mix AC. A reconstruction of regional and global temperature for the past 11,300 years. Science. 2013;339:1198–1201. doi: 10.1126/science.1228026. [DOI] [PubMed] [Google Scholar]
- 35.PALEOSENS Project Members Making sense of palaeoclimate sensitivity. Nature. 2012;491:683–691. doi: 10.1038/nature11574. [DOI] [PubMed] [Google Scholar]
- 36.Schmittner A, et al. Climate sensitivity estimated from temperature reconstructions of the last glacial maximum. Science. 2011;334:1385–1388. doi: 10.1126/science.1203513. [DOI] [PubMed] [Google Scholar]
- 37.Fyke J, Eby M. Comment on “climate sensitivity estimated from temperature reconstructions of the last glacial maximum.”. Science. 2012;337:1294. doi: 10.1126/science.1221634. [DOI] [PubMed] [Google Scholar]
- 38.Hall BL, Porter CT, Denton GH, Lowell TV, Bromley GRM. Extensive recession of Cordillera Darwin glaciers in southernmost South America during Heinrich stadial 1. Quaternary Sci Rev. 2013;62:49–55. [Google Scholar]
- 39.Boex J. Rapid thinning of the late Pleistocene Patagonian Ice Sheet followed migration of the Southern Westerlies. Sci Rep. 2013;3:2118. doi: 10.1038/srep02118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Putnam AE, et al. The last glacial maximum at 44 S documented by a 10 Be moraine chronology at Lake Ohau, Southern Alps of New Zealand. Quaternary Sci Rev. 2013;62:114–141. [Google Scholar]
- 41.Clark PU, et al. Global climate evolution during the last deglaciation. Proc Natl Acad Sci USA. 2012;109:E1134–E1142. doi: 10.1073/pnas.1116619109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kageyama M, et al. Climatic impacts of fresh water hosing under Last Glacial Maximum conditions: A multi-model study. Clim Past. 2013;9:935–953. [Google Scholar]
- 43.Timmerman A, Timm O, Stott L, Menviel L. The roles of and orbital forcing in driving Southern Hemispheric temperature variations during the last 21000 yr. J Clim. 2009;22:1626–1640. [Google Scholar]
- 44.Moreno PI, et al. Radiocarbon chronology of the last glacial maximum and its termination in northwestern Patagonia. Quaternary Sci Rev. 2015;122:233–249. [Google Scholar]
- 45.Doughty AM, et al. Mismatch of glacier extent and summer insolation in Southern Hemisphere mid-latitudes. Geology. 2015;43:407–410. [Google Scholar]
- 46.Marcott SA, et al. Centennial-scale changes in the global carbon cycle during the last deglaciation. Nature. 2014;514:616–619. doi: 10.1038/nature13799. [DOI] [PubMed] [Google Scholar]
- 47.Buizert C, et al. The WAIS divide deep ice core WD2014 chronology–part 1: Methane synchronization (6831 ka bp) and the gas age–ice age difference. Clim Past. 2015;11:153–173. [Google Scholar]
- 48.Fudge TJ, et al. Variable relationship between accumulation and temperature in West Antarctica for the past 31,000 years. Geophys Res Lett. 2016;43(8):3795–3803. [Google Scholar]
- 49.Patankar SV. Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing; Washington, DC: 1980. [Google Scholar]
- 50.Clow GD. USGS polar temperature logging system, description and measurement uncertainties: US Geological Survey Techniques and Methods 2–E3. US Geological Survey; Reston, VA: 2008. p. 24. [Google Scholar]
- 51.Clow GD. Temperature data acquired from the DOI/GTN-P Deep Borehole Array on the Arctic Slope of Alaska, 1973–2013. Earth Syst Sci Data. 2014;6:201–218. [Google Scholar]
- 52.Orsi AJ, Cornuelle BD, Severinghaus JP. Little Ice Age cold interval in West Antarctica: Evidence from borehole temperature at the West Antarctic Ice Sheet (WAIS) divide. Geophys Res Lett. 2012;39:L09710. [Google Scholar]
- 53.Sigl M, et al. The WAIS divide deep ice core WD2014 chronology–part 2: Annual-layer counting (0–31 ka bp) Clim Past. 2016;12:769–786. [Google Scholar]
- 54.Barnola J-M, Pimienta P, Raynaud D, Korotkevich YS. -climate relationship as deduced from the Vostok ice core: A re-examination based on new measurements and on a re-evaluation of the air dating. Tellus B. 1991;43:83–90. [Google Scholar]
- 55.Petrenko VV, Severinghaus JP, Brook EJ, Reeh N, Schaefer H. Gas records from the West Greenland ice margin covering the last glacial termination: A horizontal ice core. Quaternary Sci Rev. 2006;25:865–875. [Google Scholar]
- 56.Severinghaus JP, Baudette R, Headly MA, Taylor K, Brook EJ. Oxygen-18 of records the impact of abrupt climate change on the terrestrial biosphere. Science. 2009;324:1431–1434. doi: 10.1126/science.1169473. [DOI] [PubMed] [Google Scholar]
- 57.Yen Y. 1981. Review of thermal properties of snow, ice and sea ice. (US Army Corps of Engineers, Cold Regions Research and Engineering Laboratory, Hanover, NH), Tech Rep CR 81–10, p 34.
- 58.Waite WF, Gilbert LY, Winters WJ, Mason DH. Estimating thermal diffusivity and specific heat from needle probe thermal conductivity data. Rev Sci Instrum. 2006;77(4):044904. [Google Scholar]
- 59.Pollard D, Chang W, Haran M, Applegate P, DeConto R. Large ensemble modeling of last deglacial retreat of the West Antarctic Ice Sheet: Comparison of simple and advanced statistical techniques. Geosci Model Devel Disc. 2015;8:9925–9963. [Google Scholar]
- 60.Golledge NR, et al. Antarctic contribution to meltwater pulse 1A from reduced Southern Ocean overturning. Nat Commun. 2014;5:5107. doi: 10.1038/ncomms6107. [DOI] [PubMed] [Google Scholar]
- 61.Steig EJ, et al. Warming of the Antarctic ice-sheet surface since the 1957 International Geophysical Year. Nature. 2009;457:459–462. doi: 10.1038/nature07669. [DOI] [PubMed] [Google Scholar]
- 62.Price SF, Waddington ED, Conway H. A full-stress, thermomechanical flow band model using the finite volume method. J Geophys Res. 2007;112:F03020. [Google Scholar]
- 63.Koutnik MR, et al. Holocene accumulation and ice flow near the West Antarctic Ice Sheet Divide ice core site. J Geophys Res. 2016;121:907–924. [Google Scholar]
- 64.Steig EJ, et al. West Antarctic ice sheet elevation changes. Antarct Res. 2001;77:75–90. [Google Scholar]
- 65.Conway H, Hall BL, Denton GH, Gades AM, Waddington ED. Past and future grounding-line retreat of the West Antarctic ice sheet. Science. 1999;286:280–283. doi: 10.1126/science.286.5438.280. [DOI] [PubMed] [Google Scholar]
- 66.Ackert RP, Jr, et al. Measurements of past ice sheet elevations in interior West Antarctica. Science. 1999;286:276–280. doi: 10.1126/science.286.5438.276. [DOI] [PubMed] [Google Scholar]
- 67.Peltier WR, Argus DF, Drummond R. Space geodesy constrains ice-age terminal deglaciation: The global ICE-6G_C (VM5a) model. J Geophys Res Solid Earth. 2015;120(1):450–487. [Google Scholar]
- 68.Resplandy L, et al. Constraints on oceanic meridional heat transport from combined measurements of oxygen and carbon. Clim Dynam. 2016;47:3335–3357. [Google Scholar]
- 69.Rind D, et al. Effects of glacial meltwater in the GISS coupled atmosphere-ocean model. 2. A bipolar seesaw in Atlantic Deep Water production. J Geophys Res. 2001;106(D21):27355–27365. [Google Scholar]
- 70.Barker S, et al. Interhemispheric Atlantic seesaw response during the last deglaciation. Nature. 2009;457:1097–1102. doi: 10.1038/nature07770. [DOI] [PubMed] [Google Scholar]
- 71.Broccoli AJ, Dahl KA, Stouffer RJ. Response of the ITCZ to Northern Hemisphere cooling. Geophys Res Lett. 2006;33:L01702. [Google Scholar]
- 72.Felzer B, Oglesby RJ, Webb T, Hyman DE. Sensitivity of a general circulation model to changes in northern hemisphere ice sheets. J Geophys Res. 1996;101(D14):19077–19092. [Google Scholar]
- 73.Zhu J, Liu Z, Zhang X, Eisenman I, Liu W. Linear weakening of the AMOC in response to receding glacial ice sheets in CCSM3. Geophys Res Lett. 2014;41:6252–6258. [Google Scholar]
- 74.Lee S-Y, Chiang JCH, Chang P. Tropical Pacific response to continental ice sheet topography. Clim Dynam. 2015;44:2429–2446. [Google Scholar]
- 75.Anderson RF. Wind-driven upwelling in the Southern Ocean and the deglacial rise in atmospheric . Science. 2009;323:1443–1448. doi: 10.1126/science.1167441. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data are available online through the U.S. Antarctic Program Data Center (http://www.usap-data.org/).