Maximizing the potential of multi-parental crop populations

Abstract

Most agriculturally significant crop traits are quantitatively inherited which limits the ease and efficiency of trait dissection. Multi-parent populations overcome the limitations of traditional trait mapping and offer new potential to accurately define the genetic basis of complex crop traits. The increasing popularity and use of nested association mapping (NAM) and multi-parent advanced generation intercross (MAGIC) populations raises questions about the optimal design and allocation of resources in their creation. In this paper we review strategies for the creation of multi-parent populations and describe two complementary in silico studies addressing the design and construction of NAM and MAGIC populations. The first simulates the selection of diverse founder parents and the second the influence of multi-parent crossing schemes (and number of founders) on haplotype creation and diversity. We present and apply two open software resources to simulate alternate strategies for the development of multi-parent populations.

1. Introduction

Expanded genetic diversity is required to address the perpetual challenges of quantitative trait dissection. In crops, mapping populations developed from two contrasting parents have been popular for creating novel recombinants and haplotypes for key crop traits (e.g. the UK wheat reference population Avalon × Cadenza; see www.wgin.org.uk; Ma et al., 2015). Bi-parental mapping populations are simple to develop and possess high power for QTL detection (Semagn et al., 2006, Xu et al., 2016). However, combining the genomes of only two parents results in a relatively narrow genetic base and inadequately represents wider allelic diversity (Jannink, 2007). Despite this, linkage based quantitative trait locus (QTL) mapping using bi-parental populations is the most widely used method of identifying regions of genome controlling phenotypic variation (Bernardo, 2008).

Genome-wide association (GWA) or linkage disequilibrium mapping is a complementary method exploiting linkage disequilibrium (LD) as a function of historical recombination for QTL mapping. GWA studies however are prone to detection of false positive QTLs due to unknown population structure and genetic relatedness among the lines (Lewis, 2002, Zhao et al., 2007) and statistical approaches may also over-compensate for population structure (Segura et al., 2012), thereby lowering the accuracy of QTL detection. In addition, low frequency rare variant QTLs may be undetected despite having large effects (Breseghello and Sorrells, 2006, Mackay and Powell, 2007).

Multi-parent populations (MPPs) have emerged as next-generation mapping resources combining diverse genetic founder contributions with high levels of recombination (Mackay and Powell, 2007, Cavanagh et al., 2008), overcoming some of the limitations of bi-parental and GWA populations (Huang et al., 2011). The two most commonly developed forms of MPPs in crop genetics are nested association mapping (NAM) and multi-founder advanced generation inter-cross (MAGIC) populations. Derivation from greater than two parents and structured inter-mating maximizes allelic diversity and facilitates the inclusion of novel recombinants. Creating controlled populations from crosses between multiple well-characterized parents allows the derivation of individuals which feature diverse levels and patterns of recombination and new genotype and haplotype combinations. These features are exploited for trait mapping with the contribution of multiple founders increasing the potential genetic diversity in advanced lines (Yu et al., 2008).

NAM populations were designed to increase the power and precision of QTL mapping by combining the advantages of association mapping and bi-parental populations. NAM populations can effectively capture rare alleles allowing new loci to be seen (McMullen et al., 2009). Populations are derived by crossing a single inbred parent to a successive collection of diverse inbred lines. The first NAM population was created in maize, derived from crosses between the maize reference line B73 and 25 diverse inbred lines to produce 5000 recombinant inbred lines (RILs) (Yu et al., 2008). These capture thousands of recombination events but recombination and segregation distortion varies among different families which can limit the precision of genetic dissection of quantitative traits (McMullen et al., 2009). The maize NAM has been used to study the genetic architecture of a number of morphological and disease resistance traits (Buckler et al., 2009, Tian et al., 2011, Cook et al., 2012, Bajgain et al., 2016). A NAM derived advanced backcross population has been recently developed for barley which combines wild barley landraces into the exotic background Rasmusson (Nice et al., 2016).

MAGIC populations are developed by inter-crossing multiple (typically four, eight or sixteen) parental lines in a balanced funnel crossing scheme. The resulting RILs are highly recombined mosaics of the founder genomes. Multi-cross populations were first proposed for mouse known as heterogeneous stock and collaborative cross populations (Mott et al., 2000, Valdar et al., 2006b, Threadgill and Churchill, 2012) and for plants by Mackay and Powell (2007). They are also similar to the Arabidopsis multi-parent recombinant inbred line (AMPRIL) population described by Huang et al. (2011) which was developed from diallel crossing of eight Arabidopsis accessions from diverse geographical origins. In MAGIC, high levels of recombination result in low LD and give high mapping resolution. A high density MAGIC linkage map has recently been developed in wheat (Gardner et al., 2016). MAGIC populations have being developed in many plant species including Arabidopsis (Kover et al., 2009), tomato (Pascual et al., 2015), barley (Sannemann et al., 2015), maize (Dell'Acqua et al., 2015), sorghum (Higgins et al., 2014), wheat (Huang et al., 2012, Mackay et al., 2014) and rice (Bandillo et al., 2013).

Trait mapping in structured MPPs involves the use of statistical models developed based on their theoretical properties. Many models for genetic data analysis have been generated by computer simulation to determine the properties and outcomes of an experimental design. For example, simulation studies in MPPs can be applied to determine the optimal number of founder lines, crosses and the size of the population needed to effectively track the genetic architecture of quantitative traits (Myles et al., 2009). Kover et al. (2009) simulated the effects of MPP size on mapping resolution and power for QTL detection determining that QTL detection error rates decreased when population size increased and QTL could be mapped to smaller intervals. Simulation studies typically generate in silico data describing population specific genetic polymorphism which are then used to describe, solve or predict. Because in silico data sets are not subject to the same inconsistencies as real datasets, they predict outcomes for specified scenarios (Yu et al., 2006, Yu et al., 2008, Hoban et al., 2011). Verbyla et al. (2014) simulated the effect of a joint analyses of multiple environmental and multiple trait datasets on QTL detection accuracy and to infer QTL-by-environment interactions in MAGIC.

MPPs are increasingly used in crop genetics and schemes for their creation vary in design. In this paper we present simulations using two open source software applications that analyse the selection of founders and the properties of both NAM and MAGIC population types. We compare schemes in which the number of crosses and the number of parents vary. The function of MPPs can be viewed as the creation of haplotype diversity for fine mapping and selection and the different schemes were therefore quantified as the number of haplotypes created for a range of MPP configurations.

2. Materials and methods

2.1. Selecting founders

Two methods of selecting subsets of individuals from populations to maximize genetic diversity have previously been implemented using PowerMarker analysis software (Liu and Muse, 2005) and can be used to select founding individuals for MPPs. These methods are (i) selection using total number of segregating alleles and (ii) selection using average gene diversity (Nei, 1973). The PowerMarker analysis software used a simulated annealing algorithm that allowed for efficient selection of individuals from within a large set of germplasm for which performing an exhaustive search would be infeasible. However, PowerMarker is no longer actively supported and a functional version of the software is no longer publicly available. To fill this void, we implemented a complementary method using genetic algorithms. These genetic algorithms were developed using the R package ‘GA’ (Scrucca, 2013) which provides a flexible, general-purpose package for this purpose. This flexibility was used to define custom objective functions and genetic operators for implementing each method. The scripts used to implement these methods are available (http://www.niab.com/pages/id/326/Resources) and are also available as Supplementary information.

The performance of these methods was examined using the 376 wheat varieties in the TriticeaeGenome association mapping panel (Bentley et al., 2014; dataset available as above). Each line was genotyped with 2535 polymorphic DArT markers (Jaccoud et al., 2001). Each method was used to select two, four, eight, sixteen and twenty six line subsets that could be used to generate MPPs. Average performance of each method was measured across ten replicates and compared to selection of random individuals on the basis of percentage of polymorphic loci and average gene diversity. Selection of the two line subset was compared against the best possible subset for percentage of polymorphic loci and average gene diversity using an exhaustive search of all possible combinations.

In addition, we compared different MPPs for the diversity they captured and for the probability that they were segregating. We compared a bi-parental cross, MAGIC populations with four, eight, sixteen and 26 founders, and a NAM population with 25 nested families, sampling founders from source populations segregating for a bi-allelic locus with minor allele frequencies of 0.01, 0.1, 0.2, 0.4 and 0.5. We also considered a bi-allelic locus with an infinite number of alleles (i.e. all sampled individuals carrying different alleles). Diversity was measured as:

$$1-\mathrm{\Sigma p}{{}_{\mathrm{i}}}^2$$

where p_i is the frequency of the ith allele (Weir, 1996). We calculated the probability that a mapping population was segregating from the allele frequency in the source population and the binomial distribution.

2.2. Simulating multi-parent populations

2.2.1. Pedigrees

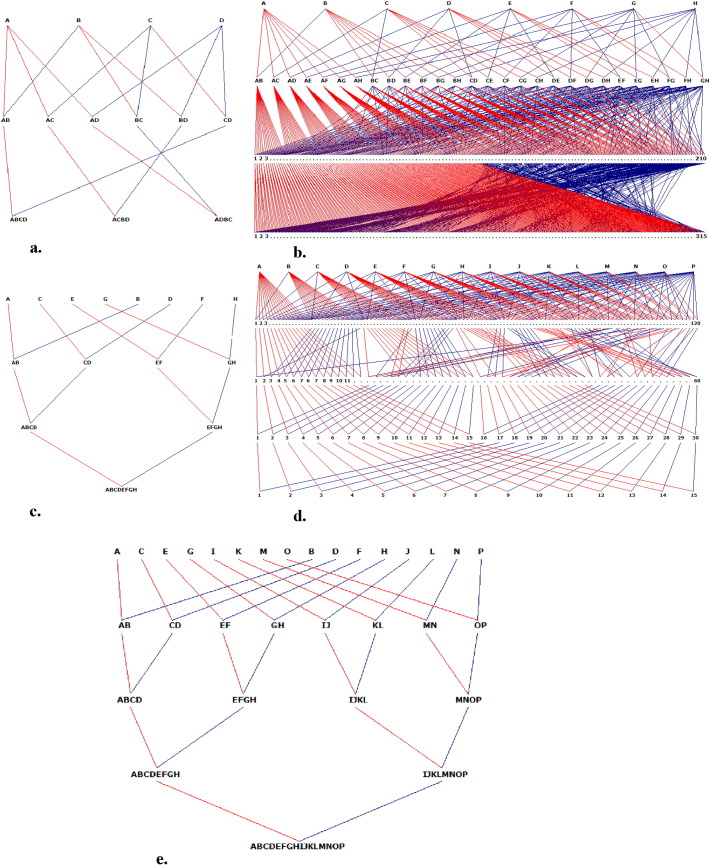
The creation of MAGIC populations is based around simple funnel crossing schemes (Huang et al., 2015) of the form, for example for an eight parent population, {[(A × B) × (C × D)] × [(E × F) × (G × H)]} where the matched brackets ( ), [ ] , { } delineate the four two-way, two four-way and one eight-way crosses respectively and the letters denote the eight parents. To sample diversity among the parents and to reduce LD within the population (for greater precision in mapping), multiple funnel crosses should be used in creating the population. For example, in the case above, there is greater scope for recombination between chromosome segments from lines A and B than there is from lines A and H. For this reason, we searched for crossing schemes which provide balance among the parental origins and contributions at each cycle of crossing. As described in Mackay et al. (2014), for an eight founder population, there are 28 possible F₁ combinations, 210 4-way combinations among unrelated F₁s and 315 eight-way crosses (as the four-way cross ABCD can be paired with EFGH, EGFH and EHFG). For the sixteen-way MAGIC, creating all possible crosses at each generation is very labour intensive, even in a large crossing program. We therefore reduced the number of crosses, while maintaining the equality of the contribution to the next generation and opportunities for recombination among chromosome tracts originating from different founders.

Following the crossing stage, inbred lines are produced. In these simulations, all individuals at the final stage of crossing were inbred for four generations by single seed descent (SSD). The final population size was maintained as close to 1000 recombinant inbred lines (RILs) as possible. All founders used in all simulations were assumed to be completely inbred. All schemes were balanced so that the expected contribution of any founder to any derived RIL was equal. MAGIC pedigrees from four, eight and sixteen parents were simulated.

The four-parent MAGIC pedigree was designed as follows: four genetically distinct founders, assumed to be completely inbred were inter-crossed in a half diallel pattern to produce six F₁s, each F₁ was then crossed to a complementary F₁ to create three four-way hybrids which are mosaics of the four parents. Each four-way cross was replicated 111 times and from each cross, three individuals were sampled to make a population of 999 plants which were inbred by SSD for four generations (Fig. 1a).

Fig. 1.

Pedigree representation of all simulated MAGIC populations. (a) Four-parent MAGIC. (b) Eight-parent MAGIC population, multiple funnel MAGIC crossing scheme. (c) Eight-parent, single funnel crossing scheme. (d) Sixteen-parent, multiple funnel crossing scheme. (e) Sixteen-parent, single funnel crossing scheme.

For the eight-parent MAGIC, two pedigree schemes were simulated. In the first scheme, all eight parents were inter-crossed in a half diallel to create 28 F₁s. Each F₁ was then systematically crossed to 15 complementary F₁s to avoid inbreeding producing 210 four-way hybrids. Each four-way hybrid was subsequently crossed to three complementary four-way hybrids to produce 315 eight-way individuals (Fig. 1b). Each eight-way cross was made in three replicates, explicitly using separate parents sampled from the segregating four-way crosses, to make a population of 945 lines which were inbred for four generations by SSD. In the second scheme, inter-crossing between pairs of parents was made in a single funnel (Fig. 1c). Founders were paired to create four F₁s followed by two four-way crosses and one eight-way cross. The eight-way crosses were made in 315 replicates (630 different parents) to make the two schemes comparable and to maximize recombination and to avoid the effect of genetic drift. From each of these eight-way crosses, three individuals were sampled to produce a population of 945 individuals which were inbred for four generations by SSD.

Two crossing schemes were also used to develop the sixteen-founder MAGIC population. The first scheme was a multiple funnel (Fig. 1d) and parents were inter-crossed in a half diallel to create 120 F₁s. Every F₁ was next paired to one unrelated F₁ to make 60 four-way crosses. Each four-way was in turn paired with an unrelated four-way to make 30 eight-way crosses and using the same method, fifteen sixteen-way crosses were made, making sure to avoid inbreeding and reciprocal crossing in the resulting sixteen-founder individuals. The number of lines in the final generation of sixteen-way lines was made up to 300 lines by replicating each eight-way cross 20 times to create 600 eight-way individuals. In the second scheme, the parents were mixed in a single funnel by creating eight F₁s, four four-way hybrids, two eight-way hybrids and finally one sixteen-way hybrid, with each parent paired only once (Fig. 1e). To make the two schemes for sixteen-way populations comparable, each four-way cross was replicated 15 times to create sixty four-way hybrids. This was next used to produce 600 eight-way hybrids by making 20 replicates of each cross. This gave 300 lines in the final sixteen-way population. Both populations were increased to 1005 lines by sampling three to four individuals from each sixteen-way hybrid.

The NAM population was made up of 25 standard mapping populations, each producing 200 RILs, giving 5000 lines in total. Each of the 25 populations had one common parent and one unique parent.

2.2.2. Simulations

Initial simulations were based on two chromosomes and four loci with all founders carrying unique alleles at all loci so all combinations of founder contributions and recombinations were tagged. The first chromosome (denoted A) had two loci 5 cM apart while the second chromosome (denoted B) had two loci 10 cM apart. A second round of simulations were made to examine expanded diversity based on the 376 wheat varieties in the TriticeaeGenome association mapping panel (Bentley et al., 2014) as above. Using the above founder selection program, four, eight and sixteen founders were selected to maximize allele number. MAGIC pedigrees were simulated as described above using sixteen polymorphic DArT markers evenly distributed along chromosomes to assess the number of realized haplotypes from these crosses.

Gene dropping was introduced by MacCluer et al. (1986) as a means of stochastic simulation of the distribution of alleles at a locus among members of a pedigree. Genotypes are assigned to founder individuals, either by sampling from a distribution of genotypes or by assigning known genotypes. Alleles are sampled at random from the founders and transmitted to progeny. Alleles from the simulated genotypes of the progeny are then sampled in turn and transmitted to the next generation. This process continues until genotypes for all members of the pedigree are simulated. Repetition of the simulations generates a probability distribution of genotype and allele frequencies in the pedigree, conditional on the founder genotypes. Gene dropping is the standard method for simulation of genotypes in pedigrees and the extension to multiple loci simply involves sampling gametes, or haplotypes from multi-locus genotypes for transmission to the next generation while allowing for recombination in generating the transmitted haplotypes.

We created the program GeneDrop specifically to simulate the properties of MAGIC and other MPPs and it was used for all the simulations presented here. GeneDrop conducts gene dropping (MacCluer et al., 1986) simulations using csv files containing a known pedigree, genetic map and founder genotypes as input. It has been developed to overcome the limitations of alternative gene dropping software which are often incompatible with plant pedigrees involving hermaphroditic individuals and selfing. The program is written in C ++ and is available to download from http://www.niab.com/pages/id/326/Resources.

All six population/pedigree designs were simulated 1000 times for both single and multiple funnel schemes. Simulated data were processed in R (R Core Team, 2011) to compute the average number of two-locus recombinant haplotypes and haplotype diversity for all MAGIC and NAM populations per simulation. For the different population schemes, recombinant haplotypes between loci on the same chromosome and from different chromosomes were assessed. For the second round of MAGIC population simulations, the number of unique haplotypes created was assessed by counting the total number of haplotypes created in incremental steps of four DArT markers. All simulations were performed on a Windows 7.0 laptop with 1000 simulations taking approximately fifteen minutes.

3. Results

3.1. Selecting founders

Two methods for using genetic algorithms to identify founder individuals of MPPs, maximizing segregating alleles or maximizing average gene diversity, were compared against random sampling (Table 1). Both methods selected subsets with higher percentages of polymorphic markers and greater average gene diversity than random sampling. Relative to each other, the genetic algorithm for segregating alleles found solutions capturing slightly higher percentages of polymorphic loci and the genetic algorithm for average gene diversity found solutions with slightly higher average gene diversity. The average gene diversity in genetic algorithm selected subsets of four or more lines exceeded the average gene diversity for the entire set of 376 lines.

Table 1.

Average values over ten replications for percentage of polymorphic loci and average gene diversity for subsets chosen from 376 lines of the TriticeaeGenome association mapping panel. The subsets were chosen using random selection, a genetic algorithm for maximizing total segregating alleles, or a genetic algorithm for maximizing average gene diversity. The maximum obtainable values for subsets of size two were calculated using an exhaustive search.

Summary statistic	Selection method	Subset size
		2	4	8	16	26
Polymorphic loci (%)	Random	26.7	51.6	73.7	85.1	91.9
	Alleles	45.7	75.8	91.6	98.4	99.9
	Diversity	45.9	75.5	89.7	96.6	98.7
	Maximum	46.4	–	–	–	–
Average gene diversity	Random	0.134	0.215	0.267	0.280	0.286
	Alleles	0.299	0.317	0.331	0.330	0.324
	Diversity	0.230	0.316	0.351	0.364	0.365
	Maximum	0.232	–	–	–	–

For the subsets containing two lines, neither method succeeded in finding the best subset in all replications. The segregating allele method identified the best subset for polymorphic loci in three out of the ten replications and the gene diversity method identified the best subset for gene diversity twice. However, on average the chosen subsets were nearly equivalent to the best subsets for both percentage of polymorphic loci and average gene diversity.

With infinite alleles, all mapping populations will be segregating. Diversity increases asymptotically toward one with increase in founder number for MAGIC populations. However, for NAM, the founder used as common parent contributes half the alleles to the population which reduces diversity to below that for a four-way MAGIC design (Table 2). Table 3 shows segregation probabilities and diversities for founders selected from a source population with varying allele frequencies. Higher minor allele frequencies and larger numbers of founders both increase diversity and the probability that the mapping population is segregating at the locus. As before, the unequal contribution of founders to the NAM population reduces its diversity. In this respect, the 26 founder MAGIC population would be best. In practice, however, a 32 founder MAGIC population would take no longer to establish and the sixteen founder population compares favourably with the NAM for all metrics assessed via simulation in this study.

Table 2.

Comparison of diversity created from different MPP types from simulations in which each cross is segregating and every parent has a different allele.

MPP type	No. alleles	p(segregating)	Diversity
2-way bi-parental	2	1	0.500
4-way MAGIC	4	1	0.750
8-way MAGIC	8	1	0.875
16-way MAGIC	16	1	0.938
26-way MAGIC	26	1	0.962
NAMa	26	1	0.740
Source	Infinite	1	1.000

^a25 parents with frequency 1/50 and one with frequency 0.5.

Table 3.

Simulated segregation probabilities and diversity for founders selected from a source population segregating for a bi-allelic locus with varying minor allele frequencies (0.01, 0.1, 0.2, 0.4 and 0.5). The simulated lines are sampled from a population in Hardy-Weinberg equilibrium.

	p(segregating)					Diversity
MPP type	0.01	0.1	0.25	0.4	0.5	0.01	0.1	0.25	0.4	0.5
2-way	0.020	0.180	0.375	0.480	0.500	0.010	0.090	0.188	0.240	0.250
4-way	0.039	0.344	0.680	0.845	0.875	0.015	0.135	0.281	0.360	0.375
8-way	0.077	0.570	0.900	0.983	0.992	0.017	0.158	0.328	0.420	0.438
16-way	0.149	0.815	0.990	1.000	1.000	0.019	0.169	0.352	0.450	0.469
26-way	0.230	0.935	0.999	1.000	1.000	0.019	0.173	0.361	0.462	0.481
NAM	0.230	0.935	0.999	1.000	1.000	0.015	0.135	0.281	0.360	0.375
Source	1.000	1.000	1.000	1.000	1.000	0.020	0.180	0.375	0.480	0.500

3.2. Simulating multi-parent populations

We assessed the capability of each MPP type to generate new haplotypes as a measure of its potential to increase diversity for trait mapping. For the MAGIC populations, for n founders, the maximum number of recombinant haplotypes possible from two loci is n² − n. To drive recombination, and to avoid genetic drift, we found it preferable to replicate crosses starting from the second generation of the mixing stage to the last generation. This enhanced full recovery of all possible haplotypes (parental haplotypes and recombinant haplotypes) per simulation for the MAGIC populations. For NAM, the maximum number is 50 (two from each of the 25 bi-parental crosses).

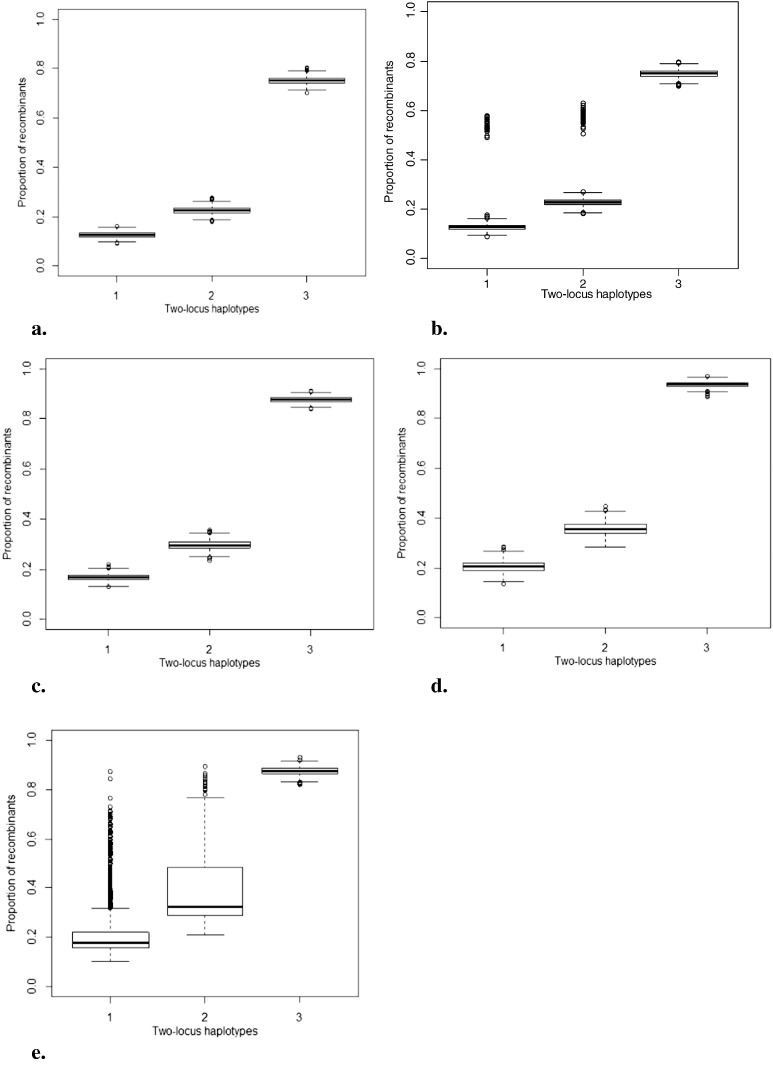
Simulations were used to evaluate the creation of recombinant haplotypes between two loci on the same chromosome and on different chromosomes. For the NAM population, all 50 possible two-locus haplotypes were observed in every simulation at all recombination frequencies. For the four-parent MAGIC population all sixteen possible two-locus haplotypes were observed at all recombination frequencies. The average number of recombinant haplotypes at 5 cM was 253.5 and at 10 cM was 452.1, giving an average ratio of 3.5 to 1 non-recombinant to recombinant haplotypes and 1.71 to 1 non-recombinant to recombinant haplotypes at 5 and 10 cM, respectively. The average number of recombinant haplotypes between different chromosomes was 1499.6 to 498.4 non-recombinants over the 1000 simulations (a three to one ratio of recombined to non-recombined haplotypes, as expected for unlinked loci at equilibrium). The proportion of recombinant haplotypes observed for three two-locus haplotypes for the four-parent MAGIC population is summarized in Fig. 2a. Across all simulations, none of the expected haplotypes were missing.

Fig. 2.

Level of recombination between pairs of loci in the MAGIC populations. Numbers 1 and 2 on the x-axis are linked locus pairs, 5 and 10 cM apart respectively, while 3 represents recombination between unlinked loci for (a) four-parent, (b) eight-parent, multiple funnel crossing scheme, (c) eight-parent, single funnel crossing scheme, (d) sixteen-parent, multiple funnel crossing scheme and (e) sixteen-parent, single funnel crossing scheme.

For the eight-parent MAGIC, two crossing schemes were simulated to compare levels of recombination using haplotype number. Observed haplotype number was compared to expected haplotype number for each scheme. For an eight-parent MAGIC population, we expect a maximum of 64 haplotypes per pair of loci. For the first scheme (multiple funnel; requiring more crosses than the second), with a distance of 5 cM between loci, we observed all possible haplotypes in only 31 of 1000 simulations; at least one haplotype was missing from 969 simulations. At 10 cM between loci, all haplotypes were observed in 634 simulations. For unlinked loci, all haplotypes were observed at an average ratio of seven to one recombinant to non-recombinant haplotype, in agreement with the expectation at linkage equilibrium (Table 4). In the second scheme, eight-parent individuals were created by mixing founders in a single funnel. At 5 cM, all haplotypes were observed in only five simulations; at least one haplotype was missing for 995 simulations. At 10 cM all haplotypes were observed in 317 simulations, about one-third of the times. Similar to the multiple funnel schemes, all simulated haplotypes were observed for all unlinked loci at an average ratio of seven to one recombinant to non-recombinant haplotypes (Table 4).

Table 4.

Observed number of missing haplotypes from simulations of the two crossing schemes of the eight-parent MAGIC population. (Maximum number = 64).

Number of missing haplotypes	Multiple funnel scheme		Single funnel
	5 cM	10 cM	5 cM	10 cM
0	31	634	5	317
1	102	286	20	377
2	196	67	47	198
3	216	11	136	79
4	204	2	174	22
5	122	0	173	6
6	72	0	161	1
7	35	0	143	0
8	10	0	86	0
9	10	0	32	0
10	2	0	13	0
11	0	0	8	0
12	0	0	2	0

The proportion of recombinant haplotypes observed per two locus pair for the multiple funnel scheme was less varied (Fig. 2b) over all simulations compared to the single funnel scheme where recombinant haplotypes were observed to be fewer in number and highly variable across simulations (Fig. 2c).

For the sixteen-parent MAGIC populations comparisons were made between the two schemes in the number of two-locus haplotypes found in the RILs. In the first scheme in which founders were mixed in fifteen funnels, all sixteen parental haplotypes were recovered in every simulation for all recombination frequencies; for the single funnel scheme however, only eight parental haplotypes were recovered in any simulation. For a sixteen-parent MAGIC population, we expect a maximum of 256 haplotypes including recombinant and parental haplotypes. The number of haplotypes observed per recombinant haplotype class in the multiple and single funnel crossing schemes are shown in Table 5. Fewer haplotypes were observed for the single compared to the multiple funnel scheme. It was also observed that in the single funnel scheme recombination levels were highly variable within the different simulated populations (Fig. 2d) when compared to the multiple funnel MAGIC scheme (Fig. 2e).

Table 5.

Number of haplotypes over all simulations for both schemes of the sixteen-parent MAGIC population (maximum possible = 256).

	Multiple funnel			Single funnel scheme
Chromosome	Min	Max	Mean	Min	Max	Mean
5 cM	99	147	124.0	44	61	52.5
10 cM	144	186	166.9	46	63	58.5
Unlinked	208	245	230.6	58	64	63.7

In the simulations based on DArT marker data, we examined the number of unique haplotypes that would potentially be created when founders are selected to maximize allele number. This was achieved by counting unique haplotypes incrementally in steps of four markers. Results from these simulations were consistent with previous findings. Across all simulations in the multiple and single funnel crosses, the number of haplotypes increased with increasing number of founders (Table 6).

Table 6.

Unique haplotypes generated from simulation of four, eight and sixteen-parent MAGIC populations using multiple and single funnel schemes with sixteen DArT markers.

	Multiple funnel									Single funnel
	4-parent			8-parent			16-parent			8-parent			16-parent
Markers	Min	Max	Mean	Min	Max	Mean	Min	Max	Mean	Min	Max	Mean	Min	Max	Mean
4	3	3	3	6	6	6	7	14	10.3	1	6	3.9	4	14	7.4
8	10	18	13.8	26	41	33.6	42	71	56.5	2	43	15.6	14	67	37.3
12	50	76	60.8	85	136	105.4	137	215	176.1	10	110	45.4	34	193	106.6
16	74	104	86.8	151	222	183.3	266	401	342.7	18	190	81.0	78	354	209.1

4. Discussion

We have used simulation to consider selection of parents to establish MPPs, and to assess the value of two forms: MAGIC and NAM. NAM is a flexible approach as it involves fewer crosses (compared to MAGIC) with potential to add crosses over time. However, although multiple parental lines (typically 26), are involved the creation of haplotype diversity is limited: at most 50 recombinant haplotypes are created. Although even with modest population sizes all 50 are virtually guaranteed to be produced unless linkage is very tight. A greater limitation may be that these 50 will always involve the common parent and therefore no novel haplotypes are generated between the 25 unique parents.

In order to assist in the selection of MPP founders we present a simple script using a genetic algorithm, although we have not directly addressed the process of selection of founders for the simulated crossing schemes presented. Founders can also be selected on breeding utility, or on diversity with the merits dependent on the biological questions to be addressed. For example, in using association mapping it is often difficult to pull together sufficient lines if there is a constraint on the agro-ecological adaptability of the parents. In this case MAGIC is probably the only option as it generates a large number of lines for genetical studies. Results in rice and wheat have shown that doing this also creates novel recombinants of direct interest to breeders (Bandillo et al., 2013, Mackay et al., 2014). In contrast to MAGIC, NAM is more highly influenced by the choice of the recurrent (common) parent. This has led to the suggestion that NAM should be extended to include more than one recurrent parent (Guo et al., 2010). To some extent, the two approaches can be viewed as having different objectives: MAGIC was intended to map QTL in breeders' germplasm to intervals of a few cM, suitable for marker assisted selection, whereas NAM is focused on positional cloning of QTL (Paux et al., 2012). Clearly, there is a complementary role for both in modern crop genetics.

NIAB have created two wheat MAGIC populations of relevance to UK and European winter wheat breeding. The first, termed MAGIC Elite (Mackay et al., 2014), was created from eight parental lines, all of which were commercially grown at the time the project started. The second, termed MAGIC Diverse, was created from sixteen parental lines to capture maximum genetic diversity without reference to trait values but conditional on each founder being adapted to the UK winter sown environment. NIAB are also developing four wheat NAM populations to incorporate diversity from wheat's ancestors as part of the UK Wheat Improvement Strategic Programme (WISP; www.wheatisp.org; Moore, 2015).

The use of multiple NAM founders would create more haplotype diversity, but simulations here show the potential for haplotype diversity is not as great as with MAGIC populations. The maize NAM consists of 200 lines from each of the 25 constituting bi-parental mapping populations giving 5000 lines in total, compared to 1000 for the MAGIC populations. At 5 and 10 cM the simulated multi-funnel eight-parent MAGIC population recovers on average 60.5 (minimum 54) and 63.5 (minimum 60) novel haplotypes respectively, but 64 for the unlinked loci (data not shown). In contrast, the NAM has more lines but only creates 50 haplotypes. This means that the eight-founder MAGIC population does better than the NAM for loose linkage as simulated here. The sixteen-parent MAGIC population, with the potential to create 240 recombinant two-locus haplotypes, is always better than the NAM as even at 5 cM 124 (minimum 99) haplotypes are created. Simulations based on DArT markers showed similar trends in the generation of haplotypes although there was a higher variance in haplotype number and lower probability of achieving certain recombinant types where frequencies were lower.

There are additional opportunities to further advance MAGIC. Following creation of individual RIL populations, it is advantageous to advance through additional generations of crossing thereby creating a second resource for mapping. These yet more advanced intercrosses can be used to replicate QTL detected in the initial population. It is also possible to optimise the use of the two populations for power and precision of QTL detection under constrained genotyping and phenotyping resources, though this has not been covered in the simulations presented here. However, there is no point in crossing indefinitely as the generation of novel haplotypes through recombination is balanced by the loss of haplotypes through drift. Although schemes exist to reduce the rate of inbreeding (Crow and Kimura (1970) in Fraser, 1972), these only reduce the rate of inbreeding, but do not eliminate it (Valdar et al., 2006a).

Creation of MPPs represents a greater investment of time and effort compared to traditional bi-parental populations. Despite this, numerous crop research groups throughout the world have developed, or are developing, MPPs. This paper broadly demonstrates that more founders and large populations are best. MAGIC outperforms NAM, even with smaller population sizes, provided that at least eight founders and multi-funnel MAGIC crossing schemes are used. Although only a few possible MAGIC schemes have been studied, GeneDrop simulations and counts of haplotype numbers are a simple way of quantifying the merits of different schemes and we have provided easy-to-use, open source, open access software to enable this.