Abstract
Ripples are high-frequency oscillations associated with population bursts in area CA1 of the hippocampus that play a prominent role in theories of memory consolidation. While spiking during ripples has been extensively studied, our understanding of the subthreshold behavior of hippocampal neurons during these events remains incomplete. Here, we combine in vivo whole-cell and multisite extracellular recordings to characterize the membrane potential dynamics of identified CA1 pyramidal neurons during ripples. We find that the subthreshold depolarization during ripples is uncorrelated with the net excitatory input to CA1, while the post-ripple hyperpolarization varies proportionately. This clarifies the circuit mechanism keeping most neurons silent during ripples. On a finer time scale, the phase delay between intracellular and extracellular ripple oscillations varies systematically with membrane potential. Such smoothly varying delays are inconsistent with models of intracellular ripple generation involving perisomatic inhibition alone. Instead, they suggest that ripple-frequency excitation leading inhibition shapes intracellular ripple oscillations.
Introduction
The hippocampal formation plays a critical role for the encoding, consolidation, and retrieval of new episodic memories (Squire, 1992), but the underlying neuronal mechanisms remain elusive. During quiet wakefulness and slow-wave sleep, brief (50–100 ms), high-frequency (80–250 Hz) ripple oscillations appear in the local field potential (LFP) and are associated with the near-synchronous discharge of principal cells (O’Keefe, 1976, Buzsaki et al., 1983). These population bursts produce coordinated output within the windows of synaptic integration and plasticity, powerfully entrain downstream brain regions, and are believed to contribute to the gradual establishment of memory representations across distributed neocortical circuits (Buzsaki, 1989, Chrobak and Buzsaki, 1996, Siapas and Wilson, 1998, Wierzynski et al., 2009, Diekelmann and Born, 2010, Carr et al., 2011, Logothetis et al., 2012, Buzsaki, 2015).
The circuit mechanisms generating ripple events have been the subject of much inquiry. The predominant conjecture is that hippocampal ripples are spontaneously initiated within the recurrent CA3 network. A population burst in CA3 provides excitatory input onto the dendrites of CA1 pyramidal cells, producing an intracellular depolarization and an associated negative sharp wave in the LFP of stratum radiatum (Buzsaki, 1986, Ylinen et al., 1995). Consequently, the amplitude of the LFP sharp wave correlates with the magnitude of net excitatory input to CA1. In support of this, the depth profile and pharmacological dependence of spontaneous sharp waves is very similar to field EPSPs evoked by stimulation of the Schaffer collaterals (Buzsaki, 1984, Buzsaki, 2015). The amplitude and slope of field EPSPs have been used extensively as a proxy for synaptic strength, since their size correlates with the magnitude of the synaptic currents and the number of activated input fibers (Bliss and Collingridge, 1993). Similarly, previous slice work has reported a correlation between the size of spontaneous sharp waves and the amplitude of excitatory currents in CA1 pyramidal cells (Mizunuma et al., 2014). The CA3 burst also recruits local CA1 interneurons, providing a source of feed-forward inhibition with a short delay (~2 ms) to CA1 pyramidal neurons (Alger and Nicoll, 1982, Pouille and Scanziani, 2001, Somogyi et al., 2014). Since CA3 exerts both direct excitatory and indirect feed-forward inhibitory influence on CA1 pyramidal cells, the consequences of scaling the magnitude of CA3 input on the membrane potential (Vm) of CA1 neurons are hard to predict in vivo. Individual CA1 pyramidal neurons receive ~30,000 excitatory inputs (Megias et al., 2001), and hence have the potential to be activated by many combinations of presynaptic partners. However, previous experiments suggest that CA1 pyramidal neurons fire only in a small subset of ripples, in a way that reflects previous experience (Wilson and McNaughton, 1994, Foster and Wilson, 2006, O’Neill et al., 2006, Diba and Buzsaki, 2007). The mechanisms enforcing such sparseness and selectivity of CA1 firing during ripples remain unknown.
Spiking of pyramidal cells and specific classes of interneurons is phase-locked to LFP ripple oscillations recorded in the pyramidal cell layer (Buzsaki et al., 1992, Klausberger et al., 2003). Hence, ripple oscillations coordinate spike timing within the CA1 population bursts. Three models of ripple generation have been proposed, each making different predictions regarding the spatiotemporal distribution of inputs onto CA1 neurons and their impact on membrane potential dynamics. First, sparse axo-axonal gap junctions between CA1 pyramidal neurons are thought to aid in the generation and propagation of ripple-frequency action potentials (Draguhn et al., 1998, Traub and Bibbig, 2000). This model predicts the presence of “spikelets” reflecting the antidromic propagation of action potentials from ectopic generation sites. Second, pyramidal cells receive ripple-frequency somatic inhibition due to reciprocal interactions within interneuron networks, pyramidal-interneuron interactions, or both (Ylinen et al., 1995, Stark et al., 2014, Buzsaki, 2015). According to this model, as neurons are hyperpolarized towards the reversal potential for inhibition, the phase of intracellular ripple oscillations should remain constant. Below the inhibitory reversal potential, their phase should abruptly flip 180 degrees. A third model, based on in vitro slice experiments, suggests that, in addition to inhibition, CA1 pyramidal cells might also receive ripple-frequency excitation (Maier et al., 2011). If this were true, the phase of intracellular ripple oscillations should vary continuously with Vm, as the relative contribution of excitation and inhibition changes due to differences in electrical driving force.
These competing hypotheses regarding the spatiotemporal distribution of excitatory and inhibitory inputs onto CA1 pyramidal neurons make specific predictions regarding their impact on the membrane potential. Yet, few studies have examined the membrane potential dynamics of CA1 pyramidal neurons during ripples in vivo (Ylinen et al., 1995, Kamondi et al., 1998, Maier et al., 2011, English et al., 2014, Valero et al., 2015). Here, we combine multisite LFP measurements with simultaneous whole-cell recordings in awake mice. Using this approach, we characterize the relationship between the strength of net excitatory input to CA1 and the membrane potential dynamics around ripples. In addition, we provide the first quantitative description of the phase relationship between spiking, intracellular, and LFP ripple oscillations in awake animals. Lastly, we discuss the consequences of our experimental observations for circuit models of ripple generation.
Results
The Average Membrane Potential Response During Ripples Has Three Components
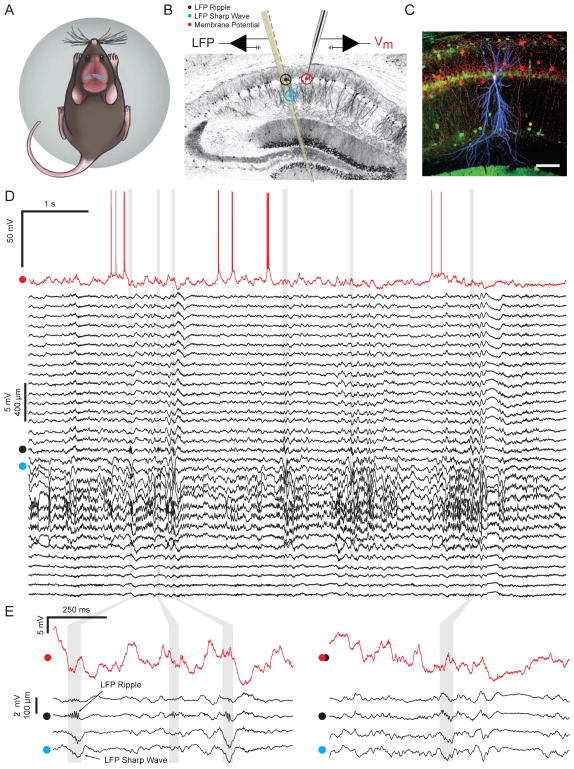
To investigate the membrane potential dynamics of pyramidal cells during ripple events, we combined whole-cell recordings from identified CA1 pyramidal neurons with simultaneous LFP measurements from a nearby (200–250 μm) multisite silicon probe in awake, head-fixed mice (Figure 1A–C). Before performing whole-cell recordings, a recording site from the silicon probe was carefully positioned within the CA1 pyramidal cell layer, where LFP ripple oscillations are reliably observed. Negative sharp waves, reflecting excitatory input onto the dendrites of CA1 pyramidal neurons, were observed in stratum radiatum and often co-occurred with ripples (Figure 1D–E). Mice were free to walk or run on a spherical treadmill, but spent the majority of their time in a state of quiet wakefulness, when the hippocampal LFP showed large irregular activity with associated high-frequency ripples in the CA1 pyramidal cell layer. Figure 1D shows an example of simultaneous whole-cell and LFP recordings from 32 sites spanning the neocortex, hippocampal formation, and parts of thalamus during a period of quiet wakefulness with six ripples. While the occurrence of ripples is apparent by inspecting the LFP, large ongoing membrane potential fluctuations and the diversity in the intracellular response during ripples makes it harder to identify these events in the Vm (Figure 1E; Figure S1).
Figure 1. In vivo whole-cell recordings from identified CA1 pyramidal neurons with simultaneous multisite extracellular measurements in awake mice.
(A) Schematic of a mouse on the spherical treadmill. The approximate whole-cell (red dot) and LFP (black dot) recording locations are marked on top of dorsal CA1.
(B) Illustration of the placement of the multisite silicon probe and patch pipette on a coronal slice of the dorsal hippocampus. Black, cyan, and red dots mark the locations of LFP ripple, LFP sharp wave, and whole-cell recordings, respectively.
(C) Confocal image of 100 μm thick coronal section showing biocytin stained CA1 pyramidal neuron (blue) with combined immunohistochemistry against parvalbumin (red) and calbindin (green). Scale bar is 100 μm.
(D) Example of simultaneous intracellular (red) and multisite LFP (black) recordings of spontaneous activity in an awake mouse. LFPs come from 32 channels spanning the neocortex, the hippocampal formation, and parts of the thalamus. The red dot next to the intracellular recording marks −55 mV. The black dot marks the channel within the CA1 pyramidal cell layer showing LFP ripple oscillations. The cyan dot marks the channel showing LFP sharp waves. Grey vertical bands mark the ripples detected in this segment.
(E) Same as in (D), but enlarged to show subthreshold Vm (red), and sharp waves and ripples in the LFP (black traces are 4 of the 32 LFP channels shown in D).
See also Figure S1.
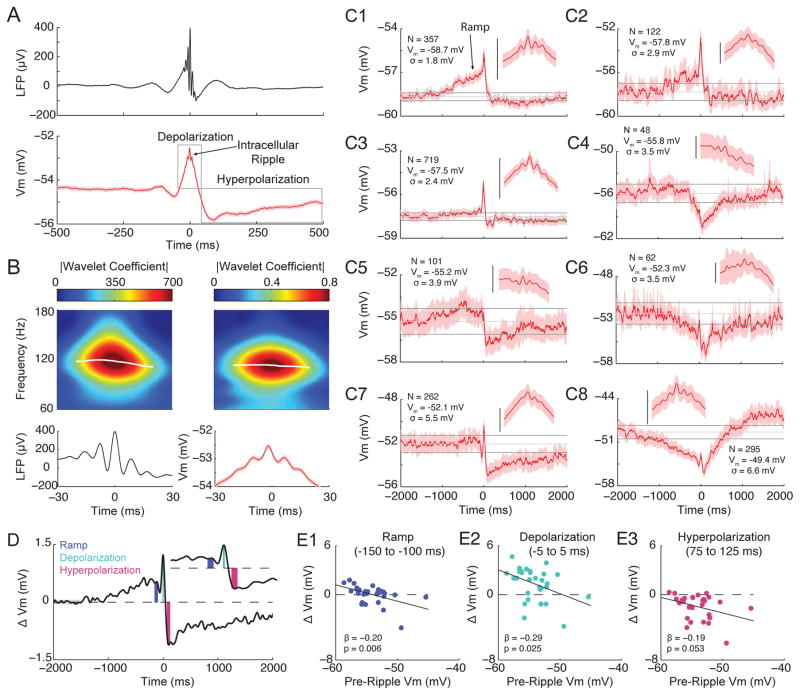
Across a total of ~8 hours of spontaneous activity from 30 neurons, we detected 4769 LFP ripples based on ripple-band power from the probe site located in the CA1 pyramidal cell layer. We then analyzed the membrane potential triggered on LFP ripples. Despite the variability in the membrane potential dynamics during single ripples, averaging across all ripples revealed a stereotyped waveform composed of three components: a sharp wave-associated depolarization (depolarization), superimposed ripple-frequency Vm oscillations (intracellular ripple), and a post-ripple hyperpolarization (hyperpolarization) lasting hundreds of milliseconds (Figure 2A)(Ylinen et al., 1995, Maier et al., 2011, English et al., 2014). A time-frequency decomposition showed that LFP ripple oscillations (LFP ripples) and intracellular ripples are restricted in both time and frequency and have similar structure (Figure 2B).
Figure 2. Average membrane potential dynamics during ripples.
(A) Ripple-triggered averages of the LFP from the CA1 pyramidal cell layer (top) and subthreshold Vm (bottom) for 4769 ripples. Shaded regions mark mean ± SEM. Note 3 components to the average intracellular response: a sharp wave associated depolarization (depolarization), superimposed ripple-frequency Vm oscillations (intracellular ripple), and a prolonged, post-ripple hyperpolarization (hyperpolarization).
(B) Enlarged view from (A) showing average ripple oscillations in the LFP (bottom, left) and Vm (bottom, right). Above each average are the wavelet-derived spectrograms showing that the average LFP and intracellular ripple are restricted in time/frequency. The magnitude of the wavelet coefficient was used as the instantaneous power. The white traces on the spectrograms mark the instantaneous frequency with the largest power at each sample.
(C1–C8) Examples of ripple-triggered averages of the subthreshold Vm for individual neurons, arranged according to their pre-ripple Vm (−2 to −1.5 s). The shaded region marks the 95% confidence intervals for each sample. The upper and lower horizontal grey lines are the mean confidence intervals of the pre-ripple Vm. The middle grey line marks the mean Vm from this same interval. The inset shows a magnification (± 30 ms) of intracellular ripple oscillations. Scale bars are 2 mV. The number of ripples, the pre-ripple Vm, and the standard deviation of the pre-ripple Vm are listed for each neuron. Note the presence of depolarizing (C1, C2, C5) and hyperpolarizing (C6, C8) ramps in the Vm for a subset of neurons starting approximately 1 second before the ripple event. Note also that more hyperpolarized neurons (top panels) tend to have depolarizing ramps and larger sharp-wave associated depolarizations, while more depolarized neurons (bottom panels) tend to have larger post-ripple hyperpolarizations.
(D) Schematic showing quantification of intracellular response amplitude in short windows at the end of the ramp (blue; −150 to −100 ms), and during the depolarization (turquoise; −5 to 5 ms) and hyperpolarization (pink; 75 to 125 ms). The component amplitudes (colored bars) were computed as the difference between the median Vm in these windows and the pre-ripple Vm (grey bar; average from −2 to −1.5 s). The inset shows a magnified view around the component windows.
(E1–E3) Scatter plots showing the relationship between pre-ripple Vm and the amplitude of the ramp (E1), the depolarization (E2), and the hyperpolarization (E3).
See also Figure S2.
Diverse Single Neuron Membrane Potential Dynamics During Ripples
Pyramidal neurons in CA1 are a heterogeneous population of cells that differ in terms of their morphology, connectivity, and gene expression patterns (Graves et al., 2012, Lee et al., 2014). Therefore, individual pyramidal neurons may show cell-specific responses during ripples (Valero et al., 2015). To investigate this possibility, we computed the average ripple-triggered Vm for each neuron. Figure 2C1–C8 shows example neuron-averages arranged according to their pre-ripple Vm. The intracellular depolarization, ripple, and hyperpolarization could be identified for nearly every neuron, but with a range of amplitudes that showed no obvious clustering of response type. This analysis also revealed a subset of neurons that slowly ramp their Vm beginning approximately one second before ripple onset. Three neurons had significant depolarizing ramps (Figure 2C1, C2, C5) and two neurons had significant hyperpolarizing ramps (Figure 2C6, C8), though most neurons showed no obvious ramping on average (N=25).
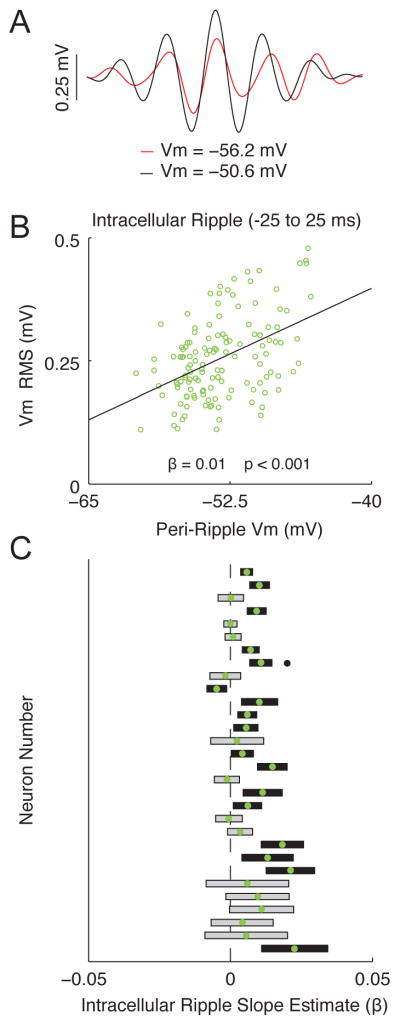
What underlies the diversity in single neuron responses during ripples? One contributing factor could be the resting membrane potential via its effect on the electrical driving force for excitation and inhibition. Indeed, more hyperpolarized neurons (top panels of Figure 2C) have depolarizing ramps and bigger sharp wave associated depolarizations, while depolarized neurons (bottom panels of Figure 2C) tend to have larger post-ripple hyperpolarizations (Figure 2D–E). Similarly, the majority of neurons (16 of 30) had significantly larger intracellular ripples when they were more depolarized (Figure 3), though this was not observed in the neuron averages (p=0.91; not shown). Together, these results further support the notion that CA1 pyramidal neurons are a heterogeneous population and suggest the state of individual neurons, as reflected in their resting membrane potential, affects the intracellular response during ripples.
Figure 3. Membrane potential dependence of intracellular ripple oscillation amplitude.
(A) Average ripple-band Vm (intracellular ripple) from the most depolarized half (black) and hyperpolarized half (red) of ripples from a single neuron.
(B) Scatter plot showing relationship between peri-ripple Vm (± 25 ms average) and intracellular ripple RMS for all single ripples from the same neuron as in (A). Note that ripples occurring at more depolarized levels tend to be larger, giving rise to a positive slope estimate (β>0; p<0.001).
(C) Comparison of slope estimates (β) computed as in (B) across all 30 neurons, sorted by the number of ripples for each neuron. Neurons with the largest number of ripples are on top. Green dots mark slope estimates. Rectangles are the 95% confidence intervals. Black rectangles indicate slope estimates that are significantly different from 0 (grey otherwise). Black dot marks location of neuron used in (A–B). Note that the majority of neurons (26 of 30) tended to have larger intracellular ripples at more depolarized levels, as indicated by positive slope estimates (β > 0), which is statistically different (p<0.01) from the expected proportion of 0.5 using a two-sided binomial test.
Membrane Potential Dynamics Vary With LFP Sharp Wave Amplitude
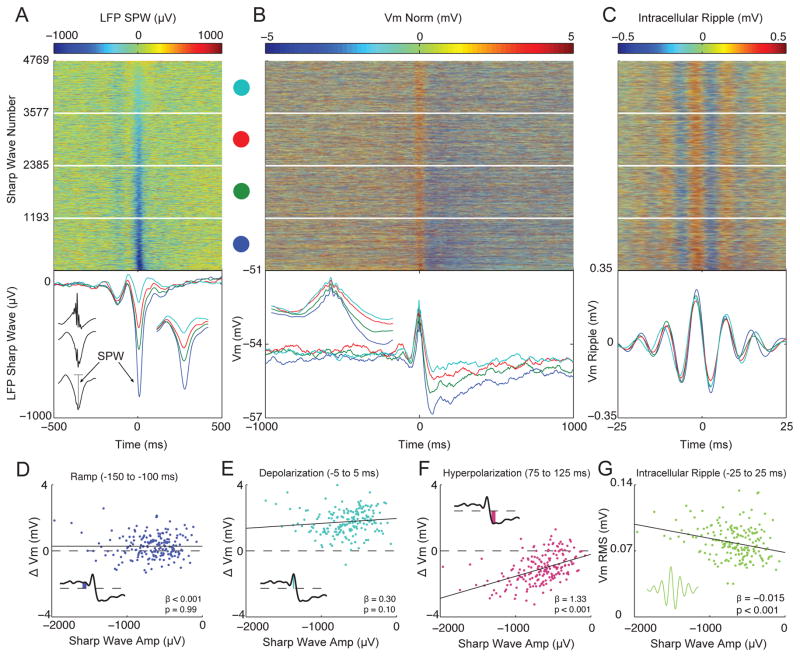
Hippocampal ripples often co-occur with negative sharp waves in the LFP of stratum radiatum (Figure 1). Sharp waves reflect excitatory input from area CA3 impinging on the dendrites of CA1 pyramidal neurons, and their amplitude correlates with, and therefore serves as a proxy for, the magnitude of the excitatory synaptic currents (Figure S3). Excitatory input from CA3 also recruits local CA1 interneurons, producing feed-forward inhibition onto CA1 pyramidal neurons. Therefore, by characterizing how the intracellular response varies as a function of sharp wave amplitude, we can assess the interplay between excitation and inhibition as a function of input strength.
To characterize how the membrane potential dynamics change with input strength, we sorted all 4769 intracellular responses by the amplitude of the LFP sharp wave and examined how the shape of the intracellular response varied (Figure 4A–C). Surprisingly, the amplitude of the intracellular depolarization was relatively independent of sharp wave amplitude. In contrast, larger LFP sharp waves were associated with a larger post-ripple hyperpolarization and larger intracellular ripple oscillations (Figure 4B–C). Only a negligible post-ripple hyperpolarization occurred with the smallest sharp waves. To statistically assess these relationships, we performed linear regressions between sharp wave amplitude and the amplitude of the intracellular components (Figure 4D–G). Consistent with the quartile-averages, larger sharp waves were associated with larger post-ripple hyperpolarizations (p<0.001) and intracellular ripples (p<0.001), while the ramp (p=0.99) and intracellular depolarization (p= 0.10) were invariant. These results suggest that larger excitatory currents are balanced by a proportional inhibition, such that the net current depolarizing the soma is invariant to sharp wave amplitude, on average. Under hyperpolarizing current injection, when the driving force for inhibition is reduced and this balance is altered, larger LFP sharp waves are associated with a larger intracellular depolarization (Figure S3).
Figure 4. Membrane potential dynamics vary with sharp wave amplitude.
(A) Top: Ripple-triggered LFP from stratum radiatum, sorted by sharp wave amplitude for all 4769 ripples. Bottom: Quartile averages color coded according to dots above. The inset to the left shows the average LFP sharp wave (bottom trace) along with its amplitude (vertical grey line). The inset to the right shows a magnified view of the quartile averages (± 100 ms).
(B) Top: Subthreshold Vm sorted by sharp wave amplitude from (A). Each row is normalized to have 0 mean (Vm Norm). Quartile averages shown below. The inset shows a magnified view of the depolarization (± 100 ms). Note that larger sharp waves are associated with a larger post-ripple hyperpolarization, while the depolarization is relatively unaffected.
(C) Top: Ripple-band Vm sorted by sharp wave amplitude from (A). Quartile averages shown below.
(D) Scatter plot between LFP sharp wave amplitude and intracellular ramp amplitude. For D–G, to get an estimate of the component’s amplitude, the sharp wave sorted response matrices (from A–C) were divided into 190 blocked averages of 25 sharp waves each, and the amplitude of each component was computed as in Figures 2/3. The inset shows a schematic of how ramp amplitude was computed.
(E) Same as in D, but for the amplitude of the depolarization.
(F) Same as in D, but for the amplitude of the hyperpolarization.
(G) Same as in D, but for the RMS amplitude of intracellular ripples. Notice that only the hyperpolarization and intracellular ripple change systematically as a function of sharp wave amplitude, while the ramp and depolarization remain invariant.
See also Figure S3.
Phase Relationships Between Spiking, Intracellular, and LFP Ripple Oscillations
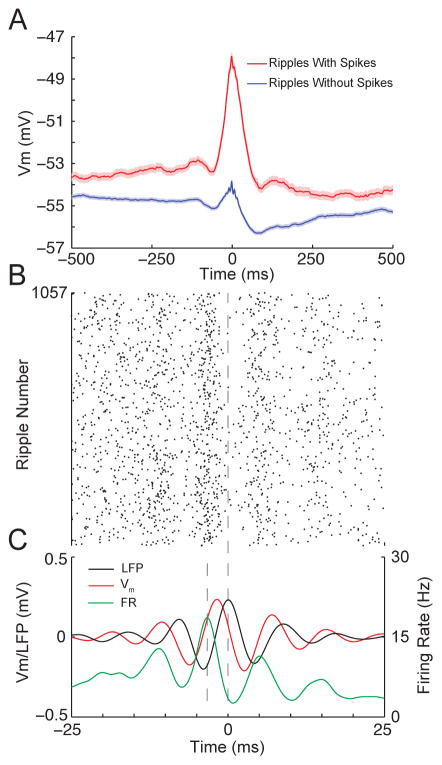
Ripple oscillations are thought to be functionally important for controlling spike timing and bringing CA1 output within the windows of synaptic integration and plasticity, but the factors that determine whether and when a neuron fires during a given ripple remain poorly understood. As shown in Figure 5A, ripples where the neuron fired had an intracellular depolarization several times larger than the average intracellular depolarization in ripples with no spikes. Moreover, the ripple-triggered raster plot of pyramidal cell firing (Figure 5B) demonstrates that spikes occurred around the trough of LFP ripples (Figure 5C; Figure S4). Importantly, this occurred when the slope of the membrane potential was near its maximum. This suggests that the amplitude of the intracellular depolarization is primarily responsible for bringing neurons to spike threshold while the fast, transient depolarizations during intracellular ripple oscillations are particularly effective at controlling spike timing.
Figure 5. Large intracellular depolarizations bring neurons to spike threshold, while intracellular ripple oscillations control the precise spike timing.
(A) Averages of the subthreshold Vm for ripples where the neuron fired at least one action potential (red; N=1057) or did not fire (blue; N=3712). Shaded regions mark mean ± SEM. Note that for ripples with at least one spike, the Vm had a depolarization several times larger than the average depolarization for ripples with no spikes.
(B) Ripple-triggered raster plot of spike times from whole-cell recordings.
(C) Average LFP ripple (black), intracellular ripple (red), and firing rate (green). The firing rate was computed by smoothing spike times with a gaussian (σ=1 ms) and averaging across all ripples. Vertical dashed lines mark the time of the peak firing rate and peak LFP ripple oscillation. Note that the peak firing rate occurs near the trough of LFP ripple oscillation, when the slope of the intracellular ripple is near its maximum.
See also Figure S4.
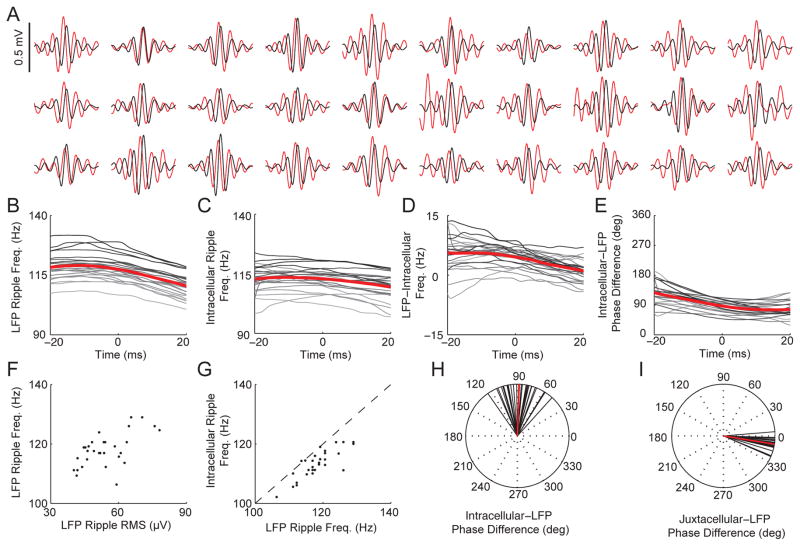
To investigate the relationship between intracellular and LFP ripple oscillations in more detail, we computed the average Vm and LFP in the ripple frequency band for each neuron. As shown in Figure 6A, LFP ripples lagged intracellular ripples for all 30 neurons. A time-frequency decomposition of intracellular and LFP ripples revealed significant differences in their frequencies, relative phases, and their temporal evolution. As shown in Figure 6B, LFP ripple frequency decreased from 118.3±1.15 Hz near the beginning (−20 ms) of ripples to 110.5±1.07 Hz near the end (20 ms) of ripples (p<10−13; paired t-test). In contrast, the frequency of intracellular ripples was more stable, but still showed a significant decline from 112.5±1.22 Hz to 109.4±1.23 Hz (p<0.001, paired t-test; Figure 6C). Hence, LFP ripples were initially faster than intracellular ripples (5.7±0.96 Hz; p<0.01; unpaired t-test), but as their frequencies converged, the difference became insignificant (1.0±0.59 Hz, p=0.52 unpaired t-test). Consistent with this observation, LFP ripples lagged intracellular ripples by 128.0 degrees (111.7 to 144.4; 95% CI) near the beginning of the ripples, compared to 76.7 degrees (65.6 to 87.8; 95% CI) near the end (Figure 6E). At LFP ripple center, LFP ripples (117.5±1.09 Hz) were 4.5±0.50 Hz faster (p<0.01; unpaired t-test) than intracellular ripples (112.9±1.00 Hz; Figure 6D), and lagged intracellular ripples by 86.8 degrees (79.3 to 94.3; 95% CI; Figure 6H). Across the population, larger LFP ripples had a faster frequency (p<10−3; Figure 6F), and faster LFP ripples were associated with faster Vm ripples (p<10−7; Figure 6G). These findings highlight the dynamic nature of ripple generation and regulation, and reveal important differences between the intracellular and LFP ripple oscillations.
Figure 6. Intracellular ripple oscillations lead LFP ripple oscillations by ~90 degrees and are ~5 Hz slower.
(A) Each neuron’s average intracellular ripple (red) and LFP ripple (black) from −25 to 25 ms around LFP ripple center. Ripples where the intracellularly recorded neuron fired were excluded since action potentials have a duration comparable to a ripple cycle, making phase estimation of the intracellular ripple difficult. Note that for all neurons the central peak in the LFP lags behind the central peak in the Vm.
(B) Instantaneous frequency of LFP ripples for each neuron. Time 0 marks the ripple center (time of central LFP peak). For B–E, Each neuron’s average is grey scaled according to its LFP ripple frequency at time 0. Averages are shown in red. Only neurons (22/30) with reliable phase/frequency estimates in a ± 20 ms window were included in B–E. Instantaneous frequency and phase are computed from a continuous wavelet transform using complex Morlet wavelets. For each sample, the frequency with the largest power was identified and its phase and frequency taken as the waveform’s instantaneous value (white lines shown in Figure 2B).
(C) Instantaneous frequency of intracellular ripples for each neuron.
(D) Difference between LFP and intracellular ripple frequency for each neuron. Note that LFP ripples are initially faster than intracellular ripples, and the frequency difference decreases with time.
(E) Instantaneous phase difference between intracellular and LFP ripples.
(F) LFP ripple frequency (at time 0) plotted as a function of its LFP ripple RMS for each neuron.
(G) Intracellular ripple frequency (at time 0) plotted as a function of LFP ripple frequency for each neuron. Note that for all but one neuron, intracellular ripples are slower than LFP ripples.
(H) Intracellular-LFP ripple phase difference (at time 0) for all 30 neurons (black lines). Average shown in red.
(I) Juxtacellular ripple - LFP ripple phase difference (at time 0) for all 28 juxtacellular recordings (black lines) performed in same mice and anatomical location as whole-cell recordings and with similar glass pipettes. Average shown in red.
See also Figure S5.
While the distance between the probe site measuring LFP ripples and the whole-cell recording in CA1 was small (200–250 μm), the spatial separation could introduce biases in the phase and frequency comparisons. To address this, we performed juxtacellular recordings from putative CA1 pyramidal neurons and LFP ripples (Juxtacellular ripples) from the same anatomical location and with similar glass pipettes as whole-cell recordings and compared them to LFP ripples occurring simultaneously on the probe site in the CA1 pyramidal cell layer (probe ripples). On average, LFP ripples on the probe led Juxtacellular ripples by just 9.1 degrees (6.66 to 11.53; 95% CI; Figure 6I) and had nearly identical frequencies as ripples recorded on the probe (Figure S5 A–D), ruling out biases in the phase/frequency comparisons due to the spatial separation between the multisite probe and pipette. Taking this 9 degree distance-related phase difference into account suggests that LFP ripples lag intracellular ripples by 96 degrees on average.
Though the time constant of the patch pipettes was considerably faster than ripples, the low-pass filtering properties of patch pipettes could in principle reduce the frequency and introduce phase delays in intracellular ripples. However, there was only a weak relationship between the magnitude of the access resistance and the phase difference between intracellular and LFP ripples (Figure S5 F). Moreover, juxtacellular ripples, which were subject to similar low-pass filtering since they were recorded with similar pipettes, had frequencies that were nearly identical to ripples from the probe, as noted above. There was a stronger relationship between the neuron’s input resistance and the intracellular-LFP phase delay (Figure S5 E), suggesting that passive properties of the neurons may contribute to the observed phase delays. However, this cannot explain the evolution of intracellular and LFP ripple frequency and relative phase across time.
The Phase Difference Between Intracellular And LFP Ripple Oscillations Changes Systematically With Membrane Potential
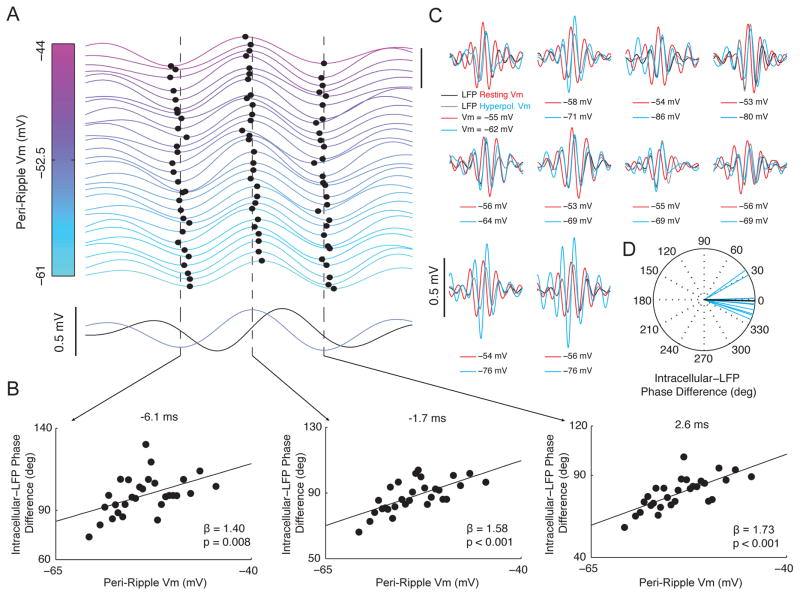
Competing models of ripple oscillation generation offer different predictions regarding how the phase of intracellular ripple oscillations should vary with membrane potential (Figure 8). In order to evaluate these competing hypotheses, we investigated how intracellular ripple phase depends on Vm in vivo. As shown in Figure 7A, ripples occurred at spontaneous membrane potential levels ranging from −61 mV to −44 mV. Interestingly, the time of the central Vm peak and the preceding/subsequent troughs varied systematically with Vm. Indeed, at more hyperpolarized levels, the phase lag between intracellular and LFP ripples was smaller compared to more depolarized levels (Figure 7B). In particular, a 1 mV hyperpolarization in Vm was associated with approximately a 1.6 degree phase shift of intracellular ripples towards LFP ripples.
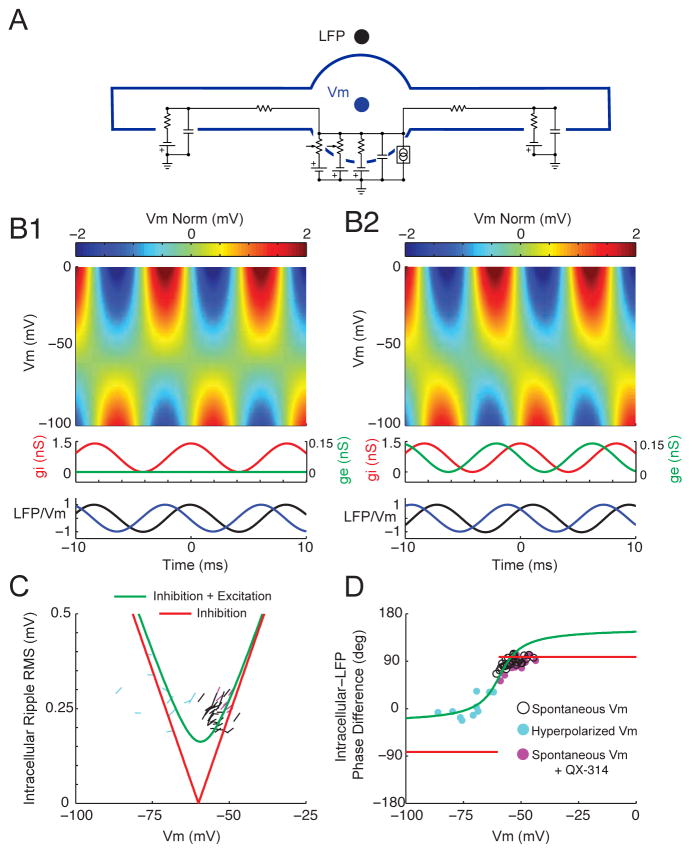
Figure 8. A simple conductance-based model of ripple generation consistent with the experimental data.
(A) Schematic of three-compartment model used in simulations (see experimental procedures).
(B1) Model with ripple-frequency (120 Hz) perisomatic inhibition. Top: intracellular ripples as a function of Vm. Each row is normalized to have 0 mean (Vm Norm). White line marks the timing of the intracellular ripple peak for each Vm level. Middle: Perisomatic synaptic conductances. Peak inhibitory (gi) amplitude of 1.4 nS. Peak excitatory (ge) amplitude of 0 nS. Bottom: Intracellular and LFP ripples at resting Vm (−55 mV) normalized to have a peak of 1. The peak in the inhibitory conductance was used as time 0.
(B2) Model with ripple-frequency perisomatic excitation leading inhibition. Same as in B1, but the excitatory conductance was 0.14 nS and led the inhibitory conductance by 90 degrees. Note the phase shift of intracellular ripples as a function of Vm.
(C) Amplitude of intracellular ripples as a function of Vm for the perisomatic inhibition model from B1 (red) and the model combining excitation leading inhibition from B2 (green). The slopes of the black lines are the estimates for all 30 neurons from Figure 3. Cyan lines are slope estimates from 10 neurons during hyperpolarizing current injection. Magenta lines are slope estimates from 7 neurons with intracellular QX-314 to block voltage-gated sodium channels (Figure S6). Note that both models predict that intracellular ripples should be larger at more depolarized levels within the range of spontaneous Vm fluctuations, consistent with black lines and Figure 3.
(D) Phase difference between intracellular ripples and LFP ripples as a function of Vm for the perisomatic inhibition model from B1 (red) and the model combining excitation leading inhibition from B2 (green). The black dots are the intracellular-LFP phase difference from Figure 7B at the time of the central intracellular peak (−1.7 ms; middle panel). The cyan dots are the intracellular-LFP phase difference for the 10 neurons under hyperpolarizing current injection at the time of the central intracellular peak. Similarly, the magenta dots are the intracellular-LFP phase difference at spontaneous Vm levels with intracellular QX-314 from Figure S6 F. Notice that the data are consistent with the model involving rhythmic excitation leading inhibition (B2; green), but not rhythmic inhibition alone (B1; red).
Figure 7. Intracellular ripple phase changes systematically with membrane potential.
(A) Top: Average intracellular ripple (from −8 to 12 ms) plotted as a function of Vm for the range of spontaneous Vm fluctuations. All ripples lacking intracellular action potentials were sorted by their peri-ripple Vm (±25 ms average), and 29 averages of 125 ripples each are displayed. Traces are separated by 0.1 mV (scale bar in upper right is 0.5 mV) and colored according to their peri-ripple Vm. The central peak and the preceding/subsequent troughs are marked by black dots for each trace. Vertical bars mark average time of preceding trough (−6.1 ms), central peak (−1.7 ms), and subsequent trough (2.6 ms). Note that hyperpolarized ripples (cyan) are phase delayed relative to depolarized ripples (pink). Bottom: Average LFP ripple (black) and intracellular ripple (light blue).
(B) Intracellular-LFP ripple phase difference plotted as a function of Vm for traces in (A).
(C) Average intracellular (red) and LFP (black) ripple at resting Vm, along with the intracellular (cyan) and LFP (grey) ripple with hyperpolarizing current injection (N=10 neurons). Scale bar marks 0.5 mV. Note that the central peak of intracellular ripples occurring under hyperpolarizing current injection (cyan) nearly aligns with LFP ripples (black/gray).
(D) Each neuron’s Intracellular-LFP ripple phase difference (at time 0) for intracellular ripples during hyperpolarizing current injection (cyan; N=10 neurons). The average is shown in black.
See also Figure S6.
To further test the voltage dependence of intracellular ripple phase, we injected hyperpolarizing DC currents into a subset of neurons (N=10) to bring them between 7 mV to 32 mV below their resting Vm. Hyperpolarization resulted in intracellular ripples that had almost zero phase difference with LFP ripples, without producing consistent changes in intracellular ripple amplitude (Figure 7C–D). At the time of the central LFP peak, intracellular ripples lagged LFP ripples by 1.4 degrees (−14.5 to 11.7; 95% CI). To examine the possibility that the voltage dependence of intracellular ripple phase is due to the activation of fast voltage-gated sodium channels, we blocked their activity intracellularly using QX-314 in an additional 7 neurons (Figure S6). Intracellular QX-314 abolished sodium spikes (Grienberger et al., 2014), but had no effect on the average intracellular-LFP phase difference or its voltage dependence.
As discussed below, these results are inconsistent with models of ripple generation involving rhythmic inhibition alone. Instead, they suggest that an interplay between rhythmic excitation leading inhibition shapes intracellular ripples in vivo (Figure 8).
Discussion
By combining in vivo whole-cell recordings from identified CA1 pyramidal neurons with nearby multisite extracellular measurements of network activity, we investigated the membrane potential dynamics underlying hippocampal ripples and found that: (1) the average membrane potential around ripples is composed of a sharp wave associated depolarization, superimposed intracellular ripple oscillations, and a post-ripple hyperpolarization. (2) Individual neurons have diverse intracellular responses, which can be partially explained by differences in membrane potential. (3) Bigger LFP sharp waves are associated with a larger post-ripple hyperpolarization and larger intracellular ripples, while the amplitude of the depolarization stays relatively constant. (4) Pyramidal neuron spikes phase-lock near the trough of LFP ripples, when the slope of the membrane potential is near its maximum. (5) The phase delay between intracellular and LFP ripples changes systematically with membrane potential.
What gives rise to the three components of the intracellular response during ripples? Ripples in CA1 are thought to be driven by excitatory input arising from a population burst spontaneously generated through the recurrent network of area CA3. Synaptic input from CA3 terminates on the apical dendrites of CA1 pyramidal neurons, and the associated synaptic currents produce a negative sharp wave in the LFP of stratum radiatum (Buzsaki, 1986). The intracellular depolarization likely reflects this excitatory input (Ylinen et al., 1995, Maier et al., 2011, English et al., 2014, Valero et al., 2015). As excitation builds up in CA1, populations of pyramidal cells and interneurons begin firing at ripple frequency, phase-locked to LFP ripple oscillations (Buzsaki et al., 1992, Klausberger et al., 2003, Klausberger et al., 2004, Somogyi et al., 2014). Consistent with this, we observe intracellular ripple-frequency oscillations superimposed on the sharp wave associated depolarization. Inhibition also produces a hyperpolarization lasting hundreds of milliseconds beyond the end of the ripple, suggesting a dependence on GABAB receptor activation (Ulrich and Bettler, 2007, English et al., 2014). The shape of the average intracellular response varied across individual neurons. One contributing factor to this variability is differences in membrane potential through its effects on the electrical driving forces for excitation and inhibition, while other factors likely include differences in gene expression and connectivity (Lee et al., 2014). Indeed, a recent study found a difference in the ripple response between superficial and deep pyramidal cells (Valero et al., 2015), consistent with our observed neuron-to-neuron variability (Figure 2).
One key finding is that the amplitude of the intracellular depolarization is insensitive to the magnitude of the sharp wave observed in stratum radiatum. This is particularly striking because the amplitudes of the intracellular ripple and post-ripple hyperpolarization scale with sharp wave amplitude (Figure 4). This indicates the presence of a circuit mechanism that provides an intricate balance between excitation and inhibition during the ripple. In particular, larger excitatory currents must be balanced by proportional inhibitory currents during the population burst, such that the net current depolarizing the soma is independent of input strength. One way to achieve this is for inhibition to be negligible up to a threshold input magnitude, and grow at the same rate as excitation beyond this threshold (Figure S7). This would ensure that the difference between excitation and inhibition (net somatic current) would stay constant as a function of input strength. What are the circuit elements that could account for this? Area CA3 provides direct excitatory input to CA1 neurons, and proportional feed-forward inhibition through local interneurons (Alger and Nicoll, 1982, Maccaferri and Dingledine, 2002, Pouille et al., 2009). Since feed-forward interneurons will fire in proportion to CA3 input only past the threshold for spiking, the resulting inhibition is a likely candidate for the requisite inhibitory current (Mizunuma et al., 2014). Consistent with this view, at resting Vm the post-ripple hyperpolarization scales with input size, when excitation has already decayed. Furthermore, under hyperpolarizing current injection, when the inhibitory driving force for the balancing inhibition is reduced, the amplitude of the intracellular depolarization scales with sharp wave amplitude (Figure S3). For low input strengths, the post-ripple hyperpolarization is negligible, further indicating the involvement of GABAB receptors, which are selectively activated under strong stimulus intensities (Dutar and Nicoll, 1988, Ulrich and Bettler, 2007).
What controls if and when neurons fire during ripples? The intracellular depolarization during ripples in which a neuron fires is significantly larger compared to ripples in which the neuron remained silent (Figure 5). Furthermore, when neurons do not fire during ripples, they exhibit a remarkably consistent subthreshold depolarization over a wide range of input strengths, suggesting an intricate balance of excitation and inhibition as discussed above. This ensures that neurons remain silent for most ripples, and fire only when specific subsets of synapses are co-activated to overcome the balancing inhibition. Hence, the specific identity, rather than the sheer number, of active CA3 neurons likely determines whether a postsynaptic CA1 neuron fires or not. We hypothesize that the depolarization brings neurons close to firing threshold, while the superimposed intracellular ripple oscillations control the precise spike timing. Indeed, we observe that spikes preferentially occur on the rising phase of the intracellular ripple oscillation, when the slope of the membrane potential is near its maximum. This is consistent with previous slice work showing that spike-timing precision is enhanced by fast, transient depolarizations (Mainen and Sejnowski, 1995).
How do the experimental observations fit with circuit models of ripple oscillations (Cutsuridis and Taxidis, 2013, Buzsaki, 2015, Gulyas and Freund, 2015, Patel, 2015)? Three main classes of models of ripple oscillations have been proposed, each making different predictions regarding the types of input CA1 pyramidal neurons receive. First, previous studies have proposed that the axons of CA1 pyramidal neurons are electrically coupled through sparse axo-axonal gap junctions, endowing the resulting axonal plexus with the ability to propagate action potentials and oscillate at ripple frequency (Draguhn et al., 1998, Traub and Bibbig, 2000). These models predict the presence of “spikelets” representing the antidromic propagation of action potentials from ectopic generation sites to the soma. Spikelets have been demonstrated in vitro (Schmitz et al., 2001) and in vivo (Spencer and Kandel, 1961, Epsztein et al., 2010, Chorev and Brecht, 2012), but at present there is little direct evidence linking their generation to the existence of pyramidal axo-axonal gap junctions, especially during ripples in vivo (English et al., 2014). Our data do not support a role for spikelets and axo-axonal gap junctions in ripple generation, since none of our 30 neurons showed spikelets during ripples, and, unlike previous slice work (Bahner et al., 2011), hyperpolarizing current injection completely abolished spiking, arguing against an ectopic site of action potential generation.
A second class of models suggests that rhythmic perisomatic inhibition alone is responsible for intracellular ripple oscillations (Ylinen et al., 1995, Stark et al., 2014, Buzsaki, 2015). Pyramidal cells are hypothesized to receive strong ripple-frequency somatic inhibition due to reciprocal interactions within interneuron networks, pyramidal-interneuron feedback loops, or both. And while several classes of interneurons, each targeting specific subcellular pyramidal cell domains, are known to be active during ripples, a prominent role for fast-spiking, parvalbumin (PV)-positive positive basket cells has emerged. Indeed, these interneurons have reciprocal connections with pyramidal cells, target their axons to the pyramidal cell soma, fire at ripple-frequency phase locked to LFP ripple oscillations, inhibit other PV-positive basket cells, and are endowed with a host of conductances supporting fast rhythmogenesis (Klausberger et al., 2003, Chiovini et al., 2014, Hu et al., 2014, Lee et al., 2014). As shown with a three-compartment conductance-based model in Figure 8 (see supplementary experimental procedures), with perisomatic inhibition alone (Figure 8B1), as the membrane potential is hyperpolarized towards the inhibitory reversal potential, the phase difference between intracellular and LFP ripple oscillations remains constant (red trace; Figure 8D). Below this level, it abruptly flips 180 degrees, as claimed in previous work in anesthetized rats (Ylinen et al., 1995). In contrast, our data demonstrates that the phase difference varies smoothly with membrane potential, and approaches zero (rather than −90) degrees below the reversal potential for inhibition. Therefore, our data provides strong evidence against models based on perisomatic inhibition alone.
Is there a simple addition to the perisomatic inhibition model that can account for the data? Recent in vitro work has suggested that CA1 pyramidal neurons receive ripple-frequency excitation in addition to inhibition (Maier et al., 2011). Moreover, because most interneurons, including PV-positive basket cells, fire 1–2 ms after pyramidal neurons (Csicsvari et al., 1999, Klausberger et al., 2004, Sullivan et al., 2011, Varga et al., 2012, Stark et al., 2014, Varga et al., 2014), excitation should lead inhibition (Maier et al., 2011). As shown in Figure 8B2, with weak ripple-frequency excitation leading inhibition by 90 degrees (~2 ms), intracellular ripples show a systematic phase shift with membrane potential. As the membrane potential is hyperpolarized towards the reversal potential for inhibition, the phase difference between intracellular and LFP ripples approaches zero (green trace; Figure 8D), as observed experimentally (colored dots in Figure 8D; Figure 7). This occurs because the phase of intracellular ripple oscillations depends upon the relative contribution of the excitatory and inhibitory currents, which varies with membrane potential due to corresponding changes in electrical driving force. The direction of the experimentally observed phase shift is non-trivial, as an identical model with inhibition leading excitation gives rise to a phase shift of the opposite direction. Moreover, the fact that the amplitude of intracellular ripples grows with membrane depolarization around resting Vm argues for weaker excitatory influence at the soma relative to inhibition (Figure 8C, Figure 3). Hence, rhythmic excitation leading inhibition provides one possible explanation for the data.
What could be the source of ripple-frequency excitation? First, CA1 pyramidal neurons are known to have sparse recurrent connections (Deuchars and Thomson, 1996, Yang et al., 2014). The phase-locked firing of CA1 neurons during ripples would produce rhythmic excitatory inputs in the recurrently connected CA1 cells. In agreement with this, slice work has demonstrated that ripples and ripple-frequency excitatory post-synaptic currents (EPSCs) persist in CA1 mini-slices presumed to be devoid of CA3 input (Maier et al., 2011). Second, rhythmic excitation might also come from CA3 pyramidal neurons bursting at ripple frequency (Sullivan et al., 2011). To the extent that this input could survive passive dendritic filtering, CA3 could provide a source of ripple-frequency excitation to the soma. Third, ripple-frequency shunting inhibition may modulate slow dendritic excitation to cause ripple-frequency depolarizing currents to enter the soma (but see (Maier et al., 2011). Regardless of its source, our data suggests that ripple-frequency excitation plays a key role in shaping intracellular ripple oscillations, thereby contributing to the regulation of spike timing across the subset of active cells.
The proposed simple model does not capture the full complexity of the intact circuit. In particular, a number of additional factors will influence the phase of the extracellular and intracellular ripples. First, the detailed cell morphology and the precise spatiotemporal distribution of excitatory and inhibitory synaptic currents will shape both intracellular and LFP ripples. Second, active conductances can have important effects on how these synaptic inputs are integrated at the soma. Third, currents associated with the synaptic inputs and spiking of multiple nearby neurons will influence the extracellular LFP (Schomburg et al., 2012). Future studies are needed to characterize the detailed contributions of these factors.
By combining in vivo whole-cell recordings with multisite LFP measurements, we reveal the presence of a circuit mechanism providing an intricate balance between excitation and inhibition during ripples. This mechanism ensures that the majority of ripples results in only a modest subthreshold depolarization, independent of input size. In contrast, firing within a ripple requires a much larger depolarization that must be sensitive to the precise identity of CA3 inputs, as opposed to their sheer number. The spike timing within a ripple is controlled by intracellular ripple oscillations, which in turn likely depends on the combination of both ripple-frequency excitation and inhibition. This could be particularly important for determining the firing order of active cells, which has functional implications for the mechanisms of ripple-induced plasticity and the circuit mechanisms of replay.
Experimental Procedures
Awake, in vivo recordings
Male mice (C57BL/6-E; Strain Code 475; Charles River Laboratories) were head-fixed on a spherical treadmill and allowed to run and walk freely. A single-shank, 32-site silicon probe with 100 μm site spacing was inserted in the coronal plane to a depth of 2600–3000 μm. The probe was adjusted so that a recording site was positioned in the CA1 pyramidal cell layer for reliably recording LFP ripple oscillations. To compare the structure of LFP ripples recorded on the probe to those from a pipette, we used artificial cerebrospinal spinal fluid filled pipettes to perform one to three juxtacellular (Pinault, 1996) recordings per mouse from putative CA1 pyramidal neurons (N=28). At the depth of the CA1 layer, the probe and pipette were separated by approximately 200 μm in the anterior-posterior direction and 100 μm in the medial-lateral.
Whole-cell recordings were performed after the depth of the CA1 layer had been identified. Pipettes were filled with an internal solution containing (in mM): 115 K-Gluconate, 10 KCl, 10 NaCl, 10 Hepes, 0.1 EGTA, 10 Tris-phosphocreatine, 5 KOH, 13.4 Biocytin, 5 Mg-ATP, 0.3 Tris-GTP. The internal solution had an osmolarity of 300 mOsm and a pH of 7.27 at room temperature. In a subset of experiments, 2 mM of QX-314 was added to the internal solution to block voltage-gated sodium channels. The membrane potential was not corrected for the liquid junction potential. Whole-cell recordings were obtained “blind” according to previously described methods (Margrie et al., 2002). Capacitance neutralization was set prior to establishing the GΩ seal. Access resistance was estimated online by fitting the voltage response to hyperpolarizing current steps (see supplemental experimental procedures). Recordings were aborted when the access resistance exceeded 120 MΩ or the action potential peak dropped below 0 mV. One to five whole-cell recordings (N=37) were performed per mouse.
Statistical analysis
To assess the significance of pre-ripple ramping in the neuron-averaged, ripple-triggered Vm traces (Figure 2C), 95% confidence intervals on the Vm were constructed at each sample from −2 s to 2 s. Pre-ripple confidence intervals were computed as the average of the upper/lower 95% confidence intervals from −2 to −1.5 seconds. The mean Vm was considered significantly different (p<0.05) from baseline if it went above/below the upper/lower baseline confidence intervals. Neurons were considered to have significant ramps if their average Vm spent at least 150 ms continuously above or below the 95% baseline confidence intervals between −1 s and −100 ms. Linear regression was used to estimate the relationship between baseline Vm and component amplitudes (Figure 2), LFP ripple power and frequency (Figure 6F), LFP and intracellular ripple frequency (Figure 6G), and Vm and intracellular ripple phase (Figure 7B). Least squares estimates of the slope (β) were used to assess significance at the p<0.05 level, except for Figures 3 and 4, which employed robust regression implemented using iteratively reweighted least squares and a bisquare weighting function on the residuals to mitigate the effect single ripple outliers. Averages are reported as mean ± standard error of the mean (SEM) unless otherwise stated. All circular statistics were performed using the CircStat toolbox (Berens, 2009).
Supplementary Material
Highlights.
Depolarization of CA1 neurons during ripples is independent of net excitatory input
This suggests a circuit mechanism keeping most neurons silent during ripples
Intracellular ripple phase varies continuously with membrane potential
This rejects a model of ripple generation involving perisomatic inhibition alone
Acknowledgments
We thank Stijn Cassenaer, Andreas Hoenselaar, Gilles Laurent, Maria Papadopoulou, Jacob Reimer, Britton Sauerbrei, and Kevin Shan for helpful discussion and comments on the manuscript, Andreas Hoenselaar and Mike Walsh for help with instrumentation, Lee-Peng Mok for help with immunohistochemistry, and Stephan Junek and the Max Planck Institute for Brain Science in Frankfurt for help with Fig. 1B. All other confocal imaging was performed in the Caltech Biological Imaging Facility, with the support of the Caltech Beckman Institute and the Beckman Foundations. This work was supported by the Mathers Foundation, the Moore Foundation, NIH 1DP1OD008255/5DP1MH099907, and NSF IOS-1146871.
Footnotes
Author Contributions:
B.K.H., L.C.M., E.V.L., and A.G.S. designed the experiments. B.K.H. performed the experiments. L.C.M. helped implement whole-cell recordings in awake mice. B.K.H., E.V.L., and A.G.S. analyzed the data. B.K.H. wrote the analysis programs and generated the figures. B.K.H., L.C.M., E.V.L., and A.G.S. wrote the paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alger BE, Nicoll RA. Feed-forward dendritic inhibition in rat hippocampal pyramidal cells studied in vitro. J Physiol. 1982;328:105–23. doi: 10.1113/jphysiol.1982.sp014255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahner F, Weiss EK, Birke G, Maier N, Schmitz D, Rudolph U, Frotscher M, Traub RD, Both M, Draguhn A. Cellular correlate of assembly formation in oscillating hippocampal networks in vitro. Proc Natl Acad Sci U S A. 2011;108:E607–16. doi: 10.1073/pnas.1103546108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P. CircStat: A MATLAB Toolbox for Circular Statistics. Journal of Statistical Software. 2009;31:1–21. [Google Scholar]
- Bliss TV, Collingridge GL. A synaptic model of memory: long-term potentiation in the hippocampus. Nature. 1993;361:31–9. doi: 10.1038/361031a0. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Long-term changes of hippocampal sharp-waves following high frequency afferent activation. Brain Res. 1984;300:179–82. doi: 10.1016/0006-8993(84)91356-8. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Hippocampal sharp waves: their origin and significance. Brain Res. 1986;398:242–52. doi: 10.1016/0006-8993(86)91483-6. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Two-stage model of memory trace formation: a role for “noisy” brain states. Neuroscience. 1989;31:551–70. doi: 10.1016/0306-4522(89)90423-5. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Hippocampal sharp wave-ripple: A cognitive biomarker for episodic memory and planning. Hippocampus. 2015 doi: 10.1002/hipo.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G, Horvath Z, Urioste R, Hetke J, Wise K. High-frequency network oscillation in the hippocampus. Science. 1992;256:1025–7. doi: 10.1126/science.1589772. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Leung LW, Vanderwolf CH. Cellular bases of hippocampal EEG in the behaving rat. Brain Res. 1983;287:139–71. doi: 10.1016/0165-0173(83)90037-1. [DOI] [PubMed] [Google Scholar]
- Carr MF, Jadhav SP, Frank LM. Hippocampal replay in the awake state: a potential substrate for memory consolidation and retrieval. Nat Neurosci. 2011;14:147–53. doi: 10.1038/nn.2732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiovini B, Turi GF, Katona G, Kaszas A, Palfi D, Maak P, Szalay G, Szabo MF, Szabo G, Szadai Z, et al. Dendritic spikes induce ripples in parvalbumin interneurons during hippocampal sharp waves. Neuron. 2014;82:908–24. doi: 10.1016/j.neuron.2014.04.004. [DOI] [PubMed] [Google Scholar]
- Chorev E, Brecht M. In vivo dual intra- and extracellular recordings suggest bidirectional coupling between CA1 pyramidal neurons. Journal of neurophysiology. 2012;108:1584–93. doi: 10.1152/jn.01115.2011. [DOI] [PubMed] [Google Scholar]
- Chrobak JJ, Buzsaki G. High-frequency oscillations in the output networks of the hippocampal-entorhinal axis of the freely behaving rat. J Neurosci. 1996;16:3056–66. doi: 10.1523/JNEUROSCI.16-09-03056.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurko A, Mamiya A, Buzsaki G. Oscillatory coupling of hippocampal pyramidal cells and interneurons in the behaving Rat. J Neurosci. 1999;19:274–87. doi: 10.1523/JNEUROSCI.19-01-00274.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutsuridis V, Taxidis J. Deciphering the role of CA1 inhibitory circuits in sharp wave-ripple complexes. Front Syst Neurosci. 2013;7:13. doi: 10.3389/fnsys.2013.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deuchars J, Thomson AM. CA1 pyramid-pyramid connections in rat hippocampus in vitro: dual intracellular recordings with biocytin filling. Neuroscience. 1996;74:1009–18. doi: 10.1016/0306-4522(96)00251-5. [DOI] [PubMed] [Google Scholar]
- Diba K, Buzsaki G. Forward and reverse hippocampal place-cell sequences during ripples. Nat Neurosci. 2007;10:1241–2. doi: 10.1038/nn1961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diekelmann S, Born J. The memory function of sleep. Nat Rev Neurosci. 2010;11:114–26. doi: 10.1038/nrn2762. [DOI] [PubMed] [Google Scholar]
- Draguhn A, Traub RD, Schmitz D, Jefferys JG. Electrical coupling underlies high-frequency oscillations in the hippocampus in vitro. Nature. 1998;394:189–92. doi: 10.1038/28184. [DOI] [PubMed] [Google Scholar]
- Dutar P, Nicoll RA. Stimulation of phosphatidylinositol (PI) turnover may mediate the muscarinic suppression of the M-current in hippocampal pyramidal cells. Neurosci Lett. 1988;85:89–94. doi: 10.1016/0304-3940(88)90434-x. [DOI] [PubMed] [Google Scholar]
- English DF, Peyrache A, Stark E, Roux L, Vallentin D, Long MA, Buzsaki G. Excitation and inhibition compete to control spiking during hippocampal ripples: intracellular study in behaving mice. J Neurosci. 2014;34:16509–17. doi: 10.1523/JNEUROSCI.2600-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epsztein J, Lee AK, Chorev E, Brecht M. Impact of spikelets on hippocampal CA1 pyramidal cell activity during spatial exploration. Science (New York, N Y) 2010;327:474–7. doi: 10.1126/science.1182773. [DOI] [PubMed] [Google Scholar]
- Foster DJ, Wilson MA. Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature. 2006;440:680–3. doi: 10.1038/nature04587. [DOI] [PubMed] [Google Scholar]
- Graves AR, Moore SJ, Bloss EB, Mensh BD, Kath WL, Spruston N. Hippocampal pyramidal neurons comprise two distinct cell types that are countermodulated by metabotropic receptors. Neuron. 2012;76:776–89. doi: 10.1016/j.neuron.2012.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grienberger C, Chen X, Konnerth A. NMDA receptor-dependent multidendrite Ca(2+) spikes required for hippocampal burst firing in vivo. Neuron. 2014;81:1274–81. doi: 10.1016/j.neuron.2014.01.014. [DOI] [PubMed] [Google Scholar]
- Gulyas AI, Freund TT. Generation of physiological and pathological high frequency oscillations: the role of perisomatic inhibition in sharp-wave ripple and interictal spike generation. Curr Opin Neurobiol. 2015;31:26–32. doi: 10.1016/j.conb.2014.07.020. [DOI] [PubMed] [Google Scholar]
- Hu H, Gan J, Jonas P. Interneurons. Fast-spiking, parvalbumin(+) GABAergic interneurons: from cellular design to microcircuit function. Science. 2014;345:1255263. doi: 10.1126/science.1255263. [DOI] [PubMed] [Google Scholar]
- Kamondi A, Acsady L, Buzsaki G. Dendritic spikes are enhanced by cooperative network activity in the intact hippocampus. J Neurosci. 1998;18:3919–28. doi: 10.1523/JNEUROSCI.18-10-03919.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klausberger T, Magill PJ, Marton LF, Roberts JD, Cobden PM, Buzsaki G, Somogyi P. Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo. Nature. 2003;421:844–8. doi: 10.1038/nature01374. [DOI] [PubMed] [Google Scholar]
- Klausberger T, Marton LF, Baude A, Roberts JD, Magill PJ, Somogyi P. Spike timing of dendrite-targeting bistratified cells during hippocampal network oscillations in vivo. Nat Neurosci. 2004;7:41–7. doi: 10.1038/nn1159. [DOI] [PubMed] [Google Scholar]
- Lee SH, Marchionni I, Bezaire M, Varga C, Danielson N, Lovett-Barron M, Losonczy A, Soltesz I. Parvalbumin-positive basket cells differentiate among hippocampal pyramidal cells. Neuron. 2014;82:1129–44. doi: 10.1016/j.neuron.2014.03.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Eschenko O, Murayama Y, Augath M, Steudel T, Evrard HC, Besserve M, Oeltermann A. Hippocampal-cortical interaction during periods of subcortical silence. Nature. 2012;491:547–53. doi: 10.1038/nature11618. [DOI] [PubMed] [Google Scholar]
- Maccaferri G, Dingledine R. Control of feedforward dendritic inhibition by NMDA receptor-dependent spike timing in hippocampal interneurons. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2002;22:5462–72. doi: 10.1523/JNEUROSCI.22-13-05462.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier N, Tejero-Cantero A, Dorrn AL, Winterer J, Beed PS, Morris G, Kempter R, Poulet JF, Leibold C, Schmitz D. Coherent phasic excitation during hippocampal ripples. Neuron. 2011;72:137–52. doi: 10.1016/j.neuron.2011.08.016. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268:1503–6. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- Margrie TW, Brecht M, Sakmann B. In vivo, low-resistance, whole-cell recordings from neurons in the anaesthetized and awake mammalian brain. Pflugers Arch. 2002;444:491–8. doi: 10.1007/s00424-002-0831-z. [DOI] [PubMed] [Google Scholar]
- Megias M, Emri Z, Freund TF, Gulyas AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience. 2001;102:527–40. doi: 10.1016/s0306-4522(00)00496-6. [DOI] [PubMed] [Google Scholar]
- Mizunuma M, Norimoto H, Tao K, Egawa T, Hanaoka K, Sakaguchi T, Hioki H, Kaneko T, Yamaguchi S, Nagano T, et al. Unbalanced excitability underlies offline reactivation of behaviorally activated neurons. Nat Neurosci. 2014;17:503–5. doi: 10.1038/nn.3674. [DOI] [PubMed] [Google Scholar]
- O’Keefe J. Place units in the hippocampus of the freely moving rat. Exp Neurol. 1976;51:78–109. doi: 10.1016/0014-4886(76)90055-8. [DOI] [PubMed] [Google Scholar]
- O’Neill J, Senior T, Csicsvari J. Place-selective firing of CA1 pyramidal cells during sharp wave/ripple network patterns in exploratory behavior. Neuron. 2006;49:143–55. doi: 10.1016/j.neuron.2005.10.037. [DOI] [PubMed] [Google Scholar]
- Patel J. Network mechanisms underlying the initiation and generation of sharp-wave-associated ripple oscillations. J Neurosci. 2015;35:2323–5. doi: 10.1523/JNEUROSCI.4215-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinault D. A novel single-cell staining procedure performed in vivo under electrophysiological control: morpho-functional features of juxtacellularly labeled thalamic cells and other central neurons with biocytin or Neurobiotin. J Neurosci Methods. 1996;65:113–36. doi: 10.1016/0165-0270(95)00144-1. [DOI] [PubMed] [Google Scholar]
- Pouille F, Marin-Burgin A, Adesnik H, Atallah BV, Scanziani M. Input normalization by global feedforward inhibition expands cortical dynamic range. Nat Neurosci. 2009;12:1577–85. doi: 10.1038/nn.2441. [DOI] [PubMed] [Google Scholar]
- Pouille F, Scanziani M. Enforcement of temporal fidelity in pyramidal cells by somatic feed-forward inhibition. Science. 2001;293:1159–63. doi: 10.1126/science.1060342. [DOI] [PubMed] [Google Scholar]
- Schmitz D, Schuchmann S, Fisahn A, Draguhn A, Buhl EH, Petrasch-Parwez E, Dermietzel R, Heinemann U, Traub RD. Axo-axonal coupling. a novel mechanism for ultrafast neuronal communication. Neuron. 2001;31:831–40. doi: 10.1016/s0896-6273(01)00410-x. [DOI] [PubMed] [Google Scholar]
- Schomburg EW, Anastassiou CA, Buzsaki G, Koch C. The spiking component of oscillatory extracellular potentials in the rat hippocampus. J Neurosci. 2012;32:11798–811. doi: 10.1523/JNEUROSCI.0656-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siapas AG, Wilson MA. Coordinated interactions between hippocampal ripples and cortical spindles during slow-wave sleep. Neuron. 1998;21:1123–8. doi: 10.1016/s0896-6273(00)80629-7. [DOI] [PubMed] [Google Scholar]
- Somogyi P, Katona L, Klausberger T, Lasztoczi B, Viney TJ. Temporal redistribution of inhibition over neuronal subcellular domains underlies state-dependent rhythmic change of excitability in the hippocampus. Philos Trans R Soc Lond B Biol Sci. 2014;369:20120518. doi: 10.1098/rstb.2012.0518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer WA, Kandel ER. Electrophysiology of Hippocampal Neurons: Iv. Fast Prepotentials. J Neurophysiol. 1961;24:272–85. doi: 10.1152/jn.1961.24.3.272. [DOI] [PubMed] [Google Scholar]
- Squire LR. Memory and the hippocampus: a synthesis from findings with rats, monkeys, and humans. Psychol Rev. 1992;99:195–231. doi: 10.1037/0033-295x.99.2.195. [DOI] [PubMed] [Google Scholar]
- Stark E, Roux L, Eichler R, Senzai Y, Royer S, Buzsaki G. Pyramidal cell-interneuron interactions underlie hippocampal ripple oscillations. Neuron. 2014;83:467–80. doi: 10.1016/j.neuron.2014.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan D, Csicsvari J, Mizuseki K, Montgomery S, Diba K, Buzsaki G. Relationships between hippocampal sharp waves, ripples, and fast gamma oscillation: influence of dentate and entorhinal cortical activity. J Neurosci. 2011;31:8605–16. doi: 10.1523/JNEUROSCI.0294-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traub RD, Bibbig A. A model of high-frequency ripples in the hippocampus based on synaptic coupling plus axon-axon gap junctions between pyramidal neurons. J Neurosci. 2000;20:2086–93. doi: 10.1523/JNEUROSCI.20-06-02086.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulrich D, Bettler B. GABA(B) receptors: synaptic functions and mechanisms of diversity. Curr Opin Neurobiol. 2007;17:298–303. doi: 10.1016/j.conb.2007.04.001. [DOI] [PubMed] [Google Scholar]
- Valero M, Cid E, Averkin RG, Aguilar J, Sanchez-Aguilera A, Viney TJ, Gomez-Dominguez D, Bellistri E, de la Prida LM. Determinants of different deep and superficial CA1 pyramidal cell dynamics during sharp-wave ripples. Nat Neurosci. 2015;18:1281–90. doi: 10.1038/nn.4074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varga C, Golshani P, Soltesz I. Frequency-invariant temporal ordering of interneuronal discharges during hippocampal oscillations in awake mice. Proc Natl Acad Sci U S A. 2012;109:E2726–34. doi: 10.1073/pnas.1210929109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varga C, Oijala M, Lish J, Szabo GG, Bezaire M, Marchionni I, Golshani P, Soltesz I. Functional fission of parvalbumin interneuron classes during fast network events. Elife. 2014;3 doi: 10.7554/eLife.04006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wierzynski CM, Lubenov EV, Gu M, Siapas AG. State-dependent spike-timing relationships between hippocampal and prefrontal circuits during sleep. Neuron. 2009;61:587–96. doi: 10.1016/j.neuron.2009.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson MA, McNaughton BL. Reactivation of hippocampal ensemble memories during sleep. Science. 1994;265:676–9. doi: 10.1126/science.8036517. [DOI] [PubMed] [Google Scholar]
- Yang S, Yang S, Moreira T, Hoffman G, Carlson GC, Bender KJ, Alger BE, Tang CM. Interlamellar CA1 network in the hippocampus. Proc Natl Acad Sci U S A. 2014;111:12919–24. doi: 10.1073/pnas.1405468111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ylinen A, Bragin A, Nadasdy Z, Jando G, Szabo I, Sik A, Buzsaki G. Sharp wave-associated high-frequency oscillation (200 Hz) in the intact hippocampus: network and intracellular mechanisms. J Neurosci. 1995;15:30–46. doi: 10.1523/JNEUROSCI.15-01-00030.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.