Date of origin of the SARS coronavirus strains

Abstract

Background

A new respiratory infectious epidemic, severe acute respiratory syndrome (SARS), broke out and spread throughout the world. By now the putative pathogen of SARS has been identified as a new coronavirus, a single positive-strand RNA virus. RNA viruses commonly have a high rate of genetic mutation. It is therefore important to know the mutation rate of the SARS coronavirus as it spreads through the population. Moreover, finding a date for the last common ancestor of SARS coronavirus strains would be useful for understanding the circumstances surrounding the emergence of the SARS pandemic and the rate at which SARS coronavirus diverge.

Methods

We propose a mathematical model to estimate the evolution rate of the SARS coronavirus genome and the time of the last common ancestor of the sequenced SARS strains. Under some common assumptions and justifiable simplifications, a few simple equations incorporating the evolution rate (K) and time of the last common ancestor of the strains (T₀) can be deduced. We then implemented the least square method to estimate K and T₀ from the dataset of sequences and corresponding times. Monte Carlo stimulation was employed to discuss the results.

Results

Based on 6 strains with accurate dates of host death, we estimated the time of the last common ancestor to be about August or September 2002, and the evolution rate to be about 0.16 base/day, that is, the SARS coronavirus would on average change a base every seven days. We validated our method by dividing the strains into two groups, which coincided with the results from comparative genomics.

Conclusion

The applied method is simple to implement and avoid the difficulty and subjectivity of choosing the root of phylogenetic tree. Based on 6 strains with accurate date of host death, we estimated a time of the last common ancestor, which is coincident with epidemic investigations, and an evolution rate in the same range as that reported for the HIV-1 virus.

Background

A new respiratory infectious epidemic, severe acute respiratory syndrome (SARS), broke out and spread throughout the world, affecting over 8,000 individuals in 32 countries[1,2]. In response to this outbreak, a global network of international collaborating laboratories was immediately sponsored and established by World Health Organization (WHO) to facilitate the identification of the causative agent of SARS. By now the putative pathogen of SARS has been identified, by experimental proof and by Koch's postulates, as a new coronavirus, a single positive-strand RNA virus [3-5]]. The whole genome of SARS coronavirus was first sequenced by the British Columbia Centre for Disease Control (CDC) in Canada on 23, April 2003 [6], and subsequently a total of 16 SARS coronavirus strains isolated from Hanoi, mainland China, Hong Kong, Singapore, and Taiwan were sequenced within short time[7,8]. Phylogenetic analysis and comparative genomic studies based on these genomic sequences indicate that the SARS coronavirus is distinct from any of the previously characterized coronaviruses. Epidemiological investigations further indicate the SARS coronavirus strains may be divided into two different genotypes[9].

RNA viruses commonly have a high rate of genetic mutation, by which the viruses escape from host defence and evolve into novel viral strains. It is therefore important to know the mutation rate of the SARS coronavirus as it spreads through the population. Moreover, finding a date for the last common ancestor of SARS coronavirus strains would be useful for understanding the circumstances surrounding the emergence of the SARS pandemic and the rate at which SARS coronavirus diverge.

Many attempts have been made to extrapolate the age of the common ancestor of sequenced genomes. Most of them are based on accurate phylogenetic tree reconstructions, which demand a large amount computation, because of their application of the maximum likelihood strategy. Common for these methods is that it is critical to choose a sequence as the root of the phylogenetic tree. Korber et al. [10] implemented a parsimonious strategy, which used the consensus sequence including the most common bases appearing in strains as the ancestral sequence.

Methods

Among the 16 full-length SARS coronavirus genomes, we selected 6 strains for which the accurate date of host death is known, and on which our modelling was based. Our model performed calculation under two hypotheses, which are commonly adopted and have lead to accurate prediction in the study of HIV-1 virus [10]: first, nucleotide variation of these strains occurred by independent mutations at random positions in a single ancestral sequence; second, there exist a molecular clock and a constant rate of evolution. In addition, we simplified the calculation by neglecting trivial non-linear effects of multi-mutation for a base, i.e. there has only been one mutation for a base at a specific position of all the sequences during SARS infection time. This simplification can be justified by further discussion (see Additional file: 1).

For an ancestor sequence S₀ of a strain S, we can deduce for the assumptions above that

E(D(S₀, S)) ≈ K(T - T₀),

where D(S₀, S) is difference of the two sequences (as depicted by Hamming distance), T₀ is the date of the last ancestor, T is the date of host death (as an estimate of sampling date), and K is the evolution rate constant. The formula gives the expectation of sequence differences in proportion to the time of evolution.

If S₀ is the last common ancestor of S and S', then we have E(D(S,S')) = E(D(S₀,S)) + E(D(S₀,S')) (Fig. 1(a)). The equation takes this form under the simplification that along the total of the infection paths of the two sequences, mutation at any specific point of the sequences could, at most, only occur once. Thus E(D(S,S')) ≈ K(T + T' - 2T₀).

Figure 1.

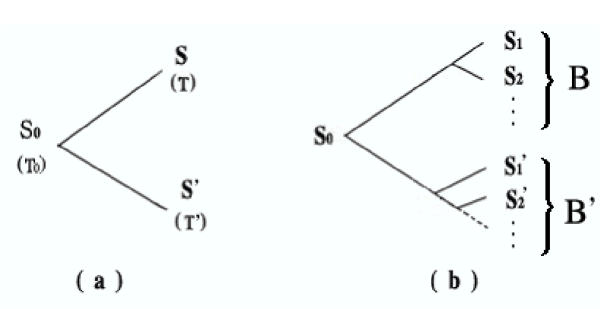
Phylogenetic Tree a) For two strains; b) For several strains, these can be divided into two groups from the last common ancestor.

The last common ancestor S₀ of all the sequences is the root of the hidden phylogenetic tree with the strains as nodes. From the time T₀, the sequences should at least evolve along two different routes. Therefore, there should be a partition of the strains into B and B' such that every pair of strains S ∈ B and S' ∈ B' should share the root of the tree as their last common ancestor (Fig. 1(b)), i.e., for each pair <S, S'>, E(D(S,S')) should be linear to (T + T') with same parameter T₀. Therefore, we can implement the least square method to estimate K and T₀ from the dataset.

Since the real partition cannot be known in advance, we carried out calculations for all of the possible partitions of these 6 strains. For each division we use the estimated K to calculate the possible T₀(S,S') of each sequence pair. The division with the minimum variance of T₀(S,S') is taken as our best solution to the problem, and the corresponding K as an estimation of the mutation rate.

To analyze how the parameters affect the results and support our fitting method, the Monte Carlo method was employed. At first, we produced a phylogenetic tree (See Fig. 3(c)) and a table of parameters (See Table 3) including the evolution rate and the times of the sequences. From the time of the last common ancestor S₀ of the other sequences, every base of a given sequence has the possibility to mutate over time according to the given evolution rate. So the other sequences, included intermediate sequences (I) and final sequences (F), can be obtained in steps in the stimulation according to the given phylogenetic tree and the time parameters. After the sequences were obtained, we used our fitting method to get the evolution rate, without including the hidden parameters. By analysis of the estimated K from the data, we can get to know how the parameters affect our fitting results and the quality of our method.

Figure 3.

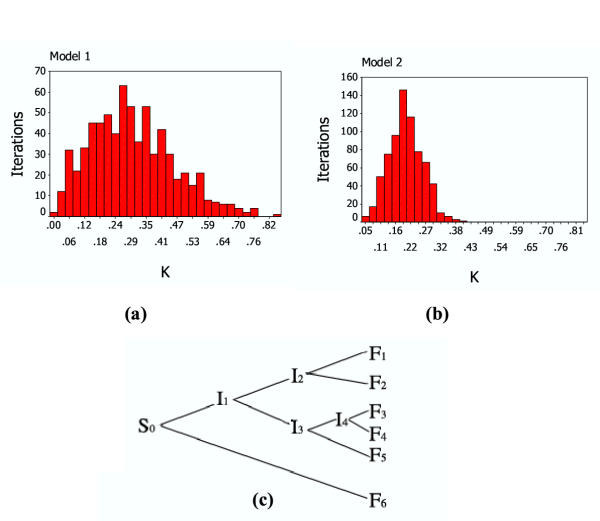
Estimated K for Monte Carlo Simulation The distribution of estimated K is shown in a) and b): a) Model 1; b) Model 2. The common phylogenetic tree is shown in c)

Table 3.

Parameters in the Monte Carlo stimulation

	K	T0	TI1	TI2	TI3	TI4	TF1	TF2	TF3	TF4	TF5	TF6
	base/day	Day	day	day	day	day	day	day	day	day	day	day
Model 1	0.2	-123	-100	-30	-60	-40	19	10	34	13	13	-13
Model 2	0.2	-180	-120	0	-90	-60	60	30	0	-30	-60	-90

Results

Of the 16 SARS coronavirus strains submitted to Genbank before June, 2003, 6 had accurate date of host death recorded. We chose these 6 to estimate the last common ancestor and the mutation rate of the SARS coronavirus (Table 1). We performed the calculation, and the fitting result of the best division (See Table 2) is shown in Fig. 2, including the differences between sequences D(S,S') versus the time factor (T + T'). The evolution rate K was estimated to be 0.16 base/day, which is similar to the reported evolution rate of HIV-1 virus [10]. The date of the last common ancestor T₀ was found to be about August or September, 2002, which is also in accordance with the epidemic investigations finding that the first verifiable SARS case was reported as early as on November 11, 2002.

Table 1.

Dates of hosts' death

ID	Strain	Date of host death	Date form Feb. 22
1	BJ01	03-08-2003	13
2	BJ02	03-08-2003	13
3	GZ01	02-10-2003	-13
4	SIN2500	03-14-2003	19
5	TOR2	03-05-2003	10
6	US	03-29-2003	34

Table 2.

Grouping of the strains

Si	Sj	D(Si, Sj)	T0*(i, j)	Annotation
GZ01	BJ02	55	-172	Best Division	G1
GZ01	TOR2	53	-167	Best Division	G1
GZ01	US	56	-165	Best Division	G1
GZ01	SIN2500	53	-163	Best Division	G1
GZ01	BJ01	49	-153	Best Division	G1
BJ02	TOR2	24	-64		G1
BJ02	US	27	-61		G1
BJ02	SIN2500	24	-59		G1
BJ01	BJ02	16	-37		G1
BJ01	TOR2	14	-32		G1
BJ01	US	17	-30		G1
BJ01	SIN2500	14	-28		G1
TOR2	US	7	0		G2
SIN2500	TOR2	4	2		G2
SIN2500	US	7	5		G2

Note: The best division is shown to the top, where one group include GZ01 and the other include the other strains. And from the time of the last common ancestor T₀*(i, j), the strains can be classified into G₁ = {GZ01,BJ01,BJ02} and G₂ = {TOR2,US,SIN2500}.

Figure 2.

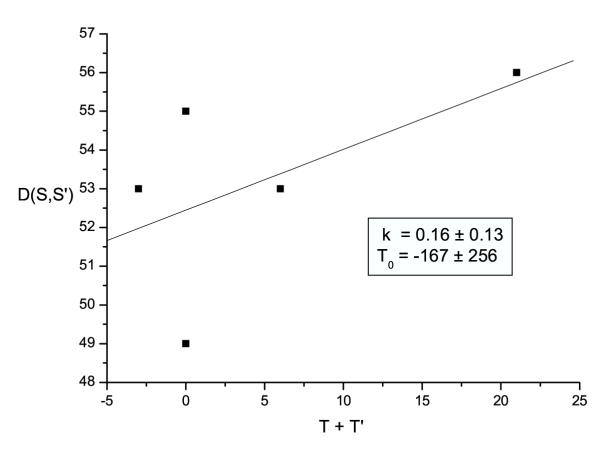
The linear relation between D(S,S') and (T+T') The parameters were estimated from the best division of 6 strains, where K is the evolution rate (base/day) and T₀ is the time (day) of the last common ancestor.

We validated our estimation of the evolutionary rate by grouping strains according to the estimated date of their pair wise last common ancestor. Applying the estimated K = 0.16, we can determine a date T₀*(i, j) of the last common ancestor for each pair <S_i, S_j> by E(D(S,S)) = K(T_i + T_j - 2T₀*(i, j)) [Table 2], and then divide the 6 into two groups, G₁ = {BJ01, BJ02, GZ01} and G₂ = {TOR2,SIN2500,US}. It is apparent that every two members in G₁ have a last common ancestor with a date T₀*(i, j) > 0, while every two members in G₂ have corresponding T₀*(i, j) < 0. This would imply that the strains in G₁ have a more recent last common ancestor than those in G₂. This partition of strains was supported by Ruan et al [9].

Discussion

Analysis by Monte Carlo Method was employed to test our fitting method and explain why the error of the evolution rate and time of last common ancestor was so large in our prediction. In a simulation of the simplified evolution model, sequences were generated according to a given phylogenetic tree, with parameters including evolution rate and times for each sequence. Two sets of parameters were used for a common phylogenetic tree, the evolution rate kept constant while time parameters differed (See Fig. 3(c) and Table 3). In model 1 there is a narrow time distribution two month of final sequences, while model 2 had a wider time distribution of five months.

Hundreds of iterations of sequence data from the stimulation were given according to the parameters. For each result, we could get estimated parameters by our fitting method. The estimated K distribution of the results (shown in Fig 3) is in support of our fitting method, as in both models the estimates for the evolutionary rate converged on the set parameter (0.2). Model 2 with wide time distribution had a narrower distribution of K, which indicates the fitted parameter has a smaller error. The difference between the two models hints a narrow sampling time window as a partially explanation of the large error on the estimated K for the real data.

Ideally, an estimation of evolution rate and the date of last ancestor for the SARS coronavirus should be based on sampling dates, with possible adjustments for culturing time and conditions. As such data were neither included in the submissions to Genbank, nor obtainable by direct contacts to the sequencing labs, we were left to choose between less ideal age estimates for the strains, such as date of host death, sequencing date, or submission date to Genbank. Sequencing dates were no more available than sampling dates, and for some groups several sequences were submitted to Genbank on the same date. In addition large part of the GenBank sequence were submitted long after June 2003, when no or very few SARS patient were available for sampling, also rendering submission date a not very accurate estimate for strain time. This basically left us with little other choice than to accept the date of host death as the most accurate available estimate for the age of each strain. Assuming that in most cases samples were taken a few days before to just after the death of the host, we think these dates represent acceptable, though not ideal, estimates of the endpoint of strain time.

In summary, certain inherent features of the situation around the SARS epidemic prevented our method from rendering more accurate estimates. First, as national and international efforts fortunately succeeded in stemming the spread of fledgling epidemic by summer 2003, all the samples used to obtain the 16 sequences were collected within a relatively short period of time (two months), which makes the error of D(S₀, S_i) is relative large. Second, because the date of host death is not good reflection of real time of sequences, the error of time is quite large. Third, as useful time data for the submitted sequences were scarce, the subset of sequences available for modelling was too small. Finally, as data on pre-sequencing culturing times and conditions have not been made available, differences in evolutions rates between in vivo and in vitro conditions cannot be estimated, and the basic assumption, that only a constant evolution rate may not be completely valid. A more accurate model considering two evolution rate parameters may produce a more accurate estimation, particularly on a larger dataset with accurate sampling and sequencing times.

Conclusions

We have proposed a mathematical model to estimate the evolution rate of the SARS coronavirus genome as well as the time of the last common ancestor of the various SARS coronavirus strains. The method is simple to implement and avoids the difficulty and subjectivity of choosing the root of phylogenetic tree. Based on 6 strains with accurate dates of host death, we estimated a time of the last common ancestor, which is coincident with epidemic investigations, and an evolution rate in the same range as that reported for the HIV-1 virus.

Competing interests

None declared.

Authors' contributions

Lu and Bu built the model including proposing the assumptions, deriving the system of equations, programmed and analyzed the data. Zhao, Wang, Li, Zhu, Sun, Cai collected data and analyzed them. Zhang, Xu programmed and prepared for the paper, Chen, Bu, Ling led the group to complete work related to the paper.

Pre-publication history

The pre-publication history for this paper can be accessed here:

http://www.biomedcentral.com/1471-2334/4/3/prepub