Polyelectrolyte multilayer electrostatic gating of graphene field-effect transistors

Abstract

We apply polyelectrolyte multilayer films by consecutive alternate adsorption of positively charged polyallylamine hydrochloride and negatively charged sodium polystyrene sulfonate to the surface of graphene field effect transistors. Oscillations in the Dirac voltage shift with alternating positive and negative layers clearly demonstrate the electrostatic gating effect in this simple model system. A simple electrostatic model accounts well for the sign and magnitude of the Dirac voltage shift. Using this system, we are able to create p-type or n-type graphene at will. This model serves as the basis for understanding the mechanism of charged polymer sensing using graphene devices, a potentially technologically important application of graphene in areas such as DNA sequencing, biomarker assays for cancer detection, and other protein sensing applications.

1 Introduction

Due to their planar nature and atomic thickness, graphene field-effect transistors (FETs) are potential candidates for a variety of chemical and biological sensors [1]. For liquid based sensors, most germane to physiologically relevant assays, a liquid electrolyte is typically in direct contact with the graphene surface. Broadly speaking the sensing assays can be divided into sensing three classes of moieties: (1) pH, (2) electrolyte concentration, (3) small quantities of charged analytes, especially charged biopolymers such as DNA [2] and proteins [3]. Because the liquid electrolyte or species to be sensed are in direct contact with the graphene, it is important to elucidate the physical interaction and mechanism of modulation of charge transport, especially the 3^rd class (charged polymers).

In the case of the first two classes (pH and electrolyte concentration sensing), considerable controversy about the mechanism persists, in spite of general agreement that the mechanism is some combination of (1) changes of the surface charge density due to ionizable side groups or OH⁻/H⁺ adsorption, and (2) changes in the Debye layer screening of this surface charge. Dekker et al. presented a model of two ionizable impurities, both with pKa 4.5, one negative, and one positive that would be ionized at different pH [4]. They attributed this to residual resist and organics from the process of the fabrication, but argued that the graphene itself was pristine. Two other groups using different methods (electrochemical capacitance measurements [5], molecular modeling [6], as well as different substrate effects [7]), have argued against this hypothesis, claiming the OH⁻ and H⁺ specifically adsorb to the sidewalls of pristine graphene, causing electrostatic gating effects. However, the molecular modeling was based on the assumption of graphene hydrophobicity, which is not always the case on hydrophilic substrates [8]. A third mechanism has been proposed, in which ionization of dangling bonds at cracks or other graphene impurities changes in response to pH [9]. This is based on low pH sensitivity measured using putatively pristine (defect free) graphene, together with arguments of hydrophobicity being incompatible with OH⁻ or H⁺ adsorption, which again neglects the hydrophilicity of graphene on hydrophilic substrates. In spite of this controversy, the mechanism of electrolyte and pH sensing is generally agreed upon to be due to two effects: Change of the surface charge and changes in the Debye layer screening of this surface charge.

In contrast to the first two cases, which have been well studied, the third and most important (and complex) case of the sensing of charged polymers has only been phenomenologically observed, but not studied in any model system. Given the potential technological significance of charged polymer sensing (in e.g. DNA sequencing, biomarker assays for cancer detection, etc.), it is important to elucidate the mechanism of sensing of charged polymers in graphene biosensors.

Nominally, graphene FETs detect the changes at the surface due to adsorption of charged species. These charged species may change the charge carrier density of graphene via one of two possible mechanisms. The first one is a capacitive gating mechanism like an electrostatic field effect transistor (gating). This mechanism does not involve the transfer of charge from the gating moiety to the graphene. For example, the applied voltage from the back of Si wafer or from the electrolyte solution to the graphene FETs will generate an electrostatic gating effect [4, 10], even though no charge is transferred from the silicon back gate to the graphene. The second mechanism is surface charge doping by partial electron transfer to or from graphene. As an example of such charge transfer, a classical dopant in a semiconductor involves an atom which “gives away” an entire extra outer shell electron to the conduction band of the semiconductor. Arguably, the most significant sensing applications of graphene will involve charged species (such as DNA and proteins, both charged biopolymers) which adsorb to the graphene surface. However, discerning the sensing mechanism (either doping or electrostatic gating) is non-trivial for charged species in direct physical contact with the surface of graphene, because both effects can contribute to the conductance change in response to adsorption.

In this work, we use a well defined charged polymer system (having both positive and negative charges determined at will) in direct contact with the graphene as a model system to investigate the interaction of charged polymer species with graphene. In order to study the exact nature of this interaction, we employed both positively and negatively charged multilayers—polyallylamine hydrochloride (PAH) and sodium polystyrene sulfonate (PSS), respectively—to mimic charged polymers on graphene’s surface. These polyelectrolyte multilayers (PEMs) are prepared by the layer-by-layer deposition of polyanions and polycations from aqueous solution. With this technique, polyanion/polycation complexes are formed with charge reversal after each successive layer. Using these species, we can control and predict the shift of the graphene’s Dirac point by the adsorption of different polymer layers, and effectively change the graphene from p-type to n-type at will. The Dirac point of graphene displays periodic behavior during sequential addition of positively and negatively charged polymers. A simple electrostatic model is applied to interpret these results, and demonstrates that electrostatic gating can account for the interaction of charged polymer species with graphene in an electrolyte gated system, the most promising sensing application envisioned for graphene biosensors. We compare this work to similar work on silicon on insulators, silicon oxide, silicon nanowires, and carbon nanotubes, each with a qualitatively different set of electrostatic and chemical properties, quite distinct from graphene which presents a planar, nominally uniform, inert surface directly to the gating electrolyte.

2 Experimental

2.1 Materials

Chemical Vapor deposition (CVD)-grown graphene was obtained from Graphene Supermarket. PAH (M_W = 58,000) and PSS (M_W = 70,000) were purchased from Sigma-Aldrich. The polyelectrolyte solution NaCl was prepared with deionized water obtained from a Millipore system.

2.2 Fabrication and measurement of graphene transistors

The graphene transistors were fabricated by employing direct transfer CVD-grown graphene on a polydimethylsiloxane (PDMS) block [11]. Then a second PDMS well with a 2 mm × 5 mm window was attached on top of the graphene to insulate the solution from two electrodes. The electrolyte was 100 mM NaCl and the gate voltage was applied using a Ag/AgCl reference electrode. The drain–source current vs. gate voltage was measured using an Agilent 34401A multimeter.

2.3 Deposition of polyelectrolyte PAH and PSS on graphene transistors

The polyelectrolyte film was formed by dropping a solution of 1.5 mM PSS or PAH dissolved in deionized (DI) water in the PDMS open window on the graphene surface for 30 min. After the polymer solution was taken out, the graphene surface was rinsed with DI water several times. Finally, the polyelectrolyte film was dried at room temperature overnight. For the polyelectrolyte multilayers, the above process was repeated sequentially, alternating between PSS and PAH until the desired number of layers was achieved.

2.4 Characterization

Scanning electron microscopy (SEM) images were obtained by FEI Quanta 3D FEG Dual Beam. Raman spectra were measured with a 532 nm excitation laser and a 50X objective lens. The specimens were prepared by PDMS transfer printing graphene onto SiO₂. Fourier transform infrared spectroscopy (FTIR) spectra were obtained with a PerkinElmer System 2000 FTIR. The samples for the FTIR were prepared by PDMS transfer printing graphene on calcium fluoride substrates.

3 Results and discussion

Figure 1(a) shows a schematic illustration of PEMs of PAH and PSS on the graphene surface. The graphene device is made using a direct fabrication transfer method of CVD grown graphene to a PDMS substrate which does not require a sacrificial transfer layer, thus providing less contamination than standard methods, described in detail in our recent publication [11]. Figure 1(b) shows an optical image of a single layer graphene device. To determine the quality of the graphene, the sample was transferred to a silicon substrate for subsequent Raman spectroscopy Fig. 1(c). Graphene’s two major peaks are the G and 2D bands at ~1,563 and ~2,670 cm⁻¹, respectively. The defect-related peak is at 1,324 cm⁻¹. Figure 1(d) presents the liquid-gated ambipolar field-effect response of the graphene device in 100 mM NaCl and V_ds = 0.1 V. A Ag/AgCl reference electrode is employed to apply the electrolyte gate voltage. The ambipolar behavior is almost symmetric for both electron and hole conduction. The liquid-gated hole and electron mobilities of the graphene FETs are 1,556 and 992 cm²/(V·s), respectively, determined as described in detail in Ref. [11].

Figure 1.

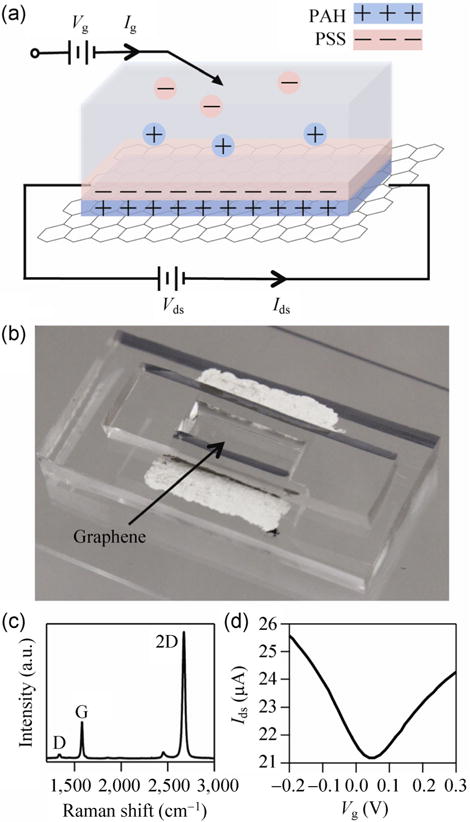
(a) Schematic illustration of polyelectrolyte multilayers of PAH and PSS deposited on the surface of single layer graphene. (b) Optical image of single layer graphene transistor device. (c) Raman spectrum of single layer graphene transfer-printed from PDMS block to SiO₂/Si substrate. (d) Liquid-gated ambipolar field-effect response of graphene device in 100 mM NaCl and V_ds = 0.1 V.

In order to study the effect of polyelectrolyte films on the electronic properties of graphene, we initially deposited only a single layer of either PAH or PSS film on the graphene FET. In subsequent experiments, polyelectrolyte multilayers were formed by alternating deposition of PAH and PSS inside the open PDMS chamber. We varied the size from 3–7 mm², and found no effect of the geometry on the deposition of polyelectrolyte multilayers on graphene surface or the Dirac voltage shift. However, previous work has shown that the edges can be doped using a variety of chemistries [12], and we would expect similar effects with the polyelectrolyte deposition onto nanoribbons or similar structures. The PAH and PSS films were characterized using a variety of techniques including SEM imaging of the deposited layers (see the Electronic Supplementary Material (ESM) 1), Raman spectroscopy of the polymer electrolyte coated graphene (ESM 2), FTIR spectroscopy of the polymer electrolyte on graphene (ESM 3), and ellipsometry characterization of the polymer electrolyte thickness (ESM 5). This characterization is comparable to “industry standard” data from other similar papers on this topic, specifically the work of Noy [13] et al. involving PEMs on nanotubes, as well as that of Neff [14] investigating the effect of PEM on silicon on insulator devices. It should be noted that direct evidence of the alternating layers of PAH and PSS has been provided in the literature using identical recipes to those we used in this work [15, 16].

In order to develop an electrostatic model, we first discuss the results for a single layer of PAH or PSS on graphene. Figure 2 presents the transfer characteristics of graphene FETs for bare graphene, PAH/graphene and PSS/graphene in (a) 1 and (b) 100 mM NaCl at V_ds = 0.1 V. The Dirac point of bare graphene is at 90 mV at 1 mM (Fig. 2(a)) and 10 mV at 100 mM (Fig. 2(b)). This residual background doping is presumably due to substrate impurities and is consistent with similar work in the literature. After the positively charged polyelectrolyte film PAH is deposited on the graphene surface, the Dirac point shifts to a more negative gate voltage. Similarly, after the negatively charged polyelectrolyte film PSS is deposited on the graphene surface, the Dirac point shifts to a more positive gate voltage. We also found the magnitude of the Dirac voltage shift can be controlled by adjusting the adsorption concentrations (the change of Dirac point is proportional to the concentration of PAH and PSS). Precise control of the Dirac point shift requires control of both the concentration and thickness (see model below); control of one parameter alone does not guarantee consistent tunability. The ability to controllably shift the Dirac point opens up more opportunities for applications. We now describe this effect in terms of a simple electrostatic gating model.

Figure 2.

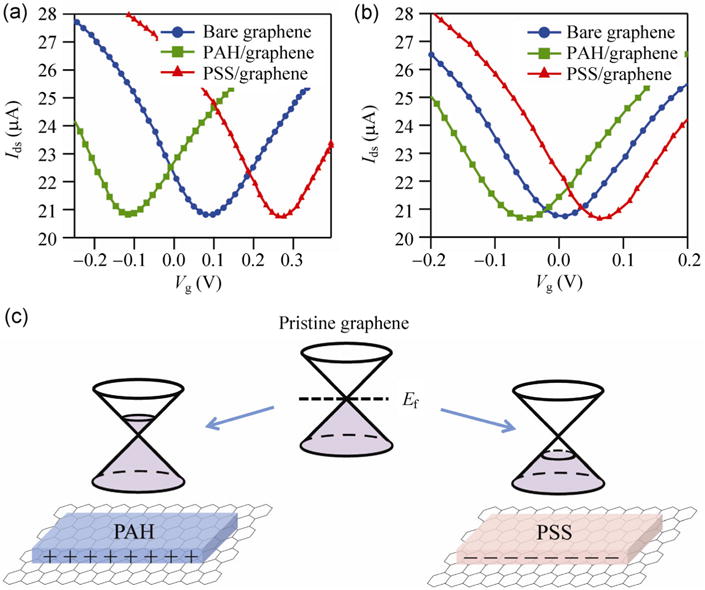
Transfer characteristic of graphene FETs for bare graphene, PAH/graphene and PSS/graphene in (a) 1 and (b) 100 mM NaCl at V_ds = 0.1 V. (c) The relationship between the Fermi energy shift and the deposition of PAH and PSS on the graphene surface.

In Fig. 3 we present a simple electrostatic model explaining the interaction between the charged polymer and the electrolyte which accounts for our observed Dirac voltage shifts. Figures 3(a)–3(c) depict a capacitor equivalent circuit model (a), the classical example (provided for a well-studied comparison to graphene) of an electrolyte in contact with a metal with no specifically adsorbed species (b), and the analogous case of graphene in contact with an electrolyte (c). Application of a positive potential to an electrolyte in contact with a classic metal induces a negative charge on the metal (Fig. 3(b)), balanced by a positive layer of charged cations adsorbed to the surface of the metal (the double layer). An analogous situation occurs when the electrode is a graphene electrode (Fig. 3(c)). In the case of graphene, the induced negative charge on the graphene shifts the Fermi energy into the conduction band. Key assumeptions in this model are that (1) there are no redox reactions between the electrolyte and the electrode; (2) at zero applied bias to the electrolyte, there are no specifically adsorbed charges species on the surface of the metal (Fig. 3(b)) or graphene (Fig. 3(c)) electrode; (3) there is no charge transfer from the adsorbed ions to the graphene (Fig. 3(c)). We will revisit these key assumptions (which differentiate this work from analogous work on silicon, silicon nanowires, and carbon nanotubes) later in the paper. For now, we will make the case that this explains the effect of the PAH on graphene in a simple way.

Figure 3.

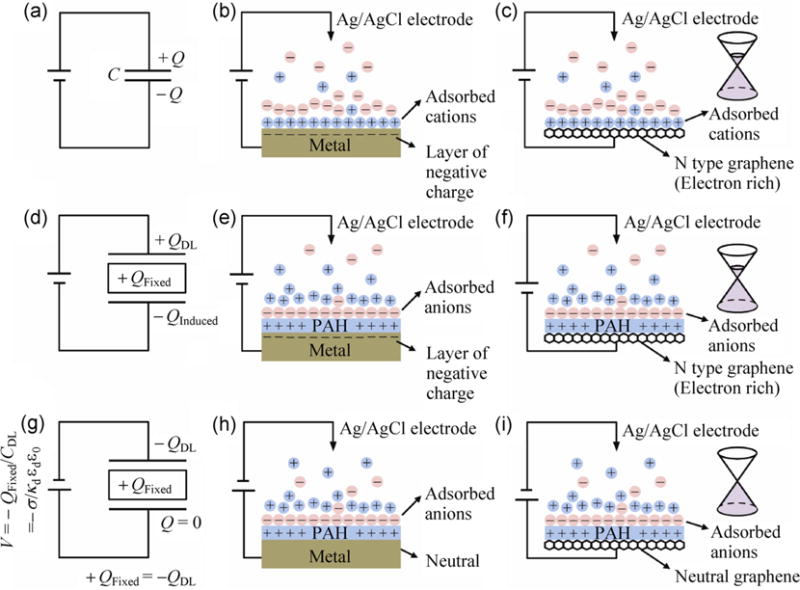
Explanation of electrostatic gating model of PAH on graphene. In the top row, for comparison, we show (a) the circuit model for an electrolyte in contact with an electrode, (b) the buildup of charge at a metal electrode in response to an applied voltage on the electrolyte, and (c) the analogous case for graphene in contact with an electrolyte. In the second row, we present the modification to the electrostatics when (d) a fixed charge is placed in between the capacitor plates, (e) a fixed charge of finite thickness is deposited on a metal in the presence of an electrolyte, and (f) a fixed charge of finite thickness is deposited on the surface of graphene. In the bottom row, we present the special case of a negative applied voltage that exactly cancels the induced charge. In circuit terms, (g), at a specific applied voltage, the fixed charge exactly balances the double layer, (h) the induced charge on the metal is zero, and (i) the graphene charge is zero, i.e. the Dirac voltage is shifted from zero to Q_Fixed/C_DL, where C_DL is the double layer capacitance, Aκ_dε_dε₀. (Symbols are defined in the text.)

We next consider what happens when a positively charged PAH is deposited onto a solid surface. Two possible scenarios emerge. The first is that the positive charges are complemented by negatively charged anions in solution inside the PAH, resulting in a net zero charge density. This happens if the layer thickness is large compared to the Debye screening length. The second is that the charges are not compensated, and that there is a net positive charge density. Although there is not universal agreement on this, it is generally believed that the latter case (uncompensated charges) occurs when the layer thickness is less than the Debye screening length [17, 18]. Simply put, the positive charges of the PAH are not shielded and leave a net positive charge density on top of the electrode. We now consider the effects of this on the electrostatic gating effect.

The positively charged PAH attracts a layer of negatively charged adsorbed anions on the surface. In addition, the positively charged PAH layers induces a negative charge on the surface of the metal (Fig. 3(e)) or graphene Fig. 3(f). The three charges (the double layer charge Q_DL, the PAH charged which is fixed Q_Fixed, and the induced charge Q_Induced) are not necessarily equal; only Q_Fixed remains independent of the bias voltage. Even at zero applied bias, all three charges are not necessarily zero. As the bias voltage on the Ag/AgCl electrode is reduced further to become negative, the induced charge on the metal (Fig. 3(e)) or graphene (Fig. 3(f)) electrodes is reduced and eventually becomes zero. In this case, the double layer charge Q_DL exactly balances the fixed PAH charge Q_Fixed, and the induced charge density on the metal (Fig. 3(h)) or graphene (Fig. 3(i)) is zero. This corresponds to the Dirac point of graphene. The double layer capacitance can be modeled [19] as C_DL = Aκ_dε_dε₀, where A is area, κ_d is the Debye screening length, ε_d is the relative dielectric constant in water, and ε₀ = 8.85 × 10⁻¹² F/m. In this model, the Dirac voltage will shift by

$$\mathrm{\Delta }{V}_{\text{Dirac}}=-Q_{\text{Fixed}}/C_{\text{DL}}=-\sigma /{\kappa }_{\mathrm{d}}{\mathrm{\epsilon }}_{\mathrm{d}}{\mathrm{\epsilon }}_0$$ (1)

Where σ is the polymer areal charge density. Similarly, if the polymer is negatively charged, the Dirac voltage will shift in the opposite direction. As the double layer capacitance depends on the screening length, which in turn depends on the electrolyte molarity, this predicts a different Dirac voltage shift depending on the KCl concentration.

This model explains quantitatively the features we observe when a single layer of positively (PAH) or negatively (PSS) charged polymer is deposited on the graphene surface: The voltage shift is positive or negative, as expected from the model (Figs. 2(a) and 2(b)). In addition, the magnitude of the voltage shift is larger at smaller NaCl concentrations, consistent with the model: At smaller NaCl concentrations, the Debye screening length is larger, hence the double layer capacitance is smaller, and hence the Dirac voltage shift is larger, as Eq. (1). Using estimated values of 7.2 and 72 μF/cm² at 1 and 100 mM NaCl [19], and the measured Dirac voltage shift of 0.18 and 0.06 V respectively, yields values of σ of 0.013 and 0.043 C/m², for the polymer surface charge density, consistent with reported literature values for PEMs deposited under similar conditions [16].

In our next series of experiments, we sequentially deposited positively charged polymer PAH and negatively charged polymer PSS on graphene FETs for up to six layers, and measured the shift in the Dirac voltage in response to each layer. Figure 4 shows the transfer characteristics of graphene FETs as a function of PAH/PSS multilayers measured in (a) 1 mM NaCl and (b) 100 mM NaCl. The Dirac voltage shifts back and forth in response to addition of each layer, with almost no Dirac voltage shift at even layer numbers (i.e. the total deposited charge is zero). A simple model to explain this shift is based on alternating layers of positive and negative charges. From the basic model presented for a single layer, we expect that if an even number of layers is present, they will cancel (the net fixed charged will be zero), and the Dirac voltage will shift back to the original position. This is indeed what we observe experimentally. If the number of layers is odd, the net charged will be positive. The negative gate voltage will be required to balance it in order to observe the Dirac point.

Figure 4.

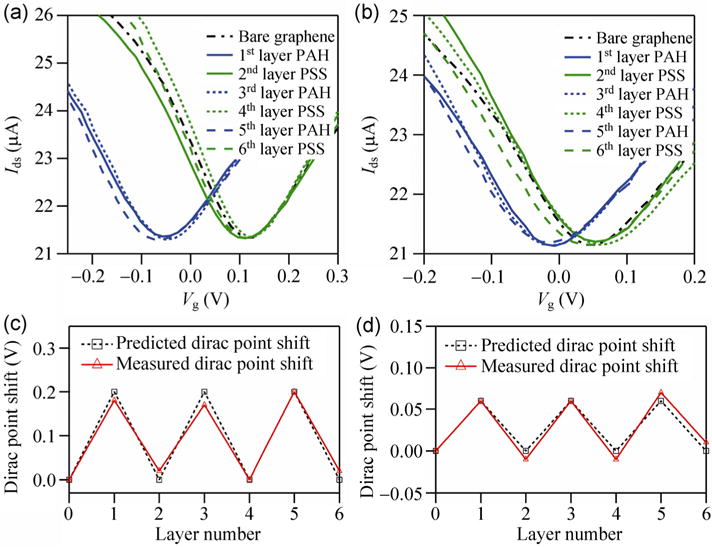
Transfer characteristics of graphene FET devices as a function of the number of PAH/PSS multilayers measured in (a) 1 mM NaCl and (b) 100 mM NaCl at V_ds = 0.1 V. Transfer characteristics of the device before (black dashed and dotted line) and after polymer coating with PAH (blue lines) and PSS (green lines). 1^st and 2^nd layers are solid lines. 3^rd and 4^th layers are dotted lines. 5^th and 6^th layers are dashed lines. Measured (red triangles) and predicted (black squares) device Dirac point voltage shift vs. the number of coating polymer layers for (c) 1 mM NaCl and (d) 100 mM NaCl. The Dirac point voltage of the uncoated device is regarded as the reference point.

If the number of layers becomes sufficiently large, then the total thickness will exceed the Debye screening length. In that case, the simple model presented above will no longer apply, and a more sophisticated model which takes into account the finite screening length needs to be developed. Briefly, the fixed PEM charges will be screened and a solution for the spatial profile of the potential needs to be developed. Such a model was presented in Ref. [16], and gives rise to the following prediction for the shift in the Dirac voltage with layer number

$$\mathrm{\Delta }{V}_{\text{Dirac}}(N)=\sigma /C_{\mathrm{D}}[(C_{\mathrm{p}}/C_{\mathrm{D}})\sin h({\kappa }_{\mathrm{p}}Nd)+\cos h({\kappa }_{\mathrm{p}}Nd)]$$ (2)

where C_p = κ_pε_pε₀ and C_D = κ_dε_dε₀ are the capacitances (per area) for polymer multilayer and electrolyte solution, κ_p and κ_d are the Debye lengths of polymer film and electrolyte solution [20], ε_p and ε_d are the dielectric constant for polymer film and electrolyte solution [16, 20], the number of polymer layers is N, the thickness of each layer is d [20], and σ is the polymer layer’s surface charge density. In our case, the parameter κ_pNd is less than one (0.05), so the dependence on N is mild and the simple model we presented above is actually quite close to the experimental data, as expected.

Taken collectively, our experiments indicate that electrostatic gating by charged polymers can dominate the Dirac voltage shift, which is a different mechanism from the sensing mechanism for the first two classes of sensing introduced in the beginning of this paper, which involves ionization of dangling bonds of residual organic impurities from the processing, ionization of dangling bonds in the graphene itself, or specific adsorption of OH⁻ or H⁺, or shielding of these charges. This work demonstrates a clear and simple canonical example of sensing of charged polymers by graphene.

We now compare this work to similar work on silicon on insulators, silicon oxide, silicon nanowires, and carbon nanotubes, each with a qualitatively different set of electrostatic and chemical properties, quite distinct from graphene. The history of polymer electrolytes on silicon and silicon oxide (which is charged and ionizable in a way that directly affects quantum transport, doping, and gating electrostatics) is very mature, and its effects have been applied in silicon nanowire biosensors. The work presented here follows that of Neff on silicon on insulator planar devices [16], where the surface presents an electrostatic potential sensitive conductance. However, the difference with graphene is that it is putatively non-reactive, with fewer dangling bonds. In contrast, the work of Neff, as well as other subsequent work using silicon nanowires [21, 22], relied heavily on the more reactive silanol groups for the sensing mechanism. This has both advantages and disadvantages, the most significant advantage being the ability to covalently functionalize the surface with different moieties. Carbon nanotubes were also investigated using this technique by Noy [15]. There, the dominant sensing mechanism was changed in the substrate (NOT the nanotube) electrostatics, which indirectly affected the nanotube conductance via local gating effects. In that work, the mechanism of electrostatic gating effects was more complicated because the single carbon nanotube is affected by the polyelectrolyte multilayer as well as the silicon oxide substrate, with ionizable side groups that change the electrostatics in the vicinity of the nanotube.

During the preparation of this manuscript, a similar paper was published using a solvent n-type doping [23]. Our work is complementary, in that we study charged polymers (rather then small molecules), and our polymers can be both positively or negatively charged, allowing a more thorough investigation of the gating mechanism, as well as the ability to create both n-type or p-type graphene at will. In addition, in contrast to Ref. [23], our approach can in principle be extended to dry (solvent free) operation.

4 Conclusions

We have demonstrated an electrostatic gating effect on graphene FETs using a simple, well known charged polymer system. We observed the shift of the Dirac point while depositing positively charged polymer PAH and negatively charged polymer PSS. A simple electrostatic model accounts well for the sign and magnitude of the Dirac voltage shift. Using this simple system, we are able to create p-type or n-type graphene at will. This model serves as the basis for understanding the mechanism of charged polymer sensing using graphene devices, a potentially technologically important application of graphene in areas such as DNA sequencing, biomarker assays for cancer detection, and other protein sensing applications.