Abstract
In this work, we successfully synthesize the single crystal Cr11Ge19. The magnetism of the noncentrosymmetric Cr11Ge19 with itinerant ferromagnetic ground state is thoroughly investigated on the single crystal. Based on the variation measurements including the angular rotation, temperature, and magnetic field dependence of magnetization, we find that this material exhibits strong magnetic anisotropy along the c-axis. To clearly reveal the magnetic interactions, the critical behavior is studied using the modified Arrott plot, the Kouvel-Fisher method, and the critical isotherm technique. Combining these different methods, three main critical exponents (β, γ, and δ) are obtained. The critical exponent β is close to the theoretical prediction of a three-dimensional XY model with spin-dimensionality n = 2, indicating two-dimensional magnetic coupling. Meanwhile, the critical exponent γ suggests that the magnetic interaction is of long-range type with magnetic exchange distance decaying as J(r) ≈ r−4.61. We propose that the ferromagnetic ground state of Cr11Ge19 is formed by the polarized magnetic moments along the c-axis, while the long-range magnetic coupling is established within the ab plane.
Itinerant ferromagnets, which are characterized by low saturation moment and Curie temperature, have been extensively studied due to their exotic physical phenomena such as superconductivity, quantum critical behavior, non-Fermi-liquid behavior, and unusual magnetic excitation1,2,3,4,5,6,7. According to the band theory of electrons, magnetic moments in these systems stem from the exchange splitting of bands8. Because of the extremely small band splitting, the saturation moment is only a fraction of a Bohr magneton, which is very close to the nonmagnetic phase boundary. Therefore, a small perturbation can arouse a large change to the electronic and magnetic properties9,10. The thermodynamical properties of itinerant ferromagnets have usually been explained by conventional Stoner-Wohlfarth theory of band ferromagnetism based on Hartree-Fock mean-field theory11. On the other hand, the theoretical model based on the self-consistent renormalization considering spin fluctuations is found to be more satisfactory for describing the electronic and magnetic behaviors in these systems12,13. Recently, noncentrosymmetric itinerant ferromagnets exhibiting chiral magnetic ordering have attracted considerable attention because of the discovery of magnetic particle-like configurations, such as skyrmion, magnetic soliton, and chiral bobber14,15,16,17. The lack of an inversion center in noncentrosymmetry usually results in Dzyaloshinsky-Moriya (DM) interaction, which is 1~2 orders of magnitude smaller than that of the ferromagnetic coupling. The competition between the DM interaction and ferromagnetic coupling often results in non-collinear magnetic ordering states such as helimagnetism, conical ordering state, and magnetic particle-like configurations. Due to the extra perturbation brought by the noncentrosymmetry, the investigation of noncentrosymmetric itinerant ferromagnet is of great importance in understanding the exotic phenomena in these systems.
The noncentrosymmetric Cr11Ge19, which exhibits tetragonal structure with the space group 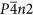 , is crystallized belonging to a family of compounds known as Nowotny chimney ladders18. A chiral structure of Cr-Cr bonds arranges along the c-axis. Due to the noncentrosymmetric characteristic, the DM interaction may exist in Cr11Ge19, which makes it a candidate possessing a magnetic particle-like configuration19. The Cr11Ge19 exhibits complex ferromagnetic ground state20,21,22. Early work has demonstrated that the ground state of Cr11Ge19 is a p-type semi-metallic ferromagnetism22. However, a linear muffin tin orbital (LMTO) calculation of electronic density of states has suggested it to be an itinerant ferromagnet with low magnetic moment23. Recent studies have manifested that Cr11Ge19 displays complex itinerant ferromagnetism. However, the magnetic behavior cannot be explained by the Stoner model which is a conventional theory describing the itinerant ferromagnet24. Both the experimental results and calculations have indicated that Cr11Ge19 is a good example of an itinerant electron ferromagnet, with signatures of spin wave excitation and magnetic fluctuation24.
, is crystallized belonging to a family of compounds known as Nowotny chimney ladders18. A chiral structure of Cr-Cr bonds arranges along the c-axis. Due to the noncentrosymmetric characteristic, the DM interaction may exist in Cr11Ge19, which makes it a candidate possessing a magnetic particle-like configuration19. The Cr11Ge19 exhibits complex ferromagnetic ground state20,21,22. Early work has demonstrated that the ground state of Cr11Ge19 is a p-type semi-metallic ferromagnetism22. However, a linear muffin tin orbital (LMTO) calculation of electronic density of states has suggested it to be an itinerant ferromagnet with low magnetic moment23. Recent studies have manifested that Cr11Ge19 displays complex itinerant ferromagnetism. However, the magnetic behavior cannot be explained by the Stoner model which is a conventional theory describing the itinerant ferromagnet24. Both the experimental results and calculations have indicated that Cr11Ge19 is a good example of an itinerant electron ferromagnet, with signatures of spin wave excitation and magnetic fluctuation24.
In this work, we successfully synthesize the single crystal Cr11Ge19. The magnetism of Cr11Ge19 on the single crystal is investigated. We find that the magnetization of Cr11Ge19 exhibits strong magnetic anisotropy along the c-axis in the ferromagnetic phase. Moreover, the study of critical behavior suggests that the magnetic interaction is of long-range type with two-dimensional magnetic coupling.
Results and Discussion
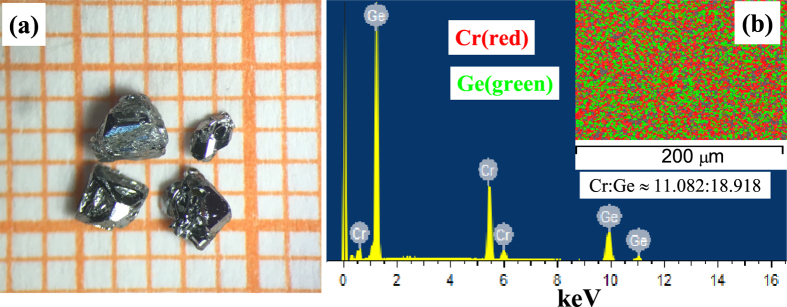
Figure 1(a) presents the photograph of Cr11Ge19 single crystals, which shows that the typical sizes of these single crystals are in millimeter scale. The shapes of the single crystals are three-dimensional graininess with small bright surfaces. Figure 1(b) gives a typical EDX spectrum of the Cr11Ge19 single crystal. The EDX spectra measured at different points indicate that the proportion of Cr:Ge is close to 11:19 (Please see the Supplementary Information). The inset of Fig. 1 gives the distribution of the elements, which indicates that Cr and Ge are distributed homogeneously. The left inset of Fig. 2(a) depicts the morphology of a typical single crystal with size of 885 × 861 μm. The bright surface was checked by XRD as shown in Fig. 2(a), which indicates that the surface is (200) plane. The right inset of Fig. 2(a) presents the rock curve of the (200) diffraction peak. The full-width-at-half-maximum (FWHM) of the rock curve is Δθ = 0.005°. The single peak and narrow FWHM of the rock curve indicate high quality of the single crystal sample without twin crystal. The other crystal orientations in the bc plane are determined by Laue photograph. The crystal orientations are marked on the single crystal in the left inset of Fig. 2(a). Figure 2(b) shows the XRD pattern for powder Cr11Ge19 ground from several pieces of single crystals. The powder XRD pattern also indicates a single phase of Cr11Ge19 without impurities. The fitting results give the lattice constants a = b = 5.803(7) Å and c = 52.343(1) Å, which is in agreement with previous reports20,22,24.
Figure 1.
(a) The photograph of Cr11Ge19 single crystals; (b) a typical EDX spectrum for single crystal Cr11Ge19 (the inset shows the distribution of elements).
Figure 2.
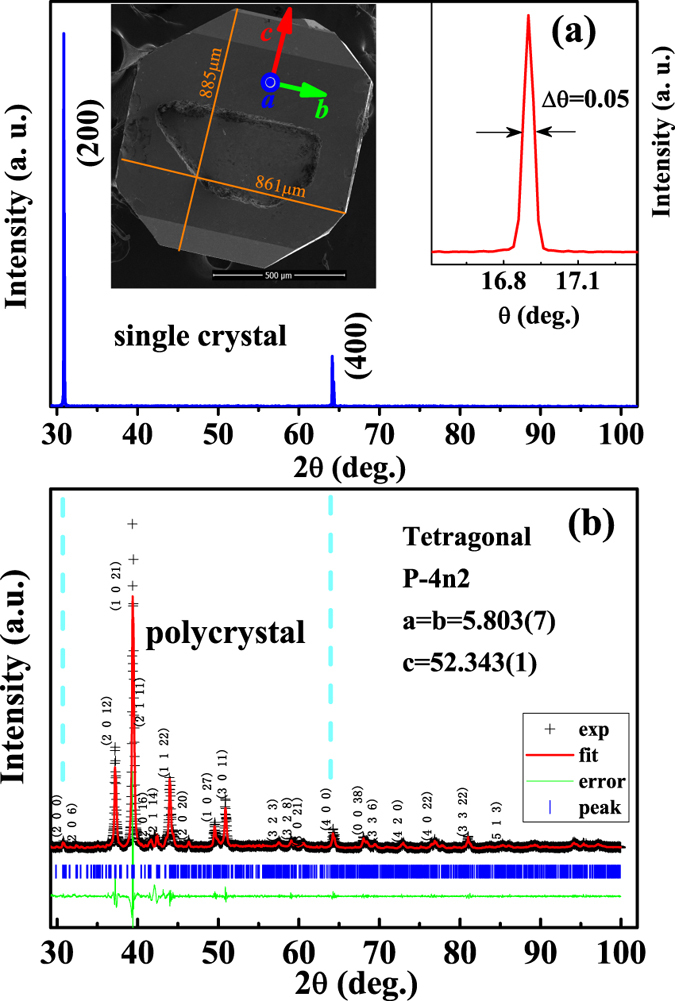
(a) The XRD pattern of the surface at room temperature for the single crystal (the left inset shows the morphology of the single crystal; the right inset gives the rock curve of (200) plane) (b) the XRD pattern at room temperature for powder Cr11Ge19.
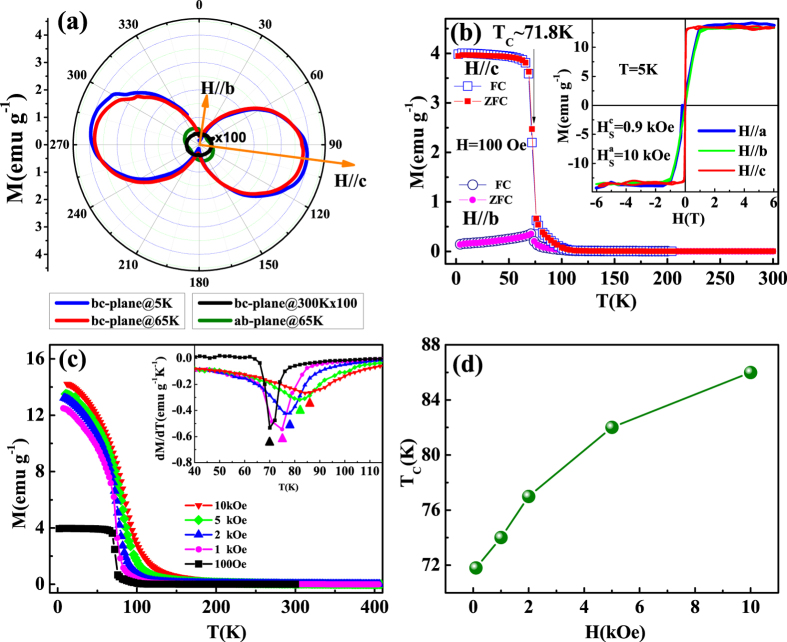
Figure 3(a) gives the magnetization as a function of rotation angle [M(φ)] under H = 100 Oe. The M(φ) curves in both ab and bc planes are measured. In the bc plane, it can be seen that the value M along the c-axis is much larger than that along the b-axis at temperatures of 65 K and 5 K, revealing strong magnetic anisotropy along the c-axis. However, there is no magnetic anisotropy at 300 K. In the ab plane, much weaker magnetic anisotropy is observed at 65 K. The variation of M(φ) curves indicates that Cr11Ge19 displays strong magnetic anisotropy, and the easy magnetization orientation is along the c-axis. It is noted that the cell of Cr11Ge19 is tetragonal with equal a and b axes, while the Nowotny chimney ladders are found along the c-axis24. Therefore, the exhibition of strong magnetic anisotropy along the c-axis corresponds closely to the tetragonal crystal structure. Figure 3(b) displays the temperature dependence of magnetization [M(T)] under zero-field-cooling (ZFC) and field-cooling (FC) with H = 100 Oe along c- and b-axis. The M(T) curves with H//c exhibit a typical paramagnetic-ferromagnetic transition. The M(T) curves with H//b are different from those with H//c. The values of M are much smaller and the transition becomes un-obvious when H//b. This result implies that the paramagnetic-ferromagnetic transition is mainly determined by the magnetization along the c-axis. The inset of Fig. 3(b) displays the isothermal magnetization [M(H)] at 5 K with H//a, H//b, and H//c. The M(H) curves with H//a and H//b are well overlapped with each other, which become saturated when H exceeds ~10 kOe. However, for M(H) curve with H//c, the situation magnetic field HS (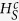 ~ 0.9 kOe) is much smaller than that with H//a or H//b (
~ 0.9 kOe) is much smaller than that with H//a or H//b (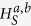 ~ 10 kOe). When H exceeds 10 kOe, the three M(H) curves overlap with each other reaching the same saturated moment MS. The obtained MS is 0.43 μB/Cr, which is in agreement with the previous report in a polycrystalline sample24. The strong magnetic anisotropy only appears when H is weaker than HS. When H exceeds HS, spins of all directions are polarized along the orientation of applied field H, regardless of H//a, H//b, or H//c. This is a process of spin rotation from unsaturated state to saturated one. The transition temperature TC ~ 71.8 K is determined from the sharpest point of the phase transition, as shown in Fig. 3(b). Generally, TC is actually difficult to be determined from magnetism because it is usually dependent on the external field. Figure 3(c) shows the M(T) curves under different fields with H//c, and the inset gives the dM/dT vs. T. The field dependence of TC determined from the minimum from dM/dT(T) curves is depicted in Fig. 3(d), which shows that TC increases monotonously with the increase of H. The TC is ~86 K when H = 10 kOe, which is close to that of 86 K reported by V. L. Zagryazhskii, et al.22 and 88 K by N. J. Ghimire, et al.24 from the polycrystalline sample.
~ 10 kOe). When H exceeds 10 kOe, the three M(H) curves overlap with each other reaching the same saturated moment MS. The obtained MS is 0.43 μB/Cr, which is in agreement with the previous report in a polycrystalline sample24. The strong magnetic anisotropy only appears when H is weaker than HS. When H exceeds HS, spins of all directions are polarized along the orientation of applied field H, regardless of H//a, H//b, or H//c. This is a process of spin rotation from unsaturated state to saturated one. The transition temperature TC ~ 71.8 K is determined from the sharpest point of the phase transition, as shown in Fig. 3(b). Generally, TC is actually difficult to be determined from magnetism because it is usually dependent on the external field. Figure 3(c) shows the M(T) curves under different fields with H//c, and the inset gives the dM/dT vs. T. The field dependence of TC determined from the minimum from dM/dT(T) curves is depicted in Fig. 3(d), which shows that TC increases monotonously with the increase of H. The TC is ~86 K when H = 10 kOe, which is close to that of 86 K reported by V. L. Zagryazhskii, et al.22 and 88 K by N. J. Ghimire, et al.24 from the polycrystalline sample.
Figure 3.
(a) The magnetization as a function of rotation angel [M(φ)]; (b) the temperature dependence of magnetization [M(T)] with the isothermal magnetization [M(H)] at 5 K in the inset; (c) M(T) curves along the c-axis under different H (the inset gives the dM/dT vs. T); (d) the field dependence of TC determined from the minimum from dM/dT curves.
According to the Stoner model, the itinerant ferromagnet should follow25,26,27:
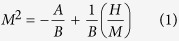 |
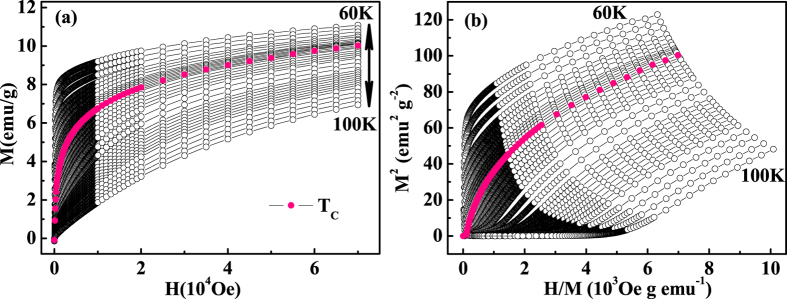
where A and B are parameters independent of H. Thus, the Arrott plot of M2 vs. H/M can be constructed, where the M2 vs. H/M relations should present a series of straight lines around TC28. Meanwhile, M2 vs. H/M at TC should just pass through the origin28. Figure 4(a) shows the initial isothermal M(H) curves around TC with H//c (i. e. the easy magnetization axis), and Fig. 4(b) gives the Arrott plot of M2 vs. H/M for Cr11Ge19. All curves of the Arrott plot show nonlinear behaviors even in the high field region, which suggests that the critical behavior of Cr11Ge19 cannot be described by the conventional Stoner model. The order of the phase transition can be determined by the slope from the Arrott plot according to the Banerjee’s criterion, where a negative slope corresponds to a first-order transition and a positive slope suggests a second-order one29. The positive slopes of M2 vs. H/M curves reveal that the phase transition in Cr11Ge19 is of a second order. However, the nonlinear of the M2 vs. H/M curves indicates that the conventional Arrott plot is invalid for Cr11Ge19.
Figure 4.
(a) The isothermal initial magnetization measured along the c-axis around TC for Cr11Ge19; (b) the Arrott plot of M2 vs. H/M.
For a second order magnetic phase transition, the magnetic interaction can be identified by the investigation of critical behavior. In the vicinity of the ferromagnetic transition, the spontaneous magnetization MS and initial susceptibility χ0 can be described by a series of functions30,31:
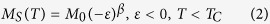 |
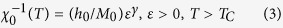 |
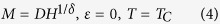 |
where ε = (T − TC)/TC is the reduced temperature; M0/h0 and D are critical amplitudes. The parameters β (associated with MS), γ (associated with χ0), and δ (associated with TC) are the critical exponents. The critical behavior around the critical temperature can be described by a series of critical exponents, which follow the Arrott-Noakes equation of state in asymptotic critical region32:
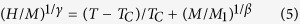 |
The critical exponents give significant clues about the magnetic interactions, such as the correlating length, spin-dimensionality, and decaying distance of magnetic coupling.
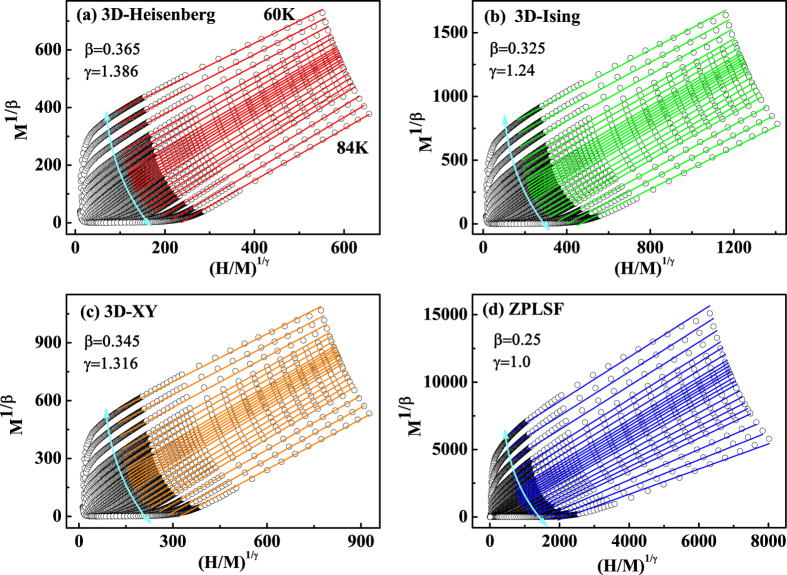
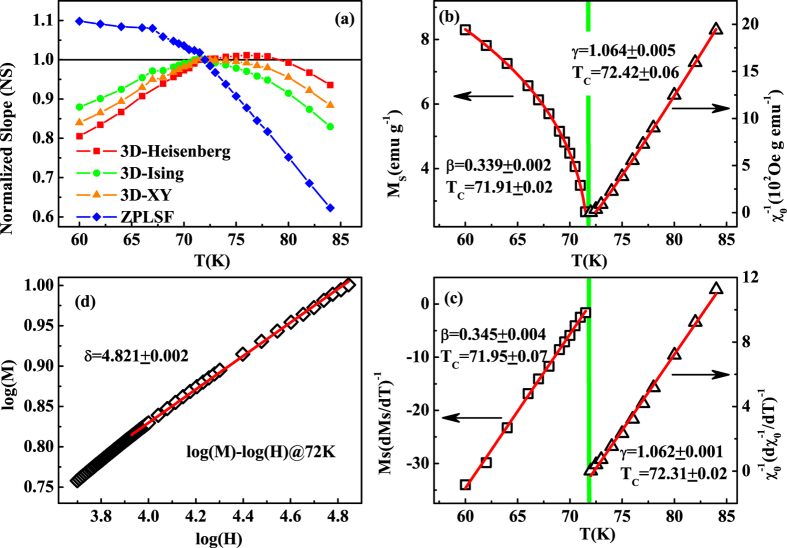
In view of the dissatisfaction of conventional Arrott plot for Cr11Ge19, a modified Arrott plot (MAP) of M1/β vs. H/M1/γ could be employed. Three kinds of modes belonging to the 3D-Heisenberg model (β = 0.365, γ = 1.336), 3D-Ising model (β = 0.325, γ = 1.24), and 3D-XY model (β = 0.345, γ = 1.316) are tried to construct the modified Arrott plots33,34, as shown in Fig. 5(a–c) respectively. According to the theoretical model suggested by Takahashi considering the zero point local spin fluctuation (ZPLSF), M4 vs. H/M should exhibit straight lines in high field region (i.e. M1/β vs. H/M1/γ with β = 0.25, γ = 1.0)13,24. Therefore, M4 vs. H/M curves are plotted in Fig. 5(d). All the curves in these four constructions exhibit quasi-straight lines in high field region. However, the lines in Fig. 5(d) are not parallel to each other, indicating that the theoretical model suggested by Takahashi is not satisfied for Cr11Ge19. For Fig. 5(a–c), it is difficult to distinguish which model is the best. For an ideal model, the modified Arrott plot should display a series of parallel lines in high field region with the same slope, where the slope is defined as S(T) = dM1/β/d(H/M)1/γ. The normalized slope (NS) is defined as NS = S(T)/S(TC), which enables us to distinguish the most suitable model by comparing the NS with the ideal value of ‘1’35,36,37. Plots of NS vs. T for the four different models are shown in Fig. 6(a). It can be seen that the NS of 3D-Heisenberg model is close to ‘1’ mostly above TC, while that of 3D-Ising model is the best below TC. This result indicates that the critical behavior of Cr11Ge19 does not belong to a single universality class.
Figure 5.
The isotherms of M1/β vs. (H/M)1/γ with parameters of (a) 3D-Heisenberg model, (b) 3D-Ising model, (c) 3D-XY model, and (d) the theoretical model considering zero point local spin fluctuation (ZPLSF).
Figure 6.
(a) Temperature dependence of normalized slope (NS); (b) the MS (left) and χ0−1 (right) as a function of temperature for Cr11Ge19; (c) the Kouvel-Fisher plot for MS(T) (left) and χ0−1(T) (right); (d) isothermal M(H) at TC with log-log scale (all red solid curves are fitted).
The precise values of the critical exponents β and γ can be obtained by an iterative method38. The linear extrapolation from the high field region to the intercepts with the axes M1/β and (H/M)1/γ yields reliable values of MS(T, 0) and 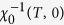 . A set of β and γ values can be obtained by fitting data to Eqs (2) and (3). These obtained β and γ values are used to reconstruct a new modified Arrott plot. Subsequently, new MS(T, 0) and
. A set of β and γ values can be obtained by fitting data to Eqs (2) and (3). These obtained β and γ values are used to reconstruct a new modified Arrott plot. Subsequently, new MS(T, 0) and 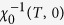 are generated from the linear extrapolation from the high field region. Therefore, another set of β and γ can be yielded. This procedure is repeated until β and γ do not change. By this method, the obtained critical exponents are hardly dependent on the initial parameters. The final MS(T, 0) and
are generated from the linear extrapolation from the high field region. Therefore, another set of β and γ can be yielded. This procedure is repeated until β and γ do not change. By this method, the obtained critical exponents are hardly dependent on the initial parameters. The final MS(T, 0) and 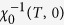 are plotted as a function of temperature in Fig. 6(b). Consequently, exponents β = 0.339 ± 0.002 with TC = 71.92 ± 0.02 K and γ = 1.064 ± 0.006 with TC = 72.42 ± 0.06 K are obtained.
are plotted as a function of temperature in Fig. 6(b). Consequently, exponents β = 0.339 ± 0.002 with TC = 71.92 ± 0.02 K and γ = 1.064 ± 0.006 with TC = 72.42 ± 0.06 K are obtained.
Alternatively, critical exponents can be determined by the Kouvel-Fisher (KF) method39:
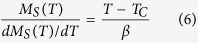 |
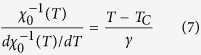 |
It can be seen that the MS(T)/dMS(T)/dT and 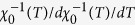 are as linear functions of temperature with slopes of 1/β and 1/γ respectively. Figure 6(c) plots the MS(T)/[dMS(T)/dT] and
are as linear functions of temperature with slopes of 1/β and 1/γ respectively. Figure 6(c) plots the MS(T)/[dMS(T)/dT] and 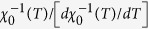 vs. T relations, which give more actual exponents β = 0.345 ± 0.004 with TC = 71.95 ± 0.07 K and γ = 1.062 ± 0.001 with TC = 72.31 ± 0.02 K. The critical exponent δ can be calculated by fitting to critical isothermal (CI) magnetization M(H) at TC following Eq. (4). Figure 6(d) shows the M(H) at TC = 72 K on log-log scale, which gives that δ = 4.821 ± 0.002.
vs. T relations, which give more actual exponents β = 0.345 ± 0.004 with TC = 71.95 ± 0.07 K and γ = 1.062 ± 0.001 with TC = 72.31 ± 0.02 K. The critical exponent δ can be calculated by fitting to critical isothermal (CI) magnetization M(H) at TC following Eq. (4). Figure 6(d) shows the M(H) at TC = 72 K on log-log scale, which gives that δ = 4.821 ± 0.002.
These critical exponents should follow the scaling equations. In the asymptotic critical region, the scaling equations can be written as31:
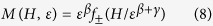 |
where f± are regular functions denoted as f+ for T > TC and f− for T < TC. Defining the renormalized magnetization m ≡ ε−βM(H, ε), and the renormalized field h ≡ Hε−(β+γ), the scaling equations indicate that m vs. h forms two universal branches for T > TC and T < TC, respectively40,41. Based on the scaling equation [m = f±(h)], the isothermal magnetization around the critical temperatures for Cr11Ge19 are replotted in Fig. 7(a), with log-log scale in the inset. It can be seen that all experimental data, including those in low field region, collapse into two universal curves. Meanwhile, the m2 vs. h/m curves also collapse into two independent branches as shown in Fig. 7(b). Furthermore, the scaling equation of state takes another form31,41:
Figure 7.
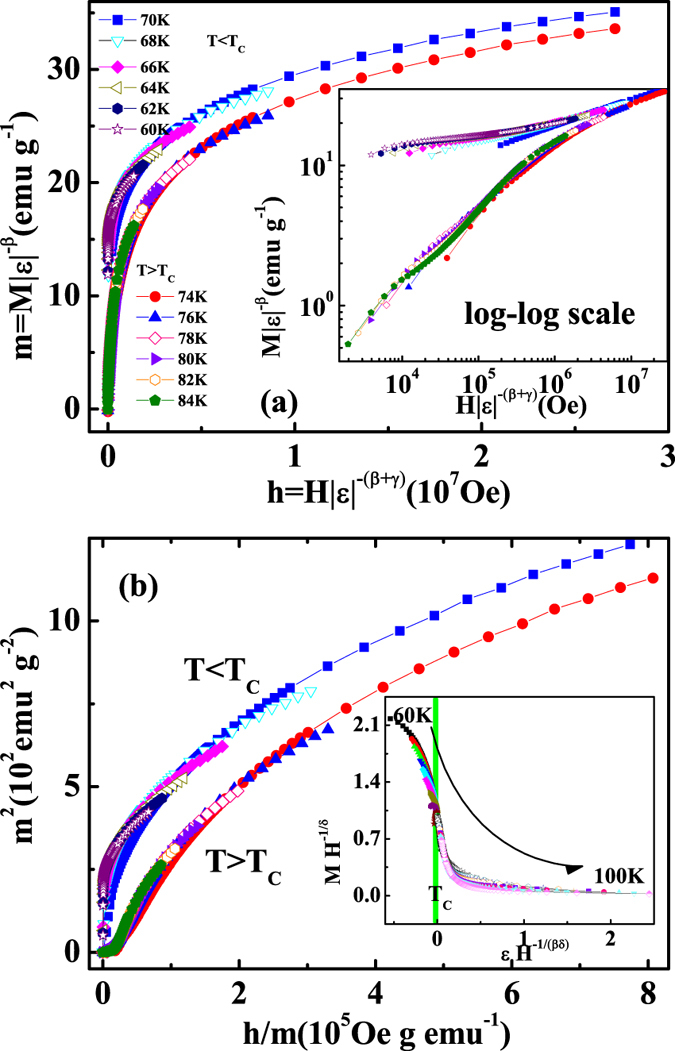
Scaling plots of m vs. h around TC; (b) m2 vs. h/m (the inset shows the re-scaling of the M(H) curves by MH−1/δ vs. εH−1/βδ).
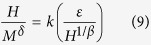 |
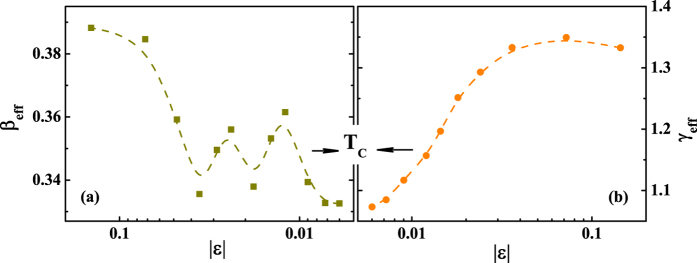
where k(x) is the scaling function. Equation (9) suggests that all experimental curves plotted on MH−1/δ vs. εH−1/(βδ) will collapse into a single one41. The inset of Fig. 7(b) shows the MH−1/δ vs. εH−1/(βδ) for Cr11Ge19, where the experimental data collapse into a single curve, and TC locates at the zero point of the horizontal axis. The well scaling and collapse of the curves demonstrate the reliability of the experimentally obtained exponents. Generally, for a single theoretical model, the critical exponents should fulfill the Widom scaling law δ = 1 + γ/β according to statistical theory42. For Cr11Ge19, it is calculated that δ = 4.078 ± 0.004 according to the Widom scaling law, which slightly deviates from that obtained from the experiment. The slightly deviation from the Widom scaling law indicates that the critical behavior of Cr11Ge19 does not belong to a single universality class, which may be caused by the complex competition of several magnetic interactions. In this case of an itinerant ferromagnet, this deviation may be attributed to the discrepancy of γ caused by the length scale of the interaction43. Actually, these critical exponents are experimentally convergent, which can be confirmed by the effective exponents βeff and γeff obtained as ref. 44:
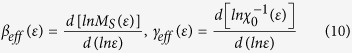 |
The βeff and γeff vs. ε for Cr11Ge19 are plotted in Fig. 8. It can be seen that βeff and γeff are convergent when temperature approaching TC.
Figure 8.
Effective exponents (a) βeff and (b) γeff as a function of the reduced temperature ε for Cr11Ge19 (dashed curves are guided on eye).
The obtained critical exponents of Cr11Ge19, as well as those of different theoretical models and related itinerant ferromagnetic materials, are listed in Table 1 for comparison. For a magnetic material, in addition to the spatial-dimensionality (d) of the crystal symmetry, the spin-dimensionality (n) also plays an important role in determination of the magnetic behavior45,46. For Cr11Ge19, due to the three-dimensional characteristic of its crystal structure, it gives that the spatial-dimensionality d = 3. However, for the spin-dimensionality, it is determined by the magnetic interaction. The critical exponent β of Cr11Ge19 approaches exactly that of the 3D-XY model, which means that d = 3 and n = 247. It can be seen that d = 3 is in agreement with the structural characteristic of Cr11Ge19. Meanwhile, that n = 2 suggests a two-dimensional magnetic coupling. The value γ is close to the mean-field model, meaning a long-range magnetic interaction. The long-range magnetic interaction deduced from γ is in agreement with the characteristic of an itinerant ferromagnet, such as MnSi48, AlCMn335, and Y2Ni743. In fact, γ in Y2Ni7 approaches the theoretical prediction of 2D-Ising model with long-range coupling with d = 2 and n = 1 (γ = 1.392)43,46.
Table 1. Comparison of critical exponents of Cr11Ge19 with different theoretical models and other itinerant ferromagnets (MAP = modified Arrott plot; KF = Kouvel-Fisher method; CI = critical isothermal fitting).
| Composition | Technique | Ref. | TC(K) | β | γ | δ |
|---|---|---|---|---|---|---|
| Cr11Ge19 | MAP | This work | 71.91 ± 0.02 | 0.339 ± 0.002 | 1.064 ± 0.005 | — |
| Cr11Ge19 | KF | This work | 71.95 ± 0.07 | 0.345 ± 0.004 | 1.062 ± 0.001 | — |
| Cr11Ge19 | CI | This work | 72 | — | — | 4.821 ± 0.002 |
| 3D-Heisenberg | theory | 33 | — | 0.365 | 1.386 | 4.80 |
| 3D-XY | theory | 33 | — | 0.346 | 1.316 | 4.81 |
| 3D-Ising | theory | 33 | — | 0.325 | 1.241 | 4.82 |
| Mean-field | theory | 33 | — | 0.5 | 1.0 | 3.0 |
| ZPLSF | theory | 13 | — | 0.25 | 1.0 | 5.0 |
| MnSi | MAP | 48 | 30.5 | 0.242 ± 0.006 | 0.915 ± 0.003 | 4.734 ± 0.006 |
| AlCMn3 | KF | 35 | 288.5 | 0.606 ± 0.009 | 1.177 ± 0.008 | 2.971 ± 0.002 |
| YNi72D−Ising | MAP | 43 | 53 | 0.306 ± 0.002 | 1.401 ± 0.002 | 5.35 |
As we know, for a homogeneous magnet, the universality class of the magnetic phase transition depends on the exchange distance J(r). M. E. Fisher et al. have theoretically treated this kind of magnetic ordering as an attractive interaction of spins. Subsequently, according to the renormalization group theory, the long-range interaction decays with distance r as refs 49,50:
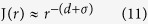 |
where d is the spatial-dimensionality and σ is a positive constant. Moreover, there is refs 46,50:
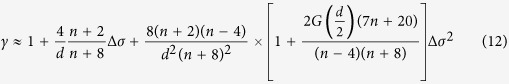 |
where 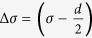 and
and 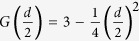 , n is the spin-dimensionality. For a three-dimensional material (d = 3), we have J(r) ≈ r−(3+σ). When σ ≥ 2, the Heisenberg model is valid for the three-dimensional isotropic magnet, where J(r) decreases faster than r−5. When σ ≤ 3/2, conditions for the mean-field model are satisfied, expecting that J(r) decreases slower than r−4.5. From Eq. (12), it is calculated that σ = 1.6054 ± 0.004 when n = 2. Finally, we yield J(r) ≈ r−4.61, indicating a long-range magnetic coupling. Moreover, the correlation length critical exponent is obtained as ν = 0.662 ± 0.004 (where ν = γ/σ, ξ = ξ0|(T − TC)/TC|−ν).
, n is the spin-dimensionality. For a three-dimensional material (d = 3), we have J(r) ≈ r−(3+σ). When σ ≥ 2, the Heisenberg model is valid for the three-dimensional isotropic magnet, where J(r) decreases faster than r−5. When σ ≤ 3/2, conditions for the mean-field model are satisfied, expecting that J(r) decreases slower than r−4.5. From Eq. (12), it is calculated that σ = 1.6054 ± 0.004 when n = 2. Finally, we yield J(r) ≈ r−4.61, indicating a long-range magnetic coupling. Moreover, the correlation length critical exponent is obtained as ν = 0.662 ± 0.004 (where ν = γ/σ, ξ = ξ0|(T − TC)/TC|−ν).
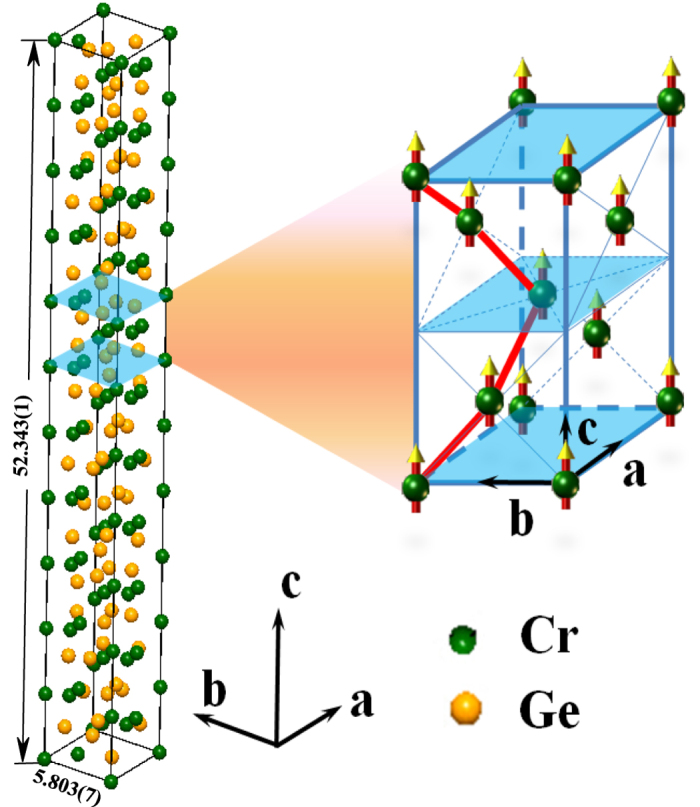
Figure 9 shows the crystal and magnetic structure for Cr11Ge19. Due to the tetragonal crystal cell of Cr11Ge19, a and b directions are equivalent in structure. Moreover, as mentioned above, a- and b-axis are also equivalent in magnetism, as shown in Fig. 3. Due to the 3D-XY characteristic, it can be concluded that the two-dimensional magnetic interaction should be within the ab plane, which means that the magnetic coupling strength exhibits relation Ja = Jb < Jc. This is analogous to a two-dimensional material, where the in-plane coupling is much stronger than that of the inter-layers. However, for Cr11Ge19, it is not a two-dimensional material but a three-dimensional network. Due to the anisotropy of the Nowotny chimney ladders structure, Cr11Ge19 exhibits very strong magnetic anisotropy along the c-axis [see Fig. 9]. The present experimental results indicate the magnetic coupling in ab plane is much stronger than that along the c-axis. The investigation of magnetism suggests that the complex magnetic structure of Cr11Ge19 correlates closely with the crystal structure. The strong correlation between the magnetic and crystal structure should response the complex magnetic behavior in Cr11Ge19, indicating strong magneto-elastic coupling in this system. Moreover, the magneto-elastic coupling has also been confirmed by the larger abnormal change of lattice parameters in the ferromagnetic state24.
Figure 9. The chiral structure of Cr-Cr bonds and the magnetic structure for Cr11Ge19.
It is meaningful to compare the magnetic behavior of Cr11Ge19 with itinerant ferromagnets with noncentrosymmetry. Recently, a chiral magnetic soliton state has been revealed in layered Cr1/3NbS2 with noncentrosymmetry51. The magnetic coupling in layered Cr1/3NbS2 is demonstrated within the ab plane52, which is analogous to that in Cr11Ge19. However, the magnetic moments in Cr1/3NbS2 are arranged helically within the ab plane53, which is different with that in Cr11Ge19. On the other hand, the itinerant ferromagnetic characteristic of Cr11Ge19 is similar to that of noncentrosymmetric MnSi which exhibits a skyrmion state48. However, the crystal structure of MnSi is cubic, which does not exhibit so strong crystalline anisotropy as that in Cr11Ge19. The investigation of magnetism in noncentrosymmetric Cr11Ge19 indicates that it is special among the itinerant ferromagnets.
Conclusion
In summary, the magnetism of Cr11Ge19 has been thoroughly investigated on single crystal. The angular rotation, temperature, and magnetic field dependence of magnetization [M(φ), M(T), and M(H)] display that the Cr11Ge19 exhibits strong magnetic anisotropy and the easy magnetization orientation is along the c-axis. Based on the study of the critical behavior, reliable critical exponents (β, γ, and δ) are obtained. The critical exponent β is close to the theoretical prediction of the 3D-XY model, which indicates two-dimensional magnetic coupling. The critical exponent γ suggests that the magnetic coupling is of long-range type, and that the magnetic exchange distance decays as J(r) ≈ r−4.61. We suggest that the ferromagnetic ground state of Cr11Ge19 is formed by the polarized magnetic moments along the c-axis, while the long-range magnetic coupling is established within the ab plane.
Methods
A single crystal Cr11Ge19 was prepared by the chemical vapor transport (CVT) method. The elementary substance pieces of chromium and germanium in mol ratio of 45:55 and about 50 mg iodine were put in an evacuated quartz tube with inner diameter of 15 mm and length of about 200 mm. The tube was then placed in a two zone furnace. After heating at 1053 K for 4 days, the source end was kept at 1053 K and growth zone was raised to 1153 K. After 10 days growth, crystals in millimeter size can be obtained.
The chemical compositions were carefully checked by Energy Dispersive X-ray (EDX) spectrometry. The crystal structure was confirmed by the Rigaku-TTR3 X-ray diffractometer using high-intensity graphite monochromatized Cu Kα radiation. The crystal orientations were determined by the Laue photography and X-ray diffraction (XRD). The magnetization was measured using a Quantum Design Vibrating Sample Magnetometer (SQUID-VSM). The no-overshoot mode was applied to ensure a precise magnetic field. The magnetic field was relaxed for two minutes before data collection. For the measurement of initial isothermal magnetization, the sample was firstly heated adequately above TC for ten minutes, then cooled to the target temperature under zero magnetic field. Then the initial isothermal magnetization was performed with the magnetic field parallel to the c-axis (Please see the Supplementary Information).
Additional Information
How to cite this article: Han, H. et al. Anisotropic magnetic coupling with a two-dimensional characteristic in noncentrosymmetric Cr11Ge19. Sci. Rep. 6, 39338; doi: 10.1038/srep39338 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Material
Acknowledgments
This work was supported by the State Key Project of Fundamental Research of China through Grant No. 2011CBA00111, the National Natural Science Foundation of China (Grant Nos 11574322, U1332140, 11474289, U1532267, 11474290, 11104281, and 11204288), the Foundation for Users with Potential of Hefei Science Center (CAS) through Grant No. 2015HSC-UP001.
Footnotes
Author Contributions H.H. and L.Z. conducted all of the experiments and wrote the paper. X.D.Z. and H.F.D. synthesized the samples. M.G. and L.S.L. performed the magnetic measurements. C.J.Z., L.P. and Y.H.Z. analyzed the experimental results.
References
- Shimizu M. Itinerant electron magnetism. Rep. Prog. Phys. 44, 329 (1981). [Google Scholar]
- Uhlarz M., Pfleiderer C. & Hayden S. M. Quantum Phase Transitions in the Itinerant Ferromagnet ZrZn2. Phys. Rev. Lett. 93, 256404 (2004). [DOI] [PubMed] [Google Scholar]
- Manyala N. et al. Agnetoresistance from quantum interference effects in ferromagnets. Nature (London) 404, 581 (2000). [DOI] [PubMed] [Google Scholar]
- Pfleiderer C., Julian S. R. & Lonzarich G. G. Non-Fermi-liquid nature of the normal state of itinerant-electron ferromagnets. Nature (London) 414, 427 (2001). [DOI] [PubMed] [Google Scholar]
- Watanabe H., Parameswaran S. A., Raghu S. & Vishwanath A. Anomalous Fermi-liquid phase in metallic skyrmion crystals. Phys. Rev. B 90, 045145 (2014). [Google Scholar]
- Pfleiderer C., McMullan G. J., Julian S. R. & Lonzarich G. G. Magnetic quantum phase transition in MnSi under hydrostatic pressure. Phys. Rev. B 55, 8330 (1997). [Google Scholar]
- Saxena S. S. et al. Superconductivity on the border of itinerant-electron ferromagnetism in UGe2. Nature (London) 406, 587 (2000). [DOI] [PubMed] [Google Scholar]
- Blanco J. A. & Pisonero J. Itinerant band weak ferromagnetism from the Stoner equations. Eur. J. Phys. 20, 289 (1999). [Google Scholar]
- Sokolov D. A., Aronson M. C., Gannon W. & Fisk Z. Critical Phenomena and the Quantum Critical Point of Ferromagnetic Zr1−xNbxZn2. Phys. Rev. Lett. 96, 116404 (2006). [DOI] [PubMed] [Google Scholar]
- Zhou J. S. et al. Critical Behavior of the Ferromagnetic Perovskite BaRuO3. Phys. Rev. Lett. 101, 077206 (2008). [DOI] [PubMed] [Google Scholar]
- Wohlfarth E. P. The Theoretical and Experimental Status of the Collective Electron Theory of Ferromagnetism. Rev. Mod. Phys. 25, 211 (1953). [Google Scholar]
- Moriya T. Theory of itinerant electron magnetism. J. Magn. Magn. Mater. 14, 1 (1979). [Google Scholar]
- Takahashi Y. On the origin of the Curie-Weiss Law of the Magnetic susceptibility in Itinerant electron Ferromagnetism. J. Phys. Soc. Jpn. 55, 3553 (1986). [Google Scholar]
- Yu X. Y. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature (London) 465, 901 (2010). [DOI] [PubMed] [Google Scholar]
- Rybakov F. N., Borisov A. B., Blugel S. & Kiselev N. S. New Type of Stable Particle-like States in Chiral Magnets. Phys. Rev. Lett. 115, 117201 (2015). [DOI] [PubMed] [Google Scholar]
- Muuhlbauer S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915 (2009). [DOI] [PubMed] [Google Scholar]
- Roβler U. K., Bogdanov A. N. & Pfleiderer C. Spontaneous skyrmion ground states in magnetic metals. Nature (London) 442, 797 (2006). [DOI] [PubMed] [Google Scholar]
- Caillat T., Fleurial J. P. & Borshchevsky A. Growth and some properties of Cr11Ge19. J. Alloys Compd. 252, 12–15 (1997). [Google Scholar]
- Wilson M. N., Butenko A. B., Bogdanov A. N. & Monchesky T. L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 89, 094411 (2014). [Google Scholar]
- Voellenkle H., Preisinger A., Nowotny H. & Wittmann A. The crystal structure of Cr11Ge19, Mo13Ge23, and V17Ge3. Z. Kristallog. 124, 9–25 (1967). [Google Scholar]
- Kolenda M., Stoch J. & Szytula A. Esca and magnetic studies of the Cr-Ge system. J. Magn. Magn. Mater. 20, 99–106 (1980). [Google Scholar]
- Zagryazhskii V. L., Geld P. V. & Shtolts A. K. Magnetic Susceptibility and Electrical Conductivity of the Highest Chromium Germanide. Sov. Phys. J 11, 23 (1968). [Google Scholar]
- Pecheur P., Toussaint G., Kenzari H., Malaman B. & Welter R. Ferromagnetism of the chimney-ladder compound Cr11Ge19. J. Alloys Compd. 262–263, 363–365 (1997). [Google Scholar]
- Ghimire N. J. et al. Complex itinerant ferromagnetism in noncentrosymmetric Cr11Ge19. Phys. Rev. B 85, 224405 (2012). [Google Scholar]
- Wohlfarth E. P. Thermodynamic aspects of itinerant electron magnetism. Physica B 91, 305–314 (1977). [Google Scholar]
- Wohlfarth E. P. Very Weak Itinerant Ferromagnets Application to ZrZn2. J. Appl. Phys. 39, 1061 (1968). [Google Scholar]
- Edwards D. M. & Wohlfarth E. P. Magnetic Isotherms in the Band Model of Ferromagnetism. Proc. Roy. Soc. A 303, 127 (1968). [Google Scholar]
- Arrott A. Criterion for ferromagnetism from observations of magnetic isotherms. Phys. Rev. 108, 1394–1396 (1957). [Google Scholar]
- Banerjee S. K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 12, 16–17 (1964). [Google Scholar]
- Fisher M. E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 30, 615–730 (1967). [Google Scholar]
- Stanley H. E. Introduction to Phase Transitions and Critical Phenomena (Oxford University Press, London, 1971). [Google Scholar]
- Arrott A. & Noakes J. Approximate equation of state for Nickel near its critical temperature. Phys. Rev. Lett. 19, 786 (1967). [Google Scholar]
- Kaul S. N. Static critical phenomena in ferromagnets with quenched disorder. J. Magn. Magn. Mater. 53, 5–53 (1985). [Google Scholar]
- Huang K. Statistical Mechanics. 2nd ed. (Wiley, New York, 1987). [Google Scholar]
- Zhang L. et al. Critical behavior in the antiperovskite ferromagnet AlCMn3. Phys. Rev. B 85, 104419 (2012). [Google Scholar]
- Zhang L. et al. Critical properties of the 3D-Heisenberg ferromagnet CdCr2Se4. Europhys. Lett. 91, 57001 (2010). [Google Scholar]
- Fan J. Y. et al. Critical properties of the perovskite manganite La0.1Nd0.6Sr0.3MnO3. Phys. Rev. B 81, 144426 (2010). [Google Scholar]
- Zhang L. et al. Critical behavior of single crystal CuCr2Se4−x Brx (x = 0.25). Appl. Phys. A 113, 201–206 (2013). [Google Scholar]
- Kouvel J. S. & Fisher M. E. Detailed Magnetic Behavior of Nickel Near its Curie Point. Phys. Rev. 136, A1626 (1964). [Google Scholar]
- Khan N. et al. Critical behavior in single-crystalline La0.67Sr0.33CoO3. Phys. Rev. B 82, 064422 (2010). [Google Scholar]
- Phan M. H. et al. Tricritical point and critical exponents of La0.7Ca0.3−xSrxMnO3 (x = 0, 0.05, 0.1, 0.2, 0.25) single crystals. J. Alloys Compd. 508, 238–244 (2010). [Google Scholar]
- Kadanoff L. P. Scaling laws for Ising models near TC. Physics 2, 263–272 (1966). [Google Scholar]
- Bhattacharyya A., Jain D., Ganesan V., Giri S. & Majumdar S. Investigation of weak itinerant ferromagnetism and critical behavior of Y2Ni7. Phys. Rev. B 84, 184414 (2011). [Google Scholar]
- Perumal A., Srinivas V., Rao V. V. & Dunlap R. A. Quenched disorder and the critical behavior of a partially frustrated system. Phys. Rev. Lett. 91, 137202 (2003). [DOI] [PubMed] [Google Scholar]
- Gerber P. R. Spin-Dimensionality Dependence of Critical Parameters. Z. Physik B 32, 327 333 (1979). [Google Scholar]
- Fischer S. F., Kaul S. N. & Kronmuller H. Critical magnetic properties of disordered polycrystalline Cr75Fe25 and Cr70Fe30 alloys, Phys. Rev. B 65, 064443 (2002). [Google Scholar]
- Fisher M. E. The renormalization group in the theory of critical behavior, Rev. Mod. Phys. 46, 597–616 (1974). [Google Scholar]
- Zhang L. et al. Critical behavior of the single-crystal helimagnet MnSi. Phys. Rev. B 91, 024403 (2015). [Google Scholar]
- Ghosh K. et al. Critical phenomena in the double-exchange ferromagnet La0.7Sr0.3MnO3. Phys. Rev. Lett. 81, 4740 (1998). [Google Scholar]
- Fisher M. E., Ma S. K. & Nickel B. G. Critical exponents for long-range interactions. Phys. Rev. Lett. 29, 917–920 (1972). [Google Scholar]
- Togawa Y. et al. Chiral Magnetic Soliton Lattice on a Chiral Helimagnet. Phys. Rev. Lett. 108, 107202 (2012). [DOI] [PubMed] [Google Scholar]
- Koumpouras K., Bergman A., Eriksson O. & Yudin D. A spin dynamics approach to solitonics. Sci. Rep. 6, 25685 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghimire N. J. et al. Magnetic phase transition in single crystals of the chiral helimagnet Cr1/3NbS2. Phys. Rev. B 87, 104403 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.