Genetic Algorithms Applied to Multi-Class Clustering for Gene Expression Data

Abstract

A hybrid GA (genetic algorithm)-based clustering (HGACLUS) schema, combining merits of the Simulated Annealing, was described for finding an optimal or near-optimal set of medoids. This schema maximized the clustering success by achieving internal cluster cohesion and external cluster isolation. The performance of HGACLUS and other methods was compared by using simulated data and open microarray gene-expression datasets. HGACLUS was generally found to be more accurate and robust than other methods discussed in this paper by the exact validation strategy and the explicit cluster number.

Introduction

The increasing use of DNA microarrays to generate large-scale datasets of gene expression has led to several important statistical and analytical challenges. Microarray experiments are increasingly being carried out in biological and medical researches to address a wide range of problems, including the classification of tumors ^{1., 2., 3., 4., 5., 6., 7.}. Tumor clustering is very valuable in clinical cancer studies because there is often interest in determining if gene expression profiles define molecular subtypes of diseases. An essential aspect of the clustering problem is to allocate tumor samples accurately to their clusters and assess the confidence of cluster assignments for individual samples. In a clinical application of microarray-based cancer diagnosis, an important statistical problem associated with tumor classification is the identification of new tumor classes using gene expression profiles. However, inaccurate cluster assignments could lead to erroneous diagnoses and unsuitable treatment protocols. Hence a reliable and precise clustering algorithm is essential for successful diagnosis and treatment of cancer.

Clustering methods have emerged as popular approaches to DNA microarray data analysis ^{1., 4., 5., 7., 8.}, because they are able to consider the full vector of gene expression variables to perform class discovery. But these methods have some limitations, one of which is that they are not always able to find optimum clusters. The traditional clustering methods, such as agglomerative or divisive hierarchical and partitional clustering, use a greedy algorithm, which puts observations into a particular cluster that is deemed the best at that point in the algorithm, but may not be the best globally when all information is considered. Recently, the use of global optimization techniques such as Simulated Annealing and Genetic Algorithms (GAs) has emerged in the clustering fields ^{9., 10.}.

Genetic Algorithms introduced by Holland (11) are randomized search and optimization techniques guided by the principle of evolution and natural genetics. Because they are aided by large amounts of implicit parallelism (12), GAs are capable of searching for optimal or near-optimal solutions on complex, large spaces of possible solutions. Furthermore, GAs allow searching of these spaces of solutions by simultaneously considering multiple interacting attributes. Because of these advantages, GAs may represent another useful tool in the classification of biological phenotypes based on gene expression data, such as class prediction problems (13).

In this paper, we used the parallelism searching capability of GAs to design a clustering schema (HGACLUS) combining merits of the Simulated Annealing to find an optimal or near-optimal set of medoids whose size was predefined. According to this optimal set of medoids, each observation was allocated to the nearest medoid and the best k clusters were then constructed. We evaluated HGACLUS and the considered methods by the exact validation strategy and the number of clusters to be used with the simulated datasets and the real datasets.

Systems and Methodology

Partitional clustering techniques

Many partitional clustering methods are based on trying to minimize or maximize a global objective function. The clustering problem then becomes an optimization problem, which, in theory, can be solved by enumerating all possible ways of dividing the points into clusters and evaluating the “goodness” of each potential set of clusters by using the given objective function. However, this “exhaustive” approach is computationally infeasible (NP complete) and as a result, a number of practical techniques for optimizing a global objective function have been developed. One approach is to use greedy algorithms to optimize the objective function to find good but not optimal solutions, such as the K-Means clustering algorithm (14) which tries to minimize the sum of the squared distance (error) between objects and their cluster centers, and the PAM (Partitioning Around Medoids) procedure (15) which is based on the search for k good representative points or medoids among the observations and then k clusters are constructed by assigning each observation to the nearest medoid. The goal of PAM is to find k medoids that minimize the sum of the distance of the observations to their closest medoid. The PAM uses the steepest descent algorithm for the objective function to find a local minimum. Other approaches such as COWCLUS (9) and KGACLUS (10) use the global optimization techniques—GAs to find optimal or near-optimal clusters, and may avoid the solution to get stuck at the local optimal solution.

Genetic Algorithms

In GAs, the search space of a problem is represented as a collection of individuals. The individuals are represented by character strings, which are referred to as chromosomes. A collection of such strings is called the population. The purpose is to find the individual from search space with the best “genetic material”. The quality of an individual is measured with an objective function or the fitness function. Based on the principle of survival of the fittest, a few of the strings are selected and each is assigned to a number of copies that go into the mating pool. Biologically inspired operators like crossover and mutation are applied on these strings to yield a new generation of strings. The process of selection, crossover and mutation continues for a fixed number of generations or till the termination condition is satisfied.

Implementation of HGACLUS

String representation

An individual is a string of length k with each position taking a different value from {1, 2, …, n}. Each individual is a subset of medoids of size k (k was the cluster number) as suggested by Kaufman and Rousseeuw (15). Therefore we transformed a clustering problem into a subset selection problem. Once the medoids were chosen, the clusters were deterministically established by assigning the points to the nearest medoid. A string would be denoted as s_h= [m₁,m₂, …, m_i, …, m_k], where m_i is the index of the i-th medoid, and h = 1, 2, …, p, p is the population size.

Initialization and evaluation

An initial population was formed by generating p random strings, p was fixed. A random string was produced by randomly generating k integers in the range [0, n]. Each string was evaluated using the following fitness function,

$$f\left({\mathrm{s}}_h\right)=\frac{\mathrm{traceB}/\left(k-1\right)}{\mathrm{traceW}/\left(n-k\right)}$$

where n and k are the total number of points and the number of clusters in the partition, respectively. B and W are the covariance matrices of between-cluster sums and the pooled within-cluster sums of squares, respectively. In fact, this function is the Variance Ratio Criterion (VRC; ref. 16), which was chosen to be the fitness function due to its high intuitive appeal as to what constitutes “true” cluster structures, and was also being used as fitness function by Cowgill et al. (9). According to each string, k clusters were constructed by assigning each observation to the nearest medoid. VRC was then calculated by the obtained class index.

Selection

The selection process selects the chromosomes for the mating pool directed by the survival of the fitness concept of natural genetic system.

There are two potential problems during genetic optimization. First, in the initialization stage there may be a few individuals with very high values of fitness. These individuals will reproduce abundantly and become preponderant, then the population will lose the variety and result in prematurity. Second, in the terminative stage of the genetic algorithm, the fitness values of all individuals are close to each other, the selection probability of each individual is almost equivalent. The capability of searching the optimal solution will not be improved prominently, and the optimization process will be stagnated.

In order to resolve the above-mentioned problems, we calculated the selection probability via the following formula:

$$p\left(s_h\right)=\frac{\exp \left(f\left({\mathrm{s}}_h\right)/T\right)}{{\displaystyle \sum _{h=1}^p}\exp \left(f\left({\mathrm{s}}_h\right)/T\right)},h=1,2,\mathrm{..}.,p.$$

where T>0 is a cooling temperature. We proposed the cooling schedule function as:

$$T\left(g\right)=\frac{G-g}{G}{T}_0,g=0,1,\dots ,G-1.$$

where T₀ is the initial temperature that is always a large value, and G is the number of generation.

In the initialization stage, T is a big value. Through this formula adjustment, it could preserve the variety of the population and prevent a few individuals, whose fitness values are large, from dominating the population. Consequently the algorithm may not get into prematurity. Along with the iteration, T is cooling gradually. In the terminative stage, through this formula adjustment, it could enlarge the diversity of the individuals and avoid the optimization process to be stagnated. Accordingly, it could help to find the optimal solution effectively.

After the probabilities of the individuals were calculated, the Stochastic Universal Sampling (SUS; ref. 17) was used to select the strings for the mating pool.

Crossover and mutation

Crossover operations were performed by randomly choosing a pair of chromosomes from the mating pool, and then applied a crossover operation on the selected strings pair with probability p_c. Two offspring strings were produced through the exchange of genetic information between the two parents. This probabilistic process was repeated until all parent strings in the mating pool were considered.

In HGACLUS, we employed the uniform crossover operation (18). Uniform crossover helps to overcome the bias in single-point crossover towards short substrings, without requiring precise understanding of the significance of the individual locus in the string.

Each of the offspring from crossover underwent mutation with probability p_m. We applied the following mutation by replacing the value of each mutation gene with a uniform random value generated between 0 and n, n was the size of genes or observations.

After mutation, each chromosome was checked for validity. The index in each chromosome should be unique, and should be destroyed if it was duplicate and invalid, generating new chromosomes whose numbers were equal to the number of the destroyed ones. The new chromosomes went to the next iteration.

Termination

The process of fitness computation, selection, crossover, and mutation was executed for G generation. After the entire run was completed, the chromosome with the best fitness of all generations was outputted as the optimal solution. The chromosome with the best overall fitness in a particular run may not necessarily always correspond to the “best” chromosome in the final or last generation. In order to determine the ultimate chromosome with the highest overall fitness, it is common to preserve each “best” chromosome in each generation and compare all the “best” chromosomes with one another. After obtaining the optimal set of k medoids, the best k clusters were constructed by this set.

Implementation Results

K-Means and PAM were implemented in the cluster package—S-Plus. The experimental results of the comparation of HGACLUS with K-Means, PAM and two publicly available versions of KGACLUS (10), COWCLUS (9) were provided for two simulation datasets (Models 1 and 2) and two real gene expression datasets, respectively.

Simulation data

Model 1

Suppose that there were three groups of patients corresponding with three distinct types of cancers. To generate such kind of data, we sampled three groups of 15, 10 and 15 subjects respectively from three multivariate normal distributions with diagonal covariance matrices, which differed only in their mean vectors. All genes had a common standard deviation of 2.0. In the first subpopulation, the first 20 genes had u=1.0 (up-regulation genes), genes 41-60 had u=–1.0 (down-regulation genes) and the other 20 genes had mean zero. In the second subpopulation, genes 21-40 had u=2.0 and the other 40 genes had mean zero. In the third subpopulation, genes 1-20 had u=–2.0, genes 41-60 had u=2.0 and the other 20 genes had mean zero. The clusters were well separated.

Model 2

Suppose that there were five groups of patients corresponding with five types of cancers. To generate such data, we sampled five groups of 10, 10, 8, 4 and 8 subjects respectively from five multivariate normal distributions with diagonal covariance matrices, which differed only in their mean vectors. All genes had a common standard deviation of 2.0. In the first subpopulation, the first 10 genes had u=3.0 and the other 40 genes had mean zero. In the second subpopulation, genes 11-20 had u=2.0 and the other 40 genes had mean zero. In the third subpopulation, genes 21-30 had u=2.0 and the other 40 genes had mean zero. In the fourth subpopulation, genes 31-40 had u=2.0 and the other 40 genes had mean zero. In the last subpopulation, genes 41-50 had u=1.5 and the other 40 genes had mean zero. One tenth of the data values were replaced with random noises. The clusters were overlapped.

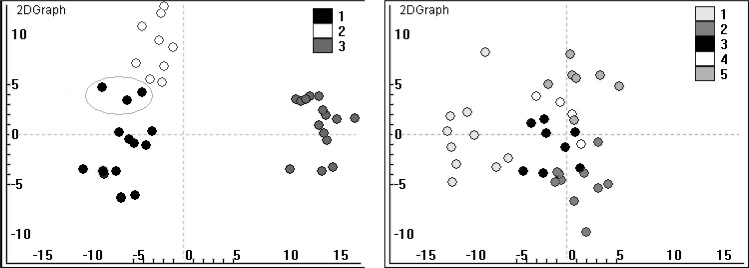
After PCA, the first two PCs were extracted. The cluster patterns were shown in Figure 1.

Fig. 1.

The 2-dimensional graphs of Models 1 and 2 of the first two gene components extracted by PCA.

Real-life data

Embryonal CNS data

(1) The dataset consisted of 34 samples of medulloblastoma tumors (9 desmoplastic medulloblastomas and 25 classic medulloblastomas). Genes were ranked by signal-to-noise metric according to their correlation with the classic versus desmoplastic distinction. 140 genes that were more highly correlated with the distinction were picked to describe the expression levels of the subtypes of cancers. The value of k was therefore chosen to be 2 for this dataset.

(2) The dataset comprised 42 samples (10 medulloblastomas, 10 malignant gliomas, 10 AT/RTs, 8 PNETs and 4 normal cerebella). Signal-to-noise ranking of genes compared each sample type to all other combined ones. Fifty genes were selected to describe the expression levels. The value of k was therefore chosen to be 5 for this dataset.

These datasets were obtained from a study published by Pomeroy et al (6). The original data and experimental methods are available at http://www.genome.wi.mit.edu/MPR/CNS.

NCI60

In this study, cDNA microarrays were used to examine the variation in gene expression among the 60 cell lines from the anti-cancer drug screen of the National Cancer Institute (NCI60; http://genome-www.stanford.edu/nci60; ref. 7). The cell lines were derived from tumors with different sites of origin: 7 from breast, 6 from central nervous system (CNS), 7 from colon, 6 from leukemia, 8 from melanoma, 9 from non-small-cell-lung-carcinoma (NSCLC), 6 from ovary, 2 from prostate, 8 from kidney, and one was unknown (ADR-RES). In addition, the unknown cell line was excluded from our analysis. We selected 50 most variable genes to describe the gene expression levels. The value of k was therefore chosen to be 9 for this dataset.

GA-based clustering algorithms (KGACLUS, COWCLUS and HGACLUS) were implemented with the following parameters: p_c=0.8, p_m=0.001, the number of generations G=30, the population size P=50 for Model 1 and Embryonal CNS (1). For Model 2, Embryonal CNS (2) and NCI60, the parameters p_c=0.9, p_m=0.01, G=50 and P=100 were used. K-Means and PAM were implemented once by S-plus procedure and three GA-based algorithms were run 50 times for each dataset, respectively.

Validation indices

Validation approach means that an algorithm should be rewarded for consistency. For clustering algorithms, researchers in general have posited the existence of clusters as distinct groups possessing the qualities of internal cohesion and external isolation. VRC and Silhouette Width appear to reflect such a description.

VRC

VRC has been defined above, because it shares an isomorphism with the F statistic which gauges the size of differences among groups in the context of an ANOVA. VRC measures the degree of separation between clusters and homogeneity within clusters. Furthermore, for all partitions the following relation remains constant: trace (T) = trace (B) + trace (W), where T is the covariance matrices of the total sums of squares. Hence, a better clustering algorithm is expected to have a relatively larger VRC value.

Silhouette Width

Silhouette Width is a composite index reflecting the compactness and separation of the clusters, and can be applied to different distance metrics. For each object i, its silhouette width s(i) is defined as:

$$s\left(i\right)=\frac{a\left(i\right)-b\left(i\right)}{\max \left(a\left(i\right),b\left(i\right)\right)}$$

where a(i) is the average distance of object i to other objects in the same cluster, b(i) is the average distance of object i to the objects in its nearest neighboring cluster. The average of s(i) across all objects reflects the overall quality of the clustering result. A larger averaged silhouette width indicates a better overall quality of the clustering result.

Comparison

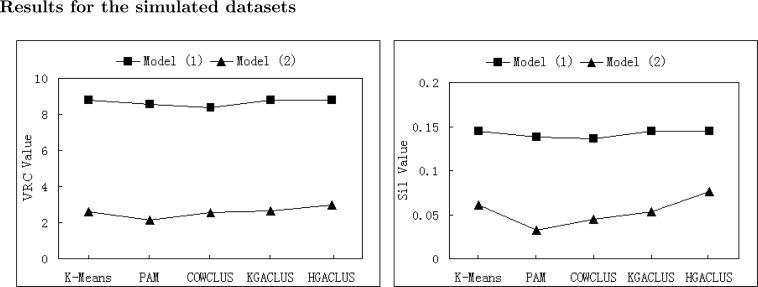
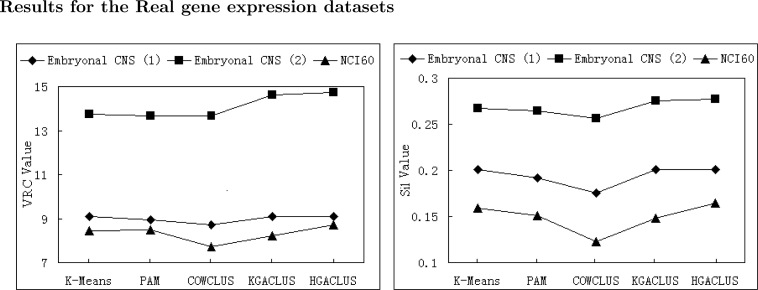
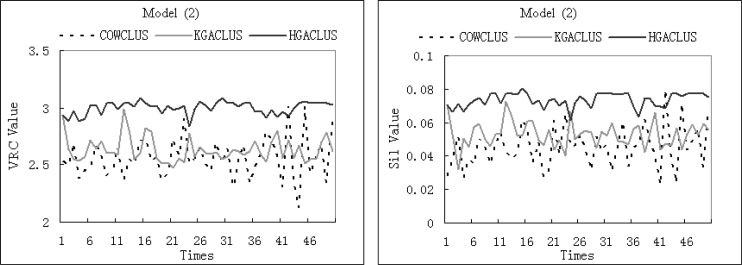
We computed the VRC and the Silhouette Width values of each algorithm for each simulated dataset and real gene expression dataset. The results were presented in following figures. Since K-Means and PAM were implemented once by S-plus, the validation indices were explicitly calculated for each dataset with an exact cluster number. The average validation indices of 50 runs implemented by three GA-based clustering techniques were computed for each dataset. Since GA-based clustering techniques are randomized search and optimization techniques, each run may obtain different cluster result. The performance of each clustering method evaluated by two validation indices was displayed in Fig. 2A, Fig. 3A. Furthermore, in order to compare the stability and optimization of three GA-based clustering methods, the validation indices of 50 runs were shown by curves in Fig. 2B, Fig. 3B. In each plot, a profile further to the horizontal axis indicated better performance.

Fig. 2A.

The average VRC and Silhouette Width values of five clustering methods for Models 1 and 2.

Fig. 3A.

The VRC and Silhouette Width values of five clustering methods for real gene expression datasets.

Fig. 2B.

The VRC and Silhouette Width values of three GA-based clustering methods for Model 2 with 50 runs.

Fig. 3B.

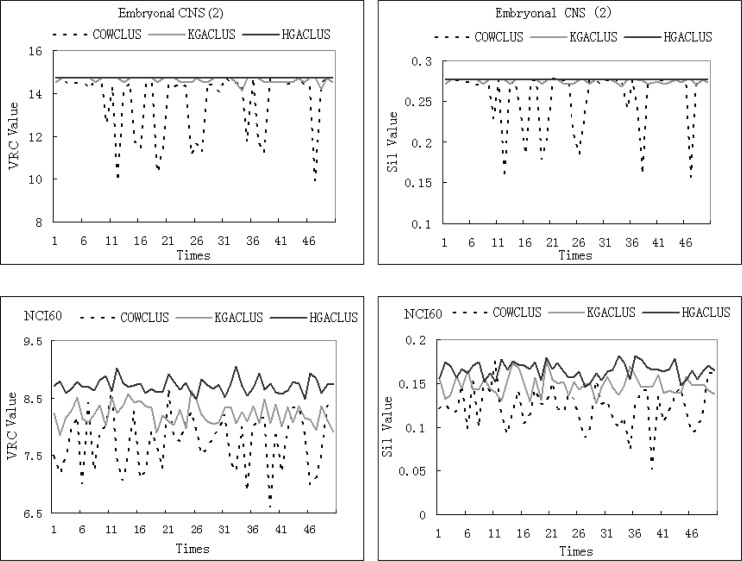
The VRC and Silhouette Width values of three GA-based clustering methods for Embryonal CNS (2) and NCI60 with 50 runs.

From Fig. 2A, Fig. 3A, it was found that the performance of COWCLUS was worse than the other four methods, and HGACLUS was a robust and stable method as judged by VRC and Silhouette Width evaluation indices.

For Model 1, it was obvious that the performance of all methods was perfect. K-Means and HGACLUS correctly recovered the true structure. However, KGACLUS allocated each point to its own cluster 7 times out of 50 runs. PAM allocated three points that in fact belong to the cluster 1 to cluster 2 (Figure 1, left plot). COWCLUS got stuck at premature solution half times (Figure 2A).

For Model 2, since it was the over-lapping dataset, the true cluster was not known. According to the two validation indices, it could be seen that HGACLUS was a little better than other methods. PAM had the worst performance. KGACLUS and COWCLUS had similar results (Figure 2A). The worst solution found by HGACLUS was better than the solutions obtained by K-Means and PAM (result not shown).

For Embryonal CNS (1), K-Means, PAM, KGACLUS and HGACLUS attained similar solutions.They all got a good solution while COWCLUS had a little worse performance than them (Figure 3A).

For Embryonal CNS (2), K-Means attained a local optimal solution while KGACLUS and HGACLUS obtained a better solution than the other methods (Figure 3A). However, the performance of KGACLUS was a little worse than HGACLUS, because the former found a sub-optimal solution (VRC was 9.08947 and Silhouette Width was 0.201284, respectively) 10 times out of 50 runs (Figure 3B).

For NCI60, three GA-based clustering methods all fluctuated more dramatically than other cases (Figure 3B). However, HGACLUS found a best solution (VRC was 9.04766 and Silhouette Width was 0.181216) that was better than the solution obtained by K-Means and PAM. For this case, K-Means and PAM had similar performance and COWCLUS had the worst performance (Figure 3A).

On the other hand, from Fig. 2B, Fig. 3B, the curve of HGACLUS was higher than KGACLUS and COWCLUS in most cases. It can be seen that the stability and optimization of HGACLUS is better than KGACLUS and COWCLUS.

Discussion

It was showed that optimal or near-optimal clustering results could be obtained by using HGACLUS that combined merits of the Simulated Annealing. The traditional K-Means are known to provide suboptimal solutions by the steepest descent techniques and strongly depend on the choice of the initial cluster centers. In order to avoid the limitations of the traditional K-Means, different strategies were suggested including GA-based clustering algorithms such as KGACLUS and COWCLUS. Comparing to the traditional K-Means, they may provide a rather steady solution. However, they may get into prematurity in comparison with HGACLUS. This is because KGACLUS may not provide the effective crossover operator (KGACLUS adopted the single-point crossover) and directly apply Roulette Wheel Selection (RWS) without adjusting the fitness value. The definition of codification and the design of operators for this codification of COWCLUS may not be very closely related. So they may lose the variety during the optimization process and get into prematurity.

Furthermore, it is a noticeable fact that a center almost never corresponds to an actual data point while a medoid is the representative point in a group of points and it is required to be an actual data point. Medoids are robust representations of the cluster centers that are less sensitive to outliers than other cluster profiles. This robustness is particularly important in the common context that many elements do not belong well to any cluster. KGACLUS and COWCLUS were based on the cluster centers to search the space of possible partitions while HGACLUS was to search a good set of well-scattered representative points (medoids) capturing the shape and extent of the cluster. This technique is similar to PAM. However, PAM adopts the steepest descent technique and may get stuck at a local optimal value in most cases. We adopted the cooling schedule in Simulated Annealing to propose an effective selection strategy in order to avoid the genetic algorithms resulting in prematurity in the initialization stage and losing the variety of the population in the terminative stage. HGACLUS utilized the capability of GAs for providing the requisite perturbation to bring PAM out of the local optima. This combination was effective because the definition of codification and the design of operators and fitness function for this codification may be related. With regard to the criteria of external isolation and internal consistency, HGACLUS appeared to perform as well as or better than any of the other mentioned methods for multi-class clustering.

The key point is that the squared-error criterion is not always a good measure of the with-cluster variation across all the partitions when there are large differences in the sizes or geometries of different clusters. In this situation, the square-error method could split large clusters to minimize the square-error. In this paper, we adopted VRC which is alike the square-error criterion as the fitness function to evaluate the string quality. So it is necessary to propose an effective criterion to measure the quality of strings.

In this paper, we supposed the cluster number k as a prior. A further issue is developing a robust methodology that can estimate the cluster number correctly for the complex multi-class gene expression data. Optimal selection of the number cluster k is a difficult problem. However, there have been some papers discussing this issue ^{19., 20.}. If there is a methodology that can estimate the number of clusters and allocate gene or tumor samples to their clusters correctly, biologists will benefit from this method.