Classifying Genomic Sequences by Sequence Feature Analysis

Abstract

Traditional sequence analysis depends on sequence alignment. In this study, we analyzed various functional regions of the human genome based on sequence features, including word frequency, dinucleotide relative abundance, and base-base correlation. We analyzed the human chromosome 22 and classified the upstream, exon, intron, downstream, and intergenic regions by principal component analysis and discriminant analysis of these features. The results show that we could classify the functional regions of genome based on sequence feature and discriminant analysis.

Introduction

Since the beginning of the Human Genome Project, a huge amount of genomic sequences have been generated. It becomes more and more important to annotate these raw sequences. Eukaryotes have genes that contain upstream, exon, intron, and downstream regions. It is even more important to classify these various functional regions. Seeking appropriate features is the key to solve this problem. In recent years, several sequence features have been proposed, including word frequency (WF; ref. 1), synonymous codon choice, amino acid usage, G+C content (2), and nucleotide composition constraint (3). In this study, we present a novel sequence feature extraction algorithm and multidimensional statistical analysis to classify genomic sequences.

Results and Discussion

We extracted the sequence feature information from the collected sequence data of the human chromosome 22, reduced the dimensionality of sequence feature vector by principal component analysis (PCA), and classified the datasets by discriminant analysis.

Word frequency

Reinert et al. (4) provided the concept of word frequency. Since a DNA sequence is formed by using an alphabet of four letters (A, T, C, G) denoting four DNA bases, we can define DNA k-words, which are k-tuples formed by using these four letters. For an integer k ≥ 1, clearly there are 4^k possible k-words. We assume that f_w is the frequency of w in the DNA sequences with the length of L:

$$f_w=\frac{n_w}{L}$$

In this study, we analyze mainly 2-word and 3-word frequencies, which form 4²=16 and 4³=64 dimensional frequency vectors, respectively.

Dinucleotide relative abundance

Karlin and Burge (5) defined the formula of dinucleotide relative abundance (DRA) as the following:

$$T_{ij}=\frac{p_{ij}}{p_i{p}_j}$$

in which p_i or p_j means the frequency of appearance of a single base i or j, and p_ij means that of joint probabilities of bases i and j. The DRA feature formsa 16-dimensional vector. If one sequence is completely stochastic and the bases are mutually independent, then theoretically p_ij = p_ip_j and the value of T_ij is 1. Therefore, the deviation of T_ij of one sequence opposite to 1 could evaluate the bias of dinucleotide.

Base-base correlation

We have proposed a novel feature called base-base correlation (BBC) with the following formula:

$$T_{ij}(k)=\sum _{i=l}^k{p}_{ij}(l)\cdot {\log }_2\left(\frac{p_{ij}}{p_i{p}_j}\right)i,j\in \left\{1,2,3,4\right\}$$

Here, p_i and p_j are defined as above, while p_ij(l) means the joint probabilities of bases i and j at a distance of l. T_ij(k) represents the average relevance of the two-base combination with different gaps from 1 to k. It reflects a local feature of two bases with an interval of k. The BBC feature forms a 16-dimensional vector.

For a given DNA sequence, the features of 2-word, 3-word, DRA, and BBC form a 112-dimensional vector in all.

Principal component analysis

Let X₁, X₂, …, X_p denote the p index considered, then we have

$$S=\left[\begin{array}{cccc}{S}_{11}& S_{12}& \cdots & S_{1p}\\ S_{21}& S_{22}& \cdots & S_{2p}\\ ⋮& ⋮\hfill & & ⋮\hfill \\ S_{p1}& S_{p2}& \cdots & S_{pp}\end{array}\right]$$

The above matrix is the covariance matrix of X₁, X₂, …, X_p, in which the principal diagonal elements S₁₁, S₂₂, …, S_pp represent the variance of X₁, X₂, …, X_p, respectively, reflecting the p index variation degree. Therefore, S₁₁ + S₂₂ + ··· + S_pp means the total variation degree of the p index.

Now we seek a new index y₁ = a₁₁x₁ + a₁₂x₂ + ··· + a_1px_p instead of the original p index. Moreover, we expect this new index could contain the original information as far as possible. We suppose λ₁ ≥ λ₂ ≥ ··· ≥ λ_γ (γ ≤ p) is the non-vanishing characteristic root. Then S₁₁ + S₂₂ + ··· + S_pp = λ₁ + λ₂ + ··· + λ_γ. Thus we extract the γ overall index of y₁, y₂, …, y_γ, whose variance is equal to the original p index variance, that is to say, the information that the γ index contains is equal to the information that the original p index contains. If γ is much smaller than p, the method greatly reduces the index but does not affect the analysis result. Because the overall index y₁ = a₁₁x₁ + a₁₂x₂ + ··· + a_1px_p is the biggest when the variance is λ₁, so the ability of synthesizing the p index of y₁ is the strongest. We define y₁, y₂, …, y_γ as the first, second, …, and the γ^th principal component, respectively. Then

$$\frac{{\lambda }_{\gamma }}{{\lambda }_1+{\lambda }_2+\cdots +{\lambda }_{\gamma }}=\frac{{\lambda }_{\gamma }}{S_{11}+S_{22}+\cdots +S_{pp}}$$

which expresses the proportion of y_γ variance in the total variance, and it is called the variance contribution rate of the γ^th principal component (6).

Here we reduced the original 112-dimensional vector to a 21-dimensional vector according to whether the eigenvalue is bigger than 1 (Table 1).

Table 1.

The Result of Principal Component Analysis

Component	Initial eigenvalue			Extraction sum of squared loadings
	Total	Variance (%)	Cumulation (%)	Total	Variance (%)	Cumulation (%)
1	31.128	27.793	27.793	31.128	27.793	27.793
2	12.589	11.240	39.033	12.589	11.240	39.033
3	8.365	7.469	46.503	8.365	7.469	46.503
4	8.075	7.210	53.713	8.075	7.210	53.713
5	4.726	4.220	57.933	4.726	4.220	57.933
6	4.192	3.743	61.675	4.192	3.743	61.675
7	3.836	3.425	65.100	3.836	3.425	65.100
8	3.425	3.058	68.158	3.425	3.058	68.158
9	2.938	2.624	70.782	2.938	2.624	70.782
10	2.775	2.478	73.259	2.775	2.478	73.259
11	2.606	2.327	75.586	2.606	2.327	75.586
12	1.928	1.721	77.308	1.928	1.721	77.308
13	1.880	1.678	78.986	1.880	1.678	78.986
14	1.663	1.485	80.471	1.663	1.485	80.471
15	1.565	1.397	81.868	1.565	1.397	81.868
16	1.515	1.353	83.221	1.515	1.353	83.221
17	1.293	1.154	84.375	1.293	1.154	84.375
18	1.276	1.139	85.515	1.276	1.139	85.515
19	1.170	1.045	86.559	1.170	1.045	86.559
20	1.067	0.953	87.512	1.067	0.953	87.512
21	1.052	0.939	88.451	1.052	0.939	88.451
22	0.925	0.826	89.277
23	0.831	0.742	90.019
24	0.786	0.702	90.721
25	0.677	0.605	91.326

Discriminant analysis

The basic principle of discriminant analysis is that the studied object that could be portrayed by the p index could also be described with the stochastic vector X = (X₁, X₂, …, X_p)^T. Let π₁, π₂, …, π_s denote the s kinds of the object that we study. If an object belongs to the j^th kind, then it is recorded as X ∈ π_j. The main goal of discriminant analysis is to seek the decision function g(X) of X according to different discriminative criteria, and to determine the category of X based on the attribute of g(X). The main criteria to construct discriminative function include the shortest distance criterion, the smallest expectation loss criterion, the Fisher criterion, and so on. Sandberg et al. (7) used a naïve Bayesian classifier to capture whole-genome characteristics in short sequences. In our method, we use the Fisher criterion whose basic principle is to find the most appropriate projection axis to make the two kinds of samples that project on this axis to be the least, thus make the classified effect to be the best.

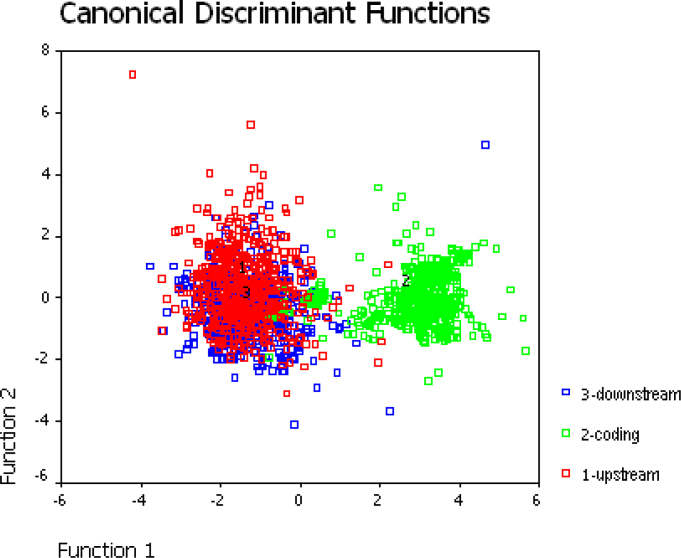
We firstly analyzed the upstream, coding, and downstream regions of the sequence (Figure 1). The scatter plots in Figure 1 show the values of the cases on two discriminant functions, and we can see obvious differences among the coding, upstream, and downstream regions. It is observed that the coding regions (green) prefer to appear on the positive side of Function 1, whereas the upstream (red) and downstream (blue) regions prefer to appear on the negative side. The two discriminant functions cannot distinguish between upstream and downstream regions. We think the reason is that regulatory elements are located in upstream regions and the gene regulatory information is not considered when we use these three sequence features. Therefore, we may seek a more effective sequence feature related to known gene regulatory knowledge to distinguish the two regions.

Fig. 1.

Classification of the upstream (red), coding (green), and downstream (blue) regions. The horizontal axis represents the function value of the first linear distinction, and the vertical axis represents the function value of the second linear distinction, which is based on calculations from the variable value.

In order to further investigate non-coding regions, we expanded the datasets from three kinds to five kinds, and selected three features, namely WF, DRA, and BBC, which constructed a 112-dimensional vector as mentioned above. The SPSS software (8) was applied to carry on discriminant analysis and the result is shown in Table 2, which was used to assess how well the discriminant function works. From the result, we can see that the classification accuracy of the exon, intron, upstream, downstream, and intergenic regions is 94%, 86%, 71%, 69%, and 69%, respectively. The classification accuracy of exon and intron is relatively high, while that of upstream, downstream, and intergenic regions is relatively low. This can help us identify genes and study the gene structure (exonintron arrangement). The 3-word frequency can help us reveal hidden sequence features in coding regions. Recent discoveries have suggested that non-coding regions may not be merely “junk DNA” as previously thought. High densities of long interspersed nuclear elements (LINEs) and short interspersed nuclear elements (SINEs) occur in non-coding regions as the signal to start methylating a region of DNA 9., 10.. The sequence features that we have used may not match inherent sequence features in non-coding regions. Therefore, the classification accuracy of non-coding regions is lower than that of coding regions. Our future project is to further improve the classification accuracy of non-coding regions by seeking new features and more efficient algorithms.

Table 2.

The Statistical Result of Discriminant Analysis^*

Result	Predicted group membership						Total
	Group	1	2	3	4	5
Original	1	71	0	7	8	14	100
	2	1	94	0	2	3	100
	3	7	0	86	5	2	100
	4	4	1	13	69	13	100
	5	5	2	12	12	69	100
Cross-validated	1	68	4	8	7	13	100
	2	1	94	0	2	3	100
	3	7	0	86	5	2	100
	4	6	2	16	57	19	100
	5	9	4	18	13	56	100

^*“Original” is the classification result of each observated sample, and “Cross-validated” is the alternately confirmed result. Groups 1 to 5 represent the upstream, exon, intron, downstream, and intergenic regions, respectively. In “Predicted group membership”, the established discriminative function reclassifies the source data and is compared with the primary variable value to compute the probability of mistaken discriminant. For example, for the 1^st group of samples with the total number of 100, the constructed discriminative function based on the original data predicts that the number belongs to the 1^st, 2^nd, 3^rd, 4^th, and 5^th group is 71, 0, 7, 8, and 14, respectively.

Conclusion

Nowadays algorithms and software for gene prediction have been developed widely. However, to our knowledge, researches on how to effectually distinguish the exon, intron, and intergenic regions have not made breakthrough. We have proposed a novel analysis method of genomic sequences based on sequence feature and statistic analysis. The results show that our analysis algorithm could improve the identification accuracy of the upstream, exon, intron, downstream, and intergenic regions from DNA sequences, especially the exon (94%) and intron (86%) regions.

Materials

We used the human chromosome 22 and collected the upstream (1,000 bp), exon, intron, downstream (1,000 bp), and intergenic regions (1,000 bp) according to the gene annotation database of the University of Santa Cruz Golden Path human genome sequence (http://genome.cse.ucsc.edu).