The Statistics and Mathematics of High Dimension Low Sample Size Asymptotics

Abstract

The aim of this paper is to establish several deep theoretical properties of principal component analysis for multiple-component spike covariance models. Our new results reveal an asymptotic conical structure in critical sample eigendirections under the spike models with distinguishable (or indistinguishable) eigenvalues, when the sample size and/or the number of variables (or dimension) tend to infinity. The consistency of the sample eigenvectors relative to their population counterparts is determined by the ratio between the dimension and the product of the sample size with the spike size. When this ratio converges to a nonzero constant, the sample eigenvector converges to a cone, with a certain angle to its corresponding population eigenvector. In the High Dimension, Low Sample Size case, the angle between the sample eigenvector and its population counterpart converges to a limiting distribution. Several generalizations of the multi-spike covariance models are also explored, and additional theoretical results are presented.

1 Introduction

As the field of statistics continues to evolve, there is ongoing discussion about the role that should be played by mathematics. There is a full range of opinions available, from those who wish to focus as much on data as possible and thus base their work on experiential insights, to those who will never actuaIly work with data, but instead develop mathematical ideas about how data should be analyzed. Among the many mathematical methods that have been used to gain statistical insights, asymptotic techniques stand out as having provided a large number of insights over the years.

An issue that is perhaps not sufficiently discussed among statisticians is: What is the value of asymptotics? Mathematics phobes might say one should never consider asymptotics on the grounds that one never has an infinite sample size. A number of people view asymptotics as “understanding what happens in situations where the sample size grows”. Some take the latter notion to an extreme by insisting that all asymptotics should “follow some type of sampling process”. An important point of this paper is a different view of asymptotics. In particular, the focus is moved beyond mere sampling to any type of limiting operation that gives statistical insights. Furthermore it will be seen that the role of asymptotic insights can go far beyond academic indulgence to becoming critical to understanding even the most basic statistical concepts in challenging modern data analytic settings.

A currently fashionable statistical topic is Big Data. Almost everyone is aware that this notion goes well beyond simply a large sample size, and also includes high dimension. What fewer people realize, but statisticians should be emphasizing, is that while size of modern data sets indeed presents serious statistical challenges, complexity of modern data sets is an even more serious and challenging aspect. Useful terminology for approaching a complex data set is object oriented data analysis, introduced in Wang and Marron (2007) and more recently discussed in Marron and Alonso (2014).

An impact of Big Data on mathematical statistics has been a realization by many that asymptotics should include calculation of limits as the dimension grows. One could try to justify this by a line of reasoning parallel to that of the sampling considerations above. For example in the biological field of gene expression, the technology of microarrays (see Murillo et al. (2008) for an overview) enabled the measurement of expressions of tens of thousands of genes at once. One could say this leads to vectors which are then effectively understood by a limiting process of growing dimension. Mathematical purists could counter that the number of genes in an organism is after all finite (tens of thousands for most complex organisms), so such a limit is inappropriate. This line of discussion could be continued in the direction of RNAseq techonology (see Denoeud et al. (2008) for an introduction), where instead of a single number for each gene, expression estimates at the level of resolution of genetic base pairs are available, thus resulting in a factor of around ten thousand more dimensions. But this is actually a moot point, from the perspective of this paper that the goal of asymptotics is to find insightful simple structure that underlies complex statistical contexts.

There are a number of ways that growing dimension asymptotics have been studied. Pioneering work by Portnoy (1984) and Portnoy et al. (1988) studied cases where the dimension grew relatively slowly, resulting in an asymptotic domain that was not far from classical fixed dimensional analysis. A very different asymptotic domain, called random matrix theory, arises when the dimension and sample size grow at the same rate. Deep work in this area has been done mostly outside of the statistical community, with landmark results including Marčenko and Pastur (1967) on the distribution of eigenvalues of the sample covariance matrix and Tracy and Widom (1996) on the distribution of the largest eigenvalue. Good overview of the large literature in this area can be found in Bai and Silverstein (2009). Statistical implications have been developed in a series of papers by Johnstone and co-authors, see e.g. Johnstone and Lu (2009) and a number of others since.

An asymptotic domain whose importance has only recently begun to be realized is where the dimension grows more rapidly than the sample size. Hall et al. (2005) coined the terminology High Dimension Low Sample Size (HDLSS) for the case where the sample size is fixed while the dimension grows.

2 HDLSS Backround

As noted in Hall et al. (2005), the world of HDLSS asymptotics is full of concepts and ideas that can run quite counter to the intuition of most people, many of which are discussed in the following. For example, in the limit as the dimension d → ∞ with a fixed sample size n, a standard Gaussian sample will lie near the surface of a growing sphere of radius d^1/2 and the angle between each pair of points with vertex at the origin will approach 90°. Thus the increasing randomness inherent to growing dimension tends towards random rotation, and modulo that random rotation and scaling by a factor of d^−1/2, the data tend to lie near vertices of the unit simplex. This phenomenon was called geometric representation, and leads to a number of interesting statistical insights as discussed in that paper.

As noted in Beran (1996) and Beran et al. (2010), some of these ideas lie at the heart of the famous paper of Stein et al. (1956) on inadmissability of the sample mean. Explicit early mathematics using HDLSS asymptotics in the Stein estimation context can be found in Casella and Hwang (1982).

A closely related asymptotic domain has been called ultra high dimension by Fan and Lv (2008), who consider the case of d = exp(cn^a), for constants c and a, in the classical limit as n → ∞. The ultra high case can also be equivalently formulated as n = (log(d)/c)^1/a in the limit as d → ∞. While these formulation appear to be equivalent at first glance, note that only the latter reveals that this case is quite near to the HDLSS context.

The HDLSS geometric representation has been established under a range of conditions. Hall et al. (2005) went beyond the independent Gaussian case by assuming the data vectors satisfy a mixing condition. Ahn et al. (2007) proposed a more palatable eigenvalue condition for geometric representation. In unpublished correspondence John Kent pointed out, using a Gaussian scale mixture example, that more than univariate moment conditions are needed. Conditions that are especially appealing because they are based only on the covariance matrix (with no assumption of Gaussianity) have been developed in a series of papers (Yata and Aoshima, 2009, 2010b; Aoshima and Yata, 2011; Yata and Aoshima, 2012a; Aoshima and Yata, 2015). A non-Gaussian condition that makes intuitive sense based on the types of data found in genomics can be found in Jung and Marron (2009).

3 PCA and HDLSS Asymptotics

Principal Component Analysis (PCA), see Jolliffe (2005) for excellent introduction and overview, is a well proven workhorse method for many tasks involving high dimensional data. A strong indicator of its utility comes from the fact that it has been rediscovered and renamed a number of times. For example, it is called empirical orthogonal functions in the earth/climate sciences, proper orthogonal decomposition in applied mathematics, the Karhunen Loeve expansion in electrical engineering and probability and factor analysis in a number of non-statistical areas, despite the fact that the term refers to a more complicated likelihood algorithm in psychometrics where the method was invented.

A misperception on the part of some is that PCA only works for Gaussian data, perhaps rooted in the fact that one can motivate PCA from a Gaussian likelihood viewpoint. However, it is more generally viewed as a fully nonparameteric method, with a number of purposes. Many view PCA as mostly being a dimension reduction method, but it is arguably even more useful for data visualization in high dimensional contexts, such as Functional Data Analysis, see Ramsay and Silverman (2002), Ramsay (2005), and Ferraty and Vieu (2004).

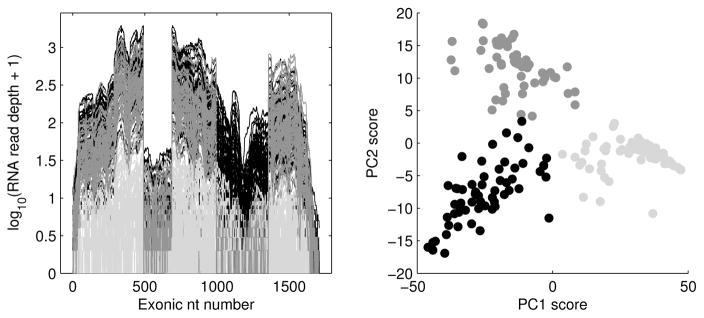
An example of PCA data visualization is shown in Figure 1. The curves in the left panel are read depth curves from RNAseq measurements (Wilhelm and Landry, 2009) from n = 180 lung cancer patients. Each curve is a very detailed measurement of biological expression of the gene CDKN2A for one tissue sample, with the horizontal axis indicating d = 1709 base pair locations of the reference genome, and the height of the curve being a log₁₀ count that indicates level of gene expression. Insight into how the curves relate to each other comes from the PCA scatterplot in the right panel of Figure 1. The axes of the scatterplot are the first two principal component scores. There is some apparent interesting structure, in the form of three distinct clusters. To explore the relevance of these clusters, they have been brushed, i.e. colored with grey levels. These same colors have been used on the curves in the left panel. Note that the lightest grey curves tend to be much lower than the others, representing cases where the CDKN2A gene is essentially not expressed (typical in some cases). The genome location of the gene includes several disconnected loci called exons, which here have been connected giving the block-like structure apparent in the other curves. Note that the third exon shows very low levels of expression for all cases. The fifth exon is interesting because it is fully expressed for only the black cases, while all others show a very low level of expression. This phenomenon is called alternate splicing, and is very important in cancer research because it can become the target of drug treatments. This example motivated a search for alternate splice events, based on screening for clusters in read depth curves, over all genes. An important challenge to the implemention of this was the assessment of the statistical significance of clusters in very high dimensions, which was done using the SigClust method of Liu et al. (2008). This screening method has been named SigFuge by Kimes and Cabanski (2013), who report on the results of a full genome screen which found previously unknown splicing events, one of which was then confirmed by a biological experiment. The main point of this example, that becomes crucial later in this paper, is that PCA found important structure in this HDLSS data set, through visualizing the PC scores, i.e. projections of the data onto the sample eigenvectors.

Figure 1.

PCA of RNAseq log read depth maps, for the union of exons in the gene CDKN2A. Left panel shows data curves. Right panel is the PC1 vs. Pc2 scores scatter-plot, showing three distinct clusters (brushed with gray levels). Use of these same colors in the left panel shows essentially unexpressed cases (lightest grey), and a clear alternate splicing event (other grey shades). This is an HDLSS example where PCA clearly reveals important biological structure.

The asymptotic underpinnings of PCA in HDLSS contexts were first considered by Ahn et al. (2007), and more deeply by Jung and Marron (2009). Insight into the behavior of PCA comes from study of the spike covariance model, made popular in statistics by Paul (2007) and Johnstone and Lu (2009). In the simplest form of the spike covariance model, there is a single large eigenvalue with all of the rest much smaller and constant, where the largest eigenvalue has size of growing order d^α. In this case the key result is that, in the limit as d → ∞, with n fixed, letting u₁ and û₁ denote the first population and sample eigenvectors respectively,

$$\text{angle}<{\widehat{u}}_1,u_1>\to \{\begin{array}{ccc}90°& \mathit{for}& \alpha <1\\ 0& \mathit{for}& \alpha >1\end{array}.$$ (3.1)

This defines a notion of consistency when the spike is large in the sense that α > 1, and also a notion called strong inconsistency when the spike is small meaning that α < 1. Furthermore, one or the other holds in almost all such settings, with the exception being only the boundary case of α = 1. The reason the boundary is at α = 1 can be understood from the geometric representation discussed in Section 2. There it is seen that in the HDLSS limit, standard Gaussian data tends to lie on the surface of the sphere at the origin, with radius d^1/2. In the spike model, when α > 1, the distribution reaches outside of this sphere (recall eigenvalues are on the scale of variance, so the corresponding largest standard deviation is much greater than $d^{\frac{1}{2}}$), which results in consistency of the first eigendirection. Conversely, when α < 1, the distribution is essentially contained within the sphere, so the first eigendirection will be random, and it is known again from geometric representation ideas that random directions are asymptotically orthogonal to any given direction. The strong dichotomy of cases between consistency and strong inconsistency established in (3.1) is an important component of the discussion in Section 4.

Deeper related results, under various assumptions including conditions only on the covariance matrix, are available in the above referenced series of papers by Yata and Aoshima (2009, 2010a, 2012a, 2013). Related new insights about sparse PCA were dicovered by Shen et al. (2012a). See Shen et al. (2012b) for far broader results in this spirit, including all combinations of n and d tending to infinity. Deeper limiting behavior in the boundary case of α = 1 was first explored by Jung et al. (2012) in the HDLSS case. Those ideas are taken in the novel conical limit theorem direction, under a far broader range of contexts, in Section 5 below. In addition, Yata and Aoshima (2012a) proposed a noise reduction estimator that relaxes the boundary of the eigenvalue estimator to $\alpha =\frac{1}{2}$ in the HDLSS case.

While (3.1) shows that when there is a sufficiently strong signal in the covariance structure PCA can find the right direction vectors, estimation of the eigenvalues is more challenging. Indeed, letting λ₁ and λ̂₁ denote the population (and sample resp.) first eignevalues, there are a number of results in the spirit of

$$\frac{{\widehat{\lambda }}_1}{{\lambda }_1}\stackrel{\mathrm{L}}{\to }\frac{{\chi }_n^2}{n},$$ (3.2)

under various HDLSS conditions. Thus sample eigenvalues are generally inconsistent when the sample size is fixed, but as noted by Yata and Aoshima (2009, 2010b), sample eignevalues are consistent if it is further assumed that in addition to d → ∞, n → ∞ as well. The case where n grows more slowly than d has been called High Dimension Moderate Sample Size by Borysov et al. (2014). Yata and Aoshima (2010a, 2012a, 2013) have also invented modified versions of PCA which provide eigenvalue estimates that are consistent.

4 Understanding Variation in Scores

Another apparently paradoxical property of PCA in HDLSS situations is that the scores, which form the basis of informative scatterplots, such as Figure 1, are generally inconsistent in the HDLSS limit. In particular, the ratio of the sample and population PC scores converge to a nondegenerate random variable, as formulated here in Section 4.2. At first glance, this comes as a surprise to statisticians who routinely use PC scores scatterpots to analyze high dimensional data, and find scientifically important structure in those plots.

The seeming paradox is resolved by taking a more careful look at the actual mathematics in Section 4.2. For a given component, the ratios for each data point indeed converge to a random variable, but it is the same realization of the random variable for each data point. Thus while all the scores are off by a random factor, it is the same factor for each data point. So in scatterplots such as Figure 1 the axis labels are off by a random factor, but the critical relationship between the points (usually the main data analytic content of such plots) is still correct.

This issue was presaged in Yata and Aoshima (2009) and is quite similar to the eignevalue inconsistency in equation (3.2). The improved variation of PCA proposed in Yata and Aoshima (2012a, 2013) gives asymptotically correct scalings. Moreover, Lee et al. (2010) and Hellton and Thoresen (2014) have considered other viewpoints on the inconsistency of scores. Specifically, under the random matrix framework, Lee et al. (2010) showed that the ratios of the sample and population PC scores converge to a constant. Hellton and Thoresen (2014) used the ideas of pervasive signal and visual content to explore this inconsistent phenomenon.

4.1 Assumptions and Notation

Let {(λ_k, u_k) : k = 1, ⋯, d} be the eigenvalue-eigenvector pairs of the covariance matrix Σ such that λ₁ ≥ λ₂ ≥ … ≥ λ_d > 0. Then Σ has the following eigen-decomposition

$$\mathrm{\sum }=U\mathrm{\Lambda }{U}^T,$$ (4.1)

where Λ = diag(λ₁, …, λ_d) and U = [u₁, …, u_d].

Assume that X₁, …, X_n are i.i.d. d-dimensional random sample vectors with the following representation

$$X_i=\sum _{j=1}^d{\lambda }_j^{\frac{1}{2}}{z}_{i,j}{u}_j,$$ (4.2)

where the z_i,j’s are i.i.d random variables with zero mean, unit variance and finite fourth moment. An important special case is that X_is’ follow normal distribution N(0, Σ).

Assumption 4.1

X₁, …, X_n are i.i.d random vectors from a d-dimensional distribution in (4.2)

Let’s consider a simple example when X_i are i.i.d. N (ξ, Σ) with ξ ≠ 0. As discussed in Paul and Johnstone (2007), it is well known that

$$\sum _{i=1}^n(X_i-\overline{X}){(X_i-\overline{X})}^T\text{has}\text{the}\text{same}\text{distribution}\text{as}\sum _{i=1}^{n-1}{Y}_i{Y}_i^T,$$

where X̄ is the sample mean and Y_i are i.i.d. N(0, Σ). Then the asymptotic properties of PCA can be studied through Y_i. Since the sample covariance matrix is location invariant, we can assume without loss of generality that X_i has zero mean at least for the normal case. In general, one has to consider the theoretical properties of X̄−μ, which have been widely investigated in the literature (Rollin, 2013; Chernozhukov et al., 2014) even when d is much larger than n.

Denote the jth normalized population PC score vector as

$$S_j={(S_{1,j},\dots ,S_{n,j})}^T={\lambda }_j^{-\frac{1}{2}}{(u_j^T{X}_1,\cdots ,u_j^T{X}_n)}^T,j=1,\cdots ,d.$$ (4.3)

Denote the data matrix X = [X₁, ⋯, X_n] and then the sample covariance matrix $\widehat{\mathrm{\sum }}=\frac{1}{n}X{X}^T$. Similarly, the sample covariance matrix Σ̂ can be decomposed as

$$\widehat{\mathrm{\sum }}=\widehat{U}\widehat{\mathrm{\Lambda }}{\widehat{U}}^T,$$ (4.4)

where the diagonal eigenvalue matrix Λ̂ = diag(λ̂₁, …, λ̂_d) and the eigenvector matrix Û = [û₁, …, û_d]. Since the data matrix $n^{-\frac{1}{2}}X$ has the singular value decomposition such that

$$n^{-\frac{1}{2}}X=\sum _{j=1}^d{\widehat{\lambda }}_j^{\frac{1}{2}}{\widehat{u}}_j{\widehat{v}}_j^T,\text{where}{\widehat{v}}_j={({\widehat{v}}_{1,j},\cdots ,{\widehat{v}}_{n,j})}^T,j=1,\cdots ,d,$$

then the jth normalized sample PC score vector is given by

$${\widehat{S}}_j={({\widehat{S}}_{1,j},\cdots ,{\widehat{S}}_{n,j})}^T=n^{\frac{1}{2}}{({\widehat{v}}_{1,j},\cdots ,{\widehat{v}}_{n,j})}^T,j=1,\cdots ,d.$$ (4.5)

We introduce the following notions to help understand the assumptions in our theorems. Assume that {a_k : k = 1, …, ∞} and {b_k : k = 1, …, ∞} are two sequence of constants, where k can stand for either n or d.

• Denote a_k ≫ b_k if ${lim}_{k\to \infty }\frac{b_k}{a_k}=0$.

• Denote a_k ~ b_k if $c_2\le {\underset{\_}{lim}}_{k\to \infty }\frac{a_k}{b_k}\le {\overline{lim}}_{k\to \infty }\frac{a_k}{b_k}\le c_1$ for two constants c₁ ≥ c₂ > 0.

In addition, we introduce an asymptotic notation. Assume that {ξ_k : k = 1, …, ∞} is a sequence of random variables and {e_k : k = 1, …, ∞} is a sequence of constants.

• Denote ξ_k = O_a.s (e_k) if ${\overline{lim}}_{k\to \infty }\left|\frac{{\xi }_k}{e_k}\right|\le \zeta$ almost surely with P(0 < ζ < ∞) = 1.

4.2 HDLSS Inconsistency

In this subsection, we shows the asymptotic properties of PC scores in HDLSS, where the sample size n is fixed and the dimension d → ∞. We consider multiple spike models (Jung and Marron, 2009) under which, as d → ∞,

$${\lambda }_1\gg \cdots \gg {\lambda }_m\gg {\lambda }_{m+1}~\cdots ~{\lambda }_d~1,$$ (4.6)

where m ∈ [1, n ∧ d] is a finite number. Under the above spike models, Jung and Marron (2009) showed that when n is fixed, if $\frac{d}{{\lambda }_m}\to 0$, the angle between each of the first m sample eigenvectors û_j and its corresponding population eigenvector u_j goes to 0 with probability 1, which is defined as the consistency of the sample eigenvector.

However, under the same assumptions, a paradoxical phenomenon is identified in that the sample PC scores are not consistent. In addition, our analysis suggests that, for a particular principal component, the proportion between the sample PC scores and the corresponding population scores converges to a random variable, the realization of which remains the same for all data points. These results are summarized in the following Theorem 4.1. The findings suggest that it remains valid to use score scatter plots (e.g. right panel of Figure 1) as a graphical tool to identify interesting features in high dimension low sample size data. Since we study the proportion between the sample and the population PC scores, that is Ŝ_i,j/S_i,j, we need the following assumption

$$P(z_{i,j}\ne 0)=1,i=1,\cdots ,n,j=1,\cdots ,m,$$ (4.7)

to ensure that P(S_i,j ≠ 0) = 1 (S_i,j = z_i,j from (4.2) and (4.3)). In addition, we need several definitions to understand the results of Theorem 4.1. Define

$${\stackrel{\sim }{Z}}_j={(z_{1,j},\cdots ,z_{n,j})}^T\text{and}{R}_j=\frac{{\stackrel{\sim }{Z}}_j^T{\stackrel{\sim }{Z}}_j}{n},j=1,\cdots ,d,$$ (4.8)

where z_i,j is defined in (4.2).

Theorem 4.1

Under Assumption 4.1, spike model (4.6) and (4.7), and for the fixed n, as d → ∞, if $\frac{d}{{\lambda }_m}\to 0$, then the proportion between the sample and population principal component scores satisfies

$$\left|\frac{{\widehat{S}}_{i,j}}{S_{i,j}}\right|\stackrel{a.s}{\to }{R}_j^{-\frac{1}{2}},i=1,\cdots n,j=1,\cdots ,m,$$ (4.9)

where $\stackrel{a.s}{\to }$ stands for almost sure convergence and R_j is defined in (4.8). In addition, if Assumption 4.1 is strengthened to normal distribution, then R_j has the same distribution as $\frac{{\chi }_n^2}{n}$ with ${\chi }_n^2$ being the Chi-square distribution with n degrees of freedom.

Remark 4.1

The results in Theorems 4.1 are different from those in Lee et al. (2010). Under the random matrix framework with n ~ d → ∞ and λ_j < ∞, Lee et al. (2010) showed that the ratios between the sample and population eigenvalues converge to a constant. In addition, Lee et al. (2010) did not consider theoretical properties of PC scores under the framework min(n, d, λ_j) → ∞, which is shown in Theorem 4.2.

Remark 4.2

It follows from (4.9) that the ratio R_j only depends on j (the index of the principal components), but not i (the index of the data points). This particular scaling suggests that the scores scatter plot, such as right panel of Figure 1, has incorrectly labeled axes (by the common factor R_j for the corresponding axis), and yet asymptotically correct relative positions of the points; hence the scatter plot still enables meaningful identification of useful scientific features as demonstrated in right panel.

Remark 4.3

If we consider the non-normalized PC scores with $S_{i,j}^o=u_j^T{X}_i={\lambda }_j^{\frac{1}{2}}{S}_{i,j}$ and ${\widehat{S}}_{i,j}^o={\widehat{\lambda }}_j^{\frac{1}{2}}{\widehat{S}}_{i,j}$, then $\left|{\widehat{S}}_{i,j}^o/S_{i,j}^o\right|\stackrel{a.s.}{\to }1$ for i = 1, …, n and j = 1, …, m under the assumptions of Theorem 4.1.

4.3 Growing Sample Size Analysis

In this subsection, we consider growing sample size contexts, where n → ∞, and then study the asymptotic properties of the PC scores. Unlike the low sample size setting, the apparent inconsistency paradox now disappears. This means that both the sample eigenvectors and the sample principal component scores can be consistent.

We consider the following multiple spike models, as n, d → ∞,

$${\lambda }_1>\cdots >{\lambda }_m\gg {\lambda }_{m+1}~\cdots ~{\lambda }_d~1.$$ (4.10)

Theorem 4.2 suggests that as n → ∞, the proportion between the sample scores and the corresponding population scores tends to 1. This connects with the above results, from the fact that the ratio R_j in (4.9) converges almost surely to 1 as n → ∞. Thus, it is not surprising that the apparent inconsistency disappears as the sample size grows.

Theorem 4.2

Under Assumption 4.1, (4.7) and spike model (4.10), and as n, d → ∞, if $\frac{d}{n^{\frac{1}{2}}{\lambda }_m}\to 0$, then the proportion between the sample and population principal component scores satisfies

$$\left|\frac{{\widehat{S}}_{i,j}}{S_{i,j}}\right|\stackrel{a.s.}{\to }1,i=1,\cdots n,j=1,\cdots ,m.$$ (4.11)

Remark 4.4

Under the current context, the consistency of the sample PC scores fits as expected, with the fact that the sample eigenvectors are consistent under the assumptions of Theorem 4.2. In particular, Shen et al. (2012b) have shown that, under the same assumptions, the angle between the sample eigenvector û_j and the corresponding population eigenvector u_j for j = 1, ⋯, m converges almost surely to 0.

5 Deeper Conical Behavior

This section is to reveal an asymptotic conical structure in critical sample eigendirections under the spike models with distinguishable (or indistinguishable) eigenvalues, when the sample size and/or the number of variables (or dimension) tend to infinity. The consistency of the sample eigenvectors relative to their population counterparts is determined by the ratio between the dimension and the product of the sample size with the spike size. When this ratio converges to a nonzero constant, the sample eigenvector converges to a cone, with a certain angle to its corresponding population eigenvector. In the HDLSS case, the angle between the sample eigenvector and its population counterpart converges to a limiting distribution. Several generalizations of the multi-spike covariance models are also explored, and additional theoretical results are presented.

We first introduce two illustrative examples to help understand the asymptotic results of conical structure for sample eigendirections, where the eigenvalues are respectively asymptotically distinguishable (Example 5.1) and indistinguishable (Example 5.2). Our theorems are applicable to a much broader class of general spike models.

Example 5.1

(Multiple-component spike models with distinguishable eigenvalues) Assume that X₁, …, X_n are random sample vectors from distribution (4.2), where the population eigenvalues have the following properties: as n, d → ∞,

$$\{\begin{array}{l}{\lambda }_1>{\lambda }_2>{\lambda }_3\gg {\lambda }_4=\cdots ={\lambda }_d=1,\hfill \\ \frac{d}{n{\lambda }_j}\to c_j,j=1,2,3,\text{with}0\le c_1<c_2<c_3\le \infty .\hfill \end{array}$$

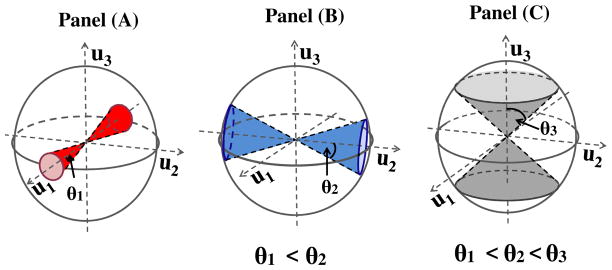
In Figure 2, the sphere represents the space of all possible sample eigen-directions, with the first three population eigenvectors as the coordinate axes. For this particular example, our general Theorem 5.1 suggests that

Figure 2.

Geometric representation of PC directions in Example 5.1. The sphere represents the space of possible sample eigenvectors. Panel (A) shows that the first sample eigenvector tends to lie in the red cone, with the θ₁ angle. Similarly, Panels (B) and (C) show that the second and the third sample eigenvectors respectively tend to lie in the blue and the gray cones, whose angles are θ₂ and θ₃. Note that the angle of the red cone is less than the blue cone, whose angle is again less than the gray cone.

• As n, d → ∞, the sample eigenvector û₁ lies in the red cone, shown in Panel (A) of Fig. 2, where the angle of the cone is ${\theta }_1=arccos(\frac{1}{\sqrt{1+c_1}})$. Similarly, as n, d → ∞, the sample eigenvectors û₂ and û₃ respectively lie in the blue and dark gray cones, shown in Panels (B) and (C) of Fig. 2, whereas the angles are respectively ${\theta }_2=arccos(\frac{1}{\sqrt{1+c_2}})$ and ${\theta }_3=arccos(\frac{1}{\sqrt{1+c_3}})$. Note that for c₁ < c₂ < c₃, we have θ₁ < θ₂ < θ₃, as shown in Figure 2.

In addition, our Proposition S4.1 in the supplementary material (Shen et al., 2015) includes the two boundary cases studied by Shen et al. (2012b) as special cases:

• When c₁ = c₂ = c₃ = 0, it follows that θ₁ = θ₂ = θ₃ = 0. This puts us in the domain of consistency (Shen et al., 2012b).

• In the opposite boundary case of c₁ = c₂ = c₃ = ∞, we have that θ₁ = θ₂ = θ₃ = 90 degrees. This leads to strong inconsistency (Shen et al., 2012b).

Hence, our new results go well beyond the work of Shen et al. (2012b), and completely characterize the transition between consistency and strong inconsistency.

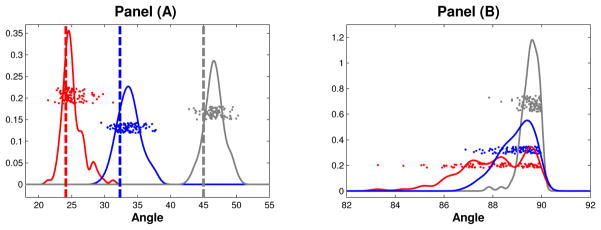
We investigated this theoretical convergence, using simulations, over a range of settings, with n = 50, 100, 200, 500, 1000, 2000, where $\frac{d}{n}=50$, and c₁ = 0.2, c₂ = 0.4, c₃ = 1. The full sequence, illustrating this convergence, is shown in Figure A of the supplementary material (Shen et al., 2015). Figure 3 shows the intermediate case of n = 200. For one data set with this distribution, we compute angles between the sample and population eigenvectors. Repeating this procedure over 100 replications, we get 100 angles for each of the first three eigenvectors, which are shown as red, blue and gray points in Panel (A). The red, blue, gray curves are the corresponding kernel density estimates. Panel (A) shows that the simulated angles are very close to the corresponding theoretical angles θ_j, j = 1, 2, 3, shown as dashed vertical lines.

Figure 3.

Example 5.1: Simulated angles between sample and population eigenvectors. Panel (A) shows realizations of angles between sample and population eigenvectors as colored dots (red is first, blue is second, gray is third). Distributions are studied using kernel density estimates, and compared with the theoretical values θ_j for j = 1, 2, 3, shown as dashed lines. Panel (B) studies randomness of eigen-directions within the cones shown in Figure 2, by showing the distribution of pairwise angles between realizations of the sample eigenvectors. All 3 colors are overlaid here, and all angles are very close to 90 degrees, which is very consistent with the randomness of the respective sample eigenvectors within the cones.

Panel (B) in Figure 3 studies randomness of eigen-directions within the cones shown in Figure 2. We calculate pairwise angles between realizations of the sample eigenvectors for the three cones, showing angles and kernel density estimates using colors as in Panel (A) of Figure 3. All angles are very close to 90 degrees, which is consistent with randomness in high dimensions, see Hall et al. (2005); Yata and Aoshima (2012a); Jung and Marron (2009); Jung et al. (2012) and the more recent work of Cai et al. (2013). In fact, the regions represented by circles in Figure 1, are actually d-1 dimensional hyperspheres, so the sample eigenvectors should be thought of as d-1 dimensional as n, d → ∞.

Example 5.2

(Multiple-component spike models with indistinguishable eigen-values) We again assume that X₁, …, X_n are random sample vectors from distribution (4.2). Different from Example 5.1, the six leading population eigenvalues fall into three asymptotically separable pairs as follows: as n, d → ∞

$$\{\begin{array}{l}{\lambda }_1={\lambda }_2>{\lambda }_3={\lambda }_4>{\lambda }_5={\lambda }_6\gg {\lambda }_7=\cdots ={\lambda }_d=1,\hfill \\ \frac{d}{n{\lambda }_{2j-1}}\to c_j,j=1,2,3,\text{with}0\le c_1<c_2<c_3\le \infty .\hfill \end{array}$$

Our general Theorem 5.2, when applied to the current example, reveals the following insights:

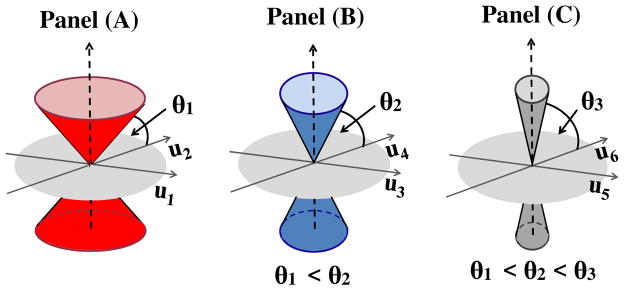
• Panel (A) in Figure 4 shows, as a red cone, the region where the first group of sample eigenvectors û₁ and û₂ lie in the limit as n, d → ∞. This has the angle ${\theta }_1=arccos(\frac{1}{\sqrt{1+c_1}})$ with the gray subspace, generated by the first group of population eigenvectors u₁ and u₂. Similarly, Panel (B) (Panel (C)) presents, as a blue (gray) cone, the region where the second (third) group of sample eigenvectors û₃ and û₄ (û₅ and û₆) lie in the limit as n, d → ∞. This has the angle ${\theta }_2=arccos(\frac{1}{\sqrt{1+c_2}})({\theta }_3=arccos(\frac{1}{\sqrt{1+c_3}}))$ with the subspace, generated by the second (third) group of population eigenvectors u₃ and u₄ (u₅ and u₆). Note that for c₁ < c₂ < c₃, we have θ₁ < θ₂ < θ₃, as shown in Figure 4.

Figure 4.

Example 5.2: Geometric representation of PC directions. Panel (A) shows the cone to which the first group of sample eigenvectors converge in the red. This cone has angle θ₁ with the gray subspace, generated by the first group of population eigenvectors. Similarly, Panel (B) (Panel (C)) shows the cone to which the second (third) group of sample eigenvectors converges shown as a blue (dark gray) cone, which has angle θ₂ (θ₃) with the subspace, generated by the second (third) group of population eigenvectors.

Furthermore, our Proposition S2.1 in the supplementary document of Shen et al. (2015) considers boundary cases of our general framework, which includes the results of Shen et al. (2012b) as special cases:

• For c₁ = c₂ = c₃ = 0, it follows that θ₁ = θ₂ = θ₃ = 0. This puts us in the domain of subspace consistency, as studied in Theorem 4.3 of Shen et al. (2012b).

• When c₁ = c₂ = c₃ = ∞, we have that θ₁ = θ₂ = θ₃ = 90 degrees. This leads to strong inconsistency, as studied in Theorem 4.3 of Shen et al. (2012b).

The rest of the section is organized as follows. Section 5.1 studies the asymptotic properties of sample eigenvalues and eigenvectors for multiple spike models with distinguishable (or indistinguishable) eigenvalues as n → ∞. Section 5.2 studies the theoretical properties of sample eigenvalues and eigenvectors in the HDLSS contexts. Section 8 contains the technical proofs of the main theorems. Additional simulation studies and proofs can be found in the supplementary document (Shen et al., 2015).

5.1 Growing sample size asymptotics

We now study asymptotic properties of PCA as n → ∞. We consider multiple component spike models with distinguishable population eigenvalues in Section 5.1.1 and with indistinguishable eigenvalues in Section 5.1.2. Moreover, we vary d from d ≪ n, through the random matrix version with d ~ n, all the way to the high dimension medium sample size (HDMSS) asymptotics of Cabanski et al. (2010); Yata and Aoshima (2012b); Aoshima and Yata (2015) with d ≫ n → ∞. Aoshima and Yata (2015) improves the results of Yata and Aoshima (2012b) under mild conditions.

5.1.1 Multiple component spike models with distinguishable eigenvalues

We consider multiple component spike models, where the population eigenvalues are assumed to satisfy the following two assumptions:

• 𝒜1. As n, d → ∞, λ₁ > ⋯ > λ_m ≫ λ_m+1 → ⋯ → λ_d = 1.

• 𝒜2. As n, d → ∞, $\frac{d}{n{\lambda }_j}\to c_j$, where 0 < c₁ < ⋯ < c_m < ∞.

We first make several comments about Assumptions 𝒜1 and 𝒜2.

• Assumption 𝒜1 includes two separate parts:

  1. The λ₁ > ⋯ > λ_m part makes it possible to separately consider the first m principle component signals and study the corresponding asymptotic properties.

  2. The λ_m ≫ λ_m+1 → ⋯ → λ_d = 1 enables clear separation of the signal (contained in the first m components) from the noise (in the higher order components), which then helps to derive the asymptotic properties of the first m sample eigenvalues and eigenvectors.

• Assumption 𝒜2 is the critical case, in which the positive information and the negative are of the same order. In particular, increasing n and the spike positively impacts the consistency of PCA, whereas increasing d has a negative impact.

While the main focus of our results is the signal eigenvectors, some notation for the noise eigenvectors is also useful. According to Assumption 𝒜1, the noise sample eigenvalues whose indices are greater than m can not be asymptotically distinguished, so the corresponding eigenvectors should be treated as a whole. Therefore, we define the noise index set H = {m + 1, ⋯, d}, and denote the space spanned by these noise eigenvectors as

$$\mathbb{S}=\text{span}\{u_j,j\in H\}.$$ (5.1)

For each sample eigenvector û_j, j ∈ H, we study the angle between û_j and the space 𝕊, as defined in Jung and Marron (2009); Shen et al. (2012b) and illustrated in Figure B of of the supplementary material Shen et al. (2015).

The following theorem derives the asymptotic properties of the first m sample eigenvalues and eigenvectors. In addition, the theorem also shows that, for j = m + 1, ⋯, [n ∧ d], the angle between û_j and u_j goes to 90 degrees, whereas the angle between û_j and the space 𝕊 goes to 0.

Theorem 5.1

Under Assumptions 4.1, 𝒜1, and 𝒜2, as n, d → ∞, the sample eigenvalues satisfy

$$\{\begin{array}{l}\frac{{\widehat{\lambda }}_j}{{\lambda }_j}\stackrel{\text{a.s}}{\to }1+c_j,1\le j\le m,\hfill \\ \frac{n{\widehat{\lambda }}_j}{d{\lambda }_j}\stackrel{\text{a.s}}{\to }1,m+1\le j\le [n\wedge d],\hfill \end{array}$$ (5.2)

and the sample eigenvectors satisfy

$$\{\begin{array}{l}\mid <{\widehat{u}}_j,u_j>\mid \stackrel{a.s}{\to }{(1+c_j)}^{-\frac{1}{2}},1\le j\le m,\hfill \\ \mid <{\widehat{u}}_j,u_j>\mid ={\mathrm{O}}_{\text{a.s}}\left\{{(\frac{n}{d})}^{\frac{1}{2}}\right\},m+1\le j\le [n\wedge d],\hfill \\ \mathit{angle}<{\widehat{u}}_j,\mathbb{S}>\stackrel{a.s}{\to }0,m+1\le j\le [n\wedge d].\hfill \end{array}$$ (5.3)

We now offer several remarks regarding Theorem 5.1.

Remark 5.1

The results in Theorem 5.1 are different from those in Paul (2007). The $\frac{d}{n{\lambda }_j}\to c_j$ contains three scenarios: (i) n, d, and λ_j → ∞; (ii) d, λ_j → ∞ and n < ∞ (HDLSS); and (iii) n, d → ∞ and λ_j < ∞. This paper studies the first two scenarios. Theorem 5.1 studies scenario (i) and Paul (2007) studied scenario (iii). Paul (2007)’s results are based on the normal assumption, which is unnecessary here. In addition, Paul (2007) did not study indistinguishable eigenvalues as in Theorems 5.2 and 5.3.

Remark 5.2

The results of (5.2) and (5.3) suggest that, as the eigenvalue index increases, the proportional bias between the sample and population eigenvalue increases, so the angle between the sample and corresponding population eigenvectors increases. This is because larger eigenvalues (i.e. with small indices) contain more positive information, which makes the corresponding sample eigenvalues/eigenvectors less biased. These results are graphically illustrated in Figure 1 and empirically verified in Figure 2, for the specific model in Example 5.1. More empirical support is provided in the supplementary material Shen et al. (2015).

Remark 5.3

Theorem 5.1 can be extended to include the random matrix cases and HDMSS cases, which is shown in Section S4.1 of the supplementary material.

5.1.2 Multiple component spike models with indistinguishable eigenvalues

We now consider spike models with the m leading eigenvalues being grouped into r(≥ 1) tiers, each of which contains eigenvalues that are either the same or have the same limit. The eigenvalues within different tiers have different limits. Specifically, the first m eigenvalues are grouped into r tiers, in which there are q_k eigenvalues in the kth tier such that ${\sum }_{l=1}^r{q}_l=m$. Define q₀ = 0, $q_{r+1}=d-{\sum }_{l=1}^r{q}_l$, and the index set of the eigenvalues in the kth tier as

$$H_k=\left\{\sum _{l=0}^{k-1}{q}_l+1,\sum _{l=0}^{k-1}{q}_l+2,\cdots ,\sum _{l=0}^{k-1}{q}_l+q_k\right\},k=1,\cdots ,r+1.$$ (5.4)

We make the following assumptions on the tiered eigenvalues:

• ℬ1. The eigenvalues in the kth tier have the same limit δ_k(> 0):

  $${lim}_{n,d\to \infty }\frac{{\lambda }_j}{{\delta }_k}=1,j\in H_k,k=1,\cdots ,r.$$
• ℬ2. The eigenvalues in different tiers have different limits:

  $$\text{as}n,d\to \infty ,{\delta }_1>\cdots >{\delta }_r\gg {\lambda }_{m+1}\to \cdots \to {\lambda }_d=1.$$
• ℬ3. The ratio between the dimension and the product of the sample size with eigenvalues in the same tier converges to a constant:

  $$\text{as}n,d\to \infty ,\frac{d}{n{\delta }_k}\to c_k,\text{with}0<c_1<\cdots <c_r<\infty .$$

Assumptions ℬ2 and ℬ3 are natural extensions of Assumptions 𝒜1 and 𝒜2. In Assumption ℬ2, the signal contained in the first r tiers of eigenvalues is well separated from the noise, and hence the asymptotic properties of the sample eigenvalues and eigenvectors in the first r tiers can be obtained. Assumption ℬ3 suggests that the positive information (sample size and spike size) and the negative information (dimension) are of the same order.

Since the sample eigenvalues within the same tier can not be asymptotically identified, the corresponding sample eigenvectors are indistinguishable. For j ∈ H_k, in order to study the asymptotic properties of the sample eigenvector û_j, we consider the angle between û_j and the subspace spanned by the population eigenvectors u_j in the same tier, defined as

$${\mathbb{S}}_k=\text{span}\{u_j,j\in H_k\}.$$ (5.5)

Our theoretical results are summarized in the following theorem.

Theorem 5.2

Under Assumptions 4.1, ℬ1, ℬ2 and ℬ3, as n, d → ∞, the sample eigenvalues satisfy

$$\{\begin{array}{l}\frac{{\widehat{\lambda }}_j}{{\lambda }_j}\stackrel{\text{a.s}}{\to }1+c_k,j\in H_k,k=1,\cdots ,r,\hfill \\ \frac{n{\widehat{\lambda }}_j}{d{\lambda }_j}\stackrel{\text{a.s}}{\to }1,m+1\le j\le [n\wedge d],\hfill \end{array}$$ (5.6)

and the sample eigenvectors satisfy

$$\{\begin{array}{l}\mathit{angle}<{\widehat{u}}_j,{\mathbb{S}}_k>\stackrel{a.s}{\to }arccos\left\{{(1+c_k)}^{-\frac{1}{2}}\right\},j\in H_k,k=1,\dots ,r,\hfill \\ \mid <{\widehat{u}}_j,u_j>\mid ={\mathrm{O}}_{\text{a.s}}\left\{{(\frac{n}{d})}^{\frac{1}{2}}\right\},m+1\le j\le [n\wedge d],\hfill \\ \mathit{angle}<{\widehat{u}}_j,{\mathbb{S}}_{r+1}>\stackrel{a.s}{\to }1,m+1\le j\le [n\wedge d].\hfill \end{array}$$ (5.7)

Theorem 5.2 is an extension of Theorem 5.1. For higher-order eigenvalues, the sample eigenvalues are more biased, while the angles between the sample eigenvectors and the subspaces spanned by their population counterparts in the same tiers are larger. See Figure 3 for an illustration of the specific model considered in Example 5.2. Theorem 5.2 can be extended to cover the random matrix and HDMSS cases, which is done in Section S4.2 of the supplementary material.

5.2 HDLSS asymptotics

We now study the asymptotic properties of PCA in the HDLSS context. In this case, the ratios between the sample eigenvalues and their population counterparts converge to non degenerate random variables, as do the angles between the sample eigenvectors and the space spanned by the corresponding population eigenvectors. This phenomenon of random limits does not exist when n increases to ∞ as shown in Section 5.1.

Since the sample size is fixed, we can not distinguish the two types of spike models considered respectively in Sections 5.1.1 and 5.1.2. Hence, we merge the model assumptions there into the following corresponding assumptions:

• 𝒞1. For fixed n, as d → ∞, λ₁ ≥ ⋯ ≥ λ_m ≫ λ_m+1 → ⋯ → λ_d = 1.

• 𝒞2. For fixed n, as d → ∞,

  $$\frac{d}{n{\lambda }_j}\to c_j,\text{with}0<c_1\le \cdots \le c_m<\infty .$$

In particular, Assumption 𝒞1 is parallel to Assumptions 𝒜1, ℬ1 and ℬ2, while Assumption 𝒞2 corresponds to Assumptions 𝒜2 and ℬ3.

As stated below in Theorem 5.3, the sample eigenvalues and eigenvectors converge to non-degenerate random variables rather than constants. We define several quantities in order to describe the limiting random variables. Define the m × d matrix

$$\mathbb{M}={[ℂ,0_{m\times (d-m)}]}_{m\times d},$$

where $ℂ=\text{diag}\{c_1^{-\frac{1}{2}},\cdots ,c_m^{-\frac{1}{2}}\}$ is an m × m diagonal matrix and 0_m×(d−m) is the m × (d − m) zero matrix. In addition, define the random matrices Z and 𝒲 as

$$Z={(z_{i,j})}_{n\times d}\text{and}\mathcal{W}=\mathbb{M}{Z}^{T}Z{\mathbb{M}}^T,$$ (5.8)

where z_i,j is defined in (4.2). The eigenvalues of the random matrix 𝒲 appear in the random limits of Theorem 5.3, as in (5.9) and (5.10).

Given the fixed sample size, the sample eigenvalues can not be asymptotically distinguished, nor can the corresponding sample eigenvectors. To study the asymptotic behavior of the sample eigenvectors, we need to consider the space 𝕊_k spanned by the corresponding population eigenvectors, as defined in (5.5), with the two index sets being H₁ = {1, ⋯, m} and H₂ = {m + 1, ⋯, d}.

We are now ready to state the main theorem in the HDLSS contexts.

Theorem 5.3

Under Assumptions 4.1, 𝒞1 and 𝒞2, for fixed n, as d → ∞, the sample eigenvalues satisfy

$$\{\begin{array}{l}\frac{{\widehat{\lambda }}_j}{{\lambda }_j}\stackrel{\text{a.s}}{\to }\frac{c_j}{n}{\lambda }_j(\mathcal{W})+c_j,1\le j\le m,\hfill \\ \frac{n{\widehat{\lambda }}_j}{d{\lambda }_j}\stackrel{\text{a.s}}{\to }1,m+1\le j\le n,\hfill \end{array}$$ (5.9)

where 𝒲 is defined in (5.8), and the sample eigenvectors satisfy

$$\{\begin{array}{l}\mathit{angle}<{\widehat{u}}_j,{\mathbb{S}}_1>\stackrel{a.s}{\to }arccos\left\{{\left(1+\frac{n}{{\lambda }_j(\mathcal{W})}\right)}^{-\frac{1}{2}}\right\},1\le j\le m,\hfill \\ \mid <{\widehat{u}}_j,u_j>\mid ={\mathrm{O}}_{\text{a.s}}(d^{-\frac{1}{2}}),m+1\le j\le n,\hfill \\ \mathit{angle}<{\widehat{u}}_j,{\mathbb{S}}_2>\stackrel{a.s}{\to }1,m+1\le j\le n.\hfill \end{array}$$ (5.10)

Three remarks are offered below regarding Theorem 5.3.

Remark 5.4

If Assumptions 4.1 becomes the normal distribution, then Theorem 5.3 reduces to studies in Jung et al. (2012). Theorem 5.3 shows that the results in Jung et al. (2012) can be strengthened to almost surely convergence.

Remark 5.5

For 1 ≤ j ≤ m, as the relative size of the eigenvalue decreases, the angle between û_j and 𝕊₁ increases. However, this phenomenon is not as strong as in the growing sample size settings studied in Section 5.1, where the sample eigenvectors can be separately studied, and the corresponding angles have a non-random increasing order.

Remark 5.6

Assumption 𝒞2 can be relaxed to include boundary cases, in which there exists an integer m₀ ∈ [1, m] such that c_m0 = 0, i.e. positive information dominates in the leading m₀ spikes; or c_m0+1 = ∞, i.e. negative information dominates in the remaining high-order spikes. These theoretical results are presented in Section S5 of the supplementary material Shen et al. (2015).

6 Discussion

A number of results have been presented with a common theme that some types of asymptotic behavior, with the HDLSS case lying at one extreme, of statistical methods can be hard for most people to initially understand at an intuitive level. We conclude that careful mathematical analysis is crucial for understanding what is going on. In fact we have found this research to frequently be a humbling experience because of the number of times that our a priori conceptions have been proven to be incorrect. This is an area of statistics where proper understanding of even purely data analytic concepts heavily relies on mathematics.

A question which sometimes arises is: in practice how can one check the assumptions that are made in HDLSS asymptotics. To understand this issue, it is useful to review assumption checking in classical contexts. An area where assumption checking is used to good effect on a routine basis is when applying methods that work best with Gaussian data. A Q-Q plot, histogram, or some formal hypothesis test is often very effective at agging data sets where violations of Gaussianity, such as skewness and/or the presence of outliers can yield very misleading results. In such cases, there are a host of better approaches a competent statistician can take, including various transformations and generalized linear models. But an important point is that all of these checks are one sided, in the sense that one cannot conclude Gaussianity in the mathematical sense from any of them, but instead only conclude that Gaussianity fails. But there are many other situations where even one sided assumption checking makes no sense. For example, the classical Central Limit Theorem holds under the assumption of a finite second moment. Note that from any set of data, it is impossible to prove whether or not the underlying distribution has a finite second moment or not. That whole concept is only asymptotic in nature, as is the formulation of the Central Limit Theorem itself. However, applied statisticians routinely see that very many quite Gaussian appearing data sets are out there, and the Central Limit Theorem explains why that is natural. The situation with HDLSS asymptotics and model checking is quite parallel. As with the Central Limit Theorem, useful general insights, which explain HDLSS phenomena observed in data are available from the mathematics. From that perspective, the irrelevant exercise of attempting to check such an assumption in the particular case of a particular data set is not sensible.

7 Supplementary Materials

Additional theoretical results, simulations and proofs can be found in the online supplementary materials.

8 Proofs

We now provide proofs of our theorems. For the sake of space, we only present detailed proofs for Theorems 5.1 and 5.2. Since Theorem 5.1 is a special case of Theorem 5.2, we just need to show the proof of Theorem 5.2. Section 8.1 presents the detailed proof of sample eigenvectors’ properties in Theorem 5.2, and the sample eigenvalues’ properties in Theorem 5.2 is proved in Section S6.1 of the supplementary material Shen et al. (2015).

The proofs of Theorems 4.1, 4.2 and 5.3 are presented in Sections S6 and S7 of the supplementary material, which also contains proofs of the extensions of Theorems 5.1, 5.2 and 5.3.

8.1 The proof of sample eigenvectors’ properties

This subsection shows the detailed proof for the properties of the sample eigenvectors in Theorem 5.2. The critical ideas of the proof are to first partition the sample eigenvector matrix Û into sub-matrices, corresponding to the group index H_k in (5.4). Then through careful analysis, we explore the connections between sample eigenvectors and eigenvalues and then use the sample eigenvalue properties to study the asymptotic properties of the sample eigenvectors.

The population eigenvalues are grouped into r + 1 tiers and H_k in (5.4) is the index set of the eigenvalues in the kth tier. Define

$${\widehat{u}}_j={({\widehat{u}}_{1,j},\cdots ,{\widehat{u}}_{d,j})}^T,j=1,\cdots ,d\text{and}{\widehat{U}}_{k,l}={({\widehat{u}}_{i,j})}_{i\in H_k,j\in H_l},1\le k,l\le r+1.$$

Then, the sample eigenvector matrix Û can be expressed as:

$$\widehat{U}=[{\widehat{u}}_1,{\widehat{u}}_2,\cdots ,{\widehat{u}}_d]=\left(\begin{array}{cccc}{\widehat{U}}_{1,1}& {\widehat{U}}_{1,2}& \cdots & {\widehat{U}}_{1,r+1}\\ {\widehat{U}}_{2,1}& {\widehat{U}}_{2,2}& \cdots & {\widehat{U}}_{2,r+1}\\ ⋮& ⋮& & ⋮\\ {\widehat{U}}_{r+1,1}& {\widehat{U}}_{r+1,2}& \cdots & {\widehat{U}}_{r+1,r+1}\end{array}\right).$$ (8.1)

Since u_j = e_j, j = 1, …, d, then the inner product between the sample and population eigenvectors satisfies

$${\mid <{\widehat{u}}_j,u_j>\mid }^2={\mid <{\widehat{u}}_j,e_j>\mid }^2={\widehat{u}}_{j,j}^2,$$

and the angle between the sample eigenvector and the corresponding population subspace 𝕊_k in (5.5) satisfies

$${\{cos[\text{angle}({\widehat{u}}_j,{\mathbb{S}}_k)]\}}^2=\sum _{l\in H_k}{\widehat{u}}_{l,j}^2,k=1,\cdots ,r+1.$$ (8.2)

In addition, we give out the the Bai-Yin’s law (Bai and Yin, 1993) that will be used in the following proof.

Lemma 8.1

Suppose $B=\frac{1}{s}{Z}_{s\times m}^T{Z}_{s\times m}$, where Z_s×m is an s × m random matrix whose elements are i.i.d and have zero mean, unit variance and finite fourth moment. As s → ∞ and $\frac{m}{s}\to c\in [0,\infty )$, the largest and smallest non-zero eigenvalues of B converge almost surely to ${(1+\sqrt{c})}^2$ and ${(1-\sqrt{c})}^2$, respectively.

The rest proofs are organized as following. Section 8.1.1 obtains the asymptotic properties for the sample eigenvectors whose index is greater than m. Section 8.1.2 derives asymptotic properties for the sample eigenvectors whose index is less than or equal to m.

8.1.1 Asymptotic properties of the sample eigenvectors û_j with j > m

We derive the asymptotic properties through the following two steps:

• First, we show that as n, d → ∞, the angle between û_j and u_j converges to 90 degrees:

  $${\mid <{\widehat{u}}_j,u_j>\mid }^2={\widehat{u}}_{j,j}^2={\mathrm{O}}_{\text{a.s}}\left(\frac{n}{d}\right),j=m+1,\cdots ,[n\wedge d].$$ (8.3)
• Then, we show that as n, d → ∞, the angle between û_j and the corresponding subspace 𝕊_r+1 converges to 0, where 𝕊_r+1 is defined as in (5.5):

  $$\text{angle}<{\widehat{u}}_j,{\mathbb{S}}_{r+1}>\stackrel{a.s}{\to }0,j=m+1,\cdots ,[n\wedge d].$$ (8.4)

We now provide the proof for the first step. Denote $W={\mathrm{\Lambda }}^{-\frac{1}{2}}{U}^T\widehat{U}{\widehat{\mathrm{\Lambda }}}^{\frac{1}{2}}$, where U and V are defined in (4.1) and Û and Λ̂ are defined in (4.4). It follows from (4.1), (4.2) and (4.4) that $W{W}^T=\frac{1}{n}{Z}^{T}Z$, where Z is defined in (5.8). Considering the k-th diagonal entry of the two equivalent matrices WW^T and $\frac{1}{n}{Z}^{T}Z$, and noting that $w_{k,j}={\lambda }_k^{-\frac{1}{2}}{\widehat{\lambda }}_j^{\frac{1}{2}}{\widehat{u}}_{k,j}(U=I_d)$, it follows that

$${\lambda }_k^{-1}\sum _{j=1}^d{\widehat{\lambda }}_j{\widehat{u}}_{k,j}^2=\sum _{j=1}^d{w}_{k,j}^2=\frac{1}{n}\sum _{i=1}^n{z}_{i,k}^2.k=1,\cdots ,d.$$ (8.5)

According to (8.5), we have that

$${\widehat{u}}_{j,j}^2\le \frac{{\lambda }_{m+1}}{{\widehat{\lambda }}_{[n\wedge d]}}\left(\frac{1}{n}\sum _{i=1}^n{z}_{i,j}^2\right),j=m+1,\cdots ,[n\wedge d],$$ (8.6)

Select the m + 1th to nth columns of Z in (5.8) to form the n × [n ∧ d] random matrix Z̄. Note that ${\sum }_{i=1}^n{z}_{i,j}^2$, j = m + 1, ⋯, [n ∧ d] are the diagonal elements of Z̄^TZ̄ and less than or equal to the largest eigenvalue of Z̄^TZ̄. Then it follows from (8.6) that

$${max}_{m+1\le j\le [n\wedge d]}{\widehat{u}}_{j,j}^2\le \frac{{\lambda }_{m+1}}{{\widehat{\lambda }}_{[n\wedge d]}}{\lambda }_{max}(\frac{1}{n}{\overline{Z}}^T\overline{Z}),$$ (8.7)

which, together with the asymptotic properties of the sample eigenvalues (5.6) and Lemma 8.1, yields (8.3).

We then move on to prove the second step. According to (8.2), we need to show that

$$\sum _{k=m+1}^d{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }1,j=m+1,\cdots ,[n\wedge d].$$ (8.8)

The non-zero k-th diagonal entry of W^TW is between its smallest and largest eigenvalues. Since W^TW shares the same non-zero eigenvalues as $\frac{1}{n}Z{Z}^T$, it follows that for j = 1, ⋯, [n ∧ d],

$${\lambda }_{min}(\frac{1}{n}Z{Z}^T)\le {\widehat{\lambda }}_j\sum _{k=1}^d{\lambda }_k^{-1}{\widehat{u}}_{k,j}^2=\sum _{k=1}^d{w}_{k,j}^2\le {\lambda }_{max}(\frac{1}{n}Z{Z}^T),$$ (8.9)

which yields that, for j = m + 1, ⋯, [n ∧ d],

$$\frac{{\lambda }_j}{{\widehat{\lambda }}_j}{\lambda }_{min}(\frac{1}{n}Z{Z}^T)\le \sum _{k=1}^d{\lambda }_j{\lambda }_k^{-1}{\widehat{u}}_{k,j}^2\le \frac{{\lambda }_j}{{\widehat{\lambda }}_j}{\lambda }_{max}(\frac{1}{n}Z{Z}^T).$$ (8.10)

According to Lemma 8.1 and the asymptotic properties of the sample eigenvalues (5.6), we have that, for j = m + 1, ⋯, [n ∧ d],

$$\frac{{\lambda }_j}{{\widehat{\lambda }}_j}{\lambda }_{min}\left(\frac{1}{n}Z{Z}^T\right)\text{and}\frac{{\lambda }_j}{{\widehat{\lambda }}_j}{\lambda }_{max}\left(\frac{1}{n}Z{Z}^T\right)\stackrel{a.s}{\to }1.$$ (8.11)

In addition, it follows from Assumption ℬ2 that, for j = m + 1, ⋯, [n ∧ d],

$$\{\begin{array}{ll}{\lambda }_j{\lambda }_k^{-1}\to 0,\hfill & k=1,\cdots ,m,\hfill \\ {\lambda }_j{\lambda }_k^{-1}\to 1,\hfill & k=m+1,\cdots d.\hfill \end{array}$$ (8.12)

Combining (8.10), (8.11), and (8.12), we have (8.8), which further leads to (8.4).

8.1.2 Asymptotic properties of the sample eigenvectors û_j with j ∈ [1, m]

We need to prove that, for j = 1, ⋯, m, the angle between the sample eigenvector û_j and the corresponding population subspace 𝕊_l, j ∈ H_l, converges to $arccos(\frac{1}{\sqrt{1+c_l}})$, l = 1, ⋯, r. According to (8.2), we only need to show that

$$\sum _{k\in H_l}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }\frac{1}{1+c_l},j\in H_l,l=1,\cdots ,r.$$ (8.13)

Below, we provide the detailed proof of (8.13) for l = 1, and briey illustrate how repeating the same procedure can lead to (8.13) for l > 2.

In order to show (8.13) for l = 1, we need the following lemma about the asymptotic properties of the eigenvector matrix Û in (8.1):

Lemma 8.2

Under Assumptions in Theorem 5.2 and as n, d → ∞, the rows of the eigenvector matrix Û satisfy

$$\sum _{l=1}^r(1+c_l)c_h{c}_l^{-1}\sum _{j\in H_l}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }1,k\in H_h,h=1,\cdots ,r,$$ (8.14)

and the columns of the eigenvector matrix Û satisfy

$$\sum _{h=1}^r\sum _{k\in H_h}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }\frac{1}{1+c_l},j\in H_l,l=1,\cdots ,r.$$ (8.15)

In addition, we also have

$$\sum _{l=1}^r(1+c_l)\sum _{j\in H_l}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }1,k\in H_1.$$ (8.16)

Lemma 8.2 is proven in Section S6.4.3 of the supplementary material (Shen et al., 2015). We now show how to use Lemma 8.2 to prove (8.13) for l = 1. Let h = 1 in (8.14), and then we have that

$$\sum _{l=1}^r(1+c_l)c_l{c}_l^{-1}\sum _{j\in H_l}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }1,k\in H_1.$$ (8.17)

Note that $c_l{c}_l^{-1}<1$ for l > 1, and comparing (8.16) with (8.17), we get that

$$\sum _{l=2}^r\sum _{j\in H_l}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }0,\sum _{j\in H_1}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }\frac{1}{1+c_1},k\in H_1,$$ (8.18)

which then yields that

$$\sum _{k\in H_1}\sum _{j\in H_1}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }\frac{q_1}{1+c_1},$$ (8.19)

where q₁ is the number of eigenvalues in H₁ (5.4). Summing over j ∈ H₁ in (8.15), we have that

$$\sum _{h=1}^r\sum _{k\in H_h}\sum _{j\in H_1}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }\frac{q_1}{1+c_1}.$$ (8.20)

It follows from (8.19) and (8.20) that

$$\sum _{h=2}^r\sum _{k\in H_h}\sum _{j\in H_1}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }0,$$ (8.21)

which, together with (8.15) for l = 1, yields

$$\sum _{k\in H_1}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }\frac{1}{1+c_1},j\in H_1.$$

which is (8.13) for l = 1.

We now prove (8.13) for l = 2, ⋯, r. Note that

• it follows from (8.21) that (8.14) becomes

  $$\sum _{l=2}^r(1+c_l)c_h{c}_l^{-1}\sum _{j\in H_l}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }1,k\in H_h,h=2,\cdots ,r.$$ (8.22)
• it follows from (8.18) that (8.15) becomes

  $$\sum _{h=2}^r\sum _{k\in H_h}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }\frac{1}{1+c_l},j\in H_l,l=2,\cdots ,r.$$ (8.23)
• similar to (8.16), we have

  $$\sum _{l=2}^r(1+c_l)\sum _{j\in H_l}{\widehat{u}}_{k,j}^2\stackrel{a.s}{\to }1,k\in H_2.$$ (8.24)

Finally, combining (8.22), (8.23) and (8.24), we can prove (8.13) for l = 2. We can repeat the same procedure for l = 3, ⋯, r.