IDENTIFYING CANCER SPECIFIC METABOLIC SIGNATURES USING CONSTRAINT-BASED MODELS

Abstract

Cancer metabolism differs remarkably from the metabolism of healthy surrounding tissues, and it is extremely heterogeneous across cancer types. While these metabolic differences provide promising avenues for cancer treatments, much work remains to be done in understanding how metabolism is rewired in malignant tissues. To that end, constraint-based models provide a powerful computational tool for the study of metabolism at the genome scale. To generate meaningful predictions, however, these generalized human models must first be tailored for specific cell or tissue sub-types. Here we first present two improved algorithms for (1) the generation of these context-specific metabolic models based on omics data, and (2) Monte-Carlo sampling of the metabolic model flux space. By applying these methods to generate and analyze context-specific metabolic models of diverse solid cancer cell line data, and primary leukemia pediatric patient biopsies, we demonstrate how the methodology presented in this study can generate insights into the rewiring differences across solid tumors and blood cancers.

Introduction

Cancer tissues exhibits significant metabolic differences when compared to their healthy counterparts, such as the Warburg effect¹ and glutamine addiction.² In recent years it has been revealed that these metabolic transformations are largely driven by oncogenes and subdued by tumor suppressor genes.^3,4 This regulation suggests that cancer metabolism plays an important role in tumor progression, as opposed to being a consequence of the tumor microenvironment.⁵ These findings have led to a renewed interest in the field of cancer metabolism,⁶ with particular interest in exploiting metabolic differences as therapeutic targets.⁷ Cancer metabolism, however, is also extremely heterogeneous across cancer types,⁸ and treatments targeting metabolic pathways need to be carefully tailored to specific cancer phenotypes. Consequently, a better understanding of the metabolic differences across cancer sub-types, and between healthy and cancerous tissues will greatly assist the development of novel therapeutic strategies.^7,8

Genome-Scale Models

To help elucidate the metabolic differences between cancer and healthy tissues, computational approaches can be extremely helpful. In particular, genome-scale models (GEMs) have proven extremely useful in studying human metabolism at the genome level,^9,10 with many studies dedicated specifically to cancer metabolism.^11–13 These studies have, for example, identified glycosaminoglycans as a marker for clear cell renal cell carcinoma,¹⁴ identified carnitine palmitoyltransferase 1 as a potential target for hepatocellular carcinoma,¹⁵ and identified MLYCD as a potential target for leukemia and kidney cancer.¹⁶

GEMs are defined at the core by a stoichiometric matrix S, where each row corresponds to a metabolite, each column to a metabolic reaction, and each entry to the stoichiometric coefficient of that particular metabolite in that particular reaction.¹⁷ For any given stoichiometric matrix, flux distribution column vectors (υ) can be defined where each element υ_i gives the metabolic flux (e.g. rate of metabolite conversion) through each reaction i. The matrix multiplication S · υ= m then yields a vector m where each element m_j gives the rate of change of concentration of metabolite j given the reaction fluxes defined by υ. A steady-state flux distribution is one where S · υ = 0. A more detailed description of the constraint-based model formulation is available in the supplemental information.

Metabolic Model Analysis

Although a wide array of methods have been developed to study GEMs,¹⁸ many of them are dependent on an objective function, which is most often assumed to be cellular growth.¹⁹ Mammalian cells, however, do not have a well established objective, and do not seek to optimize biomass production. One prominent unbiased and objective-independent method for GEM analysis, suited for the study of mammalian cells, is Monte-Carlo sampling (MCS). This method finds normally distributed steady-state flux distributions inside the solution space of S · υ = 0 defined by lower (lb) and upper (ub) reaction bounds, such that lb_i ≤ υ_i ≤ ub_i. Valuable insight into the metabolic capabilities of the model in question can be obtained by analyzing how different MCS conditions (e.g. different lower and upper bounds) affect the sampled reaction flux values. This approach has been used, for example, to model the metabolic exchange between M. tuberculosis and human macrophages,²⁰ and between different cell types in the human brain;²¹ to study aspirin resistance in platelet cells;²² and to characterize metabolic differences between healthy and cancerous tissues.²³

Mammals also have a complex and compartmentalized metabolism, where not every metabolic reaction takes place in all cells of the body. In order to generate predictions specific to different cell types, cancer categories or patients, generalized human GEMs then need to be tailored to specific contexts.²⁴ We recently introduced the Cost Optimization Reaction Dependency Assessment (CORDA) tissue-specific algorithm,²³ which builds tissue-specific metabolic models based on omics data and a generalized human metabolic reconstruction. The algorithm is based on a dependency assessment (DA), where reactions associated with little experimental evidence, called negative confidence reactions (NC), are assigned an arbitrarily high cost. This cost is then minimized while enforcing a small flux through medium (MC) or high (HC) confidence reactions (i.e. reactions with medium or considerable experimental evidence) in order to identify which NC reactions are beneficial for MC or HC reactions to carry flux. This DA is then used to build a tissue-specific model including all HC reactions and as many MC reactions as possible, while minimizing the inclusion of NC reactions. For additional details on the original algorithm we refer readers to the original CORDA publication.²³

Need for New Analyses

MCS of large metabolic networks is computationally expensive, and static approaches are only feasible for extremely small networks.²⁵ For MCS of higher dimensional networks, the Artificially Centered Hit and Run (ACHR) algorithm²⁶ is most frequently used. Given a set of points, or steady-state flux distributions, inside the solution space, ACHR calculates a center point as the average of all points, then moves each point i randomly along the directional vector defined by the trajectory between the center and another random point j. ACHR sampling of large networks can be extremely time consuming, however, and even small relative increments in computational efficiency can lead to fewer hours of computational time. Although alternatives to ACHR have been proposed, many of these methods are limited by sample distributions that are significantly different than ACHR outputs,^27–29 by their dependence on objective functions,²⁷ by long computational times,³⁰ or by lack of validation and parametrization in larger metabolic networks.³¹

Introduction of CORDA2 and mfACHR

Here we present two improved algorithms for the study of human GEMs. We first introduce an improved version of the CORDA algorithm to build tissue-specific metabolic models,²³ referred to here as CORDA2. CORDA2 yields tissue models very similar to the ones given by the previous algorithm, but it is considerably faster than CORDA computationally. CORDA2 is also noise-independent, thus providing unique model outputs for any given set of parameters, which facilitates the comparison of metabolic models across different modeling conditions (i.e. different cancer categories). We next introduce a new formulation of the ACHR algorithm,²⁶ referred to here as the matrix-form ACHR (mfACHR), which performs significantly faster than previous formulations.

Integrating the two new methods, we generate a panel of cell-line specific metabolic models using CORDA2 and experimental data from the Human Protein Atlas³² (HPA), and illustrate how flux samples generated using mfACHR can provide valuable insights into the metabolic profile of different cancer types, including pediatric leukemia. While we had previously shown that MCS of CORDA models can identify metabolic differences between healthy and cancerous tissues, here we show that this framework can also pinpoint metabolic differences between different cancer categories. The methods presented in this study provide significant advances in the generation and analysis of context-specific metabolic models.

Methods

Cost Optimization Reaction Dependency Assessment 2

In this work we present two modifications to CORDA, defining a new version of the algorithm referred to here as CORDA2. First, in the original algorithm, reversible reactions were split into forward and backward rates during every DA to ensure cost production regardless of directionality. That is, a reaction ‘A ⇔ B’ was split into ‘A ⇒ B + cost’ and ‘B ⇒ A + cost’. Since thousands of DAs are performed throughout the model building process, this modification was then repeated thousands of times during the algorithm. In CORDA2, this modification is performed at the beginning of the algorithm, and forward and backward rates are treated separately throughout the model building process, speeding the computational time. Furthermore, while in CORDA the reaction directionality in the tissue-model was imported from the generalized human reconstruction, CORDA2 assigns directionality based on whether the forward, backward, or both reaction parts are included in the final tissue model.

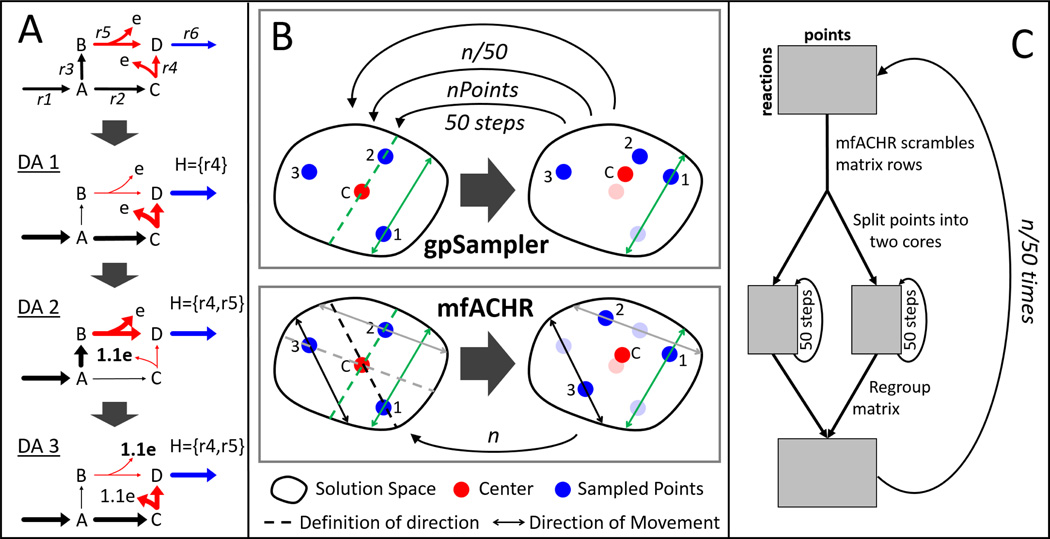
Second, pathways with similar costs are captured in CORDA by adding a small amount of noise to reaction costs during every DA. This noise-driven approach leads to different reconstructions after every run of the algorithm, and it is not guaranteed to include every alternative pathway. This approach is also inefficient since the same pathway can be sampled multiple times. In CORDA2, only undesirable reactions are assigned an arbitrarily high cost (while in CORDA all reactions received a basal cost value). This cost is then minimized during the DA, and the high cost reactions used are saved in a set H. The cost associated with the reactions in H is then increased, and the DA is performed again (Fig. 1A). This process is repeated iteratively until H is unchanged. This way, once a pathway is used, its cost is increased and another pathway with similar but now slightly lower cost is identified in the next DA. Additional details of the CORDA2 formulation, as well as the MATLAB code for its implementation, can be found in the supplemental information.

Fig. 1. Representation of the CORDA2 and mfACHR algorithms.

(A) Identification of undesirable reactions (red) beneficial for the desirable reaction (blue) to carry flux through three DAs. Pathways taken during each DA are highlighted, and H represents the set of undesirable reactions taken up to that point. After an undesirable reaction is used, its cost (e) is increased. The process is repeated until H is unchanged. (B) gpSampler moves one point at a time, 50 steps at a time. The mfACHR algorithm identifies all possible directions of movement at once and moves all points simultaneously. Vectors defining the trajectory of movement, taken as the difference between j and the center point, and the corresponding path of movement of i are color-coded. (C) During parallelization of the MCS process, the matrix of sampled points is divided into 2 cores, which are sampled for 50 steps, then re-combined.

Matrix-Form Artificially Centered Hit and Run

One of the most widely implemented ACHR formalisms is gpSampler.³³ GpSampler starts by moving a given point 50 steps as described by the ACHR algorithm, then repeats the process for each point being sampled. This whole process is then repeated $\frac{n}{50}$ times for a total of n ACHR steps (Fig. 1B). Here we propose a slightly different ACHR formulation, termed matrix-form ACHR (mfACHR). In mfACHR, all possible directions of movement are first calculated as the directional vectors defined by each sampled point and the center (dashed lines in Fig. 1B). These trajectories are then randomly assigned to each point, and each point is moved randomly along its assigned direction of movement (solid lines in Fig. 1B) within the bounds of the solution space. This whole process is repeated a total of n times for a desired number of steps. Both gpSampler and mfACHR can also be implemented in multiple cores. For that, the points being sampled are first divided into i groups, i being the number of cores used. Each group is then assigned to a core and mixed for 50 steps. All points are then re-combined and the process is repeated $\frac{n}{50}$ times for a total of n steps (Fig. 1C).

Cancer Cell Proteomics and Model Generation

Cell line gene and protein expression data were obtained from the HPA³² in order to build the cell-line specific models. Gene expression data was measured using RNA-seq and protein expression was measured by immunohistochemistry using an extensive library of well validated antibodies. Forty-four models were generated using gene expression data and fifty-two models were generated using the proteomics data. Protein expression was available for 523 (35.0%) gene products, and gene expression data was available for 1,474 (98.7%) of the 1,494 unique genes in the generalized human reconstruction Recon1.³⁴ All gene and protein expression values were categorized into not detected, low/medium, and high expression in line with threshold values from the HPA, then used to categorize reaction confidence values used in the CORDA2 algorithm. Following the reconstruction all models were sampled using mfACHR. Details of how these models were generated and sampled can be found in the supplemental information. For additional details on how the dataset was collected we refer readers to the HPA.³²

Leukemia Patient Samples

Pediatric leukemia data was obtained from bone marrow biopsies of 95 acute myeloid leukemia (AML), 57 B-cell acute lymphoblastic leukemia (B-ALL), and 16 T-cell acute lymphoblastic leukemia (T-ALL) pediatric patients, and were collected at the Texas Children’s Hospital. Protein expression level was measured using reverse phase protein array (RPPA) using 194 strictly validated antibodies.³⁵ Additional information on the pediatric leukemia data is available in the supplemental information.

Results and Discussion

Results of our study demonstrate the robustness of the CORDA2 and mfACHR methods, and their utility in analyzing diverse cell line and primary leukemia cancer metabolism. A summary of the CORDA2 and mfACHR validation is provided below, while a complete description of the algorithm validation and analysis is provided in the supplemental information.

CORDA2 Validation

In order to validate the CORDA2 algorithm, outputs of this formulation were compared to 108 tissue-specific metabolic models generated using CORDA and similar model parameters (e.g. same dataset and overlapping algorithm parameters). Overall, at least 99.7% of MC reactions, 88.9% of NC reactions, and 93% of unclassified reactions included in each of the previous 108 models are also included in the CORDA2 model, showing significant overlap between the output of both algorithms. Furthermore, CORDA2 was approximately 2.5 times faster than CORDA when the later was performed with five DAs for every reaction tested. Although performing fewer DAs in CORDA led to computational times comparable to CORDA2, the reconstructions returned in that case are not as comprehensive. In the original CORDA publication, models reconstructed using one DA were on average 2.3% smaller than models built using multiple DAs. The CORDA2 algorithm also showed very similar results across multiple metabolic tests when compared to the previous formulation. This analysis shows that CORDA2 yields models similar to CORDA in composition and behavior, while being faster and noise independent.

mfACHR Validation

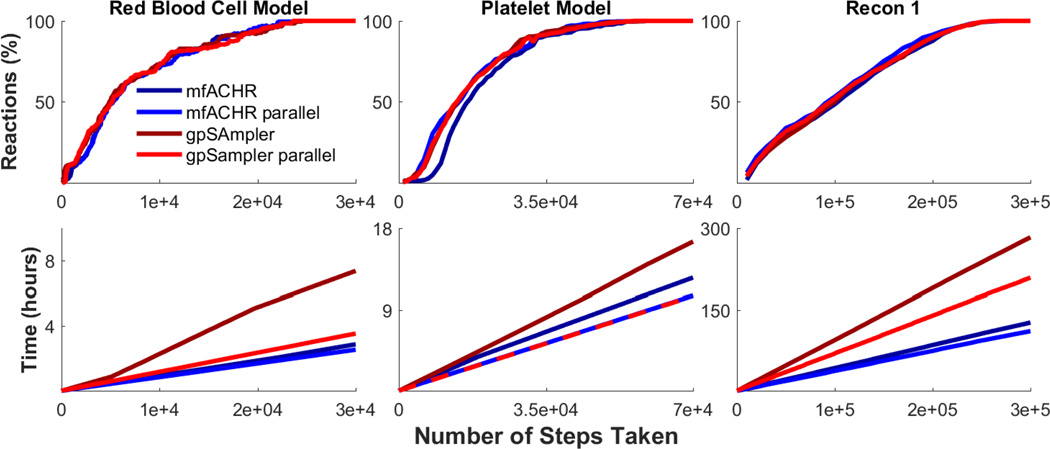
To assess the performance of mfACHR when compared to gpSampler, flux distributions and convergence speed of both formulations were compared for three different metabolic models: a red blood cell (RBC) model,³⁶ a platelet model,²² and the generalized human reconstruction Recon1.³⁴ These models have 453, 1,008, and 2,473 active reactions respectively, and were sampled for 3·10⁴, 7·10⁴, 3·10⁵ steps respectively. As an initial step in this validation, MCS outputs of four algorithm formulations (mfACHR, mfACHR parallel, gpSampler, and gpSampler parallel) were compared, and all four formulations were shown to converge to similar steady states (supplemental information).

Next, convergence speed was assessed by computational time and number of algorithm steps. Convergence based on number of steps was measured as the percentage of reactions at any given point with a Kullback-Leibler divergence (KLD) of sampled flux values below 0.05 of the final distribution. KLD represents the expected logarithmic difference between two probability distributions, and it has been previously used with a similarity threshold of 0.05 to compare sets of sampled flux distributions in metabolic models.³¹ The four tested formulations showed nearly identical conversion curves when considering the number of steps taken (Fig. 2). When considering computational times, mfACHR performed significantly better than gpSampler when both methods were performed without parallelization. When considering parallelization, mfACHR showed very similar computational times in the platelet model, slightly better times in the RBC model, and significantly better times in Recon1. Differences in computational time can be partially attributed to the fact that matrix operations performed by mfACHR are automatically parallelized in MATLAB, while the for loops performed by gpSampler are not. This allows for mfACHR to perform significantly faster than gpSampler even when the latter is performed with parallelization, and explains the low relative increase in efficiency when explicit parallelization is implemented in mfACHR. Overall, mfACHR showed consistently faster computational times when compared to gpSampler, often in the order of hours, while converging at the same speed in terms of number of algorithm steps.

Fig. 2. Conversion speed of mfACHR and gpSampler.

(Top) Percentage of reactions in the model with a KLD below 0.05 when compared to the final set of sampled points. (Bottom) Computational running time per number of algorithm steps.

Cancer Cell Models

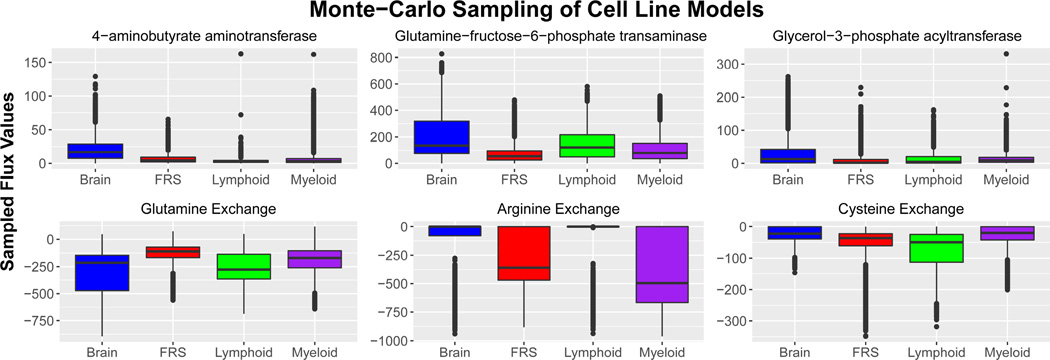
Following the validation of both algorithms, a series of cell-line specific models were generated using CORDA2 and sampled using mfACHR, as described in the methods section. Twenty-six of the cancer metabolic models were combined into four tissue categories as presented in the HPA: myeloid, lymphoid, brain, and female reproductive system (FRS) cancer cell lines. These cancer types were chosen since they had the most number of cell lines. We then identified metabolic reactions that have significantly different sampled flux distributions between the four cancer categories (Fig. 3). MCS of CORDA models previously highlighted metabolic differences between healthy and cancerous tissues.²³ That is, using CORDA we correlated high sampled flux values with metabolic pathways known to take place in healthy or cancerous phenotypes. Analogously, in this study we demonstrate that mfACHR sampling of CORDA2 models generated using HPA expression data can also highlight metabolic characteristics between different cancer categories. These characteristics include:

Fig. 3. MCS results.

Sampled flux values for six different reactions across four model categories. Boxplots represent combined flux values for a particular reaction in all models in that cancer category. For exchange reactions, negative values represent uptake of the particular metabolite, while positive values represent secretion. Colored boxes represent values within the interquartile range (IQR), ranging from the 25^th to the 75^th percentile. Horizontal line represented the median value (50^th percentile), and vertical lines indicate values within 1.5 IQR of the 25^th and 75^th percentiles. Outliers are represented by dots.

Brain tumors produce high levels of triglyceride

Lipid synthesis is an important factor for cancer survival and progression, and it has been previously suggested as a therapeutic target.^37–40 However, while most cancer types divert fatty-acids predominantly towards the production of phospholipids, not triglycerides,^39,41 glioma cells have been shown to synthesize triacylglycerol at high rates for membrane complex lipids.^42,43 Glioma cells, as well as healthy astrocytes and neurons, can also produce fatty acids from ketone-bodies,^44,45 a metabolic characteristic of brain cells which can further explain the high rate of fatty acid production in glioma cells. In the MCS results presented here, brain tumors present a significantly higher ux through glycerol-3-phosphate acyltransferase (Fig. 3) and 1-acylglycerol-3-phosphate O-acyltransferase, enzymes responsible for triacylglycerol synthesis.

Brain and lymphoid tumors have highly active glutamine metabolism

Glutamine plays an essential role in cancer metabolism,^46,47 and different tumors have been shown to utilize glutamine differently.⁴⁷ Brain tumors, in particular, have been shown to accumulate glutamine both in vitro and in vivo.^48,49 Glutamine metabolism has also been shown to play an important role in lymphoid tissues.⁵⁰ The role of this pathway in breast cancer, on the other hand, is not well defined, since basal but not luminal breast cancer cells show glutamine-dependence.⁵¹ In the results presented here, brain and lymphoid cell lines show high levels of glutamine uptake, while cell lines of the FRS show relatively low levels (Fig. 3).

Lymphoid tissues are cysteine dependent

While cysteine is not considered an essential amino-acid, lymphoid tumors have been shown to contain much lower levels of cystathionase, the last enzyme in the cysteine production pathway, when compared to healthy lymphoid tissues, and are dependent on cysteine for growth.⁵² Targeting cysteine transporters has also been shown to selectively target lymphoma cells,⁵³ and cysteine uptake has been associate with malignant progression in lymphoma cells.⁵⁴ In this study, lymphoid models presented much higher levels of cysteine uptake (Fig. 3).

Tumors show different levels of arginine dependence

Different types of cancer respond differently to arginine deprivation.⁵⁵ A study performed on 26 healthy and cancerous cell lines found that tumor cells are much more sensitive to arginine deprivation than healthy cells.⁵⁶ Furthermore, while premyelocytic and lymphoblastic leukaemia cell lines die in about two days of arginine deprivation, cell lines of the FRS died largely in three to four days, and glioma cell lines died in four to five days.⁵⁶ Interestingly, levels of arginine dependence presented in the study by Scott et. al.⁵⁶ correspond to sampled flux values of arginine uptake in the present study. Myeloid cancers, the most arginine dependent, were predicted to uptake the largest amounts of arginine, followed by models of the FRS, then brain tumors, the least arginine dependent. Acute myeloid leukemia tumors have also been shown to be dependent on arginine for proliferation.⁵⁷

Brain tumors were also predicted to have higher fluxes through the enzyme glutamine-fructose-6-phosphate transaminase (GF6PTA) (Fig 3), the rate limiting step in the hexosamines synthesis pathway (HSP), a nutrient sensor pathway.^58,59 When excess nutrients such as glucose and free fatty-acids are available, the HSP prevents cells from uptaking excess amounts from the bloodstream.⁶⁰ Furthermore, overweight and obese patients, which have excess amounts of nutrients in the bloodstream, are at an overall increased risk of mortality due to cancer.⁶¹ Interestingly, sampled flux values through the HSP presented here are anti-correlated with the increase in risk of mortality in cancer patients. According to a study of over 57,000 cancer patients, obese patients with brain tumors have a modest increase in mortality compared to non-obese glioma patients, while patients with cancer of the FRS have a high increase in risk, and patients with Non-Hodgkins lymphoma, multiple myeloma, and leukemia have a medium increase.⁶² Accordingly, brain tumor models in this study present high GF6PTA flux values, while tumors of the FRS present low fluxes, and lymphoid and myeloid tumors present intermediate values (Fig. 3). One possible explanation for this correlation is that higher fluxes through the HSP can prevent cells from uptaking excess amounts of nutrients, which in turn leads to a lower relative increase in malignancy. Further work should help elucidate these observations in context.^63,64

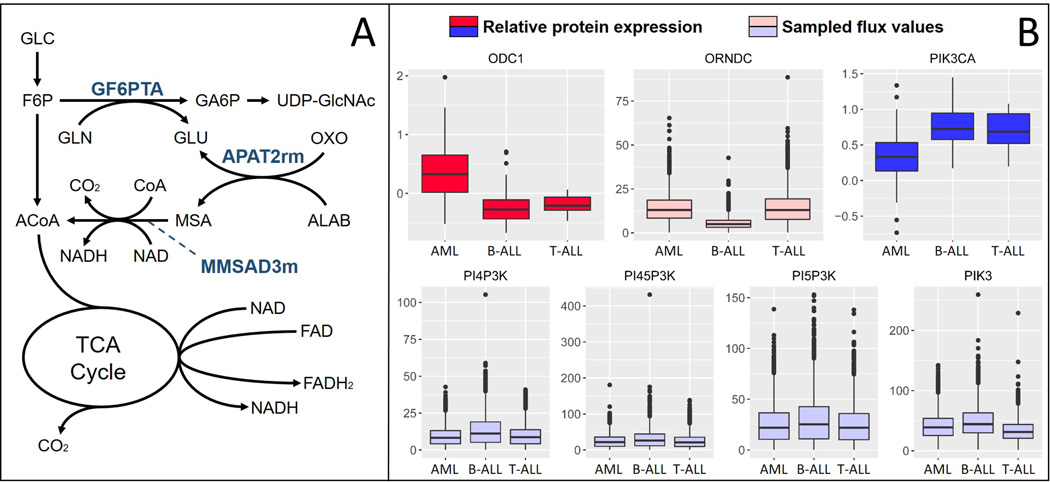
Sampled flux values also predict a high flux through the enzyme 4-aminobutyrate amino-transferase in brain cancer cells. This result is expected since this enzyme is responsible for GABA production, a pathway highly active in brain tissues. In brain cancer cells, however, this enzyme can help produce acetyl-CoA for energy production, since larger amounts of nutrients are diverted away from glycolysis and into the HSP. A diagram of this proposed mechanism is presented in Fig 4A.

Fig. 4. Model Predictions.

(A) Pathways with increased activity in brain tumors. Metabolites are glucose (GLC), fructose-6-phosphate (F6P), acetyl-CoA (ACoA), glutamine (GLN), glutamate (GLU), glucosamine-6-phosphate (GA6P), Uridine diphosphate N-acetylglucosamine (UDP-GlcNAc), oxoglutarate (OXO), beta-alanine (ALAB), and malonate semialdehyde (MSA). (B) Relative protein expression and sampled flux values for proteins differentially expressed between AML and ALL pediatric patients. ODC1 participates in the reaction Ornithine Decarboxylase (ORNDC), and PIK3CA participates in reactions PI4P3K, PI45P3K, PI5P3K, and PIK3. All reactions are labeled as in the BiGG database.⁶⁵

Primary pediatric leukemia models

We next analyzed sampled flux values in three different types of leukemia blood sample models (AML, T-ALL, and B-ALL) to clinical proteomics data collected from 168 pediatric leukemia patients as described in the methods section. Seven proteins were present both in the leukemia blood sample models and the clinical dataset, of which two were significantly differentially expressed between AML and ALL patients. The relative protein expression of these two proteins, along with the sampled flux values of reactions associated with these proteins, are presented in Fig 4B.

Sampled flux values follow trends that correlate with protein expression in both the B-ALL and AML models. That is, while AML patients show significantly higher expression levels of ODC1, the AML model showed significantly higher fluxes through Ornithine Decarboxylase (ORNDC), an ODC1 participating reaction, when compared to the B-ALL model. Likewise, while AML patients showed significantly lower expression of PIK3CA, the AML model also showed significantly lower sampled flux values through the PIK3CA reactions (Fig 4B). Sampled flux values between the AML and T-ALL model did not seem to match the differential protein expression, however. One possible explanation for this is the fact that there were considerably fewer T-ALL patients in the clinical dataset, and fewer T-ALL samples were used to generate the proteomics data used in the models building process (2 compared to 3 B-ALL and 4 AML). For instance, in the HPA, T-ALL ODC1 and PIK3CA protein scores are in between B-ALL and AML values, as opposed to much closer to B-ALL values like we see in the pediatric clinical data. This first example application to integrating RPPA leukemia data with metabolic pathway analysis demonstrates how CORDA2 and mfACHR can also be used to analyze clinical data and provide insight into patient-specific metabolic behaviors.

Conclusion

This work illustrates how Monte-Carlo sampling of metabolic models generated using CORDA2 can generate valuable predictions about context specific cancer metabolism. In applying these new optimized methods to different cancer systems, we show how this work goes beyond the identification of metabolic differences between healthy and cancerous tissues. It identifies differences in metabolism between different cancer types, paving the way to patient-specific metabolic models of cancer. In sum, the CORDA2 platform elucidates metabolic differences across cancers and provides valuable knowledge of context-specific metabolic behavior that can help guide future directed cancer therapies.