Abstract
Linkage maps constructed from genetic analysis of gene order and crossover frequency provide few clues to the basis of genomewide distribution of meiotic recombination, such as chromosome structure, that influences meiotic recombination. To bridge this gap, we have generated the first cytological recombination map that identifies individual autosomes in the male mouse. We prepared meiotic chromosome (synaptonemal complex [SC]) spreads from 110 mouse spermatocytes, identified each autosome by multicolor fluorescence in situ hybridization of chromosome-specific DNA libraries, and mapped >2,000 sites of recombination along individual autosomes, using immunolocalization of MLH1, a mismatch repair protein that marks crossover sites. We show that SC length is strongly correlated with crossover frequency and distribution. Although the length of most SCs corresponds to that predicted from their mitotic chromosome length rank, several SCs are longer or shorter than expected, with corresponding increases and decreases in MLH1 frequency. Although all bivalents share certain general recombination features, such as few crossovers near the centromeres and a high rate of distal recombination, individual bivalents have unique patterns of crossover distribution along their length. In addition to SC length, other, as-yet-unidentified, factors influence crossover distribution leading to hot regions on individual chromosomes, with recombination frequencies as much as six times higher than average, as well as cold spots with no recombination. By reprobing the SC spreads with genetically mapped BACs, we demonstrate a robust strategy for integrating genetic linkage and physical contig maps with mitotic and meiotic chromosome structure.
Introduction
Reciprocal recombination (crossing over) leads to chiasma formation during meiotic prophase and is crucial both mechanistically and genetically. Mechanistically, crossovers are converted into chiasmata that are necessary to hold homologues together and to assure their proper disjunction at anaphase I. Failure to do so results in nondisjunction and aneuploid progeny. Genetically, crossovers reshuffle the genes on the two homologues, a result that provides—along with mutations—genetic diversity, the fodder of selection and evolution. Recombination has been studied genetically and cytologically, with each method having advantages and disadvantages (Hassold et al. 2000). Genetic linkage studies allow genes to be ordered along chromosomes and can generate highly accurate information on genetic distance between markers. Typically, linkage analyses quantify recombination between only a few marker genes, but, more recently, studies have been performed that measure genomewide recombination (Broman and Weber 1999, 2000; Broman et al. 2002; Kong et al. 2002). However, linkage studies require well-characterized, polymorphic markers, so global linkage analysis is severely restricted when the objective is to examine recombination in inbred species, such as laboratory mice. On the other hand, cytological mapping of the numbers and positions of chiasmata along bivalents provides estimates of the global rate of recombination as well as revealing general patterns of crossing over on bivalents (Lawrie et al. 1995). However, in many mammals, chiasma mapping is difficult because diakinesis–metaphase I chromosomes are relatively condensed, making it difficult to identify individual bivalents or to estimate the physical distance between chiasmata on the same chromosome with any level of precision (e.g., Stack et al. 1989; Hassold et al. 2000).
Recently, an alternate approach for cytological crossover mapping in mammals has been developed that uses fluorescent antibody localization (FAL) of MLH1 protein on spreads of meiotic prophase chromosomes (bivalents) from spermatocytes (Anderson et al. 1999). MLH1 is a mismatch repair protein that is necessary for crossing over in mice and yeast (Baker et al. 1996; Hunter and Borts 1997). Evidence that MLH1 is involved in mammalian reciprocal recombination includes the following (Baker et al. 1996): (1) MLH1 localizes on the XY in the pseudoautosomal region of mouse spermatocytes. (2) Differences in frequency and distribution of MLH1 localization in spermatocytes versus oocytes reflect the known differences in recombination between male and female animals. (3) Although MLH1 disappears in late pachynema in males, in females it remains until diplonema occurs, and then it localizes to sites of chiasmata. (4) The patterns of MLH1 foci are consistent with positive genetic interference (Anderson et al. 1999). Although synapsis in Mlh1−/− mice appears normal, homologues fall apart later, indicating they are achiasmatic as they enter diplonema (Baker et al. 1996).
Combined with an antibody against SCP3, a protein component of the lateral elements of the synaptonemal complex (SC) that forms between bivalents during pachynema, an antibody raised against MLH1 has been used to determine the total number of crossover events per nucleus in species as diverse as mice, humans, and chickens (Baker et al. 1996; Barlow and Hultén 1998; Anderson et al. 1999; Pigozzi 2001; Lynn et al. 2002; Koehler et al. 2002; Tease et al. 2002). In addition, MLH1 foci have been used to map sites of recombination along SCs in meiotic prophase (Anderson et al. 1999). This technique provides higher resolution maps than does chiasma mapping. However, MLH1 mapping can be applied to individual chromosomes only when the bivalent can be distinguished. In various species, some—but not necessarily all—individual pachytene bivalents (SCs) can be identified, simply on the basis of their relative length and arm ratio, for example: humans (Solari 1980), tomatoes (Sherman and Stack 1995), and chickens (Pigozzi 2001). However, this approach is impossible in other species, such as the important mammalian model, the domestic mouse Mus musculus, in which the chromosomes are all acrocentric and show a continual gradation in size. This limitation can now be overcome by combining MLH1 immunolocalization with FISH of chromosome-specific sequences, a procedure applied to great effect to identify certain bivalents in SC spreads from human spermatocytes (Lynn et al. 2002) and oocytes (Tease et al. 2002). Heng et al. (2001) have demonstrated the feasibility of the identification of individual mouse bivalents in meiotic prophase.
Here, we have prepared detailed MLH1 recombination maps for all 19 autosomal bivalents of the mouse, using multicolor FISH (mFISH) of chromosome-specific DNA libraries to identify each bivalent. In addition, we have localized several genetically mapped mouse BACs to SCs, using mFISH spreads, thereby demonstrating a way of integrating the cytological (MLH1) recombination maps with genetic and physical maps. These MLH1 maps represent an important step toward interpreting meiotic recombination within the context of chromosome structure. In addition, this work demonstrates that the rapid integration of the genetic and cytological (MLH1) recombination maps in mouse and other species is a realistic goal.
Material and Methods
SC Spreads and Immunostaining
Three juvenile (20–21 d old) C57BL/6J mice (the same line analyzed by the Mouse Genome Sequencing Project) were used to prepare and immunolabel the SC spreads, as described elsewhere (Anderson et al. 1999). Complete sets of SCs in which the SCs were well separated but not obviously stretched or broken and that had ⩾19 MLH1 foci were selected for analysis. Three fluorescent images (4′, 6-diamino-2-phyenylindole [DAPI], SCP3, and MLH1) were captured for each SC set.
mFISH
After image acquisition of the immunofluorescence signals, the spermatocyte preparations were subjected to two or three rounds of denaturation and FISH. To identify each autosome, chromosome-specific painting probes (Rabbitts et al. 1995) were combinatorially labeled with fluorescein isothiocyanate (FITC)–2′-deoxyuridine 5′-triphosphate (dUTP), Cy5-dUTP (both from Amersham), or 6-carboxytetramethylrhodamine (TAMRA)-dUTP (Applied Biosystems) and were combined to form two different probe pools (table 1). The probes were fluorescently labeled by the incorporation of FITC-dUTP, Cy5-dUTP (both from Amersham), or TAMRA-dUTP (Applied Biosystems) during the PCR reaction. For labeling, the 2′-deoxythymidine 5′-triphosphate (dTTP) concentration in the PCR reaction mixture was reduced to 120 μM (2′-deoxyadenosine 5′-triphosphate [dATP], 2′-deoxycytidine 5′-triphosphate [dCTP], and 2′-deoxyguanosine 5′-triphosphate [dGTP] 160 μM each), and either 30 μM FITC-dUTP, 30 μM Cy5-dUTP (both from Amersham), or 10 μM TAMRA-dUTP was added. The painting probes were precipitated together with 20 μg of mouse Cot-1 DNA (Invitrogen/Life Technologies) and were dissolved in 15 μl of hybridization solution (50% formamide; 2× sodium saline citrate (SSC), pH 7.0; and 10% dextran sulfate).
Table 1.
Labeling Scheme for Whole-Chromosome Libraries
|
Chromosome |
|||||||||||||||||||
| Pool andStain | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 1: | |||||||||||||||||||
| FITC | X | X | X | X | X | ||||||||||||||
| Cy5 | X | X | X | X | X | ||||||||||||||
| TAMRA | X | X | X | X | X | ||||||||||||||
| 2: | |||||||||||||||||||
| FITC | X | X | X | X | |||||||||||||||
| Cy5 | X | X | X | X | |||||||||||||||
| TAMRA | X | X | X | X | |||||||||||||||
Five genetically mapped BAC clones (Osoegawa et al. 2000; Genetic and Physical Maps of the Mouse Chromosome Web site; Roswell Park Mouse Screening Project Web site) were hybridized to SC spreads in a third round of FISH, after chromosomes were identified using the two chromosome-painting hybridizations described above. The BAC DNA was labeled by nick translation with Cy5-dUTP (Invitrogen/Life Technologies). For each BAC, 400 ng of labeled DNA and 4 μg of mouse Cot-1 DNA were precipitated together and dissolved in 15 μl of hybridization solution. The BACs were mapped to mitotic metaphase chromosomes, using the same hybridization solutions and standard procedures.
To allow FAL analysis and sequential hybridizations on the same nuclei, the FISH protocol (Muller et al. 2002) was modified as follows: After imaging the antibody-labeled cells, the antifade solution was removed by washing the slides twice in 4× SCC/0.1% Tween-20 at 37°C for 15 min, and the slides were dehydrated in an alcohol series. The first round of denaturation was 7 min, and in situ hybridization was performed for 48 h at 37°C. After separate image acquisition of the three different colors of FISH signals, the next round of FISH (including antifade removal, dehydration, denaturation, and hybridization) was performed, as described above, except that the denaturation time was reduced to 2 min.
Fluorescence Microscopy, Image Acquisition, and Analysis
The location of each imaged, immunolabeled SC spread was recorded using a software-controlled automatic stage (Maerzhaeuser) so that it could be accurately relocated on the slide for mFISH. Digital images were obtained using a cooled CCD camera, Quantix series (Photometrics), coupled to a Zeiss Axioplan II microscope. Each color signal was acquired as a black-and-white image, using appropriate filter sets (Chroma Technologies), and was merged with SmartCaptureVP software (DigitalScientific).
Analysis of MLH1 Distribution on SCs
After the identity of each bivalent was determined by use of mFISH, the images of the corresponding SC spreads were analyzed for MLH1 distribution. For each SC, the position of each MLH1 focus was recorded as a relative distance (percentage of total length) from the centromere, using MicroMeasure (Reeves 2001). The centromeric end of each SC was identified by the surrounding DAPI-bright AT-rich heterochromatin. MLH1 foci were mapped if the MLH1 and SCP3 signals overlapped. A total of 110 sets were analyzed, and 70 SCs (3% of the total of 2,090 autosomal SCs) were eliminated from the analysis because of SC overlap near an MLH1 focus, possible SC stretching, or inconclusive FISH identification. To obtain an average absolute length for each identified SC, the average relative length of each SC was determined, then multiplied by the average absolute length of a complete set of mouse SCs (164.5 μm = 163.7 ÷ 0.995, to correct for rounding errors) (table 2) (Anderson et al. 1999). The relative position of each focus was multiplied by the average absolute length for the appropriate SC to obtain the absolute (micrometer) position of each focus. The data for each of the autosomal SCs were pooled and graphed in histogram form to demonstrate the pattern of MLH1 distribution for each SC. The 0.2-μm intervals used for graphing correspond to ∼3.44 Mb of DNA (calculated from the size, in megabases, of the autosomal fraction of the mouse genome; National Center for Biotechnology Information).
Table 2.
Characteristics of Autosomal SCs from Mouse Spermatocytes Compared with G-Banded Mitotic Chromosomes and MLH1 Frequency per Autosomal SC
| SCa |
||||||||
| Chromosome | No.Observed | LengthRank | Average RelativeLengthb (SD) | AbsoluteLengthc(μm) | Average RelativeLength of G-Banded Chromosomesd | % Difference from Expected RelativeLength Ratioe | Average No. of MLH1 Foci per SC (SD) | TotalMap Units(cM)f |
| 1 | 103 | 2 | 7.24 (.6) | 11.9 | 7.72 | −6 | 1.54 (.52) | 76.2 |
| 2 | 101 | 1 | 7.62 (.6) | 12.1 | 7.44 | 2 | 1.57 (.52) | 77.7 |
| 3 | 103 | 7 | 5.72 (.5) | 9.4 | 6.36 | −10 | 1.25 (.46) | 63.1 |
| 4 | 107 | 4 | 6.37 (.5) | 10.5 | 6.28 | 1 | 1.40 (.51) | 70.1 |
| 5 | 100 | 3 | 6.72 (.7) | 11.1 | 6.12 | 10 | 1.44 (.52) | 72.0 |
| 6 | 108 | 10 | 5.36 (.5) | 8.8 | 5.89 | −9 | 1.19 (.40) | 59.7 |
| 7 | 105 | 5 | 6.33 (.7) | 10.4 | 5.49 | 15 | 1.36 (.48) | 68.1 |
| 8 | 107 | 9 | 5.37 (.4) | 8.8 | 5.26 | 2 | 1.21 (.43) | 60.7 |
| 9 | 106 | 8 | 5.46 (.5) | 9 | 5.23 | 4 | 1.11 (.35) | 55.7 |
| 10 | 107 | 11 | 5.27 (.5) | 8.7 | 5.09 | 4 | 1.23 (.45) | 61.7 |
| 11 | 103 | 6 | 6.09 (.6) | 10 | 5.08 | 20 | 1.40 (.19) | 69.9 |
| 12 | 108 | 12 | 4.56 (.4) | 7.5 | 5.02 | −9 | 1.09 (.32) | 54.6 |
| 13 | 108 | 13 | 4.45 (.5) | 7.3 | 4.77 | −7 | 1.03 (.25) | 51.4 |
| 14 | 109 | 14 | 4.46 (.3) | 7.3 | 4.66 | −4 | 1.06 (.28) | 53.2 |
| 15 | 110 | 15 | 4.19 (.3) | 6.9 | 4.32 | −3 | .99 (.16) | 49.5 |
| 16 | 110 | 17 | 3.57 (.3) | 5.9 | 4.15 | −14 | 1.01 (.21) | 50.0 |
| 17 | 108 | 16 | 4.25 (.4) | 7 | 4.14 | 3 | 1.02 (.19) | 50.9 |
| 18 | 108 | 18 | 3.50 (.3) | 5.8 | 4.04 | −13 | 1.02 (.24) | 50.9 |
| 19 | 109 |
19 | 2.90 (.3) |
4.8 |
2.93 |
−1 | 1.00 (.14) |
50 |
| Total | 2,020 | 99.43 | 163.6 | 99.99 | 22.92 | 1,145.4 | ||
SCs were identified and numbered according to their mFISH staining pattern
Percent of total autosomal length.
Average relative length multiplied by 164.5 μm (= 163.7 ÷ .9943) for an average set of autosomal mouse SCs (Anderson et al. 1999). Because of rounding, the total absolute length does not sum to 163.7.
Percent of total autosomal G-banded mitotic chromosome length as measured by Lyon and Searle (1989).
Difference = [(average relative SC length ÷ average relative mitotic chromosome length)−1] × 100. The expected ratio is one, meaning that the average relative length is the same for mitotic chromosomes and SCs.
MLH1 focus (crossover) = 50 cM.
The interference distance between two foci on the same SC was calculated as a percentage of the euchromatic length of the SC, as described by Anderson et al. (1999). To convert MLH1 foci to distances in centimorgans, the number of MLH1 foci in each 0.2-μm SC interval was divided by the total number of SCs observed, then multiplied by 50 map units per MLH1 focus (one crossover = 50 cM).
The average number of MLH1 foci per 0.2-μm interval was determined for each autosomal SC in our sample. For the larger SCs, the average was about three; for the shorter SCs this number was slightly higher. To identify potential “hot” and “cold” regions of recombination, we added or subtracted one focus to identify regions of high (>4 for longer SCs, as high as 6 for the shorter SCs) and low (<2 for longer SCs and <4 for shorter SCs) recombination frequency, respectively.
Results
Identification of Autosomal SCs by mFISH
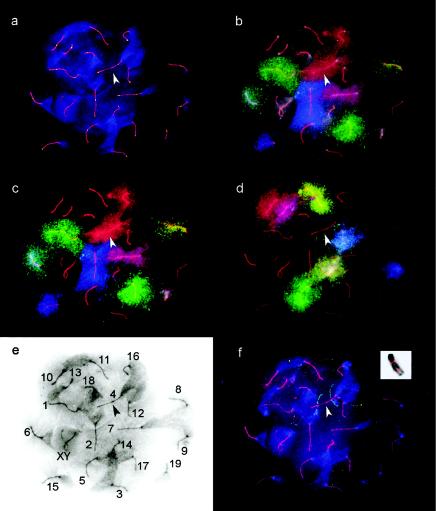
We used chromosome-specific probes (whole-chromosome libraries) labeled with FITC, Cy5, and/or TAMRA (as described in table 1) and two sequential hybridization steps to identify each SC (fig. 1). The SC number in figure 1E corresponds to the designated mitotic chromosome number. Three-color labeling allows identification of seven chromosomes at a time. To limit the sequential hybridizations to two rather than three rounds of hybridization, three pairs of chromosomes (1 and 17, 2 and 15, and 4 and 16) in pool 1 were labeled with the same color combination. In addition, chromosomes 3 and 18 were not labeled in either pool. These pairs were chosen because they could be discriminated from one another on the basis of significant length differences. This approach was validated by a third round of hybridization, using BACs that had been genetically mapped to chromosomes 3 and 4. In each case, the BACs hybridized to the longer of the two identically labeled chromosomes. Because FISH procedures interfere with immunolabeling, SC spreads were first immunolabeled with MLH1 and SCP3, and suitable spreads were photographed prior to mFISH (fig. 1A). The DAPI staining of the chromatin, as well as the retention of some SCP3 signal after mFISH, facilitated relocation of the spermatocytes and allowed precise alignment of the FISH/FAL images.
Figure 1.
Immunostaining and FISH signals of the same spermatocyte nucleus in subsequent experiments. The arrowhead identifies SC4 in all images. a, Fluorescent antibody localization of anti-SCP3 antibodies (red) and anti-MLH1-antibodies (green). The chromatin is counterstained with DAPI (blue), with the AT-rich centromeric ends staining more intensely. b, Chromosome painting with pool 1 plus DAPI. c, pool 1 without DAPI. d, pool 2 without DAPI. e, Identification of SCs on the basis of the paint signals with the SC and DAPI signals displayed in an inverted black-and-white image and with the centromeric end of each SC identified by the intense (dark) DAPI staining. f, FISH signals of two BACs: RPCI23 7-J-10, and RPCI23 219-G-3 hybridizing to the chromatin of bivalent 4 (arrow). The inset shows the mapping of the same BACs to a mitotic chromosome 4.
By splitting the probe set into two pools and leaving two chromosomes unlabeled, we significantly increased the signal-to-noise ratio and enhanced the contrast of the diffuse chromatin of the spread pachytene nuclei. The two-probe–set pool protocol also allowed us to detect nonspecific hybridization signals, since the same bivalent should not be labeled in both hybridizations. As mentioned above, we were able to reprobe the preparations a third time with BACs, with only minor degradation in signal quality.
Correspondence between Mitotic and Pachytene Chromosome (SC) Lengths
Mouse autosomes are numbered according to their mitotic lengths, from the longest chromosome, 1, to the shortest chromosome, 19 (Evans 1996). We found a good correspondence between the average relative lengths (percentage of total autosomal length) for SCs individually identified by mFISH, compared with the average relative lengths for mitotic chromosomes (table 2). A regression of these two values reveals a high r2 value, a slope near one, and an intercept near zero, as would be expected if the relative length of the autosomal chromosomes remains the same (or nearly so) in both mitotic and pachytene chromosomes (y=1.02x-0.11; r2=0.86). However, a few SCs are noticeably longer or shorter than would be expected on the basis of their relative mitotic lengths. The most extreme differences in relative lengths were recorded for chromosomes 5, 7, and 11, where the SCs are 10%–20% longer than their mitotic counterparts, and for chromosomes 3, 16, and 18, where the SCs were 10%–14% shorter than their mitotic counterparts (table 2).
Number of MLH1 Foci on Autosomal SCs
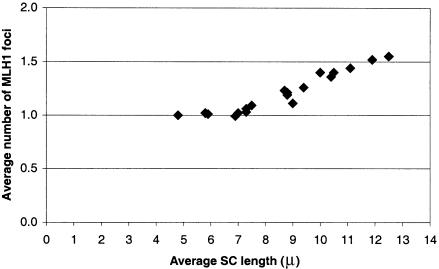
Because the average number of MLH1 foci per bivalent was not significantly different for the three mice used in the present study (P=.49), data on number and position of foci for each autosomal SC were pooled (table 2). As expected on the basis of previous studies (e.g., Anderson et al. 1999), longer SCs average more MLH1 foci than do shorter SCs. Indeed, there is an excellent relationship between average SC length and average number of MLH1 foci per SC for the longer (⩾6.9 μm) SCs (fig. 2; y=0.10x+0.30; r2=0.96), with average SC length accounting for 96% of the variation in the average number of MLH1 foci. However, this relationship does not hold for the three shortest SCs (16, 18, and 19) that average one MLH1 focus per bivalent rather than the expected frequency of less than one per bivalent. Thus, for SCs shorter than ∼6 μm, the requirement for one crossover per bivalent (necessary to assure disjunction) “trumps” the relationship between SC length and foci number.
Figure 2.
Relationship between average SC length (μm) and the average number of MLH1 foci on mouse SCs.
Because only two of the four chromatids are involved, each crossover, visualized as a MLH1 focus, is measured as 50% recombination, which translates to a 50-cM map distance. The genetic length of each SC, determined on the basis of the number of MLH1 foci, is presented in table 2. Our estimate for the total autosomal map length for the C57/BL6 male mouse is 1,145.4 cM. For the complete male genome, 50 cM must be added for the obligate crossover on the XY pair, giving a total map length of 1,195.4 cM.
Unlike Lynn et al. (2002), we did not observe a strong relationship between the total SC length for complete sets of autosomes and the total number of MLH1 foci (n=110; y=0.013x+20.7; r2=4%).
Distribution of MLH1 Foci on FISH-Identified SCs
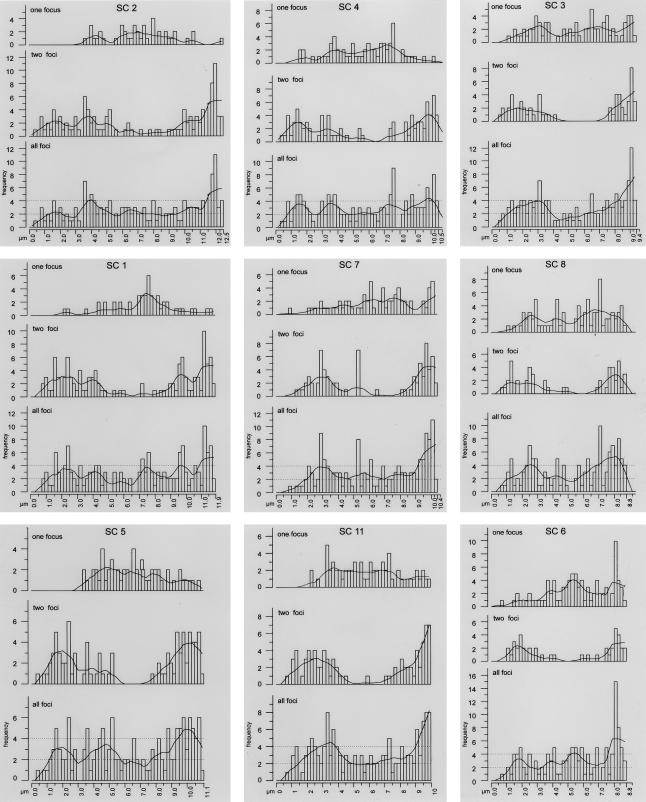
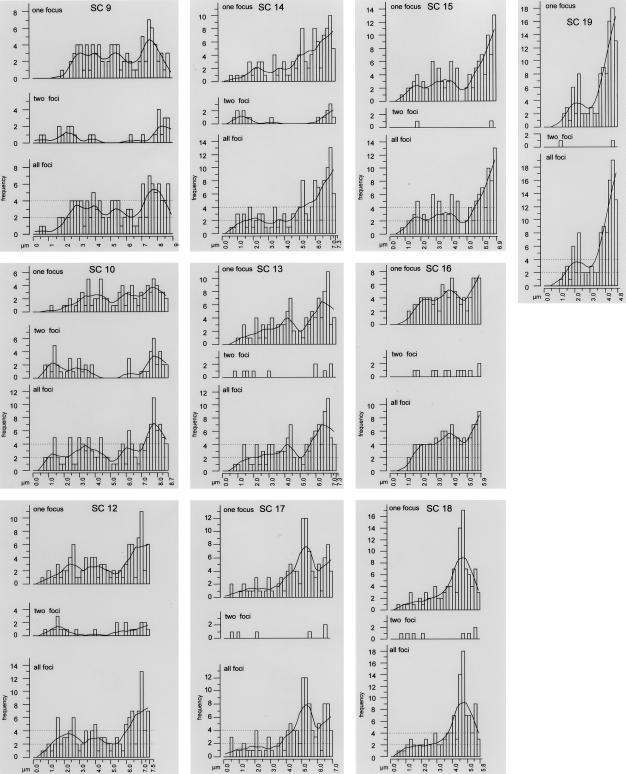
Distributions of MLH1 foci on each SC are presented in figure 3, in order of their average SC length (long to short). The graphs are all in the same orientation, with the centromeric end presented on the left and the distal end on the right. For each SC, the cumulative distribution of all foci is presented, along with the MLH1 distributions for SCs displaying one focus and distributions for SCs with two foci. No more than two foci were observed on any single SC. Superimposed over each histogram of total foci is a Lowess line that uses a mathematical function (Cleveland 1979) to smooth the data. Although this procedure effectively minimizes variation due to sampling error, it also minimizes natural variation (e.g., the high level of MLH1 foci near distal ends for almost all SCs). Nevertheless, the smoothing lines provide an easy way to compare the distribution of MLH1 foci among the various mouse SCs.
Figure 3.
Distribution of MLH1 foci along individual SCs. The X-axis represents the positions on the SCs from the centromeric end (left) to the distal telomere (right). The Y-axis indicates the frequency of MLH1 foci in each 0.2-μm interval. For each SC, three histograms are presented in a gray box. In order from top to bottom, the histograms show the results for SCs displaying a single MLH1 focus, SCs displaying two MLH1 foci, and the overall frequencies. The histograms of overall frequencies contain a smoothing curve (Lowess line), as well as thresholds indicating significantly increased or decreased recombination frequencies (dotted lines). The graphs are ordered from top to bottom, according to the SC length.
For all SCs, there is severe repression of MLH1 foci within ∼0.5–1 μm of the centromere, a region that corresponds to the large block of centromeric heterochromatin found on each mouse autosome (Evans 1989; Anderson et al. 1999). In contrast, there are many MLH1 foci near, but not necessarily at, the distal ends for all SCs (fig. 3). Despite the generally high level of recombination near distal ends, high peaks of recombination in the terminal 0.2-μm segment are most pronounced for the shorter SCs. For longer SCs, the terminal 0.2-μm segment has levels of crossing over that are about average (or lower than average for SCs 1, 5, and 7) for the SC as a whole (fig. 3). These general characteristics were noted in the first study on MLH1 localization in mouse spermatocytes (Baker et al. 1996) and have been confirmed in subsequent reports (Barlow and Hultén 1998; Anderson et al. 1999).
SC length is related not only to the average number of MLH1 foci but also to the distribution of foci (fig. 3). The six longest SCs (1, 2, 4, 5, 7, and 11) have the highest average number of MLH1 foci per SC (⩾1.36; table 2) and often have two foci. The distribution of these double foci tends to be bimodal, with one major peak near the distal end and the other peak (or sometimes two smaller peaks) nearer the centromere, whereas the distributions of single MLH1 foci are spread over a relatively broad plateau, and they “fill in” the gap located between the two peaks of double foci. Consequently, one of the two foci on doubles is usually located nearer the centromere than are singles in the one-focus group. In addition to the general patterns that are characteristic of the long SCs, distinctive patterns are also exhibited by bivalents. For example, SC 2 has a broad, low-frequency distribution of single MLH1 foci, whereas other members of this group (e.g., SCs 1 and 4) have more-prominent peaks of single MLH1 interstitial foci. It is noteworthy that SC 11, ranked sixth longest, has an MLH1 frequency and focal pattern much more characteristic of the long SCs than of the midlength cohort with which it would be placed on the basis of mitotic chromosome rank (fig. 3; table 2).
The midlength SCs (3, 6, 8, 9, 10, and 12; table 2) average 1.1–1.3 foci per SC, reflecting the decrease in bivalents with two foci. When present, the two foci exhibit a stronger bimodal distribution than do the foci of longer SCs. Although the single foci are more dispersed along the entire length of these SCs than they are in the longer group, the distribution tends toward bimodality. The proportion of foci near the centromeric heterochromatin is again higher for double than for single foci. Notice that SC 3 is ranked seventh longest of the autosomal SCs, and the distribution of MLH1 foci is typical of midlength SCs, not the longer SCs, as would be expected on the basis of mitotic metaphase rank.
The shortest SCs (13–19) have ⩽1.1 MLH1 foci per SC (table 2). These SCs rarely have two foci, but when they do, one focus is usually very proximal and one very distal. Interestingly, the distribution of single foci is bimodal for SCs 13, 15, 16, 17, and 19 but is more unimodal for SCs 14 and 18. For all of these short SCs, single foci may occur almost anywhere along their entire length, although they appear most frequently near the distal ends. SC 19 is an extreme example, in which 41% of all the foci are observed within the distal 10% (<0.5 μm) of the bivalent. These small bivalents best demonstrate the uniqueness of specific bivalents with respect to MLH1 patterns. For example, SC 18 has the most interstitial “distal” peak in the complement and has no prominent proximal peak. In contrast, SC 19 has a distinct proximal peak as well as a prominent distal peak. SC 17 has an interstitial distal peak that is more prominent than the actual distal peak, whereas the interstitial distribution of MLH1 foci for bivalent SC 16 is a fairly constant plateau.
As noted above, the relative length of some SCs is noticeably different from their relative mitotic chromosome length, and this difference is reflected in the average number of MLH1 foci for the bivalent. For example, SC 11 is 20% longer than its relative mitotic chromosome length, and the recombination rate is significantly higher (18%) than the average for mitotic chromosomes of similar size. Thus, the increased crossover rate, as measured by the frequency of MLH1 foci, corresponds very well with the increased relative length of the corresponding SC. A similar, but opposite, situation is observed for SCs 1, 3, 6, and 12, in which the relative SC lengths are shorter than those of mitotic chromosomes and in which the frequency of MLH1 foci is also reduced (table 2). Although chromosome length has long been recognized as an important determinant of recombination frequency (Mather 1937), “length” can be measured in a number of ways: genetic map length (centimorgans), DNA content (megabases), mitotic metaphase length (micrometers), or meiotic (SC) length (micrometers). Estimates of MLH1 (crossover) frequency are best predicted by SC length (r2=0.91), as compared with mitotic chromosome length (based on an average set length of 54.5 μm; r2=0.76) or chromosome size in megabases (r2=0.75). Indeed, if one disregards the three shortest chromosomes for which the recombination rate is high due to the obligatory crossover, the predictive value of SC length for recombination frequency is even higher (r2=0.96), as described above.
“Hot” and “Cold” Regions of Recombination
For each SC in figure 3, horizontal dashed lines have been inserted to indicate thresholds for regions of high and low recombination. We defined the thresholds as one crossover above or below the average number of MLH1 foci per 0.2-μm interval for each SC (see “Material and Methods” section). Prominent interstitial peaks that greatly exceed the higher threshold level occur on SCs 4, 7, 8, 11, and 17, and regions of lower recombinational activity are located on SCs 1, 4, 5, 10, and 11. Cold regions without any crossovers were observed on SCs 4, 5, and 15. Since these regions are flanked by relatively hot regions, it is likely that these represent true cold regions and are not simply due to statistical sampling artifacts. According to our maps, the hottest regions of the male mouse genome are the distal, subtelomeric regions of chromosomes 18 and 19 with recombination frequencies as much as 6.2-fold higher than the average.
Crossover Interference
When two foci are present on the same SC, they are separated by a sizeable proportion of the SC, a result suggestive of interference between the foci. We limited our analysis of interference to SCs 1–12 that had ⩾10 observations of SCs with two foci (table 3). Random placement of two foci on an SC leads to an expected average separation distance of ∼33% (Carpenter 1988). The average separation distance between two foci on SCs 1–12 was more than twice that distance (∼70%), indicating that MLH1 foci do indeed demonstrate positive interference. Interestingly, although the average absolute separation distance is significantly different for SCs of different lengths (P<.001), ranging from 4.4 μm for SC 12 to 7.6 μm for SC 2, the average relative separation distance (as a percentage of euchromatic arm length) is not significantly different between these SCs (average for SCs 1–12 = 70%; ANOVA, P=.09). The minimum separation distance between two MLH1 foci was observed for SC 7, and the two foci were only 0.34 μm (∼5 Mb) apart. However, this close proximity was rare, with separations of several microns being more common. These results are similar to those previously reported for mice (Anderson et al. 1999) and organisms as taxonomically diverse as tomatoes and birds (Sherman and Stack 1995; Pigozzi and Solari 1999; Pigozzi 2001).
Table 3.
Distance between Two Foci on the Same SC
|
Mean Distancebetween Foci (SD) |
||
| Chromosome(No. of SCs Observed) | % Euchromatic SCa | Micrometersb |
| 1 (55) | 68.6 (12.5) | 7.5 (1.4) |
| 2 (57) | 68.7 (16.4) | 7.6 (1.8) |
| 3 (28) | 77.4 (14.3) | 6.5 (1.2) |
| 4 (44) | 72.9 (18.1) | 6.9 (1.7) |
| 5 (45) | 70.3 (12.6) | 7.1 (1.3) |
| 6 (21) | 73.4 (14.7) | 5.7 (1.1) |
| 7 (38) | 63.2 (18.8) | 5.9 (1.8) |
| 8 (24) | 72.3 (15.5) | 5.7 (1.2) |
| 9 (13) | 71.9 (19.3) | 5.7 (1.6) |
| 10 (26) | 72.5 (16.3) | 5.6 (1.3) |
| 11 (41) | 70.9 (15.2) | 6.4 (1.4) |
| 12 (11) | 66.9 (24.8) | 4.4 (1.6) |
| 13 (5) | 76.0 (17.4) | 4.8 (1.1) |
| 14 (8) | 84.4 (13.5) | 5.3 (.9) |
| 15 (1) | 81.0 | 4.8 |
| 16 (3) | 82.3 (15.3) | 3.2 (.8) |
| 17 (3) | 82.3 (15.3) | 4.9 (.9) |
| 18 (4) | 79.8 (19.1) | 3.8 (.9) |
| 19 (1) | 90.0 | 3.4 |
Average relative distances between two foci for SCs 1–12 that have >10 observations each are not significantly different from one another, by ANOVA test (P=.09).
Significantly different, by ANOVA test (P<.001).
Use of BACS to Anchor the Maps
We determined the location of five genetically mapped BAC clones that were used as FISH probes on spread SCs and on mitotic metaphase chromosomes. Unlike the dotlike hybridization pattern of BACs on mitotic chromosomes (fig. 1F [insert]), the BACs that were hybridized to SC spreads produced fine threadlike signals, originating from the SC and extending approximately perpendicularly to the SC in both directions (fig. 1F). Because we observed only two threadlike signals per SC, the BAC signals most likely represent homologous chromatin loops in which the sister chromatids have not separated. These signals could be mapped quite accurate ly, since the loops were attached at their bases to the SC. The mapping precision is reflected in the lower standard deviations of the measurements of BAC signals on SCs compared with those on mitotic chromosomes (table 4). The relative positions of the BACs on SCs compared with those on mitotic chromosomes differ by 1%–7% for SC/chromosome 3 and by 11% for SC/chromosome 4. Thus, the position of a BAC on a mitotic chromosome does not necessarily match the position of the same BAC on a meiotic chromosome. Using MLH1 distributions and the hybridization location for each BAC, we estimated the linkage map position of each BAC (table 4). The linkage map positions that are estimated using BAC locations differ from the sex-averaged genetic map (Dietrich et al. 1996) by ⩽4 cM for SC 3 and by 8–11 cM for SC 4.
Table 4.
Position of Five Genetically Mapped BACs on Mitotic Compared with Meiotic (SCs) Chromosomes and the Predicted Linkage Map Assignment of the BACs on the Basis of their Position on SCs[Note]
|
% Relative Position (SD)a |
Linkage Map Position(cM from Centromere) |
||||
| BAC/Genetic Marker | Chromosome | SC Bivalent | Mitotic Chromosome | Genetic Map | Cytogenetic (MLH1) Mapb |
| 148-K-05/X97281 | 3 | 41 (2) | 47 (3) | 25 | 26 |
| 173-A-23/X91825 | 3 | 62 (2) | 63 (5) | 34 | 32 |
| 185-B-08/X58636 | 3 | 81 | 88 (1) | 45 | 41 |
| 7-J-10/MT3489 | 4 | 27 (3) | 38 (3) | 23 | 15 |
| 219-G-3/MT2557 | 4 | 74 (3) | 85 (4) | 59 | 48 |
Note.— The genetically characterized BAC information is from the Roswell Park Mouse Screening Project Web site. Linked genetic markers and centiMorgan locations are from the Genetic and Physical Maps of the Mouse Chromosome Web site.
Percent length from centromere (n=10 for all BACs except 185-B-08, in which n=1 for SC spreads).
BAC position on SC was used to estimate linkage map (cM) position on the basis of MLH1 distribution.
Discussion
We have used chromosome-specific FISH probes to identify individual meiotic bivalents (fig. 1; table 1) and to generate MLH1 (recombination) maps for each male mouse autosome (fig. 3). The utility of such maps depends on our ability to unequivocally identify each bivalent in a chromosome spread and on the suitability of MLH1 foci as indicators of meiotic recombination. In the first instance, the chromosome-specific FISH probes that we used were the same as those used by Rabbitts et al. (1995), who verified their specificity by use of chromosome banding and Robertsonian translocations. Only spreads in which all chromosomes could be unambiguously identified by FISH were used to prepare the MLH1 cytological maps. Poor spreads (by either FISH or MLH1 labeling criteria) were not used to generate the recombination map. Because it is unlikely that such cells have distinctly different recombination patterns, there is no reason to presume that their exclusion should have any impact on the MLH1 recombination maps presented here. In the second instance, prior analysis of MLH1 protein in mammals and yeast indicates that it marks crossover sites (Baker et al. 1996; Hunter and Borts 1997; Barlow and Hulten 1998; Anderson et al. 1999; Lynn et al. 2002; Tease et al. 2002), and our results regarding the frequency and distribution of MLH1 foci, as well as interference between two foci on the same SC, reinforce this conclusion. In addition, our estimated total map length of 1,195.4 cM for male mice is in good agreement with the estimated 1163.5-cM map based on chiasma counts for mouse spermatocytes (Lawrie et al. 1995). Both cytological maps are somewhat shorter than two genetic linkage maps based on molecular markers (1,361.2 cM [Dietrich et al. 1996] and 1,530 cM [Blake et al. 2002]). Although the overall correspondence of the cytological and linkage map lengths is good, the differences can be much greater when individual chromosomes are compared (see Kong et al. [2002] for discussion). These discrepancies could be due to a number of factors. One possibility is that the number of MLH1 foci is underestimated. Such underestimates would arise if some MLH1 protein was lost during the spreading procedure or was not accessible to antibodies, or if nuclei were selected in which the process involving MLH1 was just beginning or concluding and this process was asynchronous within the nucleus. However, it seems unlikely that these events, if they occurred at all, have significantly affected the map length, because the MLH1 map is actually longer than that predicted on the basis of chiasma counts (probably because two close crossovers are easier to detect as separate MLH1 foci than as two distinct chiasmata). The other alternative is that the genetic linkage maps are overestimating the amount of recombination. It is well known that errors in marker order can significantly inflate the size of the genetic linkage map (Lincoln and Lander 1992; Lynn et al. 2000; King et al. 2002; Kong et al. 2002;). In addition, genetic linkage maps in mice are sex averaged, and females have higher recombination rates than males (Dietrich et al. 1996; Broman et al. 2002). To obtain enough polymorphisms for mapping, linkage maps often utilize hybrids derived from crosses, between different inbred strains or between different subspecies of mice, that may also inflate crossing-over frequency in comparison with the inbred line that we assayed. Given that King et al. (2002) demonstrated a 1:1 correspondence between chiasmata and molecular linkage maps when the same plant population was used for both assays, it seems most likely that differences in techniques and assay populations account for much of the difference in the mouse cytological and linkage maps.
MLH1 recombination studies similar to ours have been reported recently for humans in which one or two, but not all, meiotic chromosomes were identified using chromosome-specific FISH probes (Lynn et al. 2002; Tease et al. 2002). Here, we have extended this approach to map recombination on each individually identified autosome from the male mouse. Earlier cytological studies of recombination in male mice (Lawrie et al. 1995; Anderson et al. 1999) were not able to unequivocally identify individual autosomes. In spite of this limitation, both of these earlier studies demonstrated a general dependence of crossing over on meiotic chromosome length and showed that certain recombination traits are common to all autosomal bivalents in mouse spermatocytes. These features include a high level of distal recombination (commonly observed in many male eutherian mammals) and a deficit of recombination near the centromeres (probably due, in large part, to the presence of pericentric heterochromatin) (Stack 1984; John and King 1985). Our results verify the findings from these and other earlier studies (Nachman and Churchhill 1996). In addition, we show that each chromosome has a distinct MLH1 distribution pattern (fig. 3). What factors might account for these distinct crossover patterns?
One major influence on the frequency and distribution of MLH1 foci is SC length (fig. 2; fig. 3). We found that, among three different measures of bivalent size, SC length is by far the best predictor of recombination rate and is superior, in this regard, to amount of DNA (megabases) or mitotic length (micrometers). This result accords well with the recent work of Lynn et al. (2002). Comparing two pairs of human bivalents that differed either in genetic (centimorgans) or physical (megabases) length, they showed that SC length was more closely correlated with genetic rather than with physical length. In addition, they reported a good correspondence between total SC length and the total number of MLH1 foci in complete sets from human males as well as from male and female mice (Lynn et al. 2002). In contrast, we did not observe such a relationship for the three male mice we examined. However, in many mammalian species, including mice, overall autosomal SC lengths decrease during pachytene (Moses et al. 1977), potentially obscuring any relationship between total MLH1 foci numbers and total SC set length. Any change in absolute SC length would be predicted to have little, if any, effect on our MLH1 mapping results, because relative SC lengths within a nucleus are maintained throughout pachytene (Moses et al. 1977 and results of the present study). The high reproducibility and small standard deviation we observed in the BAC localizations also indicate that relative length positions of SCs are maintained during pachynema.
In general, we found SC length to be well correlated with mitotic length when chromosomes are compared on a relative (percentage of total SC or chromosome length) basis (table 2). However, certain SCs were notably longer (5, 7, and 11) or shorter (3, 16, and 18) than would be predicted on the basis of their relative mitotic positions. Discrepancies between the meiotic and mitotic mouse karyotypes have also been reported by Heng et al. (2001). Observations of such deviations are not new. For example, Luciani et al. (1975) compared mitotic and meiotic chromosomes from humans and found that certain bivalents (16, 17, and 19) that have few chromomeres (G bands) were longer than other bivalents in the complement. Using a microspreading technique similar to that used in the present study, Solari (1980) found that these same human bivalents in spermatocytes had significantly higher relative lengths at meiosis than at mitosis, strongly suggesting that their shift in relative length is a general property of these prophase chromosomes and not a fixation artifact. Similar changes in relative meiotic versus mitotic chromosome lengths have been noted for individual chromosomes in other mammalian species, including the Chinese hamster (Pathak et al. 1976; Moses et al. 1977), and studies in mice and/or humans have shown that R-band chromatin is overrepresented in SC length compared with G-band chromatin and heterochromatin (Luciani et al. 1975, 1988; Solari 1980; Stack 1984; Holmquist 1992). Consistent with these conclusions, the differences in BAC locations on mitotic and meiotic chromosomes in the present study also indicate that chromatin is differentially packaged in meiotic prophase compared with mitotic metaphase chromosomes. Although it remains to be determined whether the final condensation of meiotic chromosomes during diplonema and diakinesis results in a restoration of mitotic metaphase ranking, the observation of a similar ranking of the mouse X chromosome in female mitotic and meiotic metaphase (Hultén et al. 1995) suggests that this is likely to be the case.
Other studies indicate that recombination occurs preferentially in R bands that are characterized by a higher density of genes and less chromatin compaction than are found in G bands (for discussion, see Holmquist 1992). More recently, Kong et al. (2002) have observed that the intensity of G-band staining is inversely related to recombination rate in humans. On the basis of these findings, we would predict that chromosomes with higher fractions of R bands would have longer SCs and higher levels of recombination than would be expected simply on the basis of their relative mitotic length. Indeed, we observed that mouse SC11 follows this pattern. It has the highest fraction of R bands (57%) of all mouse chromosomes, shows the greatest difference between its observed and expected SC length, and has a high rate of recombination compared with other meiotic chromosomes of similar size (table 2). In contrast, an SC with a high fraction of G bands (such as chromosome 6, which has the highest fraction of G bands of all mouse chromosomes) would be expected to have a relatively short SC and a lower rate of recombination, as we observed for SC 6 (table 2). Since R bands are “gene rich” compared with G bands, these observations are also consistent with studies in yeast that have found that recombination is preferentially initiated in promoter regions (Nicolas 1998) and within chromatin with a more open chromatin configuration (Wu and Lichten 1994, 1995). Thus, differences in proportion of R-band chromatin and G-band chromatin content may account for some, if not all, of the differences in overall recombination rate as well as the unique recombination patterns that we note among bivalents.
Given the preceding considerations, we had expected to detect similarities between the MLH1 crossover map distributions and the R-banding patterns of mitotic chromosomes (Evans 1996). However, most likely because of the differential contribution of R-band and G-band chromatin to SC length, we did not observe such a correlation, with one possible exception. Although recombination is high “near” chromosome ends, we find that the “near terminal” MLH1 peak may occur in any of the last four 0.2-μm intervals (fig. 3). Combining this observation with the likely preference for recombination in R-band chromatin (Holmquist 1992), one can predict that those bivalents with terminal R bands will have extreme distal MLH1 peaks. Five mouse chromosomes (4, 7, 11, 14, and 16) have terminal R bands, and two of these (11 and 16) have the distal MLH1 peak in the terminal 0.2-μm interval, with the others having peaks in the penultimate (subterminal) 0.2-μm interval. However, MLH1 also peaks in the most terminal 0.2-μm interval of two other bivalents (9 and 15) that do not have a terminal R band, suggesting that another unidentified factor may exert a powerful influence on near-terminal recombination. It is also worth noting that the presence of several large G bands in the distal third of short chromosomes, such as 14 and 16, does not seem to significantly depress the genomewide tendency for distal recombination.
Although it is tempting to use conventional terminology and to call the peaks and valleys of recombination in our maps “hot-” and “coldspots,” it is important to remember that hotspots have usually been defined genetically and that they span only a few kilobases of DNA (Schneider et al. 2002). In contrast, the cytological regions we have identified (fig. 3) are chromosomal regions encompassing several megabases. To emphasize the distinction between these differentially defined regions, we have retained the term “hotspot” for genetically defined areas in which the recombination rate per kilobase is high and have used the term “hot region” to designate cytological segments in which recombination, as measured by MLH1 frequency, is high along a bivalent. In the case of subtelomeric sequences, molecularly characterized hotspots of high recombinational activity in the human genome (Wintle et al. 1997; Badge et al. 2000) do seem to correspond in intensity to these larger cytologically defined hot regions. According to our maps, the hottest regions of the male mouse genome are the subtelomeric regions of chromosomes 18 and 19, with recombination frequencies as much as 6.2-fold higher than the average and in a range similar to that of the “hot spot” in the E-beta region of the mouse histocompatibility antigen region (equivalent to the human MHC locus) characterized by molecular studies (Lafuse and David 1986; Shenkar et al. 1991).
Another factor that influences MLH1 frequency and distribution is interference. In a study reported elsewhere, we demonstrated that two MLH1 foci on the same SC show interference, as would be expected if they mark crossover sites (Anderson et al. 1999). As discussed above, the average relative separation (interference) distance between two foci is ∼70% of the SC length, even for mouse SCs of different lengths. In comparison, interference between two crossovers on SCs of different lengths is quite variable when considered on an absolute (micrometer) length scale (table 4). To illustrate this point, consider that one would predict an average of more than two crossovers for the longest SC (SC 2), on the basis of the average interference distance between two foci for shorter bivalents SCs 8–10 (12.1 μm total length for SC 2 divided by the average separation distance of ∼5.7 μm for SCs 8–10 = 2.1 crossovers per SC 2). In actuality, SC 2 averages only 1.6 MLH1 foci, with an average separation distance of 7.6 μm between two foci. In other words, for a given length of SC interval (e.g., 6 μm), large chromosomes are less likely to have double crossovers, and they thus appear to have higher levels of interference than do smaller chromosomes. Similar results have been reported for yeast chromosomes of different sizes when intervals of the same physical distance (kilobase) were considered (Kaback et al. 1999). In comparison, Broman et al. (2002) examined double crossovers on all autosomes in the male mouse and reported that smaller chromosomes have higher levels of interference than do larger chromosomes. Like Broman et al. (2002), we did not observe many double crossovers on short chromosomes (table 4), but, when we did, the short chromosomes tended to have two foci separated by a larger percentage of the chromosome length (but usually a shorter absolute length) compared with longer chromosomes. These results demonstrate the difficulty of defining and assessing interference, and they emphasize the need for more data to be collected using a variety of techniques. For example, we do not yet know the significance of our and other’s (Sherman and Stack 1995; Pigozzi and Solari 1999) observations that SCs of different lengths have similar average relative distances between two foci. Not surprisingly, the mechanism of interference is far from understood, although current evidence suggests that the SC is somehow involved (e.g., Roeder 1997; Zickler and Kleckner 1999).
The tendency toward a bimodal distribution pattern of single foci for certain SCs, especially the midlength SCs 6, 9, and 12 (fig. 3), suggests that factors other than interference may also play important roles in determining all crossover sites, irrespective of whether they are singles or doubles (e.g., Petes 2001). As proposed by others (see Jones 1984; Stack and Anderson 1986; Zickler et al. 1992; Anderson et al. 1999), we suggest that the distribution of MLH1 foci is also related to the temporal order of synapsis, with the regions that synapse first becoming preferred sites for crossovers.
MLH1 recombination maps provide an excellent opportunity to examine the various factors involved in regulating recombination distribution. By probing meiotic preparations with BACs of known genetic and cytogenetic “addresses,” it will be possible to map regions of hot and cold recombinational activity to pre-existing genetic, physical (chromosomal), and DNA sequence maps. The mapping of a large number of BACs will anchor the maps and allow the identification of cytological as well as molecular parameters that influence recombination. Areas of special interest include the influence of band types, their role in the differential compaction of meiotic chromosomes, and their relationship (if any) to hot and cold regions of recombination. Here, we have demonstrated the feasibility of this approach in the mouse.
A major advantage of the approach of the present study is its applicability to other species. MLH1 immunolocalization has been demonstrated in mammals and birds (e.g., Barlow and Hulten 1998; Anderson et al. 1999; Pigozzi 2001), and chromosome libraries are now available for ∼20 mammalian species and for the chicken (for review, see Wienberg et al. 2000). Therefore, the combination of MLH1 detection and chromosome painting should facilitate the generation of cytological recombination maps for many important model organisms, as well as for species for which genetic mapping data are currently unavailable. More specifically for humans, significant advances have already been made in mapping BACs on mitotic chromosomes (Korenberg et al. 1999). Given the completion of the human genome sequence, the availability of chromosome-specific FISH paints and genetically mapped BACs, and the successful MLH1 localization in humans (Barlow and Hultén 1998; Lynn et al. 2002), the complete integration of the human genome sequence with both mitotic and meiotic chromosome structure is a reasonable goal for the near future.
Acknowledgments
The authors would like to thank Dr. Malcolm Ferguson Smith, for the mouse chromosome paint libraries; Katherine Uhl, for technical support; and Adelle Hack and Jaime Austin, for assistance in measuring. We also thank Drs. Roscoe Stanyon and Steve Stack for helpful advice and discussions. This work was supported by National Institutes of Health grant R01-GM55300 (to T.A.).
Electronic-Database Information
URLs for data presented herein are as follows:
- Genetic and Physical Maps of the Mouse Chromosome, http://www-genome.wi.mit.edu/cgi-bin/mouse/index/ (for BAC clones)
- Genome Sequencing, National Center for Biotechnology Information, http://www.ncbi.nlm.nih.gov/genome/seq/
- Roswell Park Mouse Screening Project, http://genomics.roswellpark.org/mouse/overview.html (for BAC clones)
References
- Anderson LK, Reeves A, Webb LM, Ashley T (1999) Distribution of crossovers on mouse chromosomes using immunofluorescent localization of MLH1 protein. Genetics 151:1569–1579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badge RM, Yardley J, Jeffreys AJ, Armour JAL (2000) Crossover breakpoint mapping identifies a subtelomeric hotspot for male meiotic recombination. Hum Mol Genet 9:1239–1244 [DOI] [PubMed] [Google Scholar]
- Baker SM, Plug AW, Prolla TA, Bronner CE, Harris AC, Yao X, Christie D-M, Monell C, Arnheim N, Bradley A, Ashley T, Liskay RM (1996) Involvement of mouse Mlh1 in DNA mismatch repair and meiotic crossing over. Nat Genet 13:336–342 [DOI] [PubMed] [Google Scholar]
- Barlow AL, Hultén MA (1998) Crossing over analysis at pachytene in man. Eur J Hum Genet 6:350–358 [DOI] [PubMed] [Google Scholar]
- Blake JA, Richardson JE, Bult CJ, Kadin JA, Eppig JT, Group at MGDB (2002) The Mouse Genome Database (MGD): the model organism database for the laboratory mouse. Nucleic Acids Res 30:113–115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broman KW, Rowe LB, Churchill GA, Paigen K (2002) Crossover interference in the mouse. Genetics 160:1123–1131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broman KW, Weber JL (1999) Long homozygous chromosomal segments in reference families from the Centre d' Etude du Polymorphisme Humain. Am J Hum Genet 65:1493–1500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- ——— (2000) Characterization of human crossover interference. Am J Hum Genet 66:1911–1926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter ATC (1988) Thoughts on recombination nodules, meiotic recombination, and chiasmata. In: Kucherlapati R, Smith GR (eds) Genetic recombination. American Society of Microbiology, Washington, DC, pp 529–548 [Google Scholar]
- Cleveland WS (1979) Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc 74:829–836 [Google Scholar]
- Dietrich WF, Miller J, Steen R, Merchant MA, Damron-Boles D, Husain Z, Dredge R, Daly MJ, Ingalls KA, O'Connor TJ (1996) A comprehensive genetic map of the mouse genome. Nature 380:149–152 [DOI] [PubMed] [Google Scholar]
- Evans EP (1989) Standard normal chromosomes. In: Lyon MP, Searle AG (eds) Genetic variants and strains of the laboratory mouse. Oxford University Press, Oxford, pp 576–578 [Google Scholar]
- Evans EP (1996) Standard idiogram. In: Lyon MF, Rastan S, Brown DM (eds) Genetic variants and strains of the laboratory mouse. Vol 2. Oxford University Press, London, p 1446 [Google Scholar]
- Hassold T, Sherman S, Hunt P (2000) Counting cross-overs: characterizing meiotic recombination in mammals. Hum Mol Genet 9:2409–2419 [DOI] [PubMed] [Google Scholar]
- Heng HH, Liu G, Lu W, Bremer S, Ye CJ, Hughes M, Moens PB (2001) Spectral karyotyping (SKY) of mouse meiotic chromosomes. Genome 44:293–298 [DOI] [PubMed] [Google Scholar]
- Holmquist G (1992) Chromosome bands, their chromatin flavors, and their functional features. Am J Hum Genet 51:17–37 [PMC free article] [PubMed] [Google Scholar]
- Hultén M, Tease C, Lawrie NM (1995) Chiasma-based genetic map of the mouse X chromosome. Chromosoma 104:223–227 [DOI] [PubMed] [Google Scholar]
- Hunter N, Borts RH (1997) Mlh1 is unique among mismatch repair proteins in its ability to promote crossing-over during meiosis. Genes Dev 11:1573–1582 [DOI] [PubMed] [Google Scholar]
- John B, King M (1985) The inter-relationship between heterochromatin distribution and chiasma distribution. Genetica 66:183–194 [Google Scholar]
- Jones GH (1984) The control of chiasma distribution. In: Evans C, Dickinson H (eds) Controlling events in meiosis. The Company of Biologist, Cambridge, United Kingdom, pp 293–320 [Google Scholar]
- Kaback DB, Barber D, Mahon J, Lamb J, You J (1999) Chromosome size–dependent control of meiotic reciprocal recombination in Saccharomyces cerevisiae: the role of crossover interference. Genetics 152:1475–1486 [DOI] [PMC free article] [PubMed] [Google Scholar]
- King J, Roberts IP, Kearsey MJ, Thomas HM, Jones RN, Huang L, Armstead IP, Morgan WG, King IP (2002) A demonstration of a 1:1 correspondence between chiasma frequency and recombination using a Lolium perenne/Festuca pratensis substitution. Genetics 161:307–314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehler KE, Cherry JP, Lynn A, Hunt PA, Hassold TJ (2002) Genetic control of mammalian meiotic recombination. I. Variation in exchange frequencies among males from inbred mouse strains. Genetics 162:297–306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong A, Gudbjartsson DE, Sainz J, Jonsdottir GM, Gudjonsson SA, Richasdsson B, Sigurdardottir S, Barnard J, Hallbeck B, Masson G, Shlien A, Palsson ST, Frigge ML, Thorgeirsson TE, Gulcher JR, Stefansson K (2002) A high-resolution recombination map of the human genome. Nat Genet 31:241–247 [DOI] [PubMed] [Google Scholar]
- Korenberg JR, Chen X-N, Devon KL, Noya D, Oster-Granite ML, Birren BW (1999) Mouse molecular cytogenetic resource: 157 BACs link the chromosomal and genetic maps. Genome Res 9:514–523 [PMC free article] [PubMed] [Google Scholar]
- Lafuse WP, David CS (1986) Recombination hot spots within the I region of the mouse H-2 complex map to the Eβ and Eα genes. Immunogenetics 24:352–360 [DOI] [PubMed] [Google Scholar]
- Lawrie NM, Tease C, Hultén MA (1995) Chiasma frequency, distribution and interference maps of mouse autosomes. Chromosoma 140:308–314 [DOI] [PubMed] [Google Scholar]
- Lincoln SE, Lander ES (1992) Systematic detection of errors in genetic linkage data. Genomics 14:604–610 [DOI] [PubMed] [Google Scholar]
- Luciani JM, Morazzani JR, Stahl A (1975) Identification of pachytene bivalents in human male meiosis using G-banding technique. Chromosoma 52:275–282 [DOI] [PubMed] [Google Scholar]
- Luciani JM, Guichaoua MR, Cau P, Divictor B, Salagnon N (1988) Differential elongation of autosomal pachytene bivalents related to their DNA content in human spermatocytes. Chromosoma 97:19–25 [DOI] [PubMed] [Google Scholar]
- Lynn A, Kashuk C, Petersen MB, Bailey JA, Cox DR, Antonarakis SE, Chakravarti A (2000) Patterns of meiotic recombination of the long arm of human chromosome 21. Gen Res 10:1319–1332 [DOI] [PubMed] [Google Scholar]
- Lynn A, Koehler KE, Judis L, Chan ER, Cherry JP, Schwartz S, Seftel A, Hunt PA, Hassold TJ (2002) Genetic length of mammalian genomes: inter-individual variation and dependence on synaptonemal complex length. Science 296:2222–2225 [DOI] [PubMed] [Google Scholar]
- Mather K (1937) The determination of position in crossing over. II. The chromosome length-chiasma frequency relation. Cytologia 8:514–526 [Google Scholar]
- Moses MJ, Slatton GH, Gambling TM, Starmer CF (1977) Synaptonemal complex karyotyping in spermatocytes of the Chinese hamster (Cricetulus griseus). III. Quantitative evaluation. Chromosoma 60:345–375 [DOI] [PubMed] [Google Scholar]
- Muller S, Neusser M, Wienberg J (2002) Toward unlimited colors for fluorescence in situ hybridization (FISH). Chrom Res 10:223–232 [DOI] [PubMed] [Google Scholar]
- Nachman MW, Churchhill GA (1996) Heterogeneity in rates of recombination across the mouse genome. Genetics 142:537–548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolas A (1998) Relationship between transcription and initiation of meiotic recombination: toward chromatin accessibility. Proc Natl Acad Sci USA 95:87–89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osoegawa K, Tateno M, Woon PY, Frengen E, Mammoser AG, Catanese JJ, Hayashizaki Y, de Jong PJ (2000) Bacterial artificial chromosome libraries for mouse sequencing and functional analysis. Genome Res 10:116–128 [PMC free article] [PubMed] [Google Scholar]
- Pathak S, Hsu TC, Markvong A (1976) Pachytene mapping of the male Chinese hamster. Cytogenet Cell Genet 17:1–8 [DOI] [PubMed] [Google Scholar]
- Petes TD (2001) Meiotic recombination hot spots and cold spots. Nat Rev Genet 2:360–369 [DOI] [PubMed] [Google Scholar]
- Pigozzi MI (2001) Distribution of MLH1foci on the synaptonemal complexes of chicken oocytes. Cytogenet Cell Genet 95:129–133 [DOI] [PubMed] [Google Scholar]
- Pigozzi MI, Solari AJ (1999) Recombination nodule mapping and chiasmata distribution in spermatocytes of the pigeon, Columba livia. Genome 42:308–314 [DOI] [PubMed] [Google Scholar]
- Rabbitts P, Impey H, Heppell-Parton A, Langford C, Tease C, Lowe N, Bailey D, Ferguson-Smith M, Carter N (1995) Chromosome specific paints from a high resolution flow karyotype of the mouse. Nature Genet 9:369–375 [DOI] [PubMed] [Google Scholar]
- Reeves A (2001) Micromeasure: a new computer program for the collection and analysis of cytogenetic data. Genome 44:439–443 [PubMed] [Google Scholar]
- Roeder GS (1997) Meiotic chromosomes: it takes two to tango. Genes Dev 11:2600–2621 [DOI] [PubMed] [Google Scholar]
- Schneider JA, Peto TEA, Boone RA, Boyce AJ, Clegg JB (2002) Direct measurement of the male recombination fraction in the human β-globin hot spot. Hum Mol Genet 11:207–215 [DOI] [PubMed] [Google Scholar]
- Shenkar R, Shen M, Arnheim N (1991) DNase I-hypersensitive sites and transcription factor-binding motifs within the mouse EB meiotic recombination hot spot. Mol Cell Biol 11:1813–1819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman JD, Stack SM (1995) Two-dimensional spreads of synaptonemal complexes from solanaceous plants. VI. High-resolution recombination nodule map for tomato (Lycopersicon esculentum). Genetics 141:683–708 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solari AJ (1980) Synaptonemal complexes and associated structures in microspread human spermatocytes. Chromosoma 81:315–337 [DOI] [PubMed] [Google Scholar]
- Stack SM (1984) Heterochromatin, the synaptonemal complex and crossing over. J Cell Sci 71:159–176 [DOI] [PubMed] [Google Scholar]
- Stack SM, Anderson LK (1986) Two-dimensional spreads of synaptonemal complexes from solanaceous plants. II. Synapsis in Lycopersicon esculentum (tomato). Am J Bot 73:264–281 [Google Scholar]
- Stack SM, Anderson LK, Sherman JD (1989) Chiasmata and recombination nodules in Lilium longifolium. Genome 32:486–498 [Google Scholar]
- Tease C, Hartshorne M, Hultén M (2002) Patterns of meiotic recombination in human fetal oocytes. Am J Hum Genet 70:1469–1479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wienberg J, Fröenicke L, Stanyon R (2000) Insights into mammalian genome organization and evolution by molecular cytogenetics. In: Clark MS (ed) Comparative genomics. Kluver, Dordrecht, Netherlands, pp 207–244 [Google Scholar]
- Wintle RF, Nygaard TG, Herbrick JA, Kvaloy K, Cox DW (1997) Genetic polymorphism and recombination in the subtelomeric region of chromosome 14q. Genomics 40:409–414 [DOI] [PubMed] [Google Scholar]
- Wu T-C, Lichten M (1994) Meiosis-induced double-strand break sites determined by yeast chromatin structure. Science 263:515–518 [DOI] [PubMed] [Google Scholar]
- ——— (1995) Factors that affect the location and frequency of meiosis-induced double-strand breaks in Saccharomyces cerevisiae. Genetics 140:55–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zickler D, Kleckner N (1999) Meiotic chromosomes: integrating structure and function. Annu Rev Genet 33:603–754 [DOI] [PubMed] [Google Scholar]
- Zickler D, Moreau PJ, Huyn AD, Slezec AM (1992) Correlation between pairing initiation sites, recombination nodules and meiotic recombination in Sordaria macrospora. Genetics 132:135–148 [DOI] [PMC free article] [PubMed] [Google Scholar]