On Stabilizing the Variance of Dynamic Functional Brain Connectivity Time Series

Abstract

Assessment of dynamic functional brain connectivity based on functional magnetic resonance imaging (fMRI) data is an increasingly popular strategy to investigate temporal dynamics of the brain's large-scale network architecture. Current practice when deriving connectivity estimates over time is to use the Fisher transformation, which aims to stabilize the variance of correlation values that fluctuate around varying true correlation values. It is, however, unclear how well the stabilization of signal variance performed by the Fisher transformation works for each connectivity time series, when the true correlation is assumed to be fluctuating. This is of importance because many subsequent analyses either assume or perform better when the time series have stable variance or adheres to an approximate Gaussian distribution. In this article, using simulations and analysis of resting-state fMRI data, we analyze the effect of applying different variance stabilization strategies on connectivity time series. We focus our investigation on the Fisher transformation, the Box–Cox (BC) transformation and an approach that combines both transformations. Our results show that, if the intention of stabilizing the variance is to use metrics on the time series, where stable variance or a Gaussian distribution is desired (e.g., clustering), the Fisher transformation is not optimal and may even skew connectivity time series away from being Gaussian. Furthermore, we show that the suboptimal performance of the Fisher transformation can be substantially improved by including an additional BC transformation after the dynamic functional connectivity time series has been Fisher transformed.

Introduction

The idea behind dynamic functional connectivity (dFC) in functional magnetic resonance imaging (fMRI) is both simple and appealing. It builds upon the previous successes of static functional connectivity (sFC), where the covariance between two brain regions is quantified over a fixed (static) interval and an inference is made regarding their relationship. To date, sFC has been applied to many areas of the brain research, from a general understanding of the network topology of the brain (De Luca et al., 2006; Fransson, 2005; Greicius et al., 2003), task modulation (Fransson, 2006), neurodevelopment (Power et al., 2010), and clinical applications (Fox and Greicius, 2010). In the case of dFC, quantitative studies of the fluctuations of signal covariance over time offers a possibility to explore the dynamics of the brain and it has already found applications; from understanding basic brain processes such as levels of consciousness (Barttfeld et al., 2015), mind wandering (Schaefer et al., 2014), and development (Hutchison and Morton, 2015), to clinical applications such as depression (Kaiser et al., 2016) and schizophrenia (Damaraju et al., 2014; Ma et al., 2014).

dFC offers an exciting perspective, but it is not without controversy. A substantial amount of work has been devoted to the issue of the accuracy of the dFC estimates obtained by the sliding window method (Allen et al., 2014; Hindrins et al., 2015; Hutchison et al., 2013; Leonardi and De Ville, 2015; Zalesky and Breakspear, 2015) and whether the fluctuations in BOLD connectivity accurately reflect the presumed underlying neuronal dynamics (Chang et al., 2013; Magri et al., 2012; Tagliazucchi et al., 2012; Thompson et al., 2013, 2014; see also Keilholz, 2014). That being said, in this article we assume that sliding window estimates of dFC are indeed fluctuations that reflect neuronal activity. The next question that arises is how to quantify fluctuations in dFC time series in an accurate manner. In this article we want to highlight a methodological aspect of dFC analysis, which often is taken for granted in the data preprocessing pipeline, namely how to stabilize the variance of time series of covariance estimates.

A dynamic functional brain connectivity time series is usually created by estimating the connectivity (most often Pearson correlation coefficients) for multiple time points across two nodes (often voxels or regions of interest [ROIs]). The resulting connectivity time series represents the degree of connectivity that fluctuates as a function of time between the two nodes. A correlation coefficient is bound to range between −1 and 1, and its expected variance is smaller as the correlation coefficient increases. The aim of stabilizing the variance is to disassociate the variance from its mean. For example, if the sampled correlations from subjects in group A are centered around a true correlation value of ρ = 0.6, and the sampled correlations from subjects in group B are centered around a true correlation value of ρ = 0.2, one would expect the variance from group B to be larger than the variance in group A. Hence, the purpose of stabilizing the variance is to achieve estimates of variance that is unbiased from the magnitude of the true correlation. In this outlined example, the Fisher transformation performs well in terms of stabilizing the variance between groups.

However, in the case of dFC fMRI we are met with a number of circumstances that complicate matters in terms of stabilizing the variance compared with the previous example. Given the assumption that dFC reflects neuronal fluctuations in brain connectivity, (1) the dFC time series reflects fluctuating true connectivity values; (2) estimates of connectivity for neighboring time points are not independent of each other when using the sliding window method; (3) given (4), the variance will then fluctuate as the true correlation value, and it is unknown how long the true correlation dwells with different true correlation values. Together, these properties differ from the original purpose of the Fisher transformation. dFC requires stable variance across an entire time series of fluctuating values, whereas the Fisher transformation is intended for stable variance around estimates of a true correlation value, making the variance independent of their correlation magnitudes.

For clarity, the Fisher transformation is intended to be used on correlation values. However, in dFC we create a time series of correlations. Moreover, in time series analysis, an established way to transform a time series to adhere to a Gaussian distribution, a distribution with stable variance, is through a Box–Cox (BC) transformation (Box and Cox, 1964). Thus, by treating dFC connectivity values as a time series, instead of just a set of correlation values, we may indeed be able to improve on the stability of the variance in dFC data. An alternative approach would be to apply two transformations to the data, first the Fisher, to transform the correlation values, and subsequently the BC, to transform the time series.

In the neuroimaging dFC literature, the variance is often stabilized by applying the Fisher transformation to the connectivity time series (a nonexhaustive list includes: Allen et al., 2014; Barttfeld et al., 2015; Damaraju et al., 2014; Elton and Gao, 2015; Hutchison and Morton, 2015; Kaiser et al., 2016; Kucyi and Davis, 2014; Leonardi et al., 2014; Schaefer et al., 2014). Generally, there are good reasons for doing so, since a reasonably stable signal variance is required to be able to accurately quantify changes in dynamic brain functional connectivity, which often is the primary goal of the analysis. In this study, we test how the Fisher transformation, the BC transformation, and a combination of both transforms performs in terms of achieving an estimate of covariance that is unbiased by the mean correlation estimate. Furthermore, we quantify to which extent the within-time series variance is stable for the tested transformations when applied to dFC fMRI time series and quantify how Gaussian the resulting distributions are. This was done because both transformations often create approximate Gaussian distributions of the data, which has a stable variance.

Materials and Methods

Simulations

A simulation was performed to demonstrate the problem of the Fisher transformation on connectivity time series and demonstrate how the BC transformation can increase performance. First, two multivariate Gaussian distributions were created. The time series where 100,000 samples long, but fluctuated in the covariance every 100 samples. The covariance was changed every 100 samples, where the new covariance was sampled from a Gaussian distribution (μ = 0.5 and σ² = 0.1). We then make 1000 “dynamic connectivity estimates” by sliding a window 100 samples long, with no overlap between windows, and performing a correlation between the time series. This entails that we have a known covariance with a Gaussian distribution (a ground truth), which we can compare with (1) the raw correlation coefficients, (2) the Fisher-transformed correlation coefficients, (3) the BC-transformed correlation coefficients, (4) first apply a Fisher transformation, then a BC transformation to the correlation coefficients. For all distributions, the skewness and Shapiro–Wilks (SW) statistic were calculated (see Quantifying the Gaussian Distributions section).

Data and preprocessing steps

One resting-state fMRI session (6 min long; 3 Tesla, TR = 2000 msec, TE = 30 msec) from 48 healthy subjects was used in the analysis (19–31 years, 24 females). Two subjects were excluded from the analysis due to incomplete data. The fMRI data was downloaded from an online repository: the Beijing Eyes Open/Eyes Closed Dataset available at http://fcon_1000.projects.nitrc.org/indi/IndiPro.html (Liu et al., 2013). Each functional volume comprised 33 axial slices (thickness/gap = 3.5/0.7 mm, in-plane resolution = 64 × 64, FOV = 200 × 200 mm). The fMRI dataset from each individual contained three different resting-state sessions, each 6 min long (two eyes closed sessions and one eyes open session). We only used data from the eyes-open condition, which was recorded in either the second or third session (counterbalanced order with respect to the second eye-closed session). Further details regarding the scanning procedure are given in Liu et al. (2013).

fMRI data were preprocessed using MATLAB (Version 2014b, MathWorks, Inc.), with the CONN (Whitfield-Gabrieli and Nieto-Castanon, 2012) and SPM8 (Friston et al., 1995) MATLAB toolboxes. Resting-state fMRI data were realigned and then normalized to the EPI MNI template as implemented in SPM. Spatial smoothing was then applied using a Gaussian filter kernel (full width at half maximum [FWHM] = 8 mm). Additional image artifact regressors attributed to head movement (Power et al., 2012; van Dijk et al., 2012) were derived by using the ART toolbox for scrubbing (www.nitrc.org/projects/artifact_detect/). Signal contributions from white brain matter, cerebrospinal fluid (CSF) and head movement (six parameters), and the ART micromovement regressors for scrubbing, were regressed out from the data using the CompCor algorithm (Behzadi et al., 2007, five principal components removed for both white matter and CSF), as implemented in CONN. After regression, data were bandpassed between 0.008 and 0.1 Hz, as well as linearly detrended and despiked. Two hundred sixty-four ROIs (sphere with a 5 mm radius) were placed throughout the brain according to the parcellation scheme provided in Power et al. (2011) (see article for coordinates). sFC was computed by the Pearson correlation coefficient across all time points for all 34,716 unique edges.

Estimation of dFC

We used the sliding window method to create dFC time series. For each time point, t, a Pearson correlation coefficient was estimated using ±31 time points (63 volumes in total equaling 126 sec) for each combination of ROIs (nodes). This resulted in a unique connectivity time series with a length of 178 time points (reduced from the full 240 time points due to the window size), for each subject and condition. At each time point there is a connectivity matrix of 34,716 unique correlation values. The chosen length of the sliding time-window is well in line with “rules of thumb” that have been previously suggested for sliding window analysis (Leonardi and Van De Ville, 2015; Zalesky and Breakspear, 2015). Different transformations were then applied to the dFC time series data.

Transformations used to stabilize the variance of dFC time series

We wanted to compare the statistical properties of four different distributions of dFC time series. First, we considered the “raw” dFC time series, which are the Pearson correlation coefficients. Second, we considered the Fisher transformation applied to the dFC time series. Third, we analyzed the BC-transformed dFC time series. Finally, we investigated a combined approach where the dFC values were first Fisher transformed and subsequently BC transformed (referred henceforth as Fisher&BC).

Fisher transformation

The Fisher transformation takes the bounded distribution of correlation coefficients (r) and makes it unbounded so that the variance is independent of the magnitude of the correlation coefficient by:

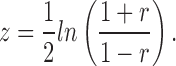The estimates of z generally approximate to a Gaussian distribution.

BC transformation

An alternative way to stabilize the variance of a non-Gaussian distributed time series is the BC transformation (Box and Cox, 1964). The BC transformation, which is a power transformation, is given by

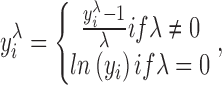where λ is set by the estimated maximum likelihood for each edge, after letting λ range from −5 to 5 in increments of 0.01. y is the time series that is applied to and i is the index of the time series. Specifically, when the parameter λ was fitted to the data, we calculated the likelihood for each possible value of λ in our specified range (−5 to 5 in increments of 0.01). It is deserved to be noted that there are other ways to optimize the finding of the maximum likelihood. If the search of optimal λ is to be performed within a certain range, we would advocate the usage of a wide range and make sure that the majority of the values are found away from the boundaries of the range. Moreover, it is recommended to examine and take into consideration the distribution of fitted λ values. Here, the estimation of λ was done by finding the maximum likelihood as outlined in Box and Cox (1964). The BC transformation, including the calculation of lambda, utilized the function boxcoxlm(), which is available in the MATLAB Central repository. (www.mathworks.com/matlabcentral/fileexchange/10419-box-cox-power-transformation-for-linear-models).

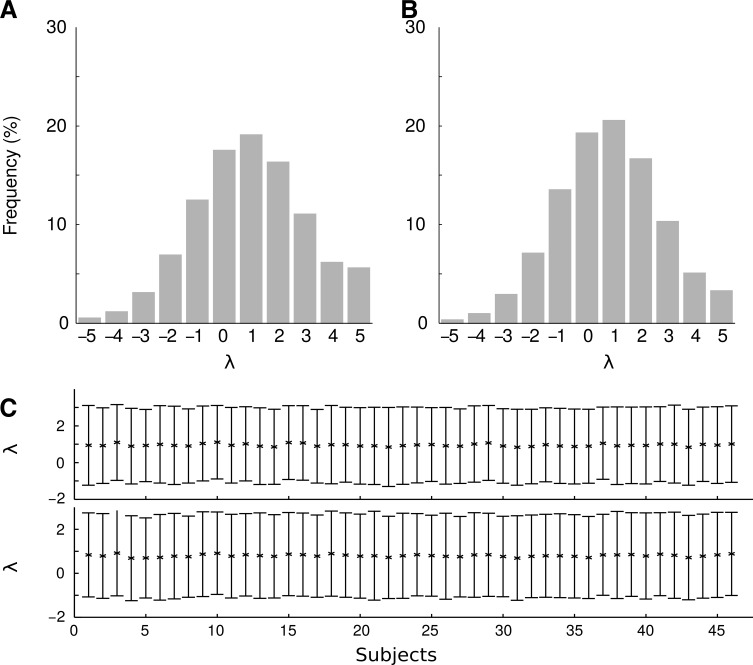
The distribution of λ for different edges is shown in Figure 1. The BC transformation was applied to both the raw dFC time series (Fig. 1A) and on the Fisher-transformed dFC time series (Fig. 1B). We also observe that subjects generally have a similar mean and standard deviation for their own distributions of λ values (Fig. 1C).

FIG. 1.

The distribution of the best-fitting value of the parameter λ included in the BC transformation when applied to all edges and subjects. (A) λ Values obtained when applying the BC transformation on the raw dFC values. (B) λ values obtained from the BC transformation on dFC values that first have undergone a Fisher transformation. (C) Mean and standard deviation of the best-fitting λ values over different edges for BC transformation (top) and Fisher&BC transformation (bottom). BC, Box–Cox; dFC, dynamic functional connectivity.

The BC transformation cannot handle values less than zero due to the natural logarithm when λ = 0. To deal with this problem, the smallest value of each dFC time series was scaled to 1 by simply adding the entire time series with the scalar |1-y_min|. This step was mandated by the fact that power transformations perform differently between 0 and 1, and by scaling the smallest value to 1, we ensured that a similar type of power transformation was applied to all time points. The BC-transformed dFC time series was subsequently scaled back so that the post-BC mean equaled the mean of the raw dFC time series. In the Fisher&BC case, the mean was scaled back to the mean of the Fisher-transformed dFC time series.

Quantifying variance stability

To quantify the variance stability within a time series, we performed a median split on the dFC time series, dividing the time series data into two separate partitions of connectivity estimates. Hence, the absolute difference of the variance in the upper and lower median partition was calculated, providing an estimate of the stability of the variance. A smaller absolute difference between the divisions (i.e., approaching 0) suggests that the variance is more stable. To make the variances of the different transformations comparable, each dFC time series was scaled between 0 and 1 before performing the median split.

Quantifying the Gaussian distributions

A time series that adheres to a Gaussian distribution will, by definition, have stable variance. We were, therefore, interested to assess how each Gaussian time series was after each transformation. We used two different methods for this: the SW test statistic and skewness (s).

SW statistic

To evaluate how closely each of the four distributions of raw, Fisher, BC, and Fisher&BC-transformed dFC data followed a Gaussian distribution, we used the SW test, which is one of the most robust methods to estimate the normality of a distribution (Razali and Wah, 2011), in particular, for cases when the number of samples in each distribution is rather small, as is the case here (178 values per distribution).

The SW test statistic, W, is calculated by:

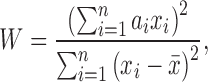where x is the ordered statistic and 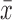is the mean. The constants a_i are given by:

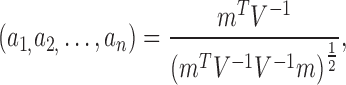where V is the covariance of the ordered statistic, and m is the expected value of the ordered statistic, given a Gaussian distribution (Shapiro and Wilk, 1965). The test statistic W was then normalized according to Royston (1992, 1993):

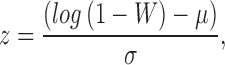where μ and σ are the mean and variance of the expected Gaussian distribution. The test statistic is usually compared against a chosen p-value threshold against the null hypothesis “the data are Gaussian.” However, this would not prove that the data are Gaussian. We, therefore, also show the SW-statistic between the proposed variance-stabilizing transformations, where a smaller normalized SW-statistic is indicative of a more Gaussian distribution.

Skewness

An additional way to quantify the Gaussian distributions is to examine how symmetric it is with the skewness (s), which is defined as:

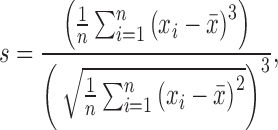for which x is the distribution to be tested (i.e., the dFC time series), s the skewness of the distribution, and 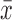is the mean of the distribution. In essence, the skewness is a measure of how much a given distribution is shifted away from a symmetric distribution toward a more fat-tailed distribution. For a unimodal distribution, a positive skewness entails that there will be a fat tail to the right of the mean, a negative skewness means a fat tail to the left of the mean. A skewness of 0 implies a symmetric distribution, which the Gaussian distribution is (but symmetric distributions could also entail other distributions such as a uniform or student's t).

Visualization of results

As the performance of the different transformations may perform differently at different correlation values, the results displayed are binned by the absolute sFC. Bins are shown between 0 and 1 in 0.025 increments. Notably, the sFC connectivity value, which are displayed on the x-axis, reflect the mean connectivity value for each of the different transformations (Supplementary Fig. S1; Supplementary Data are available online at www.liebertpub.com/brain). Unless explicitly stated, our results from different subjects are pooled across subjects. This means that we calculate all metrics for each subject independently and when visualized, edges are binned, entailing the same edge from the same subject can be in a different bin and treated independently. This is because different subjects may have different sFCs.

Results

Simulations that highlight the potential problem with the Fisher transformation and the benefit of the BC transformation

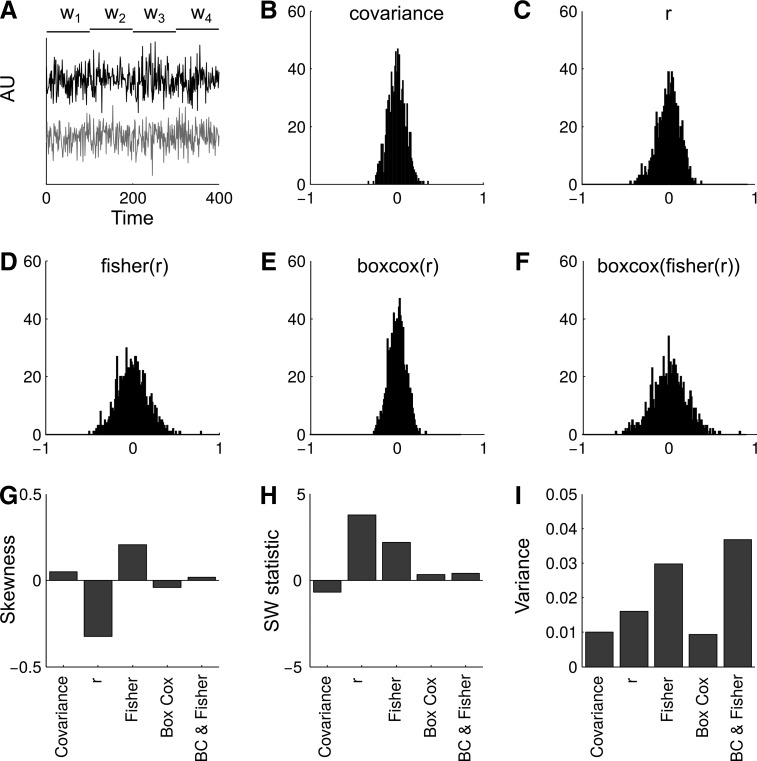
Two Gaussian time series with fluctuating covariance were simulated (total length of time series were 100,000 samples long). The covariance fluctuated every 100 samples and the new covariance was sampled from a Gaussian distribution (μ = 0.5 and σ² = 0.1). This allowed us to create 1000 windows, where the true covariance was known (Fig. 2A), and that this followed a Gaussian distribution (Fig. 2B). This distribution of the covariance “ground truth” can then be compared with the distributions after correlating each of the 1000 windows and applying each of the proposed transformations (Fig. 2C–F).

FIG. 2.

Results from simulations. (A) Snippet from the simulated time series. Two multivariate Gaussian time series were created, where the covariance fluctuated every 100 samples. These are marked by w_1, … w₄ in the figure. During these periods of known covariance, windows were created, where the covariance and correlation coefficient were estimated. In total, 1000 windows were created (4 windows are shown in the panel). (B) The mean-centered distribution of the covariance estimates for each window (ground truth). (C) The mean-centered distribution of Pearson correlation coefficients. (D) The mean-centered distribution of correlation coefficients after a Fisher transformation was applied. (E) The mean-centered distribution of the correlation coefficients after the BC transformation was applied. (F) The mean-centered distribution of the correlation coefficients after the Fisher&BC transformation was applied. (G) Skewness of the distributions in (B−F). (H) SW statistic of the distributions in (B−F). (I) Variance of the distributions in (B−F). SW, Shapiro–Wilk.

When looking at the distributions in Figure 2, applying the BC transformation leads to a distribution quite similar to the original covariance. The Fisher and the Fisher&BC transformations both have a larger variance than the original covariance distribution. The raw r values (Fig. 2C) have a slight skew toward left and the Fisher transformation skews slightly to the right. The skewness of each of the distributions can be seen in Figure 2G. The Fisher&BC transformation was the closest to the ground truth, followed closely by the BC. Both Fisher&BC and BC transformations also have low SW statistics and are closest to the ground truth. The raw and Fisher both have p-values below common thresholds of rejecting the null hypothesis that the distribution is Gaussian (p_cov = 0.7536, p_r < 0.001, p_Fisher = 0.0142, p_BC = 0.3706, p_Fisher&BC = 0.3413). The skewness and SW-statistic suggest in favor of either of the two BC distributions over the raw correlation coefficient or just the Fisher transformation.

Finally, when considering the variance of the distributions, the variance is inflated in the raw connectivity values and even more so in the two instances where the Fisher transformation is applied (Fig. 2I). Applying only the BC transformation leads to the least change in relation to the ground truth.

This simulation serves to illustrate that the Fisher transformation does not necessarily achieve a Gaussian distribution regarding the variance of a time series. We also see how it is possible for the sign of the skewness to flip between the distribution of raw correlation coefficients and the Fisher-transformed data. This simulation, however, always has the mean covariance at 0.5. We have not shown that this behavior is similar throughout the range of possible connectivity values, but instead have illustrated the possible dangers of the Fisher transformation. To show the effect throughout different connectivity values, we turn to the empirical fMRI data.

A qualitative assessment of the effect of the Fisher and BC transformations, and their combined use on empirical dFC resting-state fMRI data

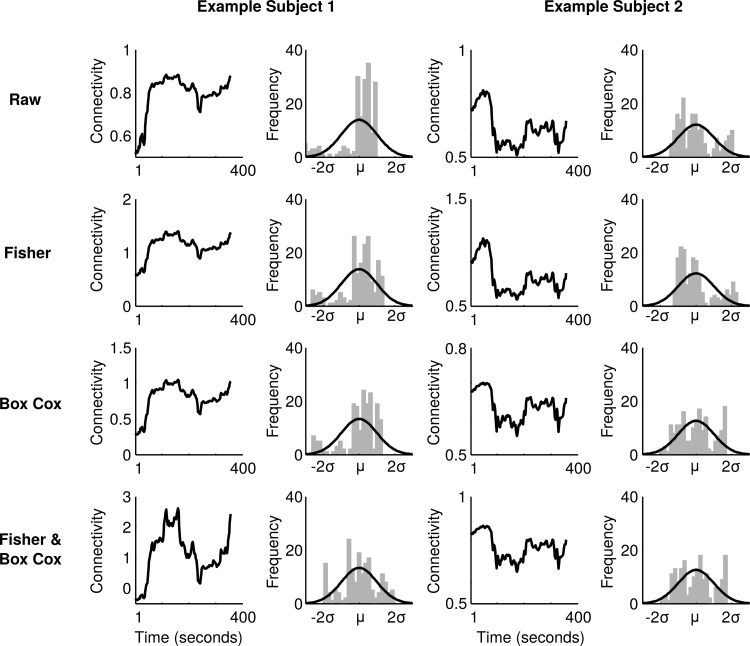
To illustrate the effects of the different transformations on empirical dFC time series data we start by presenting data from two subjects and a single edge between two nodes. Figure 3 shows the time series of dFC correlation coefficients and their corresponding distributions for four different cases. If we start by assessing the results obtained for the first subject, we note that the distribution of the raw dFC correlation coefficient values has a sharp peak of correlation coefficient values that are larger than its mean. This peak is accompanied by a greater spread of correlation coefficients in the lower regime. If we examine the corresponding Fisher-transformed distribution of dFC values (Fig. 3, second row), we can, in this case, observe that although the Fisher transformation alters the distribution so that it becomes unbounded by the −1 to 1 restriction, it still performs poorly in terms of creating a Gaussian distribution of the dFC correlation values. Similarly, the BC transformation used in isolation (Fig. 3, third row) fares no better. However, the combined Fisher&BC approach provides a rather good approximation to a Gaussian distribution (Fig. 3, last row).

FIG. 3.

dFC time series and their corresponding distributions computed for a single edge in two different subjects. The top row shows the raw dFC time series and their corresponding distributions together with a fitted Gaussian distribution (solid line). The second row shows the dynamic connectivity values after Fisher transformation. The third row displays the case of applying the BC transformation. The last row shows the result from applying first the Fisher and then the BC transformation on the same data.

Next, we proceed by examining the performance of the suggested transformations on the data obtained from the second subject (shown in the right column in Fig. 3). In this case, another potential problem with the Fisher transformation becomes apparent. Here, the raw dFC time series constitutes a distribution that appears to be Gaussian. When we apply the Fisher transformation, we can observe that the distribution is skewed away from a Gaussian distribution. However, both the BC and Fisher&BC transformations create distributions of dFC correlation coefficients that qualitatively approximate a Gaussian distribution rather well.

From the examples shown here, where data was taken from a single edge, we have illustrated two possible obstacles that pertain to the Fisher transformation in the context of stabilizing the variance of a dFC time series. First, the Fisher transformation may fail to stabilize the variance and thereby provide a poor Gaussian distribution approximation for the data, if the raw dFC time series is heavily skewed as shown for the first subject in Figure 3. Second, as exemplified for the second subject shown in Figure 3, it may skew the distribution in the opposite direction (seen also in the simulations, Fig. 2G), again performing poorly in terms of achieving a Gaussian distribution.

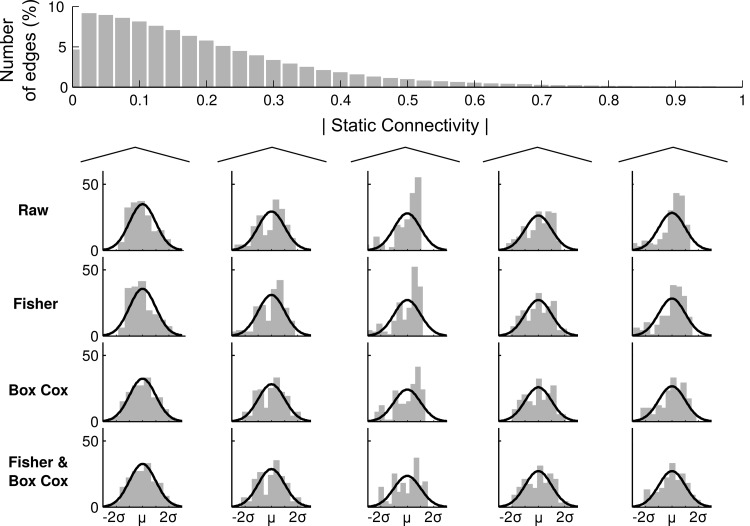
The two examples shown in Figure 3 were chosen to illustrate our concerns with the Fisher transformation's performance in the context of dFC analysis. To get a more general overview of the overall effect, we display the distribution of static connectivity values for all subjects in Figure 4. Here, we considered the same edge as shown for example subject 1 in Figure 3 so that all examples come from the same subjects that are closest to 0.1, 0.3, 0.5, 0.7, and 0.9 in absolute sFC (Fig. 4). Thereafter, we show the effect of each transformation on the edge connectivity. Similar to the qualitative examples shown in Figure 3, the results shown in Figure 4 suggest that the BC and the Fisher&BC transformations have the best performance regardless of their sFC value.

FIG. 4.

Distribution of all static functional connectivity values (pooled over subjects). Data are displayed in 0.025 increments. We here show the effect of all the transformations on edges that has its absolute static connectivity values at 0.1, 0.3, 0.5, 0.7, and 0.9, respectively.

An important observation from the results shown in Figures 3 and 4 is that a discussion of the stability of the variance from the tested transformations in terms of obtaining Gaussian distributions is warranted, although not yet confirmed. However, the data does not have stable variance (see Quantifying the Stability of the Variance of Each dFC Time Series section) and, the data does not clearly display characteristics that would suggest another candidate distribution, which the data should be transformed to instead. Thus, when we quantify the SW-statistic and skewness of dFC time series to quantify the extent of approximating a Gaussian distribution, this issue is related to the stability of the time series variance.

Quantifying the stability of the variance of each dFC time series

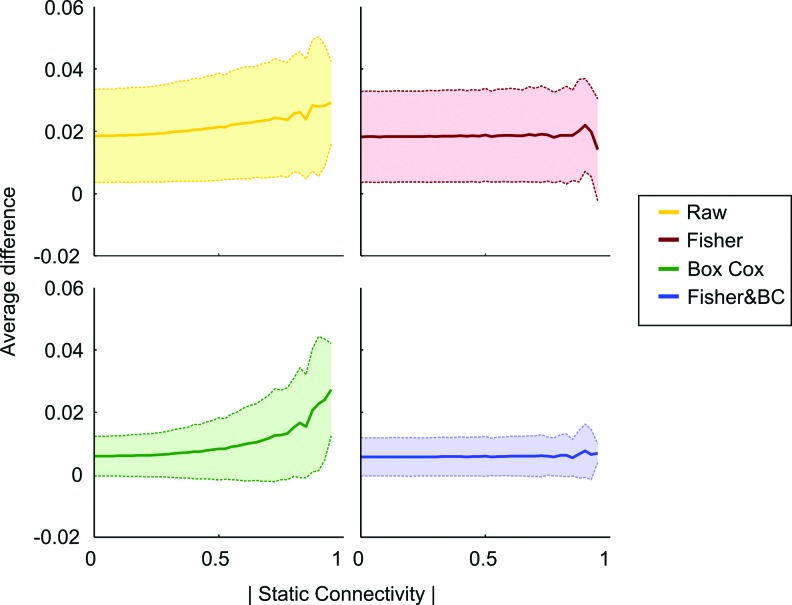
We aimed to quantify the stability of the variance in each time series across all edges and subjects and for the distributions. Ideally, the variance should be similar throughout the entire length of the dFC correlation value time series. By splitting the data into two partitions through a median split, we calculated the absolute difference in the variance between partitions. The median split procedure allowed us to investigate if the variance is similar in different parts of the time series. If the distributions had stable variance, regardless of any assumption of the distributions, the absolute difference will be zero. Figure 5 shows that the average difference in variance, binned with respect to their static connectivity values, is lowest for the combined Fisher&BC transformations, followed by the BC transformation, although it becomes less stable when the amplitude of the connectivity values increases. Larger differences were observed for the Fisher transformation, and the largest distance in variance was seen for the raw dFC time series. Both the Fisher-transformed data and the raw data had a large standard deviation. The median split analysis suggests that the within-time dFC series variance is most stable when the combined Fisher&BC data transformation strategy is used.

FIG. 5.

Differences in dFC time series variance as a function of static connectivity for the raw data and the three variance-stabilizing transformations investigated. The plot shows the averaged absolute difference in variance and binned according to its corresponding static connectivity value. The variance of connectivity was estimated as the absolute average distance of the time series connectivity values when divided into an upper and lower partition by a median split. Error bars show the standard deviation. Color images available online at www.liebertpub.com/brain

As there is high variance in Figure 5 in the raw and Fisher case, we can conclude that the variance is not stable in these cases. As the mean of Figure 5 increases for the BC and also the raw, these two do not have stable variance across the sFC range.

Quantifying normality and skewness of dFC time series

We now proceed by quantifying and evaluating the performance of the three suggested approaches to stabilize the variance in creating a Gaussian distribution for each dFC time series. We have mentioned that distributions qualitatively appear Gaussian, but this can be misleading and we now try and quantify how far each transformation is from achieving Gaussian distributions. Thereafter, we also quantify the skewness of the distributions, which deals with the symmetry of the distributions.

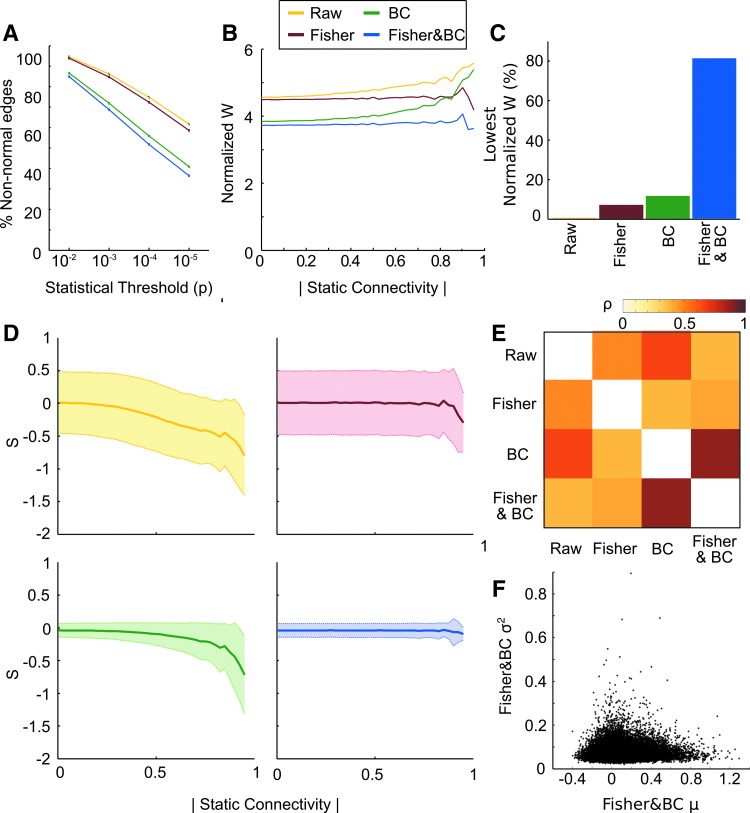
First, we noted that for many edges, their corresponding distributions were classified as being non-Gaussian by the SW tests (Fig. 6A). The Fisher&BC transformation approach had the least amount of edges classed as non-Gaussian for significance thresholds ranging from p < 0.01 to p < 0.00001. Even for the lowest statistical threshold (p < 0.00001), 36.5% of edges were still classified as non-Gaussian and for the higher threshold (p < 0.01), 84.9% of all edges were classified as non-Gaussian. The three other cases fared worse. The raw dFC time series contained 94.6% to 61.7% of non-Gaussian edges. The Fisher-transformed time series of correlation coefficients showed that non-Gaussian edges ranged from 93.9% to 58.6% and the BC-transformed data ranged from 86.6% to 40.1%. It should be noted that a significant value obtained with the SW statistic argues against the null-hypothesis, which is that the distribution of dFC values are Gaussian. Although we are unable to prove the null hypothesis for any of the proposed transformation strategies, we can still conclude that large performance differences exist for the three proposed.

FIG. 6.

(A) The percent of non-Gaussian edges for different statistical thresholds for the different distributions from the SW-statistic. (B) The normalized SW-statistic plotted against their absolute static functional connectivity values for the three different variance-stabilizing transformations together with the raw dFC distribution. (C) The percent for each of the four dFC time series that had the lowest SW-statistic. (D) Skewness for the four different distributions along different static functional connectivity values for the four different transformation possibilities. Error bars show standard deviation. (E) Spearman rank coefficient of the between-subject variance for the four different transformations computed for a single edge. All values are significant at p < 0.001, Bonferroni corrected. (F) Mean–variance relationship of the Fisher- and BC-transformed connectivity time series. Averaged over subjects, each dot represents the average mean and the average variance for each edge. Color images available online at www.liebertpub.com/brain

Next, we compared the average SW-statistic value for all edges with regard to their sFC correlation coefficient (Fig. 6B). We observe that both the raw and BC-transformed dFC time series were classified to be less Gaussian as the static connectivity value increased. The Fisher-transformed dFC data behaves worse than the BC-transformed data for lower static connectivity values, but are more on an equal footing for the case when the static connectivity value increases above 0.7 and the BC transformation is unable to perform optimally on the bounded data. For the combined Fisher&BC approach, the SW statistic quantified the distributions as being more Gaussian. This finding was consistent across all connectivity values. The Fisher&BC-transformed data had the lowest SW-statistic for 81.1% of all edges, the BC-transformed data had the lowest SW-statistic for 11.5% of all edges, followed by the Fisher-transformed data with 6.7%. The raw dFC time series data displayed a Gaussian distribution according to the SW-statistic for <1% of all edges (Fig. 6C).

The story is similar for the skewness of the transformed distributions as with the SW statistic. The raw connectivity time series becomes increasingly skewed as a function of the underlying absolute static connectivity (Fig. 6D, upper left panel). The Fisher-transformed dFC data (Fig. 6D, upper right panel) display a skewness in both positive and negative directions. The positive skewness at higher connectivity values is considerably less for the raw dFC time series and this demonstrates how the Fisher transformation can skew too much (similar to the results shown in Fig. 3B). For the BC-transformed data, the standard deviation was considerably lower than the raw and Fisher-transformed data (Fig. 6D, lower left panel), but again became destabilized at the higher connectivity values. The Fisher&BC transformation once again had the best performance by having a low standard deviation in skewness and was stable across the entire range of mean dFC values (Fig. 6D, lower right panel).

In sum, using two different tests, over the entire range of underlying connectivity, the Fisher&BC strategy performed the best.

Fluctuations of variance in dFC time series

One byproduct of the data transformations examined here is that the variance of a given dFC time series of correlation coefficients can be affected as well. To exemplify this influence, we correlated the between-subject variance of a single edge dFC time series for the different variance-stabilizing transformations examined (Fig. 6E). While all correlations had a low p-value (p < 0.001, Bonferroni corrected), this is a correlation of the variance of the same time series for the same subjects. The Spearman coefficient is quite low (often capturing below 25% of the between-subject variance). While this result is perhaps not overly surprising it shows that, without properly accounting for, it may become hard to interpret what any quantitative difference of dFC variance actually represents when contrasting data between groups or conditions—especially when there are differences in sFC as well.

The mean–variance relationship of dFC time series after a combined Fisher and BC transformation

We have previously argued that if the analysis strategy of dFC studies is to find interesting changes of connectivity in time (e.g., to make a binary time series of connectivity that used together with temporal graph theory; Thompson and Fransson, 2016), then one has to take into account the mean–variance relationship that exists for dFC fMRI time series (Thompson and Fransson, 2015). This relationship implies that different thresholding strategies used for selecting connectivity estimates of interest in time will either threshold based on those with the highest variance in connectivity or those with the highest sFC (Thompson and Fransson, 2015). Thus, it then becomes relevant to investigate if the previously shown relationship between the mean and the variance of individual edges still holds after the combined Fisher&BC transformation, as the conceptual argument discussed was based on nonstabilized variance. Figure 6F shows the variance plotted against the mean for dFC time series taken from all edges, averaged over subjects for the Fisher&BC transformation. While the variance is quite stable over edges, the fact that there are more edges when the mean is lower leads to a greater probability that some edges here have higher variance. We observe that our previous observation regarding the relationship between the mean and variance of dFC time series still holds after a Fisher&BC transformation of the dFC data. This finding implies that different (but reasonable) thresholding strategies (based on taking edges with high mean or variance) will yield different time points for different edges being marked as candidates of significant/interesting connectivity. This occurs because, despite the variance being relatively stable, the mean–variance dependence still holds and the choice of analysis strategy to be used in future studies needs to be carefully considered.

Discussion

From the results presented in this work, we can draw three conclusions. First, dFC time series, in terms of within-time series variance stability and degree of skewness compared with a Gaussian distribution, is improved when using the combined Fisher followed by a BC transformation approach compared with using the prevailing Fisher transformation strategy. Second, the problem of the mean–variance relationship for dFC data (Thompson and Fransson, 2015) is still present in data even after applying the Fisher&BC transformation strategy, meaning that the process of single out time points of interest in different connectivity time series will vary depending on the chosen thresholding strategy (i.e., giving preference to either edges with higher variance or higher mean). Third, each of suggested variance-stabilizing transformations display a relatively low degree of correlation across subjects when considering that the correlation is applied to the dFC variance of the exactly same time series with the exception of different transformations being applied (Fig. 6E). This is most likely due to a nonlinear effect on the dFC variance introduced by the variance-stabilizing transformations. Specifically, the nonlinear effect originates in the fact that when the investigated variance-stabilizing transformations are applied to dFC time series, their effect is not uniform across the range static connectivity correlations. Thus, the task of quantifying the variance of dFC time series may pose a difficult problem, since the nonlinear effects imposed by the Fisher and/or BC transformations may artificially inflate or deflate the true variance of a dFC time series. In addition, to our knowledge, it is uncertain at this time how this can be accounted for since the true variance of a given dFC time series is unknown. This means that attention has to be paid to this dependency when contrasting the variance of dFC time series between different task conditions.

One might ask oneself what is the purpose of stabilizing the variance? There are two good reasons why one may wish to do this. (1) To achieve a better estimation of whatever metric of dFC that is being estimated; (2) to allow for parametric statistic testing. While the second possibility is feasible using variance-stabilizing techniques, there is no reason (apart from perhaps simplicity) to abandon previously proposed nonparametric testing procedures that have been proposed for dFC studies (Hindriks et al., 2015). Critically, the first possibility entails more accurate and better performing analysis steps (or even meeting assumptions of different analysis techniques). Various data processing steps that are commonly applied in studies of dynamic functional brain connectivity, for example clustering, will often benefit in performance by transforming the data so that its features adhere to a Gaussian distribution. We stress that the value of the proposed pipeline and our motivation for this study was primarily to achieve an increase in performance in terms of estimating dynamic fluctuations in brain activity, not to replace previous proposals of nonparametric statistics.

It is perhaps pertinent to ask the question if the problem of variance stabilization in the context of dFC time series may after all not pose such a large methodological difficulty as it has been portrayed in this paper. To begin to provide an answer, one may ask oneself, “when could it be problematic to use the Fisher transformation with the intent to stabilize the variance for dFC time series?” We identify two possible problems with using the Fisher transformation on dFC time series. First, it becomes harder to interpret the variance measures of the time series when there are shifts in dFC variance imposed by the Fisher transformation and some of the edges are skewed away from normality by the transformation. Second, a substantial part of the dynamic functional brain connectivity literature uses k-means clustering techniques on Fisher-transformed data ( e.g., Allen et al., 2014; Barttfeld et al., 2015; Damaraju et al., 2014;). In such instances, stabilized variances will often make more robust clustering performance. dFC studies considering these types of methods would benefit from considering a BC transformation to be done on the data after the Fisher transformation has been applied as edges with varying degrees of variance stability will hamper performance.

Regarding the relationship between the mean and the variance of connectivity time series, we have previously discussed the mean–variance relationship in dFC analysis and its implications for choice of analysis strategy (Thompson and Fransson, 2015). In that study we explored the variance within a bounded range, that is, without a Fisher transformation, which was performed because we, at that time, were concerned about the Fisher transformation for the reasons addressed in this article. However, it was unclear from the Thompson and Fransson (2015) study whether the thresholding problems we addressed in that study persists for the case when the dFC time series variance was stabilized properly. To this end, we have in the present study explicitly shown when the variance has been stabilized (to the best of our ability) with first, the Fisher, then the BC transformation, we are still able to replicate our previous findings related to the mean–variance dichotomy when defining thresholds of interesting dynamical activity in the dFC fMRI time series. The implications of this relationship might be substantial as it suggests that different analysis strategies (including both choices of thresholding and clustering techniques) may be biased by the variance differences among dFC time series. We suggest that scaling (e.g., by normalizing the data, including demeaning and dividing the dFC time series by their standard deviation) should be performed to get all the dFC time series on equal mean and variance footing, which may be appropriate in many instances of data clustering and comparisons between conditions or group of subjects—otherwise it risks dFC contrasts merely illustrating an overly complicated contrast of the functional connectivity.

Although the present study clearly shows the statistical benefits of applying the BC transformation on dFC data, it is a pertinent question to ask if one should always use it in combination with the Fisher transformation. We believe that the answer depends to some degree on how the dFC data will be used. Due to the nonlinear effects of the data transformation shown in Figure 6E, we do not recommend a direct quantification of connectivity based on the mean or variance of dFC time series. Moreover, if other putative mean and variance-independent measures are used to quantify changes in dynamic connectivity, then variance stabilization achieved by the Fischer&BC transformation is not necessary and nonparametric statistical testing should be sufficient. Additionally, if data are modeled using multimodal distributions, then the transformations described in the present work are not needed. The Fischer&BC transformation, however, is useful when clustering the dFC data in some way, which is often the case in dFC studies, since variance instability will bias and hamper clustering performance. For example, the k-mean clustering technique will by necessity perform differently, and thereby be biased, for edges (features) that have a more stable variance than those with less stable variance. Finally, we are not ruling out the existence of analytical strategies to transform the dFC data so that it adheres to statistical distributions other than the Gaussian distribution, when the intent is to stabilize dFC data variance. However, the Gaussian distributions have numerous advantages and well-behaved advantages, and it can be very beneficial to work with such distributions (Wu, 2004).

We would like to emphasize the fact that nowhere in this work are we making any claims of the ontological nature of the distribution of brain connectivity in time. Our overall aim was to provide a strategy to obtain a best possible, in the sense of variance stability, connectivity time series for further analysis steps. The stabilized connectivity time series can subsequently be subjected to various measures of quantification without resorting to an implicitly assumed stability of variance, which is often the case in the literature.

To conclude, the Fisher transformation followed by a BC transformation when applied on dFC fMRI data showed superior performance terms of stabilizing the dFC time series variance across its entire range. A possible drawback with the suggested approach is that the parameter λ needs to be fitted, which poses additional work for the researcher. It is worth noting that when implementing the BC transformation on economic data, Nelson and Granger (1979) often failed to find an adequate λ estimate for their model. Indeed, we occasionally observed that the λ parameter could at times fail to fit, but these instances were relatively few in number. Potentially, an expansion of the possible range of λ for these edges could be an option or more efficient parameter searching tools to find λ.

While dFC is an exciting field of research, the present results warrant caution when computing contrasts of dynamic functional brain connectivity between subject populations and/or tasks, and that the underlying assumptions and the statistical distributions of the data should be carefully considered.

We hope that researchers will consider which of the variance-stabilizing techniques they should use and we strongly recommend that the BC or Fisher&BC data transformation is used. Without a correct stabilization of the dFC data variance, the risk of biases in the dFC results cannot be neglected.

Acknowledgment

P.F. was supported by a grant from the Swedish Research Agency (Grant No. 621-2012-4911).

Author Disclosure Statement

No competing financial interests exist.