Abstract
We propose a new optical coherence tomography (OCT) based method to measure red blood cell (RBC) velocities of single capillaries in the cortex of rodent brain. This OCT capillary velocimetry exploits quantitative laser speckle contrast analysis to estimate speckle decorrelation rate from the measured temporal OCT speckle signals, which is related to microcirculatory flow velocity. We hypothesize that OCT signal due to sub-surface capillary flow can be treated as the speckle signal in the single scattering regime and thus its time scale of speckle fluctuations can be subjected to single scattering laser speckle contrast analysis to derive characteristic decorrelation time. To validate this hypothesis, OCT measurements are conducted on a single capillary flow phantom operating at preset velocities, in which M-mode B-frames are acquired using a high-speed OCT system. Analysis is then performed on the time-varying OCT signals extracted at the capillary flow, exhibiting a typical inverse relationship between the estimated decorrelation time and absolute RBC velocity, which is then used to deduce the capillary velocities. We apply the method to in vivo measurements of mouse brain, demonstrating that the proposed approach provides additional useful information in the quantitative assessment of capillary hemodynamics, complementary to that of OCT angiography.
OCIS codes: (170.4500) Optical coherence tomography, (170.2655) Functional monitoring and imaging, (220.4000) Microstructure fabrication
1. Introduction
Capillary is the smallest blood vessel in the body. For mammals, its size is around 5 to 10μm in diameter, approximately the same order in the dimension of a red blood cell (RBC), constraining capillary blood flow to single RBC passage [1]. In brain, cerebral blood flow mainly serves to supply oxygenated blood to the capillaries, where adequate oxygen and nutrients are exchanged with local brain tissues, supporting brain cognitive function. Over the decades, many neuroscientists believe that hemodynamics in the cerebral capillary is closely coupled with the altered metabolic demands of the parenchyma associated with the change in functional activity of brain, and therefore it would play an important role in assessing the brain function. For example, Vogel et al. have reported that a moderate hypocapnia decreased the heterogeneity of capillary perfusion in rat brain [2]. Moreover, Tomita et al. have reported a neuro-capillary coupling between neurons and capillary RBC motion, in which the neuronal activation modulated regional capillary blood flow in rat brain [3]. These findings have evidenced the involvement of cerebral capillary flow dynamics with the brain pathophysiology. To probe the capillary flow dynamics, usually, laser scanning fluorescence microscopy has been employed to image the motion of RBCs in individual capillaries [4,5]. The RBC velocity was inferred either from line-scan measurements, i.e., repetitive scans of the laser along the central axis of a capillary [4], or by directly tracking individual RBC in the capillary at sufficient temporal resolution [5], where the blood vessel or RBC was fluorescently labeled with specific dyes (e.g., fluorescein isothiocyanate (FITC)). It has been reported that RBC velocities in the single capillaries of a normal rat cerebral cortex are not uniform but highly heterogeneous, ranging from 0.1mm/s to 9.4mm/s with an average velocity of 1.96 ± 1.26mm/s (mean ± s.d) [5]. While commonly used, a main limitation of these methods is to monitor only one or a few capillaries at a time within the scan lines or the limited field of view, which provides a huge challenge in the investigation of capillary flow dynamics that requires flow measurement at multiple capillaries at the same time.
Optical coherence tomography (OCT) is a label-free, noninvasive optical imaging technique utilizing a low coherent light source and confocal detection [6]. It detects an interference signal generated between lights backscattered from the sample volume in the focal zone of the imaging optics and a reference beam of the interferometer, upon which a depth-resolved reflectivity profile is extracted ('A-line'). A cross-sectional image ('B-frame') or a volumetric set of the B-frames can be collected using transverse or raster scanning of the sample beam using a pair of mechanical scanners. As OCT offers high-resolution three-dimensional (3D) structural information over an appreciable depth, it would be able to monitor more blood vessels across different depths. With the unique imaging capabilities, several OCT-based flow imaging techniques have been developed to measure blood flow at multiple blood vessels in depth. Doppler OCT (DOCT) is a representative OCT velocimetry for measurement of blood flow speed [7]. This functional OCT has provided bidirectional velocity axial projection of the transverse blood flow, well-suited for measuring blood velocity in ascending or descending vessels such as penetrating arteries and veins in brain cortex [8]. However, application of DOCT in capillary is quite challenging because the capillary flow is often transverse to the OCT incident beam [9]. Recently, OCT angiography (OCTA) has been emerged to image blood vessels in the vascular tissue beds [10–15]. OCTA works to suppress static scattering from the tissue to visualize only the dynamic scattering components caused by the motion of RBCs in the perfused blood vessels. Several algorithms and techniques for OCTA have been developed to effectively obtain the motion-based contrast [15]. While OCTA is beneficial for visualizing the capillary vasculatures [10–15], it is difficult to provide quantitative information of velocity, an important parameter for the study of capillary hemodynamics.
Alternatively, several methods based on OCT speckle signal analysis have been proposed for measuring speed or flow in transverse direction [16,17]. The methods commonly utilize the changes in the time course of the OCT speckle pattern, where a slope of normalized autocorrelation function of multiple A-scans acquired with M-mode scan (i.e., repeated A-scan at the same location) [16] or cross-correlation coefficient [17] between adjacent A-scans was used as the speckle decorrelation metric that is assumed to be linearly related to transverse flow speed without longitudinal component. These approaches have been validated in large vessel (e.g., mouse femoral artery) in vivo and scattering flow phantoms whose diameters are more than 100μm. However, no validation for cerebral capillary (<10μm in diameter) has been reported. Recently, Srinivasan et al. reported an OCT method to quantify RBC velocity in capillaries [18]. In this method, they proposed that the time scale of random fluctuations in the dynamic scattering component of complex-valued OCT signals are related to RBC velocity. They used power spectrum bandwidth of autocorrelation function of the random fluctuations to estimate velocity. Their measurement of RBC velocity in rat brain capillary was correlated with two-photon microscopy measurement [18].
In this work, we present an alternative OCT method for capillary velocimetry. The method utilizes quantitative laser speckle contrast analysis that has been used in laser speckle imaging to estimate a speckle decorrelation rate, inversely proportional to velocity. In this paper, we first describe the concept for use in the OCT speckle analysis. Then, we test the proposed approach with OCT measurements of an ex vivo capillary flow phantom, and validate it by relating the measured decorrelation time with the phantom flow velocity. Finally, the method is demonstrated by imaging velocity dynamics in capillaries of mouse brains under pathophysiological conditions.
2. Theory
2.1 Basic concept
Our proposed method essentially adopts the concept in laser speckle contrast imaging (LSCI) analysis to OCT imaging for estimating cerebral blood flow (CBF) dynamics, especially at cerebral capillaries. LSCI is a full-field technique for imaging motion, utilizing coherent laser illumination and a camera for acquisition [19,20]. Scattered light from the illuminated diffuse object produces a random interference pattern called speckle onto the camera. Movement of scattering particles (e.g., blood cells) within the random medium leads to fluctuations in the detected speckle intensity. The rate of change in the speckle pattern can be quantified by calculating temporal or spatial statistics of the speckle pattern, providing information on the motion of the scatters [19]. The statistical models have been well-established to quantitatively estimate the motion of the scatters in the form of flow or speed from the observed speckles, making it possible to extract the characteristic decorrelation time τc of the speckles, which is inversely proportional to the speed of moving scatters [19–21].
Given that OCT is a coherent imaging system, we hypothesize that backscattered signal at a single voxel of OCT cross-section can be treated as the speckle similar to that at a single pixel of camera in LSCI so that the statistical models in LSCI would be also applicable to the OCT signal. With this hypothesis, we assume that 1) a single voxel at a functional blood vessel has a time scale of random fluctuations of OCT speckle owing to random motion of RBCs passing through this voxel (here, most of constituents of blood are assumed to be red blood cells), and 2) the OCT speckle dynamics at single voxel can be quantified by using the temporal statistics of the speckle pattern. For the temporal assessment of speckle dynamics, usually, the characteristic decorrelation time τc is derived through the Siegert relation: g2(τ) = 1 + βM|g1(τ)|2 [22], where βM is a measurement-geometry specific constant, g1(τ) and g2(τ) are the autocorrelation functions of scattered electric field and intensity, respectively. However, because of difficulty in direct derivation of τc from the g1(τ), most of LSCI investigations have been focused on the spatial assessment of speckle dynamics for derivation of τc. This treatment quantifies the degree of speckle blurring that can be represented as a speckle contrast Ks, defined as a ratio of the standard deviation σs to the mean pixel intensities <Is> within small spatial window in the image taken by the camera with an exposure time duration of T; Ks = σs/<Is>. Recently, Cheng et al. [23] revealed that the temporal speckle statistics can take the same form of spatial statistics of speckle dynamics, that is, the temporal statistics can be formulated as Kt = σt/<It>, equivalent to the form of Ks, where Kt is the speckle contrast in the time dimension. <It> and σt are the mean and standard deviation of the fluctuation of time-integrated speckle intensities during a time interval of t. Based on these evidences, we purport that the dynamics of time-varying OCT signal can be quantified by the temporal speckle contrast Kt, upon which the decorrelation time τc can be derived through the proper speckle contrast analysis for velocity measurement.
2.2 Derivation of temporal decorrelation time
With the assumptions discussed above, we attempt to derive the decorrelation time from the OCT signal fluctuations at the capillary. For this, we utilize the speckle contrast analytical models that have been already well-established in the many LSCI literatures [21,22]. Table 1 shows the modified Siegert relation based speckle visibility expressions for different scattering regimes and different velocity distributions. Here, x = T/τc, where T is the camera exposure time and β is an instrumentation factor; β = Kmax2, where Kmax is the maximum attainable speckle contrast. ρ is the fraction of dynamic scattering component to the scattered light; ρ = If /(If + Is), with If the light intensity backscattered at dynamic component and Is the light intensity backscattered at static component. Cnoise is an added noise term. In the multiple scattering regime, Nd is the average number of dynamic scattering events (Nd>1). The model choice is important to retrieve accurate τc in the determination of capillary flow velocity. We note a finding in Ref. 21, suggesting the dependence of number of dynamic scattering events on flow channel size, where 3D Monte Carlo simulation of scattering within whole blood microfluidic channels having three feature sizes (65, 115, and 175μm) showed a linear increase of scattering events with the increase of the channel size. For 65μm in size, in particular, the number of scattering events in the flow channel were less than 3 regardless of objective numerical apertures (N.A.) (from 0.12 to 1.0N.A.) [21]. Therefore, it is reasonable to infer that for the channel smaller than 65μm, there would be more pronounced reduction in scattering event and that a single scattering would be predominant for very small channel like capillary (<10μm in size). Assuming directional RBC flow at capillary, we thus elected to use a speckle visibility expression with single scattering event and Gaussian velocity distribution (see Table 1). Recall the speckle visibility expression in the Table 1 as
| (1) |
If the static scattering component of the light backscattered at single capillary and the noise term are negligible, we simply put ρ to 1 (in Sec. 3.3, the presence of static scattering component will be removed prior to the decorrelation time calculation). Then, Eq. (1) can be simplified as
| (2) |
By replacing the camera exposure time T with a time interval t between OCT B-scans, Eq. (2) is rewritten as
| (3) |
Finally, from Eq. (3), a decorrelation time τc can be extracted with the temporal speckle contrast Kt obtained from OCT signal fluctuations and the known time interval t. As stated, τc should have an inverse linear relationship with flow velocity V; V = ατc−1, where α is a weighting factor depending on a combination of scatter properties and imaging geometry [22]. In Sec. 4.2, we will validate the relationship between τc and V using a scattering flow phantom, replicating real single capillary flow by the use of a microfluidic phantom.
Table 1. Speckle visibility with different scattering regimes and velocity distributions.
3. Material and method
3.1 System description
A fiber-based 1340nm spectral domain OCT system [24] was used for the capillary velocimetry experiments. The light source was a superluminescent diode (LS2000C, Thorlabs Inc.) with a spectral bandwidth of 110nm at the full-wavelength width at half maximum, yielding the axial (depth) resolution of ~7μm in tissue. A 10 × objective lens (LSM02, Thorlabs Inc.) was used in the sample arm, yielding the transverse resolution of ~7μm. The output beam from the interferometer was routed to a custom-built spectrometer designed to have the spectral resolution of ~0.141nm, providing a detectable depth range of 3mm. The imaging speed was 92,000 axial scans per second, achieved by a 1024 pixel InGaAs line scan camera (1024-LDH2, Goodrich-Sensors Unlimited Inc.). A measured signal sensitivity of the system was ~105dB and an incident light power onto sample surface was ~3.5mW. The imaging operations including beam scanning, data collection and storage were controlled by a custom software package written in Labview language.
3.2 Animal preparation
All experimental procedures performed in this study were approved by the Institutional Animal Care and Use Committee (IACUC) of the University of Washington (Protocol number: 4262-01). C57BL/6 mice (23g-25g) were prepared under isoflurane anesthesia (1.5%-2.0% in 0.2L/min oxygen, 0.8L/min air), placed on a stereotaxic frame. The body temperature of mouse was maintained at 36.8°C by a heating blanket on the frame whose temperature was controlled by a homeothermic monitoring system (50-7220F, Harvard Apparatus) that continually monitored the body temperature using rectal insertion of a temperature-sensing probe. Under anesthesia, the mice received open skull craniotomy [24], where a 4mm × 4mm area of the skull over the somatosensory cortex in right hemisphere was removed along with the dura and then the exposed somatosensory cortex was covered with a 5-mm-diameter transparent glass coverslip. The cranial window covers the territories supplied by the anterior cerebral artery (ACA) and middle cerebral artery (MCA), and anastomoses. Following the surgery, OCT imaging of the cortex was performed through the cranial window. Moreover, to investigate capillary hemodynamics in pathophysiology, we prepared two short-term studies, distal middle cerebral artery occlusion (dMCAO) and hindpaw electrical stimulation for each mouse with cranial window preparation.
3.2.1 Distal middle cerebral artery occlusion (dMCAO)
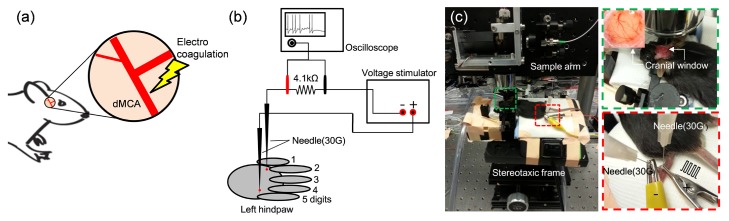
For the observation of cerebral capillary flow response to ischemic stroke, dMCAO was used as a rodent stroke model of inducing permanent focal ischemia in the cerebral cortex [25]. To induce dMCAO, a 1cm skin incision was made between the right ear and eye of the mouse, and temporal muscle below the skin was removed. Then, the temporal bone overlying the dMCA was slightly thinned to expose the dMCA. The exposed artery was permanently occluded using a microbipolar electrocoagulator (Aaron 940TM, Bovie Medical Corp.) (Fig. 1(a)).
Fig. 1.
(a) Electro-coagulation of a distal MCA (dMCA) to induce permanent dMCA occlusion (dMCAO) in mouse with cranial window preparation. (b) Schematic of hindpaw electrical stimulation of mouse and (c) its experimental set-up in the OCT sample arm.
3.2.2 Hindpaw electrical stimulation
For the observation of electrical stmulus-evoked cerebral capillary flow response, two sterile 30 gauge needles were inserted into the plantar surface of left hindpaw of the mouse, contralateral to the cranial window, where one was inserted between the fourth and fifth digits, and another one was inserted between the first and second digits of the same hindpaw as the return electrode (Fig. 1(b)). These needles were used to transmit the electrical stimulation signals to the mouse. Each needle was connected to +/− output jacks of an electronic stimulator (SD9, Grass Instruments Medical) to deliver square wave voltage pulses. A 4.1kΩ resistor was connected between the return electrode needle and the output of machine to identify the stimulus current that was calculated with a peak voltage applied to the resistor which was displayed on a digital oscilloscope. Figure 1(c) shows photographs of experimental set-up of hindpaw electrical stimulation of mouse with cranial window.
3.3 Procedures for capillary velocimetry
Figure 2 illustrates the processing steps for the capillary velocimetry. First, OCT B-scan was 100 times repeated at each location (multiple B-scan: MB scan) with a frame rate of 730fps (i.e., a time interval t = 1.37ms). Each B-scan consists of 100 A-lines covering 360μm in transverse direction. By repeating the MB scan at 100 different locations, this generates a 4D spatiotemporal OCT data set, where a total number of B-frames are 10,000. An OCT cross-section of mouse cortex (50 averaged) at the one location is shown in Fig. 2(a).
Fig. 2.
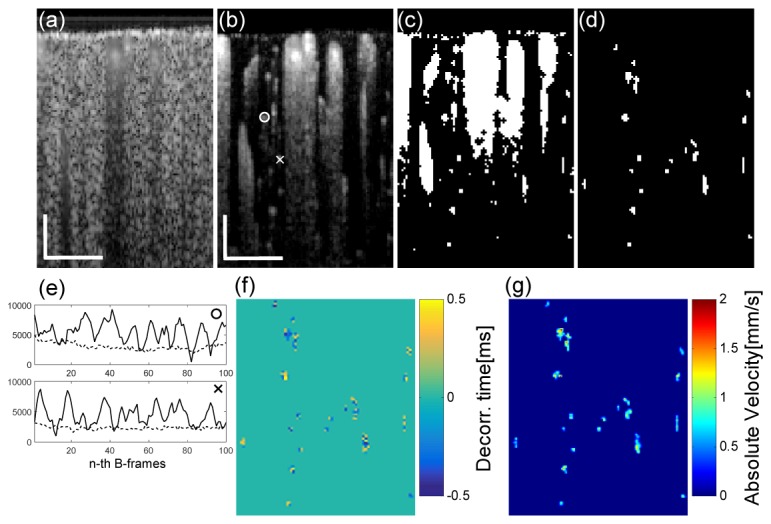
Procedure for estimating RBC velocity at single capillaries in the mouse brain cortex. (a) OCT B-scan of the mouse cortex through a cranial window. OCTA B-scan (b) at the same location as (a) and its binary image (c) are shown. (d) Capillary binary image isolated from (c). (e) Plots of intensity magnitudes extracted along with the ○ and × labeled points in (b) (solid lines) and their neighboring points in the static tissue (dotted lines). (f) Decorrelation time map. (g) Corresponding capillary absolute velocity map. Scale bars: 0.1mm.
With the data set acquired, we performed a voxel-wise temporal decorrelation estimation. In order to locate the capillaries in the OCT image, we firstly conducted OCTA with the B-scans (N = 100). Figure 2(b) is an OCTA B-scan of Fig. 2(a), which was 99 ensemble averaged. OCTA technique used was an intensity optical microangiography (OMAG) based on absolute of subtraction between inter B-frames to obtain RBC motion contrast for visualizing the functional vessels [26]. Binarization was then performed on the OCTA image with thresholding (Fig. 2(c)), where a threshold value was defined as the average of background pixel intensity (BG_Mean) plus twice the standard deviation of BG_Mean (BG_STD) [27]. Therefore, a vessel was defined as the region occupying pixels with an intensity > BG_Mean + 2*BG_STD. To isolate capillaries among vessels in the binary OCTA, the pixel areas of vessels in Fig. 2(c) were calculated, in which the vessel objects having more than at least 3 pixels or less than 15 pixels were judged as the potential capillary candidates. Figure 2(d) shows a resulting binary capillary image following the pixel area estimation as described above. The OCT intensities were extracted from the isolated pixels of 100 OCT B-frames masked by the capillary binary image and then, the decorrelation time estimate can be performed with the extracted intensity profiles. Prior to the decorrelation time calculation, we need to suppress the static scattering component from the extracted intensity profile because the OCT signal can be described as the superposition of dynamic and static scattering components and noise within a single voxel in flow region [18]. For separating the two scattering components, we assumed that for a flat and isotropic sample such as brain cortex, the static component at capillary would be presumably approximated to the scattering component at the static tissue right next to the vessel. It was identified from OCT intensity profiles (Fig. 2(e)) at pixels in two capillaries (marked as ○ and × in Fig. 2(b), respectively) and their neighboring tissue regions with no vessels, showing that the intensities (dotted lines) at the neighboring static tissue may represent the offsets of the intensity fluctuations (solid lines) at the capillaries. The offset could be realized from polynomial fit of the capillary intensity fluctuations and subtracted to suppress the static scattering.
After removal of the static scattering component, we calculated the decorrelation time with the time course intensity fluctuations at capillaries using Eq. (3). Figure 2(f) shows a calculated decorrelation times at each capillary, ranged from −0.5ms to 0.5ms (0 indicates uncorrelated). With this map, finally, an absolute capillary velocity map (Fig. 2(g)) was derived from a decorrelation-velocity relationship (Sec. 4.2). Furthermore, this process can be performed along the slow axis (C-scan) to construct a 3D velocity data set.
4. Validation
4.1 Capillary flow phantom
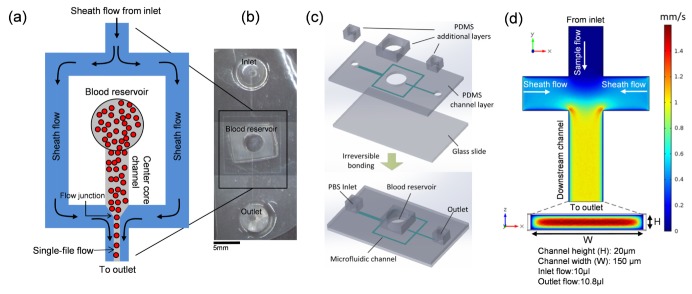
In order to establish a relationship between the decorrelation time and RBC velocity, we devised a flow phantom experiment to simulate real single capillary blood flow. The mechanism of capillary flow in the phantom is based on a hydrodynamic focusing effect in flow channel. Hydrodynamic focusing is a technique of flow cytometry to measure the properties (e.g., size) of individual flow particles [28]. Figure 3(a) shows a design of the 4 channels (connected with 2 inlets and 1 outlet) hydrodynamic focusing microfluidic system. The main inlet is connected to one channel, divided into two side sheath flow channels and anther inlet is a blood reservoir for blood storage, connected to a center core channel, through which the blood stream carrying particles (RBCs) is enclosed by the two side sheath fluids (Phosphate buffered saline, PBS) at the flow junction. These fluids are pushed through the system at slightly different pressures using syringe pumps. The sheath fluids are under high pressure and therefore, move faster. As the sheath fluid moves, it creates a drag effect that squeezes and reshapes the sample downstream, allowing for a single-cell pipeline in the particle flow [28]. The focused sample stream speed is determined by a ratio of the outlet pumping rate (μl/hr) to the microchannel crossectional area (μm2) and its width is controlled by (outlet pumping rate (μl/hr) - inlet pumping rate (μl/hr)) × microchannel width (μm) / outlet pumping rate (μl/hr), where the width can be altered with the constant sample velocity by changing the only inlet pumping rate. The microfluidic device was fabricated with multistep process (Fig. 3(c)) using polydimethylsiloxane (PDMS)-based soft lithographic technique similar to the fabrication process reported by previous literatures [29,30]. Figure 3(b) shows a top view of the fabricated microfluidic device, in which the width and height of microflow channels are 150μm and 20μm, respectively.
Fig. 3.
Design of a single capillary flow phantom. (a) Layout of the hydrodynamic focusing microfluidic device for capillary flow simulation, where the two side sheath fluids hydrodynamically focus the blood cell suspension from blood reservoir to form a single-file flow. (b) Top view of the fabricated microfluidic device. (c) Illustration of the device fabrication process. (d) COMSOL simulation result of flow velocity distribution in the microflow channels for the inlet/outlet pumping flow rate of 10/10.8μl.
Based on the physical dimensions of the flow channel in the fabricated microfluidic device, we numerically simulated flow velocity distribution through the flow channel by changing the outlet pumping rates. As mentioned above, the hydrodynamically focused sample stream velocity is defined as the ratio of the outlet pumping rate to the crossectional area of microflow channel. For the known crossectional area of channel (150 × 20 = 3,000μm2) and preset inlet/outlet flow rates (10/10.8μl/hr), COMSOL multi-physics simulation (Fig. 3(d)) displayed en face (xy) flow velocity distribution above 5μm from the bottom of the channel at intersection of the 4-microflow channels. In the downstream channel, where the single-file flow is formed at the middle of the channel, we can see that the flow velocity is approximated to be 1mm/s along the channel, and its profile in the channel cross-section appears parabolic along the channel height (H), a typical feature of the laminar flow. Considering that a theoretical velocity of the focused sample stream is 1mm/s (10.8μl/hr/3000μm2), from the simulation result, we speculated that the focused sample stream would be formed at the bottom of center of the channel and RBCs in the stream would move at speed of 1 mm/s for the given inlet/outlet flow rates. For different outlet pumping flow rates: 32.4μl, 54.0μl, and 86.4μl, the simulated velocities were 3mm/s, 5mm/s, and 8mm/s at the above 5μm from the bottom of the downstream channel (not shown here).
4.2 Establishment of a relationship between decorrelation time and velocity
Based on the simulation results, we established a relationship between the decorrelation time and velocity using the capillary flow phantom. Figure 4(a) describes a schematic of the phantom imaging set-up to measure the RBC flow in the microfluidic device. In the device, there are inlet and outlet for infuse and drain of fluids (PBS and blood), respectively, connected to individual programmable syringe pumps (Fusion 100, Chemyx Inc.) to control the flow. Thereby, velocity and width of the hydrodynamically focused sample stream are manipulated by changing the pumping flow rates of the inlet/outlet syringe pumps. Prior to hydrodynamic focusing, warming up time of 1h was required for stabilization of pumping flow and removal of possible inclusions such as dusts or bubbles in the microflow channel. After the stabilization, a fresh whole blood was prepared as sample of interest. The blood (~0.1ml) was kept in a blood collection tube (MonojetTM, EDTA, 0.05ml, Covidien) to avoid blood coagulation before storage into the reservoir. Accordingly, the sample flow was driven into the center core channel by gravity to form a hydrodynamic focus at the flow junction. OCT beam spot was placed at the downstream flow channel in the device to measure the light backscattered by RBCs in single-file flow, passing one by one across the scanning zone. The location of beam spot was identified by OCT B-scan of the channel. At the same time, a tailored inverted bright field microscope was co-aligned with the OCT objective below the device to record the RBC passage in the focused sample stream at a video rate (25fps). The device was slightly tilted to avoid strong reflection from the top surface of device during OCT measurement. Figure 4(b) is representative time-course snapshots captured by the inverted microscope (Fig. 4(a)) during the hydrodynamic focusing process at a predicted velocity of 1mm/s, showing that the sample downstream was increasingly narrowed by the sheath flow pressure, ended up with the single-file flow. Visualization 1 (4.6MB, AVI) displays the focused sample stream recorded by the inverted microscope at 25fps. MB scan was then performed at one location (indicated as an arrow in the last snapshot in Fig. 4(b)) to collect 100 repeated B-frames at 730fps. Figure 4(c) shows the OCT and OCTA B-scans of the scanned microflow channel. It was observed that the OCTA signal was seen at the bottom of the channel with confined dimensions of 7μm (height) × 12μm (width), demonstrating good focusing performance of our fluidic device, in which the RBCs in single-file flow would move at speed of 1mm/s along the downstream channel.
Fig. 4.
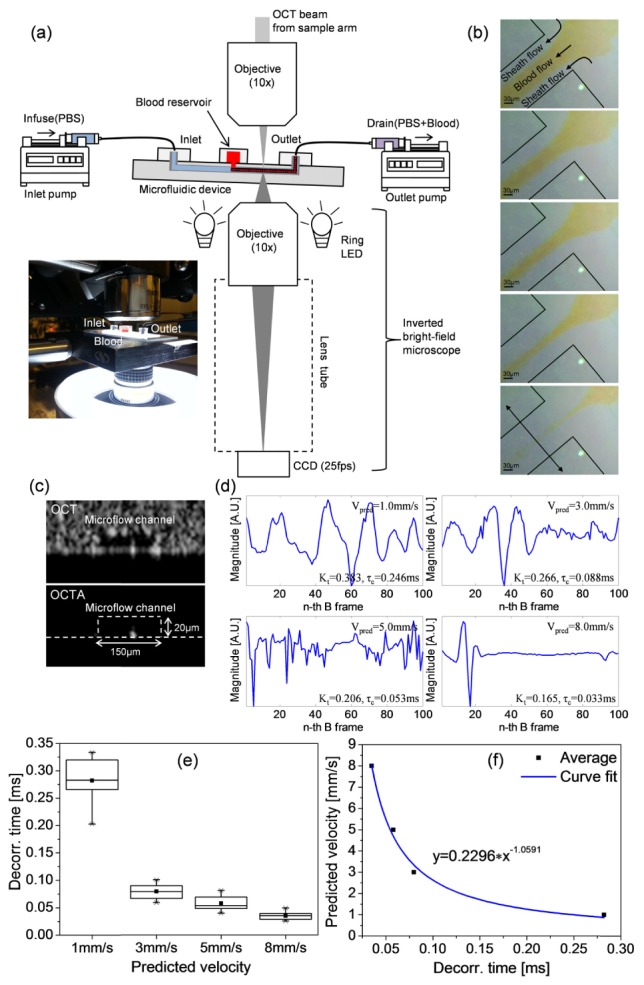
(a) Schematic of single capillary flow phantom imaging. Inset is a photograph of the set-up. (b) Time course snapshots captured by the inverted microscope (25fps) below the microfluidic device during hydrodynamic focusing of blood downstream. (c) (top) OCT B-scan of microfluidic device scanned at the location (arrow in the bottom snapshot in (b)), depicting a rectangle channel embedded in scattering PDMS, and (bottom) corresponding OCTA B-scan, highlighting the flow signal. (d) Extracted temporal profiles of OCT signals at the centroid of the focused blood streams in 100 consecutive OCT B-frames for each preset velocity: 1.0, 3.0, 5.0, and 8.0mm/s. (e) Distribution of decorrelation times repeatedly measured 15 times for each velocity. A curve fit of the average values in (e) shows the inverse relation of the decorrelation time to velocity in (f) with R2 = 0.987.
Using Eq. (3), we calculated decorrelation times τc with each OCT data set acquired at predicted velocities, 1.0, 3.0, 5.0, and 8.0mm/s. Figure 4(d) is representative time scale of OCT speckle fluctuations at the centroid across the focused sample stream for the predicted velocities, Vpred. In the decorrelation time calculation, it is noted that β in Eq. (3) was calculated to be 0.31 from Kmax of 0.56 that was referred from a previous literature in which the maximum K value was estimated from the static part of the flow phantom at a short integration time, similar to our time interval of 1.37ms [22].
In Fig. 4(d), it is observed that the magnitude in fluctuation gradually decreases while its frequency increases with increment of velocity, and at 8mm/s, the fluctuation reached to plateau. Taking into account that the RBC peak's width (FWHM of Gaussian RBC profile) is a function of the RBC speed V [9]: (ѡRBC2 + ѡvoxel2)1/2/V, where ѡRBC is a RBC size (7μm) and ѡvoxel is OCT voxel size (transverse resolution of 7μm), the temporal RBC peak's width is ~1.24ms at 8mm/s, shorter than our time interval, which is not sufficient to resolve discrete sequence of the samples (RBCs) according to Nyquist theory (sampling interval should be less than a half the current one). Eventually, this current sampling rate may limit an upper bound of velocity estimate to 8mm/s. The sampling rate can be increased either with faster line scan cameras (>92kHz) or by reducing a number of A-lines per B-frame on the current system, so that the measurable velocity range is increased. The measurements were repeated >15 times to determine the average τc for each velocity and thus, the resulting decorrelation time deviations are presented in Fig. 4(e). The averages are plotted as solid boxes with their fit (R2 = 0.987) in Fig. 4(f). The fitting curve yielded a nonlinear relationship between decorrelation time and velocity with an equation of y = 0.2296 × x-1.0591, representing the typical inverse relation of velocity to decorrelation time [19]. After the relationship is established, it is reasonable to derive the absolute velocity estimates at individual capillaries in the brain cortex through the velocimetry process described in Fig. 2. However, a lower bound of the velocity estimates in the current system may be determined using the relationship with a maximum attainable speckle contrast obtained at capillary. Assuming the maximal speckle contrast Kt of 0.56, the same as that of static part of the flow phantom, its decorrelation time would be 0.436 ms and therefore, the lower bound of the velocity would be ~0.552 mm/s.
5. Results
5.1 Capillary flow response to distal middle cerebral artery occlusion (dMCAO)
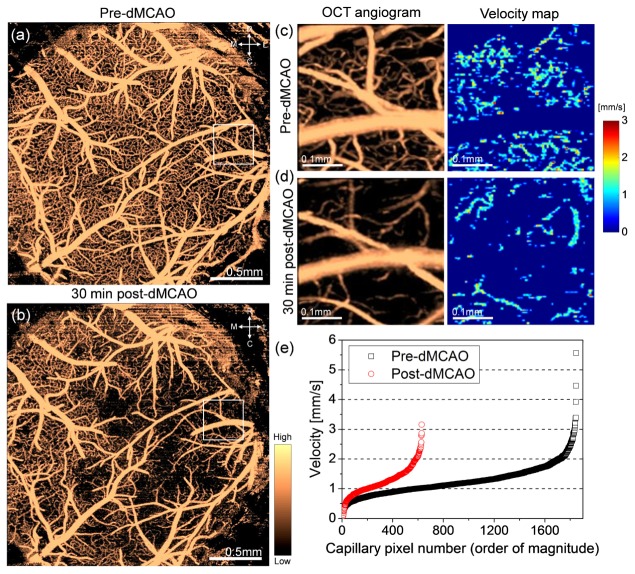
With the established relationship between the decorrelation time of temporal OCT speckle fluctuations and the corresponding capillary flow velocity, we tested the OCT capillary velocimetry for in vivo measurement. First, we imaged the brain cortex of mouse subject to dMCAO. Figures 5(a) and 5(b) show OCT angiograms (3mm × 3mm) of the mouse cortex through the cranial window before and 30min after occlusion, respectively. Here, the angiograms were made with maximum intensity projection (MIP) of OCTA signals within 400μm below the brain surface (corresponding to surface to cortical layers II/III in depth) using a scan protocol of 5 repetitions of B-scans consisting of 400 A-lines for each 400 locations unlike the scan protocol described for the velocimetry in Sec. 3.3. The dMCAO usually results in a stop of blood flow in the barrel region of the somatosensory cortex, which is represented as deficit in number of capillaries perfused with RBCs in the angiogram (Fig. 5(b)) compared to pre-dMCAO (Fig. 5(a)).
Fig. 5.
OCT capillary velocimetry in ischemic stroke model of mouse in vivo. OCT angiograms of the mouse cortex (surface to cortical layers II/III) through cranial window before (a) and 30min after (b) distal middle cerebral artery occlusion (dMCAO). Rarefaction of perfused capillaries is apparent after occlusion compared to pre-dMCAO. (c,d) OCT angiograms (boxes in (a) and (b)) (left) and corresponding capillary velocity maps (cortical layers II/III) (right) before (c) and after (d) occlusion, respectively. The velocity map post-dMCAO (d) shows reduction in velocity in the local perfused capillaries compared to pre-dMCAO (c). (e) Velocities in the capillary velocity maps before and after occlusion, plotted against the magnitude. For both pre/post-dMCAO, the RBC velocities are not constant but variable, clustered at around 1.0mm/s, but smearing at higher velocities up to 5.5mm/s before occlusion. R: rostral, C: caudal, M: medial, L: lateral.
In addition, we also observed the change in capillary flow velocity in dMCAO. Figures 5(c) and 5(d) show OCT angiograms (left) and single capillary velocity maps (right) before and after occlusion, respectively. The magnitude in the velocity map is absolute velocity, color-coded with a scale bar ranged from 0 to 3mm/s. Both images in the panels are the MIP images taken at specific cortical layers II/III (100μm-400μm in depth) in the local area (360μm × 360μm) of the somatosenosry cortex (white boxes in Figs. 5(a) and 5(b)). For pre-dMCAO, it is observed different velocities through the capillary network over the field of view. This spatiotemporal heterogeneity of capillary velocity in normal brain has been reported from previous animal studies [31,32]. For post-dMCAO, however, the capillary velocity still appears heterogeneous but its strength is overall green-bluish in color relative to that of pre-dMCAO, indicating absence of RBC velocities over 2.5mm/s. Figure 5(e) represents all velocities in individual capillaries in the pre/post-dMCAO velocity maps, which were enumerated in ascending order in the graph. The velocity distribution indicates that the normal capillary perfusion can contain RBCs with high velocities (>3mm/s), but the high-flow RBC perfusion is no longer observed following the transient blood occlusion. The mean RBC velocity in capillaries was 1.25 ± 0.49 m/s for pre-dMCAO which was in good agreement with ones measured by fluorescence scanning microscopy [33], and slightly decreased to 1.20 ± 0.49mm/s after dMCAO.
5.2 Capillary flow response to hindpaw electrical stimulation
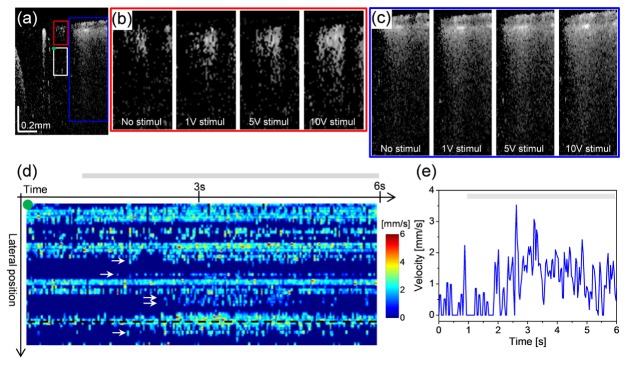
As another in vivo application of OCT capillary velocimetry, we monitored capillary flow response following hindpaw electrical stimulation as described in Sec. 3.2.2. For monitoring the rapid transitional changes in blood flow, we used multiple B-scans (MB scans) at one location that was carefully selected in the hindlimb area of mouse sensory cortex contralateral to the hindpaw underwent electrical stimulation. Figure 6(a) shows an OCTA cross-section of the mouse cortex through cranial window with no electrical stimulation. Hindpaw stimulation was performed using 6s trials. Each trial consists of a 1s pre-stimulus period, followed by 5s of stimulation with 300μs monophasic square pulses at 3Hz provided by the voltage stimulator. The stimulus amplitudes (1V, 5V, and 10V) were chosen to be just below the animal's twitch threshold as determined by palpation. A 5-minute post-stimulus period was then used to allow full recovery to the baseline. Moreover, with the applied voltage to the 4.1kΩ resistor in Fig. 1(b), the stimulus current was calculated. As the respective stimulus amplitude increases, we could observe the longer tail artifact below the surface vessels (in red and green boxes in Fig. 6(a)) as well as vascular widening in OCTA cross-sections, which are seen in Figs. 6(b) and 6(c), respectively. This is probably due to increased vessel diameter and blood velocity following electrical stimulation, leading to an increase in blood flow. Figure 6(d) is a capillary velocity graph showing the time course change in capillary flow velocities which was recorded at the cortical layers II/III (white box in Fig. 6(a)) with the stimulation trial at 10V stimulus amplitude, corresponding to a stimulus current of 0.74mA. After onset of the simulation, a rise of RBC velocities in the fraction of capillaries was visualized as the hotter colors in magnitude over time [34], while the velocity response was not instant but rather delayed 1-2 seconds after the stimulation as Fig. 6(e) (a velocity profile taken at a dotted line on Fig. 6(d)). Interestingly, we found the appearance of low velocity magnitudes since the stimulation (arrows in Fig. 6(d)). It indicates possible engagement of reserved capillaries into the hyperemic response to neuronal activation, otherwise not utilized under resting condition [34].
Fig. 6.
OCT capillary velocimetry for monitoring capillary flow response to hindpaw electrical stimulation. (a) OCTA B-scan of brain cortex through cranial window with no stimulation. During electrical stimulation, OCTA visualizes increase in diameter of surface vessels (in red and green boxes in (a)) along with the longer tail artifacts with increment of stimulus amplitudes (from 1V to 10V), highlighted in (b) and (c), respectively. (d) Time course velocity graph taken at capillary region in the cortical layers II/III (white box in (a)) at 10V stimulus amplitude, where few capillaries showed gradual increase in RBC velocities 1-2 seconds after onset of stimulation. The capillary hemodynamics is represented with a velocity profile (e) at dotted line in (d). The gray bars in (d) and (e) indicate the electrical stimulation period.
6. Discussion and conclusion
In this work, we introduced a new method of OCT velocimetry to measure velocity of RBC flow in perfused capillaries within mouse brain cortex. The method is based on measuring the time scale of random fluctuations in OCT signal intensities at single capillary, upon which to derive the characteristic decorrelation rate of the signal fluctuation that is used to estimate velocity. We adopted analytical speckle contrast expression used in laser speckle contrast imaging to derive the decorrelation time with the speckle contrast of the observed fluctuations. To identify the relation of the decorrelation with velocity, validation work was performed on in vitro single capillary flow phantom, where the measured decorrelation times were fitted against the known blood flow velocities, demonstrating the typical inverse relationship between the two flow metrics. Using the method, we demonstrated the flow dynamics in cortical micro-vessels under pathophysiological events in the mouse brain in vivo.
Decorrelation measurement to estimate velocity in our method is conceptually similar to the other decorrelation-based speckle analysis methods [16–18]. In terms of methodology, the presented method differs from them in that our method utilizes the speckle contrast of the OCT signal fluctuations, whereas other methods use the slope [16] or power spectral bandwidth [18] of its normalized autocorrelation function (ACF). We noticed that there are methods proposed in the literature that also use repeated A-scan (M-mode) acquisition to analyze correlation between the inter A-lines [16,17] to infer the velocity in the small vessels. However, such approach seems to have limited sensitivity in small vessels, such as in capillary vessels, simply because the acquisition time on the order of tens of microseconds as revealed in their study was too short to reliably derive velocities in the most capillaries in practice. The power spectral bandwidth approach [18] alleviates the sensitivity limitation by adapting the repeated B-scans similar to the present method, but because the technique is based on complex-valued OCT signal, it is phase-sensitive and therefore requires high mechanical stability of the sample and OCT system as well.
In the validation, we performed OCT velocity measurements in the scattering flow phantom specifically designed to replicate realistic single capillary blood flow. As stated in Introduction, many previous velocimetry approaches have been validated in microfluidic channels or glass tubes, or large vessels whose diameters are larger than 100 μm [16,17]. Considering cerebral capillary diameter less than 10 μm, it requires a particular caution, if applicable, when applying these methods to the smallest vessel with the decorrelation metrics described by such macro-flow phantoms. In contrast, the devised phantom in this work simulated a single file RBC passage in the confined blood flow channel whose dimension was close to the actual capillary size. Therefore, the achievement of ex vivo capillary flow phantom makes it possible for us to validate our proposed approach on one hand, and on the other hand to establish the relationship between the decorrelation time and the RBC velocity in the capillary.
Although our method has shown promise, there are several limitations. In this work, we have not considered hematocrit or RBC linear density in capillary when measuring capillary flow speed, which is known to be not constant but time-variable across segments in capillary networks [9]. The varying capillary hematocrit may cause perceivable errors in the RBC velocity measurements using the decorrelation-based methods. For example, the OCT intensity fluctuations may be different for capillaries having even the same flow speed because RBC trains in the capillaries can travel with different separations between RBCs (typically, 10μm~100μm). Therefore, it may result in rather different decorrelation times, and thus different velocities. This possible dependency of decorrelation rate on hematocrit can make it difficult to reliably measure capillary flow velocity. One possible way to compensate the hematocrit issue is to increase the number of B-scans to acquire longer time course random fluctuations, mitigating the extent of the hematocrit variation. In this way, however, it would inevitably compromise the measurable temporal resolution.
Another limitation is the effect of defocus and multiple scattering on our measurement. According to Srinivasan et al. [18], for a given velocity, the decorrelation rate depends on the voxel size (mainly determined by spatial resolution), such that the rate of decorrelation will decrease at the depth away from the focal plane because of the worsening of the transverse resolution. Furthermore, in the deeper region, multiple scattering effect will dominate due to the heterogeneity of brain tissues, which violates the assumption of single scattering for the use of speckle visible expression. Because of these effects, either individually or combined, our capillary velocity measurement was limited to superficial cortical regions such as cortical layers II/III in this study. Use of optics with a large depth of focus may reduce the fallout of decorrelation rate at the increased depth, but the voxel size can be anisotropic because of poor transverse resolution relative to the axial resolution (coherence gate), making the decorrelation to be dependent on the direction of flow [18]. Since the voxel size achieved in our study was ~7 × 7 × 7 μm3, which is isotropic and almost identical to RBC size (~7 × 7 × 3 μm3), the decorrelation time is independent of velocity direction.
Disconnectivity in capillary velocity map is likely due to some portion of capillaries whose vessel orientation is parallel to the B-scan direction. In this case, this portion can be missing when determining the capillary candidates in the binary OCTA B-scan (Fig. 2(c)) because its longitudinal cross-section is much larger than transverse cross-sections of most capillaries. The resulting velocity projection map has discrete velocity distribution, looking different from the capillary OCT angiogram.
We anticipate that our velocimetry could be used in ophthalmology to assess RBC flow at capillaries in the ocular tissues, particularly, in retina because the retinal capillaries are superficially localized to thin and translucent retinal structure. One concern in the application of the method to ophthalmology is the motion artifact due to physiological eye movements such as blinks and macro-saccades, or breathing during the OCT scans. Active eye-tracking technologies would be helpful to reduce the artifacts in OCT data acquisition [35].
In conclusion, we have described a development of capillary velocimetry in mouse brain cortex with OCT, in which temporal speckle contrast analysis was used to analyze dynamic scattering component of OCT signals. We believe that the proposed technique will provide additional functional information complementary to conventional OCT angiography technique. Further, in neuroscience, it would be beneficial to investigate hemodynamics of capillary network in pathophysiological brains in vivo.
Acknowledgments
This work was supported in part by grants from the National Heart, Lung, and Blood Institute (R01HL093140) and the National Eye Institute (R01EY024158). The content is solely the responsibility of the authors and does not necessarily represent the official views of grant giving bodies.
References and links
- 1.Mishra A., O’Farrell F. M., Reynell C., Hamilton N. B., Hall C. N., Attwell D., “Imaging pericytes and capillary diameter in brain slices and isolated retinae,” Nat. Protoc. 9(2), 323–336 (2014). 10.1038/nprot.2014.019 [DOI] [PubMed] [Google Scholar]
- 2.Vogel J., Abounader R., Schröck H., Zeller K., Duelli R., Kuschinsky W., “Parallel changes of blood flow and heterogeneity of capillary plasma perfusion in rat brains during hypocapnia,” Am. J. Physiol. 270(4 Pt 2), H1441–H1445 (1996). [DOI] [PubMed] [Google Scholar]
- 3.Tomita M., Tomita Y., Unekawa M., Toriumi H., Suzuki N., “Oscillating neuro-capillary coupling during cortical spreading depression as observed by tracking of FITC-labeled RBCs in single capillaries,” Neuroimage 56(3), 1001–1010 (2011). 10.1016/j.neuroimage.2011.02.078 [DOI] [PubMed] [Google Scholar]
- 4.Kleinfeld D., Mitra P. P., Helmchen F., Denk W., “Fluctuations and stimulus-induced changes in blood flow observed in individual capillaries in layers 2 through 4 of rat neocortex,” Proc. Natl. Acad. Sci. U.S.A. 95(26), 15741–15746 (1998). 10.1073/pnas.95.26.15741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Unekawa M., Tomita M., Osada T., Tomita Y., Toriumi H., Tatarishvili J., Suzuki N., “Frequency distribution function of red blood cell velocities in single capillaries of the rat cerebral cortex using intravital laser-scanning confocal microscopy with highspeed camera,” Asian Biomed. 2(3), 203–218 (2008). [Google Scholar]
- 6.Fercher A. F., Drexler W., Hitzenberger C. K., Lasser T., “Optical coherence tomography - principles and applications,ˮ,” Rep. Prog. Phys. 66(2), 239–303 (2003). 10.1088/0034-4885/66/2/204 [DOI] [Google Scholar]
- 7.Leitgeb R. A., Werkmeister R. M., Blatter C., Schmetterer L., “Doppler optical coherence tomography,” Prog. Retin. Eye Res. 41, 26–43 (2014). 10.1016/j.preteyeres.2014.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Srinivasan V. J., Sakadzić S., Gorczynska I., Ruvinskaya S., Wu W., Fujimoto J. G., Boas D. A., “Quantitative cerebral blood flow with optical coherence tomography,” Opt. Express 18(3), 2477–2494 (2010). 10.1364/OE.18.002477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee J., Jiang J. Y., Wu W., Lesage F., Boas D. A., “Statistical intensity variation analysis for rapid volumetric imaging of capillary network flux,” Biomed. Opt. Express 5(4), 1160–1172 (2014). 10.1364/BOE.5.001160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang R. K., Jacques S. L., Ma Z., Hurst S., Hanson S. R., Gruber A., “Three dimensional optical angiography,” Opt. Express 15(7), 4083–4097 (2007). 10.1364/OE.15.004083 [DOI] [PubMed] [Google Scholar]
- 11.Mariampillai A., Standish B. A., Moriyama E. H., Khurana M., Munce N. R., Leung M. K., Jiang J., Cable A., Wilson B. C., Vitkin I. A., Yang V. X., “Speckle variance detection of microvasculature using swept-source optical coherence tomography,” Opt. Lett. 33(13), 1530–1532 (2008). 10.1364/OL.33.001530 [DOI] [PubMed] [Google Scholar]
- 12.Vakoc B. J., Lanning R. M., Tyrrell J. A., Padera T. P., Bartlett L. A., Stylianopoulos T., Munn L. L., Tearney G. J., Fukumura D., Jain R. K., Bouma B. E., “Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging,” Nat. Med. 15(10), 1219–1223 (2009). 10.1038/nm.1971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.An L., Qin J., Wang R. K., “Ultrahigh sensitive optical microangiography for in vivo imaging of microcirculations within human skin tissue beds,” Opt. Express 18(8), 8220–8228 (2010). 10.1364/OE.18.008220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang A., Zhang Q., Chen C.-L., Wang R. K., “Methods and algorithms for optical coherence tomography-based angiography: a review and comparison,” J. Biomed. Opt. 20(10), 100901 (2015). 10.1117/1.JBO.20.10.100901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang Y., Wang R., “Autocorrelation optical coherence tomography for mapping transverse particle-flow velocity,” Opt. Lett. 35(21), 3538–3540 (2010). 10.1364/OL.35.003538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu X., Huang Y., Ramella-Roman J. C., Mathews S. A., Kang J. U., “Quantitative transverse flow measurement using optical coherence tomography speckle decorrelation analysis,” Opt. Lett. 38(5), 805–807 (2013). 10.1364/OL.38.000805 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Srinivasan V. J., Radhakrishnan H., Lo E. H., Mandeville E. T., Jiang J. Y., Barry S., Cable A. E., “OCT methods for capillary velocimetry,” Biomed. Opt. Express 3(3), 612–629 (2012). 10.1364/BOE.3.000612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Boas D. A., Dunn A. K., “Laser speckle contrast imaging in biomedical optics,” J. Biomed. Opt. 15(1), 011109 (2010). 10.1117/1.3285504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dunn A. K., “Laser speckle contrast imaging of cerebral blood flow,” Ann. Biomed. Eng. 40(2), 367–377 (2012). 10.1007/s10439-011-0469-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kazmi S. M. S., Faraji E., Davis M. A., Huang Y.-Y., Zhang X. J., Dunn A. K., “Flux or speed? Examining speckle contrast imaging of vascular flows,” Biomed. Opt. Express 6(7), 2588–2608 (2015). 10.1364/BOE.6.002588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nadort A., Woolthuis R. G., van Leeuwen T. G., Faber D. J., “Quantitative laser speckle flowmetry of the in vivo microcirculation using sidestream dark field microscopy,” Biomed. Opt. Express 4(11), 2347–2361 (2013). 10.1364/BOE.4.002347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cheng H., Yan Y., Duong T. Q., “Temporal statistical analysis of laser speckle images and its application to retinal blood-flow imaging,” Opt. Express 16(14), 10214–10219 (2008). 10.1364/OE.16.010214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baran U., Zhu W., Choi W. J., Omori M., Zhang W., Alkayed N. J., Wang R. K., “Automated segmentation and enhancement of optical coherence tomography-acquired images of rodent brain,” J. Neurosci. Methods 270, 132–137 (2016). 10.1016/j.jneumeth.2016.06.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rosell A., Agin V., Rahman M., Morancho A., Ali C., Koistinaho J., Wang X., Vivien D., Schwaninger M., Montaner J., “Distal occlusion of the middle cerebral artery in mice: are we ready to assess long-term functional outcome?” Transl. Stroke Res. 4(3), 297–307 (2013). 10.1007/s12975-012-0234-1 [DOI] [PubMed] [Google Scholar]
- 26.Choi W. J., Zhi Z., Wang R. K., “In vivo OCT microangiography of rodent iris,” Opt. Lett. 39(8), 2455–2458 (2014). 10.1364/OL.39.002455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pepple K. L., Choi W. J., Wilson L., Van Gelder R. N., Wang R. K., “Quantitative assessment of anterior segment inflammation in a rat model of uveitis using spectral-domain optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 57(8), 3567–3575 (2016). 10.1167/iovs.16-19276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee G.-B., Chang C.-C., Huang S.-B., Yang R.-J., “The hydrodynamic focusing effect inside rectangular microchannels,” J. Micromech. Microeng. 16(5), 1024–1032 (2006). 10.1088/0960-1317/16/5/020 [DOI] [Google Scholar]
- 29.Simonnet C., Groisman A., “High-throughput and high-resolution flow cytometry in molded microfluidic devices,” Anal. Chem. 78(16), 5653–5663 (2006). 10.1021/ac060340o [DOI] [PubMed] [Google Scholar]
- 30.Qin W., Schmidt L., Yang X., Wei L., Huang T., Yuan J. X., Peng X., Yuan X., Gao B. Z., “Laser guidance-based cell detection in a microfluidic biochip,” J. Biomed. Opt. 18(6), 060502 (2013). 10.1117/1.JBO.18.6.060502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hudetz A. G., “Blood flow in the cerebral capillary network: a review emphasizing observations with intravital microscopy,” Microcirculation 4(2), 233–252 (1997). 10.3109/10739689709146787 [DOI] [PubMed] [Google Scholar]
- 32.Jespersen S. N., Østergaard L., “The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism,” J. Cereb. Blood Flow Metab. 32(2), 264–277 (2012). 10.1038/jcbfm.2011.153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hutchinson E. B., Stefanovic B., Koretsky A. P., Silva A. C., “Spatial flow-volume dissociation of the cerebral microcirculatory response to mild hypercapnia,” Neuroimage 32(2), 520–530 (2006). 10.1016/j.neuroimage.2006.03.033 [DOI] [PubMed] [Google Scholar]
- 34.Schulte M. L., Wood J. D., Hudetz A. G., “Cortical electrical stimulation alters erythrocyte perfusion pattern in the cerebral capillary network of the rat,” Brain Res. 963(1-2), 81–92 (2003). 10.1016/S0006-8993(02)03848-9 [DOI] [PubMed] [Google Scholar]
- 35.Vienola K. V., Braaf B., Sheehy C. K., Yang Q., Tiruveedhula P., Arathorn D. W., de Boer J. F., Roorda A., “Real-time eye motion compensation for OCT imaging with tracking SLO,” Biomed. Opt. Express 3(11), 2950–2963 (2012). 10.1364/BOE.3.002950 [DOI] [PMC free article] [PubMed] [Google Scholar]